模型预测控制^[1-2](model predictive control，MPC)，又称为滚动时域控制(moving horizon control，MHC)或后退时域控制(receding horizon control，RHC)，是近年来被广泛讨论的一种控制策略，它是一种基于预测模型的闭环优化控制策略，通常采用在线反复优化计算并滚动实施控制作用和模型误差反馈校正^[3], 并具有控制效果好、鲁棒性强，对模型精确性要求不高的优点^[4]。因此在石油、化工、冶金、机械等工业过程控制领域具有广泛的应用前景^[5-6]，特别地，模型预测控制在汽车行业有着较为广泛的运用^[7-8]。针对以上各个行业的应用，以一类工业生产过程中实时跟踪问题，并将其这类问题具体化后，以地面导弹跟踪目标飞行器为研究背景，提出了一套基于跟踪误差的增量式模型预测控制算法。

模型预测控制最为常见的有模型算法控制(model algorithmic control，MAC)^[9]和动态矩阵控制(dynamic matrix control，DMC)^[10-11]。通常对于MAC采用脉冲响应模型进行研究，而对于DMC则采用阶跃响应模型进行研究，二者均为非参数模型预测控制，且都是在时域内由系统输出误差的平方和以及输入控制信号增量的平方和的加权系数构成优化性能指标函数。这类算法的特点是：采用增量式预测模型，选择适当的加权系数以及预测时域来保证闭环系统的稳定性，并在性能指标函数中对输入信号增量进行加权来消除系统的稳态误差。但是，传统的非参数模型预测控制研究是建立在较低阶的线性近似模型基础之上，而对于具有非线性、高阶次和强干扰的复杂工业对象，这种方法则很难达到令人满意的控制效果。为此，有学者提出把原有的模型算法控制中在指标函数中引入微分项，用以获得更好的动态性能^[12-13]；还有学者提出同时对模型算法控制和动态矩阵控制进行改进，用以减小内模截断误差，获得更好的动态性能^[14-17]，也有学者提出在模型预测控制中，引入动态输出反馈，用来辅助优化^[18]等。

显然，目前的研究，都是建立在脉冲响应模型和阶跃响应模型之上，即都采用了输出模型与预测模型的误差信号的增量式的模型预测控制，用以改善控制系统的动态性能，但是对于一类工业生产过程中实时跟踪问题，例如地面导弹跟踪目标飞行器等这类问题，原有的模型预测算法或者改进算法就无法满足系统的动态性能要求。汪纪锋老师提出了在DMC优化性能指标函数中的跟踪误差项，在指标函数中引入跟踪误差的微分项，可以使得对象动态响应更加平稳，闭环系统的鲁棒性更强^[12]。于此，在分析DMC基础上，针对工业生产过程中实时跟踪问题，笔者提出了一种基于跟踪误差的增量式模型预测控制(error Incremental model predictive control，EI-MPC)算法，将它应用到地面导弹跟踪目标飞行器系统中，它采用速度信号作为预测模型，以使得被控对象在匀加速过程中，更好的满足动态性能，且闭环鲁棒性更好；同时在建立预测模型之后，笔者利用滚动优化方法优化性能指标，且在速度信号预测模型中，采用跟踪误差增量的加权平均值，用以更好的消除稳态误差，满足系统的稳态性能。通过理论推导和计算机仿真结果表明该算法具有更好的控制品质。

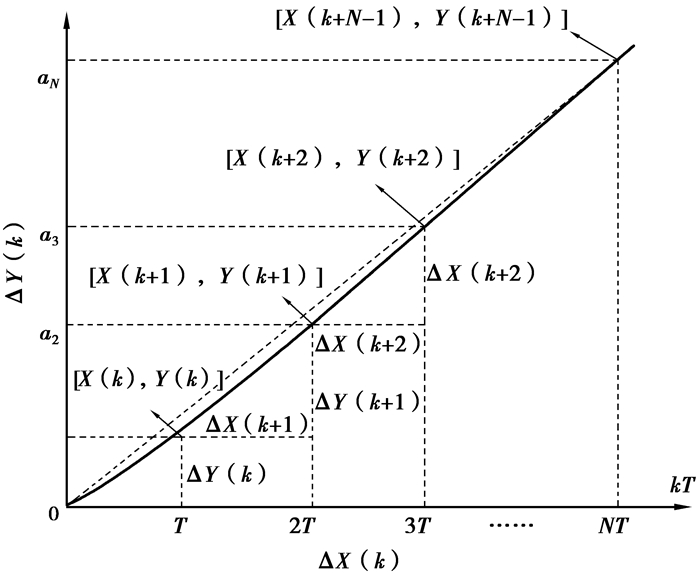
1 跟踪误差的增量式模型预测控制算法 1.1 预测模型

地面导弹跟踪目标飞行器系统中，若令a_i(i=1, 2, …, N)为被控对象的速度响应采样的纵坐标值，且有$\mathop {\lim }\limits_{i \to \infty } {a_i} = {a_s}\left( {s = N + 1, N + 2, \cdots, D} \right) $，即当i>N时，a_i已经进入稳态，即可认为a_s为响应曲线的稳态值，则速度响应的纵坐标值a_i和a_s，即为该对象速度响应的非参数预测模型。N和D称为模型时域长度，如图 1所示。

根据线性系统的比例和叠加性质，利用速度响应预测模型和给定的输入控制增量，可以预测系统未来时刻的输出值。其中, 控制输入X和Y为计算机在kT时刻的对输入信号模型采样的横坐标值和纵坐标值，控制输入增量ΔX与ΔY为计算机在kT时刻和(k-1)T时刻对输入信号模型的横坐标增量值与纵坐标增量值，输入信号模型即为以上所述的被控对象的速度响应的非参数预测模型。确定在K时刻起的m个时刻控制增量是：[Δx_(k)，Δy_(k)]，[Δx_(k+1)，Δy_(k+1)]，…，[Δx_(k+M-1)，Δy_(k+M-1)]，若在k时刻加一控制增量[Δx_(k)，Δy_(k)]，则系统在未来N个时刻的模型输出值为

$ {\mathit{\boldsymbol{y}}_{pm\left( {k + i/k} \right)}} = {\mathit{\boldsymbol{y}}_{po\left( {k + i/k} \right)}} + {a_i}\sqrt {\Delta \mathit{\boldsymbol{x}}_{\left( k \right)}^2 + \Delta \mathit{\boldsymbol{y}}_{\left( k \right)}^2}, $

(1)

式(1)中，y_pm(k+i/k)(i=1, 2, …, N)是未来N个时刻模型输出的预测值，y_po(k+i/k)(i=1, 2, …, N)是k时刻无控制增量时，N个未来时刻输出的初始值，即零输入响应，$\sqrt {\Delta \mathit{\boldsymbol{x}}_{\left( k \right)}^2 + \Delta \mathit{\boldsymbol{y}}_{\left( k \right)}^2} $为0时刻到iT时刻输入模型在iT时间间隔的速度模型增量值。若控制增量在未来M个采样间隔连续变化，[Δx_(k), Δy_(k)], [Δx_(k+1), Δy_(k+1)], …, [Δy_(k+M-1), Δy_(k+M-1)]，则系统在未来P个时刻的模型预测输出值为

$ {\mathit{\boldsymbol{y}}_{pm\left( {k + i/k} \right)}} = {\mathit{\boldsymbol{y}}_{po\left( {k + i/k} \right)}} + \sum\limits_{j = 1}^M {{a_{i - j + 1}}\sqrt {\Delta \mathit{\boldsymbol{x}}_{\left( {k + j - 1} \right)}^2 + \Delta \mathit{\boldsymbol{y}}_{\left( {k + j - 1} \right)}^2} }, $

(2)

式中Δx_(k+j-1)=x_(k+j-1)-x_(k+j-2)，Δy_(k+j-1)=y_(k+j-1)-y_(k+j-2)。式(1)也可写成向量形式

$ {\mathit{\boldsymbol{y}}_{pm\left( k \right)}} = {\mathit{\boldsymbol{y}}_{po\left( k \right)}} + \mathit{\boldsymbol{A}}\sqrt {\Delta \mathit{\boldsymbol{x}}_{\left( k \right)}^2 + \Delta \mathit{\boldsymbol{y}}_{\left( k \right)}^2}, $

(3)

其中：矩阵A为速度随动矩阵，里面的元素是描述系统动态特性的速度响应系数；M为控制时域长度；P为优化时域长度，且M≤P≤N。式中：y_pm(k)=[y_pm(k+1/k)，y_pm(k+2/k), …, y_pm(k+P/k)]^T，y_po(k)=[y_po(k+1/k)，y_po(k+2/k), …, y_po(k+P/k)]^T和$ \sqrt {\Delta \mathit{\boldsymbol{x}}_{\left( k \right)}^2 + \Delta \mathit{\boldsymbol{y}}_{\left( k \right)}^2} = $${\left[{\sqrt {\Delta \mathit{\boldsymbol{x}}_{\left( k \right)}^2 + \Delta \mathit{\boldsymbol{y}}_{\left( k \right)}^2}, \sqrt {\Delta \mathit{\boldsymbol{x}}_{\left( {k + 1} \right)}^2 + \Delta \mathit{\boldsymbol{y}}_{\left( {k + 1} \right)}^2}, \cdots, \sqrt {\Delta \mathit{\boldsymbol{x}}_{\left( {k + M-1} \right)}^2 + \Delta \mathit{\boldsymbol{y}}_{\left( {k + M-1} \right)}^2} } \right]^{\rm{T}}} $以及

$ \mathit{\boldsymbol{A}} = {\left[{\begin{array}{*{20}{c}} {{a_1}}&0& \cdots&\cdots &0\\ {{a_2}}&{{a_1}}& \cdots&\cdots &0\\ \vdots&\vdots&\ddots&\vdots&\vdots \\ {{a_M}}&{{a_{M-1}}}& \cdots&\cdots &{{a_1}}\\ \vdots&\vdots&\vdots&\vdots&\vdots \\ {{a_P}}&{{a_{P-1}}}& \cdots&\cdots &{{a_{P-M + 1}}} \end{array}} \right]_{P \times M}}, $

式(3)中，跟踪误差的增量式模型预测控制算法的预测模型由两部分组成：第一部分为系统在k时刻的输入值，即系统的自由项零输入响应；第二部分为系统在k时刻加入输入控制增量的加权平均值，即零状态响应。

1.2 滚动优化

为使预测模型和实际期望输出模型误差达到最小值，设每一时刻k开始的M个控制增量为[Δx_(k), Δy_(k)], [Δx_(k+1), Δy_(k+1)], …, [Δx_(k+M-1), Δy_(k+M-1)]，在其控制的作用下，未来P个时刻的输出预测值y_pm(k+1/k), y_pm(k+2/k), …, y_pm(k+P/k)接近实际期望输出值y_r(k+1), y_r(k+2), …, y_r(k+P)的跟踪误差增量式模型预测控制二次型优化性能指标为

$ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{J}}\left( k \right) = \sum\limits_{i = 1}^P {{q_i}{{\left[{{\mathit{\boldsymbol{y}}_{r\left( {k + i} \right)}}-{\mathit{\boldsymbol{y}}_{pm\left( {k + i/k} \right)}}} \right]}^2}} + }\\ {\sum\limits_{j = 1}^M {{r_j}{{\left[{\sqrt {\Delta \mathit{\boldsymbol{x}}_{\left( {k + j-1} \right)}^2 + \Delta \mathit{\boldsymbol{y}}_{\left( {k + j-1} \right)}^2} } \right]}^2}}, } \end{array} $

(4)

其中，[y_r(k+i)-y_pm(k+i/k)]为k+i时刻的系统跟踪误差。q_i, r_j(i=1, 2, …P; j=1, 2, …, M)分别叫做误差权系数和控制权系数，是对速度控制增量的软约束，其目的是抑制控制量的变化过于激烈。式(4)记为向量形式如下

$ \mathit{\boldsymbol{J}}\left( k \right) = \left\| {{\mathit{\boldsymbol{y}}_{r\left( k \right)}} - {\mathit{\boldsymbol{y}}_{pm\left( k \right)}}} \right\|_Q^2 + \left\| {\sqrt {\Delta \mathit{\boldsymbol{x}}_{\left( k \right)}^2 + \Delta \mathit{\boldsymbol{y}}_{\left( k \right)}^2} } \right\|_R^2, $

(5)

式中：y_r(k)=[y_r(k+1), y_r(k+2), …, y_r(k+P)]^T，为未来P个时刻期望输出向量；Q=diag(q₁, q₂, …, q_p)和R=diag(r₁, r₂, …, r_M)分别叫做误差权矩阵和控制权矩阵。将预测模型式(3)代入优化性能指标式(5)可以得到

$ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{J}}\left( k \right) = \left\| {{\mathit{\boldsymbol{y}}_{r\left( k \right)}} - {\mathit{\boldsymbol{y}}_{po\left( k \right)}} - \mathit{\boldsymbol{A}}\sqrt {\Delta \mathit{\boldsymbol{x}}_{\left( k \right)}^2 + \Delta \mathit{\boldsymbol{y}}_{\left( k \right)}^2} } \right\|_Q^2 + }\\ {\left\| {\sqrt {\Delta \mathit{\boldsymbol{x}}_{\left( k \right)}^2 + \Delta \mathit{\boldsymbol{y}}_{\left( k \right)}^2} } \right\|_R^2, } \end{array} $

(6)

根据$\left\{ \begin{gathered} \left\| \mathit{\boldsymbol{\alpha }} \right\|_x^2 = {\mathit{\boldsymbol{\alpha }}^{\rm{T}}}\mathit{\boldsymbol{x\alpha }}; \hfill \\ \frac{{{\rm{d}}{\mathit{\boldsymbol{\alpha }}^{\rm{T}}}\mathit{\boldsymbol{x\alpha }}}}{{{\rm{d}}\mathit{\boldsymbol{\alpha }}}} = 2\mathit{\boldsymbol{x\alpha }}, \hfill \\ \end{gathered} \right. $，其中α为n维列向量，x为n×n对称阵，可以得

$ \begin{array}{*{20}{c}} {\frac{{{\rm{d}}\mathit{\boldsymbol{J}}\left( k \right)}}{{{\rm{d}}\sqrt {\Delta \mathit{\boldsymbol{x}}_{\left( k \right)}^2 + \Delta \mathit{\boldsymbol{y}}_{\left( k \right)}^2} }} = - 2{\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{Q}}\left[{{\mathit{\boldsymbol{y}}_{r\left( k \right)}}-{\mathit{\boldsymbol{y}}_{po\left( k \right)}}-} \right.}\\ {\left. {\mathit{\boldsymbol{A}}\sqrt {\Delta \mathit{\boldsymbol{x}}_{\left( k \right)}^2 + \Delta \mathit{\boldsymbol{y}}_{\left( k \right)}^2} } \right] + 2\mathit{\boldsymbol{R}}\sqrt {\Delta \mathit{\boldsymbol{x}}_{\left( k \right)}^2 + \Delta \mathit{\boldsymbol{y}}_{\left( k \right)}^2}, } \end{array} $

(7)

上式代入极值条件$\frac{{{\rm{d}}{\mathit{\boldsymbol{J}}_{\left( k \right)}}}}{{{\rm{d}}\sqrt {\Delta \mathit{\boldsymbol{x}}_{\left( k \right)}^2 + \Delta \mathit{\boldsymbol{y}}_{\left( k \right)}^2} }} = 0 $，可以求得

$ \begin{array}{*{20}{c}} {\Delta \mathit{\boldsymbol{u}}\left( k \right) = \sqrt {\Delta \mathit{\boldsymbol{x}}_{\left( k \right)}^2 + \Delta \mathit{\boldsymbol{y}}_{\left( k \right)}^2} = {{\left( {{\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{QA}} + \mathit{\boldsymbol{R}}} \right)}^{ - 1}} \cdot }\\ {{\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{Q}}\left[{{\mathit{\boldsymbol{y}}_{r\left( k \right)}}-{\mathit{\boldsymbol{y}}_{po\left( k \right)}}} \right], } \end{array} $

(8)

由于在k时刻，y_r(k), y_po(k)均为已知，上式给出了k时刻起跟踪误差的增量式预测控制算法的控制律$\sqrt {\Delta \mathit{\boldsymbol{x}}_{\left( k \right)}^2 + \Delta \mathit{\boldsymbol{Y}}_{\left( k \right)}^2}, \sqrt {\Delta \mathit{\boldsymbol{x}}_{\left( {k + 1} \right)}^2 + \Delta \mathit{\boldsymbol{y}}_{\left( {k + 1} \right)}^2}, $$ \cdots, \sqrt {\Delta \mathit{\boldsymbol{x}}_{\left( {k + M-1} \right)}^2 + \Delta \mathit{\boldsymbol{y}}_{\left( {k + M-1} \right)}^2}$的最优值。现将滚动优化采用闭环控制算式，及时的控制增量为

$ \begin{array}{*{20}{c}} {\Delta \mathit{\boldsymbol{u}}\left( k \right) = \sqrt {\Delta \mathit{\boldsymbol{x}}_{\left( k \right)}^2 + \Delta \mathit{\boldsymbol{y}}_{\left( k \right)}^2} = \left( {1, 0, 0, \cdots, 0} \right) \cdot }\\ {{{\left( {{\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{QA}} + \mathit{\boldsymbol{R}}} \right)}^{ - 1}}{\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{Q}}\left[{{\mathit{\boldsymbol{y}}_{r\left( k \right)}}-{\mathit{\boldsymbol{y}}_{po\left( k \right)}}} \right], } \end{array} $

(9)

在上式中令C^T=(1, 0, 0, …, 0), d^T=C^T(A^TQA+R)^-1A^TQ[y_r(k)-y_po(k)]=[d₁, d₂, …, d_p]为本算法控制参数向量，在上式中，Q, R, M和P可以确定，那么d^T可以离线计算出来，这样使得$\sqrt {\Delta \mathit{\boldsymbol{x}}_{\left( k \right)}^2 + \Delta \mathit{\boldsymbol{y}}_{\left( k \right)}^2} $的计算方便，大大提高了系统的实时性。

但上式在k时刻起，并不是把所有的从该时刻起的M个控制增量当作实现的最优解，而只是取其中的及时控制增量$\sqrt {\Delta \mathit{\boldsymbol{x}}_{\left( k \right)}^2 + \Delta \mathit{\boldsymbol{y}}_{\left( k \right)}^2} $构成实际控制$ \sqrt {\mathit{\boldsymbol{x}}_{\left( k \right)}^2 + \mathit{\boldsymbol{y}}_{\left( k \right)}^2} $作用于对象。到下一个时刻，计算新的初始预测输出值，考虑到模型失配、不确定干扰因素等影响，取

$ {\mathit{\boldsymbol{y}}_{po\left( k \right)}} = \mathit{\boldsymbol{S}}\left[{{\mathit{\boldsymbol{y}}_{pm\left( k \right)}} + \mathit{\boldsymbol{H}}{\mathit{\boldsymbol{e}}_{\left( {k + i} \right)}}} \right], $

(10)

其中S为转移矩阵，

$ \mathit{\boldsymbol{S}} = {\left[{\begin{array}{*{20}{c}} 0&1&{}&{}&0\\ {}&0&1&{}&{}\\ {}&{}& \ddots&\ddots &{}\\ {}&{}&{}&0&1\\ 0&{}&{}&{}&1 \end{array}} \right]_{P \times P}}, $

y_pm(k)是k时刻起经过该时刻控制增量$\sqrt {\Delta \mathit{\boldsymbol{x}}_{\left( k \right)}^2 + \Delta \mathit{\boldsymbol{y}}_{\left( k \right)}^2} $作用后的输出预测值向量。e_(k+i)=y_(k+i)-y_pm(k+i/k)是k+i时刻的输出误差，H=[h₁, h₂, …, h_p]^T为P维校正向量。这样通过反馈校正向量H构成了闭环优化，来增强系统的鲁棒性，到下一时刻，重复上述优化的过程。

2 算法仿真

为了说明笔者提出的本算法具有更好的控制性能和跟踪性能，现将下述被控对象应用两种算法分别进行仿真比较。

工业生产过程中实时跟踪问题，导弹跟踪目标飞行器的控制具有稳定性、准确性以及快速性的要求，要求系统跟踪性能好，抗干扰性强等，则被控对象的差分方程为

$ {\mathit{\boldsymbol{y}}_{\left( k \right)}} + 10{\mathit{\boldsymbol{y}}_{\left( {k - 1} \right)}} + 40{\mathit{\boldsymbol{y}}_{\left( {k - 2} \right)}} = 20{\mathit{\boldsymbol{u}}_{\left( k \right)}}, $

(11)

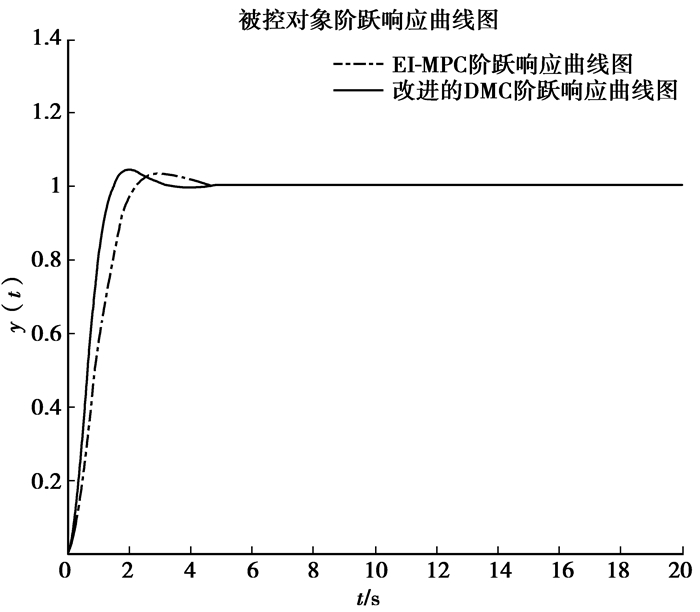
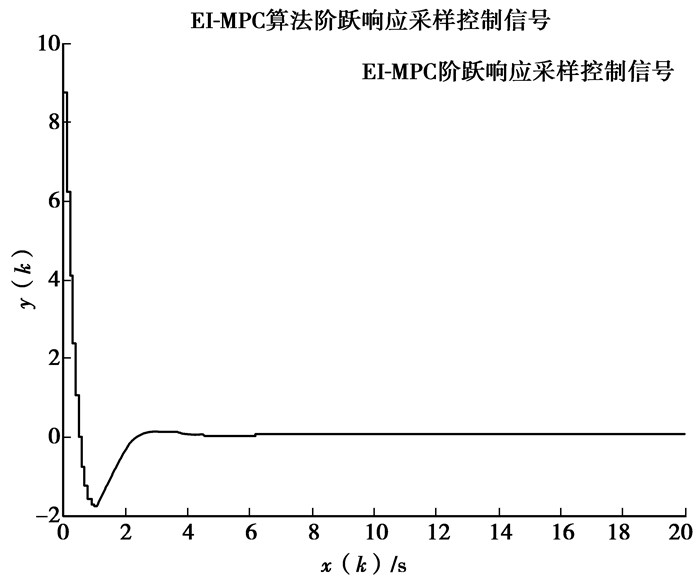
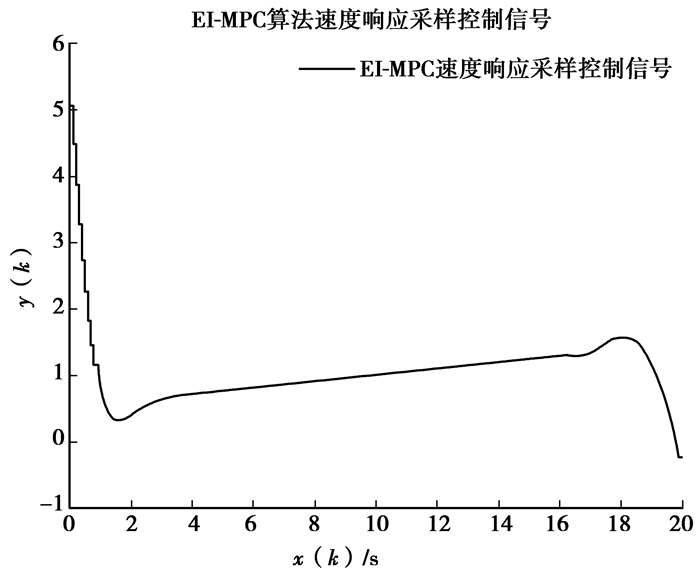
为了便于分析算法的控制性能，选取建模时域N=20，由被控对象的速度响应的动态性能，取优化时域P=10，控制时域M=6，为了建模的精确性，在本算法仿真中，选取采样时间间隔为T=0.1 s。因为被控对象无延时和非最小相位的特性，故在上式推导的矩阵按一般原则取：误差权矩阵Q=I_P×P, 控制权矩阵R=0.2I_M×M，校正向量H=[1, 1, 1, …, 1]^T, 设系统的初始输入输出为零，在k时刻输入设定的阶跃信号和速度信号，分别对两种信号使用不同的算法进行仿真，系统的响应曲线如图所示，图 2为被控对象阶跃响应曲线图，其中实线为EI-MPC算法对应的阶跃响应，虚线为改进的DMC算法的阶跃响应，可以看出，笔者提出的EI-MPC算法具有上升时间短，超调量小，过渡过程时间短，具有更好的动态性能；图 4为被控对象速度响应曲线图，其中实线为EI-MPC算法的速度响应，虚线为改进的DMC算法的速度响应，从图中可以得出，笔者提出的EI-MPC算法具有快速且稳定的跟随性能，并且可以使系统的稳态误差趋近于零，抗干扰性能更强，具有更高的稳态性能，且闭环系统的鲁棒性跟强；图 3为EI-MPC算法阶跃响应采样控制信号；图 5为EI-MPC算法速度响应采样控制信号。

3 结论

预测控制由于控制性能好、鲁棒性强等优点而具有广阔的应用前景。笔者提出的一种基于跟踪误差的增量式模型预测控制新算法，将其使用在工业生产过程中的实时跟踪系统，使系统的输出能够更好地跟踪期望输出。通过对新算法的理论推导，以及仿真结果表明，只要适当的选取各时域的参数和权矩阵，该算法具有更快的动态特性响应速度，过渡过程时间短，响应过程也更加平稳，同时也保证了系统的稳态性能，该算法改善了系统的动态性能，加强了系统的鲁棒性。