b. 重庆大学 汽车工程学院, 重庆 400044
b. School of Automotive Engineering, Chongqing University, Chongqing 400044, P. R. China
橡胶材料由于具有良好的弹性特性,被广泛用于工程和生活各个方面,然而复杂的分子特性以及材料和几何的双重非线性,使得橡胶力学性能的计算十分困难,而对橡胶材料进行真实可靠的力学行为描述具有非常重要的意义。
橡胶材料的研究已有很长的历史,橡胶本构模型的参数识别是研究中的重要内容[1]。准确的参数识别方法可以增强模型的应用性,从而更加全面地描述橡胶材料的力学特性。近年来橡胶本构模型的种类不断增多[2],但由于参数识别需要的试验数据较多,并且橡胶本构模型也比较复杂,因此模型参数的识别十分困难,且精度有限。左曙光等[3]将弹性单元、粘弹单元和塑性单元集成于橡胶本构模型,并将3种单元的分析结果转变为橡胶本构模型参数,通过有限元仿真后,证明了该模型可以准确描述橡胶的振幅相关性;桑建兵等[4]在编写的Marc子程序中,以4节点等参单元和更新的Lagrangian方法确定了橡胶本构模型参数,对橡胶接触中的力学特性取得了较好的仿真效果;在考虑激励和预载后,罗义建等[5]证明了粘弹性Maxwell模型对橡胶悬置的动力学特性计算效果更好;进行橡胶静态力学分析时,黄建龙等[6]利用最小二乘法识别了二参数MR模型和YEOH模型,并采用简单的有限元模型算例进行了验证;郑明军等[7]以单轴拉伸试验数据为基础,将简化后的一次函数模型与橡胶硬度理论结合,揭示了MR本构模型参数间的比值对橡胶静力学仿真结果有一定影响。
笔者针对橡胶材料超弹性本构模型理论,提出一种基于超静定方程的本构模型参数识别方法。采用某橡胶衬套作为试验算例,将该方法识别的参数应用于有限元仿真,其仿真结果和实验结果吻合得更好,表明该方法在参数识别精度上明显优于传统最小二乘法,能够较为准确描述橡胶制品的静态力学特性。
1 橡胶本构模型分析对橡胶本构模型进行参数识别,需要先对模型进行必要的分析。橡胶的本构模型理论主要分为两大类:一种是基于统计热力学的理论[8],另一种是基于连续介质假设的唯象理论[9]。统计法是通过对材料长链分子进行弹性研究,进而推导出宏观性质;唯象法是基于拟合出的材料参数去描述其他变形状态,两种模型均用应变能密度函数来表示,对其进行分析推导后更加便于识别参数。
1.1 Mooney-Rivlin本构模型分析Mooney-Rivlin模型[10]在超弹性力学研究中使用最为广泛,此模型公式相对简单,能描述大部分橡胶力学行为,经典二参数Mooney-Rivlin本构模型的应变能密度表达式为
| $W={{C}_{10}}({{I}_{1}}-3)\text{ }+{{C}_{01}}({{I}_{2}}-3)\text{ }+\left( J-1 \right){{~}^{2}}/D,$ | (1) |
式中:C10和C01为待定力学性能常数;D为描述材料压缩性的系数;应变不变量I1、I2和J均与拉伸比λi有关。
| $\left\{ \begin{align} & {{I}_{1}}~=~{{\lambda }_{1}}^{2}~+~{{\lambda }_{2}}^{2}~+~{{\lambda }_{3}}^{2}, \\ & {{I}_{2}}~=~{{\lambda }_{1}}^{2}{{\lambda }_{2}}^{2}~+~{{\lambda }_{1}}^{2}{{\lambda }_{3}}^{2}~+~{{\lambda }_{2}}^{2}{{\lambda }_{3}}^{2}, \\ & J\text{ }=~{{\lambda }_{1}}{{\lambda }_{2}}{{\lambda }_{3}} \\ \end{align} \right.$ | (2) |
在对橡胶等超弹性材料的力学性能进行分析时,假设材料是不可压缩的,因此有J=λ1λ2λ3=1,通过应变能函数对拉伸比求导,可以得到柯西应力表达式[11]
| ${{\sigma }_{i}}={{\lambda }_{i}}\frac{\partial W}{\partial {{\lambda }_{i}}}-p,$ | (3) |
式中p是引入的静水压力,利用各应力相减后可以消去,进而得到不同变形状态下材料的应力拉伸比关系。橡胶超弹性本构模型的参数识别一般要经过对材料标准样件进行单轴拉伸、等双轴拉伸和纯剪切等基本力学试验[12],在橡胶材料的单轴拉伸试验中,3个主拉伸比λ1=λ,λ2=λ3=λ-1/2,而3个主应力关系为σ1=σ,σ2=σ3=0[13],由式(3) 可得到所测应力与拉伸比之间的关系为
| ${{T}^{\text{uni}}}=(2{{C}_{10}}+\frac{2{{C}_{01}}}{\lambda })({{\lambda }^{2}}-\frac{1}{\lambda }),~$ | (4) |
在等双轴拉伸试验中,λ1=λ2=λ,λ3=λ-2,主应力间的关系为σ1=σ2=σ,σ3=0。
| ${{T}^{\text{bia}}}=2{{C}_{10}}({{\lambda }^{2}}-\frac{1}{{{\lambda }^{4}}})-2{{C}_{01}}(\frac{1}{{{\lambda }^{2}}}-{{\lambda }^{4}}),\text{ }$ | (5) |
在纯剪切试验中,λ1=λ,λ2=1/λ,λ3=1,主应力关系为σ1=σ,σ2=σ3=0[14]。
| ${{T}^{\text{ps}}}=2({{C}_{01}}+{{C}_{10}})\left( {{\lambda }^{2}}-1\frac{1}{{{\lambda }^{2}}} \right),~$ | (6) |
式(4) 、(5) 、(6) 由MR应变能密度表达式变形而来,但相对式(1) 更加简洁,易于参数识别。
1.2 YEOH本构模型分析YEOH模型[15]也是一种常见的超弹性本构模型,工程中常用的YEOH 3参数式为
| ${{W}_{YEOH}}={{C}_{10}}({{I}_{1}}-3)\text{ }+{{C}_{20}}({{I}_{1}}-3){{~}^{2}}+C30({{I}_{1}}-3){{~}^{3}},$ | (7) |
其中C10、C20和C30是待识别材料参数,同样利用式(3) 应变能密度函数对拉伸比求导并消去静水压力,可以得到材料在不同试验状态下的应力拉伸比关系。
| ${{T}^{\text{uni}}}=2{{C}_{10}}\lambda (\lambda -{{\lambda }^{-2}})+4{{C}_{20}}\lambda ({{\lambda }^{2}}-2{{\lambda }^{-1}}-3)\text{ }(\lambda -{{\lambda }^{-2}})+\\6{{C}_{30}}\lambda ({{\lambda }^{2}}-2{{\lambda }^{-1}}-3){{~}^{2}}(\lambda -{{\lambda }^{-2}}),$ | (8) |
| ${{T}^{\text{bia}}}=4{{C}_{10}}\lambda (\lambda -{{\lambda }^{-5}})+8{{C}_{20}}\lambda (2{{\lambda }^{2}}+{{\lambda }^{-4}}-3)\text{ }(\lambda -{{\lambda }^{-5}})+\\12{{C}_{30}}\lambda (2{{\lambda }^{2}}+{{\lambda }^{-4}}-3){{~}^{2}}(\lambda -{{\lambda }^{-5}}),$ | (9) |
| ${{T}^{\text{ps}}}=2{{C}_{10}}\lambda (\lambda -{{\lambda }^{-3}})+4{{C}_{20}}\lambda (2{{\lambda }^{2}}+{{\lambda }^{-2}}-2)\text{ }(\lambda -{{\lambda }^{-3}})+\\6{{C}_{30}}\lambda ({{\lambda }^{2}}+{{\lambda }^{-2}}-2){{~}^{2}}(\lambda -{{\lambda }^{-3}})$ | (10) |
YEOH模型较为复杂,但将应变能函数转化为应力对拉伸比的函数后,也可在标准试件试验的基础上,以超静定法对模型中待定的力学参数进行识别。
2 本构模型参数识别对于橡胶本构模型参数识别,最小二乘法是最常用方法,此外,将橡胶恢复力用幂函数分解也可分离识别参数,而为了提高精确度,可以基于超静定方程推导出一种新的识别方法。当方程个数多于未知数个数时,方程一般无精确解,但是可以求得最优近似解,以此为理论基础,可以同时通过多个应力函数对本构模型进行识别。设有方程组
| $\left\{ \begin{align} & {{a}_{11}}{{x}_{1}}+{{a}_{12}}{{x}_{2}}+\cdots +{{a}_{1}}n{{x}_{n}}={{b}_{1}}, \\ & {{a}_{21}}{{x}_{1}}+{{a}_{22}}{{x}_{2}}+\cdots +{{a}_{2}}n{{x}_{n}}={{b}_{2}}, \\ & \vdots \\ & \text{ }{{a}_{m1}}{{x}_{1}}+{{a}_{m2}}{{x}_{2}}+\cdots +{{a}_{mn}}{{x}_{n}}={{b}_{m}} \\ \end{align} \right.$ | (11) |
其中m>n。记系数矩阵为A,而b=[b1,b2,…,bm],因此方程组可以写成矩阵形式AX=b,构造新函数
| $F(x)=\sum\limits_{i=1}^{m}{{{[{{b}_{i}}-\sum\limits_{j=1}^{n}{{{a}_{ij}}{{x}_{j}}}]}^{2}}}=\left\| \mathit{\boldsymbol{b}}-Ax \right\|_{2}^{2},$ |
显然当F(x)最小时,所求得的x为方程组最优解,根据多元函数极值必要条件∂F∂x=0,即
| $\sum\limits_{i\text{ }=\text{ }1}^{m}{2}[{{b}_{i~}}-\sum\limits_{j\text{ }=\text{ }1}^{n}{{{a}_{i~}}_{j~}{{x}_{j~}}}](-{{a}_{ik~}})\text{ }=\text{ }-2\sum\limits_{i\text{ }=\text{ }1}^{m}{{{a}_{ik~}}}[{{b}_{i~}}-\sum\limits_{j\text{ }=\text{ }1}^{n}{{{a}_{i~}}_{j~}{{x}_{j~}}}]\text{ }=\text{ }0,$ | (12) |
则
| $\mathit{\boldsymbol{X}}={{({{\mathit{\boldsymbol{A}}}^{\rm{T}}}\mathit{\boldsymbol{A}})}^{-1}}{{\mathit{\boldsymbol{A}}}^{\rm{T}}}\mathit{\boldsymbol{b}}$ | (13) |
橡胶本构模型应变能公式也可写成超静定方程组形式,以求解待定参数。对于MR本构模型,首先对式(4) 、(5) 、(6) 所表示的3种形变关系式进行处理,令
| $\left\{ \begin{align} & {{Y}^{\text{uni}}}=\frac{{{T}^{\text{uni}}}}{2({{\lambda }^{2}}-{{\lambda }^{-1}})},{{X}^{\text{uni}}}={{\lambda }^{-1}}, \\ & {{Y}^{\text{bia}}}=\frac{{{T}^{\text{bia}}}}{2({{\lambda }^{2}}-{{\lambda }^{-4}})},{{X}^{\text{bia}}}={{\lambda }^{2}}, \\ & \text{ }{{Y}^{\text{ps}}}=\frac{{{T}^{\text{ps}}}}{2({{\lambda }^{2}}-{{\lambda }^{-2}})} \\ \end{align} \right.$ | (14) |
因此,橡胶3种变形关系的应力拉伸比关系式可以视为3个一次函数,并且是关于待识别参数C10和C01的二元一次超静定方程组
| $\left\{ \begin{align} & {{Y}^{\text{uni}}}={{C}_{10}}+{{C}_{01}}{{X}^{\text{uni}}}, \\ & {{Y}^{\text{uni}}}={{C}_{10}}+{{C}_{01}}{{X}^{\text{bia}}},\text{ } \\ & {{Y}^{\text{ps}}}={{C}_{10}}+{{C}_{01}} \\ \end{align} \right.$ | (15) |
通过对橡胶标准试件的单轴拉伸、等双轴拉伸和纯剪切试验,获得3种对应变形的应力T和应变ε数据,而拉伸比λ=1+ε,运用式(14) 分别对3组应力和拉伸比的试验数据做适当的处理,获得数组Yuni和Xuni、Ybia和Xbia、Yps和Xps,将所有X和Y视作已知数,而C10和C01视作未知数,即
| $\left\{ \begin{align} & {{C}_{10}}+{{C}_{01}}X_{1}^{\text{uni}}=Y_{1}^{\text{uni}}, \\ & {{C}_{10}}+{{C}_{01}}X_{2}^{\text{uni}}=Y_{2}^{\text{uni}}, \\ & \vdots \\ & {{C}_{10}}+{{C}_{01}}X_{1}^{\text{bia}}=Y_{1}^{\text{bia}}, \\ & \vdots \\ & {{C}_{10}}+{{C}_{01}}=Y_{1}^{\text{ps}}, \\ & \vdots \\ & \text{ }{{C}_{10}}+{{C}_{01}}=Y_{k}^{\text{ps}} \\ \end{align} \right.$ | (16) |
所要识别的参数C10和C01,就是方程组(16) 的解。X为系数矩阵,C为未知数矩阵:
| $\begin{array}{l} \mathit{\boldsymbol{X}} = \left[ {\begin{array}{*{20}{c}} 1&{X_1^{{\rm{uni}}}}\\ 1&{X_2^{{\rm{uni}}}}\\ \vdots & \vdots \\ 1&{X_1^{{\rm{bia}}}}\\ \vdots & \vdots \\ 1&1 \end{array}} \right],{\rm{ }}\\ \mathit{\boldsymbol{C}} = \left[ \begin{array}{l} {C_{10}}\\ {C_{01}} \end{array} \right],{\rm{ }}\\ \mathit{\boldsymbol{Y}} = \left[ \begin{array}{l} Y_1^{{\rm{uni}}}\\ Y_2^{{\rm{uni}}}\\ Y_1^{{\rm{bia}}}\\ Y_k^{{\rm{bia}}} \end{array} \right] \end{array}$ | (17) |
将变换得到的数据分别代入矩阵X和Y中,根据超静定方程矩阵求解公式(13) ,利用MATLAB软件计算得到未知数矩阵C,即得到MR本构模型的材料参数,如表 1所示。
| 表 1 MR本构模型超静定识别结果 Table 1 Parameters of MR by hyperstatic equations |
对于YEOH模型,令
| $\left\{ \begin{array}{l} {Y^{\text{uni}}} = \frac{{{T^{\text{uni}}}}}{{2({\lambda ^2} - {\lambda ^{ - 1}})}},{X^{\text{uni}}} = {\lambda ^2} - 2{\lambda ^{ - 1}} - 3;\\ {Y^{\text{bia}}} = \frac{{{T^{\text{bia}}}}}{{2({\lambda ^2} - {\lambda ^{ - 4}})}},{X^{\text{bia}}} = 2{\lambda ^2} + {\lambda ^{ - 4}} - 3;\\ {Y^{\text{ps}}} = \frac{{{T^{\text{ps}}}}}{{2({\lambda ^2} - {\lambda ^{ - 2}})}},{X^{\text{ps}}} = {\lambda ^2} + {\lambda ^{ - 2}} - 2 \end{array} \right.$ | (18) |
式(8) 、(9) 、(10) 转化为二次函数形式,因此,可以得到类似(16) 的超静定方程组
| $\left\{ \begin{align} & {{C}_{10}}~+\text{ }2{{C}_{20}}X_{1}^{\text{uni}}~+\text{ }3{{C}_{30}}X_{1}{{^{\text{uni}}}^{2}}~=~Y_{1}^{\text{uni}}, \\ & {{C}_{10}}~+\text{ }2{{C}_{20}}X_{2}^{\text{uni}}~+\text{ }3{{C}_{30}}X_{2}{{^{\text{uni}}}^{2}}~=~Y_{2}^{\text{uni}}, \\ & \vdots \\ & {{C}_{10}}~+\text{ }2{{C}_{20}}X_{1}^{\text{bia}}~+\text{ }3{{C}_{30}}X_{1}{{^{\text{bia}}}^{2}}~=~Y_{1}^{\text{uni}}, \\ & {{C}_{10}}~+\text{ }2{{C}_{20}}X_{1}^{\text{ps}}~+\text{ }3{{C}_{30}}X_{1}{{^{\text{ps}}}^{2}}~=~Y_{1}^{\text{ps}}, \\ & \vdots \\ & {{C}_{10}}~+\text{ }2{{C}_{20}}X_{k}^{\text{ps}}~+\text{ }3{{C}_{30}}X_{k}{{^{\text{ps}}}^{2}}~=~Y_{k}^{\text{ps}} \\ \end{align} \right.$ | (19) |
写出X、Y矩阵和未知数矩阵C后,同理得YEOH本构模型的材料参数见表 2。
| 表 2 YEOH本构模型超静定识别结果 Table 2 Parameters of YEOH by hyperstatic equations |
对同样的试验数据进行分析,若采用传统回归方法进行参数识别,可以得到不同结果,其中最小二乘法最具有代表性,以此为例对MR模型和YEOH模型进行参数识别,可得到这两种模型的材料参数如表 3所示。
| 表 3 最小二乘法参数识别结果 Table 3 Parameters by least square method |
为了验证参数识别效果,将最小二乘法和超静定方法识别出的MR本构模型和YEOH本构模型与橡胶标准试件的单轴拉伸、等双轴拉伸和纯剪切试验应力应变曲线进行对比,见图 1~3。

|
图 1 单轴拉伸识别效果 Figure 1 Parameter identification in uniaxial tension |

|
图 2 等双轴拉伸识别效果 Figure 2 Parameter identification in equibiaxial tension |

|
图 3 纯剪切试验识别效果 Figure 3 Parameter identification in pure shear |
从图 1~3中可以看到,采用两种方法对本构模型的参数进行识别时,MR模型和YEOH模型的超静定识别效果对橡胶试件的3种变形均有较好的拟合效果,精度较高;YEOH模型的最小二乘法识别对单轴拉伸和等双轴拉伸拟合误差较小,而对纯剪切试验的拟合效果随着应变的增大而降低;MR模型总体拟合效果较差,尤其与等双轴拉伸的试验数据相差较大。总体来看,在橡胶试件应变较小时,超静定识别方法能够更加准确拟合橡胶标准试件的应力应变曲线。
3.2 识别效果的有限元验证为进一步验证超静定识别方法的精度与可靠性,选取同种材料的某橡胶衬套进行3种静态力学试验,依次为轴向拉伸、径向变形和扭转变形试验,3种试验均将衬套外套筒固定,在轴向拉伸时,对内套筒沿轴向进行加载,而在径向变形时,对内套筒施加径向载荷使其挤压橡胶体,扭转变形则对内套筒施加扭转位移,使内外套筒发生相对转动。试验结束后获得衬套的反力和位移数据,对MR和YEOH两种模型利用最小二乘法和超静定方程法识别本构参数,将识别结果运用于有限元计算分析,比较仿真效果。
首先对橡胶衬套进行几何建模,量取实际尺寸后利用UG软件绘制出衬套模型。该衬套几何模型分别由金属内套筒、金属外套筒和橡胶体3部分组成,用ABAQUS软件对模型进行有限元分析。由于内外金属套筒刚度远远大于橡胶体,为减少计算量将其简化为刚体,同时去除一些圆角和倒角。以内套筒尺寸为基准,找到其位于轴线上的几何中心,在此建立参考点并与内套筒内壁进行耦合约束,作为加载及输出数据提取点。为了模拟衬套与内外金属套筒的硫化连接,分别将模型中内外套筒与橡胶体上对应的接触面固定,对其进行网格划分,橡胶体总共划分出40 321个C3D10H单元,如图 4所示。

|
图 4 橡胶衬套有限元模型 Figure 4 Finite element model of rubber bushing |
对橡胶衬套进行加载分析时,参照试验条件,对外套筒的外表面施加约束,将其完全固定。进行轴向拉伸时,在内套筒中心的参考点施加轴向位移载荷,径向变形时,在参考点施加垂直于套筒轴线的位移载荷,而在扭转变形时,在参考点施加绕轴线转动的位移载荷。由于实验设备所限,3种变形均在20%应变范围内进行加载。经过计算后,输出参考点在轴向拉伸和径向变形沿加载方向的位移和反力,以及在扭转变形加载方向上的转动位移和反力矩,绘制相应的力位移曲线和力矩转角曲线。对于MR本构模型,两种识别方法的仿真和试验对比结果见图 5~7。

|
图 5 MR模型轴向拉伸力位移曲线 Figure 5 Axial force-displacement curve for model MR |

|
图 6 MR模型径向变形力位移曲线 Figure 6 Radical force-displacement curve for model MR |

|
图 7 MR模型扭转变形力矩转角曲线 Figure 7 Moment-rotation curve for model MR |
图 5~7表明,利用超静定方程求解方法所识别的MR本构模型,在进行有限元仿真时,得到的橡胶衬套静态力学特性与试验结果更为接近,只有轴向拉伸变形时,利用最小二乘法识别参数的仿真效果略微好于超静定方程求解法,总体而言,超静定方程求解法识别的参数在仿真效果上优于最小二乘法。
对于YEOH模型,两种识别方法的仿真结果和试验对比见图 8~10。
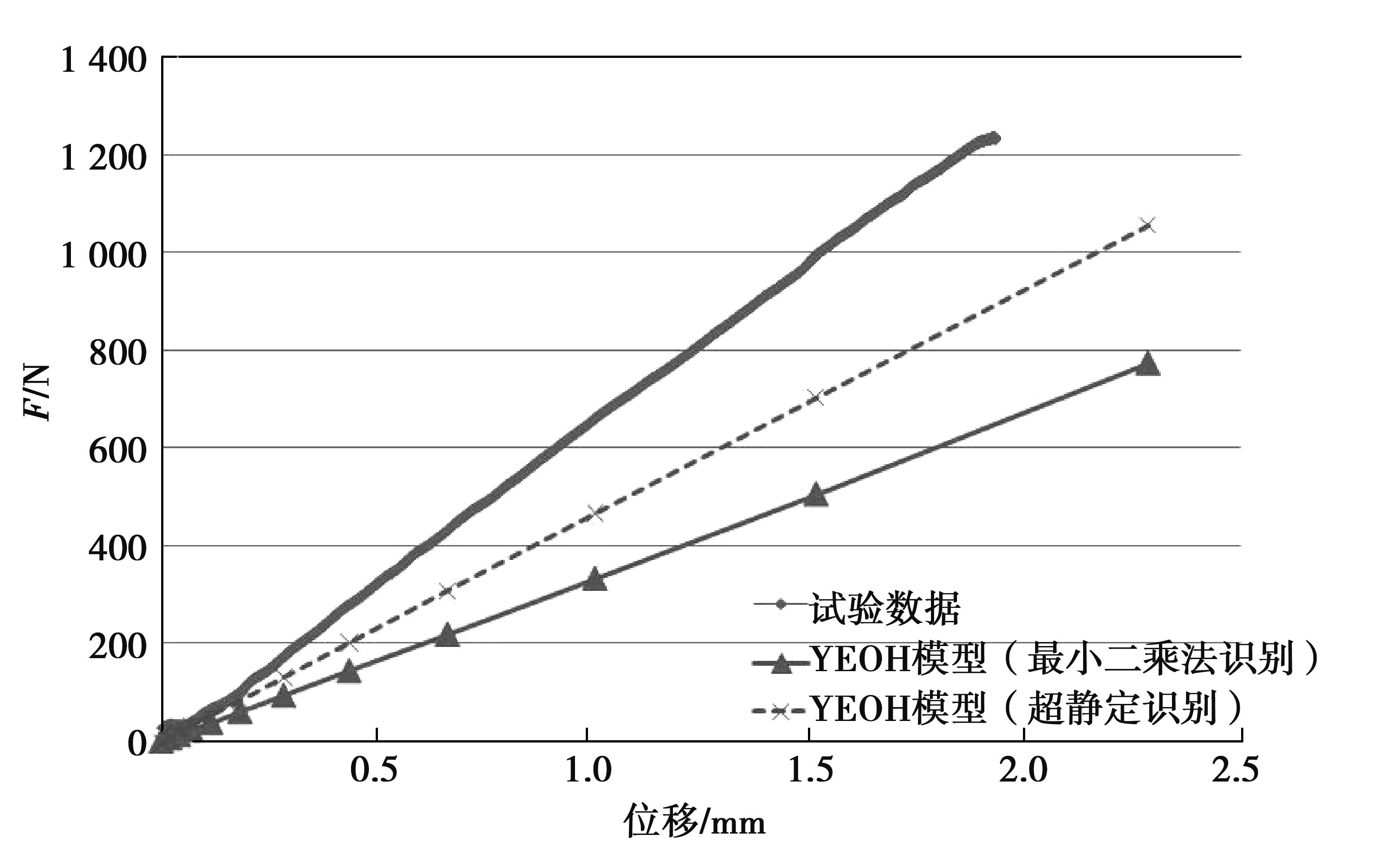
|
图 8 YEOH模型轴向拉伸力位移曲线 Figure 8 Axial force-displacement curve for model YEOH |

|
图 9 YEOH模型径向变形力位移曲线 Figure 9 Radical force-displacement curve for model YEOH |

|
图 10 YEOH模型扭转变形力矩转角曲线 Figure 10 Moment-rotation curve for model YEOH |
通过图 8~10可以看到,利用YEOH本构模型对橡胶衬套3种变形试验进行仿真,比较超静定法和最小二乘法,前者所识别的参数仿真曲线与试验曲线更为接近,仿真效果明显好于后者。
综合MR模型和YEOH模型在两种不同识别方法下的仿真精度,在图 5~10的位移轴上选取等间距的20个点,找到对应仿真曲线的力或力矩值,以实验数据作为参照,进行误差计算:
| $\eta =\frac{\left| {{F}_{仿}}-{{F}_{测}} \right|}{{{F}_{测}}}\times 100%$ | (20) |
误差对比见表 4。可以看到,在20%应变范围内,运用超静定识别方法后,橡胶衬套的仿真精度明显高于最小二乘法,与实验结果更加接近。
| 表 4 仿真误差对比 Table 4 The comparison of simulation error |
为了提高橡胶材料参数识别的精度,基于超静定方程求解原理提出了一种新的材料参数识别方法;根据试验数据识别出MR和YEOH两种模型的本构参数;参数识别结果运用于橡胶标准试件应力应变曲线拟合与有限元分析计算,对比最小二乘法,该方法能够真实可靠地描述橡胶材料的静态力学特性,而且参数识别精度有显著提高。
| [1] | Boyce M C, Arruda E M. Constitutive models of rubber elasticity:a review[J]. Rubber Chemistry and Technology, 2000, 73(3): 504–523. DOI:10.5254/1.3547602 |
| [2] | Treloar L R G. The elasticity of a network of long-chain molecules I/Ⅱ[J]. Trans Faraday Soc, 1943, 42(4): 83–94. |
| [3] |
左曙光, 朱俊兴, 吴旭东, 等.
一种考虑粘弹塑性的新型橡胶材料本构模型及其参数识别[J]. 重庆大学学报, 2014, 37(9): 1–10.
ZUO Shuguang, ZHU Junxing, WU Xudong, et al. A novel viscoelastroplastic constitutive model of rubber materials and parameter identification[J]. Journal of Chongqing University, 2014, 37(9): 1–10. (in Chinese) |
| [4] |
桑建兵, 刘波, 王志亮, 等.
橡胶类大变形材料有限元模拟及材料参数的确定[J]. 煤矿机械, 2009, 30(2): 64–66.
SANG Jianbin, LIU Bo, WANG Zhiliang, et al. Nonlinear finite element analysis of rubber like materials and determination of material parameters[J]. Coal Mine Machinery, 2009, 30(2): 64–66. (in Chinese) |
| [5] |
罗义建, 高永锋, 刘航.
考虑预载的橡胶悬置多体力学模型参数识别[J]. 重庆大学学报, 2012, 32(S1): 20–24.
LUO Yijian, GAO Yongfeng, LIU Hang. Parameter identification of rubber mounting multi-body model considering preload[J]. Journal of Chongqing University, 2012, 32(S1): 20–24. (in Chinese) |
| [6] |
黄建龙, 解广娟, 刘正伟.
基于Mooney-Rivlin和Yeoh模型的超弹性橡胶材料有限元分析[J]. 橡塑技术与设备, 2008, 34(12): 22–26.
HUANG Jianlong, XIE Guangjuan, LIU Zhengwei. Finite element analysis of super-elastic rubber materials based on the Mooney-Rivlin and Yeoh model[J]. China Rubber/Plastic Technology and Equipment, 2008, 34(12): 22–26. (in Chinese) |
| [7] |
郑明军, 王文静, 陈政南, 等.
橡胶Mooney-Rivlin模型力学性能常数的确定[J]. 橡胶工业, 2003, 50(8): 462–465.
ZHENG Mingjun, WANG Wenjing, CHEN Zhengnan, et al. Determination for mechanical constants of rubber Mooney-Rivlin model[J]. China Rubber Industry, 2003, 50(8): 462–465. (in Chinese) |
| [8] | Arruda E M, Boyce M C. A three-dimensional constitutive model for the large stretch behavior of rubber elastic materials[J]. Journal of the Mechanics and Physics of Solids, 1993, 41(2): 389–412. DOI:10.1016/0022-5096(93)90013-6 |
| [9] | Ogden R W. Large deformation isotropic elasticity:on the correlation of theory and experiment for incompressible rubberlike solids[J]. Proceedings of the Royal Society of London, 1972, 326(2): 565–584. |
| [10] | Puel G, Bourgeteau B, Aubry D. Parameter identification of nonlinear time-dependent rubber bushings models towards their integration in multibody simulations of a vehicle chassis[J]. Mechanical Systems and Signal Processing, 2013, 36(2): 354–369. DOI:10.1016/j.ymssp.2012.10.021 |
| [11] | Sasso M, Palmieri G, Chiappini G, et al. Characterization of hyperelastic rubber-like materials by biaxial and uniaxial stretching tests based on optical methods[J]. Polymer Testing, 2008, 27(8): 995–1004. DOI:10.1016/j.polymertesting.2008.09.001 |
| [12] | Pearson I, Pickering M. The determination of a highly elastic adhesive's material properties and their representation in finite element analysis[J]. Finite Elements in Analysis and Design, 2001, 37(3): 221–232. DOI:10.1016/S0168-874X(00)00031-7 |
| [13] | Darijani H, Naghdabadi R. Hyperelastic materials behavior modeling using consistent strain energy density functions[J]. Acta Mechanica, 2010, 213(3): 235–254. |
| [14] | Bechir H, Chevalier L, Chaouche M, et al. Hyperelastic constitutive model for rubber-like materials based on the first Seth strain measures invariant[J]. European Journal of Mechanics-A/Solids, 2006, 25(1): 110–124. DOI:10.1016/j.euromechsol.2005.03.005 |
| [15] | Yeoh O H. Some forms of the strain energy function for rubber[J]. Rubber Chemistry and Technology, 2012, 66(5): 754–771. |
 2017, Vol. 40
2017, Vol. 40

