高阶谱的概念是Wiener[1]在1958年提出的,定义为高阶累积量的多维傅立叶变换。文献[2-6]分析比较了各种谱估计方法,发表了有关现代谱分析的长篇综述论文。在20世纪60年代,高阶累积量就已经引起数学家们的关注,直到20世纪80年代后期,信号处理技术取得了很大进展,目前已成为信号处理的一种有力的数学工具。由于高阶累积量可以自动地抑制高斯背景噪声(有色或白色)的影响,现已应用得非常广泛。由三阶累积量进行二维傅里叶变换得出的双谱包含了信号的非对称非线性信息,可以用来描述非线性相位耦合,尤其是二次相位耦合, 并已经在机械故障诊断、电子信息等领域得到了深入研究[7-12]。文献[7-12]都是通过分析在相似的工作条件下和不同的参数情况时所采集的时间序列,这些序列得出的双谱之间存在某些差异,再将这些差异和所要分析的信号与其不同的工作状态相对应进行判别。文献[7]通过分析不同状态的溢流阀信号所得出的不同双谱所表现出来的不同特性,包括谱峰数、谱峰分布、谱峰尖锐程度等,从而判断溢流阀的工作状态。文献[6-14]对一般信号以及耦合信号的双谱进行了详细的理论分析,并利用这些方法对机械故障进行诊断。文献[7-12]的应用中都是假定所分析数据的双谱存在较为明显的差异,从而在可以进行辨别的前提下进行的,如果在实际工作状态相近的情况下采集的某些数据的双谱非常相似,则采用上述文献的方法就难以起到比较理想的效果。
基于双谱理论对各种机械振动信号进行的应用研究称之为双谱分析。鉴于单纯的双谱分析方法对于信号的相近工作状态难以进行精确的分析,文中提出了一种对原始数据先进行微分再求其双谱,然后分析其中耦合信号对于原始双谱会产生何种改变的方法。由于在不同的工作状态下,信号频率必然存在着某种程度的差别,文中提出的微分方法可以放大这种差别。因此,通过微分,在双谱中难以区分的机械工作状态变得容易区分,并将这种方法应用到铣削机床的工况分析中,取得了较好效果。
1 耦合信号微分及其双谱性质设时间序列{x(n)}为零均值k阶平稳随机过程,则该过程的三阶累积量为
| $ {c_{3x}}\left( {{\tau _1},{\tau _2}} \right) = E\left\{ {x\left( n \right)x\left( {n + {\tau _1}} \right)x\left( {n + {\tau _2}} \right)} \right\}, $ | (1) |
式中:E{x(n)x(n+τ1)x(n+τ2)}表示x(n)的三阶矩;τ1, τ2是滞后量,对其进行傅里叶变换,即得双谱为
| $ B\left( {{\omega _1},{\omega _2}} \right) = \sum\limits_{\tau 1 = - \infty }^\infty {\sum\limits_{\tau 2 = - \infty }^\infty {{c_{3x}}\left( {{\tau _1},{\tau _2}} \right){{\rm{e}}^{ - j\left( {\omega 1\tau 1 + \omega 2\tau 2} \right)}}} } 。$ | (2) |
双谱用频率特性函数可以表示为
| $ B\left( {{\omega _1},{\omega _2}} \right) = {\gamma _{3a}}H\left( {{\omega _1}} \right)H\left( {{\omega _2}} \right){H^ * }\left( {{\omega _1} + {\omega _2}} \right), $ | (3) |
式中:H*(ω)为H(ω)为共轭函数;H(ω)为频率特性函数;γ3a=E{a3(n)}为歪斜度,a(n)是一独立同分布的非高斯随机过程。
在式(3) 中,令ω1=ω2=ω,即得到双谱对角切片表达式
| $ B{S_x}\left( {\omega ,\omega } \right) = {\gamma _{3a}}{H^2}\left( \omega \right){H^ * }\left( {2\omega } \right)。$ | (4) |
如果连续函数f(t)的的傅立叶变换是F(jω),且f(t)的微分是
| $ F\left[ {\frac{{{\rm{d}}f\left( t \right)}}{{{\rm{d}}t}}} \right] = j\omega F\left[ {j\omega } \right]。$ | (5) |
当对时间序列{x(n)}一次微分以后,其双谱变为
| $ {B^1}\left( {{\omega _1},{\omega _2}} \right) = - j{\omega _1}{\omega _2}\left( {{\omega _1} + {\omega _2}} \right)H\left( {{\omega _1}} \right)H\left( {{\omega _2}} \right){H^ * }\left( {{\omega _1} + {\omega _2}} \right), $ | (6) |
双谱的对角切片表达式变为
| $ {B^1}\left( {\omega ,\omega } \right) = - j2{\omega ^3}{H^2}\left( \omega \right){H^ * }\left( {2\omega } \right), $ | (7) |
当对时间序列{x(n)}n次微分以后,其双谱变为
| $ {B^n}\left( {{\omega _1},{\omega _2}} \right) = {j^{3n}}\omega _1^n\omega _2^n{\left( {{\omega _1} + {\omega _2}} \right)^n}H\left( {{\omega _1}} \right)H\left( {{\omega _2}} \right){H^ * }\left( {{\omega _1} + {\omega _2}} \right), $ | (8) |
对角切片表达式变为
| $ {B^{1n}}\left( {\omega ,\omega } \right) = {j^{3n}}2{\omega ^{3n}}{H^2}\left( \omega \right){H^ * }\left( {2\omega } \right), $ | (9) |
再讨论耦合信号所发生的情况。
在式(3) 中,令x(n)为实数耦合信号,即令
| $ x\left( n \right) = \sum\limits_{i = 1}^3 {{A_{oi}}\cos \left( {{\omega _{oi}}n + {\varphi _{oi}}} \right)} , $ | (10) |
其中φo3=φo2+φo1。谐波分量ωo3是由谐波分量ωo1和ωo2通过二次相位耦合而成的,即x(n)为发生了耦合的信号。
为了方便说明,文中令ωo1=ω0,ωo2=2ω0,则ωo3=3ω0, φo1=φ0,φo2=2φ0,则
| $ {\varphi _{o3}} = {\varphi _{o1}} + {\varphi _{o2}} = 3{\varphi _0}。$ | (11) |
对x(n)微分以后,有
| $ \frac{{{\rm{d}}x\left( n \right)}}{{{\rm{d}}n}} = \sum\limits_{i = 1}^3 {{A_{oi}}{\omega _{oi}}\cos \left( {{\omega _{oi}}n + {\varphi _{oi}} + \frac{{\rm{\pi }}}{2}} \right)} , $ | (12) |
由式(3) 可得,x(n)的双谱如式(13) 所示。
| $ \begin{array}{l} {B_x}\left( {{\omega _1},{\omega _2}} \right) = \frac{{{A_1}{A_2}{A_3}}}{8}\left[ {\delta \left( {{\omega _1} + {\omega _0}} \right){{\rm{e}}^{ - j\varphi 0}} + \delta \left( {{\omega _1} - {\omega _0}} \right){{\rm{e}}^{j\varphi 0}} + \delta \left( {{\omega _1} + 2{\omega _0}} \right){{\rm{e}}^{ - j2\varphi 0}} + } \right.\\ \left. {\delta \left( {{\omega _1} - 2{\omega _0}} \right){{\rm{e}}^{j2\varphi 0}} + \delta \left( {{\omega _1} + 3{\omega _0}} \right){{\rm{e}}^{ - j3\varphi 0}} + \delta \left( {{\omega _1} - 3{\omega _0}} \right){{\rm{e}}^{j3\varphi 0}}} \right] \cdot \left[ {\delta \left( {{\omega _2} - {\omega _0}} \right){{\rm{e}}^{ - j\varphi 0}} + } \right.\\ \delta \left( {{\omega _2} - {\omega _0}} \right){{\rm{e}}^{j\varphi 0}} + \delta \left( {{\omega _2} + 2{\omega _0}} \right){{\rm{e}}^{ - j2\varphi 0}} + \delta \left( {{\omega _2} - 2{\omega _0}} \right){{\rm{e}}^{j2\varphi 0}} + \delta \left( {{\omega _2} + 3{\omega _0}} \right){{\rm{e}}^{ - j3\varphi 0}} + \\ \left. {\delta \left( {{\omega _2} - 3{\omega _0}} \right){{\rm{e}}^{j3\varphi 0}}} \right] \cdot \left[ {{\delta ^ * }\left( {{\omega _1} + {\omega _2} + {\omega _0}} \right){{\rm{e}}^{j\varphi 0}} + {\delta ^ * }\left( {{\omega _1} + {\omega _2} - {\omega _0}} \right){{\rm{e}}^{ - j\varphi 0}} + {\delta ^ * }\left( {{\omega _1} + } \right.} \right.\\ \left. {{\omega _2} + 2{\omega _0}} \right){{\rm{e}}^{j2\varphi 0}} + {\delta ^ * }\left( {{\omega _1} + {\omega _2} - 2{\omega _0}} \right){{\rm{e}}^{ - j2\varphi 0}} + {\delta ^ * }\left( {{\omega _1} + {\omega _2} - 3{\omega _0}} \right){{\rm{e}}^{j3\varphi 0}} + \\ \left. {{\delta ^ * }\left( {{\omega _1} + {\omega _2} - 3{\omega _0}} \right){{\rm{e}}^{ - j3\varphi 0}}} \right]。\end{array} $ | (13) |
通过式(4),可得到其双谱对角切片如式(14) 所示。
| $ \begin{array}{l} B{S_x}\left( {{\omega _1},{\omega _2}} \right) = \frac{{{A_1}{A_2}{A_3}}}{8}\left[ {\delta \left( {\omega + {\omega _0}} \right){{\rm{e}}^{ - j\varphi 0}} + \delta \left( {\omega - {\omega _0}} \right){{\rm{e}}^{j\varphi 0}} + \delta \left( {\omega + 2{\omega _0}} \right){{\rm{e}}^{ - j2\varphi 0}} + } \right.\\ {\left. {\delta \left( {\omega - 2{\omega _0}} \right){{\rm{e}}^{j2\varphi 0}} + \delta \left( {\omega + 3{\omega _0}} \right){{\rm{e}}^{ - j3\varphi 0}} + \delta \left( {\omega - 3{\omega _0}} \right){{\rm{e}}^{j3\varphi 0}}} \right]^2} \cdot \left[ {{\delta ^ * }\left( {2\omega + {\omega _0}} \right){{\rm{e}}^{j\varphi 0}} + } \right.\\ {\delta ^ * }\left( {2\omega - {\omega _0}} \right){{\rm{e}}^{ - j\varphi 0}} + {\delta ^ * }\left( {2\omega + 2{\omega _0}} \right){{\rm{e}}^{j2\varphi 0}} + {\delta ^ * }\left( {2\omega + 2{\omega _0}} \right){{\rm{e}}^{ - j2\varphi 0}} + {\delta ^ * }\left( {2\omega + 3{\omega _0}} \right) \\ {{\rm{e}}^{j3\varphi 0}} + \left. {{\delta ^ * }\left( {2\omega + 3{\omega _0}} \right){{\rm{e}}^{ - j3\varphi 0}}} \right]。\end{array} $ | (14) |
式(15) 和式(16) 分别为信号微分一次和k次后得到的双谱表达式。
| $ \begin{array}{l} {B_x}\left( {{\omega _1},{\omega _2}} \right) = \frac{{3{A_1}{A_2}{A_3}\omega _0^3}}{4}\left[ { - j\delta \left( {{\omega _1} + {\omega _0}} \right){{\rm{e}}^{ - j\varphi 0}} + j\delta \left( {{\omega _1} - {\omega _0}} \right){{\rm{e}}^{j\varphi 0}} - } \right.\\ j\delta \left( {{\omega _1} + 2{\omega _0}} \right){{\rm{e}}^{ - j2\varphi 0}} + j\delta \left( {{\omega _1} - 2{\omega _0}} \right){{\rm{e}}^{j2\varphi 0}} - j\delta \left( {{\omega _1} + 3{\omega _0}} \right){{\rm{e}}^{ - j3\varphi 0}} + \\ \left. {j\delta \left( {{\omega _1} - 3{\omega _0}} \right){{\rm{e}}^{j3\varphi 0}}} \right] \cdot \left[ { - j\delta \left( {{\omega _2} + {\omega _0}} \right){{\rm{e}}^{ - j\varphi 0}} + j\delta \left( {{\omega _2} - {\omega _0}} \right){{\rm{e}}^{j\varphi 0}} - } \right.\\ j\delta \left( {{\omega _2} + 2{\omega _0}} \right){{\rm{e}}^{ - j2\varphi 0}} + j\delta \left( {{\omega _2} - 2{\omega _0}} \right){{\rm{e}}^{j2\varphi 0}} - j\delta \left( {{\omega _2} + 3{\omega _0}} \right){{\rm{e}}^{ - j3\varphi 0}} + \\ \left. {j\delta \left( {{\omega _2} - 3{\omega _0}} \right){{\rm{e}}^{j3\varphi 0}}} \right] \cdot \left[ {j{\delta ^ * }\left( {{\omega _1} + {\omega _2} + {\omega _0}} \right){{\rm{e}}^{j\varphi 0}} - j{\delta ^ * }\left( {{\omega _1} + {\omega _2} - {\omega _0}} \right){{\rm{e}}^{ - j\varphi 0}} + } \right.\\ j{\delta ^ * }\left( {{\omega _1} + {\omega _2} + 2{\omega _0}} \right){{\rm{e}}^{2j\varphi 0}} - j{\delta ^ * }\left( {{\omega _1} + {\omega _2} - 2{\omega _0}} \right){{\rm{e}}^{ - j2\varphi 0}} + j{\delta ^ * }\left( {{\omega _1} + {\omega _2} + 3{\omega _0}} \right){{\rm{e}}^{j3\varphi 0}} - \\ \left. {j{\delta ^ * }\left( {{\omega _1} + {\omega _2} - 3{\omega _0}} \right){{\rm{e}}^{ - j3\varphi 0}}} \right], \end{array} $ | (15) |
| $ \begin{array}{l} {B_x}\left( {{\omega _1},{\omega _2}} \right) = \frac{{{2^{k - 1}} \times {3^k}{A_1}{A_2}{A_3}\omega _0^{3k}}}{4}\left[ {\delta \left( {{\omega _1} + {\omega _0}} \right){{\rm{e}}^{ - j\left( {\varphi 0 + \frac{{k{\rm{\pi }}}}{2}} \right)}} + \delta \left( {{\omega _1} - {\omega _0}} \right){{\rm{e}}^{j\left( {\varphi 0 + \frac{{k{\rm{\pi }}}}{2}} \right)}} + } \right.\\ \delta \left( {{\omega _1} + 2{\omega _0}} \right){{\rm{e}}^{ - j\left( {2\varphi 0 + \frac{{k{\rm{\pi }}}}{2}} \right)}} + \delta \left( {{\omega _1} - 2{\omega _0}} \right){{\rm{e}}^{j\left( {2\varphi 0 + \frac{{k{\rm{\pi }}}}{2}} \right)}} + \delta \left( {{\omega _1} + 3{\omega _0}} \right){{\rm{e}}^{ - j\left( {3\varphi 0 + \frac{{k{\rm{\pi }}}}{2}} \right)}} + \\ \left. {\delta \left( {{\omega _1} - 3{\omega _0}} \right){{\rm{e}}^{j\left( {3\varphi 0 + \frac{{k{\rm{\pi }}}}{2}} \right)}}} \right] \cdot \left[ {\delta \left( {{\omega _2} + {\omega _0}} \right){{\rm{e}}^{ - j\left( {\varphi 0 + \frac{{k{\rm{\pi }}}}{2}} \right)}} + \delta \left( {{\omega _2} - {\omega _0}} \right){{\rm{e}}^{j\left( {\varphi 0 + \frac{{k{\rm{\pi }}}}{2}} \right)}} + } \right.\\ \delta \left( {{\omega _2} + 2{\omega _0}} \right){{\rm{e}}^{ - j\left( {2\varphi 0 + \frac{{k{\rm{\pi }}}}{2}} \right)}} + \delta \left( {{\omega _2} - 2{\omega _0}} \right){{\rm{e}}^{j\left( {2\varphi 0 + \frac{{k{\rm{\pi }}}}{2}} \right)}} + \delta \left( {{\omega _2} + 3{\omega _0}} \right){{\rm{e}}^{ - j\left( {3\varphi 0 + \frac{{k{\rm{\pi }}}}{2}} \right)}} + \\ \left. {\delta \left( {{\omega _2} - 3{\omega _0}} \right){{\rm{e}}^{j\left( {3\varphi 0 + \frac{{k{\rm{\pi }}}}{2}} \right)}}} \right] \cdot \left[ {{\delta ^ * }\left( {{\omega _1} + {\omega _2} + {\omega _0}} \right){{\rm{e}}^{j\left( {\varphi 0 + \frac{{k{\rm{\pi }}}}{2}} \right)}} + {\delta ^ * }\left( {{\omega _1} + {\omega _2} - {\omega _0}} \right) } \right.\\ {{\rm{e}}^{ - j\left( {\varphi 0 + \frac{{k{\rm{\pi }}}}{2}} \right)}} + {\delta ^ * }\left( {{\omega _1} + {\omega _2} + 2{\omega _0}} \right){{\rm{e}}^{j\left( {2\varphi 0 + \frac{{k{\rm{\pi }}}}{2}} \right)}} + {\delta ^ * }\left( {{\omega _1} + {\omega _2} - 2{\omega _0}} \right){{\rm{e}}^{ - j\left( {2\varphi 0 + \frac{{k{\rm{\pi }}}}{2}} \right)}} + \\ \left. {{\delta ^ * }\left( {{\omega _1} + {\omega _2} + 3{\omega _0}} \right){{\rm{e}}^{j\left( {3\varphi 0 + \frac{{k{\rm{\pi }}}}{2}} \right)}} + {\delta ^ * }\left( {{\omega _1} + {\omega _2} - 3{\omega _0}} \right){{\rm{e}}^{ - j\left( {3\varphi 0 + \frac{{k{\rm{\pi }}}}{2}} \right)}}} \right]。\end{array} $ | (16) |
对x(n)进行k次微分以后,有
| $ \frac{{{{\rm{d}}^k}x\left( n \right)}}{{{{\rm{d}}^k}n}} = \sum\limits_{i = 1}^3 {{A_{oi}}\omega _{oi}^k\cos \left( {{\omega _{oi}}n + {{\bar \omega }_{oi}} + \frac{{k{\rm{\pi }}}}{2}} \right)} 。$ | (17) |
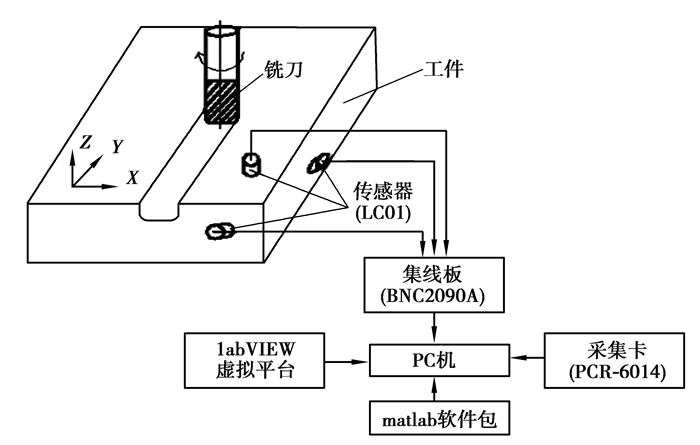
铣削加工是采用多齿刀具进行断续切削的一种加工方法。铣刀的刀齿在切削进行时,其切削力的幅值和方向都在连续发生变化,这是铣削加工的基本特征。为了获得铣削振动过程中工件的振动信号,以便于分析其振动系统的频谱特性,采用了如图 1所示的测试系统进行数据采集。该系统工作原理如下:在铣削加工过程中,由于工件在加工过程中因受热、受力发生的变形、刀具在加工过程中的磨损等因素都会使得工件发生相应的振动,通过在工件上安装加速度传感器,可以采集工件的振动信号,并通过相应的数据处理可以定性、定量地进行分析。
|
图 1 数据采集原理图 Figure 1 Data acquisition principle |
实验选用的工件材料为A3钢和45钢;选择的刀具是钨钴钛类硬质合金,牌号是YT-15、直径为20 mm的硬质合金直柄圆柱三刃螺旋铣刀;加工过程不加铣削液。利用软件LabVIEW、数据采集卡和一个加速度传感器,依次采集主轴转速、进给量及进给速度变化时数控铣床的振动信号。在测试过程中,采样频率设为1 024 Hz,读取频率为512 Hz。
本次试验中将传感器安装在夹具上,通过测量夹具各个方向振动信号来分析工件的振动情况。文中采用的7组数据,都是在进给速度为700 mm/min的情况下采集的,数据的其他控制量如表 1所示。其中数据一和数据二加工的是A3钢,其他数据加工的是45号钢。文中采用的数据个数为1 024个。
| 表 1 文中采用数据 Table 1 Data in the paper |
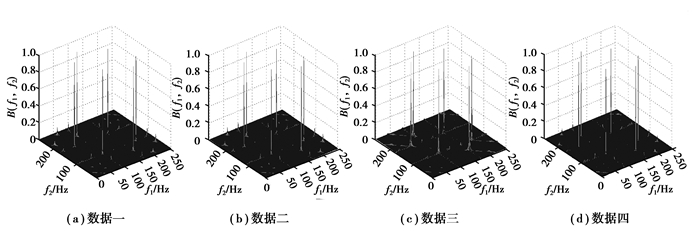
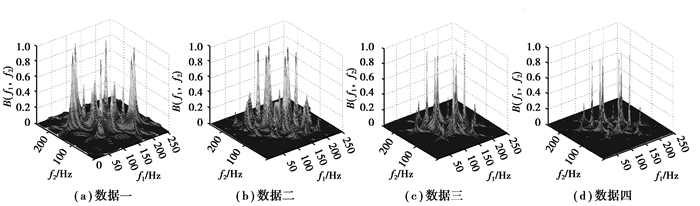
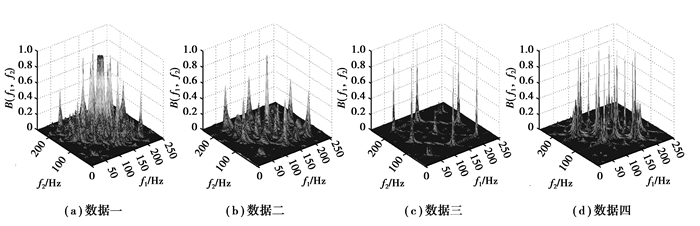
研究首先选取4组双谱相近的数据进行分析,见表 1中的数据一至数据四。从图 2可以看出,4组数据都分别有6个谱峰,且6个谱峰分布的位置分别都在(50 Hz、150 Hz)、(100 Hz、100 Hz)等处,每组数据6个相对应的谱峰的幅值都在0.7~0.9之间,因此,这4组数据的双谱无论从谱峰的数目、高度还是其分布位置来看,整体上都非常相似,难以分辨。图 3是经过一次微分以后的4组数据所得出的双谱,从图中可以看出,数据一和数据二在一次微分以后的双谱,单从谱峰的整体上来看比较相似,但仔细分析,数据一的几个主要谱峰的位置处于(50 Hz、200 Hz)、(100 Hz、230 Hz)等处,而数据二的则处于(100 Hz、150 Hz)、(120 Hz、200 Hz)等处。从表 1可以看出,数据一和数据二的主轴转速虽然不同,但加工材料都是A3钢,也就是说,数据一和数据二的双谱在微分前难以区分,但微分后可以通过谱峰的位置加以区分;而数据三和数据四的加工材料都是45#钢,且主轴转速都是3 000 r/min,只是轴向进给量和粗糙值不同,这2组数据虽然微分前后无论从谱峰的数量、位置还是幅度来看都比较相似,但微分后数据三的几个主要谱峰与数据四相比,其底部都更粗大些。再与图 2对照,可以看出,经过一次微分以后,数据一和数据二的双谱与微分前相比,其谱峰数明显增多、变粗,而数据三和数的双谱变化的程度相对要弱一些, 而且数据一和数据二作为一个整体与数据三和数据四作为一个整体进行比较, 在一次微分后, 数据一和数据二的双谱明显比数据三和数据四的谱峰更多、更粗, 这应该与数据一、数据二的加工材料和数据三、数据四的加工材料不同有关。通过前述理论分析可以看出, 微分以后, 无论是耦合信号还是非耦合信号, 其振幅都会由于微分的作用而成指数倍增加, 但由于每组数据里面发生耦合的信号不同, 因此这种不同就由于微分的作用被放大, 从而使原来通过双谱无法区分的信号变得可以区分。图 4表示四组数据二次微分后所得到的双谱。从图 4可以看出,4组数据的双谱从其谱峰的多少、粗细和分布都各不相同。为了进行进一步的分析,文中对上述4组数据进行了多次微分,图 5显示的是4组数据分别经过5次微分以后所得到的双谱图。从图 5可以看出,前2组和后2组数据再次显示出分别相似的特征。再分别对每组数据进行纵向分析,即参考图 3(a),图 4(a),图 5(a),可以看出,数据一随着微分次数的增加,其双谱的谱峰数呈现出一种减少并且变细的趋势。同样可以观察到数据二具有相似的变化规律。数据三和数据四则呈现出相反的特点,即随着微分次数的增加,其双谱的谱峰数呈现出一种增加和变粗的趋势。这些现象是否和不同的加工材料有关,是值得进一步讨论的地方。经过多次微分以后发现,4组数据在二次微分后相互间区别最大,而这种微分次数和相互间的区别是否存在着某种关联,笔者将在以后的研究中将进行进一步探讨。
|
图 2 原始数据双谱图 Figure 2 The bispectrum of original data |
|
图 3 数据1次微分后双谱图 Figure 3 Bispectrum of data after 1st differential |
|
图 4 数据2次微分后双谱图 Figure 4 Bispectrum of data after second differential |

|
图 5 数据5次微分后双谱图 Figure 5 Bispectrum of data after fifth differential |
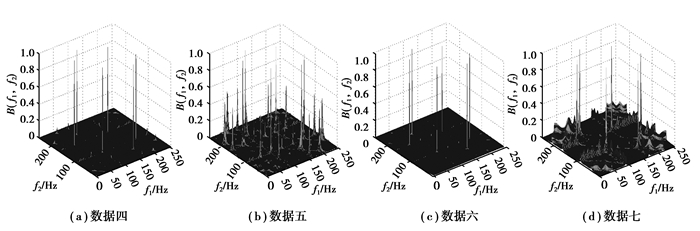
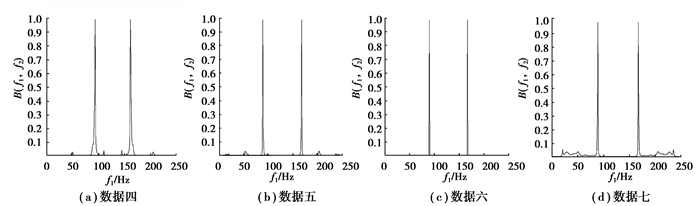
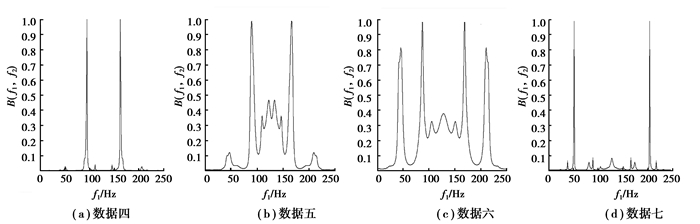
接下来再选择4组数据,即数据四至数据七,该4组数据的双谱见图 6所示。从图 6可以看出,该4组数据的双谱只有数据四和数据六的双谱相似。仔细分析这些数据可以发现, 数据四和数据六的转速、进给量和粗糙度都比较接近,而数据五的粗糙度值为2.131,比数据四和数据六的要大,数据七的转速为2 400 r/min,比其他数据的小,这应该是产生这种现象的部分原因。图 7显示的是该4组数据的双谱对角切片,从图 7可以看出,4组数据的对角切片都非常相似。对上述4组数据进行一次微分后,所得到的双谱切片如图 8所示。从图 8可以看到,4组数据在经过一次微分后,其双谱切片变得比较容易区分。图 9表示4组数据经过二次微分以后所得到的双谱切片图,从图 9可以看出,数据五和数据六的谱峰明显比其他2组数据复杂, 根据式(6), 耦合数据的振幅会随着微分次数的增加而增大, 说明数据五和数据六发生的耦合比数据四和数据七严重些, 参考表 1,数据五和数据六的粗糙度数值比数据四和数据七要大,而这种变化是否与此有关,也可以进行进一步的研究。
|
图 6 原始数据双谱图 Figure 6 Bispectrum of primary data |
|
图 7 原始数据双谱对角切片图 Figure 7 Bispectral diagonal slice of primary data |

|
图 8 数据1次微分后双谱对角切片图 Figure 8 Bispectral diagonal slice of data after 1st differential |
|
图 9 数据2次微分后双谱对角切片图 Figure 9 Bispectral diagonal slice of data after second differential |
通过上述分析, 可以看出, 由于微分放大了不同信号间发生耦合信号的差异, 而在铣削加工系统中, 各种参数比如转速、材料及粗糙度等,都与信号的耦合有关,因此可以通过调整各种参数增加或者减少这种耦合现象,从而达到改善系统功能的目的。
4 结论研究通过先对信号微分再求其双谱,然后运用到铣削机床的工况分析中,可以看到,随着微分次数的增加,信号的双谱幅值也随着发生了变化,原来难以区分的铣床振动信号变得可以区分。研究的意义在于,对于通过双谱难以区分的时间序列,可以通过对信号进行微分再求其双谱的方法进行分析;对于那些双谱对角切片相似的信号,也可以采用同样的方法进行讨论。文中提供了2种研究方法:一是对于双谱相似的不同信号,在它们经过了相同微分次数并得到其双谱后,通过对比这些双谱之间的不同点进行横向分析的方法;二是对于同一组信号,在进行不同的微分次数并得出其双谱后,再对这些双谱进行讨论的纵向分析方法。
| [1] | Wiener N, Teichmann T. Nonlinear problems in random theory[M]. Massachusetts Institute of Technology, 1958: 77. |
| [2] | Childers D G, Group I I T. Modern spectrum analysis[M]. IEEE Information Theory Group, 1978. |
| [3] | Kay S M, Marple S L. Spectrum analysis-a modern perspective[J]. Proceddings of the IEEE, 1981, 69(11): 1380–1419. DOI:10.1109/PROC.1981.12184 |
| [4] | Kesler S B. Modern spectrum analysis[M]. New York: IEEE Press, 1986. |
| [5] | Raghuveer M R. Time-domain approaches to quadratic phase coupling estimation[J]. IEEE Transactions on Automatic Control, 1990, 35(1): 48–56. DOI:10.1109/9.45142 |
| [6] |
张严, 王树勋.
非线性相位耦合的切片谱分析方法[J]. 电子学报, 1998, 26(10): 104–109.
ZHANG Yan, WANG Shuxun. The slice spectra approach to nonlinear phase coupling analysis[J]. Acta Electronic Sinica, 1998, 26(10): 104–109. DOI:10.3321/j.issn:0372-2112.1998.10.022 (in Chinese) |
| [7] |
彭志君, 黄宜坚.
基于AR双谱的溢流阀故障诊断[J]. 机械科学与技术, 2007, 26(7): 908–912.
PENG Zhijun, HUANG Yijian. Fault Diagnosis of Relief Valve Using AR Bispectrum[J]. Mechanical Science and Technology for Aerospace Engineering, 2007, 26(7): 908–912. (in Chinese) |
| [8] |
吴文兵, 黄宜坚, 陈文芗.
基于机械故障诊断的高阶谱耦合性能分析[J]. 振动、测试与诊断, 2012, 32(1): 130–134.
WU Wenbing, HUANG Yijian, CHEN Wenxiang. High order spectrum's coupling performance based on mechanical fault diagnosis[J]. Journal of Vibration, Measurement & Diagnosis, 2012, 32(1): 130–134. (in Chinese) |
| [9] |
耿文飞, 梅二召, 吴文兵.
高阶谱在分流集流阀故障诊断中的应用[J]. 煤矿机械, 2015, 36(10): 306–309.
GEN Wenfei, MEI Ershao, WU Wenbing. Application of high order spectrum in fault diagnosis of flow distributing and collecting valve[J]. Coal Mine Machinery, 2015, 36(10): 306–309. (in Chinese) |
| [10] |
吴文兵, 梅二召, 欧阳鑫, 等.
基于复数信号的三阶累积量微分性质研究及应用[J]. 哈尔滨工程大学学报, 2015, 36(8): 1073–1079.
WU Wenbing, MEI Ershao, OUYANG Xin, et al. Study on the third-order cumulant's differential features based on complex signals and its application[J]. Journal of Harbin Engineering University, 2015, 36(8): 1073–1079. (in Chinese) |
| [11] |
吴文兵, 黄宜坚.
基于故障诊断的双谱优良特性体现[J]. 中国机械工程, 2014, 25(6): 771–775.
WU Wenbing, HAUNG Yijian. Presence of bispectrum's prior performance based on fault diagnosis[J]. China Mechanical Engineering, 2014, 25(6): 771–775. (in Chinese) |
| [12] |
陈智博, 黄宜坚.
基于AR双谱的超声波电机故障诊断[J]. 中南大学学报:自然科学版, 2011, 42(12): 3728–3734.
CHEN Zhibo, HUANG Yijian. Fault diagnosis of ultrasonic motor using AR bispectrum[J]. Journal of Central South University (Science and Technology), 2011, 42(12): 3728–3734. (in Chinese) |
| [13] | Lee S K, White P R. Higher-order time-frequency analysis and its application to fault detection in rotating machinery[J]. Mechanical Systems & Signal Processing, 1997, 11(4): 637–650. |
| [14] | Hinich M J. Higher order cumulants and cumulant spectra[J]. Circuits, Systems, and Signal Processing, 1994, 13(4): 391–402. DOI:10.1007/BF01183737 |
| [15] |
陈静.
数字微分器的Matlab实现[J]. 株洲师范高等专科学校学报, 2005, 10(2): 46–48.
CHEN Jing. Matlab realization of digital differentiator[J]. Journal of Zhuzhou Teachers College, 2005, 10(2): 46–48. (in Chinese) |
 2017, Vol. 40
2017, Vol. 40

