液滴在固体表面上的铺展现象广泛存在工业应用中,如打印机将墨水喷到纸面[1]、农药喷洒在蔬菜表面[2]、表面喷涂[3]、喷雾冷却[4]等。液滴撞击壁面大致会出现3种现象:沉积、溅射和反弹[5]。很多工业应用涉及到液滴在壁面上的沉积问题[2-3, 6],为抑制液滴溅射和反弹来提高液滴在壁面上的沉积率,通常有两种途径[6]:1)加入添加剂改变流体的流变特性;2)改变固壁表面的性质。第一种方法用途广泛,例如在液体中添加聚合物使液滴呈现非牛顿性,抑制液滴在壁面上的溅射和反弹,提高药物的使用效率[2];铁轨上的摩擦改进剂,通过水溶剂中添加聚合物复合材料改变流变特性,提高沉积率,以降低机车燃料消耗和轨轮的磨损[3]等等。在流体中添加不同的成分得到的流变特性不同[7-11],例如添加弹性颗粒会促进液滴在壁面上的反弹[11],而在牛顿流体中添加高分子聚合物会使液体产生幂律流变特性[9, 12-14]。幂律流体在控制液体沉积问题中有着重要的应用,目前对于幂律流体的动态湿润理论研究虽然已经取得一些进展[14-16],但数值模拟的研究仍然较少[15]。
与传统数值方法相比,格子Boltzmann方法作为一种介观的数值方法,凭借其独特的优势在研究非牛顿流体方面得到了广泛的关注[17-21]。在格子Boltzmann方法中,最常用的是单松弛模型,由于该模型的数值稳定性较差,笔者给出了非牛顿流体的多松弛格子Boltzmann模型。目前,研究两相流界面运动常有的数值方法有水平集法、流体体积函数法(VOF)[22]、相场法[23]等,相对于其他方法,基于自由能理论的相场法在研究多组分系统中介观结构的演化等复杂现象时具有特有的优势,如多相流、接触线以及涉及复杂界面演化和相变问题;与此同时,相场法既有水平集、VOF等方法的捕捉大变形界面的能力,又无需涉及界面的重构过程,相界面的位置捕捉以及厚度大小的控制均可通过一个对流扩散的控制方程来实现,基于该方法追踪得到的两相界面较光滑且连续性好。因此,相场法是一种可以有效模拟液滴撞击固壁问题的方法。
笔者以格子Boltzmann方法为基础,基于相场理论并借助Cahn-Hilliard方程,建立了非牛顿幂律流体与牛顿流体的两相流模型,模拟了假塑性流体在不同幂律指数n(0.5≤n≤1.0)和韦伯数We(5≤We≤45)下液滴撞击壁面的铺展,该模拟结果对于通过改变流变特性控制液滴的沉积提供了参考。
1 理论 1.1 幂律(Power-law)模型对于不可压缩流体,切应力张量τ与变形速度张量
| $ \eta (\dot \gamma ) = {\eta _0}|\dot \gamma |n - 1, n > 0, $ | (1) |
式中:η0为渐进黏度;
| $ \left\{ \begin{array}{l} \frac{{\partial C}}{{\partial t}} + {\mathit{\boldsymbol{u}}} \cdot \nabla C = M{\nabla ^2}{\mu _{\rm{c}}}, \\ {\mu _{\rm{c}}} = {C^3} - 1.5{C^2} + 0.5C - {\varepsilon ^2}{\nabla ^2}C, \end{array} \right. $ | (2) |
式中:C表示体积分数,u是速度。移动系数M=M0|C(1-C)|,μc是化学势。界面的厚度取为
| $ \nabla \cdot {\mathit{\boldsymbol{u}}} = 0, $ | (3) |
| $ \rho (\frac{{\partial {\mathit{\boldsymbol{u}}}}}{{\partial t}} + {\mathit{\boldsymbol{u}}} \cdot \nabla {\mathit{\boldsymbol{u}}}) = - \nabla p + \nabla \cdot [\eta (\nabla {\mathit{\boldsymbol{u}}} + \nabla {{\mathit{\boldsymbol{u}}}^{\rm{T}}})] + {{\mathit{\boldsymbol{F}}}_{\rm{s}}}, $ | (4) |
式中:密度ρ=Cρ1+(1-C)ρ2,黏度η=Cη1+(1-C)η2,下标1和2代表不同的组分。p表示压力,
下面采用格子Boltzmann方法[25-27]来求解上述两相流流动的控制方程(3)和(4)。对于D2Q9模型,为了得到压力和速度,引入了一个变量
| $ f_\alpha ^{{\rm{eq}}} = \rho {\Gamma _\alpha }({\mathit{\boldsymbol{u}}}) = \rho {\omega _\alpha }[1 + \frac{{{{\mathit{\boldsymbol{e}}}_\alpha } \cdot {\mathit{\boldsymbol{u}}}}}{{c_{\rm{s}}^{\rm{2}}}} + \frac{{{{({{\mathit{\boldsymbol{e}}}_\alpha } \cdot {\mathit{\boldsymbol{u}}})}^2}}}{{2c_{\rm{s}}^4}} - \frac{{{\mathit{\boldsymbol{u}}} \cdot {\mathit{\boldsymbol{u}}}}}{{2c_{\rm{s}}^{\rm{2}}}}], $ | (5) |
式中eα为α方向的微观粒子的速度; ωα是相对应的权系数。马赫数Ma=|u|/cs,在低马赫数的情况下,宏观的水动力方程可由式(6)gα的离散Boltzmann方程恢复得到:
| $ \frac{{\partial {g_\alpha }}}{{\partial t}} + {e_\alpha } \cdot \nabla {g_\alpha } = - {{\mathit{\pmb{\Lambda}}} _{\alpha \beta }}({g_\beta } - g_\beta ^{{\rm{eq}}}) + ({{\mathit{\boldsymbol{e}}}_\alpha } - {\mathit{\boldsymbol{u}}}) \cdot [\nabla \rho c_{\rm{s}}^{\rm{2}}({\Gamma _\alpha } - {\Gamma _\alpha }(0)) + {\mathit{\boldsymbol{F}}}{\Gamma _\alpha }], $ | (6) |
式中采用的是多松弛时间模型。Λαβ为粒子碰撞矩阵,分子间作用力为
| $ {{\bar g}_\alpha }({\mathit{\boldsymbol{x}}} + {{\mathit{\boldsymbol{e}}}_\alpha }\delta t, t + \delta t) - {{\bar g}_\alpha }({\mathit{\boldsymbol{x}}}, t) = - ({S_{\alpha \beta }} + 2{I_{\alpha \beta }})({{\bar g}_\beta } - \bar g_\beta ^{{\rm{eq}}}) + \\\;\delta t({{\mathit{\boldsymbol{e}}}_\alpha } - {\mathit{\boldsymbol{u}}}) \cdot [\nabla \rho c_{\rm{s}}^{\rm{2}}({\Gamma _\alpha } - {\Gamma _\alpha }(0)) + {{\mathit{\boldsymbol{F}}}_{\rm{s}}}{\Gamma _\alpha }], $ | (7) |
式中粒子碰撞矩阵Sαβ+2Iαβ=
这样,宏观速度和压力可以通过
| $ \begin{array}{l} p = \sum\limits_{\alpha = 0}^8 {{{\bar g}_\alpha }} + \frac{{\delta t}}{2}{\mathit{\boldsymbol{u}}} \cdot \nabla \rho c_{\rm{s}}^{\rm{2}}, \\ {\mathit{\boldsymbol{u}}} = \frac{1}{{\rho c_{\rm{s}}^{\rm{2}}}}(\sum\limits_{\alpha = 0}^8 {{{\bar g}_\alpha }} {{\mathit{\boldsymbol{e}}}_\alpha } + \frac{{\delta t}}{2}{{\mathit{\boldsymbol{F}}}_{\rm{s}}})。\end{array} $ | (8) |
由于非牛顿流体的黏度与变形速度张量
为了验证格子Boltzmann模型模拟非牛顿幂律流体的能力和程序的可靠性,将两相流程序中的体积分数C全部设置为1,模拟了单相幂律流体在幂律指数n=0.5时的方腔流流动。其中,Re=ρU2-nLn/η0= 100, U=0.05, 计算域为[0, 200]×[0, 200]。将本文的数值结果与Neofytou的文献结果[30]相比较,从图 1中看出,两者吻合。

|
图 1 幂律流体方腔流在竖直中心线上u和水平中心线上v的分布和文献解的对比 Figure 1 Comparision between our results and Neofytou's results for power-law flow: u-velocity profiles along vertical centerline and v-velocity profiles along horizontal centerline |
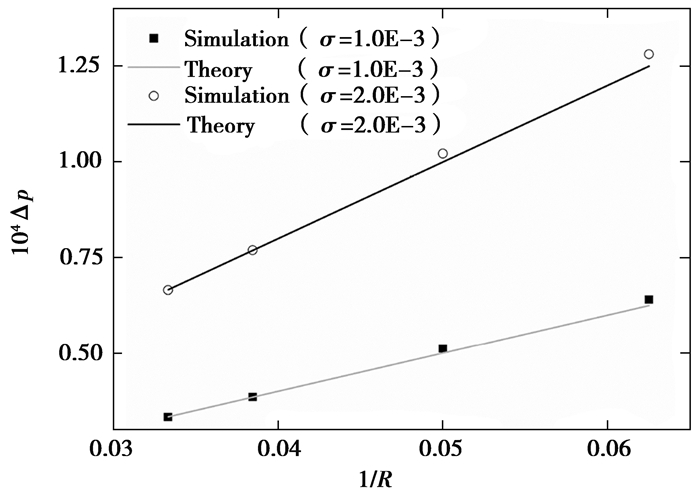
验证了基于相场法的格子Boltzmann模型模拟幂律流体、牛顿流体两相流的能力和程序的可靠性。根据Laplace定律,液滴放置在母液中,在未受其他外力的作用下,液滴达到稳定状态时,液滴内外压差与其半径以及表面张力系数存在一定的关系。对二维情况有:Δp=pin-pout=σ/R,其中R为液滴半径,pin是液滴的压力,pout是液滴外母液的压力。初始时刻液滴位于计算区域中心,计算为[0, 6R]×[0, 6R],四边均为周期性边界条件。参数n=0.5,ρ1=1.0,ρ2=1.0,η1=η2=0.1。下标1表示液滴,下标2表示液滴周围的液体,以下所涉及算例的下标含义均是如此。图 2中,在2种表面张力参数σ=1.0 E-3及σ=2.0 E-3下,数值解和理论解的相对误差均在2.53 %以内,且随着半径R的增大,相对误差随之减小。最大伪势速度在液滴界面附近,大小为10-7量级。
|
图 2 幂律液滴达到稳态时Δp和1/R的关系与理论解的对比 Figure 2 Comparision between the numerical and theoretical solution of the relationship of Δp and 1/R when power law drops reach steady state |
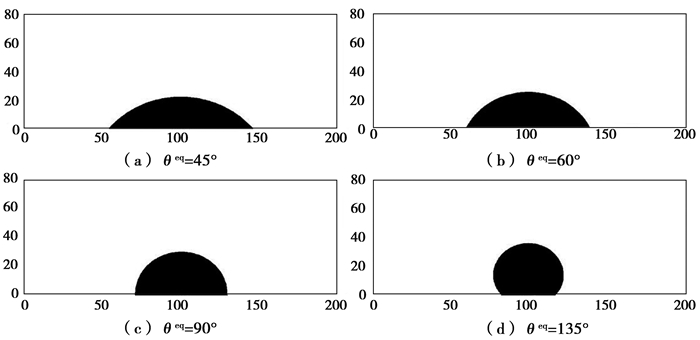
验证了在引入考虑接触角影响的边界条件后的两相流模型模拟液滴动态接触的能力和程序的正确性。首先,考察了固壁上液滴达到平衡态时,静态接触角是否跟设置值一致。初始时刻,在固壁上放置一个半圆形液滴,由于表面张力的作用,液滴会变形,直至达到平衡状态。计算域[0, 200]×[0, 80],上下边界为完全反弹边界条件,左右边界施加周期性边界条件。液滴半径R=30,其他参数为n=0.5,σ=10-3,η1=0.01,η2=0.001和ρ1=ρ2=0.1。平衡态接触角是固壁附近处界面两层网格线性拟合的直线以顺时针旋转到壁面的夹角。图 3为液滴在不同静态接触角下达到平衡状态后的形状。从表 1可以看出,数值模拟得到的平衡态接触角与理论值的相对误差的最大绝对值为3.3 %(即静态接触角为45°),稳态时的液滴面积与初始液滴面积的相对误差的最大绝对值为2.98 %。
|
图 3 幂律液滴在不同静态接触角的稳态 Figure 3 Stable configurations of power law droplet at different equilibrium contact angles |
| 表 1 不同静态接触角下的各参数相对误差 Table 1 The relative error for different equilibrium contact angles |
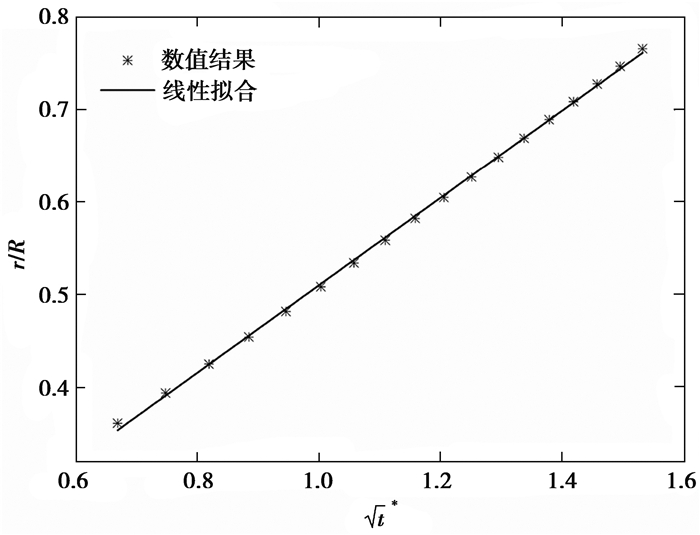
考察了移动接触线的变化规律。初始时刻,液滴刚接触固壁,在表面张力作用下液滴会变形,接触线也随之变化。液滴半径R=20,设液滴与壁面上的接触线半径为r,则量纲一的铺展长度为r/R,时间采用
|
图 4 量纲一的铺展长度r/R和量纲一的时间t*=t/ |
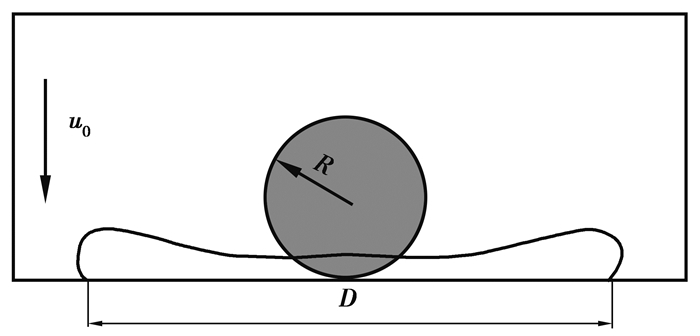
图 5为单液滴以一定速度u0撞击固壁,D是液滴的铺展长度,R为液滴半径。以下算例中均不考虑重力效应, 且黏度比均为10。上下两边施加完全反弹边界条件,左右两边界为周期性边界。计算域[0, 200]×[0, 200],其他参数R=20,θeq=90°,σ=10-3,η1=0.01,η2=0.001,ρ1=ρ2=0.1。韦伯数We=ρ1u02R/σ,奥内佐格数
|
图 5 液滴撞击壁面的示意图 Figure 5 The sketch of droplet impact on a solid surface |
首先,模拟了在We=45及Oh=0.158时幂律指数n=0.5~1.0,液滴撞击壁面上的铺展。从图 6可知,对于幂律指数n≥0.7的液滴,撞击壁面后大致可分为3个阶段:快速铺展、回缩、稳定。在快速铺展阶段,液滴迅速地铺展到最大长度,幂律指数越大,最大铺展长度越大;在回缩阶段,液滴开始由最大铺展长度向中心收缩,幂律指数越大,回缩的速度越大;最后,液滴回缩至其铺展长度达到一个恒定值,与回缩阶段相对应,液滴回缩的速度越快,越能更快达到稳定状态。对于幂律指数n=0.5的液滴,铺展过程中无回缩现象,液滴的铺展速度由初始最大值逐渐减小,当液滴铺展到最大铺展长度时,液滴即到达稳定状态。

|
图 6 不同幂律指数n下铺展长度D随时间变化的关系 Figure 6 Spreading length D as a function of time for different power exponents n |
从整体上看,对于幂律指数n≤1.0的液滴,最大铺展长度随着幂律指数n的减小而减小,且幂律指数越大,液滴越趋近于牛顿流体;幂律指数越小,液滴的非牛顿特性就越明显,表现为回缩现象不明显,达到稳态所需要的时间也变长。这些结果表明,在碰撞速度相同下,与牛顿流体相比,假塑性流体更易黏附在壁面,且n越小,流体非牛顿特性越强。
图 7为选取上述算例中幂律指数n=0.5以及n=1.0(牛顿流体)时液滴撞击壁面后形态的变化。对于牛顿液滴,初期在惯性的作用下迅速铺展,液滴两端凸起直至铺展到最大铺展长度,然后在以表面张力为主导的作用下,液滴向中心收缩,当液滴的动能全部转化为内能时,液滴最终以半圆的形态静止在壁面上。相对于牛顿流体,幂律指数n=0.5的假塑性液滴在撞击壁面后,黏性迅速增大导致液滴的铺展、变形受到抑制,液滴的拓扑结构没有发生较大变化,仍然大致呈一个圆形;铺展后期,液滴的能量耗散速度变慢,经过较长一段时间后,液滴铺展到最大铺展长度时,并以半圆形的形态静止在壁面上,液滴达到稳态。上述分析表明,相对于牛顿液滴,假塑性流体的液滴撞击壁面后的形态更稳定。
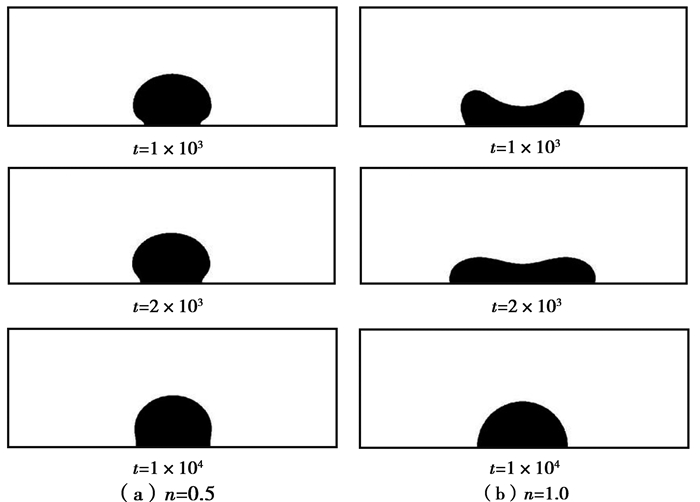
|
图 7 幂律液滴在不同时间的形态 Figure 7 Droplets configurations at different time |
然后,模拟了在Oh=0.158下幂律指数分别为n=0.5以及n=1.0时,韦伯数We=5~45液滴撞击壁面上的铺展。从图 8中可以看出,对于n=0.5的假塑性幂律流体,液滴铺展到最大铺展长度时液滴即到达稳态,稳态跟韦伯数无关。当韦伯数等于5和20时,液滴均相对较缓慢地到达稳态,到达稳态的所需时间均较长;当韦伯数继续增大至45时,液滴铺展到最大铺展长度所需要的时间急剧减小。对于n=1.0的牛顿流体,液滴的稳态也与韦伯数无关,且随着速度的增大,液滴到达最大铺展长度的所需时间变长,最大铺展长度也增大;液滴到达稳态的时间随速度增加而增长但不显著。此外,假塑性幂律流体和牛顿流体在稳态时的铺展长度均相同,碰撞速度相等时前者到达稳态的时间要比后者长,随着速度的增大,这种差异会急剧减小,例如,在We=45时假塑性液滴和牛顿液滴到达稳态的时间已基本上相同,且稳定后的铺展长度均为54.5格子长度。以上结果均表明,在高碰撞速度下,与牛顿流体相比,假塑性流体会抑制液滴的铺展,更有利于液滴在壁面上的沉积。
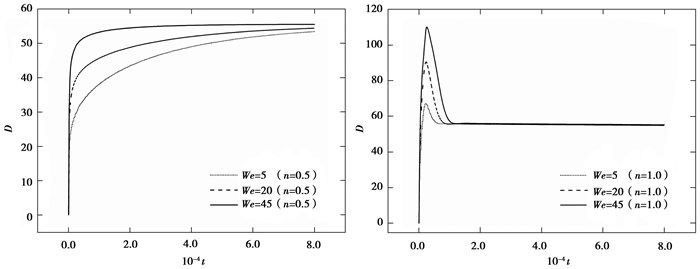
|
图 8 不同韦伯数We下幂律指数n=0.5以及1.0液滴铺展长度随时间的变化关系 Figure 8 Spreading length as a function of time at different We when the power exponent n=0.5 and n=1.0 |
在两相流格子Boltzmann模型中引入流体的非牛顿特性,建立了基于相场法的牛顿流体、非牛顿幂律流体两相流格子Boltzmann模型,并在不考虑重力作用的条件下,对不同幂律指数和不同韦伯数下液滴撞击壁面的铺展进行了数值模拟。当n<1时幂律流体的非牛顿特性会抑制液滴的铺展,且n越小,幂律流体表现的非牛顿特性就越强;韦伯数We越大,液滴到达稳定的速度越快。这些结果表明,假塑性流体的非牛顿特性有利于液滴在壁面上的沉积。
| [1] |
Son Y, Kim C. Spreading of inkjet droplet of non-Newtonian fluid on solid surface with controlled contact angle at low Weber and Reynolds numbers[J]. Journal of Non-Newtonian Fluid Mechanics, 2009, 162(1/2/3): 78-87. |
| [2] |
Bergeron V, Bonn D, Martin J Y, et al. Controlling droplet deposition with polymer additives[J]. Nature, 2000, 405(6788): 772-775. DOI:10.1038/35015525 |
| [3] |
Dressler D M, Li L K B, Green S I, et al. Newtonian and non-Newtonian spray interaction with a high-speed moving surface[J]. Atomization & Sprays, 2009, 19(1): 19-39. |
| [4] |
Healy W M, Hartley J G, Abdel-Khalik S I. On the validity of the adiabatic spreading assumption in droplet impact cooling[J]. International Journal of Heat & Mass Transfer, 2001, 44(20): 3869-3881. |
| [5] |
Yarin A L. Drop impact dynamics:Splashing, spreading, receding, bouncing…[J]. Annual Review of Fluid Mechanics, 2006, 38(1): 159-192. |
| [6] |
Bertola V. Some applications of controlled drop deposition on solid surfaces[J]. Recent Patents on Mechanical Engineering, 2008, 1(3): 167-174. DOI:10.2174/2212797610801030167 |
| [7] |
Jung S, Hoath S D, Hutchings I M. The role of viscoelasticity in drop impact and spreading for inkjet printing of polymer solution on a wettable surface[J]. Microfluidics and Nanofluidics, 2013, 14(1/2): 163-169. |
| [8] |
Bertola V. Dynamic wetting of dilute polymer solutions:The case of impacting droplets[J]. Advances in Colloid & Interface Science, 2013, 193/194: 1-11. |
| [9] |
Huh H K, Jung S, Seo K W, et al. Role of polymer concentration and molecular weight on the rebounding behaviors of polymer solution droplet impacting on hydrophobic surfaces[J]. Microfluidics and Nanofluidics, 2015, 18(5/6): 1221-1232. |
| [10] |
Wang Y L, Minh D Q, Amberg G. Dynamic wetting of viscoelastic droplets[J]. Physical Review E, 2015, 92(4). |
| [11] |
Izbassarov D, Muradoglu M. Effects of viscoelasticity on drop impact and spreading on a solid surface[J]. Physical Review Fluids, 2016, 1(2): 023302. DOI:10.1103/PhysRevFluids.1.023302 |
| [12] |
Liang Z P, Wang X D, Lee D J, et al. Spreading dynamics of power-law fluid droplets[J]. Journal of Physics:Condensed Matter, 2009, 21(46): 464117. DOI:10.1088/0953-8984/21/46/464117 |
| [13] |
Liang Z P, Wang X D, Duan Y Y, et al. Energy-based model for capillary spreading of power-law liquids on a horizontal plane[J]. Colloids & Surfaces A Physicochemical & Engineering Aspects, 2012, 403(11): 155-163. |
| [14] |
Wang Y, Zhu K Q. A study of dynamic contact angles of shear-thickening power-law fluids[J]. Physics of Fluids, 2014, 26(5): 739-423. |
| [15] |
闵琪, 段远源, 王晓东, 等. 非牛顿流体液滴铺展过程的格子Boltzmann模拟[J]. 热科学与技术, 2013, 12(4): 335-341. Min Qi, DUAN Yuanyuan, WANG Xiaodong, et al. Lattice Boltzmann simulation of droplet spreading of non-Newtonian fluid[J]. Thermal Science and Technology, 2013, 12(4): 335-341. (in Chinese) |
| [16] |
Iwamatsu M. Spreading law of non-Newtonian power-law liquids on a spherical substrate by an energy-balance approach[J]. Physical Review E, 2017, 96(4): 049902. |
| [17] |
Aharonov E, Rothman D H. Non-Newtonian flow (through porous media):A lattice-Boltzmann method[J]. Geophysical Research Letters, 1993, 20(8): 679-682. DOI:10.1029/93GL00473 |
| [18] |
Gabbanelli S, Drazer G, Koplik J. Lattice Boltzmann method for non-Newtonian (power-law) fluids[J]. Physical Review E Statistical Nonlinear & Soft Matter Physics, 2005, 72(4): 046312. |
| [19] |
Sullivan S P, Gladden L F, Johns M L. Simulation of power-law fluid flow through porous media using lattice Boltzmann techniques[J]. Journal of Non-Newtonian Fluid Mechanics, 2006, 133(2/3): 91-98. |
| [20] |
Yoshino M, Hotta Y, Hirozane T, et al. A numerical method for incompressible non-Newtonian fluid flows based on the lattice Boltzmann method[J]. Journal of Non-Newtonian Fluid Mechanics, 2007, 147(1/2): 69-78. |
| [21] |
Wang C H, Ho J R. A lattice Boltzmann approach for the non-Newtonian effect in the blood flow[J]. Computers & Mathematics with Applications, 2011, 62(1): 75-86. |
| [22] |
刘儒勋, 舒其望. 计算流体力学的若干新方法[M]. 北京: 科学出版社, 2003. LIU Ruxun, SHU Qiwang. Several new methods of computational fluid mechanics[M]. Beijing: Science Press, 2003. |
| [23] |
Takada N, Tomiyama A. A numerical method for two-phase flow based on a phase-field model[J]. JSME International Journal Series B, 2006, 49(3): 636-644. DOI:10.1299/jsmeb.49.636 |
| [24] |
Boyd J, Buick J, Green S. A second-order accurate lattice Boltzmann non-Newtonian flow model[J]. Journal of Physics A:Mathmatical and General, 2006, 39(46): 14241-14247. DOI:10.1088/0305-4470/39/46/001 |
| [25] |
Liu H H, Valocchi A J, Zhang Y H, et al. Phase-field-based lattice Boltzmann finite-difference model for simulating thermocapillary flows[J]. Physical Review E Statistical Nonlinear & Soft Matter Physics, 2013, 87: 013010. |
| [26] |
Qiao L, Zeng Z, Xie H Q, et al. Modeling thermocapillary migration of interfacial droplets by a hybrid lattice Boltzmann finite difference scheme[J]. Applied Thermal Engineering, 2018, 131: 910-919. DOI:10.1016/j.applthermaleng.2017.12.034 |
| [27] |
Fakhari Kahaki A. Phase-field modeling of multiphase flows using the lattice Boltzmann method with adaptive mesh refinement[D]. Philadelphia: University of Pennsylvania, 2015.
|
| [28] |
Ding H, Spelt P D. Wetting condition in diffuse interface simulations of contact line motion[J]. Physical Review E Statistical Nonlinear & Soft Matter Physics, 2007, 75(4): 046708. |
| [29] |
Chai Z H, Shi B C, Lin Z. Simulating high Reynolds number flow in two-dimensional lid-driven cavity by multi-relaxation-time lattice Boltzmann method[J]. Chinese Physics. B, 2006, 15(8): 1855-1863. DOI:10.1088/1009-1963/15/8/038 |
| [30] |
Neofytou P. A 3rd order upwind finite volume method for generalised Newtonian fluid flows[J]. Advances in Engineering Software, 2005, 36(10): 664-680. DOI:10.1016/j.advengsoft.2005.03.011 |
| [31] |
Winkels K G, Weijs J H, Eddi A, et al. Initial spreading of low-viscosity drops on partially wetting surfaces[J]. Physical Review E, 2012, 85(5): 055301-055301. DOI:10.1103/PhysRevE.85.055301 |
 2018, Vol. 41
2018, Vol. 41


