由于信杂比(SCR，signal-to-clutter ratio)低，目标多普勒小，强杂波背景下静止/慢速小目标(如树林、草丛中隐藏的装甲目标，近海偷渡船只，低空飞行无人机等“低小慢”目标)的检测问题，始终是雷达目标检测领域的难点问题^[1]。

极化可提高雷达的目标检测能力，对于雷达极化问题的研究始于1946年，当时美国俄亥俄州立大学天线实验室的Sinclair指出，一个雷达目标可以视作一个“极化变换器”，他用一个2×2相干散射矩阵来描述一个相干雷达目标的散射特性，即Sinclair极化散射矩阵。以此为标志，开始了雷达极化信息处理领域的最初研究。1989年，美国麻省理工学院林肯实验室的Novak提出了极化匹配滤波器(PMF, polarimetric matched filter)、极化白化滤波器(PWF, polarimetric whiten filter)、张成检测器(span detector)和最优极化检测器(OPD, optimal polarization detector)^[2]，开启了极化雷达目标检测理论的最初研究。但是，以OPD检测器为代表的上述极化检测器需要目标和杂波极化二阶矩的先验知识，而这种假设在实际应用中难以成立，为此研究人员寻求利用辅助通道数据来估计待检测单元杂波协方差矩阵以用于检测器设计^[3-4]，这包括文献[3]提出的极化广义似然比检测器和文献[4]提出的极化空时自适应检测器等。但上述2种方法假定杂波服从高斯分布，当杂波偏离高斯分布时，它们的检测性能会明显下降，因此需研究非高斯杂波条件下的检测方法。然而，非高斯杂波增加了设计有效检测器的难度。比如，文献[5]提出的相干极化自适应检验统计量仅在2个极化通道的条件下有闭合形式表达式，文献[6-7]提出的检测器对杂波协方差矩阵不具有恒虚警(CFAR, constant false alarm rate)性质。但随着雷达分辨能力的提高，杂波表现出显著的非高斯性，造成基于辅助数据估计而设计的极化检测器的实际检测性能并不理想^[8-9]。因此，亟需发展非高斯杂波条件下的极化检测算法。

近来，研究发现，将传统的收发极化由固定式变为自适应方式可显著提高极化雷达对目标的探测能力。比如，文献[10]以SCR最大为准则，提出了一种雷达波形极化优化方法，利用美国陆军实验室的装甲目标微波暗室测量数据的实验，证实波形极化优化对目标检测能力提升达4 dB。文献[11]采用矢量传感器天线作为极化雷达发射极化组件，提出了一种基于矢量传感器发射极化优化的检测算法，证实了相比于固定发射极化，发射极化优化雷达的目标检测性能更高。此外，文献[12]和文献[13]分别研究了高斯和部分高斯杂波背景下基于极化雷达波性优化设计的检测器设计问题，文献[14]则研究了非高斯杂波背景下，以提高输出信杂噪比为准则，极化雷达发射波形和接收滤波器组联合优化设计方法。上述研究结果表明，波形优化设计可显著改善极化雷达输出信杂噪比。

研究立足于解决全极化雷达的目标检测问题，利用收发极化联合优化，设计非高斯杂波背景下“低小慢”目标的极化检测器。在数学建模环节，描述了一种收发极化可变的极化雷达测量模型。在检测器设计环节，基于广义似然比方法(GLRT, generalized likelihood ratio test)设计了一种非高斯杂波背景下“低小慢”目标的极化检测器，并从理论上推导出了该检测器性能的解析表达式。在性能分析环节，采用蒙特卡洛仿真方法证实了算法具有良好的抗杂波非高斯性能，相比传统方法的性能优势。比较了收发极化联合优化雷达、发射极化优化雷达和收发极化方式固定雷达间的检测性能差异, 结果证实, 收发极化联合优化雷达的检测性能明显优于其他2种极化雷达。

1 问题模型

首先，系统模型方面, 全极化雷达发射信号可表示为

$ s\left( t \right) = \mathit{\boldsymbol{\xi }}s\left( t \right) = {\left[ {{\xi _{\rm{H}}},{\xi _{\rm{V}}}} \right]^{\rm{T}}}s\left( t \right), $

(1)

式中: s(t)为发射信号的复包络; ξ为发射天线极化矢量，且有‖ξ‖=1。

雷达接收天线极化矢量为η=[η_H, η_V]^T(‖η‖=1)，雷达回波信号不仅包含目标回波，还包含环境杂波以及接收机噪声分量。于是，全极化雷达回波信号可表示为

$ y\left( t \right) = \frac{g}{{{r^2}}}{\mathit{\boldsymbol{\eta }}^{\rm{T}}}\left( {\mathit{\boldsymbol{T}} + \mathit{\boldsymbol{C}}} \right)\mathit{\boldsymbol{\xi }}s\left( {t - \tau } \right) + n\left( t \right), $

(2)

式中：n(t)为噪声；τ为信号自发射到再次返回接收的延迟时间；r为目标到雷达的距离；g为与载频、天线增益等因素有关的常系数；T和C分别为目标和杂波的极化散射矩阵，具体形式分别为

$ \mathit{\boldsymbol{T}} = \left[ {\begin{array}{*{20}{c}} {{T_{{\rm{HH}}}}}&{{T_{{\rm{HV}}}}}\\ {{T_{{\rm{VH}}}}}&{{T_{{\rm{VV}}}}} \end{array}} \right], $

(3)

和

$ \mathit{\boldsymbol{C}} = \left[ \begin{array}{l} {C_{{\rm{HH}}}}{C_{{\rm{HV}}}}\\ {C_{{\rm{VH}}}}{C_{{\rm{VV}}}} \end{array} \right]。$

(4)

对式(2)进行数字化抽样和匹配滤波，再进行归一化处理将系数$\frac{g}{{{r}^{2}}}$并入噪声项之后，雷达接收输出为

$ y = {\mathit{\boldsymbol{\eta }}^{\rm{T}}}\left( {\mathit{\boldsymbol{T}} + \mathit{\boldsymbol{C}}} \right)\mathit{\boldsymbol{\xi }} + n。$

(5)

引入系统响应矢量

$ \mathit{\boldsymbol{h}} = \left[ {{\eta _{\rm{H}}}{\xi _{\rm{H}}},{\eta _{\rm{H}}}{\xi _{\rm{V}}},{\eta _{\rm{V}}}{\xi _{\rm{H}}},{\eta _{\rm{V}}}{\xi _{\rm{V}}}} \right], $

(6)

并将目标极化散射矩阵T和杂波极化散射矩阵C改写成矢量形式，即

$ {\mathit{\boldsymbol{x}}_t} = {\left[ {{T_{{\rm{HH}}}},{T_{{\rm{HV}}}},{T_{{\rm{VH}}}},{T_{{\rm{VV}}}}} \right]^{\rm{T}}} $

(7)

和

$ {\mathit{\boldsymbol{x}}_c} = {\left[ {{C_{{\rm{HH}}}},{C_{{\rm{HV}}}},{C_{{\rm{VH}}}},{C_{{\rm{VV}}}}} \right]^{\rm{T}}}, $

(8)

则可将式(5)改写成如下线性观测模型

$ y = \mathit{\boldsymbol{h}}{\mathit{\boldsymbol{x}}_t} + \mathit{\boldsymbol{h}}{\mathit{\boldsymbol{x}}_c} + n。$

(9)

假定相干检测在一次雷达驻留期间的观测样本数为M，有测量模型为

$ y\left( m \right) = h\left( m \right){x_t}\left( m \right) + h\left( m \right){x_c}\left( m \right) + n\left( m \right),m = 1,2, \cdots ,M。$

(10)

目标散射特性方面，由于研究对象为“低小慢”目标，假定雷达驻留期内目标的极化散射系数不变，即x_t为一确定矢量。不同于目标散射特性，距离单元内的杂波为一系列非相干散射体回波的和，故考虑杂波x_c为以∑为协方差矩阵的零均值复高斯随机矢量。此外，将噪声n看作方差为σ²的零均值复高斯随机变量，而杂波和噪声统计独立。M个观测样本满足如下统计分布形式，即

$ y\left( m \right) \sim CN\left( {\mathit{\boldsymbol{h}}{\mathit{\boldsymbol{x}}_t},\mathit{\boldsymbol{h}}\sum {{\mathit{\boldsymbol{h}}^H} + {\sigma ^2}} } \right),m = 1,2, \cdots ,M。$

(11)

式中：CN(·)表示复高斯分布；(·)^H表示共轭转置。需要指出的是，在式(11)中，雷达发射接收极化h通常是已知的，且系统噪声功率σ²也可在雷达实际工作前事先测得，因此，未知参量只剩下目标散射矢量x_t和杂波协方差矩阵∑。

2 极化检测器设计 2.1 检验统计表达式

根据上节的分析可知，目标散射矢量x_t和杂波协方差矩阵∑均为未知参量，也就是说，待解决的检测问题具有如下假设检验形式

$ \left\{ \begin{array}{l} {H_0}:{\mathit{\boldsymbol{x}}_t} = 0,\Sigma ,\\ {H_1}:{\mathit{\boldsymbol{x}}_t} \ne 0,\Sigma 。\end{array} \right. $

(12)

由纽曼-皮尔逊假设检验准则可知，对上述检测问题应采用GLRT方法。若判H₁成立，则有

$ \ln {L_{{\rm{GLR}}}} = \ln {f_1}\left( {{y_1}, \cdots ,{y_M};{{\mathit{\boldsymbol{\hat x}}}_t},{{\hat \Sigma }_1}} \right) - \ln {f_0}\left( {{y_1}, \cdots ,{y_M};{{\hat \Sigma }_0}} \right) > \ln \gamma , $

(13)

式中：f₀和f₁分别为H₀和H₁条件下的概率密度函数；${{{\hat{\Sigma }}}_{0}}$和${{{\hat{\Sigma }}}_{1}}$分别为H₀和H₁条件下∑的最大似然估计(MLE, maximum likelihood estimation)；${{{\mathit{\boldsymbol{\hat{x}}}}}_{t}}$为x_t在H₁条件下的MLE，γ为检测门限。为叙述方便，下文简记lnf₀(y₁, …, y_M; ${{{\hat{\Sigma }}}_{0}}$)为lnf₀(${{{\hat{\Sigma }}}_{0}}$)，lnf₁(y₁, …, y_M; ${{{\mathit{\boldsymbol{\hat{x}}}}}_{t}}$, ${{{\hat{\Sigma }}}_{1}}$)为lnf₁(${{{\mathit{\boldsymbol{\hat{x}}}}}_{t}}$, ${{{\hat{\Sigma }}}_{1}}$)。

在H₀假设检验条件下，有${{{\mathit{\boldsymbol{\hat{x}}}}}_{t}}$=0，相应的似然函数为

$ \ln {f_0}\left( \Sigma \right) = - M\left[ {\ln \pi + \ln \left| \mathit{\Psi } \right| + {\mathit{\Psi }^{ - 1}}{S_0}} \right], $

(14)

式中：|·|为取绝对值操作；Ψ=h∑h^H+σ²为观测数据的方差真值；S₀为样本方差且满足

$ {S_0} = \frac{1}{M}\sum\limits_{m = 1}^M {{\mathit{\boldsymbol{y}}_m}\mathit{\boldsymbol{y}}_m^ * } , $

(15)

其中(·)^*指(·)的共轭。在经一系列数学推导后可得H₀条件下∑的MLE为(具体推导过程可套用文献[16])

$ {{\hat \Sigma }_0} = {\mathit{\boldsymbol{h}}^ + }{S_0}{\mathit{\boldsymbol{h}}^{ + {\rm{H}}}} - {\sigma ^2}{\left( {{\mathit{\boldsymbol{h}}^{\rm{H}}}\mathit{\boldsymbol{h}}} \right)^{ - 1}}, $

(16)

其中h⁺=(h^Hh)^-1h^H为h的伪逆矢量。于是，H₀条件下基于∑最大似然估计的对数似然函数为

$ \ln {f_0}\left( {{{\hat \Sigma }_0}} \right) = - M\left[ {4 + \ln \pi - 3\ln \sigma + \ln \left| {{\mathit{\boldsymbol{h}}^{\rm{H}}}\mathit{\boldsymbol{h}}} \right| + {\sigma ^{ - 2}}{\mathit{\Pi }^ \bot }{S_0} + \ln \left| {{\mathit{\boldsymbol{h}}^ + }{S_0}{\mathit{\boldsymbol{h}}^{ + {\rm{H}}}}} \right|} \right], $

(17)

其中Π^⊥=1-hh⁺。

H₁假设检验条件下，名义对数似然函数为

$ \ln {f_1}\left( {\mathit{\boldsymbol{\mu }},\Sigma } \right) = - M\left[ {\ln \pi + \ln \left| \mathit{\Psi } \right| + {\mathit{\Psi }^{ - 1}}\mathit{\tilde \Psi }} \right], $

(18)

其中

$ \mathit{\tilde \Psi } = \frac{1}{M}\sum\limits_{m = 1}^M {\left( {{y_m} - \mathit{\boldsymbol{h}}{\mathit{\boldsymbol{x}}_t}} \right){{\left( {{y_m} - \mathit{\boldsymbol{h}}{\mathit{\boldsymbol{x}}_t}} \right)}^{\rm{H}}}} 。$

(19)

根据式(18)可得，H₁条件下x_t和∑的MLE分别为(具体推导过程可套用文献[11])

$ {{\mathit{\boldsymbol{\hat x}}}_t} = {\mathit{\boldsymbol{h}}^ + }\bar y $

(20)

和

$ {{\hat \Sigma }_1} = {\mathit{\boldsymbol{h}}^ + }{S_1}{\mathit{\boldsymbol{h}}^{ + {\rm{H}}}} - {\sigma ^2}{\left( {{\mathit{\boldsymbol{h}}^H}\mathit{\boldsymbol{h}}} \right)^{ - 1}}, $

(21)

式中：y为样本均值，满足$\bar{y}=\frac{1}{M}\sum\limits_{m=1}^{M}{{{y}_{m}}}$; S₁为样本方差，表达式为${{S}_{1}}=\frac{1}{M}\sum\limits_{m=1}^{M}{\left( {{y}_{m}}-\bar{y} \right)}{{\left( {{y}_{m}}-\bar{y} \right)}^{*}}$。于是，H₁假设检验条件下，基于参数x_t和∑最大似然估计的对数似然函数为

$ \ln {f_1}\left( {{{\mathit{\boldsymbol{\hat x}}}_t},{{\hat \Sigma }_1}} \right) = - M\left[ {4 + \ln \pi - 3\ln \sigma + \ln \left| {{\mathit{\boldsymbol{h}}^H}\mathit{\boldsymbol{h}}} \right| + {\sigma ^{ - 2}}{\mathit{\Pi }^ \bot }{S_0} + \ln \left| {{\mathit{\boldsymbol{h}}^ + }{S_1}{\mathit{\boldsymbol{h}}^{ + {\rm{H}}}}} \right|} \right]。$

(22)

此外，对于任意M×M维矩阵C，有

$ \ln \left| {{\mathit{\boldsymbol{h}}^ + }\mathit{\boldsymbol{C}}{\mathit{\boldsymbol{h}}^{ + {\rm{H}}}}} \right| = \ln \left( {{\mathit{\boldsymbol{h}}^H}\mathit{\boldsymbol{Ch}}} \right) - 2\ln {\mathit{\boldsymbol{h}}^{\rm{H}}}\mathit{\boldsymbol{h}}。$

(23)

将式(17)和式(22)代入式(13)得到检验统计量为

$ \ln {L_{{\rm{GLR}}}} = - M\left( {\ln \left| {{\mathit{\boldsymbol{h}}^{\rm{H}}}{S_1}\mathit{\boldsymbol{h}}} \right| - \ln \left| {{\mathit{\boldsymbol{h}}^{\rm{H}}}{S_0}\mathit{\boldsymbol{h}}} \right|} \right)。$

(24)

对于式(24)，有如下等式成立(具体推导过程可套用文献[11]附录B)

$ \left| {{\mathit{\boldsymbol{h}}^{\rm{H}}}{S_0}\mathit{\boldsymbol{h}}} \right| = \left| {{\mathit{\boldsymbol{h}}^{\rm{H}}}{S_1}\mathit{\boldsymbol{h}}} \right|\left[ {1 + {{\bar y}^ * }\mathit{\boldsymbol{h}}{{\left( {{\mathit{\boldsymbol{h}}^{\rm{H}}}{S_1}\mathit{\boldsymbol{h}}} \right)}^{ - 1}}{\mathit{\boldsymbol{h}}^{\rm{H}}}\bar y} \right]。$

(25)

所以式(24)等价于

$ \ln {L_{{\rm{GLR}}}} = M\ln \left[ {1 + {{\bar y}^ * }\mathit{\boldsymbol{h}}{{\left( {{\mathit{\boldsymbol{h}}^{\rm{H}}}{S_1}\mathit{\boldsymbol{h}}} \right)}^{ - 1}}{\mathit{\boldsymbol{h}}^{\rm{H}}}\bar y} \right]。$

(26)

观察式(26)不难看出，检验统计量lnL_GLR是参数项${{{\bar{y}}}^{*}}\mathit{\boldsymbol{h}}{{\left( {{\mathit{\boldsymbol{h}}}^{\rm{H}}}{{S}_{1}}\mathit{\boldsymbol{h}} \right)}^{-1}}{{\mathit{\boldsymbol{h}}}^{\rm{H}}}\bar{y}$的单调递增函数。于是可以将检验统计量进一步简化为

$ {T_{{\rm{GLR}}}} = {{\bar y}^ * }\mathit{\boldsymbol{h}}{\left( {{\mathit{\boldsymbol{h}}^{\rm{H}}}{S_1}\mathit{\boldsymbol{h}}} \right)^{ - 1}}{\mathit{\boldsymbol{h}}^{\rm{H}}}\bar y。$

(27)

至此，得到了文中方法检验统计量T_GLR的解析形式。

2.2 检测器的检测性能

这一节推导2.1节得到检测统计量的检测性能。令z_m=h^Hy_m(m=1, …, M)，则式可以等价写为

$ {T_{{\rm{GLR}}}} = {{\bar z}^ * }\mathit{\boldsymbol{S}}_z^{ - 1}\bar z, $

(28)

其中z和S_z分别为复高斯分布CN(h^Hhx_t, h^Hh∑h^Hh+σ²h^Hh)的样本均值矢量和协方差矩阵，满足

$ \left\{ \begin{array}{l} \mathit{\boldsymbol{\bar z = }}\frac{1}{M}\sum\limits_{m = 1}^M {{z_m}} ,\\ {\mathit{\boldsymbol{S}}_z} = \frac{1}{M}\sum\limits_{m = 1}^M {\left( {{z_m} - \bar z} \right){{\left( {{z_m} - \bar z} \right)}^{\rm{H}}}} 。\end{array} \right. $

(29)

利用文献[16]中推论5.2.1，得上述检测统计量满足如下分布

$ {T_{{\rm{GLR}}}}\frac{{M - 4}}{4} \sim \left\{ \begin{array}{l} {F_{8,2\left( {M - 4} \right)}},\\ {{F'}_{8,2\left( {M - 4} \right)}}\left( \lambda \right), \end{array} \right. $

(30)

式中：F_{v1, v2}表示双自由度为v₁和v₂的中心F分布；F′_{v1, v2}(λ)表示自由度为v₁和v₂的非中心F分布，非中心参数λ等于

$ \begin{array}{l} \lambda = 2M\mathit{\boldsymbol{x}}_t^{\rm{H}}{\mathit{\boldsymbol{h}}^{\rm{H}}}\mathit{\boldsymbol{h}}{\left[ {{\mathit{\boldsymbol{h}}^{\rm{H}}}\left( {\mathit{\boldsymbol{h}}\sum {{\mathit{\boldsymbol{h}}^H} + {\sigma ^2}} } \right)\mathit{\boldsymbol{h}}} \right]^{ - 1}}{\mathit{\boldsymbol{h}}^{\rm{H}}}\mathit{\boldsymbol{h}}{\mathit{\boldsymbol{x}}_t} = \\ 2M\mathit{\boldsymbol{x}}_t^{\rm{H}}{\left[ {{\mathit{\boldsymbol{h}}^ + }\left( {\mathit{\boldsymbol{h}}\sum {{\mathit{\boldsymbol{h}}^H} + {\sigma ^2}} } \right){\mathit{\boldsymbol{h}}^{ + {\rm{H}}}}} \right]^{ - 1}}{\mathit{\boldsymbol{x}}_t} = \\ 2M\left[ {\mathit{\boldsymbol{x}}_t^{\rm{H}}\sum {^{ - 1}{\mathit{\boldsymbol{x}}_t}} - \mathit{\boldsymbol{x}}_t^{\rm{H}}{{\left( {\Sigma + \frac{{\sum {{\mathit{\boldsymbol{h}}^H}\mathit{\boldsymbol{h}}} \Sigma }}{{{\sigma ^2}}}} \right)}^{ - 1}}{x_t}} \right]。\end{array} $

(31)

上述检测器检测性能解析表达式为

$ \left\{ \begin{array}{l} {p_{fa}} = {Q_{F8,2\left( {M - 4} \right)}}\left( {{\gamma _{{\rm{GLR}}}}} \right),\\ {p_d} = {Q_{F'8,2\left( {M - 4} \right)\left( \lambda \right)}}\left( {{\gamma _{{\rm{GLR}}}}} \right), \end{array} \right. $

(32)

式中：函数Q_{F8, 2(M-4)}(·)和Q_{F′8, 2(M-4)(λ)}(·)分别为F_{8, 2(M-4)}和F_{8, 2(M-4)}′(λ)的右尾概率函数；γ_GLR为判决门限。至此，得到了检验统计量T_GLR检测性能的解析形式。

值得注意的是，式(32)中虚警概率表达式并不依赖于杂波协方差矩阵和噪声结构，与发射信号亦不相关，也就是说，文中检测算法为CFAR检测器。

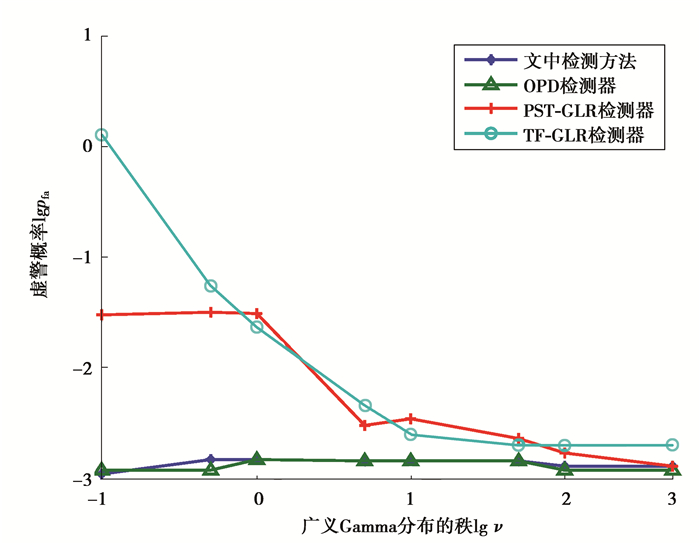
3 检测性能验证

针对杂波背景下的目标极化检测问题，研究人员提出了一系列检测算法。选取3种有代表性的极化检测器：OPD检测器、极化纹理无关广义似然比检测器(TF-GLR, texture-free GLR)^[5]和极化空时广义似然比检测器(PST-GLR, polarimetric space time GLR)^[4]，对比它们与文中方法的差异。需要说明的是，OPD检测器也即最优极化检测器，在已知目标散射矢量和杂波极化协方差矩阵先验信息的条件下，OPD检测器通常视为极化检测器的检测性能上限。TF-GLR检测器和PST-GLR检测器对目标的先验信息均未知，杂波方面，PST-GLR检测器利用辅助通道数据估计待检测单元杂波协方差矩阵，但它假定杂波满足高斯分布，故在杂波偏离高斯模型时，其检测性能可能会明显下降。TF-GLR检测器通过对辅助单元杂波数据的归一化处理移除纹理分量，故称“纹理无关”，但该检测器仅当极化通道数为2时有解析表达式，且当杂波协方差矩阵未知时，检测统计量的概率分布未知。

3.1 抗杂波非高斯性能对比及结果

文中算法的一个重要特点在于，检验统计量的结构与待检测单元数据相关，而与辅助单元数据无关，在非高斯杂波条件下能保持良好的检测性能。取杂波服从协方差矩阵为τ∑的复合高斯分布，其中τ为纹理分量，满足广义Gamma分布

$ f\left( \tau \right) = \frac{1}{{\mathit{\Gamma }\left( \nu \right)}}{\left( {\frac{\nu }{\delta }} \right)^\nu }{\tau ^{\nu - 1}}{{\rm{e}}^{ - \frac{\nu }{\delta }\tau }}, $

(33)

式中：Γ(·)为Gamma函数；δ为平均功率；ν为秩，ν的值越小，对应广义Gamma分布的非高斯性越强，相反，ν的值越大，广义Gamma分布的高斯性越强，当ν=+∞，杂波对应高斯分布。暂不考虑极化优化，假定雷达采用固定极化设计，即取ξ_H=ξ_V= $\frac{\sqrt{2}}{2}$，η_H=η_V=$\frac{\sqrt{2}}{2}$，另外，令δ=50，$\sum\nolimits_{0}{=\left[\begin{matrix} 1&0&0&0 \\ 0&0.1&0&0 \\ 0&0&0.1&0 \\ 0&0&0&1 \\ \end{matrix} \right]}$，待检测距离单元个数为N=1，保护单元个数2H=4，参考单元个数为2K=64，M=10，采用蒙特卡洛方法进行10⁵次仿真。如图 1所示给出几种检测器虚警概率随广义Gamma分布的秩ν的变化曲线。可以看出，随着杂波非高斯程度的增加(由右至左)，PST-GLR检测器和TF-GLR检测器的虚警概率明显提高，而文中算法、OPD检测器依然保持较低的虚警概率。这是由于，PST-GLR检测器和TF-GLR检测器均采用辅助单元数据估计待检测单元杂波协方差矩阵，当杂波的非高斯性越来越强时，杂波协方差矩阵的估计值偏离真实值越来越远，致使虚警概率越来越高。相反，OPD检测器已知杂波协方差的真实值，文中检测方法则利用待检测单元杂波数据估计其协方差矩阵，两者均不利用辅助单元杂波数据，所以即使杂波的非高斯性变得越来越强，但两者的虚警概率依然保持一个较低的水平。

3.2 检测性能对比及结果

杂波仿真过程和参数设置同3.1节，另外取ν=1。考虑2个目标：目标1，极化散射矢量为x_t⁽¹⁾=α[0.5, 0.1, 0.1, 0.4]^T和目标2，极化散射矢量为x_t⁽²⁾=α[0.1, 0.5, 0.5, 0.4]^T。其中α为控制SCR的因子。信杂比和杂噪比的定义如下：首先，目标功率为P_t=‖x_t‖²，其次，杂波功率为P_c=E[‖x_c‖²]=tr(∑)，于是有信杂比为${\rm{SCR}}=\frac{{{P}_{t}}}{{{P}_{c}}}$。

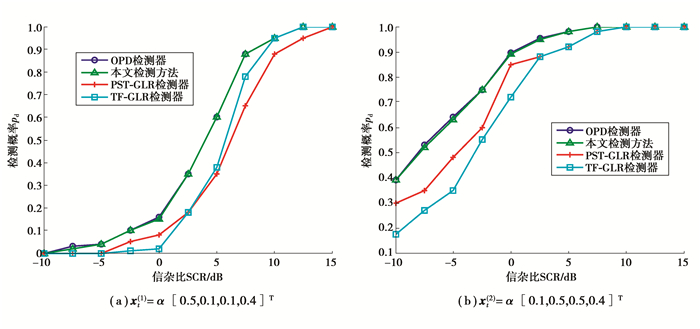
如图 2所示给出虚警概率p_fa=10^-3条件下，上述2种目标的检测概率p_d随信杂比SCR的变化曲线。可以看出，在非高斯杂波背景下(ν=1对应的杂波分布为非高斯杂波)，由于文中方法的抗杂波非高斯性优于PST-GLR检测器和TF-GLR检测器，所以无论是目标1还是目标2，文中方法的检测性能均优于上述2种目标先验信息未知的极化检测器。文中方法的检测性能接近OPD检测器的性能，究其原因，是由于目标的极化散射矢量为一常矢量，这与本文第一节的建模环节设定的目标模型是一致的，故而能达到理想的检测效果，性能趋近于目标和杂波先验信息已知的OPD检测器。事实上，如果目标为机动目标，或散射特性起伏不定，此时目标的极化散射特性不能再看作一个常矢量，此时若采用文中方法，由于目标先验模型和真实场景失配，文中方法的检测性能会严重下降。然而，由于文中方法使用场景为静止/慢速运动小目标此类“低小慢”目标的检测问题，因此，将其极化散射矢量建模为常矢量，而不是随机目标是可行的。

另外，对比图 2(a)和图 2(b)可以看出，图 2(a)对应目标1的检测性能不及图 2(b)对应目标2的检测性能。这是因为目标2极化散射矢量对应的非中心参数λ更大，故在相同的杂波背景下，检测性能更好。

3.3 极化优化设计与固定极化设计的性能比较和结果

假定x_t和∑已分别通过式(20)和式(21)估计得到，对比收发极化固定雷达、发射极化优化雷达和收发极化联合优化雷达间的检测性能差异。其中，对于收发极化固定雷达，取ξ_H=ξ_V=$\frac{\sqrt{2}}{2}$，η_H=η_V=$\frac{\sqrt{2}}{2}$；对于发射极化优化雷达，取η_H=η_V=$\frac{\sqrt{2}}{2}$，最优ξ_H和ξ_V通过网格搜索法计算，使式(31)中λ最大的{ξ_H, ξ_V}为最优发射极化；对于收发极化联合优化雷达，η_H，η_V，ξ_H和ξ_V均通过网格搜索法计算，相似地，使式(31)中λ最大的{ξ_H, ξ_V, η_H, η_V}为最优收发极化组合。

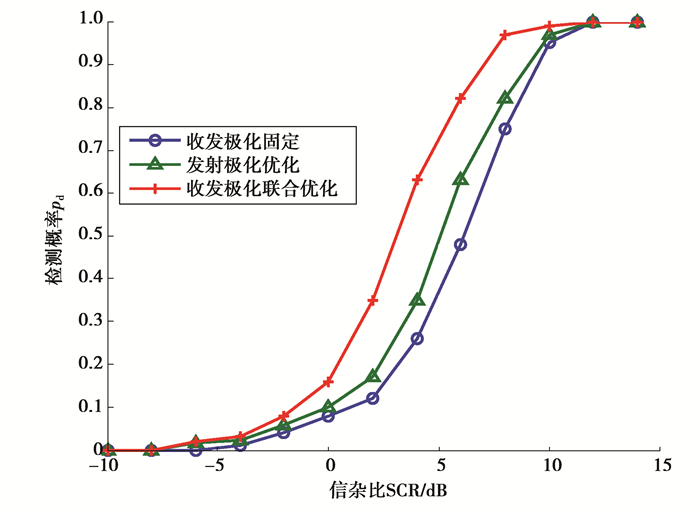
固定噪声功率σ²=0.1，虚警概率为p_fa=10^-3，改变SCR取值，且对于每个SCR进行10⁵次蒙特卡罗仿真，得到λ的均值和对应检测概率。如图 3所示给出文中检测方法分别在固定极化、发射极化优化以及收发极化联合优化条件下的检测概率随SCR变化曲线。可以看出，3种测量系统间的目标检测性能排序为：收发极化联合优化雷达＞发射极化优化雷达＞固定极化雷达。这表明，收发极化联合优化可显著提高雷达对目标的检测性能。

4 结论

设计了收发极化可变极化雷达的测量模型, 提出了一种非高斯杂波背景下的目标极化检测算法，指出了该算法的恒虚警属性以及收发极化与检测性能之间的对应关系。仿真实验首先验证了文中算法在非高斯杂波环境下的性能鲁棒性。接着, 验证了研究方法相比现有目标先验信息未知极化检测方法的性能优势。比较了收发极化联合优化雷达、发射极化优化雷达和收发极化方式固定雷达间的检测性能差异。结果表明, 收发极化联合优化雷达的检测性能明显优于发射极化优化雷达和收发极化固定雷达。