在现代生活生产中,不可压缩材料诸如凝胶[1]、橡胶[2-3]、生物组织[4]等,扮演着越来越重要的角色。虽然在大变形条件下上述材料的本构关系复杂,但是在小变形条件下,仍可将其视为线弹性材料[5]。合理利用不可压缩材料的前提是了解其力学性能,如杨氏弹性模量,硬度等,而且在超弹性模型[6]、黏弹性模型[7]中,杨氏弹性模量等也是至关重要的材料弹性常数。目前测量材料杨氏弹性模量的方法主要可归结为2种,即静态法(拉伸法、压痕法等)与动态法(共振法、超声法等)。由于压痕法[8]的测量结果较为精确且测量过程简单,研究者通常通过开展压痕分析来得到不可压缩材料的力学性能;如Zisis等[9]利用改进的压痕法得到不可压缩超弹性材料的材料性能,Feng等[10]利用压痕法结合有限元分析估计了不可压缩蛋白质组织的材料参数。
在进行材料的压痕分析时,接触半径与薄膜厚度之比直接影响着计算结果,例如接触力与压痕深度,接触半径之间的关系。当薄膜较厚时,研究者往往应用赫兹接触模型进行压痕分析,如Dimitriadis等[11]利用校正了的赫兹模型计算了材料的杨氏弹性模量。但是当薄膜厚度小于接触半径时,赫兹模型便不再适用。于是Greenwood等[12]采用积分和级数展开相结合的方法研究分析了刚性圆柱与弹性薄膜的压痕问题;Delavoipière等[13]研究了水凝胶在其压痕试验中的压痕深度与弹性薄膜厚度、压痕半径的关系;Yang[14]和Chadwick[15]给出了不可压缩弹性薄膜压痕问题的低阶渐近解。相对传统的线弹性求解手段而言,引入Kerr模型中的微分关系可以简化计算,如Ru[16]曾利用Kerr模型[17-19]解析分析了薄膜的褶皱问题。在本文中,将利用Kerr模型对不可压缩薄膜的球形压痕问题进行解析分析,推导问题的高阶渐近解,建立接触力、压痕深度以及接触半径之间的显式联系。
1 薄膜上表面接触压强p(r)与位移w(r)有一厚度为h的各向同性线弹性薄膜,底面粘结在刚性基底上,将半径为R的球形刚性压头压入弹性薄膜中,压痕深度为δ,接触半径为a(如图 1所示),该种压痕问题相对于z轴是轴对称的。
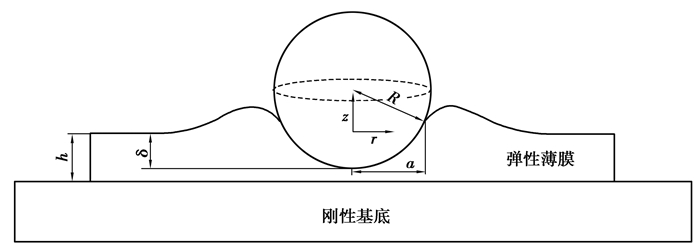
|
图 1 不可压缩弹性薄膜的球形压痕问题 Fig. 1 Spherical indentation of an incompressible elastic thin film |
假定压头与弹性薄膜之间无摩擦力作用,且R
| $ \begin{array}{l} w - {A_1}{h^2}{D^2}w + {A_2}{h^4}{D^4}w = {B_1}\frac{h}{E}p - {B_2}\frac{{{h^3}}}{E}{D^2}p,\\ {D^2} = \frac{{{\partial ^2}}}{{\partial {r^2}}} + \frac{1}{r}\frac{\partial }{{\partial r}},{D^4} = \frac{{{\partial ^4}}}{{\partial {r^4}}} + \frac{2}{r}\frac{{{\partial ^3}}}{{\partial {r^3}}} - \frac{1}{{{r^2}}}\frac{{{\partial ^2}}}{{\partial {r^2}}} + \frac{1}{{{r^3}}}\frac{\partial }{{\partial r}}, \end{array} $ | (1) |
| $ {A_1} = \frac{1}{{1 - \nu }} = 2,{A_2} = \frac{{3 - 4\nu }}{{12{{\left( {1 - \nu } \right)}^2}}} = \frac{1}{3},{B_1} = \frac{{\left( {1 - 2\nu } \right)\left( {1 + \nu } \right)}}{{1 - \nu }} = 0,{B_2} = \frac{{\left( {3 - 4\nu } \right)\left( {1 + \nu } \right)}}{{3\left( {1 - \nu } \right)}} = 1, $ | (2) |
式中:r是点到接触中心的距离;E是薄膜的杨氏弹性模量;ν为不可压缩薄膜的泊松比,大小为0.5。
在接触区内(r≤a),w(r)可通过图 1中的几何关系得出,是接触半径a和压痕深度δ的函数。结合表面压强p(r)在接触区边界r=a处的连续性条件,p(r)可根据等式(1)求出。另一方面,在接触区外(r≥a),薄膜上表面压强p(r)处处为零,根据w(r)在r=a处的连续性条件,w(r)可根据等式(1)求出。之后利用Betti互等定理得到a和δ之间的关系。最后根据力的平衡得出接触力F与接触半径a、压痕深度δ之间的关系。
1.1 接触区内的压强p(r)在接触区内(h
| $ w = \delta + \sqrt {{R^2} - {r^2}} - R \approx \delta - \frac{{{r^2}}}{{2R}},r \le a。$ | (3) |
对于不可压缩薄膜(ν=0.5),从式(2)中可以看到B1=0。因此将式(3)代入式(1)中得到
| $ - {B_2}\frac{{{h^3}}}{E}{D^2}p = \delta + 2{A_1}\frac{{{h^2}}}{R} - \frac{{{r^2}}}{{2R}}。$ | (4) |
因为在r=0处,压强应为有限值,故解得
| $ p = {c_1} + {c_2}{r^2} + {c_3}{r^4}。$ | (5) |
其中,
| $ {c_2} = - \frac{1}{{4{h^3}}}\frac{E}{{{B_2}}}\left( {\delta + 2{A_1}\frac{{{h^2}}}{R}} \right),{c_3} = \frac{1}{{32{h^3}R}}\frac{E}{{{B_2}}}\left( {1 - 4{A_1}\frac{{{h^2}}}{{{R^2}}}} \right)。$ | (6) |
因为在r=a处,压强p(r)=0,代入式(5)得
| $ {c_1} = - {c_2}{a^2} - {c_3}{a^4}。$ | (7) |
接触区外,薄膜上表面接触压强p(r)为0,等式(1)即为
| $ \begin{array}{l} v - {A_1}{h^2}\left( {\frac{{{\partial ^2}}}{{\partial {r^2}}} + \frac{1}{r}\frac{\partial }{{\partial r}}} \right)w + {A_2}{h^4}\left( {\frac{{{\partial ^4}}}{{\partial {r^4}}} + \frac{2}{r}\frac{{{\partial ^3}}}{{\partial {r^3}}} - \frac{1}{{{r^2}}}\frac{{{\partial ^2}}}{{\partial {r^2}}} + \frac{1}{{{r^3}}}\frac{\partial }{{\partial r}}} \right)w = 0;\\ w = 0,r \to \infty 。\end{array} $ | (8) |
因此
| $ \begin{array}{l} w = {d_1}{K_0}\left( {\frac{r}{{h\sqrt {{\lambda _1}} }}} \right) + {d_2}{K_0}\left( {\frac{r}{{h\sqrt {{\lambda _2}} }}} \right),r \ge a;\\ {\lambda _1} = \frac{{{A_1}}}{2}\left( {1 + \sqrt {1 - \frac{{4{A_2}}}{{A_1^2}}} } \right) = 1.82,{\lambda _2} = \frac{{{A_1}}}{2}\left( {1 - \sqrt {1 - \frac{{4{A_2}}}{{A_1^2}}} } \right) = 0.18, \end{array} $ | (9) |
式中:K0为第二类零阶的修正贝塞尔函数;d1和d2是2个实常数,可由w(r)及其斜率在r=a处的连续性条件求出。
| $ \begin{array}{l} w\left( {r = a} \right) = {d_1}{K_0}\left( {\frac{a}{{h\sqrt {{\lambda _1}} }}} \right) + {d_2}{K_0}\left( {\frac{a}{{h\sqrt {{\lambda _2}} }}} \right) \approx \delta - \frac{{{a^2}}}{{2R}},\\ - w'(r = a) = \frac{{{d_1}}}{{h\sqrt {{\lambda _1}} }}{K_1}\left( {\frac{a}{{h\sqrt {{\lambda _1}} }}} \right) + \frac{{{d_2}}}{{h\sqrt {{\lambda _2}} }}{K_1}\left( {\frac{a}{{h\sqrt {{\lambda _2}} }}} \right) \approx \frac{a}{R}。\end{array} $ | (10) |
K1为第二类一阶的修正贝塞尔函数。当h
| $ \frac{{{K_0}\left( {\frac{a}{{h\sqrt {{\lambda _1}} }}} \right)}}{{{K_1}\left( {\frac{a}{{h\sqrt {{\lambda _1}} }}} \right)}} \approx 1 - \frac{1}{2}\frac{{h\sqrt {{\lambda _1}} }}{a}。$ | (11) |
从式(10)(11),得出
| $ {d_1} = \frac{{\sqrt {{\lambda _1}} \left( {\delta - \frac{{{a^2}}}{{2R}}} \right) - \sqrt {{\lambda _1}{\lambda _2}} \frac{{ah}}{R}\left( {1 - \frac{{\sqrt {{\lambda _2}} }}{2}\frac{h}{a}} \right)}}{{{K_1}\left( {\frac{a}{{h\sqrt {{\lambda _1}} }}} \right)\left[ {\sqrt {{\lambda _1}} - \sqrt {{\lambda _2}} + \frac{1}{2}\frac{h}{a}\left( {{\lambda _2} - {\lambda _1}} \right)} \right]}},{d_2} = \frac{{\sqrt {{\lambda _2}} \left( {\delta - \frac{{{a^2}}}{{2R}}} \right) - \sqrt {{\lambda _1}{\lambda _2}} \frac{{ah}}{R}\left( {1 - \frac{{\sqrt {{\lambda _1}} }}{2}\frac{h}{a}} \right)}}{{{K_1}\left( {\frac{a}{{h\sqrt {{\lambda _2}} }}} \right)\left[ {\sqrt {{\lambda _2}} - \sqrt {{\lambda _1}} + \frac{1}{2}\frac{h}{a}\left( {{\lambda _1} - {\lambda _2}} \right)} \right]}}。$ | (12) |
假设在薄膜上施加均匀的压力P0,由式(1)可得薄膜上表面位移w(r)为0,因此,根据贝蒂互等定理可得
| $ 2{\rm{ \mathsf{ π} }}{p_0}\int\limits_0^\infty {wr{\rm{d}}r} = 2{\rm{ \mathsf{ π} }}{w_0}\int\limits_0^a {pr{\rm{d}}r} = 0。$ | (13) |
由式(13)看到线弹性不可压缩薄膜在当前球形压痕问题中,体积变化量为零。将式(3)和式(9)代入到式(13)中得
| $ {d_1}\sqrt {{\lambda _1}} {K_1}\left( {\frac{a}{{h\sqrt {{\lambda _1}} }}} \right)ah + {d_2}\sqrt {{\lambda _2}} {K_1}\left( {\frac{a}{{h\sqrt {{\lambda _2}} }}} \right)ah + \frac{{\delta {a^2}}}{2} - \frac{{{a^4}}}{{8R}} = 0。$ | (14) |
将等式(11)代入式(14)中得
| $ \frac{{\left( {\sqrt {{\lambda _1}} + \sqrt {{\lambda _2}} } \right)\left( {\delta - \frac{{{a^2}}}{{2R}}} \right)ha - \sqrt {{\lambda _1}{\lambda _2}} \frac{{{a^2}{h^2}}}{R}}}{{1 - \left( {\sqrt {{\lambda _1}} + \sqrt {{\lambda _2}} } \right)\frac{h}{a}}} + \frac{{\delta {a^2}}}{2} - \frac{{{a^4}}}{{8R}} = 0。$ | (15) |
当h
| $ \begin{array}{l} \left( {\sqrt {{\lambda _1}} + \sqrt {{\lambda _2}} } \right)\left( {\frac{{R\delta }}{{{a^2}}} - \frac{1}{2}} \right)\frac{h}{a} + {\left( {\sqrt {{\lambda _1}} + \sqrt {{\lambda _2}} } \right)^2}\left( {\frac{{R\delta }}{{{a^2}}} - \frac{1}{2}} \right)\frac{{{h^2}}}{{{a^2}}} - \\ \sqrt {{\lambda _1}{\lambda _2}} \frac{{{h^2}}}{{{a^2}}} + \frac{{R\delta }}{{2{a^2}}} - \frac{1}{8} = 0。\end{array} $ | (16) |
根据式(16)可得接触半径a与压痕深度δ之间的三阶渐近关系
| $ \begin{array}{l} \frac{{\delta R}}{{{a^2}}} = \frac{1}{4} + \alpha \left( {\frac{h}{a}} \right) + \beta {\left( {\frac{h}{a}} \right)^2} + O{\left( {\frac{h}{a}} \right)^3};\\ \alpha = \frac{1}{2}\left( {\sqrt {{\lambda _1}} + \sqrt {{\lambda _2}} } \right) = 0.89,\beta = \frac{1}{4}{\left( {\sqrt {{\lambda _1}} + \sqrt {{\lambda _2}} } \right)^2} + 2\sqrt {{\lambda _1}{\lambda _2}} - 2\alpha \left( {\sqrt {{\lambda _1}} + \sqrt {{\lambda _2}} } \right) = - 1.21。\end{array} $ | (17) |
据笔者所知,目前关于不可压缩弹性薄膜的高阶关系研究的还很少,在本文的结论中,若忽略α,β项,则“a-δ”关系(式(17))可退化为已有的渐近结果[15]。
此外,为了验证所得的高阶渐近解的精度,建立了轴对称有限元模型。在有限元模型中,压头为刚性材料,半径为8 mm,不可压缩弹性薄膜厚度为5 μm,半径为2 mm。对压头施加垂直向下的位移,在薄膜的下表面,所有方向上的位移设置为零。模型中应用了160 000个0.25 μm×0.25 μm的轴对称混合单元(CAX4RH)。球形压痕轴对称有限元几何模型如图 2所示。
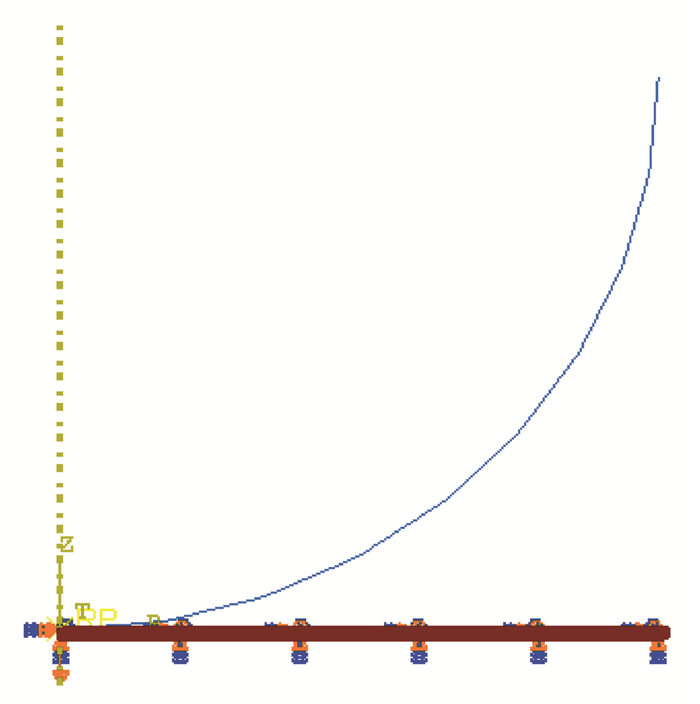
|
图 2 球形压痕问题轴对称有限元几何模型 Fig. 2 The axisymmetric finite element geometric model of spherical indentation test |
图 3反映了压痕深度δ与接触半径a的关系,与现有的低阶渐近解[15]相比,本文的高阶解更加接近已有的数值解[21]与新开展的有限元分析结果。当a/h大于3时,材料凸起现象出现。和新开展的有限元分析结果相比,本文的高阶渐近解相对误差在10%以内,精度比现有低阶渐近解高。
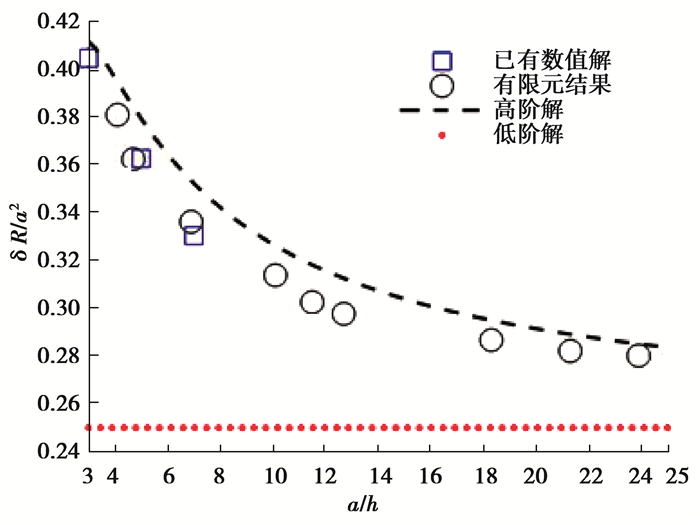
|
图 3 压痕深度δ与接触半径a的关系 Fig. 3 The relation between indentation depth δ and contact radius a |
最后,根据垂直方向上的力的平衡,可以求解接触力F
| $ 2{\rm{ \mathsf{ π} }}\int\limits_0^a {pr{\rm{d}}r} = 2{\rm{ \mathsf{ π} }}\int\limits_0^a {\left( {{c_1} + {c_2}{r^2} + {c_3}{r^4}} \right)r{\rm{d}}r} = F。$ | (18) |
由式(6)(7)(18)可得
| $ - \frac{1}{2}{c_2}{a^4} - \frac{2}{3}{c_3}{a^6} = \frac{F}{{\rm{ \mathsf{ π} }}}。$ | (19) |
由式(6)(7)(17)和(19)可得不可压缩弹性薄膜的“F-a”关系
| $ \left[ {1 + 12\alpha \frac{h}{a} + 12\left( {2{A_1} + \beta } \right)\frac{{{h^2}}}{{{a^2}}}} \right]{\left( {\frac{a}{h}} \right)^6}\frac{h}{{96R}} = \frac{{{B_2}F}}{{{\rm{ \mathsf{ π} }}E{h^2}}}。$ | (20) |
“F-a”关系(式(20))在忽略高阶项后可退化为现有的低阶渐近解[15]。图 4反映了接触力F与接触半径a的关系。当接触半径与压痕深度之比a/h较小时,本文的高阶解精度显著高于现有渐近解;随着比值的增加,两种解的精度均在提高,但本文的高阶精度始终高于现有渐近解,更加接近已有的数值解[21]与有限元分析结果。
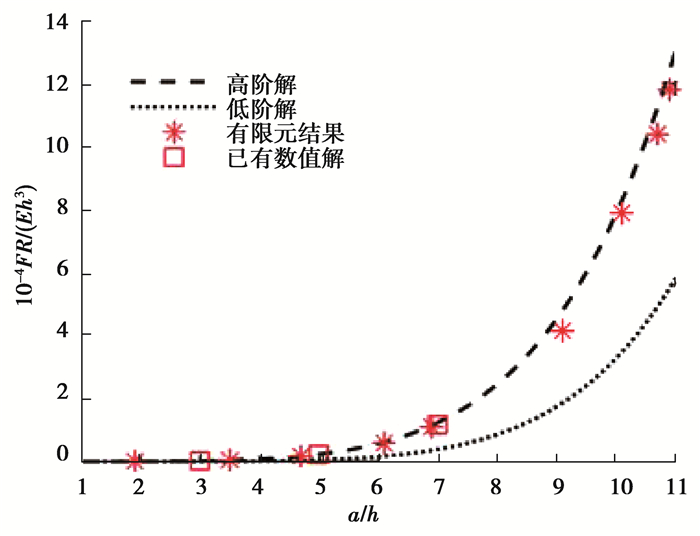
|
图 4 接触力F与接触半径a的关系 Fig. 4 The relation between contact force F and contact radius a |
由式(17)(20)得
| $ \frac{2}{3}{\left( {\frac{\delta }{h}} \right)^3}{\left( {\frac{R}{h}} \right)^2} + \left( {4{A_1} - 8{\alpha ^2}} \right){\left( {\frac{\delta }{h}} \right)^2}\frac{R}{h} = \frac{{{B_2}F}}{{{\rm{ \mathsf{ π} }}E{h^2}}}。$ | (21) |
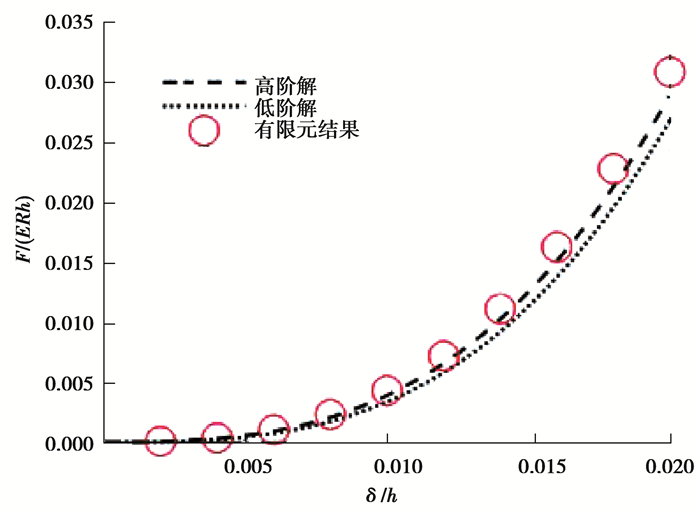
笔者所提出的高阶“F-δ”关系(21)在忽略高阶项后与已有渐近解一致[15]。将基于Kerr模型微分关系(1)得到的显式公式(21)与现有的低阶渐近解[15]以及本文中所开展的有限元结果进行了比较。图 5反映了接触力F与压痕深度δ的关系。通过对比发现,本文的高阶解比现有的低阶解更加贴近有限元分析结果,且随着压痕深度与膜厚之比δ/h的增大,本文的高阶解误差会越来越小。
|
图 5 接触力F与压痕深度δ的关系 Fig. 5 Relationship between contact force F and indentation depth δ |
利用Kerr模型推导了不可压缩弹性薄膜球形压痕问题的高阶渐近解析解。应用贝蒂互等定理,得到了接触力、压痕深度和接触半径之间的显式关系。本项工作的主要结论概述如下。
1) 与已有的低阶渐近解相比,本文的高阶渐近解与已有的数值结果和新开展的有限元分析结果更为接近,精度更高。
2) 当接触半径与膜厚之比较小时,本文的高阶解比现有低阶解明显更加接近数值解和有限元分析结果;随着接触半径与膜厚的比值的增大,两种解的精度均在提高。值得一提的是,本文的高阶解精度始终高于现有的低阶解,当接触半径与膜厚的比值大于3后,材料凸起现象出现,本文的高阶解精度可稳定在10%以内。
3) 随着压痕深度与膜厚之比的增大,本文中得出的接触力与压痕深度的关系的精度随之而增大。
| [1] |
Ramaswamy R, Bourantas G, Jülicher F, et al. A hybrid particle-mesh method for incompressible active polar viscous gels[J]. Journal of Computational Physics, 2015, 291: 334-361. DOI:10.1016/j.jcp.2015.03.007 |
| [2] |
Setiyana B, Jamari J, Khafidh M. Numerical investigation on the elastic modulus of rubber-like materials by a rigid ball indentation technique[C]//MATEC Web of Conferences. EDP Sciences: 2018, 204: 07002.
|
| [3] |
胡景, 严波, 张宏雁, 等. 覆冰导线舞动数值仿真分析[J]. 重庆大学学报(自然科学版), 2010, 33(3): 76-81. HU Jing, YAN Bo, ZHANG Hongyan, et al. Numerical simulation on galloping of iced conductors[J]. Journal of Chongqing University(Natural Science Edition), 2010, 33(3): 76-81. (in Chinese) |
| [4] |
颜功兴, 刘占芳, 郦光丰, 等. 离体培养成骨细胞的有限元分析[J]. 重庆大学学报, 2010, 33(11): 119-123. YAN Gongxing, LIU Zhanfang, LI Guangfeng, et al. The finite element analysis on electromechanical behaviors in bone tissues[J]. Journal of Chongqing University, 2010, 33(11): 119-123. (in Chinese) DOI:10.11835/j.issn.1000-582X.2010.11.020 |
| [5] |
Lopera Perez J C, Kwok C Y, Senetakis K. Effect of rubber size on the behaviour of sand-rubber mixtures:a numerical investigation[J]. Computers and Geotechnics, 2016, 80: 199-214. DOI:10.1016/j.compgeo.2016.07.005 |
| [6] |
Laino G, de Santis R, Gloria A, et al. Calorimetric and thermomechanical properties of titanium-based orthodontic wires:DSC-DMA relationship to predict the elastic modulus[J]. Journal of Biomaterials Applications, 2012, 26(7): 829-844. DOI:10.1177/0885328210388678 |
| [7] |
Hamma A, Kaci M, Mohd Ishak Z A, et al. Starch-grafted-polypropylene/kenaf fibres composites Part 1:Mechanical performances and viscoelastic behaviour[J]. Composites Part A:Applied Science and Manufacturing, 2014, 56: 328-335. DOI:10.1016/j.compositesa.2012.11.010 |
| [8] |
陈蓓, 丁培道, 程川. ZrO2层状复合陶瓷压痕开裂力学分析[J]. 重庆大学学报(自然科学版), 2004, 27(7): 65-67, 71. CHEN Bei, DING Peidao, CHENG Chuan. Indentation cracking mechanical analysis of ZrO2 laminated ceramics[J]. Journal of Chongqing University(Natural Science Edition), 2004, 27(7): 65-67, 71. (in Chinese) |
| [9] |
Zisis T, Zafiropoulou V I, Giannakopoulos A E. Evaluation of material properties of incompressible hyperelastic materials based on instrumented indentation of an equal-biaxial prestretched substrate[J]. International Journal of Solids and Structures, 2015, 64/65: 132-144. DOI:10.1016/j.ijsolstr.2015.03.019 |
| [10] |
Feng Y, Lee C H, Sun L N, et al. Characterizing white matter tissue in large strain via asymmetric indentation and inverse finite element modeling[J]. Journal of the Mechanical Behavior of Biomedical Materials, 2017, 65: 490-501. DOI:10.1016/j.jmbbm.2016.09.020 |
| [11] |
Dimitriadis E K, Horkay F, Maresca J, et al. Determination of elastic moduli of thin layers of soft material using the atomic force microscope[J]. Biophysical Journal, 2002, 82(5): 2798-2810. DOI:10.1016/S0006-3495(02)75620-8 |
| [12] |
Greenwood J A, Barber J R. Indentation of an elastic layer by a rigid cylinder[J]. International Journal of Solids and Structures, 2012, 49(21): 2962-2977. DOI:10.1016/j.ijsolstr.2012.05.036 |
| [13] |
Delavoipière J, Tran Y, Verneuil E, et al. Poroelastic indentation of mechanically confined hydrogel layers[J]. Soft Matter, 2016, 12(38): 8049-8058. DOI:10.1039/C6SM01448H |
| [14] |
Yang F Q. Axisymmetric indentation of an incompressible elastic thin film[J]. Journal of Physics D:Applied Physics, 2003, 36(1): 50-55. DOI:10.1088/0022-3727/36/1/307 |
| [15] |
Chadwick R S. Axisymmetric indentation of a thin incompressible elastic layer[J]. SIAM Journal on Applied Mathematics, 2002, 62(5): 1520-1530. DOI:10.1137/S0036139901388222 |
| [16] |
Ru C Q. Surface wrinkling of two mutually attracting elastic thin films due to van der Waals forces[J]. Journal of Applied Physics, 2001, 90(12): 6098-6104. DOI:10.1063/1.1418424 |
| [17] |
Li M, Ru C Q, Gao C F. An alternative method for indentation of an elastic thin beam by a rigid indenter[J]. International Journal of Mechanical Sciences, 2018, 149: 508-513. DOI:10.1016/j.ijmecsci.2017.07.047 |
| [18] |
Li M, Ru C Q, Gao C F. Axisymmetric indentation of an elastic thin plate by a rigid sphere revisited[J]. ZAMM-Journal of Applied Mathematics and Mechanics, 2018, 98(8): 1436-1446. DOI:10.1002/zamm.201700266 |
| [19] |
Li M, Gao C F, Ru C Q. Asymmetric indentation of an elastic beam by a rigid cylinder[J]. Zeitschrift Für Angewandte Mathematik Und Physik, 2018, 69(4): 93. DOI:10.1007/s00033-018-0987-9 |
| [20] |
Hasenhuetl E, Kasada R, Zhang Z X, et al. Evaluation of ion-irradiation hardening of tungsten single crystals by nanoindentation technique considering material pile-up effect[J]. Materials Transactions, 2017, 58(5): 749-756. DOI:10.2320/matertrans.M2016437 |
| [21] |
Jaffar M J. A numerical solution for axisymmetric contact problems involving rigid indenters on elastic layers[J]. Journal of the Mechanics and Physics of Solids, 1988, 36(4): 401-416. DOI:10.1016/0022-5096(88)90025-7 |
 2019, Vol. 42
2019, Vol. 42


