2. 北京大学 光华管理学院, 北京 1000871;
3. 中央财经大学 中国经济与管理研究院, 北京 100081
2. Guanghua School of Management, Peking University, Beijing 100871, P. R. China;
3. China Economics and Management Academy, Central University of Finance and Economics, Beijing 100081, P. R. China
企业目标的确定是企业行为研究的重要内容。所谓企业行为就是企业为实现某一或某组特定目标的决策和实施决策的过程。现代企业行为理论认为, 企业是企业内部主要主体要素, 即所有者、经理和职工或工会利益和权力关系的组合。企业厂商的主导行为目标就取决于处于主导地位的利益和权力主体的目标趋向。所以, 在传统的高度集中的国家所有制内, 主导的行为目标是完成国家计划;在古典的私有制内, 主导的行为目标是利润的不断增加;在经理主导型的股份制内, 主导行为目标是企业成长;在传统南斯拉夫社会所有制内, 主导行为目标是收入的增加。
实际上,随着理论的发展,相对于绝对偏好,相对偏好或多元化目标、非利润最大化的目标考虑了更多的因素。除了利润之外,还有市场份额、每个工人的平均收益、股东权益、管理者报酬,甚至公司的声誉,这些因素在管理理论中都有所涉及。企业受各种因素的影响,会确立不同的目标, 企业的目标不仅限于利润最大化,而且是多重目标。企业确立了目标,便会有相应的战略来实现这些目标。企业目标的变化,或者说企业偏好的变化,引致企业行为和绩效发生变化,进而影响资源的配置,从而也影响了竞争对手的企业行为。这种目标改变所带来的企业们的行为改变,也即多重目标下企业之间行为的相互影响,是本文的兴趣所在。
用经济学的范式语言描述如下:如同对于个人的偏好的分析,对于企业相对偏好的讨论也有很多方向。如偏好的变化对于企业行为的影响。如同绝对偏好,企业也会确定一个目标函数,但此目标函数,不仅包含了一定权重的利润,还包含了一定权重的其他因素,如上面提到的市场份额、每个工人的平均收益、股东权益、管理者报酬等。这些因素的存在,都有其现实基础,也表现了该企业或企业的所有者对于企业发展的看法或倾向。笔者在这里把这种更符合现实的、企业具有的多重目标称为非最大化利润的目标(non-profit maximization)。文中,笔者主要讨论了两种企业的相对偏好或者说非最大化利润目标的情况。一种是企业将它自己的收入包含进目标函数;另一种是企业将自己的利润和行业中的某个利润水平相比较,最大化此相对利润。
一、研究现状对于利润最大化目标的质疑以及对企业行为研究方式转变的建议为时已久。Berle and Means指出股东不断减弱的作用和相随的企业管理者的管理作用的增强,预示了管理理论开始走强。Cyert and March①进一步指出,企业的目标是实现一定的可以接受的利润水平,这个水平由以往的经验和外在的标准决定。Baumol认为企业最大化利润至少要实现一设定的最小利润水平,Baumol讨论了最大化收益的增长率的约束。这些研究通过将现实经验转化为约束条件,讨论在此基础上非最大化利润目标的实现。Cyert and March②认为企业是适应性的组织,他们解决遇到的各种问题而不是最大化任何目标。Oliver Williamson③把管理者的效用函数标准化(最大化效用同时有最小利润的约束),效用函数里包括实现管理者目标的方式和管理层的报酬。相关的影响因素有和管理者升迁相关的花费规模、工资、保险、权力、荣誉、专业级别,还包括令人费解的可任意使用的支出账户和办公室大小。Marris④认为管理者在最小利润的限制下最大化企业规模增长率,这里企业规模是由公司资本定义的(固定资本、存货和现金)。John Willianson⑤提供了一个对利润最大化、增长率最大化和贴现收益最大化的比较。这些作者都认为最小利润的限制来自于管理者对工作保险的兴趣:低利润(因而低股价)使他们被替换的可能性增大⑥。
① Cyert,Richard M.and March, James G.(1956),”Organizational Factors in the Theory of Oligopoly, ”Quarterly Journal of Economics, 10(2), 398-412.
② Cyert,Richard M.and March, James G.(1963),A Behavioral Theory of the Firm, Second Edition, Cambridge, MA:Blackwell.
③ Williamson,Oliver E.(1963),”Managerial Discretion and Business Behavior”, Ameriacan Economic Review, 53(5), 1032-1057. Williamson,Oliver E.(1964),The Economics of Discretionary Behavior:Mangerial Objectives in a Theory of the Firm, Englewood Cliffs, NJ:Prentice-Hall.
④ Marris,Robin, ”A Model of the ‘Manegerial’ Enterprise, ”Quarterly Journal of Economics, 77(2), 185-209.
⑤ Willianson, John,”Profit, Growth and Sales Maximization, ”Economica,33(129), 1-16.
⑥ Yarrow,G.K.(1976),”On the Predictions of Managerial Theories of the Firm, ”Journal of Industrial Economics, 24(4),267-279.
以上研究皆针对管理者管理的企业,管理者是重要影响因素,与管理者有关的经济变量被考虑进目标函数。
另一类没有假设利润最大化的模型是劳动力管理的企业。Dreze⑦和⑧作出了最初的贡献。假设雇员们参与企业的决策过程,在这个认识的基础上,劳动力管理的企业的目标被认为是最大化雇员的福利。Ward⑨认为企业应最大化每个人的净收益(收益中除去非劳动的费用)。这些目标函数考虑了雇员的效用。
⑦ Dreze,Jacques H.(1976),”Some Theory of Labor Management and Participation, ”Econometrica, 44(6), 1125-1139.
⑧ MeadeMeade,J.E.(1972),”The Theory of Labor-Management Firms and of Profit Sharing, ”Economic Journal, 82(325s), 402-428.
⑨ Ward,Benjamin(1958),”The Firm in Illyria:Markrt Syndicalism, ”American Economic Review, 48(4),566-589.
Miyazaki⑩和Neary⑪⑫定义了雇员的福利由工资和失业导致的闲暇的效用所决定。Aoki⑬把企业的目标进一步发展为股东和雇员之间博弈讨价还价的结果。1983年Aoki⑭把企业进一步假定为股东、雇员和商业伙伴的联合。
⑩ Miyazaki,Hajime(1984),”On Success and Dissolution of the Labor-managed Firm in the Capitalism Economy”, Journal of Political Economy, 92(5), 909-931.
⑪ iyazaki,Hajime and Neary(1983),”The Illyrian Firm Revisited, ”Bell Journal of Economics, 14, 259-270. Miyazaki,Hajime and Neary(1985),“Output, Work Hours and Emlpoyment in the Short Run of a Labor-Management Firm, ”Economic Journal, 95, 1035-1048.
⑫ Aoki,Masahiko(1980),”A Model of the Firm as a Stockholder-Employee Cooperative Game, ”American Economic Review, 70(4),600-610.
⑬ Aoki,Masahiko(1983),”Managerailism Revisited in the Light of Bargaining-Game Theory, ”International Journal of Industrial Organization, 1(1),1-21。Baumol,William J.(1959), Business Behavior, Value and Growth, NewYork:Macmillan.
⑭ Kaneda, M., Mastui A. 2003. Do Profit Maximizers Maximize Profit? Divergence of Objective and Result in Oligopoly. mimeo, University of Tokyo, available at http://www.e.u-tokyo.ac.jp/~amatsui/profit50.pdf.
Kaneda and Matsui⑮进一步提出了一个更广泛形式的企业的目标函数,假设它是一定权重的利润和其他目标的平均数。
⑮ Kaneda, M., Mastui A. 2003. Do Profit Maximizers Maximize Profit? Divergence of Objective and Result in Oligopoly. mimeo, University of Tokyo, available at http://www.e.u-tokyo.ac.jp/~amatsui/profit50.pdf.
上文所介绍企业的相对偏好或偏离最大化利润目标的理论,都集中在讨论当偏好发生变化时,也就是对于不同的企业目标,企业的行为如何发生改变,是目标对行为的影响。但是,这样的讨论是否合理,非最大化利润的目标是否有其理论和逻辑的合理性,这些更深入、更根本的讨论,并没有触及。
国内也有相关的理论研究。和国外的讨论类似,一方面有对理论合理性的探讨, 例如:谭顺[1]表明了对利润最大化理论的质疑。他认为在利润最大化原则运行过程中不可避免地出现了两种错误倾向:第一种倾向是把利润最大化等同于利润唯一化,强调追逐利润是经济活动的唯一目标,对其他的合理目标加以排斥;第二种倾向是把利润最大化等同于逐利合理化,从而使利润最大化原则在法律、道德上处于无可挑剔、无可争议的地位。笔者认为利润最大化是和经济可持续发展目标相背离的;王曲华[2]讨论了商业银行设立非最大化利润目标的合理性。合理设定经营效益目标,对商业银行实现稳健经营具有极其重要的意义。利润最大化只是一种理论抽象,实际工作中很难找到衡量的标准,而且极易诱发经营者的非律行为。因此,作为工作目标,商业银行应当而且只能设置适度利润的效益目标,才能推动银行业的可持续发展;郭卫,陈庆中从新古典经济学、新制度经济学、利益相关者理论角度对企业目标作了简要的分析,并针对现实经济生活中的两种目标模式作了对比。联系中国企业的实际情况,包括利润增加、企业成长、提高市场份额、职工收入增加、完成国家计划、经理收入增加等目标,指出中国企业应以维护股东利益为目标。
另一方面,就是和非最大化利润理论和现实经济相结合,探讨转型期中国的企业行为:刘小玄[3]讨论了国有企业和民营企业在转轨过程中的目标差异以及其所导致的行为差异。国有企业的目标是模糊的多元的,有时甚至是相互冲突的;民营企业的目标则是明确的和唯一的。在中国目前的转轨经济过程中,这种最基本的目标差异实质上就在于,国有企业的目标实际上就是经营者或政府管理者的利益目标,他们通过追求销售收入最大化,或者可支配收益最大化,或者可控制资源最大化,或者满足效用的支出最大化等具体的经营目标和方式,来实现其利益目标。民营企业的目标则可以简单地归结为所有者的利益目标,与这个目标相匹配、相一致的经营目标和方式就是实现利润最大化。徐传谌,高元禄和庄慧彬[4]讨论了国有企业多元化目标形成的原因,并阐述了相应的解决措施。笔者认为随着产权改革的不断深入以及公司治理结构的完善,国有企业已经不是传统意义上的国有企业,而是在产权制度现代化和管理体系市场导向两个维度都发生深刻变化的“新型国有企业”。在国有企业的身后,人们总是可以同时看到两股力量:一股是非经济的,出于政治或意识形态考虑的力量;另一股是经济的,出于实用主义考虑的力量。正是在这两股力量的交互作用下,国有企业成了一种同时拥有非经济目标和经济目标的特殊的企业组织,刘小玄[5]以利润最大化的企业行为作为效率和市场均衡的参照系,构造了一个双重目标的企业行为模型,即所有者和经营者各自具有自身最大化利益的不同目标,来分析中国经济中的企业行为,考察中国特有的产权结构和转轨过程中的市场结构对企业行为的作用及其结果。模型假定政府决定的企业行为是税收最大化,而经营者控制下的企业行为是企业可支配收益最大化,得到的关于税收最大化的行为导致的市场价格低于利润最大化的均衡价格,市场供给大于均衡供给的水平的结论。
无论是国外和国内的研究,都更多地集中于对于企业的不同目标的讨论,或者是非最大化利润理论本身的合理性,而对于确立了非最大化利润目标之后,企业之间行为的相互影响,如何影响,影响程度如何,讨论较少。这也正是本文的努力方向。
文中,笔者采用了Kaneda and Matsui提出的更广泛形式的企业的目标函数,即企业的目标是一定权重的利润和一定权重的其他目标,如收入、成本、市场份额、每个工人的平均利润等。在一个寡头竞争市场上,分析讨论目标变化引致的企业行为的变化,以及企业之间行为的相互影响、影响程度。
除了普遍形式的目标函数,笔者还讨论了两种具体的偏离最大化利润的目标函数。一种是在最大化利润的同时,还最大化企业自己的收益;另一种是将行业的某个利润水平考虑进来,企业比较自己的利润和此利润水平的差距,最大化这个利润水平的差距。在这两种目标函数下,对企业进行产量竞争和价格竞争的行为都进行了分析,并且对于第一种目标函数,采取了所有者—管理者两阶段博弈。论文的结构如下:第2部分我们讨论了普遍形式的多重目标的模型,对于两个企业之间竞争行为或战略的相互影响,以及企业对于不同目标的重视程度,进行了讨论;第3部分提出第一种目标函数下的理论模型及其相应的假设,并讨论了企业在此目标下所有权和管理权分离时,进行产量竞争和价格竞争的均衡结果;第4部分提出了第二种目标函数下的理论模型及其相应的假设,同样讨论了进行产量竞争和价格竞争的结果,对企业行为进行分析;第5部分进行了总结,并探讨了进一步可能的研究。
二、一般模型寡头市场上有两个企业和, 这两个企业都具有非最大化利润的目标函数,包括利润和利润之外的另一个目标,两个企业同时选择它们的战略变量和,这可以是产量,也可以是价格。我们假设一个较高水平的变量表明企业的比较激进的行为。比如企业的目标是最大化利润和市场份额的组合,它选择产量作为变量进行竞争,一个较高水平的产量也就表明该企业比较激进。同样,进行价格竞争的话,一个较低水平的价格是企业比较激进的标志。
目标函数如下:
| $g_i(x_i,x_j)=θ_iπ(x_i,x_j)+(1-θ_i)F(x_i,x_j)。$ | (1) |
对目标函数关于
| $\frac{∂g_j(x_i,x_j)}{∂x_j}=0,$ |
即
| $θ_i\frac{∂π(x_i,x_j)}{∂x_j}+(1-θ_j)\frac{∂F(x_i,x_j)}{∂x_i}=0。$ | (2) |
对上式全微分可得:
| $\frac{∂^2g_i}{∂x^2_i}dx_i+\frac{∂^2g_i}{∂x_i∂x_j}dx_j+\frac{∂^2g_i}{∂x_i∂θ_j}dθ_j=0,$ |
即
| $[θ_j\frac{∂^2π_j}{∂x^2_i}+(1-θ_j)\frac{∂^2F_j}{∂^2x_i}]+\\ [θ_j\frac{∂^2π_j}{∂x_i∂x_j}+(1-θ_j)\frac{∂^2F_j}{∂x_i∂x_j}]dx_j+\\ [\frac{∂π_j}{∂x_i}-\frac{∂π_j}{∂x_j}]=0。$ | (3) |
由上可得:
| $sign\left(\frac{dx_j}{dx_j}\right)=-sign(θ_i∂^2π_i/∂x_i∂x_j+(1-θ_i)∂^2F_j/\\ ∂x_i∂x_j)(θ_j∂^2π_i/∂x_j^2+(1-\\ θ_i)∂^2F_j/∂x_j^2),\\ sign\left(\frac{dx_j}{dθ_j}\right)=-sign(∂π_i/∂x_i∂x_i-∂F_j/∂x_j)$ | (4) |
| $(4)(θ_j∂^2π_i/∂x_j^2+(1-\\ θ_i)∂^2F_j/∂x_j^2)。$ | (5) |
不失一般性,我们假设
定义1:当
定义2:当
定义3:当
定义4:当
命题1:企业
(1) 当
(2) 当
(3) 当
当
若进行产量竞争,则企业选择产量
若
若
类似地,若进行价格竞争,则企业选择价格
若
当
当
在上面的讨论中,我们都是假设
所有者的目标函数是最大化利润
| $\frac{θπ_i(θ_i,θ_j)}{∂θ_i}=0。$ | (6) |
同样,对上式全微分:
| $\frac{θ^2π_i(θ_i,θ_j)}{∂θ_i^2}dθ_i+\frac{θ^2π_i(θ_i,θ_j)}{∂θ_i∂θ_j}dθ_j=0,$ | (7) |
这样,
| $sign\frac{dθ_i}{dθ_j}=-sign(∂^2π_i(θ_i,θ_j)/∂θ_i^2)(∂^2π_i(θ_i,\\ θ_j)/∂θ_i∂θ_j)。$ | (8) |
一般我们假设
当
当
一个企业将利润外的目标引入目标函数后,它的最优行为相较于利润最大化时,发生了变化,这一方面是受到企业自身对于不同目标权重的侧重,另一方面是企业的竞争对手的影响。在上面的模型中,我们从战略替代品和战略互补品的角度进行了分析,接下来将对两个具体的模型进行研究,说明这种变化。
三、包含收益的目标函数在接下来的模型中假设有两个企业,每一个企业都有一个所有者和一个管理者。我们说“所有者”,是指这个做决策的人的目标是最大化利润。“所有者”可以是实际的控制者、董事会或者CEO,而“管理者”是指所有者所雇用的、能够观察到需求和成本的情况,并且做出产量或者价格实时决策的人。
在这里我们考察一个两阶段博弈。在第一阶段,每一个企业的所有者同时决定他们的管理者的目标,企业的所有者和管理者一样,对于产品的需求和成本具有完全信息。在第二阶段,管理者进行寡头竞争,他们互相知晓自己和彼此的目标函数。
企业的管理者的目标函数是:
| $g_i(x_i,x_j)=θ_iπ(X,x_j)+(1-θ_i)R(X,x_i),$ | (9) |
我们将考察这个二阶段模型的子博弈均衡。
在第二个阶段,我们算出企业的管理者在知晓彼此的目标及需求和成本的信息的情况下做出决策后的纳什均衡。接下来我们将讨论企业的管理者进行产量竞争和价格竞争的不同情形。
在第一阶段,企业的所有者同时选择,即他们要求管理者对利润所赋予的权重,我们将考察这阶段的纳什均衡。
(一) 产量竞争假设这是同质产品市场,需求函数是线性的,
在第二阶段,企业的管理者选择
| $g_i(x_i,x_j)=θ_i(a-bX-c_i)x_i+(1-θ_i)(a-bX)x_i,$ | (10) |
企业1的反应函数是
| $x_1=\frac{1}{2b}(a-bx_2)-\frac{1}{2b}θ_1c_1,$ | (11) |
企业2具有对称的反应函数。
如果
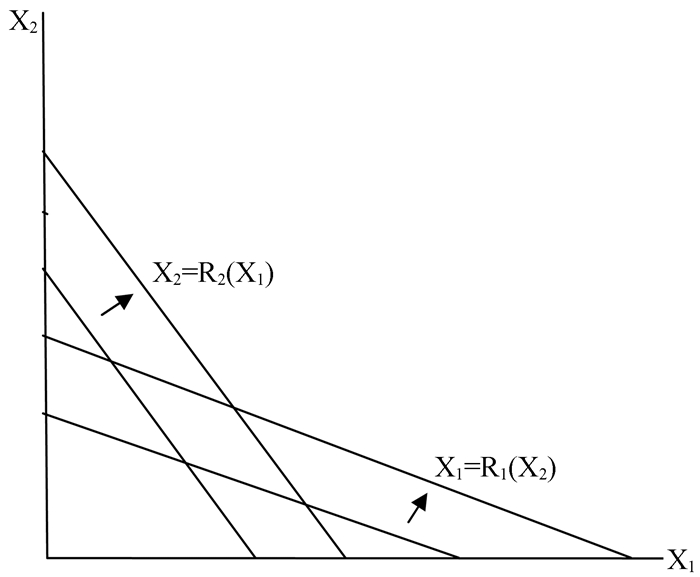
|
图 1 企业反应函数图 |
同时我们可以得到:
| $P=\frac{1}{3}(a+θ_1c_1+θ_2c_2),$ | (12) |
| $x_1(θ_1,θ_2)=\frac{1}{3b}(a-2θ_1c_1+θ_2c_2),$ | (13) |
| $π_1=\frac{1}{9b}(a+θ_1c_1+θ_2c_2-3c_1)(a-2θ_1c_1+θ_2c_2)。$ | (14) |
对于企业2,有类似的结果。
当
当
在第一阶段,企业1的所有者会选择
| $θ_1=\frac{3}{2}-\frac{a}{4c_1}-\frac{θ_2}{4}\frac{c_2}{c_1},$ | (15) |
在第一阶段,我们最终可以得到:
| $θ_1=\frac{3}{2}-\frac{a+2c_2-3c_1}{5c_1},$ | (16) |
| $x_1=\frac{1}{5b}(2a-6c_1+4c_2)。$ | (17) |
命题3:如果这两个寡头企业进行产量竞争,且都有正的产出,那么我们将会得到如下均衡结果
| $θ_i=\frac{3}{2}-\frac{a+2c_j-3c_i}{5c_i},i≠j,$ | (18) |
| $x_i=\frac{1}{5b}(2a-6c_i+4c_j),i≠j,$ | (19) |
| $P=\frac{1}{3}(a+θ_1c_1+θ_2c_2),$ | (12) |
命题4:
可以比较一下古诺竞争的结果和我们的均衡结果。均衡的总产出要大于古诺竞争的产量,而利润和价格要低于古诺竞争的情形。看一个例子,当
同时,我们也认为所有者—管理者博弈的生产也更有效率。这不仅是因为这个博弈的均衡价格要更接近边际成本,而且对于成本较低的企业,它的产量增加得更多。假设企业1是低成本的企业,我们可以算出在此均衡时的市场份额是古诺均衡时的市场份额的
在这一部分我们考察价格竞争的情形。企业具有线性需求函数是
在这里,
| $g_i(x_i,x_j)=θ(a-αP_i+βP_j)(P_i-c)+(1-θ_i)(a-αP_i+βP_j)P_i,$ | (20) |
在第二阶段,企业1最大化
企业1的反应函数是
| $P_1=\frac{α+βP_2+θ_1αc}{2α},$ | (21) |
当竞争对手提高价格的时候,企业的管理者自己也会提高价格。
我们也会得到:
| $P_i=\frac{1}{4α^2-β^2}(2αa+βa+βθ_jac)+\frac{2α^2θ_ic}{4α^2-β^2},$ | (22) |
| $π_i=\frac{1}{4α^2-β^2}(2αa+βa-4α^2+β^2c+2α^2θ_ic)(a-αP_i+βP_j)。$ | (23) |
由上面可以知道,均衡的价格要高于管理者仅最大化利润的时候的价格。当竞争对手提高价格的时候,企业的管理者自己也会提高价格。也就是,企业的管理者知道如果自己提高价格,竞争对手也会跟着提高价格。价格的反应函数将会向外移动。
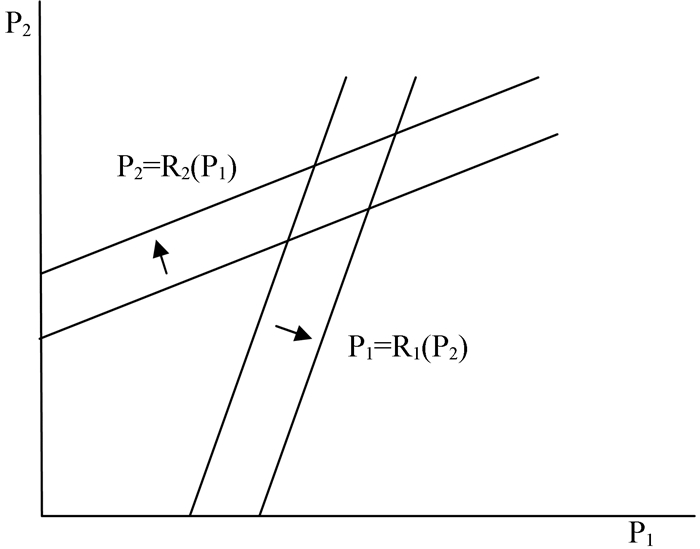
|
图 2 价格反应函数图 |
在第一阶段,企业的所有者最大化利润,可得他的反应函数
| $θ_i=m+nθ_j,$ | (24) |
其中
| $m=\frac{2αβ^2a+β^3a-6β^2α^2c+β^4c+8α^4}{4α^2(2α^2-β^2)c},$ |
| $n=\frac{β ^3}{4α^2(2α^2-β^2)},$ |
最后可得:
| $θ_i=1+\frac{(a-(β-α)c)(β^3+2β^2α)}{α(8α^3-4β^2α-β^3)c}>1。$ | (25) |
命题5:当两个寡头企业进行价格竞争的时候,我们会得到如下的均衡结果:
| $θ_i=1+\frac{(a-(β-α)c)(β^3+2β^2α)}{α(8α^3-4β^2α-β^3)c}>1,$ |
| $P_i=\frac{1}{4α^2-β^2}(2αa+βa+βθ_jαc)+\frac{2α^2θ_ic}{4α^2-β^2}。$ |
命题6:
这样使均衡时的价格要低于贝特兰竞争的价格,企业的反应要保守一些,而不是像产量竞争时比较激进,生产的产量大于古诺竞争的产量。不同于产量竞争使得均衡结果更接近于完全竞争的结果,价格竞争使得均衡价格向着垄断价格的方向增加。
四、包含行业利润水平的目标函数另外,除了将收益函数考虑进目标函数,我们还将考察另外一种情形,企业会更加注重自己的相对效益,它会比较自己的利润水平和行业的某个利润水平的差距,并将之最大化,也就是,会有如下形式的目标函数:
| $g_I(x_i,x_j)=π(X,x_i)-θ_i(π(X,x_i)+π(X,x_j))\\ =(1-θ_i)π(X,x_i)+θ_i(-π(X,x_j)),$ | (26) |
在这里我们不再考虑两阶段博弈,而是假定
同样地,我们考虑产量竞争和价格竞争的情形。
(一) 产量竞争假设这是同质产品市场,需求函数是线性的,
以企业1为例,企业1选择产量
企业1的反应函数是
| $x_1=\frac{1}{2}(a-c)+\frac{2θ_1-1}{2(1-θ_1))x_2},$ | (27) |
企业2具有对称的反应函数。
我们也会得到
| $x_1=\frac{(3-4θ_1)(1-θ_2)}{(3-2θ_1-2θ_2)}(a-c),$ | (28) |
| $P=\frac{1}{(3-2θ_1-2θ_2)}(5θ_1+5θ_2-8θ_1θ_2-3)\\ +(6-7θ_1-7θ_2+8θ_1θ_2)c),$ |
| $π_1= \frac{(5θ_1+5θ_2-8θ_1θ_2-3)(3-4θ_1)(1-θ_2)}{(3-2θ_1-2θ_2)^2} (a-c)^2,$ | (30) |
命题5:
若两个企业都有正的产出,则由
| $θ_1<\frac{3}{4},θ_2<\frac{3}{4},$ |
(1) 当
| $x_1=\frac{1}{2}(a-c),$ |
与
当
| $P=c$ |
| $π_1=π_2=0$ |
两个企业互不影响,或者说,这等同于完全竞争时的情况,就像完全竞争市场上的企业一样,这里的每个寡头企业都不具有影响市场的能力。
(2) 当
(3) 当
类似的结论也适用于企业2。
我们再考虑一个特殊的情形,
| $x_2=\frac{1}{2}(a-c),$ |
| $x_1=\frac{1}{4}(a-c),$ |
| $π_1=\frac{1}{16}(a-c)^2,$ |
| $π_1=\frac{1}{8}(a-c)^2。$ |
当企业1只关注自己的利润而企业2关注相对利润时,企业2的利润要大于企业的利润。企业2最大化相对利润,它的行动不会受到企业1的影响,而企业1因为需求函数的关系,反而会降低自己的产量,从而使自己的利润也要低于竞争对手的利润。也就是说,有这样一种情况,企业最大化自己利润的时候,实现了的利润不一定是最大利润,而当企业偏离最大化利润的目标时,它可能是最大化利润者。
(二) 价格竞争两个寡头企业
| $g_i(x_i,x_j)=(1-θ_i)(1-bP_i+P_j)P_i-θ_i(1-bP_j+P_i)P_j。$ | (31) |
对于(23) 式关于
| $P_i=\frac{1}{2b}+\frac{1-2θ_i}{2b(1-θ_i)}P_j+\frac{1}{2}c+\frac{θ_i}{2b(1-θ_i)}c。$ | (32) |
命题6:
(1) 当
(2) 当
(3) 当
我们还可以得到:
| $P_i=\frac{1}{A}[(1-θ_j)(2b+1-2(b+1)θ_i)+2(1-θ_j)b(b+\frac{1}{2}-bθ_i)],$ | (33) |
其中
当
本文讨论了企业在确立了多重目标或非最大化利润目标的情况下,怎么选择自己的竞争策略的问题。显然,企业不仅要考虑自己在不同目标之间的权重(如果不是外生的情况),还要参照竞争对手的行为确定自己的行动。
处在同一市场上的企业行为相互影响。一个企业的行动或策略会刺激或抵消它的竞争对手的行动。简单说,若两个企业的行动相互抵消(offset),则称它们的行动互为战略替代品;若两个企业的行动相互加强(reinforce), 则称它们的行动互为战略互补品。
显然,企业的目标对于企业的行为有影响,一个企业确立了多重目标,它的均衡产量、价格、利润都会发生变化,竞争对手亦是如此。但到底是怎样的影响,在什么程度上影响自己的行动,影响竞争对手的行动,进而影响最后的均衡结果,笔者从战略替代品、战略互补品等角度分析了企业的不同目标的关系和不同企业行为之间的关系,这是本文所讨论的问题,也是本文的创新之处。
企业确立不同权重的目标,可以称之为目标结构,要受到很多因素的影响,要给予企业自身的远景规划和价值取向,以及外界的影响。有时,企业暂时确立了利润之外的目标,但它的最终目的还是希望最大化远期利润。在文中所讨论的第二个例子的结论中,我们发现了一个有意思的结论,当企业确立非最大化利润目标时,它反而可能取得相对于竞争对手的更大的利润。这在一定程度上证实了对最大化利润目标或“as if ”的质疑。但并不是说最大化利润不对。实际上,一个理性的企业即使确立了多重目标,它的最优策略也和利润最大化的目标一致,这样企业才能持续繁荣,否则企业会失去持续发展的资源。
| [1] | 谭顺. 利润最大化原则与可支配经济发展——一个经济学悖论[J]. 经济学家, 2008(3): 37–43. |
| [2] | 王曲华. 银行业的效益目标是利润最大化还是适度利润[J]. 学术界, 2003(5): 36–44. |
| [3] | 刘小玄. 中国转轨过程中的企业行为和市场均衡[J]. 中国社会科学, 2003(2): 136–144. |
| [4] | 徐传谌, 高元禄, 庄慧彬. 国有大型企业集团的目标多元化问题及其解决措施[J]. 理论前沿, 2007, 511(22): 26–31. |
| [5] | 刘小玄. 双重目标的企业行为模型[J]. 经济研究, 1998(11): 16–24. DOI: 10.3969/j.issn.1002-9605.1998.11.008 |
 2013, Vol. 19
2013, Vol. 19

