根据中国经济运行的机制,企业的生存状况很大程度上受到宏观经济运行和产业政策等外部条件的影响——即企业的生存状况依赖于经济运行状况。本文讨论企业的生存状况在外生冲击的影响下将怎样变化以及哪些冲击对企业生存状况影响较大。企业生存状况基本无法直接计量,但企业数量的变化间接说明企业生存状况的变化,所以本文使用产品市场是垄断竞争的动态随机一般均衡模型(DSGE)分析企业数量的变化,讨论企业生存状况。
本文的模型把企业数量设置为内生的变量,Lewis[1]认为把企业数量设定为内生变量有三个原因:第一,根据Dixit和Stiglitz[2]、Krugman[3]设定垄断竞争的市场条件下一个企业只生产一种产品,在新企业进入的同时,也就有新产品种类被生产,由于产品差异化能满足消费者的不同偏好,这样给消费者带来一定的福利。现在统计的通货膨胀率中没有对产品多样化作出相应的调整,导致统计的通货膨胀率高估了居民生活成本。所以引入内生的企业数量可以反映真实的生活成本。第二,Bilbiie等[4]、Bergin和Corsetti[5]认为内生的企业数量变化增加了宏观经济波动的传递机制。第三,新企业的进入导致了产业内竞争加剧,使产品的差异化变小,从而产品间的替代性加强,使企业的垄断力量和价格制定能力减弱。
在国外文献中技术冲击、偏好冲击对企业数量的影响有一致的看法,Chatterjee和Cooper [6]把企业数量设定为内生变量且受消费偏好冲击和技术冲击的影响。由于企业面临的产品市场是垄断竞争市场,生产的产品是不完全替代,所以企业数量对涨价率(markup)有显著的影响,使企业具有一定的定价能力,从而企业可以长期盈利。对于有利可图的产业可以吸引新企业的进入,加剧产业内的竞争。各个在位企业为了避免在激烈的竞争中被淘汰,只能增强自己的盈利能力,不断积累资本以增大自己的生存空间;但是潜在的进入者看到该产业有利可图,更加想进入该产业,形成一个产业外部积极进入,内部不断增强自己生存能力的过程。Devereux等[7]认为企业数量的变动增加了宏观经济波动的传递途径,从而扩大了宏观经济波动的影响力。索洛余项波动导致企业数量的变化,而企业生存环境的变化促进企业专业化或者规模化以增加自己的生存能力,这又导致索洛余项的变动,形成一个循环传递过程,即企业数量变动是冲击的传递途径。Bilbiie等[4]建立了有进入成本的DSGE模型,在模型中引入内生的企业数量,分析它怎样影响经济周期的相关变量,由于企业有进入成本导致生产者要权衡是否进入产业,所以形成了与Devereux等[7]建立模型相对应的新的经济波动传播机制。Lewis[1]在其模型中引入了供给、需求、货币和进入成本的波动,考察这些波动对企业数量的影响,而供给的波动又分在位企业供给的波动和新进入企业供给的波动,认为企业数量对这些波动都有明显的反应。在国内的文献中,刘晴辉[8]使用固定效应面板数据模型分析货币政策与各产业内企业数量的关系,得到货币政策的变动能解释产业内企业数量变动的95%的结论。从国内文献可以看出对企业生产状况与外生冲击的研究还停留在实证分析上,数量模型的研究还欠缺,而国外成熟的模型又不符合中国的特点。
本文建立一个把企业数量设定为内生变量的封闭经济DSGE模型,主要考察消费偏好、生产技术和货币等外生冲击是怎样影响企业生存(数量)和应该怎样应对这些外生冲击。没有考虑开放经济问题是因为Gali[9]、徐高[10]认为政府支出、净出口等需求对经济波动的影响不大。对家庭建模时,在模型中引入了符合中国家庭实际情况的货币余额偏好,针对中国货币流通速度趋势变化的特点,在模型中也加入了一个对货币余额偏好的持久性冲击。在这个模型中把企业数量变化分析深入到产业内部,这有别于其他的讨论宏观经济波动与企业数量关系的DSGE模型。本文研究企业部门时借鉴了Jaimovich和Floetotto[11]研究涨价率与产业内企业数量的动态关系的建模方法,不同之处在于加总各个产业产出时加入了消费者对产品多样性的偏好,可以修正居民的生活成本。由于产业内部的企业间是垄断竞争的假设,企业通过垄断定价来谋取利润,形成一个前文提及的资本积累的循环过程。由于刘晴辉[8]的经验分析,所以在本文的模型中考虑政府部门时只引入货币政策,而没有考虑政府支出和税收的影响。刘斌[12]认为中国的货币政策目标是盯住货币供应量,所以本文中政府实施的货币政策也只是考虑了控制货币总量增长率而没有考虑利率等其他因素。最后本文求解模型的对称均衡,并使用校准方法对模型进行脉冲响应分析。本文第二部分是理论模型的构建与求解;第三部分是模型校准和脉冲响应分析;第四部分给出模型结论和启示。
一、模型的构建与求解本文建立了封闭经济DSGE模型,包括家庭、企业、政府三个部门。以下分别讨论各个部门。
(一) 家庭部门经济中存在连续(总测度为1) 同质且无限生存的家庭,每个家庭都最大化其一生中的期望效用之和。
| $ {{\rm{E}}_0}\sum\limits_{{\rm{t}} = 0}^\infty {{\beta ^{\rm{t}}}{U_{\rm{t}}}} $ | (1) |
其中,β是主观折现因子;Ut是家庭在t期的即期效用函数,它是消费的增函数;Ct表示消费;劳动供给的减函数,Lt表示劳动供给;货币持有量的增函数,用Mt表示货币持有量,其具体形式为
| $ {U_{\rm{t}}} = \frac{{\varepsilon _{\rm{t}}^c}}{{1 - \sigma }}C_{\rm{t}}^{1 - \sigma } - \frac{\mathit{{\phi }}}{{1 + \mathit{{\phi }}}}L_{\rm{t}}^{1 + \mathit{{\phi }}} + {e^{{d_{\rm{t}}}}}\ln \left( {\frac{{{M_{\rm{t}}}}}{{{P_{\rm{t}}}}}} \right) $ |
其中,σ是跨期消费替代弹性的倒数,φ是劳动供给弹性的倒数。εtc是消费偏好波动,服从对数化一阶自回归过程(AR(1))。ø表示劳动供给的效用相对消费和货币持有量带来效用的比例,没有引入劳动力供给波动是因为劳动供给波动对经济的影响较小[13]。Pt是价格指数,其具体形式将在对企业建模时给出。edt为每期对真实货币余额偏好的冲击,dt遵循一个带漂移的随机游走过程,行为方程为
| $ {{\rm{d}}_{\rm{t}}} = \left( {1 - {\rho _d}} \right){g_m} + {\rho _d}{{\rm{d}}_{{\rm{t}} - 1}} + {\eta _d} $ |
gm是为了体现中国货币流动速度的趋势性变化,在偏好中施加的一个持久性冲击。gm等于中国真实货币余额的增长率与真实产出增长率之间的差额。ηd是随机扰动项。
每期家庭向企业提供劳动力并获取相应的报酬。同时,家庭决定在t期的名义投资量、名义货币持有量和消费。由于只考虑货币政策,没有考虑财政政策,所以在约束等式里面没有税收和转移支付等。家庭的跨期预算约束可以表示为
| $ \begin{array}{l} {C_{\rm{t}}} + {I_{\rm{t}}} + {v_{\rm{t}}}N_{\rm{t}}^E + {M_{\rm{t}}} = {R_{{\rm{t}} - 1}}{K_{{\rm{t}} - 1}} + {W_{\rm{t}}}{L_{\rm{t}}} + \\ {\pi _{\rm{t}}}{N_{\rm{t}}} + {M_{{\rm{t}} - 1}} \end{array} $ | (2) |
其中等式左端表示支出,分别是t期的消费、t期的投资、t期投资的新企业、t期家庭货币持有量。用It表示每期投资额,vt表示企业的价值,NtE表示t期新进入的企业数量。等式右端是收入,分别是资本利得、劳动收入、企业分红、t-1期持有的货币量。用Kt表示资本,Wt表示名义工资率,Rt-1表示t-1期持有的名义资本收益率,πt表示企业利润,Nt表示企业数量。Kt、Nt是状态变量,每期有NtE数量的企业进入,δN比例的在位企业退出生产,而资本也有一定的折旧,用δ表示资本折旧率。所以Kt、Nt的行为方程为
| $ {N_{\rm{t}}} = \left( {1 - {\delta ^N}} \right){N_{{\rm{t}} - 1}} + N_{\rm{t}}^E $ |
| $ {K_{\rm{t}}} = \left( {1 - \delta } \right){K_{{\rm{t}} - 1}} + {I_{{\rm{t}} - 1}} $ |
所以(2) 表示的家庭预算约束可以改写为
| $ \begin{array}{l} \frac{{{M_{\rm{t}}}}}{{{P_{\rm{t}}}}} + \frac{{{K_{\rm{t}}}}}{{{P_{\rm{t}}}}} + {C_{\rm{t}}} + {v_{\rm{t}}}{N_{\rm{t}}} = \frac{{{M_{{\rm{t}} - 1}}}}{{{P_{\rm{t}}}}} + \left( {1 - \delta + {R_{{\rm{t}} - 1}}} \right)\\ \frac{{{K_{{\rm{t}} - 1}}}}{{{P_{\rm{t}}}}} + \frac{{{W_{\rm{t}}}}}{{{P_{\rm{t}}}}}{L_{\rm{t}}} + {\pi _{\rm{t}}}{N_{\rm{t}}} + {v_{\rm{t}}}\left( {1 - {\delta ^N}} \right){N_{{\rm{t}} - 1}} \end{array} $ | (3) |
代表性家庭在式(3) 的约束下求Ct、Lt、Mt、Kt、Nt使家庭期望效用式(1) 最大化,得到最优决策一阶条件为
| $ \varepsilon _{\rm{t}}^cC_{\rm{t}}^{ - \sigma }\frac{{{W_{\rm{t}}}}}{{{P_{\rm{t}}}}} = \mathit{{\phi }}L_{\rm{t}}^\mathit{{\phi }} $ | (4) |
| $ \beta {{\rm{E}}_{\rm{t}}}\left\{ {\left( {1 - \delta + {R_{\rm{t}}}} \right)\frac{{\varepsilon _{{\rm{t + 1}}}^cC_{{\rm{t + 1}}}^{ - \sigma }}}{{\varepsilon _{\rm{t}}^cC_{\rm{t}}^{ - \sigma }}}\frac{{{P_{\rm{t}}}}}{{{P_{{\rm{t + 1}}}}}}} \right\} = 1 $ | (5) |
| $ {e^{{d_{\rm{t}}}}}{\left( {\frac{{{M_{\rm{t}}}}}{{{P_{\rm{t}}}}}} \right)^{ - 1}} = \varepsilon _{\rm{t}}^cC_{\rm{t}}^{ - \sigma }\left( {1 - \frac{1}{{1 - \delta + {R_{\rm{t}}}}}} \right) $ | (6) |
| $ {v_{\rm{t}}} = {\pi _{\rm{t}}} + \beta \left( {1 - {\delta ^N}} \right){{\rm{E}}_{\rm{t}}}\left\{ {{v_{{\rm{t + 1}}}}\frac{{\varepsilon _{{\rm{t + 1}}}^cC_{{\rm{t + 1}}}^{ - \sigma }}}{{\varepsilon _{\rm{t}}^cC_{\rm{t}}^{ - \sigma }}}} \right\} $ | (7) |
式(4) 表示均衡时劳动与消费的边际替代率等于真实工资率,式(5) 表示均衡时资本收益率等于消费的跨期替代率,式(6) 表示均衡时真实货币持有量与消费的替代率等于货币持有成本,式(7) 表示均衡时企业价值等于企业利润加企业未来的期望价值的现值。
(二) 企业部门经济系统中有最终产品和中间产品,最终产品是使用连续且总测度为1的各个产业生产的产品进行生产。在每个产业中都有有限数量的生产中间产品的企业,它们生产不同的产品——即同一个产业中生产的产品是不完全替代的,并假设企业面临的市场是垄断竞争市场。这样会导致各个产业生产的中间产品最后加总产出时各产品之间也是不完全替代的。
最终产品使用规模报酬不变的生产函数生产,它使用各个产业生产的产品进行生产。其生产技术为
| $ {Y_{\rm{t}}} = {\left[ {\int_0^1 {{Q_{\rm{t}}}{{\left( j \right)}^\omega }{\rm{d}}j} } \right]^{\frac{1}{\omega }}},\;\;\;\;\;\;\;\omega \in \left( {0,1} \right) $ | (8) |
Yt为最终产出,Qt(j)是产业j的产出,任何两个不同的产业间生产产品的替代弹性是固定的,等于
在产业j中有数量有限且Nt>1的企业数量,它们生产不同的产品,使用CES函数形式把它们加总为产业j的产出。Nt不同于Jaimovich和Floetotto[11]的设定形式,本文引入了消费者对产品差异化的喜好程度。产业j的产出是
| $ \begin{array}{l} {Q_{\rm{t}}}\left( j \right) = {A_{\rm{t}}}{\left[ {\sum\limits_{i = 1}^{{N_{\rm{t}}}} {{q_{\rm{t}}}{{\left( {j,i} \right)}^\tau }} } \right]^{\frac{1}{\tau }}},\tau \in \left( {0,1} \right)\\ {A_{\rm{t}}} = N_{\rm{t}}^{\gamma - \frac{1}{\tau }} \end{array} $ | (9) |
其中借鉴Dixit和Stiglitz[2]的设定,γ表示消费者对产品差异化的喜好程度。qt(j, i)表示产业j中企业i的产出。产业中的企业面对垄断竞争市场,企业i生产的产品特征不同于其他同产业的企业产品特征,它们使用垄断定价能力使其利润最大化。产业内任意两个企业间生产产品的替代弹性为
每个中间产品生产企业使用资本k和劳动力l进行生产,资本市场和劳动力市场是完全竞争市场。生产函数的形式为
| $ \begin{array}{l} {q_{\rm{t}}}\left( {j,i} \right) = {z_t}k{\left( {j,i} \right)^\alpha }{l_{\rm{t}}}{\left( {j,i} \right)^{1 - \alpha }} - o,\\ \alpha \in \left[ {0,1} \right] \end{array} $ | (10) |
其中zt表示外生的技术冲击, 各个厂商之间都是相同的,其服从对数化AR(1) 过程。一般认为技术冲击是独立于货币政策的,所以过去技术冲击不会受到货币政策冲击及货币需求冲击的影响。ο是中间产品生产企业为生产支付的固定费用,中间产品生产企业把投入的ο数量的费用立即使用起来,而且把它一次消耗完。
最终产品生产者购买各个产业的产品进行生产,面对的最终产品市场是完全竞争市场。所以最终产品生产者选择投入来使其利润最大化,最后得到各个产业的需求函数为
| $ {Q_{\rm{t}}}\left( j \right) = {\left[ {\frac{{{p_{\rm{t}}}\left( j \right)}}{{{P_{\rm{t}}}}}} \right]^{\frac{1}{{\omega - 1}}}}{Y_{\rm{t}}} $ | (11) |
pt(j)是产业j在t期的价格指数,Pt表示最终产品在t期的价格指数,把式(11) 代人(8) 可以得到最终产品价格指数为
| $ {P_{\rm{t}}} = {\left[ {\int_0^1 {{p_{\rm{t}}}{{\left( j \right)}^{\frac{\omega }{{\omega - 1}}}}{\rm{d}}j} } \right]^{\frac{{\omega - 1}}{\omega }}} $ | (12) |
把产业j的企业i的价格表示为pt(j, i),使用同样的方法可以得到qt(j, i)的需求函数和产业j的价格指数。
| $ {q_{\rm{t}}}\left( {j,i} \right) = A_{\rm{t}}^{\frac{\tau }{{1 - \tau }}}{\left[ {\frac{{{p_{\rm{t}}}\left( {j,i} \right)}}{{{p_{\rm{t}}}\left( j \right)}}} \right]^{\frac{1}{{\tau - 1}}}}{Q_{\rm{t}}}\left( j \right) $ | (13) |
| $ {p_{\rm{t}}}\left( j \right) = \frac{1}{{{A_{\rm{t}}}}}{\left[ {\sum\limits_{i = 1}^{{N_{\rm{t}}}} {{p_{\rm{t}}}{{\left( {j,i} \right)}^{\frac{\tau }{{\tau - 1}}}}} } \right]^{\frac{{\tau - 1}}{\tau }}} $ | (14) |
产业内各中间产品企业的定价过程分为两步,第一步是使用资本和劳动,在生产技术的约束下使其成本最小化;第二步是带入第一步求出单位成本,中间产品生产者在需求函数的约束下,制定价格使其利润最大化。在第二步制定价格时,如果使用Dixit和Stiglitz[2]的假设,单个企业的价格不会影响经济整体的价格指数,则没有把企业定价影响考虑到最终产品价格指数和产业的价格指数中。但是Yang和Heijdra[14]认为Dixit和Stiglitz[2]的设定是当企业数量是无限时的加总方法,需要纳入企业垄断定价能力对价格指数的影响,但是仍然假设单个企业的定价只会影响到产业的价格指数,而不会影响最终产品的价格指数。由于本文中假设产业内有有限数量的企业,所以本文使用第二种设定,可得到
| $ \begin{array}{l} \frac{{{p_{\rm{t}}}\left( {j,i} \right)}}{{M{C_{\rm{t}}}\left( {j,i} \right)}} = \mu \left( {{N_{\rm{t}}}} \right) = \\ \frac{{\left( {1 - \omega } \right){N_{\rm{t}}} - \left( {\tau - \omega } \right)}}{{\tau \left( {1 - \omega } \right){N_{\rm{t}}} - \left( {\tau - \omega } \right)}} \end{array} $ | (15) |
其中MCt(j, i)表示产业j内企业i的边际成本,μ表示其涨价率,它是企业数量N的函数。同时根据定价过程,可以得到中间产品企业对资本和劳动力的需求函数
| $ \frac{{{R_{\rm{t}}}}}{{{p_{\rm{t}}}\left( {j,i} \right)}} = \frac{{{z_{\rm{t}}}}}{{\mu \left( {{N_{\rm{t}}}} \right)}}\left[ {\alpha \frac{{{k_{\rm{t}}}{{\left( {j,i} \right)}^\alpha }{l_{\rm{t}}}{{\left( {j,i} \right)}^{1 - \alpha }}}}{{{k_{\rm{t}}}\left( {j,i} \right)}}} \right] $ | (16) |
| $ \frac{{{W_{\rm{t}}}}}{{{p_{\rm{t}}}\left( {j,i} \right)}} = \frac{{{z_{\rm{t}}}}}{{\mu \left( {{N_{\rm{t}}}} \right)}}\left[ {\left( {1 - \alpha } \right)\frac{{{k_{\rm{t}}}{{\left( {j,i} \right)}^\alpha }{l_{\rm{t}}}{{\left( {j,i} \right)}^{1 - \alpha }}}}{{{l_{\rm{t}}}\left( {j,i} \right)}}} \right] $ | (17) |
根据式(10)、(16)、(17) 可以得到中间产品企业的利润,πt(j, i)为
| $ {\pi _{\rm{t}}}\left( {j,i} \right) = {p_{\rm{t}}}\left( {j,i} \right)\left[ {{q_{\rm{t}}}\left( {j,i} \right)\frac{{\mu \left( {{N_{\rm{t}}}} \right) - 1}}{{\mu \left( {{N_{\rm{t}}}} \right)}} - \frac{o}{{\mu \left( {{N_{\rm{t}}}} \right)}}} \right] $ | (18) |
潜在的进入者支付ψ的进入成本建立一家新企业。接下来企业拥有者把产品出售给家庭。它的价值确定方法是未来利润折现v,它的值等于式(7) 确定的数值。所以潜在进入者支付的最优进入成本满足的条件为
| $ {\psi _{\rm{t}}} = {v_{\rm{t}}} $ |
式(7) 可以改写为
| $ {\psi _{\rm{t}}} = {\pi _{\rm{t}}} + \beta \left( {1 - {\delta ^N}} \right){{\rm{E}}_{\rm{t}}}\left\{ {{\psi _{{\rm{t}} + 1}}\frac{{\varepsilon _{{\rm{t + 1}}}^cC_{{\rm{t + 1}}}^{ - \sigma }}}{{\varepsilon _{\rm{t}}^cC_{\rm{t}}^{ - \sigma }}}} \right\} $ | (19) |
政府是通过控制名义货币总量来实施货币政策,需要考虑的因素有上期名义产出、通货膨胀率等,为了符合中国经济运行的实际情况,其行为方程是参照李春吉和孟晓宏[15]的设定,具体形式为
| $ \begin{array}{l} \ln \left( {\Delta {m_{\rm{t}}}/\Delta m} \right) = {\rho _{my}}\ln \left( {{Y_{{\rm{t}} - 1}}/Y} \right) + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\rho _{m\Pi }}\ln \left( {{\Pi _{t - 1}}/\Pi } \right) + \eta _{\rm{t}}^m \end{array} $ | (20) |
其中
在前文提到的企业定价过程中,可以发现所有企业拥有相同的边际成本,这是由于它们面对相同的劳动力市场和资本市场。又由家庭是同质的,可以得出模型的对称均衡解。即∀(j, i)∈[0, 1]×[1, Nt]:qt(j, i)=qt、kt(j, i)=kt、lt(j, i)=lt、Nt(j)=Nt。由于各个企业拥有相同的技术和单位成本,所以它们制定的价格都是相同的,可以把价格定义为pt(j, i)=pt=1。在加总劳动和资本时可以得到Kt=ktNt、Lt=ltNt。通过加总可以得到最终产品生产者的产出、中间产品生产企业的利润、价格指数、资本需求函数和劳动需求函数为
| $ {Y_{\rm{t}}} = N_{\rm{t}}^{\gamma - 1}\left( {{z_{\rm{t}}}K_{\rm{t}}^\alpha L_{\rm{t}}^{1 - \alpha } - {N_{\rm{t}}}o} \right) $ | (21) |
| $ {\pi _{\rm{t}}} = \frac{{{Y_{\rm{t}}}}}{{N_{\rm{t}}^\gamma }}\left( {1 - \frac{1}{{\mu \left( {{N_{\rm{t}}}} \right)}}} \right) - \frac{o}{{\mu \left( {{N_{\rm{t}}}} \right)}} $ | (22) |
| $ {P_{\rm{t}}} = N_{\rm{t}}^{1 - \gamma } $ | (23) |
| $ {R_{\rm{t}}} = \frac{{{z_{\rm{t}}}}}{{\mu \left( {{N_{\rm{t}}}} \right)}}\left[ {\alpha \frac{{K_{\rm{t}}^\alpha L_{\rm{t}}^{1 - \alpha }}}{{{K_{\rm{t}}}}}} \right] $ | (24) |
| $ {W_{\rm{t}}} = \frac{{{z_{\rm{t}}}}}{{\mu \left( {{N_{\rm{t}}}} \right)}}\left[ {\left( {1 - \alpha } \right)\frac{{K_{\rm{t}}^\alpha L_{\rm{t}}^{1 - \alpha }}}{{{L_{\rm{t}}}}}} \right] $ | (25) |
由于最终产品用于消费、投资和新企业的构建,所以可以得到总资源约束方程为
| $ {Y_{\rm{t}}} = {C_{\rm{t}}} + {I_{\rm{t}}} + {\psi _{\rm{t}}}N_{\rm{t}}^E $ | (26) |
(4) -(6)、(15)、(19) -(26) 式描述了均衡时的动态系统。进行数值模拟前需要确定模型中各个结构参数的值,结构参数的校准主要考虑模拟数据序列的稳定性和参照相关文献来确定其数值,它们在参照文献中的经济含义与本文中相应参数的经济含义相同。家庭行为参数集合为{σ, φ, δ, β, δN }。基于季度数据的考虑,σ、φ、δN参数设定时参照刘斌[12]使用Bayes估计得到的值,它们分别为2.1、6.16、0.05,它们的取值意味着跨期消费和劳动供给都缺乏弹性;δ、β参照李春吉和孟晓宏[15]的设定分别为0.05、0.97。企业行为的参数集合为{α, ο, ω, τ, γ}。由于企业部分模型设定参照了Jaimovich和Floetotto[11]的设定,所以α、ο、ω、τ这部分参数也参照其给出的值,它们分别为0.3、0.127、0.001、0.949;γ参照Lewis[1]的设定,其值为0.3。外生冲击的参数集合为{gm, ρc, ρd, ρz, ρmy, ρm∏, ηc, ηd, ηz, ηm}。货币偏好的持久性冲击gm参照刘海超[16]在其博士论文中的统计数据计算得到,其值为0.038。消费冲击系数(ρc)、货币偏好冲击系数(ρd)、技术冲击系数(ρz)参照刘斌[12]的估计结果得到,它们分别为0.17、0.26、0.95。货币政策行为方程的系数ρmy、ρm∏参照李春吉和孟晓宏[15]的设定分别为-0.303 190、0.963 093。各个外生冲击的扰动项ηc、ηd、ηz、ηm的概率分布服从正态分布,具体形式分别为ηc~N(0, 0.99)、ηd~N(0, 1.13)、ηz~N(0, 0.12)、ηm~N(0, 0.12)。具体各个参数的值见表 1。
| 表 1 参数值 |
为了得到模型中各个变量的稳态值,首先应该求出各个外生冲击的稳态值。根据消费偏好冲击、货币供给冲击、技术冲击的定义,它们的稳态值都为1。由于货币偏好冲击是带有漂移的随机游走过程,根据其行为方程可知其稳态值等于gm的值。由于系统处于稳定状态时,各个动态变量是固定的值,根据式(5) 计算出R的稳态值为0.080 928。本文中参照Jaimovich和Floetotto[11]对涨价率的设定,μ(涨价率)的稳态值为1.3,根据涨价率的等式(15) 计算出企业数量的稳态值N为1.218 163。得到N的稳态值后,根据式(23) 计算出P的稳态值为1.148 137。本文设定L的值为1,它代表一个工作日有8个小时,根据式(24) 得到K的稳态值为4.468 011。由式(25) 计算得到W的稳态值为0.843 702。由前面计算的这几个变量的稳态值,根据式(21) 得到Y的稳态值为1.229 965。得到Y的稳态值后,从式(22) 得到π的稳态值为0.169 829。从式(19) 计算出ψ的稳态值为2.163 431。由N、K的行为方程计算得到NE、I的稳态值分别为0.060 908、0.223 401。然后根据式(26) 计算出C的稳态值为0.874 793。从式(6) 得到M的稳态值为30.017 693。ø是一个静态变量,在给定其他参数的值和其他变量的稳态值后,由式(4) 计算其值为0.973 181,可以看到劳动占消费和货币持有量的效用比例非常大。根据∏的定义,在稳定状态时有Pt=Pt-1,所以其值为1。各个变量的稳态值计算结果见表 2。
| 表 2 变量的稳态值 |
为了清楚了解各个冲击对企业数量的动态影响,本文考查了企业数量对技术、货币偏好冲击的脉冲响应函数(图 1)。
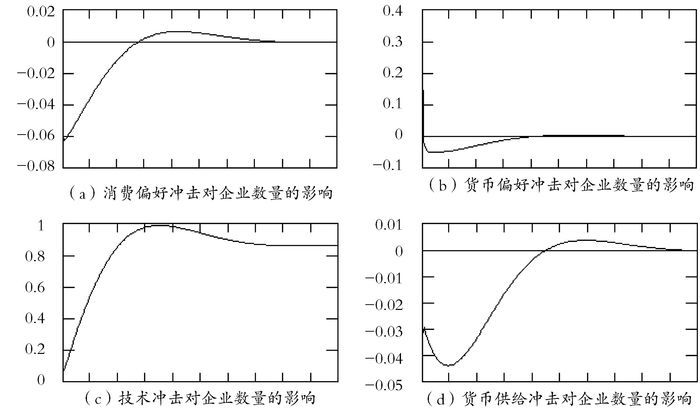
|
图 1 各个冲击对企业数量的脉冲响应函数 注:横轴表示时间(每个刻度20期),纵轴表示单位标准差的冲击给企业数量带来百分比变化。 |
从图 1中可以看到,技术冲击对企业数量的影响最大,技术冲击对企业数量只有正面的影响。在技术冲击的影响下,企业数量会偏离原来的稳定状态,在经过140期后达到一个新的稳定状态,最大偏离发生在70期的时候,其值为1%。从脉冲响应图中还可以看到,企业数量对技术冲击滞后70期是影响最大,属于滞后型波动。在现实中,技术的传播过程也总是部分企业先进行技术创新,然后是其他企业纷纷模仿这些企业的技术,进入该行业,使该行业的企业数量增加。该行业的企业数量达到一定数量后,竞争加剧,部分企业消亡,其他企业为了生存,只有加快技术创新的步伐,这样才能立于不败之地。货币偏好的冲击对企业数量只有负面作用,从图 1中可以看到,货币偏好冲击几乎立即使企业数量的波动达到最大。可以说,家庭的货币偏好,对企业数量有立竿见影的作用,这属于一致性波动。最后大约在60期的时候恢复到稳定状态,偏离程度最大的时候是0.15%。在经济中,企业的建立需要资本的投入,而家庭的货币偏好冲击是持有货币,而不是把这些货币用于投资或者消费。在本模型中,家庭把货币投资于企业,获得分红,当货币偏好冲击发生时,家庭就偏好持有更多货币,企业不能获得资本投入,所以对企业数量具有负面的影响。
三、结论与启示本文采用DSGE分析框架建立了一个企业数量内生化的封闭经济模型,研究外生冲击对企业数量的影响,也即分析外生冲击对企业生存状况的影响。使用参数校准模拟发现货币偏好冲击对企业的生存状况的影响比较小,最大影响只有0.15%,但其影响的持续时间比较长。技术冲击对企业数量有比较大且持久的正面积极影响,最大影响达到1%。
这些结论给我们的启示有两点:其一,货币偏好冲击给企业生存状况带来负面影响且整个过程是长期的,但是其对企业生存状况的影响都比较小,所以对企业的生存状况的作用平缓,即货币偏好变化,不会给企业生存状况带来太大影响。由于这个外生冲击的影响是长期的,如果要避免企业生存能力不会出现长期波动,那么就要有相对稳定的政策去引导家庭的货币偏好。其二,由于垄断竞争的假设,一个企业只生产一种产品,企业数量的增加,意味着产品间的可替代性增强,各个企业为了生存可以通过技术创新带来盈利,从而提升自己的生存能力,而潜在的进入者看到这个产业有利可图,也设法进入该产业,使整个产业形成一个积极的技术创新过程。所以应该鼓励企业技术创新,不断增强自己的生存能力,以增强整个经济的活力。
| [1] | LEWIS V.Macroeconomic fluctuations and firm entry:Theory and evidence[R].National Bank of Belgium Working paper research, 2006. |
| [2] | DIXIT A K, STIGLITZ J E. Monopolistic competition and optimum product diversity[J]. American Economic Review, 1977, 6(3): 297–308. |
| [3] | KRUGMAN P R. Increasing returns, monopolistic competition and international trade[J]. Journal of International Economics, 1979, 9: 469–479. DOI: 10.1016/0022-1996(79)90017-5 |
| [4] | BILBⅡE F O, GHIRONI F, MELITZ M J.Business cycles and firm dynamics[R].Manuscript, 2005. |
| [5] | BERGIN P, CORSETTI G.Towards a theory of firm entry and stabilization policy[R].NBER Working Paper, 2005. |
| [6] | CHATTERJEE S, COOPER R W.Entry and exit, product variety and the business cycle[R].NBER Working Paper, 1993. |
| [7] | DEVEREUX M B, HEAD A C, LAPHAM B J. Aggregate fluctuations and increasing returns to specialization and scale[J]. Journal of Economic Dynamics and Control, 1996, 20: 627–656. DOI: 10.1016/0165-1889(95)00868-3 |
| [8] | 刘晴辉. 货币政策、企业行为与商业周期: 基于动态随机一般均衡的模拟分析[D]. 上海: 复旦大学, 2010. http://cdmd.cnki.com.cn/Article/CDMD-10246-2010194269.htm |
| [9] | GALI J. Monetary policy, inflation, and the business cycle[M]. Princeton: Princeton University Press, 2008. |
| [10] | 徐高. 基于动态随机一般均衡模型的中国经济波动数量分析[D]. 北京: 北京大学, 2008. |
| [11] | JAIMOVICH N, FLOETOTTO M. Firm dynamics, markup variations, and the business cycle[J]. Journal of Monetary Economics, 2008, 55: 1238–1252. DOI: 10.1016/j.jmoneco.2008.08.008 |
| [12] | 刘斌. 我国DSGE模型的开发及在货币政策分析中的应用[J]. 金融研究, 2008, 10: 1–22. DOI: 10.3969/j.issn.1007-9041.2008.02.001 |
| [13] | WALSH C E. Monetary theory and policy[M]. second edition. Massachusetts: The MIT Press, 2003. |
| [14] | YANG X, HEIJDRA J B. Monopolistic competition and optimum product diversity[J]. American Economic Review, 1993, 83(1): 295–301. |
| [15] | 李春吉, 孟晓宏. 中国经济波动——基于新凯恩斯主义垄断竞争模型的分析[J]. 经济研究, 2006(10): 72–82. |
| [16] | 刘海超. 钉住汇率制度的宏观经济绩效——亚洲金融危机前后比较分析[D]. 成都: 西南财经大学, 2007. |
 2013, Vol. 19
2013, Vol. 19

