商业银行汇率风险是指汇率变动可能给银行的当期收益或价值带来损失的风险，它是由汇率波动的时间差、地区差及银行表内外业务币种和期限结构不匹配等原因造成的。汇率风险源于包括固定汇率和浮动汇率的两大国际货币制度。固定汇率风险较浮动汇率风险要小得多，浮动汇率波动频繁且波动幅度大，所产生的汇率风险也难以度量，是商业银行风险控制的主要内容之一。

中国目前实行以市场供求为基础，单一的、有管理的浮动汇率制度，在这种汇率制度下，人民币汇率保持了基本的稳定。然而，人民币面临很大的升值压力，从市场均衡角度看，主要是外汇供大于求，截至2011年6月30日，中国外汇储备达到3.19万亿美元，外汇储备的不断增加以及贸易逆差、热钱涌入使得人民币面临更大的升值压力。纵观当前形势，人民币升值已势在必然，对于中国商业银行而言，必须密切关注人民币汇率走势，做好外汇资产的合理分配和保值增值，有效防范汇率风险。早在20世纪90年代，国外学者就展开了对均衡汇率及其风险的研究，如Willianmson提出了基本要素均衡汇率模型FEER^[1]，Stein提出了自然均衡实际汇率模型NATREXR^[2]，MacDonald提出了行为均衡汇率模型^[3]，这些模型都以发达国家为研究对象，很少考虑发展中国家常见的制度性干预因素，如外汇管制、贸易壁垒和黑市汇率等。中国一些学者直接利用上述模型对人民币汇率进行了测算，如张晓朴^[4]、施建淮和余海丰^[5]分别采用FEER模型对1984年1季度至1999年1季度和1991年1季度至2004年3季度的人民币汇率进行了估计。施建

淮和余海丰认为自20世纪90年代以来，人民币实际实质汇率在大部分时期偏离人民币均衡实质汇率轨迹，表现为人民币实质汇率的失调^[5]。因此，在人民币实际汇率失调的情况下很难采用传统方法度量人民币汇率的风险。对于商业银行而言，要有效管理汇率风险，首先应比较准确地度量汇率风险。在2005年7月汇率改革以来，人民币兑主要发达国家货币的汇率越来越市场化，导致汇率呈现出尖峰厚尾的非对称性，传统的VaR方法无法刻画这类风险，而GARCH模型则能较好地反映金融市场上的非线性波动特征。本文在传统VaR方法的基础上，引入GARCH模型，构造了VaR-GARCH(1, 1) 模型来计算商业银行的汇率风险，以便刻画汇率波动中的制度性干扰因素。

一、研究设计 (一) VaR方法 1. VaR概述

VaR的含义是在险价值，指市场正常波动下，某一金融资产或证券组合的最大可能损失^[6]，更为确切地是指，在一定的概率水平下（置信度），某一金融资产或证券组合在未来特定的一段时间内的最大可能损失，其数学表达式为：

$\text{Pr}ob(\text{ΔP}>\text{VaR)}=1－c$

(1)

其中$\text{Δ}P$为金融资产在持有期$\text{Δ}t$内的损失；VaR为置信水平c下的在险价值。直观上讲，在假定市场正常波动的情况下，某银行的VaR是指这样的损失：给定的概率为c，持有期为$\text{Δt}$，在$\text{Δt}$日内超过这一损失的概率为$1－c$。

从统计学的角度来看，VaR实际上是金融资产收益分布的一个百分位数，换言之，如果给出某一金融资产价值的统计分布图，根据定义就可直观地找到与置信度相对应的分位数，即VaR值。在VaR定义中，有两个重要参数：持有期和置信水平。

持有期是计算VaR的时间范围。由于波动性与时间长度正相关，所以VaR随持有期的增加而增加。金融机构选择持有期时往往要考虑流动性、正态性、头寸调整、数据约束四种因素。一般而言，交易头寸流动性好则持有期可以较短，否则较长。但当持有期较短时，收益的实际分布会更接近于正态分布的假设，所估计的结果也更加合理。而且持有期较短时，组合头寸也会尽量保持不变，这有利于VaR的计算。

置信水平的选取反映了金融机构对风险的厌恶程度，置信水平越高，厌恶风险的程度也越大。置信水平一般选择在90%到99%之间。具体的选择依赖于对VaR验证的需要、内部风险资本需要、监管要求以及在不同机构之间进行比较的需要。风险厌恶程度越高，所需用于补偿额外损失的资本量就越大。设置较高的置信水平对监管当局而言可以维持金融系统的稳定性。同时为了统计和比较不同金融资产间的置信水平，需要选择中等或较高的置信水平。目前全球几大金融机构选用的置信度为：银行信托公司99%，花旗银行95.5%，JP.摩根银行95%，美洲银行95%。根据需要，本文设置了95%、99%和99.9%等三种置信水平。

2. 传统VaR计算方法

考虑一个外汇资产组合，假定$P_0$为外汇资产的初始价值，R是持有期内的投资回报率，则在持有期末，外汇资产的价值可以表示为$P=P_0(1+R)$。假定收益率R的期望收益和波动性分别为$μ$和$σ$。如果在某一置信度c下，外汇资产的最低价格为$P^*=P_0{(1+R^*)。}$则根据VaR的定义，外汇资产组合价值的均值（期望收益）的VaR，即相对VaR为：

$\text{VaR}_R=\text{E}(P)－P^*=－P_0(R^*－μ)$

(2)

如果不以组合价值的均值（期望收益）为基准，可以定义绝对VaR为：

$\text{VaR}_A=P_0－P^*=－P_0R^*$

(3)

根据以上定义，计算VaR就相当于计算最小值$P^*$或最低收益率$R^*$。考虑外汇资产组合未来交易日收益行为的随机过程，假定其未来收益的概率密度函数为$f(p)$，则对于某一置信度水平c下的外汇资产组合最低值$P^*$有$c=\text{∫}^∞_{P^*}f(p)\text{d}p$或$1－c=\text{∫}^{P^*}_∞f(p)\text{d}p$，无论分布是离散的还是连续的，厚尾还是瘦尾，这种表示方式对于任何分布都是有效的。

在此基础上，对外汇资产VaR的计算还扩展为方差—协方差法、历史模拟法和蒙特卡罗模拟法等三种方法。方差—协方差法是基于对参数标准差的估计，而不是从经验分布上确定百分位数，因此该方法又被称为参数法^[7]。它的基本思想是在假设资产组合服从正态分布的前提下，对资产组合收益的方差—协方差矩阵进行估计，求出一定置信度下收益分布偏离均值程度的偏离值，然后计算出VaR值。

方差—协方差方法的关键在于在假定组合收益服从正态分布的前提下，对组合资产的标准差进行估计。历史模拟法假定外汇资产收益的未来发展趋势将会延续过去。它的核心在于根据市场因子的历史样本变化模拟证券组合的未来损益分布，利用分位数给出一定置信度下的VaR估计^[8]。“模拟”的核心是将当前的权数放到历史的资产收益时间序列中：

$R_{p,k}=∑\limits^N_{i=1}w_{i,t}R_{i,k}(k=1,...,\text{t})$

(4)

（4）式中，$R_{p,k}$指外汇资产组合在时间k的收益率，是构造的虚拟收益率；$w_{i,\text{t}}$指当前时间t的投资权重；$R_{i,k}$指组合中第i种外汇在时间k的收益率。

历史模拟法的概念直观、计算简单，无需进行分布假设，可以有效地处理非对称和厚尾等问题，而且历史模拟法可以较好地处理非线性、市场大幅波动等情况，可以捕捉各种风险。但是，历史模拟法的缺点也是显而易见的：首先，它假定市场因子的未来变化与历史完全一样，这与实际金融市场的变化不一致；其次，历史模拟法需要大量的历史数据，通常认为，历史模拟法需要的样本数据不能少于1 500个；最后，历史模拟法的计算量非常大，对计算能力要求较高。

蒙特卡罗模拟亦称随机模拟法，其基本思想是，为了求解科学、工程技术和经济金融等方面的问题，首先建立一个概率模型或随机过程，使它的参数等于问题的解，然后通过对模型或过程的观察计算所求参数的统计特征，最后给出随机问题的近似值^[8]。历史模拟法计算的VaR是基于历史市场价格变化得到组合收益的各种可能结果，从而在观察到的损益分布基础上通过分位数计算VaR。蒙特卡罗模拟法模拟的VaR的计算原理与此类似，不同之处在于市场因子的变化不是来自历史观察值，而是通过随机数模拟得到。其基本思路是重复模拟外汇资产变量的随机过程，使模拟值包括大部分可能情况，这样通过模拟就可以得到组合价值的整体分布情况，在此基础上就可以求出VaR。

蒙特卡罗模拟法的优点在于它是一种全值估计方法，可以处理非线性、大幅波动及厚尾问题；它产生大量情景，比历史模拟法更精确和可靠。但蒙特卡罗模拟法也存在不少缺点，如依赖特定的随机过程和所选择的历史数据；计算量大、计算时间长。

3. 传统VaR计算方法的不足

VaR三种主要计算方法都有特定的假设条件和使用范围。对于包含期权和隐含期权的组合，模拟方法（包括历史模拟法和蒙特卡罗模拟法）能够较好地计算。但模拟方法较参数方法在实施上具有很大难度，两种模拟方法都需要大量样本数据，这些样本数据在收集和处理上都需要很高的要求。在向高层管理者解释方面，历史模拟法由于计算原理简单，易于向高层管理者解释，但参数法和蒙特卡罗方法需要统计等专业方面的知识，解释起来较难。从三种方法计算结果可靠性角度看，参数法和历史模拟法都选取历史数据进行计算和模拟，因此数据的选取直接影响结果的准确性，蒙特卡罗模拟法能选择市场因子的统计分布，但管理者可能会作出错误的选择，使选择的分布不能体现市场因子的实际分布。在实践中，要根据实际情况选用不同的方法，才能得到较为精确的VaR估计结果，对金融风险产生有效的控制和度量。为此，本文提出用GARCH(1, 1) 模型来计算商业银行外汇资产的风险。

(二) 基于GARCH(1, 1) 的VaR计算方法

GARCH模型又称异方差自回归模型（Auto-Regressivie Conditional Heteroskedustic Model），是Bollerslev于1986年提出的。GARCH模型定义为：

$σ^2_\text{t}=α_0+∑\limits^p_{i=1}α_ir^2_{\text{t}－i}+∑\limits^q_{j=1}α_jσ^2_{\text{t}－j}$

(5)

其中$r_\text{t}=σ_\text{t}ε_\text{t}$，$ε_\text{t}$~I.I.D，$\text{E}(ε_\text{t})=0$，$\text{VaR}(ε_\text{t})=1$，并对系数有以下要求：$α_0>0$，$∀$i，j有$α_i≥0,β_j≥0$，且$∑^{\text{max}(p,q)}_{i=1}(α_i+β_j)<1$，则称$r_t$服从GARCH（p，q）模型。

GARCH模型一般由两个方程组成：条件均值方程（6）；条件方差方程——标准的回归方程（7）：

$r_\text{t}=μ+ε_\text{t}$

(6)

$σ^2_\text{t}=ω+αε^2_{\text{t}－1}+βσ^2_{\text{t}－1}$

(7)

其中$μ$是无条件均值，$σ^2_\text{t}$表示条件方差，$ω$，$α$，$β$为常数。基于GARCH模型的VaR计算一般要求先建立GARCH（1, 1）模型：

$GARCH=C(1)+C(2)·RESID(－1)^{∧2}+{C(3)·GARCH(－1)}$

(8)

其中GARCH表示收益率$R_t$的条件方差，$RESID(－1)^∧2$表示残差平方和的滞后一阶，GARCH(-1) 表示条件方差的滞后一阶。模型建立后计算一定置信度下的VaR值步骤如下：

第一步：运用GARCH（1, 1）模型得到未来交易日的条件方差；

第二步：计算出外汇资产组合收益率序列间的相关系数$ρ_{ij}$，根据公式$\text{Cov}(R_i,R_j)=ρ_{ij}σ_iσ_j$得到协方差矩阵$\mathit Σ$的预测值；

第三步：根据各收益率序列在组合中比重得到组合整体条件方差$σ^2_p$：$σ^2_p=w′∑w$；

第四步：取一定的置信水平，得到在该置信水平下的VaR值，$\text{VaR}_p=αW_0\sqrt{w′∑w}$。其中$W_0$为初始风险头寸，$α$为相应置信度下的分位数值。

基于GARCH模型的VaR计算相比于传统VaR计算方法的主要优点在于：相比于历史模拟法对数据的利用更充分有效；计算过程较蒙特卡罗模拟法更简单；计算结果比传统方法更精确。

二、实证结果及分析 (一) 样本来源

为了更加全面地研究中国商业银行汇率风险问题，我们选取2003年1月1日至2005年7月21日中国汇改前、2005年7月22日至2008年9月15日汇改后至金融危机爆发前以及2008年9月16日至2009年12月30日金融危机爆发后三个不同时段人民币对美元、欧元、日元与港币的汇率中间价，共1 698个有效数据，全部数据来源于国家统计外汇管理局网站。汇率日收益率采用对数收益率，即$R_t=\text{ln}(P_t)－\text{ln}(P_{t－1})$，其中$P_t$表示t期的汇率，$R_t$表示t期的汇率日收益率。

(二) 日收益率的描述性统计（表 1）

表 1为外汇收益率的描述性统计，其中Panel A为2003年1月1日至2005年7月21日的描述性统计，Panel B为2005年7月22日至2008年9月15日的描述性统计，Panel C为2008年9月16日至2009年12月30日的描述性统计。由Panel A知2003年1月1日至2005年7月21日期间美元、欧元、日元和港币的日收益率序列的偏度系数均大于0，右偏，峰度系数也均大于0，具有尖峰特征。由Panel B知2005年7月22日至2008年9月15日期间欧元、日元的日收益序列的偏度系数大于0，右偏，美元和港币日收益序列的偏度系数小于0，左偏，峰度系数均大于0，具有尖峰特征，美元和港币峰度系数远大于0，尖峰特征异常明显。由Panel C知2008年9月16日期间美元、欧元和日元具有负的偏度系数，正的峰度系数，右偏尖峰，港币日收益序列具有正的偏度系数，负的峰度系数，左偏尖峰。从表 1 ADF检验值显著不为零知4种外汇收益率序列在1%水平上都拒绝单位根假设，即收益率序列是协方差平稳的。

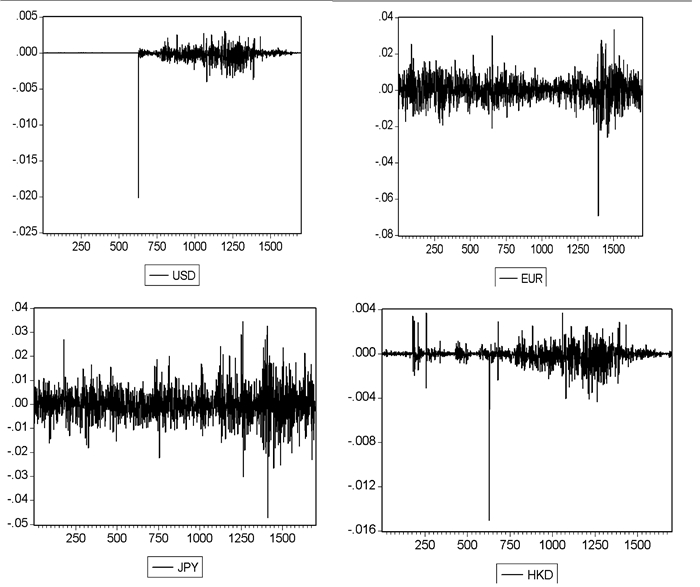
从图 1可以看出收益率序列大幅度的波动后紧跟着是较大幅度的波动，较小幅度的波动后紧跟着是较小幅度的波动，即这4种序列存在波动性集聚特性。而且我们从图 1美元波动图中可以明显看出汇率改革之前汇率管理采取人民币盯住美元的汇率政策，波动性几乎为0，汇率改革后实施人民币与美元浮动汇率政策，表现在波动图上具有明显的波动性。2008年9月15日后随着全球金融危机的爆发，为了使中国经济衰退不至于太大，中国实施稳定的汇率政策，确保金融体系的稳定，在这段时间内人民币对美元的汇率波动也较为平稳。

(三) 正态性检验

表 2为我们对三个时间段序列的四种外币进行One-Sample K-S Test的检验结果，从检验结果我们可以看出在汇率改革前以及金融危机爆发后两时期日元的K-S检验的P值分别为0.694、0.545，均大于0.05，欧元在三个时期的K-S检验的P值分别为0.285、0.211、0.143，均大于0.05，即在5%的显著性水平下，这些序列在相应期间内是不能拒绝正态分布的原假设，而在其他情形下，相应的P值小于0.05，即在5%的水平下，其序列的分布与正态分布有显著差异。

(四) GARCH(1, 1) 模型的构建

我们针对三个时间段的美元、欧元、日元以及港币汇率的时间序列分别建立GARCH(1, 1) 模型，并对各模型进行估计及检验，检验结果见表 3，其中Panel A表示汇率改革前外币日收益率时间序列的模型估计及检验结果，Panel B表示汇率改革后至金融危机爆发前外币日收益率序列的估计结果，Panel C表示金融危机爆发后外币日收益率序列的评估结果。在模型估计中，GARCH表示收益率$R_t$的条件方差，$RESID(－1)^∧2$表示残差平方和的滞后一阶，GARCH(-1) 表示条件方差的滞后一阶。由表 3可以看出条件方差的滞后一阶估计系数C（3）在1%置信度下显著，残差平方和滞后一阶的估计系数C（2）在1%置信度下也显著，但欧元和日元不显著，参数C(1) 除2003-2005时段港币显著外其余都不够显著。由表 3的ARCH-LM检验结果知ARCH效应已经消失，综合可知GARCH（1，1）模型模拟各外币序列是较好的。

由表 3知GARCH(1, 1) 模型各项均显著不为零，说明条件异方差性明显，汇率波动具有集群性。同时我们从表中还可以看出，人民币/美元、人民币/港币的滞后系数（C3）均小于人民币/欧元、人民币/日元，即人民币/欧元、人民币/日元的波动性比人民币/美元、人民币/港币的更持久。而且人民币/欧元、人民币/日元的回报系数（C2）均比人民币/美元、人民币/港币的回报系数小，即人民币/美元、人民币/港币的波动性对市场运动反应更加迅速，其波动性更长而尖。

(五) 外汇投资组合的VaR-GARCH(1, 1) 计算

假设在2009年12月30日，某商业银行有欧元、日元各100万的外汇投资组合（美元、港币由于日收益率的分布是非正态的，因此不包含），下面我们来计算95%置信度下该投资组合的日VaR。

把当天的外汇头寸按当天汇率换算成等价的人民币。当天的汇率分别为1欧元=9.783 6元人民币，1日元=0.074 217元人民币，可以得到由各种外币换来的人民币风险头寸共9 857 817元。

采用GARCH模型来预测2010年1月4日（1-3日为假日）的条件方差及协方差。

用2008年9月16日至2009年12月30日人民币/欧元、人民币/日元两时间序列通过GARCH模型获得在2010年1月4日的条件方差及它们之间的相关系数ρ_ij，然后再根据公式$\text{Cov}(R_{i},R_{j})=ρ_{ij}σ_{i}σ_{j}$得到协方差矩阵∑的预测值。

计算外汇投资组合的日VaR。首先计算各外币在组合中所占的市值比重向量w，接着得到组合的整体条件方差$σ^2_p$：$σ^2_p=w′∑w$ = 7.87247E-09，最后由公式$\text{VaR}_p=αW_0\sqrt{w′∑w}$，取$α=1.645$得出95%置信度下该组合的VaR为：$\text{VaR}_p=$1.645*985 781 7^*$\sqrt{7.872 47E－09}$=2 550.216，取$α$=2.326得出99%置信度下组合的VaR值为$\text{VaR}_p={2.326}*985 781 7*\sqrt{7.872 47E－09}$=360 5.959，取$α$=3.09得出99.9%置信度下组合的VaR值为$\text{VaR}_p=3.09*985 781 7*\sqrt{7.872 47E－09}$=4 790.376，计算结果表明在95%、99%以及99.9%置信度下投资组合（100万欧元和100万日元）在2010年1月4日的潜在最大损失分别为人民币2 550.216元、3 605.959元以及4 790.376元。

三、结论

本文采用VaR-GARCH(1, 1) 模型，选取2003年至2009年人民币对四种外汇的交易数据度量了商业银行外汇资产组合的风险。通过对四种外汇收益率序列的研究发现，四种收益率序列具有尖峰特征且在1%置信度下这些汇率不一定服从正态分布假设，此时采用传统VaR方法估计的汇率风险将是有偏的。而随着中国进出口贸易量的持续高速增长，商业银行不可避免地持有越来越多的外汇头寸，必须对外汇风险进行较准确的计量。从本文构造的GARCH模型的估计和检验来看，外汇收益序列具有波动集聚性特点，因此GARCH（1, 1）模型能够有效地刻画收益率序列。从欧元和日元组成的模拟外汇资产组合来看，在99.9%置信水平下，用VaR-GARCH(1, 1) 估计的最大潜在损失约为头一交易日市场价值的0.05%，以此度量了商业银行的汇率风险。实践中，商业银行可以以估计日之前若干交易日（如500或1 000等）的数据为基础，来滚动地估计未来交易日外汇头寸的潜在最大损失值，并做好相应的预防准备。