周内效应指证券市场一周之内各交易日收益率及其波动性存在差异,具体分为“收益率周内效应”和“波动性周内效应”。其中最常见的有周一效应(周一收益率最小、但风险最大)、周五效应(周五收益率最高、但风险最小),此外也有周二效应和周四效应。研究周内效应,其理论意义在于合理评价股票市场的有效性和发展更为现实的资产定价模型,其现实意义在于指导证券市场的监管和帮助投资者制定更为精确的投资策略。从Ferd C.Kelly首次发现周一收益率异常波动的事实,对股票市场周内效应的研究就一直没有间断过。早期的研究如Fama[1],Cross[2],French[3],Keim[4]等都证实了美国股票市场上存在周内效应。20世纪80年代中期,周内效应的研究范围从股票市场延伸到债券和期货等市场。Cornell[5],Dyl和Moberly[6]的研究发现美国的股指期货市场、政府债券市场都存在周内效应。Singleton和Wingender[7]对债务资本的收益率进行了研究,发现债务资本周一收益率为负数,而且长期债务资本比短期债务资本具有更明显的周内效应。Jaffe和Westerfield[8]研究了英国、日本、加拿大和澳大利亚股票市场的日收益率,结果显示这些证券市场均存在周内效应,但是与美国股票市场不同,澳大利亚与日本周二的平均收益率最低,而美国的股票市场周一的平均收益率最低。Barone[9]发现意大利市场的周内效应与澳大利亚和日本相似。G. Kohers等[10]的研究发现因为市场效率的不断提高,20世纪80年代美国市场存在的周内效应在90年代和21世纪却逐渐消失了,许多研究转向转型和新兴市场经济国家。Choudhry发现在许多发展中国家如印度尼西亚、马来西亚和泰国,其金融市场同样存在周内效应。Richard[11]通过对东欧转型和新兴市场经济国家研究发现广泛存在周内效应。
中国学者对周内效应的研究,在方法上经历了从简单的平均值判断到复杂的GARCH及非参数检验的过程,在样本上经历了从整个样本区间的研究到分区间研究的过程。俞乔[12],戴国强和陆蓉[13],范钛和张明善[14]的研究发现中国证券市场存在周内效应,并且沪市的周内效应更为明显。刘彤[15],田华、陆庆春[16]的研究表明上证市场存在“二五效应”。周少甫和陈千里[17]应用无条件波动的修正Levene检验和条件波动的GARCH模型对上海股市的周内效应进行研究,结果显示上海股市存在显著的周一高波动现象。何兴强[18]的检验发现上证综合指数收益和波动性都存在显著的星期效应:周五平均收益最高,周一平均收益最低,周四波动最大,周五波动最小。李凌波、吴启芳和汪寿阳[19]对中国开放式基金和封闭式基金的周内效应进行了实证检验,结果表明,中国基金市场存在一定的日历效应。上海基金指数和大部分样本开放式基金周一收益率相对更高,上半月的日收益率均值低于下半月的日收益率均值,这与股票市场的周内效应特点是不同的。崔婧等[20]、王如丰[21]的实证结果显示,牛市和熊市中的周内效应存在着显著差异,牛市时期表现出显著正向的周一效应,其收益率显著高于其他四个交易日,周四的收益率低于其他四个交易日;而在熊市时期则同时存在着显著为负的周一、周四效应,以及正向的弱周二效应。张晨曦、杨一文[22]运用混合密度网络法研究了股市流动性的周内效应, 实证研究发现沪深股市在一段时间中存在负的“星期五效应”。
本文在已有研究的基础上扩展了研究样本容量,采用1995年5月5日至2009年7月27日期间上证综合指数和深证成分指数日收益率为样本,共计3 452个样本,极大弥补了早期研究样本容量不足的问题;并分区间研究中国涨跌停板制度的实施对收益率及其波动性周末效应的影响,采用条件异方差模型对时间序列的残差进行拟合,并且每一样本区间均采用GARCH模型、GARCH-M模型和E-GARCH模型对其进行检验,后两者分别就风险对收益率的影响和“好坏消息”对收益率影响进行了实证检验。
二、数据及分析方法 (一) 数据及其描述性统计分析鉴于1995年以前,中国股票市场的交易制度为T+0制度,从1995年开始实行T+1制度,而且1995年以前的市场规范性较差,因此我们选取1995年5月5日至2009年7月27日沪深两市的股票价格作为研究样本。1996年12月26日,中国开始实行涨跌板制度,因此我们在运用模型识别法(即波动率模型)时就全样本、1995年5月5日至1996年12月25日和1996年12月26日至2009年7月27日进行分析比较,检验涨跌停板制度对周内效应的影响。因为描述统计不涉及变量系数的显著性分析,所以统计分析只对全样本进行比较(表 1、表 2)。本文数据来源于深圳国泰安信息技术开发有限公司的CSMAR数据库,采用上证综合指数和深证成分指数的日收益率HR和SR作为研究对象,其中HR=lnPt-lnPt-1,SR同样定义,Pt表示第t期指数收盘价格。
| 表 1 沪深两市日收益率全样本描述性统计 |
| 表 2 沪深两市周一到周五描述性统计 |
从表 1可以看出,沪深两市的股票收益率的分布有左偏且峰度远大于3,有尖峰胖尾特征,而且J-B统计量远大于临界值都说明了沪深两市的股票日收益率非正态分布。
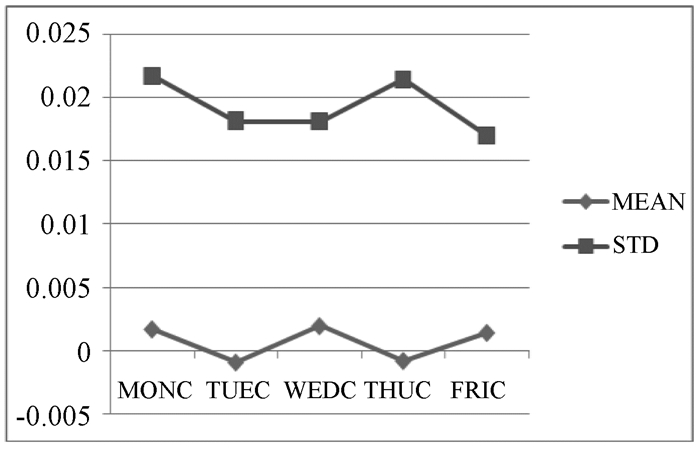
在表 2中,(1) 从均值看,两市具有相似性,两个市场中周二与周四的平均值都为负,且周二的日均收益率一周最低;周一、周三和周五的平均值都为正,周三为最高, 周五次高,两者相差不大。因此就收益率的均值看,沪深两市的确存在着刘彤的“二五效应”,只是周三收益率更高。(2) 从标准差分析,即从日均收益率的波动性看,两市的最大标准差均出现在周一,说明经过三天的信息量集中反映在周一,导致其波动性最大,这也与国际股票市场的“周一效应”相符。(3) 需要注意的是,两市中周三的平均收益率是最大的,而标准差是最小的,这与风险溢价理论不符合,需要进一步探讨。(4) 从偏度、峰度和J-B统计量看,两市的股票平均收益率都呈非正态分布,因为峰度大于3,J-B统计量远远大于临界值。结合沪市和深市的收益率与标准差图形(图 1、2)可以有更直观的认识。
|
图 1 沪市交易日收益率与标准差关系图 |
|
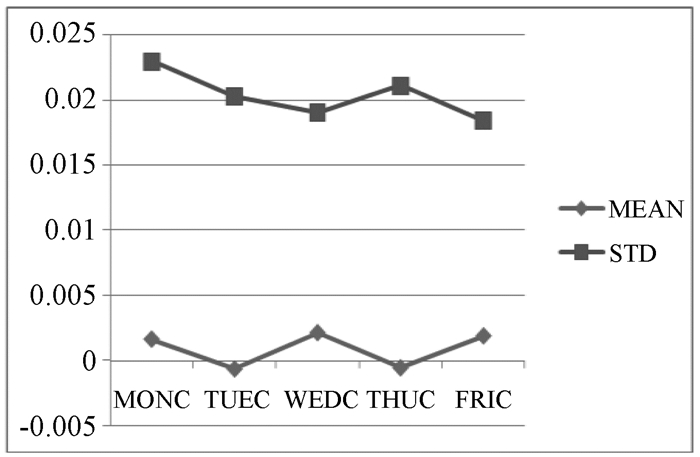
图 2 深市交易日收益率与标准差关系图 |
但是,描述性统计的结果推导出的结论并不一定可靠,其结论不具有一般性,必须进行严格的统计与计量检验,才能说明收益率与波动性的显著性。
(二) 研究模型及方法目前,对于股票市场周内效应的主流研究方法主要包括模型识别法、非参数检验法。本文主要采用前一种方法对沪深两市的股票收益率进行实证检验。整个检验过程通过EVIEWS6.0实现,主要步骤如下:(1) 对股票收益率进行平稳性检验,通过单位根检验(ADF)实现。(2) 用股票收益率HR或者SR对虚拟变量周内交易日(i=2, 3, 4, 5) 进行OLS回归,含常数项;首先对回归的残差进行序列相关检验,以判断收益率是否存在自相关性,若存在自相关性,同时要确定自相关阶数,并进行修正。(3) 对步骤2的回归方程的残差,进行ARCH-LM检验,以确定是否存在条件异方差性。(4) 如果步骤3验证模型存在条件异方差,就要分别建立GARCH、GARCH-M和EGARCH模型检验风险对收益率的影响是否显著和正面信息与反面信息对收益率变化的影响是否对称,最终通过AIC准则和SIC准则选择最优的模型。(5) 实证分析结果陈述。
ARCH和GARCH模型都属于波动率模型,是对一般回归模型的方差进行拟合。在金融市场上,金融资产收益率的波动率(用条件方差反映)往往具有以下特征:波动率存在聚类性(volatility clustering),即大的变化之后是大的变化,小的变化之后是小的变化;波动率不趋于无穷,在一定范围内变化;波动率具有杠杆效应,研究表明当股票价格下跌时,收益率的波动率变大,即坏消息带来了更大的波动性,这表现为波动率变化的非对称性。这些波动率的变化特征表现为条件异方差,由此产生了条件异方差模型(ARCH)。
Bollerslev对ARCH模型进行了推广,提出了广义自回归条件异方差模型,即GARCH模型。GARCH只是ARCH的延伸,如果说ARCH是关于条件方差的自回归模型,那么GARCH就是条件方差的自回归平滑(ARMA)模型。本文将运用GARCH(1, 1)-M和EGARCH(1, 1) 模型,分别是均值方程和条件异方差方程,在此给出两者的表达式及检验指标。
GARCH(1, 1)-M的均值方程:
| $ {R_{\rm{t}}} = c + {\lambda _{\rm{t}}}TUE + {\lambda _{\rm{w}}}WED + {\lambda _{{\rm{th}}}}THU + {\lambda _{\rm{F}}}FRI + {\xi _{\rm{t}}}\sqrt {{h_{\rm{t}}}} + {\varepsilon _{\rm{t}}} $ |
其中关键系数为ξt,若ξt为正且显著,表明收益率风险自身(方差)能够增加收益率,即满足风险溢价定理;若ξt不显著,则不存在风险增加收益的效果。
EGARCH(1, 1) 的条件方差方程:
| $ \begin{array}{l} {\rm{log(}}{{h}_{\rm{t}}}{\rm{) = }}{c}{\rm{(6) + }}{c}{\rm{(7)}}\left| {\frac{{{\varepsilon _{{\rm{t - 1}}}}}}{{\sqrt {{h_{\rm{t}}}} }}} \right| + {c}{\rm{(8)}}\frac{{{\varepsilon _{{\rm{t - 1}}}}}}{{\sqrt {{h_{\rm{t}}}} }}({{h}_{{\rm{t - 1}}}} + {c}{\rm{(9)log(}}{{h}_{{\rm{t - 1}}}}{\rm{)}}) + {c}{\rm{(10)}} * TUE + {c}{\rm{(11)}} * WED \\+ {c}{\rm{(12)}} * TUE + {c}{\rm{(13)}} * FRI \end{array} $ |
其中关键检验系数为c(8),若c(8)>0,则说明市场中正面消息对股票收益率波动性带来的影响大于负面消息带来的影响,股票市场中存在波动率杠杆效应;若c(8) < 0,则结论相反。
根据平均收益率的变化情况,我们可知其波动率存在聚集性,同时与GARCH模型相结合,我们建立如下模型,其中R为HR或SR。
均值方程:
Rt=c+λtTUE+λwWED+λthTHU+λFFRI+εt
条件方差方程:
| $ {h_{\rm{t}}} = {\alpha _0} + \sum\limits_{i = 1}^p {{\beta _{\rm{t}}}} {h_{{\rm{t - 1}}}} + \sum\limits_{j = 1}^1 {{\alpha _j}} \varepsilon _{{\rm{t - }}j}^2 + {\eta _{\rm{t}}}TUE + {\eta _{\rm{w}}}WED + {\eta _{{\rm{th}}}}THU + {\eta _{\rm{F}}}FRI $ |
| $ {\varepsilon _{t}} = \sqrt {{h_{\rm{t}}}{v_{\rm{t}}}} $ |
vt独立同分布白噪声过程,并且E(vt)=0, Var(vt)=1。
根据虚拟变量选择规则,一般选择m -1个虚拟变量,以避免进入“虚拟变量陷阱”。虚拟变量含义为,以TUE为例,当t是为周二时TUE=1, 其他情况等于0。其余同样定义。需要注意的是,在方程中当所有虚拟变量都为0时,常数项为周一(MONDAY)的系数,而其他虚拟变量的系数须加上常数项后才为其自身对平均收益率的影响程度。
三、实证分析与结果检验 (一) 收益率均值周内效应检验对沪市、深市股票收益率进行平稳性检验,检验结果如表 3所示。
| 表 3 沪市、深市股票收益率平稳性检验 |
通过ADF检验,统计量绝对值大于1%和5%的临界值,同时其相伴概率小于0.01,因此拒绝零假设(序列存在单位根),接受备择假设。因此沪市和深市的股票收益率均不存在单位根,因此其时间序列是平稳的,可以用最小二乘法进行检验。
根据前述均值方程Rt=c+λtTUE+λwWED+λthTHU+λFFRI+ε,进行最小二乘法回归(OLS)。分别对沪深两市全样本、1995年5月5日至1996年12月25日和1996年12月26日至2009年7月27日进行回归检验,结果如表 4。
| 表 4 最小二乘法的估计结果 |
从OLS结果来看,(1) 在全样本区间,沪深两市周内交易日的系数呈现不显著的特征,深市的一阶自回归系数通过显著性检验,说明深市上期的收益率会明显影响下期的日均收益率;(2) 在1995-1996年区间,沪市的收益率序列存在一阶自相关,深市在周二的收益率为周内最低,并且显著为负,周一的系数同样显著,但是为正,因此本区间收益率存在周二效应;(3)1996-2009年区间内,类似全样本区间,只有深市存在一阶自相关,其他均不显著。造成系数不能通过显著性检验的原因很可能是回归方程的残差存在条件异方差,导致假设检验失效。下面进行收益率的ARCH效应检验。
对步骤2的回归残差进行ARCH效应的Q统计量检验和ARCH-LM检验,结果见表 5。为确保检验的有效性,阶数取12。
| 表 5 ARCH效应的Q统计量和LM检验 |
通过ARCH效应的Q统计量和LM检验可以看出,统计量均远远大于临界值,而且两者相伴概率也均说明沪深两市的股票收益率存在明显的ARCH效应,有必要建立ARCH模型。
本文对全样本区间、1995-1996年区间和1996-2009年样本区间的股票收益率分别建立了GARCH(1, 1)、GARCH-M(1, 1) 和EGARCH(1, 1) 模型,从AIC和SIC准则、R-adjusted等检验准则出发,选择各自最合适的模型进行分析。分析将按照时间区间对沪深两市的收益率模型进行检验。
对于全样本区间,沪市和深市的三个模型的AIC准则量见表 6。
| 表 6 全样本期间三个模型的AIC准则量 |
表 6说明对于沪市和深市在全样本区间都是GARCH(1, 1)-M的AIC准则最小,因此我们又综合考虑了R-adjusted和SIC准则,在全样本区间两市均选择GARCH(1, 1)-M模型。其实证分析结果见表 7。
| 表 7 全样本区间GARCH估计结果 |
在全样本区间,沪市在周四的系数显著为负,且为一周的次低水平,最低出现在周二但是不显著,因此沪市的收益率均值并未表现出与前述文献相符的周内效应,但是其
沪市在全样本区间并未显示显著的周内效应,这可能反映了上海股市消息的平衡性,另一方面也预示着两个股票市场在信息的吸收、消化上存在着差异,或者表明所用的模型并没有能够很好地反映出上海股市报酬所隐含的内在特性,因此有必要进一步探讨。
我们对所有的周一进行细化,并定义为M1、M2、M3、M4和M5,分别表示每月的第一个周一、第二个周一、第三个周一、第四个周一和第五个周一。在原模型中加入这五个变量,以期发现沪市股票市场的内在规律性。三个模型中,GARCH(1, 1) 更好地反映了其规律。但是EGARCH中c(8)=-0.021 168,并且显著,说明沪市负面消息对收益波动率的影响大于正面消息带来的影响。GARCH(1,1) 的估计结果见表 8。
| 表 8 GARCH(1,1) 的估计结果 |
鉴于沪市股票收益率在全样本区间的特殊性,在此将其均值方程与条件方差方程一并讨论。从均值方程来看,平均收益率在M5时显著为负,并低于其他交易日的收益率,周三和周五的系数均显著为正,并且周三大于周五,因此沪市的收益率特点是:在第五个周一具有最低周内收益率,在周三具有最高收益率,可以称为“一三效应”;从条件方差方程看,除去第三个周一不显著外,其他交易日的系数均显著,其中最高波动率出现在每月的第一个周一,其系数显著正,说明每月的第一个周一可能由于月末的积累信息对月初开始的股票价格造成波动。最低波动率出现在周二并且其系数显著为负。
鉴于1996年12月26日开始实行涨跌停板制度,我们将全部样本分为1995年5月5日至1996年12月25日和1996年12月26日至2009年7月29日两个区间,在此对其周内效应的变化进行对比分析。两个区间中GARCH(1, 1)、GARCH-M(1, 1) 和EGARCH(1, 1) 模型的AIC准则量见表 9。
| 表 9 分阶段区间模型AIC准则量 |
由以上AIC判定并结合可决系数和SIC准则,在1995-1996年区间沪市选择EGARCH(1, 1) 模型,深市选择GARCH-M(1, 1) 模型;在1996-2009年区间,沪市选择GARCH-M(1,1) 模型,深市选择EGARCH(1,1) 模型。其均值方程的估计结果见表 10。
| 表 10 沪深两市分区间实证检验 |
1995-1996年期间,沪市通过EGARCH(1, 1) 分析,均值没有表现出显著的周内效应,深市则表现出显著的周五效应,周五的系数为正,而且通过5%显著性水平下的检验。
由此对比分析看出,1995-1996年间,沪市没有明显周内效应,而到1996-2009年间,具有了明显的周一效应;深市从具有周五效应转至其后的周一效应。而且在1996-2009年间,沪市和深市均表现出显著的周一效应。这一结论与马丹的涨跌停板制度削弱了周内效应的结论不一致。涨跌板停制度并未对股票市场的有效性有显著的效果。
(二) 收益率波动性周内效应检验股票市场的周内效应不仅表现在收益率均值随着交易日的变化而改变,同时也表现在收益率的波动性上,即其条件方差随着各交易日的不同而各异。我们通过构造条件方差方程进行波动率的实证分析。
| $ {{h}_{\rm{t}}} = {\alpha _0} + \mathop \sum \limits_{i = 1}^p {\beta _i}{{h}_{{\rm{t - i}}}} + \mathop \sum \limits_{j = 1}^q {\alpha _j}\varepsilon _{{\rm{t - }}{j}}^2 + {\eta _{\rm{t}}}TUE + {\eta _{\rm{w}}}WED + {\eta _{{\rm{th}}}}THU + {\eta _{\rm{F}}}FRI $ |
| $ {\varepsilon _{\rm{t}}} = \sqrt {{h_{\rm{t}}}{v_{\rm{t}}}} $ |
而各个时期模型的选择与上述的AIC准则应该一致,以保持均值方程与方差方程的一致。其分析结果见表 11和表 12。
| 表 11 GARCH-M方差方程分析 |
| 表 12 EGARCH(1, 1) 方差方程分析 |
如前所述在全样本区间,沪深两市通过GARCH(1, 1)-M模型检验,沪市周五的系数显著为正,说明周五的报酬波动性大于其他交易日;深市则表现出周一显著为正,说明从1995-2009年期间,股市报酬波动率都有周一效应发生,但是具体波动性的时间段表现不一致,可能是风险传递机制的差异造成。
在1995-1996年期间,运用EGARCH(1, 1) 对沪市进行检验,如前所述,若c(8) < 0且显著,则表明股票市场负面消息的影响大于正面消息,而沪市在这一期间c(8) < 0, 且通过了5%显著性水平的检验,周一、周二和周五的系数均显著,后两者为负,而周五的波动率波动性表现为周内最小,这与前述的波动率周五效应是相符的。深市在周三周四和周五均通过显著性检验,而且最低的波动率出现在周三。
在1996-2009年期间,运用GARCH(1, 1)-M对沪市进行检验,整个周内交易日都通过了5%显著性水平下的检验,且周二表现出最低的波动率水平,但是周五与其相差不大同时也显著为负,因此可以认为存在弱的周五效应;运用EGARCH(1, 1) 对深市进行分析发现,c(8) < 0且显著,表明深市股票收益波动性存在杠杆效应。而周二至周五的波动率也显著为负,且在周二达到最低水平,这与沪市的波动率水平相符,表明1996-2009年期间,股票市场的波动率周内效应,具体表现为周二效应。
与均值方正周内效应的结果相似,通过比较分析认为,涨跌停板制度削弱股票市场波动率的周内效应同样不显著,2006年后股票市场的有效性仍未有很大提高。而整个样本区间,沪深股票市场的报酬波动率同样具有显著的周内效应。
四、结论通过以上实证检验和分析,我们发现以下结论:(1) 在全样本区间,就均值方程而言,深证市场存在显著的周内效应,周一的收益率为一周最低,而周五的收益率为一周内最高,与前述文献的周内效应概念相符;而沪市的周一和周三的收益率分别显著地为周内最低和最高,表明沪市同样存在周内效应,只是其具体分布与前述分布有所差异。而从条件方差看,沪市和深市的收益率波动性也具有明显的周内效应,但是分别出现在周五和周一。(2) 从分段区间的比较发现,涨跌停板制度对于股票收益率均值的周内效应及其波动率的周内效应均表现出明显的削弱作用。(3) 本文运用GARCH(1, 1)-M模型对股票市场风险(波动性)对于其收益率的影响进行了检验,发现在深市的全样本区间和1995-1996年区间、沪市1996-2009年区间,随着股票自身风险的增加其收益率也显著地增加,这与风险溢价理论是相符的。(4) 本文还运用EGARCH(1, 1) 模型对沪深两市股票波动率的杠杆效应进行了实证,发现在沪市的全样本区间和1995-1996年区间、深市的1996-2009年区间,负面信息对股票收益率波动性的影响大于正面信息带来的影响,也说明在这些区间上,波动率杠杆效应的存在。由以上结论,可以看出中国股票市场的周内效应是较为明显的,主要是因为中国股市坏消息在周末到周一出现的频率较高,而好消息均匀分布在一周之内,加上中国股市投机气氛浓厚和多年形成的“政策依赖症”,短线炒作者在周末博利好消息推高周五的股价,造成周五的高收益率。而在下周一,无论是猜中利好消息而获利,还是出现利空而亏损或消息真空,短线投资者都会抛出股票,从而造成周一的低收益率。另外投资者的情绪也会对周内效应产生影响。总之,市场的有效性还有待进一步提高,而这些需要交易制度进一步规范,信息发布进一步公开。
| [1] | FAMA E F. The behavior of stock prices[J]. Journal of the Business, 1965(1): 34–1051. |
| [2] | CROSS F. The behavior of stock prices on fridays and mondays[J]. Financial Analysts Journal, 1973, 29(6): 67–69. DOI: 10.2469/faj.v29.n6.67 |
| [3] | KENNETH F. Stock return and the weekend effect[J]. Journal of Financial Economics, 1980(5): 55–69. |
| [4] | KEIM D B, STAMBOUGH R F. Further investigation of the weekend in stock returns[J]. Journal of Finance, 1987, 39: 819–835. |
| [5] | CORNELL B. The weekly pattern in stock returns:Cash versus futures:A note[J]. Journal of Finance, 1985(2): 583–588. |
| [6] | DYL E A, MOBERLY E D. The daily distribution of changes in the price of stock index futures[J]. Journal of Futures Markets, 1986, 6(4): 513–521. DOI: 10.1002/(ISSN)1096-9934 |
| [7] | SINGLETON J CL, WINGENDER J R. The nonparallel weekend effect in the stock and bond market[J]. Journal of Financial Research, 1994, 17(4): 581–538. |
| [8] | JAFFE, WESTERIELD. The week-end effect in common stock returns:The international evidence[J]. Journal of Finance, 1985, 40(2): 433–454. DOI: 10.1111/j.1540-6261.1985.tb04966.x |
| [9] | BARONE E. The Italian stock market:Efficiency and calendar anomalies[J]. Journal of Banking and Finance, 1990, 14: 483–510. DOI: 10.1016/0378-4266(90)90061-6 |
| [10] | KOHERS G, KOHERS N, PANDEY V, et al. The disappearing day-of-the-week effect in the world's largest equity markets[J]. Applied Economics Letters, 2004, 11(3): 167–171. DOI: 10.1080/1350485042000203797 |
| [11] | RICHARD A, SEYED M, MARK J. The day-of-the-week effect in stock returns:Further evidence from eastern European emerging markets[J]. Emerging Markets Finance and Trade, 2004, 40(4): 53–62. |
| [12] | 俞乔. 市场有效、周期异常与股价波动[J]. 经济研究, 1994(9): 43–50. |
| [13] | 戴国强, 陆蓉. 中国股票市场的周末效应检验[J]. 金融研究, 1999(4): 48–54. |
| [14] | 范钛, 张明善. 中国证券市场周末效应研究[J]. 中国管理科学, 2002(2): 92–95. |
| [15] | 刘彤. 利用非参数方法对上海股市周末效应的研究[J]. 数理统计与管理, 2003(1): 28–33. |
| [16] | 田华, 陆庆春. 上海股市周日效应GARCH模型族的实证研究[J]. 系统工程理论与实践, 2003(7): 75–79. |
| [17] | 周少甫, 陈千里. 上海股市波动的周末效应检验[J]. 数理统计与管理, 2004(3): 57–60. |
| [18] | 何兴强. 上证指数收益和波动性的星期效应检验[J]. 中山大学学报:社会科学版, 2003(6): 89–93. |
| [19] | 李凌波, 吴启芳, 汪寿阳. 周内效应和月度效应:中国证券投资经济市场的实证研究[J]. 管理学报, 2004(1): 41–46. |
| [20] | 崔婧, 杨扬, 程刚, 等. 周内效应在牛市、熊市中的异化现象—关于中国证券市场的一个实证研究[J]. 系统工程理论与实践, 2008(8): 17–25. |
| [21] | 王如丰. 不同股市行情下的星期效应研究—基于沪深股市的实证检验[J]. 上海金融学院学报, 2009(1): 32–38. |
| [22] | 张晨曦, 杨一文. 基于混合密度网络测度股市流动性"周内效应"[J]. 中国证券期货, 2010(9): 38–40. |
 2014, Vol. 20
2014, Vol. 20
