一直以来,股票市场收益与通货膨胀两者之间的关系是研究股票市场与宏观经济环境之间关系、评价股票市场有效性的重要途径之一。从客观上讲,股票市场价格的波动受通货膨胀直接或者间接的影响,但是,就影响程度而言,学术界尚未形成一致的结论。
股票收益率是指投资于股票所获得的收益总额与原始投资额的比率。著名的费雪假说[1]指出,资产的价格是随通胀率变动而变化的,如果通胀率发生变化时,资产名义收益率会发生相应变化,而实际收益率则维持现状,保持不变。然而,Fama & Schwert[2]却针对费雪假说提出了两条重要假设:一是股票市场必须是有效的;二是股票真实收益率与通胀率之间相互独立,互不影响。由此可以推断,股票的名义收益率与通胀率客观上存在正相关,并且能够有效对冲通货膨胀所带损失的保值品。目前,部分学者的研究结论也支持该假说,Boudhouch[3]研究了美国1802-1990年度数据后,发现股票收益率与通胀率存在正相关,与费雪假说一致。Westerlund[4]对1890-1997年14个OECD国家的面板数据进行协整检验,结果也支持费雪假说。
然而,也有部分学者通过实证研究发现通胀率与股票收益率之间存在显著负相关。例如,Gultekin[5]、Kaul[6]均发现了股票收益不能对冲通货膨胀所带来的损失,因此,其研究结论不支持费雪假说。由此,有不少学者致力于解释有悖于费雪假说现象的原因,归纳起来存在以下三个方面。
一是货币幻觉假说。所谓货币幻觉,实际上就是倾向于从货币的名义价值而不是实际价值的角度进行思考。Cohn & Modigliani[7]认为,在高通货膨胀时期,如果投资者错误地使用名义利率作为真实现金流的贴现率,随着通胀率的提高,名义利率也会上升,从而提高了未来真实现金流的贴现率,因此,股票价值容易被投资者错误低估,导致通胀率与股票收益率之间存在显著的负相关。Ritter & Warr[8]、Campbell & Vuolteenaho[9]分别研究了1983-2000年、1927-2002年的美国股票市场数据,发现通货膨胀与股票市场错误估值之间存在显著的相关性,当处于通货膨胀时期,投资者无法正确调整对未来收益增长率的预期,这就是所谓的货币幻觉假说,但不存在代理效应与通货膨胀风险溢价效应。
二是代理假说。基于美国1953年后的数据,Fama[10]建立了关于货币与实际经济的理性预期模型,发现了通胀率与股票收益率之间并无直接联系,其原因在于,虽然未来经济活动与当前的通胀率存在负相关,但是未来实体经济活动却与当前股票收益率存在正相关。因此,随着通胀率上升,投资者预期未来公司的盈利能力会下滑,红利下降,公司股票估值下降,投资者将卖出股票,股价下跌。Geske & Roll[11]扩展了Fama的研究,提出负债的货币化是对未来实体经济变化预期的体现,因此,负债的货币化也是美国股票收益率与通胀率存在负相关的成因之一。Sharpe[12]指出,从长期来看,市场对真实收益的预期与预期通货膨胀存在负相关,其中一个原因就是因为生产率降低。Bahram Adrangi等[13]对1990-1996年秘鲁和1985-1995年智利两国的通胀率、产出率以及股票收益率的关系进行了实证研究,发现两国通货膨胀与真实产出变动之间均存在显著的负相关,真实产出变动与真实收益存在正相关,这就说明了秘鲁、智利两国存在明显的代理假说效应。同时,他们也发现如果排除代理效应之外,通货膨胀与真实收益率之间仍然存在显著的负相关。Brunnermeier & Julliard[14]将这种关系应用到估值关系上,称之为代理效应。
三是风险溢价假说。Brandt & Wang[15]提出了风险溢价假说,持续上升的通胀率增加了未来金融资产的风险,提高了投资者所要求的风险溢价,以及现金流的贴现率,使股票估值水平下降,投资者抛售股票,导致股票价格下跌,收益率下降。
综上所述,通胀率对股票真实收益率产生负面影响主要源于影响未来实体经济产出、风险溢价和名义利率等间接因素,但两者之间并不存在直接的因果关系。
中国股市起步较晚,学术界对通货膨胀与股票收益关系的研究文献不多,但大部分研究表明通胀率与股票收益存在负相关。靳云汇[16]认为中国股票价格与通胀率存在反向变动关系,符合代理问题假说。赵兴球[17]也支持代理问题假说,他发现中国股票收益率与通胀率显著负相关,产出与股票收益正相关,但控制了产出对通货膨胀的影响后,股票收益与通货膨胀之间的负相关消失。刘金全[18]等分别从通货膨胀波动率与股票收益率负相关、通胀率与通胀波动率正相关的角度来解释中国股票收益与通货膨胀之间的负相关关系。韩学红[19]从产生通胀率的两大原因:供给冲击和需求冲击对股票收益的影响角度解释了股票收益率与通货膨胀率的关系。刘仁和[20]应用动态Gordon增长模型,解释了红利—股价比与通胀率正相关的原因。
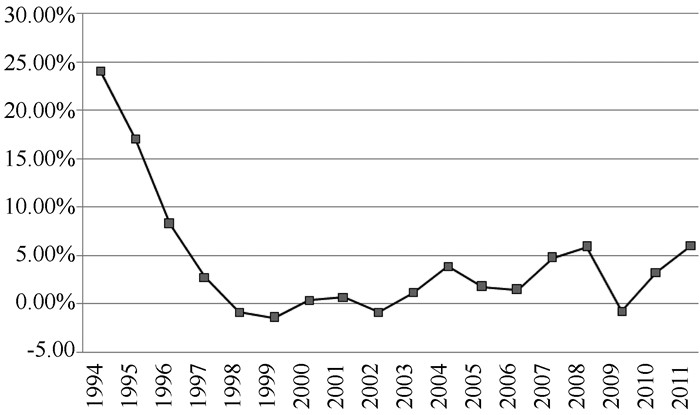
国内学者的研究在一定程度上解释了通胀率与中国股票收益率关系的产生机理,但有两个问题值得注意:(1)作为国民经济“晴雨表”的股票市场,股票收益的变动在一定程度上直接反映投资者基于未来相关估值要素的预期变化所产生的估值变动,正如Fama利用美国1953-1987年月度、季度和年度数据进行回归,发现股市收益率与未来实际产出变动显著正相关,他认为,这是投资者对于上市公司未来现金流的预期在现期股价上的体现;同时通胀率与各估值要素并非只存在单边的因果关系(即只考虑经济实体产出,而货币政策也是产生通胀的原因),在很大程度上通胀率也会对未来各估值要素(如实体经济形势、货币政策以及市场风险状态)产生不同程度的影响。而从该角度来解释股票收益率与通胀率相关关系的却较为罕见。(2)上述国内外文献对样本区间选择几乎没有考虑存在不同的宏观经济状态,而不同的宏观经济状态也可能会导致股票收益率对通胀率反应的差异。从中国通胀率趋势看,1994年1月至2011年9月,中国通胀率趋势曾呈现出不一致的发展格局,1994-1999年主要表现为通胀率的快速下滑,2000-2011年主要表现为通胀率的震荡攀升两种不同的状态(图 1),而不同的状态可能对股票收益与通胀率的关系产生不同的影响。
|
图 1 1994-2011年中国通胀率趋势 数据来源:中国经济信息网,2011年。 |
综上所述,根据中国股票市场的实际情况,本文基于Boyd等[21]的研究思路,将货币幻觉假说纳入其中,利用Gordon固定增长模型,将股票真实收益率对于通胀率的变动分解为代理效应、风险溢价效应和货币幻觉效应,分析验证在不同状态下,三种效应对中国股票收益率变动的影响途径以及显著程度,并且在清除三种效应影响后,检验通胀率与股票真实收益率有无直接的变动关系。
二、通胀率对股票收益波动影响的传导机制为了表达未来名义利率、风险溢价以及实体经济活动对股票实际收益的影响,现借鉴Gordon模型:
| $ P = \frac{{D\left( {1 + g} \right)}}{{r + \rho - g}} $ | (1) |
其中,D为当前红利水平,g代表未来预期的真实红利增长率,ρ代表投资者根据未来金融资产风险所要求的风险溢价,r代表未来预期的无风险真实利率,P代表当前股票真实价值。现对式(1)求全微分:
| $ \begin{array}{l} RR = \frac{{\Delta P}}{P} = - \frac{P}{{D\left( {1 + g} \right)}}\left[ {\Delta r + \Delta \rho - \left( {\frac{{P + D}}{P}} \right)\Delta g} \right] = \left[ { - \frac{P}{{D\left( {1 + g} \right)}}} \right]\Delta r + \left[ { - \frac{P}{{D\left( {1 + g} \right)}}} \right]\Delta \rho + \\ \left[ {\frac{{P + D}}{{D\left( {1 + g} \right)}}} \right]\Delta g \end{array} $ | (2) |
其中,
如式(2)表现的数量关系,Boyd等认为,当前股票收益率水平实际上与未来预期的实际利率、风险溢价以及实际红利增长变动有直接联系,而其他宏观经济要素对当前证券资产收益的影响主要是通过对未来这3种要素的影响而间接产生的。根据货币幻觉假说,随着通胀率的攀升,尽管未来名义利率也会上升,但是,这并不会使未来实际利率有明显变化,因此,在投资者理性估值情况下,股票实际收益率不会因为名义利率变动而发生显著变动。Cohn & Modigliani却认为,事实上,证券投资人就是错误地将名义利率作为真实现金流的贴现率,导致证券资产被错误估值,最后影响了该资产的收益率大小。为了反映这种现象,本文又将名义利率r′作为贴现率,以此来表现货币幻觉效应对股票收益率的影响,从而可以得到在错误估值情况下的股票真实收益率RR′:
| $ RR' = \left[ { - \frac{P}{{D\left( {1 + g} \right)}}} \right]\Delta r' + \left[ { - \frac{P}{{D\left( {1 + g} \right)}}} \right]\Delta \rho + \left[ {\frac{{P + D}}{{D\left( {1 + g} \right)}}} \right]\Delta g $ | (3) |
根据Cohn & Modigliani提出的货币幻觉假说,名义利率可以由名义货币供应增长率进行表达。令Δr′=θΔm,Δm代表名义流通货币供应的对数增长率,根据宏观经济理论,本文假定Δm与名义利率r′的变动量成负相关关系,θ < 0表示名义流通货币对名义利率的敏感系数。现将Δr′=θΔm带入式(3):
| $ RR' = \left[ { - \frac{{P\theta }}{{D\left( {1 + g} \right)}}} \right]\Delta m + \left[ { - \frac{P}{{D\left( {1 + g} \right)}}} \right]\Delta \rho + \left[ {\frac{{P + D}}{{D\left( {1 + g} \right)}}} \right]\Delta g $ | (4) |
式(4)表明,在错误估值情况下,当前股票实际收益率RR′取决于未来名义货币供应增长率Δm、风险溢价变动Δρ以及实体经济产出的变动水平Δg。同时,根据Fama提出的代理问题,未来实际产出与股票实际收益正相关,通胀率与未来实际产出负相关,而未来实际产出最后反映到未来上市公司的实际红利增长率的变动中,因此,可以用实际产出增长变动来代替红利增长率的变动。同理,根据Brandt等提出的风险溢价效应,也可以由估值模型中的风险溢价变动进行表达。
为了验证股票真实收益率与通胀率的变动关系的产生机理,在式(4)的基础上,本文继续对错误估计情况下的真实收益率RR′求关于通胀率I的一阶导数:
| $ \begin{array}{l} \frac{{{\rm{d}}RR'}}{{{\rm{d}}I}} = \left[ { - \frac{P}{{D\left( {1 + g} \right)}}} \right]\frac{{{\rm{d}}\left( {\Delta r'} \right)}}{{{\rm{d}}I}} + \left[ { - \frac{P}{{D\left( {1 + g} \right)}}} \right]\frac{{{\rm{d}}\left( {\Delta \rho } \right)}}{{{\rm{d}}I}} + \left[ {\frac{{P + D}}{{D\left( {1 + g} \right)}}} \right]\frac{{{\rm{d}}\left( {\Delta g} \right)}}{{{\rm{d}}I}} = \\ \left[ { - \frac{{P\theta }}{{D\left( {1 + g} \right)}}} \right]\frac{{{\rm{d}}\left( {\Delta m} \right)}}{{{\rm{d}}I}} + \left[ { - \frac{P}{{D\left( {1 + g} \right)}}} \right]\frac{{{\rm{d}}\left( {\Delta \rho } \right)}}{{{\rm{d}}I}} + \left[ {\frac{{P + D}}{{D\left( {1 + g} \right)}}} \right]\frac{{{\rm{d}}\left( {\Delta g} \right)}}{{{\rm{d}}I}} = {\mathit{\Lambda }_1} + {\mathit{\Lambda }_2} + {\mathit{\Lambda }_3} \end{array} $ | (5) |
其中,I为通胀率,dI为通胀率波动。从式(5)可知,RR′相对通胀率的变动水平
基于以上论述,无论是费雪效应,还是货币幻觉效应、代理效应、风险溢价效应,均建立在利率市场化的基础之上,而利率市场化对货币政策的有效性能够产生重大作用,因此,在国外的相关理论中,以上论述的若干效应都成立。由于中国的利率并非市场化,必然会影响到资产价格的变动,从而资产价格的变动与通胀率的关系是否仍旧符合费雪效应、Gordon股价模型有待论证,因此,本文提出了以下4个命题作为实证研究部分的验证目标。
命题A:当同时存在三种效应时,中国股票真实收益率RR与通胀率I之间存在着负相关。
命题B:中国股票真实收益率RR与未来实体经济活动变动Δg存在正相关,与未来货币供给增速Δm存在正相关,与未来风险溢价变动Δρ存在负相关。
命题C:在中国股市中,通胀率I与未来实体经济活动变动Δg存在负相关,与未来货币供给增速Δm存在负相关,与未来风险溢价变动Δρ存在正相关。
命题D:在中国股市中,通胀率I与股票真实收益率RR在排除三种效应影响后,并不存在显著负相关。
三、数据与模型变量的选择 (一) 代理变量假设与数据分析为保证数据的信度与效度,本文从中国经济信息网与中国人民银行官方网站选取了1994年1月至2011年9月的数据作为研究对象。从现实分析,由于中国无风险名义利率水平的一年期存款利率长期保持不变,因此,如果选用该指标会使利率的变动量长期为零,模型的估计就没有意义。由于中国利率并非市场化,货币管理当局实际上长期控制着名义利率以及货币供应量的变化,这两个指标共同作为当局货币政策工具,是影响未来实体经济和控制通胀率趋势的两大调控手段,两者具有很高的配套性。因此,针对预期的名义利率的变动情况,我们实际选择了1994年1月至2011年9月狭义货币供应量M1的对数增长率
① 韩学红等(2008)认为对数货币供给增长率与名义利率变动存在反向变动关系。
在代理效应假说中,表示实体经济活动②变化的代理变量选用中国1994年1月至2011年9月的工业实际增加值增速的一阶差分Δg。由于剔除了价格因素,本文所描述的工业增加值增速实际上反映的是工业实际生产量的增长速度,与工业生产指数的含义近似。
② 实体经济活动一般应用GDP来代表,由于中国GDP增长率无月度数据,而工业增加值与GDP有很好的关联性,可以代表实体经济活动(Ghatrath,1997)。
Lee,Myers & Swaminthan[22]验证了Dow30股票的内在价值与股票价格比值(
在通胀率处理上,选取中国1994年1月至2011年9月的通胀率(同比)I′,将该数据对数化为ln(1+I′),然后根据Campbell & Vuolteenaho的方法对指数进行平滑处理后得到通货膨胀率I。
在股票收益率处理上,上证指数收益率采用对数化收益率R,利用中银国际交易软件数据收市指数IS,得到当月股票收益率
③ 由于(同比)通胀率I实际反应的是相邻两年同月通胀率大小,因此在计算月实际收益时要对I进行平均化处理, 得i=I/12。
(二) 通胀率趋势状态划分同一消息对于金融资产来说,有时候是利好的,有时候又是利空的,这取决于经济状态[23]。Johan Kniff[24]在研究美国的非预期通胀率与股票收益率关系时,发现两者关系取决于该国所处的经济状态。中国1994年1月至1999年12月时期为通胀率下跌时期,该时期的通胀率从20%以上的高水平迅速下滑,而1997-1998年的亚洲金融危机恰好使中国宏观经济扩张速度减缓;2000年1月至2011年9月则是通胀率的震荡攀升时期,在此时期中国经济形势持续好转。
(三) HP滤波分解通胀率本文将通货膨胀分为预期通货膨胀与非预期通货膨胀。HP滤波分析将时间序列看作不同频率成分的叠加,本文采用HP滤波分析方法,将通胀率的时间序列分解为趋势序列与偏离趋势的非预期离差序列。其中,趋势序列作为预期通胀率EIt,非预期通胀部分作为循环变动序列,更接近于实际状态。本文采用HP滤波分析主要是使不可观测部分—预期通胀率EIt达到最小:
| $ \min \left\{ {\sum\nolimits_{{\rm{t}} = 0}^{\rm{T}} {{{\left( {{I_{\rm{t}}} - E{I_{\rm{t}}}} \right)}^2}} + \lambda \sum\nolimits_{{\rm{t}} = 2}^{{\rm{T}} - 1} {{{\left[ {\left( {E{I_{{\rm{t}} + 1}} - E{I_{\rm{t}}}} \right) - \left( {E{I_{\rm{t}}} - E{I_{{\rm{t}} - {\rm{1}}}}} \right)} \right]}^2}} } \right\} $ | (6) |
λ越大,估计趋势越接近线性函数,由于采用月度数据,选取λ=14 400[25]。由式(6)得到的实际是非预期通胀部分的估计趋势,这也是后续研究的基础。从货币中性的角度分析,预期通货膨胀是不会有效应的,只有非预期通货膨胀才会有实际效应,这也是本文采用HP滤波分析的原因。
四、通胀率与中国股票收益率之间关系的实证研究以下实证研究中国股票市场收益波动与通胀率冲击之间的费雪效应、代理假说、风险溢价以及货币幻觉效应是否在中国股票市场成立。由于以上各代理变量均是时间序列数据,必须对模型变量进行单位根检验和判断变量平稳性。所谓时间序列的平稳性检验,是指检验一个序列的均值、方差和自协方差是否稳定,假若一个时间序列具有稳定的均值、方差和自协方差则这个序列是平稳的,否则被视为不稳定。如果直接对非平稳的时间序列进行回归分析,可能会造成虚假回归等问题。
(一) 单位根检验本文采用ADF检验法对以下代理变量进行平稳性检验(表 1)。
| 表 1 各代理变量ADF检验结果 |
由表 1结果可知,本文中设置的各代理变量的一阶差分均表现出平稳性,因此,可以进行回归分析。
(二) 中国股市的费雪效应检验关于股票收益的费雪效应假说的实证检验可用如下估计模型表达式:
| $ R{R_{\rm{t}}} = \alpha + \beta \left( {{I_{\rm{t}}}\left| {{\mathit{\Omega }_{{\rm{t}} - 1}}} \right.} \right) + {\varepsilon _{\rm{t}}} $ | (7) |
RRt为真实收益率,It为当期通胀率,Ωt-1在t-1时刻获得的信息,ε为随机扰动项。但是,在大量的研究中常假设股票收益不仅能很好对冲期望通胀带来的损失,而且也能对冲非预期通胀带来的损失。因此,在式(7)基础上,本文进行了拓展,引入了非预期通胀率,对于验证费雪效应更加客观,估计模型表达如下:
| $ R{R_{\rm{t}}} = \alpha + {\beta _1}\left( {E{I_{\rm{t}}}\left| {{\mathit{\Omega }_{{\rm{t}} - 1}}} \right.} \right) + {\beta _2}\left( {U{I_{\rm{t}}}\left| {{\mathit{\Omega }_{{\rm{t}} - 1}}} \right.} \right) + {\varepsilon _{\rm{t}}} $ | (8) |
式(8)中,EI为预期通胀率,UI为非预期通胀率。Fama & Schwert认为,如果β1=0那么股票投资能很好对冲期望通胀带来的损失;如果β1=β2=0,那么股票投资能同时完美地对冲预期通胀和非预期通胀,则费雪效应假说成立。
在式(8)基础上,本文又引入经济状态因素,建立了式(9)、(10)估计模型来研究1994年1月至2011年9月中国股市对通胀率影响的费雪效应:式(9)是基于非预期通胀率对中国股票真实收益的估值,而式(10)则是基于当期通胀率对中国股票真实收益的估值:
| $ R{R_{\rm{t}}} = \delta + {d_{\rm{t}}}\left( {{\kappa _1}U{I_{\rm{t}}}} \right) + \left( {1 - {d_{\rm{t}}}} \right)\left( {{\kappa _2}U{I_{\rm{t}}}} \right) + {\varepsilon _{\rm{t}}} $ | (9) |
| $ R{R_{\rm{t}}} = \delta + {d_{\rm{t}}}\left( {{\varphi _1}{I_{\rm{t}}}} \right) + \left( {1 - {d_{\rm{t}}}} \right)\left( {{\varphi _2}{I_{\rm{t}}}} \right) + {\varepsilon _{\rm{t}}} $ | (10) |
式(9)、(10)中以dt为虚拟变量,重点在于衡量分界点1999年12月前后截然不同的通胀率变化趋势状态的影响。在1994年1月至1999年12月期间,通胀率呈快速下滑趋势,故dt=1;在2000年1月至2011年9月期间,通胀率则进入震荡攀升状态,故dt=0。大量实证研究表明,股票收益率与通胀率之间呈负相关关系,即κ1 < 0,κ2 < 0,φ1 < 0,φ2 < 0。以上两式间接反映了股票真实收益率与非预期通胀率、通胀率之间的关系。
| 表 2 1994年1月至2011年9月股票真实收益率与通胀率关系 |
表 2中第二行显示,在通胀率攀升时期,中国股票市场的真实收益率RRt和非预期通胀率UIt之间存在显著的负相关;在通胀率下滑时期,中国股票的真实收益率RRt和非预期通胀率UIt之间却表现出不太明显的正相关,显著性和相关系数绝对值的大小都弱于通胀攀升时期。这说明,在不同经济状态中,金融市场和投资者对非预期通胀率的态度是不同的。通胀率下滑时期,投资者把非期望通胀率的上涨解释为一个好消息,例如,在通胀率下滑趋势状态中,物价的意外上涨使投资者预期消费者信心持续增加以及商品劳务真实需求的回升。而在通胀率攀升时期,投资者又把非预期通胀率的上涨理解为一个坏消息,例如,在通胀率攀升状态中,非预期价格的上涨增加了投资者对中央银行提高利率,缩紧银根,降低通胀率,经济增长放缓的担忧。同时,κ1、κ2各自的绝对值大小以及显著程度,说明在通胀率下滑时期,投资者对非预期通胀率的反应程度要远远弱于通胀率攀升时期投资者对非预期通胀率的反应程度。值得注意的是,在通货紧缩时期,费雪效应成立,而在通货膨胀时期,费雪效应并不成立。
第三行显示,总体上讲,中国股票的真实收益率RRt与通货膨胀It之间存在负相关(φ1 < 0,φ2 < 0),其结论与国内外大量的实证研究结论一致。但是,无论从φ1和φ2的绝对值大小以及显著性判断,在通胀率下滑期间,这种负相关非常不显著,要弱于通胀率攀升时期,与费雪效应不矛盾。然而,在通胀率攀升时期,负相关却较为显著,从而费雪效应不成立。从研究结论看,反映了投资者对同样的通胀率信息在不同经济运行环境中的反应程度不一致,这种差异可能来源于两个方面:在不同物价变动趋势状态中,通胀率对Gordon固定增长模型中各种估值要素影响存在差异,同时,投资者对未来估值要素反应有差异。
结合式(9)、(10),不难发现中国股票真实收益率与通胀率的关系具有一定程度的不确定性,故命题A不完全成立。
(三) 代理问题、风险溢价与货币幻觉效应检验Bahram Adrangi等在研究秘鲁和智利两国实际收益与通胀率负相关的原因时,使用了如下估计模型来验证两国的代理效益:
| $ R{R_{\rm{t}}} = \delta + \sum\nolimits_{k = i} {{\lambda _k}\Delta {g_{{\rm{t}} + k}} + {\varepsilon _{\rm{t}}}} $ | (11) |
| $ {I_{\rm{t}}} = \alpha + \sum\nolimits_{k = i} {{\mathit{{ø}}_k}\Delta {g_{{\rm{t}} + k}} + {\omega _{\rm{t}}}} $ | (12) |
| $ R{R_{\rm{t}}} = \delta + \sum\nolimits_{k = i} {{\lambda _k}\Delta {g_{{\rm{t}} + k}} + \eta {\omega _{\rm{t}}} + {\varepsilon _{\rm{t}}}} $ | (13) |
其中,Δgt+k代表未来第k时期的对数工业生产指数的一阶差分,RRt代表当前的真实收益率,It代表当前通胀率,ωt代表不能被Δgt+k解释的剩余通胀率。Bahram Adrangi等认为,如果代理效应成立,则式(11)中λk>0,式(12)中∅k < 0,而且式(13)中ωt的相关系数η将会变得不显著。在实证研究过程中,Bahram Adrangi等发现秘鲁和智利两国时期收益率与未来实体产出变化显著正相关,而通胀率与未来实体产出变化显著负相关,支持了代理问题效应。可是研究也发现,当排除代理问题效应之后,剩余通胀率与实际通胀率依然成显著的负相关。产生这种结果的原因可能在于上述模型并没有考虑货币幻觉效应与风险溢价的影响。
为了综合、有效验证中国股票市场的代理问题、风险溢价及货币幻觉效应,在式(11)、(12)、(13)基础上,本文又增加了对风险溢价变动以及货币供应增速两个因素的考量,并提出了不同经济状态时期的各种变量之间的关系变化:
| $ \begin{array}{l} R{R_{\rm{t}}} = \delta + {d_{\rm{t}}}\left( {\sum\nolimits_{k = i} {{\lambda _k}\Delta {g_{{\rm{t}} + k}}} + \sum\nolimits_{k = i} {{\tau _k}\Delta {\rho _{{\rm{t}} + k}}} + \sum\nolimits_{k = i} {{\chi _k}\Delta {m_{{\rm{t}} + k}}} } \right) + \left( {1 - {d_{\rm{t}}}} \right)\\\left( {\sum\nolimits_{k = i} {{{\lambda '}_k}\Delta {g_{{\rm{t}} + k}}} + \sum\nolimits_{k = i} {{{\tau '}_k}\Delta {\rho _{{\rm{t}} + k}}} + } \right. \;\;\;\;\;\;\;\;\;\;\left. {\sum\nolimits_{k = i} {{{\chi '}_k}\Delta {m_{{\rm{t}} + k}}} } \right) + {\varepsilon _{\rm{t}}} \end{array} $ | (14) |
| $ \begin{array}{l} U{I_{\rm{t}}} = \alpha + {d_{\rm{t}}}\left( {\sum\nolimits_{k = i} {{\mathit{{ø}}_k}\Delta {g_{{\rm{t}} + k}}} + \sum\nolimits_{k = i} {{\gamma _k}\Delta {\rho _{{\rm{t}} + k}}} + \sum\nolimits_{k = i} {{\eta _k}\Delta {m_{{\rm{t}} + k}}} } \right) + \left( {1 - {d_{\rm{t}}}} \right)\\\left( {\sum\nolimits_{k = i} {{{\mathit{{ø}'}}_k}\Delta {g_{{\rm{t}} + k}}} + \sum\nolimits_{k = i} {{{\gamma '}_k}\Delta {\rho _{{\rm{t}} + k}}} + } \right. \;\;\;\;\;\;\;\;\;\;\left. {\sum\nolimits_{k = i} {{{\eta '}_k}\Delta {m_{{\rm{t}} + k}}} } \right) + {\varepsilon _{\rm{t}}} \end{array} $ | (15) |
| $ \begin{array}{l} {I_{\rm{t}}} = \alpha + {d_{\rm{t}}}\left( {\sum\nolimits_{k = i} {{\mathit{{ø}}_k}\Delta {g_{{\rm{t}} + k}}} + \sum\nolimits_{k = i} {{\gamma _k}\Delta {\rho _{{\rm{t}} + k}}} + \sum\nolimits_{k = i} {{\eta _k}\Delta {m_{{\rm{t}} + k}}} } \right) + \left( {1 - {d_{\rm{t}}}} \right)\\\left( {\sum\nolimits_{k = i} {{{\mathit{{ø}'}}_k}\Delta {g_{{\rm{t}} + k}}} + \sum\nolimits_{k = i} {{{\gamma '}_k}\Delta {\rho _{{\rm{t}} + k}}} + } \right. \;\;\;\;\;\;\;\;\;\;\left. {\sum\nolimits_{k = i} {{{\eta '}_k}\Delta {m_{{\rm{t}} + k}}} } \right) + {\omega _{\rm{t}}} \end{array} $ | (16) |
| $ \begin{align} R{{R}_{\rm{t}}}=\delta +{{d}_{\rm{t}}}\left( \sum\nolimits_{k=i}{{{\lambda }_{k}}\Delta {{g}_{\rm{t}+k}}}+\sum\nolimits_{k=i}{{{\tau }_{k}}\Delta {{\rho }_{\rm{t}+k}}}+\sum\nolimits_{k=i}{{{\chi }_{k}}\Delta {{m}_{\rm{t}+k}}+\eta {{\omega }_{\rm{t}}}} \right)\\+\left( 1-{{d}_{\rm{t}}} \right)\left( {{\sum }_{k=i}}{{{{\phi }'}}_{k}}\Delta {{g}_{\rm{t}+k}}+\sum\nolimits_{k=i}{{{{{\gamma }'}}_{k}}\Delta {{\rho }_{\rm{t}+k}}}+ \right.\\ \left. \ \ \ \ \ \ \ \ \ \ \ \ \sum\nolimits_{k=i}{{{{{\eta }'}}_{k}}\Delta {{m}_{\rm{t}+k}}}+{\eta }'{{m}_{\rm{t}}} \right)+{{\varepsilon }_{\rm{t}}} \\ \end{align} $ | (17) |
在上述估计模型中,Δg表示经济实体增长率的一阶差分,Δρ表示收益波动率的一阶差分,Δm表示货币供应量的对数增长率,间接反映了名义利率水平的变动情况,RRt表示股票真实收益,UIt表示非预期通胀率,It表示当期实际通胀率。
在式(14)、(15)和(16)中,如果系数∅i < 0,λi>0且显著,表示通胀率与未来实体经济活动之间存在负相关,而未来实体经济活动又与股票收益成正相关,则代理问题效应应当成立;如果γi>0,τi < 0且显著,表示通胀率与未来资产风险溢价变动成正相关,资产风险溢价变动与股票收益成负相关,则风险溢价效应应当成立;如果ηi < 0,χi>0且显著,表示通胀率与未来货币流动性之间成负相关,货币流动性与股票收益率之间成正相关,则货币幻觉效应成立。在式(17)中,由于剩余通胀率已经排除了包含未来3种估值要素变动信息的通胀率部分,所以如果剩余通胀率的回归系数η不显著,则说明3种效应能很好解释通胀率与实际收益率之间的影响。
在实际估计过程中,本文选择OLS与Newey-West异方差自相关一致协方差修正参数估计量的标准差方法,而采用非向量自回归系统的原因在于本文主要目的是区分其中存在的短期传导机制。在进行了平稳性检验之后,本文必须确定式(14)-(17)的最优滞后期k,滞后期的选择应使残差εt成为白噪声,可由AIC或SC信息准则来确定。如果滞后期太短,随机误差项的自相关会很严重,并导致参数的非一致估计。因此,经数据量计算,取最优滞后期k=3。
1. 各估值要素变动对股票真实收益之间的相关性现选用模型式(14)进行实证研究,在1994年1月至2011年9月期间,中国股票收益与各估值要素之间主要存在以下相关关系(表 3)。
| 表 3 各估值要素与股票收益率的关系 |
由表 3分析可知,从总体回归系数看,在通胀率下滑和通胀率攀升两个时期内,中国股票真实收益总体与实体经济增速变动Δg之间存在正相关,与风险溢价变动Δρ存在负相关,与货币供给增速Δm存在正相关,与命题B是一致的。然而,两时期股票市场对未来估值要素的敏感性存在非对称性,在通胀率下滑时期,未来3个月各估值要素变动对股票真实收益率的影响并不显著,这说明该时期投资者对各种估值信息的预期变化反应并不明显。
在通胀率攀升时期,股票真实收益对经济实体增速变动、货币供应增速有非常显著的反应,同时,对风险溢价变动的反应也较为明显,其原因在于,投资者对中国经济抱有乐观的期望,即在一定的通胀率上,经济增长率要比实际的高得多,对通货膨胀的估计不足,从而容易受非预期通货膨胀的影响,因此,货币幻觉、风险溢价以及代理问题效应比较显著。
2. 通胀率对各估值要素变动的影响关系以下主要研究中国非预期通货膨胀和当期通货膨胀对未来各估值要素变动的影响。现分别使用模型(15)与(16)进行估值。先对式(15)进行估值(表 4)。
| 表 4 非预期通货膨胀UIt与估值要素变动的关系 |
从表 4可以发现通胀率下滑时期,非预期通货膨胀率与经济增速变动成微弱的正相关关系,不符合命题C的假定,与代理效应矛盾。这说明,在通货紧缩时期,非预期通胀率对实体经济活动是一个正向信号,物价的意外上涨反应了持续增加的消费者信心以及商品劳务需求的回升;而与风险溢价变动成非常显著的负相关关系,同样不符合命题C的假定,也不支持风险溢价效应,这说明,对投资者来说,非预期通胀率作为经济复苏的信号,未来风险溢价增长趋势放缓;非预期通胀率与货币供应增速呈比较显著的负相关关系,符合命题C的假定,因此,货币幻觉效应成立。但是,由于货币幻觉效应的负冲击抵消不了经济实体变动与风险溢价变动的正冲击,这也就解释了该时期股票真实收益率与非预期通胀微弱的正相关现象的原因。
在通胀率攀升时期,非预期通胀率分别与未来实体经济增速变动、货币供给增速成比较显著的负相关,符合命题C的假定。而非预期通胀率与风险溢价变动并无不明显的正相关关系。因此,该时期股票真实收益与非预期通胀率显著的负相关关系。主要来源于比较显著的代理效应与货币幻觉效应,而风险溢价效应并不明显。原因在于,在高通胀期间,中国投资者对通货膨胀预期不足,对经济增长持乐观态度,容易产生货币幻觉,使得非预期通货膨胀能够对中国股票真实收益产生作用。
现又对式(16)进行估值(表 5)。
| 表 5 当期通货膨胀It与估值要素变动的关系 |
在通胀率下滑时期,通胀率与实体经济增长变动表现出比较显著的负相关,与命题C基本一致;而通胀率与风险溢价之间却存在微弱负关系,与货币供应增速存在比较显著的正相关,都不支持命题C。在通货紧缩时期,股票收益率与通胀率微弱的负相关主要来源于微弱的代理问题效应,然而,风险溢价效应与货币幻觉效应却并不成立。
在通胀率的上升期间,通胀率与未来实体经济增长变动趋势表现为显著的负相关,与货币增速变量之间也表现为显著的负相关,与命题C一致,因此,该时期代理效应与货币幻觉效应表现尤为显著;而风险溢价效应不明显,与通胀率之间也没有明显的正相关,因此,该时期通胀率与股票收益率之间的显著负相关来源于非常显著的货币幻觉效应和较为显著的代理效应,而风险溢价效应则并不明显。
综上所述,在通货紧缩时期,中国政府为了刺激经济增长,采取了利率管制策略,降低基准利率,实施较为宽松的货币政策,提高货币供给增速。但是,对于投资者而言,他们已经习惯了中国央行通过行政手段调整利率以刺激经济增长的方法,他们也能够意识到名义利率与实际利率之间的差异。实际上,这一时期的央行基准利率下调必然会向投资者传递一个信号,即通货紧缩信号,当货币工资减少时,投资者能够准确判断通货紧缩,并且也会用实际利率对股票实际盈利资本化。
虽然中国也客观存在通货膨胀,由于高货币工资、高物价水平,政府、投资者对通货膨胀的预期不足,无法及时调整名义工资、名义价格等,因此,非预期通货膨胀必然会产生作用。实际上,无论政府、或者投资者都很难分清楚经济增长与通货膨胀,而央行调整利率的行为并非分离均衡,而是混同均衡,因此,政府与投资者很可能会低估通胀率。
3. 剩余通胀率对股票真实收益率的直接影响为了验证通胀率与股票收益率是否存在直接的影响关系,本文对模型式(17)进行估计(表 6)。
| 表 6 剩余通货膨胀对股票真实收益率的直接影响 |
表 6估计的Δg、Δρ和Δm回归系数λi,τi,χi的大小以及显著性跟前部分结论一致,通胀率率下滑时期ω的回归系数η=-0.095(t=-0.559)和通胀率攀升时期ω的回归系数η′=-0.385(t=-0.807),与前文估计模型中各时期通胀率对收益率的回归系数φ1=-0.242(t=-0.878),φ2=-0.952(t=-2.107)相比,系数的绝对值大小和显著性都明显降低,而且在通胀率攀升时期,通胀率与股票真实收益负相关关系不再显著。这说明剩余通胀率对股票真实收益率不具备明显的直接因果关系,代理、风险溢价和货币幻觉效应能很好地解释中国通胀率对股票真实收益率负相关关系,与命题D一致。
五、结论及政策建议根据中国股票市场实际情况,本文实证结果表明:(1)在通胀率下降期间,费雪效应应当成立,相反,在通胀率上升期间费雪效应则不成立。(2)不同时期通胀率与股票真实收益率的关系并不完全为负相关,当通胀率处于下降时期,非预期通胀率与股票真实收益率之间表现为微弱的正相关关系,产生该现象的原因在于非预期通胀与经济增长之间的微弱正相关以及与风险溢价之间显著的负相关。(3)在通胀率下降时期,通胀率与股票真实收益的微弱负相关主要来源于微弱的代理效应,风险溢价效应与货币幻觉效应并不成立;在通胀率上升时期,通胀率与股票真实收益的显著负相关主要来源于尤为显著的货币幻觉效益与较为显著的代理效应,风险溢价效应则不明显。在通胀率上升时期,股票市场对宏观经济变动的敏感程度要明显强于通货率下滑时期。(4)通胀率与股票真实收益不构成直接的因果关系,通胀率主要是通过影响未来估值要素变动对当期收益率产生间接影响。
通过实证研究通胀率对中国股票市场波动的影响,本文发现,在不同通胀率趋势下,股票市场对未来各估值要素的变动以及当期通胀率反应的敏感程度不一致。通胀率攀升时期,通胀率会对股票市场产生非常明显的负面影响,并且代表错误估值的货币幻觉效应尤其显著,其根源问题就在于,中国利率并非市场化,而是利率管制,从而扭曲了宏观经济的实际运行轨迹,因此,为了维持股票市场的稳定,本文提出如下建议。
首先,将利率市场化作为金融改革核心。央行的利率管制行为实际上并未有效解决宏观经济系统存在的问题,甚至于根本不能达到预期目标,相反更容易扭曲现实经济运行的轨迹。对于通货膨胀而言,政府的盲目乐观必然会使利率不能产生信号传递作用。因此,利率市场化有利于帮助政府、投资者对通货膨胀形势作判断。中国利率市场化应当是循序渐进的过程,主要涉及货币市场与债券市场的利率市场化,其中存、贷款利率市场化是利率市场化改革的主要目标。
其次,促进利率市场化以增强货币政策有效性,完善金融机构的利率定价机制。主要依靠货币政策工具来引导利率市场化制度的变革,优化货币传导机制,增加货币政策有效性。根据风险与收益对称原则,建立合理有效的利率定价管理与利率风险管理体系以及风险溢价测评体系。同时,也要建立内部转移价格制度和正向激励机制,完善内部资本约束制度。
最后,完善金融机构利率风险防范机制。客观上讲,利率市场化有利于增强利率政策效应,一是强化银行职能。在利率市场化条件下,对金融机构可能存在的过度或不正当竞争行为应当防范在先,维持金融机构的竞争秩序。二是加速企业现代化和银行商业化。合格的企业和银行是实现利率市场化的必要条件之一。完善现代企业制度,加快国有银行商业化改革,有利于促进金融市场的稳定繁荣。三是建立存款保险制度。在利率市场化条件下,金融机构必须承担风险、自负盈亏,金融业内部必须建立有效的风险转嫁机制,保证金融系统的稳定。
| [1] | FISHER I. The theory of interest[M]. New York: Maxmillan, 1930. |
| [2] | FAMA F, SCHWERT G W. Asset return and inflation[J]. Journal of Financial Economics, 1977, 5: 115–146. DOI: 10.1016/0304-405X(77)90014-9 |
| [3] | BOUDOUCH J, RICHARDSON M. Stock returns, inflation:A long-horizon perspective[J]. American Economic Review, 1993, 83: 1346–1355. |
| [4] | WESTERHUND J. Panel cointegration tests of the Fisher hypothesis[R].Department of Economics, Lund University, Sweden, 2005. https://lup.lub.lu.se/search/search/publication/ebe0c136-3c57-4568-9dd4-1d7127afb3e2 |
| [5] | GULTEKIN N B. Stock market returns and inflation:Evidence from other countries[J]. Journal of Finance, 1983, 38: 49–65. DOI: 10.1111/j.1540-6261.1983.tb03625.x |
| [6] | KAUL G. Stock market returns, inflation:The role of monetary sector[J]. Journal of Financial Economics, 1987, 18: 253–276. DOI: 10.1016/0304-405X(87)90041-9 |
| [7] | COHN R A, MODIGLIANI F. Inflation, rational valuation and the market[J]. Financial Analysts Journal, 1979, 37(3): 24–44. |
| [8] | RITTER J R, WARR R S. The decline of inflation and the bull market of 1982-1999[J]. Journal of Financial and Quantitative Analysis, 2002, 37: 29–61. DOI: 10.2307/3594994 |
| [9] | CAMPBELL J Y, VUOLTEENAHO T. Inflation illusion and stock prices[J]. American Economic Review, 2004, 94(2): 19–23. DOI: 10.1257/0002828041301533 |
| [10] | FAMA E F. Stock returns, real activity, inflation and money[J]. American Economic Review, 1981, 71(4): 545–565. |
| [11] | GESKE R, ROLL R. The fiscal and monetary linkage between stock returns and inflation[J]. Journal of Finance, 1983, 38: 854–865. |
| [12] | SHARPE S A.Stock prices, expected returns, and inflation[C].Finance and Economics Discussion Series, 1999. |
| [13] | ADRANGI B, CHATRATH A, SHANK T M. Inflation, output and stock prices:Evidence from Latin America[J]. Managerial and Decision Economics, 1999, 20(2): 63–74. DOI: 10.1002/(ISSN)1099-1468 |
| [14] | BRUNNERMEIER M, JULLIARD C. Money illusion and housing frenzies[J]. Review of Financial Studies, 2008, 21(1): 135–180. DOI: 10.1093/rfs/hhm043 |
| [15] | BRANDT M W, WANG K Q. Time-varying risk aversion and unexpected inflation[J]. Journal of Monetary Economics, 2003, 50: 1457–1498. DOI: 10.1016/j.jmoneco.2003.08.001 |
| [16] | 靳云汇, 余存高. 中国股票市场与国民经济关系的实证研究(上)[J]. 金融研究, 1998(3): 40–45. |
| [17] | 赵兴球. 通胀、产出与股票价格关系实证研究[J]. 统计研究, 1999(5): 264–265. |
| [18] | 刘金全, 王风云. 资产收益率与通货膨胀率的实证研究[J]. 财经研究, 2004(1): 123–128. |
| [19] | 韩学红, 郑妍妍, 伍超明. 对我国股票收益率与通货膨胀率关系的解释[J]. 金融研究, 2008(4): 21–36. |
| [20] | 刘仁和. 通货膨胀与中国股票价格波动—基于货币幻觉假说的解释[J]. 数量经济技术经济研究, 2009(6): 149–161. |
| [21] | BOYD J H, HU J, JAGANNATHAN R. The stock market's reaction to unemployment news:Why bad news is usually good for stocks[J]. Journal of Finance, 2005, 60: 649–672. DOI: 10.1111/j.1540-6261.2005.00742.x |
| [22] | L EE, CHARLES M C, MYERS J, et al. What is the intrinsic value of the Dow?[J]. Journal of Finance, 1999, 54(5): 1693–1741. DOI: 10.1111/0022-1082.00164 |
| [23] | BLANCHARD, OLIVER J. Output, the stock market, and interest rates[J]. American Economic Review, 1981, 71: 132–143. |
| [24] | KNIF J, KOLARI J, PYNNONEN S. Stock market reaction to good and bad inflation news[J]. The Journal of Financial Research, 2008(2): 141–166. |
| [25] | 李晓芳, 高铁梅. 应用HP滤波方法构造我国增长循环的合成指数[J]. 数量经济技术经济研究, 2001(9): 100–103. |
 2014, Vol. 20
2014, Vol. 20

