中国的产业技术创新战略联盟(以下简称“联盟”)是一种在政府引导与推动下,以提升技术创新能力为目标,以产学研为主要合作形式的战略联盟。根据2008年国家六部门联合发布的《关于推动产业技术创新战略联盟构建的指导意见》,产业技术创新战略联盟是指由企业、高校、科研机构或其他组织机构,以企业的发展需求和各方的共同利益为基础,以提升产业技术创新能力为目标,以具有法律约束力的契约为保障,形成的联合开发、优势互补、利益共享、风险共担的技术创新合作组织。《国务院关于加快培育和发展战略性新兴产业的决定》指出,要结合国家技术创新工程的实施,加快构建一批产业技术创新战略联盟。产业技术创新战略联盟作为集中建设技术创新体系中的三大载体之一,在国家技术创新体系建设中的地位不可小觑,在整个转变经济发展方式中也占据着重要地位。因此,产业技术创新战略联盟已经成为相关学术界与实践界研究、实践的热点[1]。
目前中国产业技术创新战略联盟主要存在合作行为非长期化,合作关系不稳定,尚未形成实质的战略伙伴关系等问题[1-2]。而对于造成联盟不稳定的原因,部分学者进行了探究:第一,联盟的不稳定性受到联盟内各主体沟通不畅的影响;第二,联盟的不稳定性受到联盟内各主体的核心能力的影响;第三,联盟的不稳定性是由于联盟内部各主体对于联盟整体利益与自身利益认识的冲突,即各主体追求的最优目标存在差异造成的。已有文献从多个角度对联盟的不稳定性进行了探析,原因最终归结为各个主体之间目标与定位的差异性。这些差异性由于主体的异质性,是难以消除的,而已有研究并没有验证在产业技术创新战略联盟这种异质互利共生的联盟中,到底能不能存在一个平衡点,使各主体在合作提高联盟的总体效率的同时使自身的利益最大化。基于此,笔者采用三维Lotka-Volterra合作系统模型对联盟最终能够形成长期稳定的合作关系进行证明,并应用二维Lotka-Volterra竞争与合作模型对联盟中的高校与科研机构因为一定相似目标而形成的“类似竞争”关系进行稳定性分析。
产业技术创新战略联盟是在主体各方共同利益的基础上形成的联合开发、优势互补、利益共享、风险共担的技术创新合作组织。要构建有效的联盟,联盟中的各个主体之间应该有相互依存、互相支撑的关系[3]。从某种程度上说,这种主体之间在资源共享基础上相互促进、共同发展的关系类似于生态学中的共生关系[4]。基于此,笔者引入共生理论,对产业技术创新战略联盟的共生本质及其形成的共生系统的稳定性进行分析。
二、相关研究综述 (一) 共生理论的相关应用1998年袁纯清将“共生理论”应用到国内小型经济的研究,“共生”这一生态学概念开始在国内从自然现象研究转向社会现象研究,尤其是经济领域。“共生”的概念来源于生态学,是1897年德国生物学家德贝里提出,它的本义是指不同的生物种属按照某种物质联系而生活在一起。而在本文中,将产业技术创新战略联盟看成是一个共生系统,即在共生环境中,共生单元按照某种共生模式构成共生关系的集合[5]。
近年来,学术界除了将共生理论引入到战略联盟的构建、城市圈经济一体化及产业共生机理研究等理论方面,越来越多的学者开始应用共生理论进行产业内、企业间的共生模型构建[6]。邹磊、孙长雄采用共生程度或共生关系研究了其对企业共生行为的影响及相应的效应;李玉琼、朱桂龙借用自然生态学中的共生系统理论,构建了企业生态系统竞争的共生战略模型,并推导了企业之间从竞争到合作再到竞争共生的平衡条件;而胡浩、李子彪、胡宝民利用共生理论构建了区域创新系统多创新极共生演化动力模型;除此之外,王晓雪、周柏翔还构建了基于共生理论的联盟中的知识转移模型,促使企业保持长期稳定的共生状态。综上所述,共生的概念越来越为学术界接受并应用于企业联盟、产业集群等方面的研究中。因此,共生理论对于产业技术创新联盟本质探究是具有可行性的[5]。
(二) Lotka-Volterra模型的相关应用Lotka-Volterra模型(种间竞争模型)是Lotka和Volterra提出的种间竞争方程模型,最初用来描述同一生态环境下的共享同种资源的两种种群的增长情况。作为Logistic方程(逻辑斯蒂)的延伸,由于其中的竞争关系与种群发展与产业集群、企业联盟等有竞争关系存在的经济联盟情况相似,Lotka-Volterra模型像逻辑斯蒂方程一样,被越来越广泛地应用到相关经济组织的研究中。徐爱东、龙勇利用Lotka-Volterra模型模拟了中国移动和中国联通竞争动态演变模型,分析其二者之间的竞争稳定性与演变轨迹,并进行了实证分析;蒙灼、严静对Lotka-Volterra模型进行扩展与改进,建立了能源产业之间的竞争模型,对竞争关系及度量进行了验证。虽然Lotka-Volterra模型大多用在2个不同的竞争对手间以描述其竞争关系,但高长元、杜鹏除了在高技术虚拟产业集群成员间引入Lotka-Volterra竞争模型而外,也构建了其集群成员之间的合作模型,并拓展了大于2维的Lotka-Volterra模型[8],从数学角度求解出了高技术虚拟产业集群成员间从竞争到合作的平衡条件。因此,基于产业技术创新战略联盟各主体之间的关系与生态系统中种群生存竞争的相似性,对于企业、高校和科研机构所构成的合作联盟,Lotka-Volterra竞争模型也是适用的。
三、产业技术创新战略联盟共生系统Lotka-Volterra模型构建 (一) 产业技术创新战略联盟共生系统构建根据袁纯清[5]所阐述的共生系统构成的判据,可以得知产业技术创新战略联盟能够构建共生系统。产业技术创新战略联盟由企业、高校和科研机构通过某种方式进行联合,共同对涉及的技术创新、产业化推广和人才培养等事项进行合作,以提高联盟运行效率与效果。根据共生理论,可对联盟共生系统作以下分析。
1. 共生单元产业技术创新战略联盟作为一个共生系统,主要由企业、高校和科研机构等共生单元组成。其中企业是技术的需求者,其优势在于产品市场的开发;高校知识创新水平较领先;科研机构在应用研究方面有专长。由于各共生单元拥有优势资源的差异性,共生系统中的各共生单元在资源共享、优势互补提高整个系统运行效率与效果的同时,只有实现各相关主体个体的目标与利益,才能促使共生系统长久有效地发展。因此,联盟的共生系统是优势互补、利益共享的互利共生关系。
2. 联盟的共生模式产业技术创新战略联盟是统一的整体,它由企业、科研机构、高校等主体要素和资金、人才、技术、物资基础、信息等客体要素构成。客体要素在各主体要素之间和内部流动和配置,促成系统的运行和发展,产生比形成共生系统之前更大的利益,这种利益就是共生系统的共生能量。
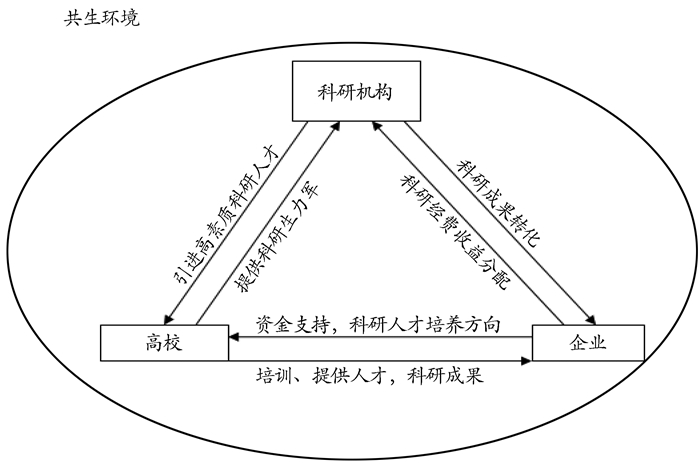
在联盟共生系统中,各共生单元之间存在一种互惠互利的关系(图 1)。高校从科研机构引进高素质的科研人才提高自身科研能力的同时,也为科研机构提供科研的生力军;科研机构通过企业将科研成果转化成为市场产品,同时企业为科研机构提供一定的科研经费;高校为企业培训、提供相关的技术人才,使企业能够转化更多的科研成果以获取利益,同时企业也为高校给予了必要的资金支持,为科研人才的培养提供一定的方向性建议。
|
图 1 联盟共生系统中各共生单元之间的互惠互利的关系 |
总之,联盟共生系统中的各主体之间是一种相互支持、共同发展的关系。对称互惠一体化是联盟共生系统运行最有效的共生模式,也是增强自主创新能力的必由之路。企业、高校、科研机构拥有不同优势资源,采取共生系统中各单元对称互惠一体化的共生模式,有利于优势互补、资源共享,使创新活动和创新成果的内在价值得到市场检验,加快科研成果转化,进而实现产业化,变为现实生产力。不仅实现各单元的目标与个体利益,也促使整个共生系统更好发展。
3. 联盟所处的共生环境联盟所处的外部环境以及联盟当下的运行条件,就是联盟共生系统的共生环境。产业技术创新战略联盟的产生有利于高校、科研机构和企业发挥各自优势,并通过相互密切结合,形成整体的综合竞争力,推动科技和经济的发展。在市场经济条件下,通过联盟可以极大提高有关技术创新、产业化推广、人才培养、经济发展、社会进步等事项的运行绩效。联盟的顺利运行影响产业与国民经济的发展,政府、金融机构等中介机构,都对联盟共生系统给予尽可能大的支持。基于此,联盟共生系统的共生环境有利于联盟的发展。
(二) 产业技术创新战略联盟共生系统的Lotka-Volterra模型构建 1. 基本构建思想联盟中各共生单元追求的目标与利益存在差异,各主体自身的定位不一致,其对于技术创新、产业化推广和人才培养等联盟的合作事项的需求程度和关联程度不同。当两个以上的联盟主体的联合与合作的运行效率与效果超过单个主体的运行效率与效果时,联盟共生系统就能形成长期稳定的关系。对于企业来讲,在联盟中更看重经济效益的增加,这可以从高校与科研机构科研成果在市场上的转化率来衡量;对于高校与科研机构来讲,在联盟中更看重科研成果的产出,文中通过科研成果的增长率来表示。从整体上说,企业、高校和科研机构为了提高联盟总体效率,应该是互利互惠的合作关系。但是,对于高校和科研机构来说,在相同的资源基础上,同样看重各自的科研成果产出率,因此,他们之间除了存在相互促进的合作关系外,还存在比较微妙的“类似竞争”关系。作为联盟共生系统的重要组成部分,高校与科研机构之间的相互作用状态是竞争或合作将直接影响共生系统的稳定性,有必要对其平衡条件及稳定性进行探究。因此,模型的构建将分两部分:关于联盟总体3个主体之间的三维Lotka-Volterra合作模型;关于高校与科研机构的二维Lotka-Volterra竞争与合作模型。
2. 基本假设假设某产业技术联盟构成的共生系统为A,而由高校和科研机构组成的二元共生系统为A1。
对于共生系统A。假设X1、X2 、X3 分别表示A共生系统中的企业、高校和科研机构。x1、x2、x3分别表示企业的科研成果市场转化率、高校的科研成果产出率和科研机构的科研成果产出率;t为时间;aii(i=1, 2, 3,且aii ≥0) 表示对应xi的自然增长率[10],
对于共生系统A1 。假设X、Y分别表示共生系统中的高校和科研机构;r1 、r2 为2种互补的资源(技术、知识等)。当高校和科研机构都以联盟整体的效率为追求目标,即高校与科研机构进行合作时,共享各自拥有的资源r1 、r2 ;反之,当高校和科研机构都以各自的利益(科研成果产出率)为追求目标,即二者之间存在“类似竞争”关系,争夺共生系统中的资源r1 。x、y分别表示高校和科研机构的科研成果产出率;t为时间,则
由基本假设及已有研究成果可以构建共生系统A的三维Lotka-Volterra合作模型[9]和共生系统A1 的二维Lotka-Volterra竞争与合作模型[8]如下。
(1) 产业技术创新战略联盟共生系统A的三维合作模型。
| $ \frac{{{\rm{d}}{x_1}}}{{{\rm{dt}}}} = {x_1}\left( {{a_{11}} - \frac{{{a_{11}}}}{{{k_1}}}{x_1} + {a_{12}}{x_2} + {a_{13}}{x_3}} \right) $ | (1) |
| $ \frac{{{\rm{d}}{x_2}}}{{{\rm{dt}}}} = {x_2}\left( {{a_{22}} - {a_{21}}{x_1} - \frac{{{a_{12}}}}{{{k_2}}}{x_2} + {a_{33}}{x_3}} \right) $ | (2) |
| $ \frac{{{\rm{d}}{x_3}}}{{{\rm{dt}}}} = {x_3}\left( {{a_{33}} + {a_{31}}{x_1} + {a_{32}}{x_2} - \frac{{{a_{33}}}}{{{k_3}}}{x_3}} \right) $ | (3) |
(2) 高校与科研机构共生系统A1 的二维模型。竞争模型:
| $ \frac{{{\rm{d}}x}}{{{\rm{dt}}}} = x\left( {{a_x} - {a_{{\rm{t}}x}}x - \frac{x}{k} + {a_{sx}} + {a_{rx}}} \right) - {\alpha _x}{\beta _{xy}}xy $ | (4) |
| $ \frac{{{\rm{d}}y}}{{{\rm{dt}}}} = y\left( {{a_y} - {a_{{\rm{t}}y}}y - \frac{y}{k} + {a_{sy}} + {a_{ry}}} \right) - {\alpha _y}{\beta _{yx}}xy $ | (5) |
合作模型:
| $ \frac{{{\rm{d}}x}}{{{\rm{dt}}}} = x\left( {{a_x} - {a_{{\rm{t}}x}}x - \frac{x}{{{k_1}}} + {a_{sx}} + {a_{rx}}} \right) - {\alpha _x}{\beta _{xy}}xy $ | (6) |
| $ \frac{{{\rm{d}}y}}{{{\rm{dt}}}} = y\left( {{a_y} - {a_{{\rm{t}}y}}y - \frac{y}{{{k_1}}} + {a_{sy}} + {a_{ry}}} \right) - {\alpha _y}{\beta _{yx}}xy $ | (7) |
由式(1)-(3) 可知,要使共生系统A达到全局平衡,即共生系统中各主体在相同的环境与资源基础上的相互作用达到平衡状态,3个主体都有利可图,就是求解方程组的根(共生系统全局平衡点)。
设矩阵B为共生系统A中3个主体之间的相互作用矩阵,则
| $ B = \left( {\begin{array}{*{20}{c}} { - \frac{{{a_{11}}}}{{{k_1}}}}&{{a_{12}}}&{{a_{13}}}\\ {{a_{21}}}&{ - \frac{{{a_{22}}}}{{{k_2}}}}&{{a_{23}}}\\ {{a_{31}}}&{{a_{32}}}&{ - \frac{{{a_{33}}}}{{{k_3}}}} \end{array}} \right) $ | (8) |
根据已有相关定理[9],若︱B︱<0,则共生系统中存在内部平衡点E(x1*,x2* ,x3*),且平衡点唯一。若能求解出满足此条件的平衡点,则说明在产业技术创新战略联盟形成的共生系统A中,不管目前企业、高校与科研机构对于自身在联盟共生系统中的定位与目标认识差异有多大,共生单元通过调节与适应,最终可以达到多赢共生状态。对此观点证明如下。
将B矩阵的行列式︱ B︱依次从按行展开,则按第一行展开时
| $ \begin{array}{l} \left| B \right| = - \frac{{{a_{11}}}}{{{k_1}{k_2}{k_3}}}\left( {{a_{22}}{a_{33}} - {a_{23}}{a_{32}}{k_2}{k_3}} \right) + \\ \frac{{{a_{12}}}}{{{k_3}}}\left( {{a_{21}}{a_{31}} + {a_{23}}{a_{31}}{k_3}} \right) + \frac{{{a_{13}}}}{{{k_2}}}\left( {{a_{22}}{a_{31}} + {a_{21}}{a_{32}}{k_2}} \right) \end{array} $ | (9) |
由已知假设可知,式(9) 中后两项都是大于0的,只要满足式(10),︱B︱<0就成立。
| $ {a_{22}}{a_{33}} - {a_{23}}{a_{32}}{k_2}{k_3} > 0 $ | (10) |
同理可知,当︱B︱分别按第二行、第三行展开行列式时,为使︱B︱<0成立,应有:
| $ {a_{11}}{a_{33}} - {a_{13}}{a_{31}}{k_1}{k_3} > 0 $ | (11) |
| $ {a_{11}}{a_{22}} - {a_{12}}{a_{21}}{k_1}{k_2} > 0 $ | (12) |
因此,当企业、高校和科研机构三者的科研成果市场转化率、科研成果产出率的自然增长率中两两主体的合作系数,即相互作用力与其为了实现增长目标已占用的资源之间满足式(10)-(12),共生系统就能达到平衡状态,并且在此平衡状态下,3个主体所追求的变化(即
| $ - \frac{{{a_{11}}}}{{{k_1}}}{x_1} + {a_{12}}{x_2} + {a_{13}}{x_3} = - {a_{11}} $ | (13) |
| $ {a_{21}}{x_1} - \frac{{{a_{22}}}}{{{k_2}}}{x_2} + {a_{23}}{x_3} = - {a_{22}} $ | (14) |
| $ {a_{31}}{x_1} + {a_{32}}{x_2} - \frac{{{a_{33}}}}{{{k_3}}}{x_3} = - {a_{33}} $ | (15) |
解方程组得:
| $ \begin{array}{l} x_1^ * = \frac{1}{{\left| B \right|}}\left[ { - \frac{{{a_{11}}}}{{{k_2}{k_3}}}\left( {{a_{22}}{a_{33}} - {a_{23}}{a_{32}}{k_2}{k_3}} \right) - \frac{{{a_{22}}}}{{{k_3}}}\left( {{a_{12}}{a_{33}} + {a_{12}}{a_{32}}{k_3}} \right) - } \right.\\ \;\;\;\;\;\;\;\left. {\frac{{{a_{33}}}}{{{k_2}}}\left( {{a_{22}}{a_{13}} + {a_{12}}{a_{23}}{k_2}} \right)} \right] = \frac{{{I_1}}}{{\left| B \right|}} \end{array} $ | (16) |
| $ \begin{array}{l} x_2^ * = \frac{1}{{\left| B \right|}}\left[ { - \frac{{{a_{11}}}}{{{k_3}}}\left( {{a_{21}}{a_{33}} - {a_{23}}{a_{31}}{k_3}} \right) - \frac{{{a_{22}}}}{{{k_1}{k_3}}}\left( {{a_{11}}{a_{23}} + {a_{13}}{a_{31}}{k_1}{k_3}} \right) - } \right.\\ \;\;\;\;\;\;\;\left. {\frac{{{a_{33}}}}{{{k_1}}}\left( {{a_{11}}{a_{23}} + {a_{13}}{a_{21}}{k_1}} \right)} \right] = \frac{{{I_2}}}{{\left| B \right|}} \end{array} $ | (17) |
| $ \begin{array}{l} x_3^ * = \frac{1}{{\left| B \right|}}\left[ { - \frac{{{a_{11}}}}{{{k_2}}}\left( {{a_{22}}{a_{31}} - {a_{21}}{a_{32}}{k_2}} \right) - \frac{{{a_{22}}}}{{{k_1}}}\left( {{a_{11}}{a_{32}} + {a_{12}}{a_{31}}{k_1}} \right) - } \right.\\ \;\;\;\;\;\;\;\left. {\frac{{{a_{33}}}}{{{k_1}{k_2}}}\left( {{a_{11}}{a_{22}} + {a_{12}}{a_{21}}{k_1}{k_2}} \right)} \right] = \frac{{{I_3}}}{{\left| B \right|}} \end{array} $ | (18) |
因为满足式(10)-(12),则I1、I2、I3都小于0;而︱B︱<0成立。可推知,式(16)-(18) 平衡点E(x1*,x2*,x 3*)中xi*>0(i=1, 2, 3)。共生系统A能够在一定条件下形成互利共生的平衡合作关系。
产业技术创新战略联盟所谋求的平衡并不是暂时的,而是建立一种长期稳定的战略合作关系。基于此,我们将对共生系统中存在的这一平衡点的稳定性进行验证,以表明产业技术创新战略联盟这一共生系统是可以形成长期稳定合作关系的产学研一体化联盟。
设平衡点E(x1*,x2* ,x3*)所形成的矩阵为C。根据Hurwitz定理,系统
| $ C = \left( {\begin{array}{*{20}{c}} { - \frac{{{a_{11}}}}{{{k_1}}}x_1^ * }&{{a_{12}}x_1^ * }&{{a_{13}}x_1^ * }\\ {{a_{21}}x_2^ * }&{ - \frac{{{a_{22}}}}{{{k_2}}}x_2^ * }&{{a_{23}}x_2^ * }\\ {{a_{31}}x_3^ * }&{{a_{32}}x_3^ * }&{ - \frac{{{a_{33}}}}{{{k_3}}}x_3^ * } \end{array}} \right) \\= \left( {\begin{array}{*{20}{c}} {x_1^ * }&0&0\\ 0&{x_2^ * }&0\\ 0&0&{x_3^ * } \end{array}} \right)\left( {\begin{array}{*{20}{c}} { - \frac{{{a_{11}}}}{{{k_1}}}}&{{a_{12}}}&{{a_{13}}}\\ {{a_{21}}}&{ - \frac{{{a_{22}}}}{{{k_2}}}}&{{a_{23}}}\\ {{a_{31}}}&{{a_{32}}}&{ - \frac{{{a_{33}}}}{{{k_3}}}} \end{array}} \right) = DB $ | (19) |
则有
二维共生系统中高校与科研机构处于竞争状态时,若要保持系统平衡,则二者的科研成果产出率不再变化。令
| $ \frac{{{\rm{d}}x}}{{{\rm{dt}}}} = \frac{{{\rm{d}}y}}{{{\rm{dt}}}} = 0 $ | (20) |
由式(4)、(5) 有
| $ x\left( {{a_x} - {a_{{\rm{t}}x}}x - \frac{x}{k} + {a_{sx}} + {a_{rx}}} \right) - {\alpha _x}{\beta _{xy}}xy = 0 $ | (21) |
| $ y\left( {{a_y} - {a_{{\rm{t}}y}}y - \frac{y}{k} + {a_{sy}} + {a_{ry}}} \right) - {\alpha _y}{\beta _{yx}}xy = 0 $ | (22) |
对高校X和科研机构Y来说,通过两点法可得知其各自科研成果产出率增加在x、y轴上的交点分别为
| $ {F_1}\left( {{f_{11}},{f_{12}}} \right) = \left( {\frac{{{a_x} + {a_{sx}} + {a_{rx}}}}{{{a_{tx}} + \frac{1}{k}}},0} \right),{F_2}\left( {{f_{21}},{f_{22}}} \right) = \left( {0,\frac{{{a_x} + {a_{sx}} + {a_{rx}}}}{{{\partial _x}{\beta _{xy}}}}} \right) $ |
| $ {F_3}\left( {{f_{31}},{f_{32}}} \right) = \left( {\frac{{{a_y} + {a_{sy}} + {a_{ry}}}}{{{\partial _y}{\beta _{yx}}}},0} \right),{F_4}\left( {{f_{41}},{f_{42}}} \right) = \left( {0,\frac{{{a_y} + {a_{sy}} + {a_{ry}}}}{{{a_{ty}} + \frac{1}{k}}}} \right) $ |
由以上的交点可知,若将高校和科研机构的科研成果产出率变化放到同一象限,将有4种情况。
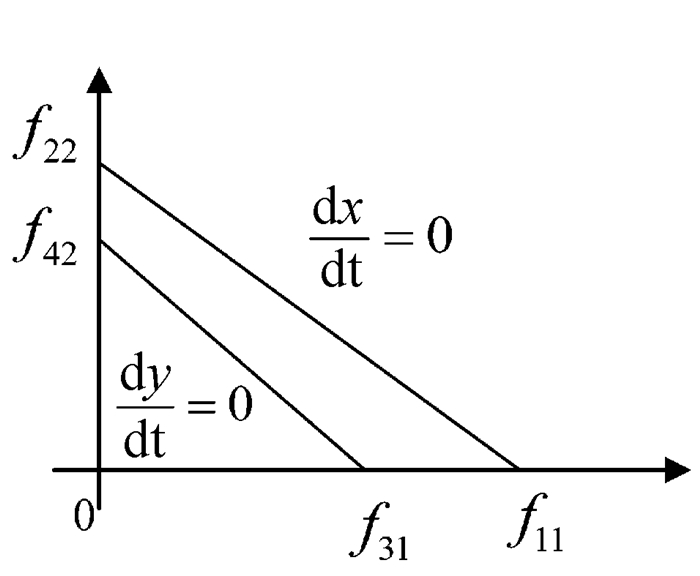
(1) 当f11>f31,f22>f42时,即高校比科研机构更具竞争力,科研机构不能与高校竞争资源以增加科研成果产出率,则高校X与科研机构Y科研成果产出率增加值
|
图 2 高校比科研机构更具竞争力 |
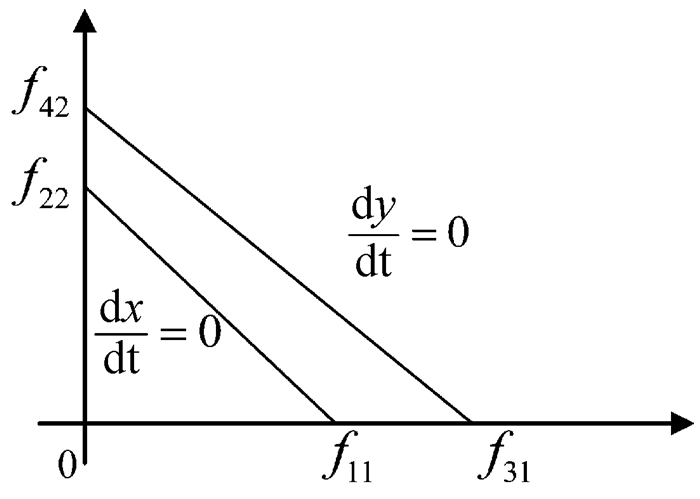
(2) 当f11<f31,f22<f42时,即科研机构比高校更具竞争力,高校不能与科研机构竞争资源以增加科研成果产出率。,则高校X与科研机构Y科研成果产出率增加值
|
图 3 科研机构比高校更具竞争力 |
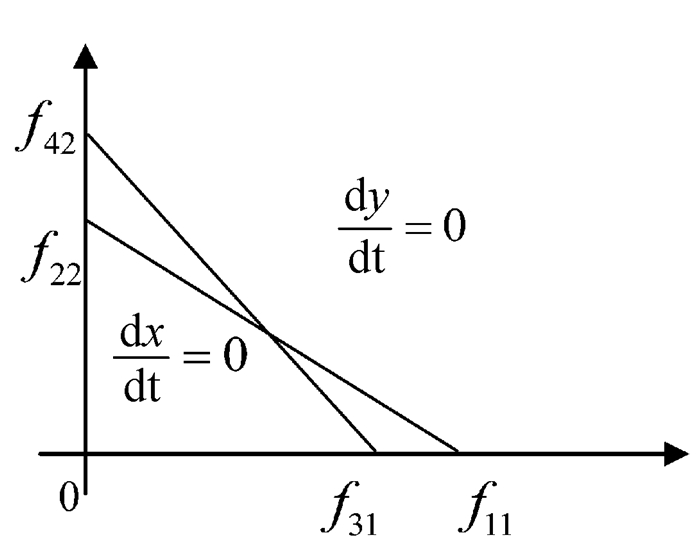
在以上两种情况下,毫无疑问无法达到共生系统A1的平衡状态。从数学角度解析,要使共生系统A1在竞争状态下实现平衡,则
|
图 4 高校和科研机构竞争情况一 |
|
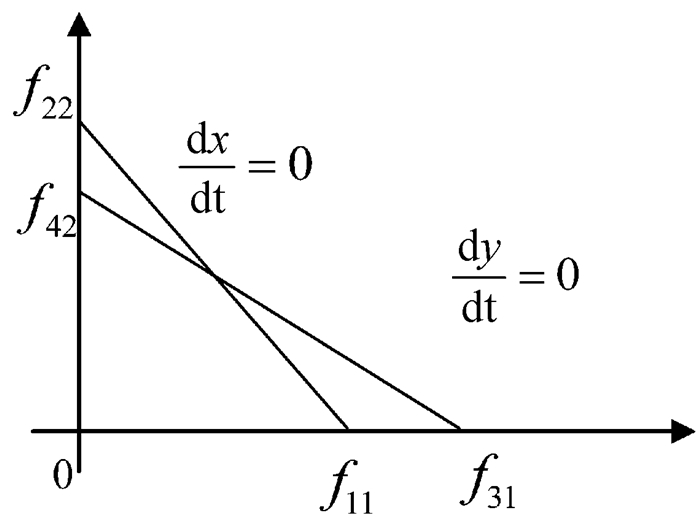
图 5 高校和科研机构竞争情况二 |
(3) 以图 5为例,f11<f31,f22>f42,即
二维共生系统中高校与科研机构处于合作状态时,同样,若要保持系统平衡,则二者的科研成果产出率不再变化。则令
| $ \frac{{{\rm{d}}x}}{{{\rm{dt}}}} = \frac{{{\rm{d}}y}}{{{\rm{dt}}}} = 0 $ | (23) |
由式(6)、(7) 有
| $ x\left( {{a_x} - {a_{{\rm{t}}x}}x - \frac{x}{{{k_1}}} + {a_{sx}} + {a_{rx}}} \right) + {\alpha _x}{\beta _{xy}}xy = 0 $ | (24) |
| $ y\left( {{a_y} - {a_{{\rm{t}}y}}y - \frac{y}{{{k_1}}} + {a_{sy}} + {a_{ry}}} \right) + {\alpha _y}{\beta _{yx}}xy = 0 $ | (25) |
解方程组,可得高校X与科研机构Y在合作状态下的共生系统A1的互利共生平衡条件,即
| $ x = \frac{{\left( {{a_x} + {a_{sx}} + {a_{rx}}} \right)\left( {{a_{ty}} + \frac{1}{k}} \right) + \left( {{a_y} + {a_{sy}} + {a_{ry}}} \right){\alpha _x}{\beta _{xy}}}}{{\left( {{a_{tx}} + \frac{1}{k}} \right)\left( {{a_{ty}} + \frac{1}{k}} \right) - {\alpha _x}{\beta _{xy}}{\alpha _y}{\beta _{yx}}}} $ | (26) |
| $ y = \frac{{\left( {{a_x} + {a_{sx}} + {a_{rx}}} \right)\left( {{\alpha _y}{\beta _{yx}}} \right) + \left( {{a_y} + {a_{sy}} + {a_{ry}}} \right)\left( {{a_{tx}} + \frac{1}{{{k_1}}}} \right)}}{{\left( {{a_{tx}} + \frac{1}{{{k_1}}}} \right)\left( {{a_{ty}} + \frac{1}{{{k_1}}}} \right) - {\alpha _x}{\beta _{xy}}{\alpha _y}{\beta _{yx}}}} $ | (27) |
当高校X和科研机构Y在合作状态下共生时,应该是二者的科研成果产出率变化为正,即x>0,y>0。此时,由式(26)、(27) 可知,(x,y)应在第一象限,则可知
| $ \left( {{a_{tx}} + \frac{1}{{{k_1}}}} \right)\left( {{a_{ty}} + \frac{1}{{{k_1}}}} \right) - {\alpha _x}{\beta _{xy}}{\alpha _y}{\beta _{yx}} > 0 $ | (28) |
式(28) 为共生系统A1中高校X和科研机构Y下,达到合作互利共生平衡的条件。从条件不等式中也可以看出,即便在合作状态下,高校与科研机构的科研成果产出率一直增加,但因为受到共生系统及共生单元成长周期的影响,这种增长将趋于稳定,空间将越来越小直至达到一个定值。
五、结论与决策建议本文在Lotka-Volterra种间竞争生态模型的基础上,构建了产业技术创新战略联盟共生系统的三维(企业、高校和科研机构)合作模型,并对其中的高校和科研机构“类似竞争”的关系构建了二维竞争与合作模型。三维合作模型从整体验证了联盟共生系统3个主体达到互利共生平衡的条件及其稳定性,二维竞争与合作模型分析了高校与科研机构在不同相互作用力下共生系统的平衡条件及其稳定性。
通过对产业技术创新战略联盟共生系统相关模型的建立与分析,主要得到以下结论。
(一) 产业技术创新战略联盟可以实现互利共生平衡对三维Lotka-Volterra合作模型方程组求解,求出方程组的唯一平衡点E(x1*,x2*,x3*),说明联盟中的企业、高校和科研机构可以构建互利共生的平衡关系。但是,这种平衡的实现需要一定的前提:
| $ {a_{22}}{a_{33}} - {a_{23}}{a_{32}}{k_2}{k_3} > 0 $ | (29) |
| $ {a_{11}}{a_{33}} - {a_{13}}{a_{31}}{k_1}{k_3} > 0 $ | (30) |
| $ {a_{11}}{a_{22}} - {a_{12}}{a_{21}}{k_1}{k_2} > 0 $ | (31) |
式(29)-(31) 可以变形为:
| $ \frac{{{a_{22}}}}{{{K_2}}} \times \frac{{{a_{33}}}}{{{K_3}}} > {a_{23}} \times {a_{32}} $ | (32) |
| $ \frac{{{a_{11}}}}{{{K_1}}} \times \frac{{{a_{33}}}}{{{K_3}}} > {a_{13}} \times {a_{31}} $ | (33) |
| $ \frac{{{a_{11}}}}{{{K_1}}} \times \frac{{{a_{22}}}}{{{K_2}}} > {a_{12}} \times {a_{21}} $ | (34) |
其中,
因此,虽然各共生单元追求的目标存在差异,其对于在联盟共生系统中的定位不清晰,但是当企业、高校和科研机构三者的科研成果市场转化率、科研成果产出率的自然增长率、合作系数,即相互作用力与其为了实现增长目标已占用的资源满足上述条件时,联盟共生系统总能达到平衡。
(二) 产业技术创新战略联盟中各主体之间存在稳定的互利共生关系产业技术创新战略联盟的建立并不是暂时的,联盟的建立应该以长期稳定的互惠合作关系为基础,这样才能在战略层面实现产业经济增长,使企业增强自主创新能力,高校和科研机构在进行良好知识互动的同时,增强自身的科研能力,为企业、高校和科研机构带来长久的积极影响[10]。
设平衡点 E(x1*,x2*,x3*)形成的矩阵为C。对共生系统中存在唯一平衡点E(x1*,x2*,x3*)的稳定性进行验证,证明产业技术创新战略联盟这一共生系统是可以形成长期稳定合作关系的产学研一体化联盟。
| $ C = \left( {\begin{array}{*{20}{c}} { - \frac{{{a_{11}}}}{{{k_1}}}x_1^ * }&{{a_{12}}x_1^ * }&{{a_{13}}x_1^ * }\\ {{a_{21}}x_2^ * }&{ - \frac{{{a_{22}}}}{{{k_2}}}x_2^ * }&{{a_{23}}x_2^ * }\\ {{a_{31}}x_3^ * }&{{a_{32}}x_3^ * }&{ - \frac{{{a_{33}}}}{{{k_3}}}x_3^ * } \end{array}} \right) \\= \left( {\begin{array}{*{20}{c}} {x_1^ * }&0&0\\ 0&{x_2^ * }&0\\ 0&0&{x_3^ * } \end{array}} \right)\left( {\begin{array}{*{20}{c}} { - \frac{{{a_{11}}}}{{{k_1}}}}&{{a_{12}}}&{{a_{13}}}\\ {{a_{21}}}&{ - \frac{{{a_{22}}}}{{{k_2}}}}&{{a_{23}}}\\ {{a_{31}}}&{{a_{32}}}&{ - \frac{{{a_{33}}}}{{{k_3}}}} \end{array}} \right) \\= DB $ | (35) |
则有
从模型的相关求解可知,构建联盟应以战略合作为基础,联盟主体间形成长期的战略关系是可行的。若企业、高校和科研机构在组建联盟时有长期合作、资源共享、优势互补的战略意识,形成良好的互利共生平衡,就能使共生系统平衡的稳定性更加持久。
(三) 联盟中更倾向于“类似竞争”的某两个主体之间可以达到共生平衡,但是这种平衡将会被打破二维共生系统中高校与科研机构倾向于“类似竞争”关系时,保持系统平衡的条件是二者的科研成果产出率的变化量相等且为零。令
| $ \frac{{{\rm{d}}x}}{{{\rm{dt}}}} = \frac{{{\rm{d}}y}}{{{\rm{dt}}}} = 0 $ | (36) |
通过运算可知,只要满足不等式
基于此,在联盟中要尽力构建主体之间(不仅是高校和科研机构之间,还包括企业与高校、企业与科研机构之间)良性竞争甚至是促成实质的合作关系。当联盟主体间的实质合作关系建立之后,能有效促进联盟的整体运行效果与效率的改进,使整个联盟最终成为互利共生的共生系统,实现多赢发展模式。
(四) 联盟中更倾向于合作的某两个主体之间可以达到共生平衡,促进二者利益的增长,但这种增长将趋于饱和二维共生系统中高校与科研机构倾向于合作关系时,保持系统平衡的条件是二者的科研成果产出率变化量相等且为零。即
| $ \frac{{{\rm{d}}x}}{{{\rm{dt}}}} = \frac{{{\rm{d}}y}}{{{\rm{dt}}}} = 0 $ | (37) |
通过求解可知,高校与科研机构在合作状态下互利共生平衡条件为
| $ \left( {{a_{tx}} + \frac{1}{{{k_1}}}} \right)\left( {{a_{ty}} + \frac{1}{{{k_1}}}} \right) - {\alpha _x}{\beta _{xy}}{\alpha _y}{\beta _{yx}} > 0 $ | (38) |
不等式(38) 表明,即便在合作状态下,高校与科研机构的科研成果产出率一直增加,但因为受到共生系统及共生单元成长周期的影响,这种增长将趋于稳定,空间将越来越小直至达到一个定值。
因此,联盟中的某两个主体之间更倾向于合作时,二者的共生系统虽然能形成较稳定的共生平衡关系,使总体和个体的追求的增长目标都得以实现,但是这种增长最终将趋向饱和。政府、企业、高校和科研机构应该采取积极措施尽量延长联盟及其主体利益增长的时间。
针对所构建模型中的方程求解结果及结论,笔者提出以下相关决策建议。
第一,正确引导联盟主体树立构建稳定联盟关系的合作意识。企业、高校和科研机构都应该对联盟充满信心。而政府也应当从适当的方向引导三方的合作,并出台相关政策促使联盟主体构建长期的战略关系。将联盟中的各主体看成统一的总体来给予支持,并且对于其中实力较弱的一方要提供必要的协助。不断引导企业、高校与科研机构强化彼此之间共生意识,使联盟的总体效率提高的同时使主体自身也获得比参与联盟之前更大的利益满足。
第二,进行持续的阶段性监督与政策支持。产业技术创新联盟的构建并不是为了某一个合作项目或迎合某一阶段的创新口号,而是关系到一个产业战略性的发展。三方主体在加入到联盟时应该是以战略合作为起点,政府应在联盟发展过程中不断进行阶段性的监督,并根据联盟发展客观情况制定相关的政策使联盟中的各主体建立长期有效的信用等相关机制,以维系其战略合作关系以至达到联盟共生系统的平衡状态。
第三,进一步规范联盟中各主体的合作与竞争行为。政府及相关部门应该完善相关政策法规,建立较全面的联盟总体与各主体的相关评价机制,以规范各主体在共生系统中的利益分享与风险共担的行为。
第四,不断加强联盟各主体的核心竞争力。政府及有关部门应制定企业、高校与科研机构的一体化发展战略及指导文件,不断地引导共生主体积极进行有效的合作模式与共生系统运行机制的探索,使企业、高校和科研机构不断提高自身核心能力,进行及时的技术创新,增强主体的名誉度,努力延长联盟成长生命周期中的稳定期,避免联盟的效率改进趋近饱和,以使联盟共生系统不断处于活跃的创新环境中,在提高自身核心竞争力的同时,促进联盟总体的共同发展。
| [1] | 谭建伟, 叶丽, 李攀艺. 基于产学研的技术创新战略联盟运行机制研究述评与展望[J]. 重庆理工大学学报:社会科学版, 2012(6): 32–36. |
| [2] | 胡枭峰. 产业技术创新战略联盟研究评述[J]. 商业现代化, 2010(7): 8–9. |
| [3] | 李林, 肖玉超, 王永宁. 基于产业集群的产学研战略联盟合作机制构建研究[J]. 重庆大学学报:社会科学版, 2010(2): 11–15. |
| [4] | 徐刚, 梁淑静, 高静. 产业技术创新战略联盟本质与运行难点[J]. 商业研究, 2012(7): 112–116. |
| [5] | 袁纯清. 共生理论及其对小型经济的应用研究(上)[J]. 改革, 1998(2): 101–105. |
| [6] | 胡坚. 在不同学科的交汇行进—评袁纯清同志著[J]. 重庆大学学报:社会科学版, 1999(5): 92–94. |
| [7] | FREEDMAN H I A.Deterministic mathematical models in population ecology[M]. NY:Marcel Dekker Inc., 1980. http://onlinelibrary.wiley.com/doi/10.2307/3556198/abstract |
| [8] | 高长元, 杜鹏. 基于Lotka-Vovterra的高技术虚拟产业集群成员间合作与竞争模型[J]. 科技进步与对策, 2009(23): 72–75. |
| [9] | 权宏顺. 3维Lotka-Volterra合作系统的全局稳定性[J]. 应用数学, 1991(1): 53–57. |
| [10] | RAO B P, SRINIVAS K, REDDY A. Dynamic to the analysis of strategic alliances[J]. International Business Review, 1995, 4(4): 499–518. DOI: 10.1016/0969-5931(96)81750-1 |
 2014, Vol. 20
2014, Vol. 20

