2012年7月北京大暴雨,为北京带来了前所未有的困难和考验,城区多处积水严重,路面交通中断,部分地铁停运,500多架次航班取消或延误。这说明中国城市在基础设施建设,尤其是在道路、交通、排涝应急等公共设施方面,存在很大的短板,同时也说明公共基础设施之间的关联性是造成某种自然风险因素扩散性传递的重要载体。作为不可抗力的风险因素,管理者并不能改变其存在和发展的客观性,但是如果能很好地预知这类风险带给公共基础设施的损失及其扩大路径,对于风险发生之后的损失控制方案制定有很大意义。因此,准确把握公共基础设施之间的关联性与风险形成、传递规律,应当作为城市公共工程风险应急管理的重要内容。目前关于基础设施系统内部关联性的研究集中于内部关联性特征和基于关联性的外界互动研究两个方面。研究方法则以数学模型和复杂网络方法为主。基于数学以及模拟仿真技术针对城市基础设施系统内部关联状况进行模拟的研究,基本上统一于对内部关联性存在的认可,并可以一定的方式进行描述,如Nozick等利用马尔可夫特性描述了关键基础设施网络的关联关系[1],刘健等则采用系统动力学和Multi-Agents混合建模方法模拟了城市基础设施系统内部的关联关系[2];另一类则基于这种关联性考虑系统受到外部因素影响时的效应分析,这方面研究以Haimes等将Leontief经济学模型应用其中,提出失效输入/输出模型为主要标志,提供了城市基础设施系统与外界因素交互作用研究的新模式[3]。后续学者基于此模式具体分析了在特定外界因素作用下,城市基础设施系统内部的关联性变化规律,如Garg等利用最小费用流算法模拟城市基础设施网络部分系统失效情况下的运行和恢复情况[4];吴之立等在肯定城市基础设施系统存在复杂关联的前提下,建立了供需关系网络模型以应对紧急状态下备用资源的分配问题[5];胡爱军等以极端天气这一自然风险因素为例说明了基础设施在风险影响下的间接经济损失的评估问题[6];除此之外,还包括了部分学者对公共基础设施风险的定性分析[7]。总体而言,对城市基础设施系统内部关联性的认识是统一的,但缺乏针对这一系统面临风险因素的影响时基于设施关联性发生的传递效应的分析,尤其是各设施本身具有的抗风险能力这一能动性要素未被考虑。因此,本文基于公共基础设施的风险传递机理构建其不可操作性风险的传递模型,以说明基础设施系统中风险的形成和扩散过程。
一、公共基础设施项目及其特点公共基础设施是指为公众设置,公众可以共享,不允许某个人独占或排他的一些基础性设施,包括具有一定规模的建筑、交通、能源、通信等服务于社会公众,与群众日常生活联系紧密,具有广泛社会影响,关系城市或者区域可持续发展的重大工程,通常具有重要使用功能和重大社会意义的标志性工程。除了具有一般项目的一次性、独特性、投资周期长等特点,还具有公共性、服务性、社会关注度高、配套设施条件、安全性与关联性要求高等特点[8]。
公共性是指公共基础设施的需求根源以及委托方都是公众,项目成果应当为公众共同享用。服务性是指公共基础设施具有为公众的物质文化生活提供服务的功能,是实现公共服务的载体。社会关注度高。一般来说公共基础设施投资多、建设规模大、公共资源消耗多,涉及社会公众生活的各个方面,从根本上花的是纳税人的钱,对区域经济文化具有战略意义,因此一般会受到较高的社会关注。安全性要求高。公共基础设施受众面大,一旦发生安全问题,造成的损失将不可估量,因此要求公共基础设施要保障公众及周边环境的安全。
需求导向明显。相对于一般商业项目,大型公共基础设施基本是完全需求导向型的,也就是基于公众的需求开发建设。
关联性高。这是公共基础设施系统内部的重要特征,一般来说可以分为四类[9]:(1) 实体相依性。如果两个关键基础设施系统之间是实体相依性,则一系统依赖另一系统提供原料或是服务,方能运作。如供水系统须依赖电力系统所产出的电力才能顺利提供供水服务。(2) 信息相依性。透过信息的连接将关键基础设施系统连接称为信息相依性,如一发电厂的控制讯号通过光纤等通讯网络传递到总控制中心,才能正确配电给服务范围内各项设施,故称两者之间具有信息相依性。(3) 地理相依性。如果本地环境事件造成本地的一些关键基础设施的状态变化,则这些关键基础设施系统具有地理上的相关性。举例来说,输水管线与电力配送系统在同一条桥上,当桥梁损毁时输水管线与电力配送系统将会同时发生状况。(4) 逻辑相依性。是指不同设施所属机关相同,当发生风险事件时可能因为资源分配问题彼此之间存在间接影响。如电力系统与供水系统都由同一家公司管理,当公司财务发生问题时对电力系统与供水系统的监控与注意力都会下降,就会造成供水系统或电力系统破坏的可能性大幅提高。
二、公共基础设施不可操作性风险的形成 (一) 公共基础设施不可操作性风险的定义综合各主流学说对风险的不同定义,风险的实质就是一个事件发生某个后果的不确定性(或然性)及造成损失的严重程度,可用函数R=F(P, C)来表示,R代表风险,P 代表事件发生的概率,C代表事件发生的结果。还有一种定义将风险情景因素考虑其中,给出了R=F(S, P, C),其中S为某种风险情景。
本文将公共基础设施项目的不可操作风险定义为不确定性事件或条件对公共基础设施项目期望目标值存在的影响。这种影响包含两层含义:一是风险因素对公共基础设施本身的直接影响;二是基于公共基础设施系统的复杂性和关联性,非直接的影响作用以设施本身为载体向其他设施进行传递,包括风险的放大和减弱两种情形。基于公共基础设施的主要功能要求,其不可操作性风险表现为设施受到内部或者外界风险因素影响时,其部分或整体功能失效。我们将其定义为系统在行使其规定的功能时表现出来的无效,这一特征由于设施不同而有不同的表现形式,如交通中断、电力系统瘫痪等。以概率方式可以表示为:
| $ C = P\left[{E\left( X \right) < X} \right] $ | (1) |
其中C为不可操作性风险结果,X 为基础设施要求的操作性水平,可以财富损失或者人员伤亡表示其风险后果。
以实物形态来说,公共基础设施不可操作性风险主要表现为:(1) 扩散效应。当一设施毁坏后,与其串联的各个设施皆会中止服务或毁坏。如通往发电厂的道路损毁,造成电力不足,电力系统的中断造成通讯中断,进而产生更多问题。(2) 渐升效应。当一设施毁坏后,另一设施的损毁程度增加或复原时间增加。如通讯系统中断,通常将使许多设施的修复时间加长。(3) 共同原因损坏。一些设施可能因同一原因,几乎同时间一起损坏。
(二) 公共基础设施不可操作性风险传递风险因素、风险事故与风险损失之间的关系是风险因素导致风险事件的发生,风险事件在一定条件下引起风险后果。也就是说,风险因素是造成损失的内在原因,而风险事件则是造成损失的外在原因。关于风险的形成,亨利希的骨牌理论形象地说明了风险的形成要素之间的关系。在他的理论中,这些骨牌依次是:遗产及社会环境、人的缺点、人的不安全行为和物的不安全状态、事故与伤害。他认为风险事故的发生是一连串事件互为因果按照一定顺序发生的结果[10]。也就是说,在一串骨牌中,如果一块骨牌倒下,后面的骨牌将发生连锁反应顺序倒下。
基于骨牌理论,我们将风险分为三种类型:一是风险的直接形成,表示风险因素直接造成风险客体的风险损失;二是由于客体之间的相关性,在直接风险形成后同时形成相关性风险;三是风险的传递。风险的传递现象又因为载体的不同表现为两种类型:一是由于项目任务之间的关联性导致同一种风险的扩大或减弱;二是由于人为的理解或者操作导致风险的放大或减弱。前者的传递载体是项目任务之间的关联性,后者的载体则主要是信息传播。由于公共项目的属性,经常以基础设施的形态出现,而基础设施之间的相互依赖性和相互关联性成为风险传递的载体,导致发生风险的复杂化,这种现象属于第一种风险传递类型。因此,基础设施实体的关联性是风险传递的基础。
我们考虑由n项彼此关联的基础设施组成一个公共基础设施系统,每个基础设施可以作为一个实体,其可操作性水平取决于其他基础设施所提供资源的可用性。那么这个系统中的要素可能遭受外界风险事件或者内部自身功能失效的影响,造成这一要素的不可操作性风险。由于不同基础设施之间的直接依赖关系导致循环和相互依存关系等形式的关联性关系的存在,即一个事件降低了第i项基础设施的可操作性,还可能引发与第i项基础设施关联的其他基础设施的可操作性水平的变化。这些变化将以关联性的物质载体传递到其他基础设施。当然基础设施的不可操作性状况在一定时间内是稳定的,即不考虑其自我恢复性。在这样的系统中,某种风险因素可能直接影响单个的基础设施,再在关联性系统中进行传递;也有可能是风险因素同时影响多个基础设施,并发生传递,扩大影响的范围。需要说明的是风险传递只能说明风险影响结果的扩散性,但不一定是风险的增大。
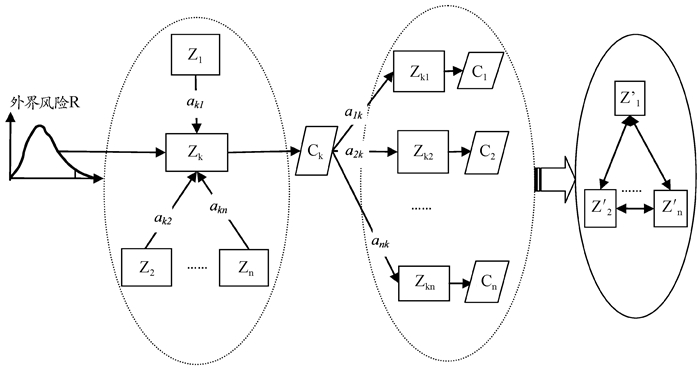
这一传递过程机理如图 1所示。图中基础设施系统由n项相关联的要素构成,R 表示基础设施受到的外界风险因素的影响,一般以概率分布描述;Z 表示基础设施内部任务结构,也可以看作其抗风险能力;aij是内部风险响应状态,表示第j项基础设施对第i项基础设施不可操作性的贡献;Ci表示第i项基础设施在受到风险冲击之后表现出来的不可操作性风险结果,是风险传递的阶段性产物;基于基础设施之间的关联性,Ci 以传递的形式对系统中的其他基础设施的可操作性造成冲击,各自形成了一定的不可操作性风险结果,最终形成了公共基础设施的另一种操作性均衡水平[Zi′]。
|
图 1 基于关联性的公共基础设施不可操作性风险传递 |
美国经济学家瓦西里·列昂惕夫在《美国经济结构,1919-1929》一书中详细介绍了“投入产出分析”的基本内容[11]。这一方法是研究经济体中均衡行为的框架,促进了对一个经济体中不同部分之间的互联性的理解,同时说明了某部分的变化对其他部分带来的影响的预测。投入产出(IO)模型已被高度多样化地应用,包括评估经济的相互依存关系[12]、环境建模[13]以及灾害影响分析[14]。随后,Haimes[15]与Santos[16]等在Leontief的投入产出模型基础上,提出了不可操作投入产出模型(Inoperability input-output modeling,IIM)。IIM模型是Leontief投入产出(IO)模型的延伸,是各种故障来源包括恐怖主义、自然灾害和意外事故引发的基础设施的级联效应评估的分析工具。
基础设施面临的第三种风险传递是基于基础设施之间的关联性而导致的设施不可操作风险的扩大或减弱的结果,表现为外力作用下关联性系统的风险投入和产出的问题。因此,我们可以基于Leontief的IO模型建立公共基础设施面临风险时由于内部设施关联性导致的实体不可操作风险传递的模型。
假设:xj表示第j个基础设施面临的整体风险。xij表示系统中第j项基础设施受到风险因素的影响造成不可操作性对第i个基础设施不可操作性的影响。aij为第j项基础设施对第i项基础设施贡献的不可操作性概率,表示第i项基础设施对第j项基础设施的依赖程度。aij=1表示两个基础设施之间有明确的关联性,即第i项基础设施的不可操作风险一定会导致j项基础设施的故障;而aij=aji=0表示在第i项基础设施和基础设施j 之间不存在物理性连接。Ci表示第i项基础设施受到风险因素的影响,即不可操作性风险。
| $ 由此,{X_i} = \sum\nolimits_{j = 1}^n {{X_{ij}} + {C_k}\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;i, j = 1, 2, \cdots \cdots, n} $ | (2) |
针对不可操作性风险的传递模型则有:
| $ {X_i} = \sum\nolimits_{j = 1}^n {{a_{ij}}{X_j} + {C_k}\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;i, j = 1, 2, \cdots \cdots, n} $ | (3) |
其中,
I为n × n 的单位矩阵,则由上式可以求得基础设施系统不可操作向量:
| $ X = {\left( {I-A} \right)^{-1}}C $ | (4) |
需要说明的是,aij表示基础设施不可操作性风险的传递系数,因此A矩阵数值的确定应当是这一模型精确性的关键所在。很多学者用专家调查法、模糊法来确定[17-18]。但是主观判断与客观存在之间难免存在误差,如果不能很好地描述公共基础设施系统的内部关联性,那么对于整个系统的不可操作性风险的预测将会不可避免地出现误差。相比而言,公开的投入产出表比实际领域的调查和访谈更为优越,因此本文应用投入产出表中的数据作为基础数据来获得这一依赖性关系矩阵。另外,在以前IIM的应用中,经常假设向量C由常量元素组成。例如,电力系统为第i项基础设施,是唯一直接受影响的部门,如果20%的电力服务能力下降,将对应Ci = 0.2,所有其他元素都是零。事实上,自然灾害类的风险因素很多情况下不只对一项基础设施产生直接影响,而是同时直接影响多项基础设施的可操作性。而且风险因素的不确定性导致了基础设施面临不可操作性风险损失的不确定性,应考虑其以某种概率分布情况存在,而不是常量,且一般情况下,自然灾害的发生属于极端事件。
(二) 模型应用为说明公共基础设施系统不可操作性风险传递模型的应用,本文选择5项基础设施:(1) 电力、热力系统;(2) 燃气供应系统;(3) 供水系统;(4) 城市公共交通;(5) 信息传输系统。j=1, 2, 3, 4, 5分别表示这5项基础设施。这些子系统之间的关联系数矩阵(A)如表 1-表 3所示,根据中国2007年投入产出表中数据计算得出。
| 表 1 基础设施关联系数矩阵 |
| 表 2 (I-A)系数矩阵 |
| 表 3 (I-A)-1系数矩阵 |
在基础数据确定的情况下,本文假定基础设施受到风险因素影响后在一定时间内的不可操作性不变,来说明这一模型的应用过程。
假设第一种情况,只有供水系统受到袭击,导致其可操作性降低了30%,即C3=0.3,其他4项基础设施不受风险的直接影响,有C= [0 0 0.3 0 0]T。根据式(4) 可求得由于供水系统受到风险直接影响后,相互关联的基础设施系统不可操作风险向量为:X= [0.092 0.001 0.301 0 0.001]T
这说明在供水子系统可操作性降低30%之后,由于基础设施的关联性,其他设施也不可避免地受到这一风险的影响,不可操作性风险传递结果显示供电和热力子系统是仅次于供水系统本身的受害体。
如果多项基础设施同时遭受风险,则基础设施系统不可操作性风险传递的结果也可用同样方法得到。
第二种情况,基础设施面临的风险因素发生服从某种概率分布,因此只能得到某项基础设施遭受的不可操作风险的概率分布,而不是点估计值,即自然风险发生的概率分布假设为g ,则基础设施不可操作性风险发生的概率分布为f (g)。这种情况下,其他基础设施的不可操作性风险水平也以一种新的概率分布发生。
假设供水子系统受到风险因素影响之后不可操作性风险降低f1,其他设施不受风险因素的直接影响,则同理可得,基础设施系统的不可操作性水平变为:X=[0.307f1 0.003f1 1.004f1 0 0.004f1]T
同时可知f1的取值范围是0≤f1≤0.996,因为f1>0.996,在f1>0.996的情形下,供水子系统将全面崩溃。
如果多项以上基础设施同时受到风险因素的直接影响,在一定时间内不考虑恢复效应,假定供水子系统和通信子系统同时受到侵袭,这种侵袭的风险来源可能是相同的一种,也可能是不同的风险因素,其各自的不可操作性向量分别为f1和f2,同样可以得到整个基础设施系统的不可操作性风险向量为:
| $ X = \left[\begin{array}{l} 0.307{f_1} + 0.045{f_2}\\ \begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {}&{0.003{f_{\rm{1}}}}&{} \end{array}} \end{array}\\ 1.004{f_1} + 0.002{f_2}\\ \begin{array}{*{20}{c}} {}&{0.001{f_2}}&{} \end{array}\\ 0.004{f_1} + 1.012{f_2} \end{array} \right] $ |
此时由于风险因素的组合效应,f1和f2的取值范围为:0≤f1≤0.994, 0≤f2≤0.988。
这一方法除了能有效预测基础设施系统不可操作性风险的传递效应之外,还可以逆向考虑,即可获知当某几项基础设施性能水平提高的情况下整个基础设施系统性能的改善情况。如要求提升某城市整体基础设施系统的稳定性水平20%,那么基于这种关联性的传递效应,我们可以用同样的方法获知在基础设施系统内部,各项基础设施功能可操作性的有效提升空间。
四、结论系统内部的关联性对基础设施面临的风险形成和发展造成了更大的传递性和复杂性。本文在分析了公共基础设施风险传递的特性之后,基于Leontief投入产出模型,构建了基础设施系统不可操作风险的传递模型,并以实例说明模型的应用性。公共基础设施的不可操作性风险传递模型为管理者提供了一个框架,帮助管理者分析如何对存在关联性的基础设施(或部门)系统进行有效的风险管理,尤其是为建立基础设施之间的风险联动防范机制提供了参考依据,同时也为基础设施改善性功能分配建设提供了借鉴。
| [1] | NOZICK L K, TURNQUIST M A, JONES D A, et al. Assessing the performance of interdependent infrastructures and optimizing investments[J]. International Journal of Critical Infrastructure, 2005, 1(2): 144–154. |
| [2] | 刘健, 刘晓, 吴之立. 网络化关键基础设施依存关系建模与仿真方法研究[J]. 中国安全科学学报, 2011, 21(10): 29–37. DOI: 10.3969/j.issn.1003-3033.2011.10.005 |
| [3] | HAIMES Y, JIANG P. Leontief-based model of risk in complex interconnected infrastructures[J]. Journal of Infrastructure System, 2001, 7(1): 1–12. DOI: 10.1061/(ASCE)1076-0342(2001)7:1(1) |
| [4] | GARG M, SMTTH J C. Models and algorithms for the design of survivable multi-commodity flow networks with general failure scenarios[J]. International Journal of Management Science, 2008, 36(6): 1057–1071. |
| [5] | 吴之立, 刘晓. 突发事件下城市关键基础设施应急策略研究[J]. 中国安全科学学报, 2011, 21(6): 168–176. |
| [6] | 胡爱军, 李宁, 史培军, 等. 极端天气事件导致基础设施破坏间接经济损失评估[J]. 经济地理, 2009, 29(4): 529–535. |
| [7] | 韩豫, 陈亮, 成虎. 大型公共建筑风险的系统分析[J]. 现代城市研究, 2010(10): 92–96. DOI: 10.3969/j.issn.1009-6000.2010.10.013 |
| [8] | 王元明, 徐大海. 大型公共项目风险结构分析[J]. 北京理工大学学报:社会科学版, 2012(5): 84–88. |
| [9] | RINALDI S, PEERENBOOM J, KELLY T. Identifying, understanding, and analyzing critical infrastructure independencies[J]. IEEE Control Systems Magazine, 2001(21): 11–25. |
| [10] | HEINRICH H W. Industrial accident prevention:A safety management approach[M]. NewYork: McGraw-Hill, 1979: 14-19. |
| [11] | LEONTIEF, WASSILY W. structure of American economy, 1919-1939:An empirical application of equilibrium analysis[M]. New York: Oxford University Press, 1951. |
| [12] | MIDMORE P, MUNDAY M, ROBERTS A. Assessing industry linkages using regional input-output tables[J]. Regional Studies, 2006, 40: 329–343. DOI: 10.1080/00343400600631673 |
| [13] | HOEKSTRA R, JANSSEN M. Environmental responsibility and policy in a two-country dynamic input-output model[J]. Economic Systems Research, 2006, 18: 61–84. DOI: 10.1080/09535310500440894 |
| [14] | ROSE A. Economic principles, issues, and research priorities in hazard loss estimation[M]. . |
| [15] | HAIMES Y, HOROWITZ B, LAMBERT J, et al. Inoperability input-output model (ⅡM) for interdependent infrastructure sectors:Theory and methodology[J]. Journal of Infrastructure Systems, 2005(11): 67–79. |
| [16] | SANTOS J. Inoperability input-output modeling of disruptions to interdependent economic systems[J]. Systems Engineering, 2006(9): 20–34. |
| [17] | 魏海蕊. 分布式能源供应链的规划与鲁棒运作研究[M]. 上海: 上海交通大学出版社, 2010. |
| [18] | 李鹏, 易立新, 王晓荣, 等. 重要基础设施的依赖性模型及应用[J]. 中国安全科学学报, 2010, 20(2): 59–63. |
 2014, Vol. 20
2014, Vol. 20

