重庆是集大城市、大农村、大山区、大库区和少数民族地区为一体的西部直辖市,各区县地理环境、资源禀赋、风俗人文等差异很大,经济社会发展极不平衡。统筹城乡发展,是新形势下促进城市与乡村协调发展,缩小城乡差距、区域差距、贫富差距,实现共同富裕的必由之路,是从根本上解决新形势下“三农”问题、全面推进农村小康建设的客观要求。坚持城乡统筹,必须着眼于破除城乡二元结构突出矛盾,切实处理好工农关系和城乡关系,把推进城镇化建设与优化城乡经济和人口布局、调整城乡利益关系结合起来,推动城乡经济社会协调互动发展。因此,在新型城镇化的战略背景下,研究和探讨重庆全市和各区域板块城乡收入差距演化规律,对优化城乡统筹战略,调整城乡利益关系,推动新型城镇化科学稳健发展,具有十分重要的意义。
(一) 城乡收入差距的研究现状在国内外理论界,对城市化与城乡收入差距的关注由来已久。早期的刘易斯模型[1],库兹涅茨倒U形曲线假说[2],拉尼斯和费景汉模型[3],乔根森模型[4]以及托达罗模型[5],从人口流动、人力资本及产业结构等方面不同程度揭示了城市化与城乡收入差距的关系。近年来,中国学者也从不同的角度对城乡收入差距问题进行了大量研究,认为影响中国城乡收入差距及其变动的因素众多,如经济发展水平[6]、经济开放程度[7]、金融发展水平[8-11]、要素积累差异[12-14]、城市发展水平[15-16]、城市偏向政策[17-19]等。在城市化与城乡收入差距的关系方面,一部分学者认为中国的城市化导致了城乡收入差距进一步拉大[16, 20-22]。同时,一些学者认为城市化能够缩小中国城乡收入差距[8, 18, 23-24]。
(二) 面板数据向量自回归(PVAR)模型的研究现状面板数据能够获得更多的样本观测值,为有效估计向量自回归模型参数提供条件。Pearran和Smith[25]对面板数据向量自回归模型进行了开创性研究,发现对于宏观面板数据(即观测样本较少、观测时点较大),可以通过对每个变量的个体平均时间序列数据建立时间序列向量自回归模型的方法估计模型参数,并且这种估计是一致的。Binder、Hsiao和Pesaran[26]对纵剖面时间序列独立的微观面板数据进行了研究,给出了个体固定效应面板数据向量自回归模型的QML估计、GMM估计和MSE估计,并且发现3种参数估计方法都是渐进正态分布的一致估计。Canova和Ciccarelli[27]、Canova等[28]对纵剖面时间序列相关的微观面板数据进行了研究,提出了一种基于分层贝叶斯后验估计方法(Hierarchical Bayesian Posteriori Estimation Method,BPE)的面板数据向量自回归模型,并且将PVAR模型和指数模型[29]相结合,采用贝叶斯后验估计方法和马尔科夫链蒙特卡洛模拟方法(Markov Chain Monte Carlo Simulation Method,MCMC),解决了不同个体和不同变量的模型系数存在时间变异的问题,在应用中具有良好的性质。
二、研究设计 (一) 变量选取及分析 1. 城乡收入泰尔指数(THEIL)国内外学者提出很多测量居民收入差距的指标,比较有代表性的指标有城乡居民人均可支配收入比、城乡居民人均消费支出比以及基尼系数(Gini coefficient)、泰尔指数(Theil index)等。在现有文献中,常用城镇人均可支配收入与农村人均纯收入之比作为度量城乡收入差距的指标。由于中国是一个农业大国,城乡经济呈现出显著的二元结构,农村人口占有较大的比重,因此这一度量方法没有反映城乡人口所占比重的变化,不能准确度量城乡收入差距[30]。鉴于城乡收入差距因二元经济结构特征主要体现为两端的变化,本文借鉴Shorrocks的研究选择泰尔指数(THEIL)作为度量城乡收入差距的指标。以THEILt表示t时期的泰尔指数,其计算公式为:
| $ THEI{L_{\rm{t}}} = \sum\limits_{j = 1}^2 {(\frac{{{R_{jt}}}}{{{R_{\rm{t}}}}})} {\rm{In}}({\rm{ }}\frac{{{R_{jt}}}}{{{R_{\rm{t}}}}}/\;\frac{{{N_{jt}}}}{{{N_{\rm{t}}}}}) = (\frac{{{R_{1{\rm{t}}}}}}{{{R_{\rm{t}}}}}){\rm{In}}({\rm{ }}\frac{{{R_{1{\rm{t}}}}}}{{{R_{\rm{t}}}}}/\frac{{{R_{1{\rm{t}}}}}}{{{R_{\rm{t}}}}}\;) + (\frac{{{R_{2{\rm{t}}}}}}{{{R_{\rm{t}}}}}){\rm{In}}({\rm{ }}\frac{{{R_{2{\rm{t}}}}}}{{{R_{\rm{t}}}}}/\frac{{{R_{2{\rm{t}}}}}}{{{R_{\rm{t}}}}}\;) $ |
其中,j =1、2分别表示城镇地区和农村地区,Njt表示城镇地区(j =1) 或农村地区(j =2) 的常住人口数量,Nt表示常住人口总量,Rjt表示城镇地区(j =1) 或农村地区(j =2) 的收入总额(用相应的常住人口数量和人均收入之积表示),Rt表示收入总额。
2. 城镇化率(URB)城镇化率又称城市化率、城市化度、城市化水平指标,通常用市人口和镇驻地聚集区人口占全部人口(人口数据均用常住人口而非户籍人口)的百分比来表示,是一个国家或地区经济发展的重要标志。近年来,针对城市日益多元的综合性发展,协同考虑人口、土地、文化、环境等多因素,国内外众多研究机构和学者纷纷从不同角度构建了一系列复合型城镇化评价指标体系,但在评价因子和评价权重方面带有较强的主观性和随意性。因此,本文选择城镇化率作为反映人口向城镇聚集过程和聚集程度的指标,并做对数化处理,以消除变量之间的量纲差异和可能存在的异方差。以URBt表示t时期的城镇化率,其计算公式为:
| $ UR{B_{\rm{t}}}{\rm{ = }}\frac{{{N_{{j}{\rm{t}}}}}}{{{N_{\rm{t}}}}} \times 100\% $ |
工业化有狭义与广义之分。狭义的工业化通常被定义为工业(特别是其中的制造业)或第二产业产值(或收入)在国民生产总值(或国民收入)中比重不断上升的过程。工业发展是工业化的显著特征之一,但工业化并不能狭隘地理解为工业发展,因为工业化是以工业发展为核心、由传统农业社会向现代工业社会转变的过程。在此过程中,工业发展不是孤立进行的,而总是与交通运输、仓储和邮政业、信息传输、计算机服务和软件业、批发和零售业、金融业等生产服务部门的发展相辅相成的。十六大报告对新型工业化道路的战略部署中特别指出,通过推进产业结构的优化升级,形成以高技术产业为先导,基础产业和制造业为支撑,服务业全面发展的产业格局。所以,工业化进程在广义上可以理解为以农业增加值比重下降和非农产业增加值比重上升的经济结构优化升级的过程。非农产值比是第二产业增加值与第三产业增加值之和在地区生产总值中的比重。考虑到数据的可得性以及指标的使用惯例,本文选择非农增加值比重作为广义工业化进程和水平的代理变量,也做对数化处理。以INDt表示t时期的非农产值比,其计算公式为:
| $ IN{D_{\rm{t}}} = \frac{{{V_{2{\rm{t}}}} + {V_{3{\rm{t}}}}}}{{{V_{\rm{t}}}}} \times 100\% $ |
其中,V2t、V3t分别表示第二产业和第三产业的增加值,Vt表示地区生产总值。
(二) 数据选择与描述样本期间选择2000-2012年,包含38个区县横截面单元,原始数据来自《重庆统计年鉴》。由于2000-2006年各区县城镇居民人均可支配收入数据不全,本文根据2007-2012年城镇居民人均可支配收入占城镇非私营单位就业人员年平均工资的比率,乘以2000-2006年各区县城镇非私营单位就业人员年平均工资,推算出相应城镇居民人均可支配收入数据。2007年5月,重庆市第三次党代会立足全市城镇体系现状和产业发展布局,提出了“一圈两翼”的发展战略,即以主城为核心、以大约1小时通勤距离为半径范围的城市经济区(“一圈”),建设以万州为中心的三峡库区城镇群(“渝东北翼”)和以黔江为中心的渝东南城镇群(“渝东南翼”)。同时,考虑到主城核心的九区与“一圈”外围区县的经济发展水平存在梯次差距,我们将“一圈”进一步划分为“主城核心区”和“1小时经济圈”两个板块。因而,从重庆市区域经济板块研究的角度,我们将重庆38个区县分为主城核心区、1小时经济圈、渝东北翼、渝东南翼共4个区域板块,如表 1所示。
| 表 1 各区域板块区县一览 |
| 表 2 各区域板块面板数据变量统计特征 |
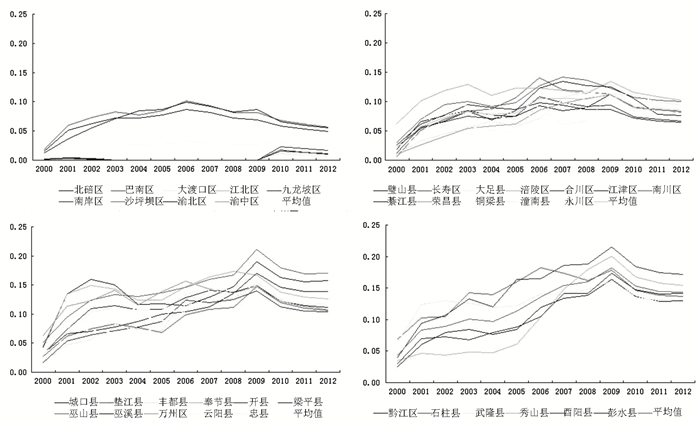
根据城乡收入泰尔指数计算公式,分区域板块绘制出各区县的城乡收入泰尔指数变化图,如图 1所示。
|
图 1 2000-2012年重庆市各区域板块城乡收入泰尔指数变化图 |
从图 1可以看出,2000-2012年重庆市绝大多数区县城乡收入泰尔指数曲线呈现出显著的倒U型特征。但各个区域板块在总体呈现倒U型特征的基础上,也具有自身特点。从倒U型曲线最高点的相应数值看,渝东南翼和渝东北翼两大板块内各区县最高点的数值较大,酉阳县城乡收入泰尔指数最高值0.215 6,巫山县城乡收入泰尔指数最高值0.210 8,分别位于渝东南翼和渝东北翼各区县首位。1小时经济圈内各区县最高点的数值略低,长寿区城乡收入泰尔指数最高值0.120 1,位于1小时经济圈各区县首位。主城核心区内各区县最高点的数值最低,巴南区城乡收入泰尔指数最高值0.101 4,位于主城核心区各区县首位。从倒U型曲线最高点出现的时间看,主城核心区各区县最高点出现时间最早,集中在2006年;1小时经济圈各区县最高点出现时间略晚,陆续分布在2006-2009年之间;渝东南翼和渝东北翼各区县最高点出现时间最晚,集中在2009年。渝东北翼各区县在2002年曾达到阶段性高点,在2003-2005年之间出现阶段性下降,此后又出现反弹性上升;渝东南翼则总体上处于持续上升状态,在2005-2009年之间上升速度尤为明显。这种状况是由于城镇化对城乡收入差异的多种方向相同和/或方向相反的作用相互叠加或抵消,使城镇化对城乡收入差异的净效应错综复杂,往往在不同地区和不同时期表现出不同特征。库兹涅茨倒U型曲线假说认为,工业化和城市化进程中,城乡收入差距在一个相当长的时间内会随着城市化水平的提高而提高,当城市化水平达到一定的程度后,城乡收入差距将逐步减少,直至基本平衡。重庆绝大多数区县城乡收入泰尔指数曲线呈现出显著的倒U型特征,在形态上与库兹涅茨倒U型曲线较为相似,这在很大程度上反映了各区县城镇化水平和所处发展阶段的差异,但考虑到本文时间跨度相对较短,是否在长期趋势上符合库兹涅茨倒U型曲线假说有待后续在更长时间跨度上加以检验。
三、实证分析 (一) 模型设定与估计方法借鉴Binder、Hsiao和Pesaran[26]建立的面板数据自回归系统:
| $ {Y_{i{\rm{t}}}} - {\phi _{\rm{t}}}{Y_{i, {\rm{t}} - 1}} - {\phi _2}{Y_{i, {\rm{t}} - 2}} - \cdots - {\phi _i}{Y_{i, {\rm{t}} - p}} - {\psi _1}{X_{i, {\rm{t}} - 1}} \\- {\psi _2}{X_{i, {\rm{t}} - 2}} - \cdots - {\psi _P}{X_{i, {\rm{t}} - P}} = {\gamma _i} + {u_{i{\rm{t}}}} $ |
其中,i =1,2,
| $ \mathit{\Phi }{\rm{(}}\mathit{L}{\rm{)(}}{{\rm{Y}}_{\mathit{i}{\rm{t}}}}{\rm{ - }}{\eta _\mathit{i}}{\rm{ - }}{\delta _{\rm{t}}}{\rm{) = }}{\mathit{u}_{\mathit{i}{\rm{t}}}} $ |
由于存在不可观测的个体固定效应Yi,所以在估计模型前要将它们消除。剔除个体固定效应Yi的常用方法是在原始模型的基础上估计一阶差分模型,即:
| $ \begin{array}{l} \Delta {Y_{i{\rm{t}}}} - \delta = {\mathit{\Phi }_{\rm{1}}}{\rm{(}}\Delta {Y_{i, {\rm{t}} - 1}} - \delta {\rm{) + }}{\mathit{\Phi }_{\rm{2}}}{\rm{(}}\Delta {Y_{i, {\rm{t}} - 2}} - \delta {\rm{) + }} \cdots {\rm{ + }}{\mathit{\Phi }_\mathit{p}}{\rm{(}}\Delta {Y_{i, {\rm{t}} - p}} - \delta {\rm{) + }}\\ {\psi _{\rm{1}}}{\rm{(}}\Delta {Y_{i, {\rm{t}} - 1}} - \delta {\rm{) + }}{\psi _{\rm{2}}}{\rm{(}}\Delta {Y_{i, {\rm{t}} - 2}} - \delta {\rm{) + }} \cdots {\rm{ + }}{\psi _\mathit{P}}{\rm{(}}\Delta {X_{i, {\rm{t}} - P}} - \delta {\rm{) + }}\Delta {u_{i{\rm{t}}}} \end{array} $ |
令
| $ {\rm{mi}}n\left\{ {\begin{array}{*{20}{l}} {[\sum\limits_{i = 1}^N {((} {Q_i} \otimes {I_m})Vec(\Delta {Y_i}) - ({Q_i}{R_i} \otimes {I_m})Vec(\mathit{\Lambda })){]^\prime }}\\ { \times [\sum\limits_{i = 1}^N {({Q_i} \otimes {I_m})} Vec(\Delta {Y_i}){\rm{ - }}({Q_i}{R_i} \otimes {I_m})Vec(\mathit{\Lambda }))]}\\ { \times {{[\sum\limits_{i = 1}^N {({Q_i} \otimes {I_m})} \sum ({Q_i} \otimes {I_m})']}^{ - 1}}} \end{array}} \right\} $ |
为确保估计结果的稳健性,在对变量进行计量分析前,要对各面板数据序列的平稳性进行单位根检验,面板单位根检验可以使用LLC、IPS、Breintung、ADF-Fisher、PP-Fisher、Hadri等方法。本文对全市层面、主城核心区、1小时经济圈、渝东北翼和渝东南翼的THEIL、logURB和logIND三个变量的面板数据分别进行了检验,检验结果如表 3所示。从检验结果看,全市层面logIND变量面板数据ADF-Fisher统计量显示能够在5%的显著水平下拒绝“存在有效的单位根过程”,全市层面的其他变量的面板数据以及其他各区域板块THEIL、logURB和logIND三个变量面板数据的各个检验统计量均显示能够在1%的显著水平下拒绝存在单位根的原假设,这说明全市层面和各区域板块的THEIL、logURB和logIND三个变量均为平稳序列。
| 表 3 各区域板块面板数据变量平稳性检验结果 |
本文的面板数据时期跨度T相对较小,但全市及各区域板块均有多个区县观测样本,因此我们选择面板数据向量自回归(PVAR)模型进行实证研究。为了避免模型设定差异引起的比较偏误,本文对全市层面和各区域板块的PVAR模型采取相同的滞后阶数。T=13^(1/4)≈1.90,把滞后阶数确定为2,建立滞后2阶的PVAR(2) 模型。本文估计PVAR模型基于STATA11计量软件,并参考了世界银行Ⅰ.love关于PanelVAR的程序代码,运用Helmert程序对原始面板数据进行前向均值差分处理,消除原始面板数据包含的固定效应。为比较全市层面和各区域板块城乡收入差异对城镇化、工业化的影响程度,对全市层面、主城核心区、1小时经济圈、渝东北翼和渝东南翼的面板数据分别进行了PVAR模型估计,估计结果如表 4所示。
| 表 4 各区域板块PVAR模型估计结果 |
考虑到VAR模型主要考察变量之间的动态反馈关系,且考虑到各区域板块VAR模型估计时的结构一致性,因而无论参数的估计值有无显著性,我们都保留在模型之中。从以上估计结果可以看出,全市层面和各个区域板块的泰尔指数(THEIL)PVAR模型解释程度总体较高,对比全市层面和各个区域板块的估计参数可以得到以下实证信息。
泰尔指数的短期动态自强化特征。在滞后1期时,无论全市层面还是各个区域板块层面,ΔTHEIL(-1) 的系数均为正,说明城乡收入差距具有自强化特征;从自强化程度看,全市层面和主城核心区、1小时经济圈、渝东北翼、渝东南翼四大板块滞后1期的系数分别是0.412 9、0.994 3、0.889 1、0.906 8和1.083 4,城乡收入差距自强化程度渝东南翼最强,主城核心区和渝东北翼次之,1小时经济圈最弱。在滞后2期时,全市层面及主城核心区ΔTHEIL(-2) 的系数均为正,说明城乡收入差距的自强化特征还在持续,但强度已经大幅下降;1小时经济圈、渝东北翼、渝东南翼三大板块ΔTHEIL(-2) 的系数均为负,表明城乡收入差距在滞后1期自强化的基础上,在滞后2期时略有回调。
城镇化率对泰尔指数的短期动态影响关系。在滞后1期时,全市层面及1小时经济圈ΔlogURB(-1) 的系数分别为-0.008 0和-0.007 5,这种负数说明城镇化率对城乡收入差距具有负向影响;主城核心区、渝东北翼、渝东南翼三大板块ΔlogURB(-2) 的系数分别为0.097 1、0.050 5和0.032 1,说明城镇化率对城乡收入差距具有正向影响。在滞后2期时,全市层面和主城核心区的ΔlogURB(-2) 系数分别为0.007 8和0.022 6,1小时经济圈、渝东北翼、渝东南翼3大板块的ΔlogURB(-2) 系数分别为-0.002 5、-0.023 7和0.085 6,表明城镇化率对城乡收入差距的影响开始有所分化,影响程度依然很强。
非农产值比对泰尔指数的短期动态影响关系。在滞后1期时,全市层面及主城核心区、渝东北翼、渝东南翼三大板块ΔlogIND(-1) 的系数为-0.005 9、-2.548 5、-0.062 5和-0.314 4,这种负数说明非农产值比对城乡收入差距具有负向影响;1小时经济圈ΔlogIND(-1) 的系数为0.012 8,说明非农产值比对城乡收入差距具有正向影响。在滞后2期时,全市层面和1小时经济圈、渝东北翼、渝东南翼ΔlogIND(-2) 系数分别为-0.118 8、-0.026 6、-0.038 6和-0.281 1,主城核心区ΔlogIND(-2) 的系数为1.592 5,表明非农产值比对城乡收入差距的影响有所衰减。
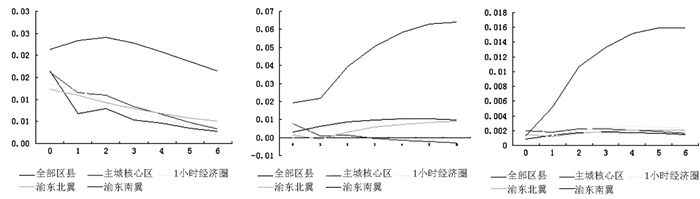
(四) PVAR模型脉冲响应分析为比较城乡收入差异对城镇化、工业化冲击的响应过程,本文在PVAR模型的基础上,分别提取全市层面和各区域板块城乡收入差异对城镇化、工业化的的脉冲响应函数,提取结果如图 2所示。
|
图 2 各区域板块城乡收入泰尔指数脉冲响应过程比较 |
对来自THEIL的标准差冲击,渝东南翼反应最强,其他区域板块相对较为温和,全市层面反应最弱。从响应趋势来看,渝东南翼的响应在前两期不断增强,在第2期达到最高0.024 1,此后逐渐衰减,在第6期达到0.016 4。其他区域板块的响应总体上持续减弱,其中主城核心区的衰减速度最快,在第6期达到0.002 7;1小时经济圈衰减速度次之,在第6期达到0.003 0;渝东北翼最慢,在第6期达到0.003 0。全市层面的响应由初期的0.016 5迅速衰减到第一期的0.006 8,此后小幅回升,在第二期达到0.008 0,此后保持平稳衰减态势,在第6期达到0.002 7。
对来自logURB的标准差冲击,渝东南翼反应最强,全市层面和1小时经济圈、渝东北翼相对较为温和,主城核心区的反应最弱。从响应趋势来看,渝东南翼的响应第1期略有增强,达到最高0.021 6,此后迅速增强,在第6期达到0.064 1。渝东北翼的响应前两期总体平稳中略有减弱,在第2期达到最低-0.000 9,此后持续小幅回升,在第6期达到0.008 9。1小时经济圈的响应前四期持续小幅增强,在第4期达到最高0.009 6,此后持续小幅衰减,在第6期达到0.008 8。主城核心区前三期为正向反应且持续衰减,在第4期达到最高0.001 4,此后转为正向反应并持续小幅增强,在第6期达到-0.002 8。全市层面的响应前四期持续小幅增强,在第4期达到最高0.010 4,此后持续小幅衰减,在第6期达到0.009 8。
对来自logIND的标准差冲击,渝东南翼的累计响应最强,1小时经济圈、主城核心区和渝东北翼的累计响应相对较为温和,全市层面的累计响应最弱。从响应趋势来看,渝东南翼的响应持续快速增强,在第6期达到0.015 9。渝东北翼的响应在第1期略有减弱,达到最低0.001 2,此后持续小幅回升,在第6期达到0.002 1。1小时经济圈的响应前两期明显减弱,在第2期达到最低0.001 4,此后小幅回升最高达到0.002 6,在第6期达到0.002 3。主城核心区的响应在0.001 6和0.002 2之间波动,在第6期达到最低0.001 6。全市层面的响应前三期持续小幅增强,在第3期达到最高0.001 8,此后持续小幅衰减,在第6期达到0.001 5。
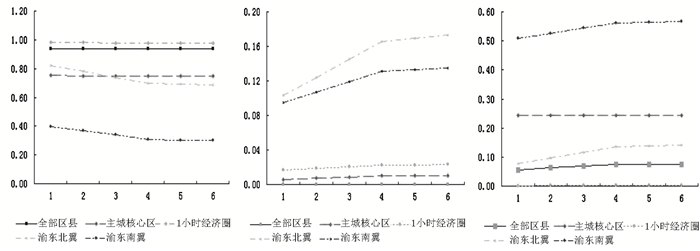
(五) PVAR模型方差分解分析本文提取了全市层面和主城核心区、1小时经济圈、渝东北翼、渝东南翼四大区域板块THEIL、logURB、logIND在第1期至第6期的方差分解结果,提取结果如图 3所示。
|
图 3 各区域板块城乡收入泰尔指数方差分解分析比较 |
从THEIL自身的贡献度来看,全市层面的贡献度最大,平均贡献度为93.72%,1小时经济圈、主城核心区、渝东北翼三大板块的贡献度次之,平均贡献度分别为97.77%、74.81%和73.61%,渝东南翼的贡献度最低,平均贡献度为33.57%。而且,均呈现不同程度的下降趋势。从logURB对THEIL变化的贡献度来看,渝东北翼的贡献度最大,平均贡献度为14.67%,渝东南翼、1小时经济圈、主城核心区3大板块的贡献度次之,平均贡献度分别为11.96%、2.07%和0.88%,全市层面的贡献度最低,平均贡献度为0.03%。从logIND对THEIL变化的贡献度来看,渝东南翼的贡献度最大,平均贡献度为54.47%,主城核心区、渝东北翼两大板块和全市层面的贡献度次之,平均贡献度分别为24.32%、11.72%和6.88%,1小时经济圈的贡献度最低,平均贡献度为0.17%,而且在趋势上均呈现不同程度的下降趋势。同时,logURB、logIND对THEIL变化的贡献度均呈现不同程度的增强趋势。
四、结论与启示在重庆市38个区县面板数据的基础上,运用面板数据向量自回归模型对全市层面和各区域板块城镇化与城乡收入差距的关系进行了现实考察和计量分析。结果发现:第一,2000-2012年重庆市绝大多数区县城乡收入泰尔指数曲线总体上呈现出显著的倒U型特征,但在倒U型曲线顶点的绝对数值和出现时间具有鲜明的区域差异,在形态上与库兹涅茨倒U型曲线较为相似,这在很大程度上反映了各区县城镇化水平和所处发展阶段的差异。第二,全市层面和各个区域板块城乡收入泰尔指数的脉冲响应过程存在显著差异。其中,渝东南翼城乡收入差距会作出同向脉冲响应,即城镇化率和非农产值比提高对城乡收入差距会产生扩大效应,且这种效应在全市层面和各个区域板块中最强;其他区域板块城乡收入差距也会同向扩大,但响应强度相对较为温和;仅有主城核心区城乡收入差距对城镇化率冲击会最终作出反向脉冲响应,即城镇化率提高会对城乡收入差距产生缩小效应。进一步的方差分解表明,全市层面和各个区域板块城乡收入差距对自身变化的贡献度均呈下降趋势,城镇化率和非农产值比对城乡收入差距变化的贡献度均呈增强趋势。
我们认为,城镇化率和非农产值比重对城乡收入差距的净效应取决于城镇化带来的城市收入增长和农村收入增长之间的对比关系。依据现有经济学理论框架,城镇化对城乡收入增长的作用机制主要有3种渠道:一是要素渠道。一方面,农村劳动力流向城市,城市地区劳动力要素投入增长推动城市地区收入增长,而农村地区劳动力要素投入减少抑制农村地区收入增长;另一方面,农村劳动力流向城市,城市地区劳动力供给增加,劳动力边际产出下降,对城市地区收入增长的推动作用减弱,而农村地区劳动力供给减少,劳动力边际产出增加,对农村地区收入增长的推动作用增强。二是市场渠道。城镇化率和和非农产值比重提高,将为农村地区产业发展提供更大的市场需求,从而促进农村地区产业发展和人均收入增长。三是投资渠道。城镇化率和和非农产值比重提高,城市地区资本和劳动力边际收益递减,一部分资本和劳动力回流农村,加快农业现代化,从而推动农村人均收入增长。本文实证发现1小时经济圈、渝东北翼、渝东南翼城镇化率和非农产值比提高对城乡收入差距会产生扩大效应,其原因可能在于农村地区劳动力要素外流问题较为突出,对农村地区收入增长的抑制作用较大,而城市地区得益于劳动力要素投入增加,收入增长较快,但由于城市规模和城市发展水平总体较低,对农村地区的市场拉动和产业投资效应尚未充分发挥;主城核心区城镇化率对城乡收入差距会产生缩小效应,其原因可能在于城市地区劳动力供给过剩,城镇化带来的新增劳动力边际产出较小,而另一方面城市地区对农村地区的市场拉动和产业投资效应已经得到较强发挥。
根据实证研究的结果,得到的启示是:新型城镇化尽管成绩斐然,但仍任重道远,由于各种不合理的制度约束和政策偏差,城镇化和工业化对城乡收入差距的净效应仍表现为扩大效应。要在推进新型城镇化的同时逐步缩小城乡收入差距,必须寻求一条符合本国国情的、科学合理的发展模式和政策框架,加快破除各种导致城乡收入分配不平等的制度约束,在此基础上逐步形成公平、合理的城乡收入分配格局,使城乡居民共享经济发展的成果,从而实现全面建设小康社会的目标。
| [1] | LEWIS W A. Economic development with unlimited supply of labor[J]. The Manchester School of Economic and Social Studies, 1954, 22(2): 139–191. DOI: 10.1111/j.1467-9957.1954.tb00021.x |
| [2] | KUZNETS S. Economic growth and income inequality[J]. American Economic Review, 1955, 45(March): 1–28. |
| [3] | RANIS G, FEI H A. Theory of economic development[J]. American Economic Review, 1961, 51(4): 533–558. |
| [4] | JORGENSON D W. Surplus agricultural labor and the development of a dual economy[J]. Oxford Economic Papers, New Series, 1967, 19(3): 288–312. DOI: 10.1093/oxfordjournals.oep.a041051 |
| [5] | TODARO M P. A model of labor migration and urban unemployment in less developed countries[J]. The American Economic Review, 1969, 59(1): 138–148. |
| [6] | 罗楚亮. 经济增长、收入差距与农村贫困[J]. 经济研究, 2012(2): 15–27. |
| [7] | 曾国平, 王韧. 二元结构、经济开放与中国收入差距的变动趋势[J]. 数量经济技术经济研究, 2006(10): 15–25. DOI: 10.3969/j.issn.1000-3894.2006.10.002 |
| [8] | 姚耀军. 金融发展、城市化与城乡收入差距—协整分析及其Granger因果检验[J]. 中国农村观察, 2005(2): 2–8. |
| [9] | 冉光和, 鲁钊阳. 金融发展、外商直接投资与城乡收入差距—基于我国省级面板数据的门槛模型分析[J]. 系统工程, 2011(7): 19–25. |
| [10] | 孙永强, 万玉琳. 金融发展、对外开放与城乡居民收入差距—基于1978-2008年省际面板数据的实证分析[J]. 金融研究, 2011(1): 28–39. |
| [11] | 王征, 鲁钊阳. 农村金融发展与城乡收入差距—基于我国省级动态面板数据模型的实证研究[J]. 财贸经济, 2011(7): 55–62. |
| [12] | 郭剑雄, 吴佩. 内生增长要素与城乡收入差距[J]. 清华大学学报:哲学社会科学版, 2006(3): 120–124. |
| [13] | 侯风云, 付洁, 张凤兵. 城乡收入不平等及其动态演化模型构建—中国城乡收入差距变化的理论机制[J]. 财经研究, 2009(1): 4–15. |
| [14] | 韩其恒, 李俊青. 二元经济下的中国城乡收入差距的动态演化研究[J]. 金融研究, 2011(8): 15–30. |
| [15] | 丁志国, 赵宣凯, 赵晶. 直接影响与空间溢出效应:我国城市化进程对城乡收入差距的影响路径识别[J]. 数量经济技术经济研究, 2011(9): 118–130. |
| [16] | 程开明. 聚集抑或扩散—城市规模影响城乡收入差距的理论机制及实证分析[J]. 经济理论与经济管理, 2011(8): 14–23. |
| [17] | 蔡昉. 城乡收入差距与制度变革的临界点[J]. 中国社会科学, 2003(5): 16–25. |
| [18] | 陆铭, 陈钊. 城市化、城市倾向的经济政策与城乡收入差距[J]. 经济研究, 2004(6): 50–58. |
| [19] | 陈斌开, 张鹏飞, 杨汝岱. 政府教育投入、人力资本投资与中国城乡收入差距[J]. 管理世界, 2010(1): 36–43. |
| [20] | 陈迅, 童华建. 城市化与城乡收入差距变动的实证研究—基于1985年-2003年中国数据[J]. 生产力研究, 2007(10): 64–65. |
| [21] | 许秀川, 王钊. 重庆市城市化、剩余劳动力转移与城乡收入差距的系统动力学分析[J]. 农业技术经济, 2008(1): 91–97. |
| [22] | 周云波. 城市化、城乡差距以及全国居民总体收入差距的变动—收入差距倒U形假说的实证检验[J]. 经济学(季刊), 2009(7): 1239–1256. |
| [23] | 余静文. 重庆统筹城乡改革缩小了城乡收入差距吗?—基于合成控制法的经验研究[J]. 西部论坛, 2013(1): 1–10. |
| [24] | 杨志海, 刘雪芬, 王雅鹏. 县域城镇化能缩小城乡收入差距吗?—基于1523个县(市)面板数据的实证检验[J]. 华中农业大学学报:社会科学版, 2013(4): 42–48. |
| [25] | PESARAN M H, SMITH R. Estimating long-run relationships from dynamic heterogeneous panels[J]. Journal of Econometrics, 1995, 68(1): 79–113. DOI: 10.1016/0304-4076(94)01644-F |
| [26] | BINDER M, HSIAO C, PESARAN M H. Estimation and inference in short panel vector autoregressions with unit roots and cointegration[J]. Econometric Theory, 2005, 21(4): 795–837. |
| [27] | CANOVA F, CICCARELLI M. Forecasting and turning point predictions in a Bayesian panel VAR model[J]. Journal of Econometrics, 2004, 120: 327–359. DOI: 10.1016/S0304-4076(03)00216-1 |
| [28] | CANOVA F, CICCARELLI M, ORTEGA E.Similarities and convergence in G7 cycles[R].CEPR Discussion Papers 4534, C.E.P.R., 2004. https://dialnet.unirioja.es/servlet/articulo?codigo=802055&info=resumen&idioma=ENG |
| [29] | STOCK J H, WATSON M W.New indexes coincident and leading economic indicators[M]//Macroeconomics Annual. Cambridge:MIT Press, 1989. http://www.sciencedirect.com/science/article/pii/S0927539899000158 |
| [30] | 王少平, 欧阳志刚. 我国城乡收入差距的度量及其对经济增长的效应[J]. 经济研究, 2007(10): 44–55. DOI: 10.3969/j.issn.1002-9605.2007.10.016 |
 2014, Vol. 20
2014, Vol. 20

