资本市场是一个易受政策信息与各种消息面影响的系统,特别在中国,由于资本市场发展仍不够完善,信息冲击的产生与传播在资本市场屡见不鲜。一方面由于制度上的不完善,常有内幕信息等不同信息冲击发生;另一方面,由于投资者主体的差异,易造成对信息反应的异常现象。同时由于不同市场的相互作用,信息在不同市场间的传播与互动使信息冲击对资本市场的影响复杂多变。深入挖掘不同资本市场信息冲击规律对于把握中国资本市场微观结构,完善不同资本市场的制度建设具有重要意义。为此,本文将依据信息冲击特征,通过向量移动平均(VMA)模型,来探讨中国股票市场和债券市场的信息冲击关系。
关于股票市场与债券市场相互关系的研究虽然也有较长的历史,但早期的研究对信息在金融市场的冲击的考虑较少,许多研究只是基于互动关系的均衡存在性或相互关系类型进行分析,如文献[1-2]等对股票价格与债券价格是否运动一致做了研究。文献[3-5]对股票收益和债券收益的相互关系做了研究。
另外,以往关于信息对金融市场冲击的研究绝大多数只是将股票市场与债券市场分开来单独研究,因此对两市的信息传递与互动关系的研究仍不够。实际上,由于跨市场套利机会的存在以及不同市场的相关性使股票市场与债券市场之间存在大量的信息传递与互动现象,只有基于信息冲击影响来研究跨市场互动关系,才能更深刻地把握不同市场的关系。在这方面的研究还不是很多。文献[6]研究了债券价格对股票回购信息的反应。文献[7]将盈利公告(earnings announcement)分解为预期的(expected)和非预期的(unexpected or “surprise”)两部分,认为只有非预期的部分才包含有信息,并检验了收益的变化是否在债券市场传递某种信息,发现债券价格对非预期的收益增加(减少)存在显著的正(负)反应。Kwan检验了个股收益和与之对应的公司发行的债券个债收益的相关关系,并发现两者存在负相关和同步相关(contemporaneously correlated),说明个股和对应的债券受特定公司的信息驱使。文献[8]检验了公共信息(common information)对股票市场和债券市场波动的联系性的作用。文献[9]利用高收益公司债券日和时的交易价格数据分析了高收益公司债券市场的信息效率,以及债券价格与对应的公司的标的股票(underlying stocks)价格的关系。文献[10]利用很大样本的交易活跃的股票和美国国债数据检验了如下假定:股票市场和债券市场的交易活动包含整个市场重要的定价信息(marketwide pricing information)。
由于中国资本市场发展较晚,对资本市场的研究还主要是跟随于国外学者的研究,许多研究只是借鉴国外的研究思路与方法分析国内资本市场问题。其中,国内学者对资本市场信息冲击的研究还处于起步阶段,大部分研究还局限于对单个市场异常现象的研究。如文献[11]通过构造测度中国证券市场非公开信息的知情交易概率(Probability of Informed Trading),研究了非公开信息对中国证券收益率的影响。文献[12]通过建立一个两变量向量自回归模型,着重考察了A股市场的股票收益率和交易量对私人信息和公开信息冲击的不同反应。
国内学者关于股票市场与债券市场的互动关系问题虽然已有不少相关研究,但这些研究主要是基于两市相互关系的检验与分析,以及对影响联动关系的一些经济因素的探讨。文献[13]研究了中国股市和债市溢出效应影响因素,并探讨了投资者情绪这一主观因素对两市的波动影响。文献[14]使用非对称动态条件相关系数(ADCC)模型,研究债券市场与股票市场的相关系数随时间变化的情况。文献[15]实证分析了股票市场与债券市场之间收益率和流动性的相关关系,并分析了影响这种相关关系的宏观经济因素。可见,国内文献很少有基于信息冲击视角下对股票市场与债券市场相互关系的研究,基本上研究股票市场与债券市场关系的文献都未专门考虑信息冲击效应对两市互动关系的影响。
总之,国内学者基于信息冲击对股票市场与债券市场互动关系的研究可谓凤毛麟角,国外学者对相关问题虽然有一些研究,但还不够系统深入,仍存在许多问题值得进一步探讨。如不同市场各种信息冲击的识别方法的研究,股票市场与债券市场对信息冲击反应特点的异同,两市收益率及波动关系如何受信息冲击的影响,其相互关系有何规律等。本文试图围绕这些问题,基于信息冲击分解的视角,对中国股市与债市的互动关系进行实证分析。
二、模型构建与信息识别研究股票市场与债券市场收益关系如何受市场信息影响的一个难点是对信息冲击的识别与测度。如要研究公开信息与私人信息的冲击效应,一种比较常见的办法是寻找代理变量,如采用构造类似于文献[16]提出的知情交易概率的某种度量。但要找到多个不同的代理变量来识别股票市场与债券市场的多种不同信息几乎不可能。另外,也可以通过计量模型的构建来识别,如利用信息冲击的特征通过对移动平均模型的限制来识别不同的信息冲击。如文献[17]根据收益率与交易量随私人信息与公开信息反应的不同特点对双变量移动平均模型(BMAR)施加限制,利用股票市场的收益率与交易量两个变量来识别与估计这两种信息的冲击序列。而若将股票市场和债券市场放在一起研究时,就必须进一步分解市场的信息类型,找出信息冲击对两市不同变量的影响特征,从而找到合适的向量移动平均模型的限制条件来识别市场的不同信息。
由于投资者通常对公开信息和私人信息的反应存在差异[17],同时由于不同市场套利机会的存在以及市场结构的差异,使各种信息在不同市场的传递与作用规律有所不同。文献[18]研究表明市场信息进入股票市场和债券市场的先后顺序不同,会对市场产生不同的影响。为了更细致地挖掘这些信息冲击的特征,本文将市场信息依次分解为公共的公开信息与私人信息,先入股票市场的公开信息与私人信息,先入债券市场的公开信息与私人信息6类。同时,本文分别选择了股票市场和债券市场的收益率、收益波动率和交易量6个变量构建模型来识别不同的信息冲击。如果假定不同市场的交易量、收益率及其波动风险随不同信息的冲击而发生变化,则可用如下VMA模型反映不同信息冲击对这些变量影响的时间路径:
| $ {y_{\rm{t}}} = B({L}){\varepsilon _{\rm{t}}} $ | (1) |
其中:yt= [Rts, Rtb, σts, σtb, Vts, Vtb]T,
| $ {\varepsilon _{\rm{t}}}{\rm{ = }}{[{\varepsilon _{\rm{t}}}^{{\rm{cpublic}}},{\varepsilon _{\rm{t}}}^{{\rm{cprivate}}},{\varepsilon _{\rm{t}}}^{{\rm{spublic}}},{\varepsilon _{\rm{t}}}^{{\rm{bpuclic}}},{\varepsilon _{\rm{t}}}^{{\rm{bprivate}}}]^T} $ |
| $ B(L) = \left[ {\begin{array}{*{20}{l}} {{B_{11}}(L),{B_{{\rm{12}}}}(L),{{B}_{{\rm{13}}}}(L),{{B}_{{\rm{14}}}}(L),{{B}_{{\rm{15}}}}(L),{{B}_{{\rm{16}}}}(L)}\\ {{B_{21}}(L),{B_{{\rm{22}}}}(L),{{B}_{{\rm{23}}}}(L),{{B}_{{\rm{24}}}}(L),{{B}_{{\rm{25}}}}(L),{{B}_{{\rm{26}}}}(L)}\\ {{B_{31}}(L),{B_{{\rm{32}}}}(L),{{B}_{{\rm{33}}}}(L),{{B}_{{\rm{34}}}}(L),{{B}_{{\rm{35}}}}(L),{{B}_{{\rm{36}}}}(L)}\\ {{B_{41}}(L),{B_{{\rm{42}}}}(L),{{B}_{{\rm{43}}}}(L),{{B}_{{\rm{44}}}}(L),{{B}_{{\rm{45}}}}(L),{{B}_{{\rm{46}}}}(L)}\\ {{B_{51}}(L),{B_{{\rm{52}}}}(L),{{B}_{{\rm{53}}}}(L),{{B}_{{\rm{54}}}}(L),{{B}_{{\rm{55}}}}(L),{{B}_{{\rm{56}}}}(L)}\\ {{B_{61}}(L),{B_{{\rm{62}}}}(L),{{B}_{{\rm{63}}}}(L),{{B}_{{\rm{64}}}}(L),{{B}_{{\rm{65}}}}(L),{{B}_{{\rm{66}}}}(L)} \end{array}} \right] $ |
Rts, Rtb分别是股市和债市收益率,σts, σtb分别是股市和债市收益波动风险,Vts, Vtb分别是去除了趋势的股市和债市交易量。εtcpublic, εtcprivate, εtspublic, εtsprivate, εtbpublic, εtbprivate依次为公共的公开信息与私人信息,先入股票市场的公开信息与私人信息,先入债券市场的公开信息与私人信息所带来的冲击,εt是对yt标准正交化的冲击,所以cov(εt)是一个秩为6的单位矩阵。
由于这些信息冲击不可直接观测,利用上述VMA模型(式(1))仍不能估计出各类信息序列。为了能够利用数据估计出上述模型,则必须对其施加一定条件,使它可以通过VAR模型求逆导出。为此,考虑如下VAR(6) 模型:
| $ {y_{\text{t}}} = A(L){y_{{\text{t}} - 1}} + {u_{\text{t}}} $ | (2) |
其中:
在满足可逆条件下,对方程(2)求逆,并结合式(1)可以得到下式:
| $ {y_{\rm{t}}} = B({L}){\varepsilon _{\rm{t}}} = {[{I}-A({L}){L}]^{ - 1}}{u_{\rm{t}}} = {[{I}-A({L}){L}]^{ - 1}}{B^0}{\varepsilon _{\rm{t}}} $ | (3) |
其中:I是秩为6的单位矩阵,
| $ {B^0}{\varepsilon _{\rm{t}}} = {u_{\rm{t}}} $ | (4) |
可见ut冲击是εt冲击的线性组合,因此ut代表一种复合冲击。为了得到可识别的结构性冲击εt= (B0)-1ut,需对矩阵B0的系数作出约束,使矩阵B0具有可逆性,从而保证VMA模型可识别。这样,通过对B0系数的估计,就可以得到冲击B0-1ut的估计值。因此,估计εt的一个关键步骤就是结合经济理论对矩阵B0施加约束。根据不同市场公开信息与私人信息对各变量的影响差异,本文作出如下假定①:(1) 私人信息的冲击对交易量有同步的影响,而公开信息的冲击对交易量没有同步的影响或者影响滞后,所以b51=b61=b53=b63=b55=b65=0;(2) 先入股票市场的信息对债券市场的收益、风险和交易量没有同步的影响或者影响滞后,所以b23=b24=b43=b44=b64=0;(3) 先入债券市场的信息对股票市场的收益、风险和交易量没有同步的影响或者影响滞后,所以b15=b16=b35=b36=b56=0。
① 模型(3) 的内生变量个数k为6,需要施加k(k-1)/2=15个约束条件才能满足模型的恰好识别条件,本文施加了16个约束条件,因此存在过度识别。
基于以上假设,本文待估计的反映当期关系的系数矩阵B0为:
| $ {B^0} = \left[\begin{array}{l} {b_{11}}\;\;\;{b_{12}}\;\;{b_{13}}\;\;{b_{14}}\;\;0\;\;\;\;0\\ {b_2}_1\;\;{b_{22}}\;\;0\;\;\;\;0\;\;\;\;{b_{25}}\;\;{b_{26}}\\ {b_{31}}\;\;{b_{32}}\;\;{b_{33}}\;\;{b_{24}}\;\;0\;\;\;\;0\\ 0\;\;\;\;{b_{52}}\;\;0\;\;\;\;{b_{44}}\;\;0\;\;\;\;0\\ 0\;\;\;\;{b_{62}}\;\;0\;\;\;\;0\;\;\;\;0\;\;\;\;{b_{66}} \end{array} \right] $ |
这样我们就可以使用完全信息极大似然法来估计得到模型(1) 的所有未知参数,从而估计和识别出不同信息的冲击。
三、数据处理与变量分析本文所采用的研究数据为上证指数(代码:999999) 和国债指数(代码:000012) 每日收盘指数和日成交量序列(单位:百万股), 时间跨度为2005年2月24日至2011年12月1日,共1 658个数据,数据均来自光大证券的交易软件数据库。
(一) 收益率与交易量序列分析定义日收益率Rt由日收盘指数pt按式(5) 计算得来。
| $ {R_{\rm{t}}} = {\rm{In}}(\frac{{{p_{\rm{t}}}}}{{{p_{{\rm{t}} - 1}}}}) $ | (5) |
从成交量数据看,股票市场与债券市场成交量明显随着时间推移而逐渐上升。以往的研究表明成交量序列既含有线性趋势又含有非线性趋势,在剔除交易量的时间趋势时也都采用Gallant的假定[19-20] ,用含有二次时间趋势项的模型回归了交易量序列。本文沿用文献[6]的办法,假定中国股市的交易量同时含有线性和非线性趋势。为了考虑非线性趋势影响,对交易量做如下回归:
| $ {V_{\rm{t}}} = {a_0} + {a_1}{\rm{t}} + {a_2}{{\rm{t}}^2} + {u_{\rm{t}}} $ | (6) |
其中:Vt为原始(对数)交易量序列,t为线性时间趋势,t2为非线性时间趋势。对上式进行最小二乘回归后,发现拟合效果很好,其残差估计值便是剔除了时间趋势后的交易量序列,简称为“去势交易量”。
(二) 风险变量的估计根据金融理论知,股票资产的收益应当与其风险成正相关。因此,本文选择能体现这一关系的GARCH-M模型来估计收益率波动值②。首先利用对数收益对式Rt=ω+ut(ω为常数)进行OLS回归,并进行ARCH效应的LM检验。发现残差序列存在ARCH效应。比较多种估计结果后最终选择构建GARCH-M(2, 1) 模型。在残差的条件分布服从广义误差分布情况下估计的结果如下:
② 本文也做了非对称ARCH模型的估计,但发现,这期间两市的收益波动的不对称性不明显,因此,最终根据数据诊断选用了对称的GARCH-M模型。
| $ 均值方程\begin{array}{l} R_{\rm{t}}^{\rm{s}} = 0.01066 + 0.001153{\rm{In}}(\sigma _{\rm{t}}^2)\\ (2.275973)(2.116702) \end{array} $ | (7) |
| $ 均值方程\begin{array}{l} \sigma _{\rm{t}}^{\rm{2}} = 03000003103 + 0.07666u_{{\rm{t - 1}}}^2 + 0.9179\sigma _{{\rm{t - 1}}}^2\\ (2.241906)\;\;(5.630481)\;(68.04871) \end{array} $ | (8) |
| $ 均值方程\begin{array}{l} R_{\rm{t}}^{\rm{b}} = 0.0006966 + 0.00004037{\rm{In(}}\sigma _{\rm{t}}^2{\rm{)}}\\ {\rm{(2}}{\rm{.490307)}}\;\;{\rm{(2}}{\rm{.116046)}} \end{array} $ | (9) |
| $ 均值方程\begin{array}{l} \sigma _{\rm{t}}^2 = 0.00000002004 + 0.1439u_{{\rm{t - 1}}}^2 + 0.8556\sigma _{{\rm{t - 1}}}^2\\ (3.667913)\;\;(6.551986)\;\;(47.80715) \end{array} $ | (10) |
方程(7) 与(8) 是反映股市收益波动风险的GARCH-M模型,方程(9) 与(10) 是反映债市收益波动风险的GARCH-M模型。其中,方程下括号里的数值为相应变量系数的t检验统计量,根据估计结果看出,各系数的估计结果都很显著。此时,通过对标准化的残差序列进行ARCH效应的LM检验,结果表明ARCH效应也消失了。估计结果表明股票市场的收益波动明显比债券市场的收益波动大,这与其他学者[8]的研究结果一致,也与现实相吻合。因此,这两个模型都能较好地反映股票市场与债券市场的收益与风险的相互关系。利用这两个估计的模型可以计算出相应的自回归条件异方差序列,本文将此估计的自回归条件方差序列作为中国的股市与债市收益波动风险值。
(三) 变量的单位根检验本文选用ADF单位根检验来检验各变量的平稳性。由表 1的检验结果可知,所有变量都是平稳的,如果对它们直接进行回归不会出现虚假回归现象,因此可以直接利用这些变量估计向量自回归模型。
| 表 1 有关变量的ADF单位根检验 |
本文根据变量研究的重要性,确定各变量在VAR模型中的先后顺序依次为Rts, Rtb, σts, σtb, Vts, Vtb。建模时,首先根据SC准则选择滞后2期;观察知该VAR(2) 模型特征多项式的逆根都在单位圆内,因此该VAR(2) 模型是稳定的。利用极大似然估计法,可以估计出矩阵B0,进而求得εt值。
由于本文的VMA模型存在过度识别,此时需要对模型进行过度识别检验,从过度识别(over-identification)的LR统计检验看,Chi-square(1)0=0.633 824,伴随概率水平为0.426 0,说明模型使用的假设具有合理性。
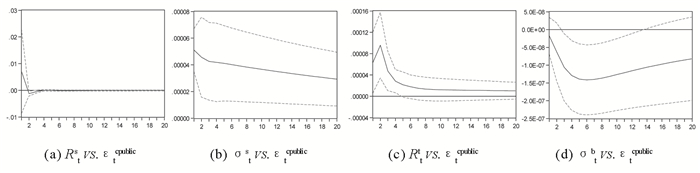
不同信息(εtcpublic, εtcprivate, εtspublic, εtsprivate, εtbpublic, εtbprivate)的冲击效果可用脉冲响应图描绘出来。根据所估计模型,可以得到以下脉冲响应图(图 1-图 8),图中的实线为冲击效果,虚线为冲击的正负两倍标准差偏离带。
|
图 1 Rts,σts,Rtb,σtb对公共公开信息冲击响应 |
|
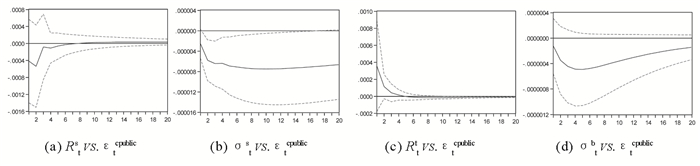
图 2 Rts,σts,Rtb,σtb对公共私人信息冲击响应 |
|
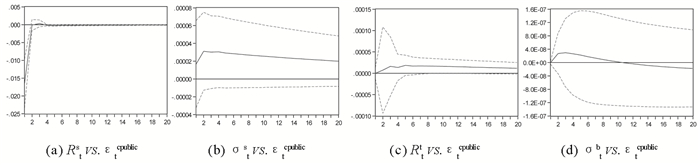
图 3 Rts,σts,Rtb,σtb对股市公开信息冲击响应 |
|
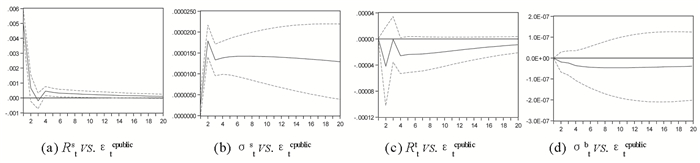
图 4 Rts,σts,Rtb,σtb对股市私人信息冲击响应 |
|
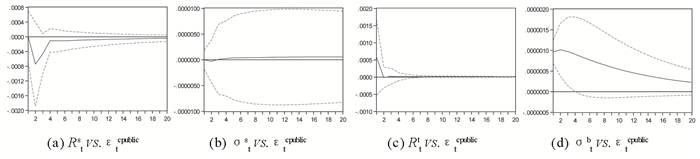
图 5 Rts,σts,Rtb,σtb对债市公开信息冲击响应 |
|
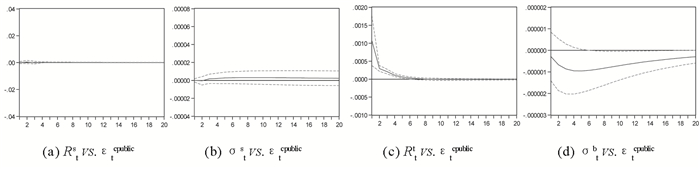
图 6 Rts,σts,Rtb,σtb对债市私人信息冲击响应 |
|
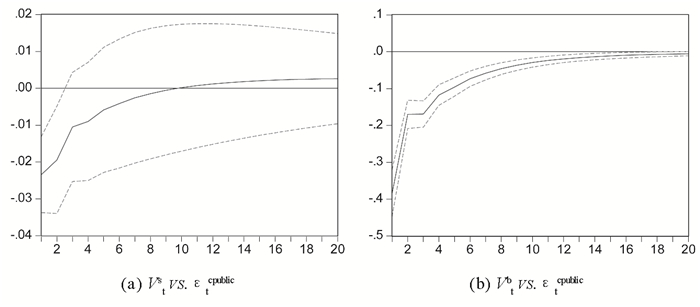
图 7 Vts,Vtb对公共私人信息冲击响应 |
|
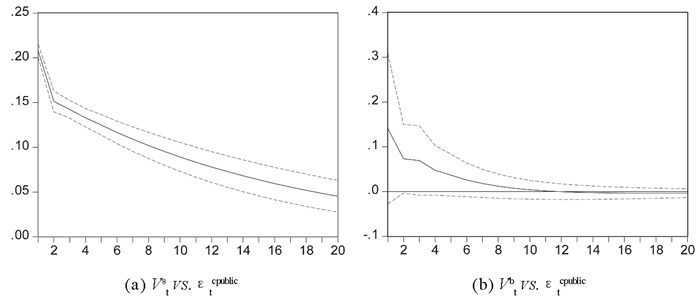
图 8 Vts对股市及Vtb对债市的私人信息冲击响应 |
根据图 1,若公共的公开信息对股市收益带来负的冲击,会相应给债市收益带来正的冲击;另外,若公共的公开信息对股市收益波动带来正的冲击,会相应给债市收益波动带来负的冲击。从统计显著性角度看,公共的公开信息对股市收益的冲击不具有统计显著性,但对债市收益的冲击比较显著。另外,公共的公开信息对股市收益波动的冲击效应随着时间的推移逐渐递减,而其对债市收益的冲击效应存在先增大,大概在第六天达到最大值,随后再逐渐减小的趋势。总体上,在公共的公开信息的主导下,两市的收益呈现短期正相关关系,而两市收益波动风险呈现负相关关系。
根据图 2,若公共的私人信息对股市收益带来负的冲击,会相应给债市收益带来正的冲击;另外,若公共的私人信息对股市收益波动带来负的冲击,会相应给债市收益波动带来负的冲击。不过除了对股市收益波动的冲击具用统计显著性外,对另外三者的冲击在统计意义上不是很显著。因此,粗略看,在公共的私人信息的主导下,两市的收益呈现短期微弱的负相关关系,而两市收益波动风险呈现微弱的正相关关系。
根据图 3,先入股市公开信息对股市收益存在显著的冲击影响,但不具有持续性,其对股市收益波动、债市收益及其波动的冲击不是很显著。总体上,若先入股市公开信息对股市收益带来负的冲击,会相应给债市收益带来微弱的正冲击。因此先入股市的公开信息的主导下,两市的收益呈现负相关关系,而两市收益波动风险的相关关系带有不确定性。
根据图 4,若先入股市的私人信息对股市收益带来正的冲击,会相应给债市收益带来负的冲击;另外,若先入股市的私人信息对股市收益波动带来正的冲击,会相应给债市收益波动带来负的冲击。其中,先入股市的私人信息对股市收益及其波动的冲击具有很强的统计显著性,但对债市收益及其波动的冲击不是很显著。总体上,在先入股市的私人信息的主导下,两市的收益及其波动都呈现正相关关系。
根据图 5,先入债市公开信息对债市收益波动存在较显著的冲击影响,而对其他三者的冲击不具用统计显著性,特别的,其对股市收益波动几乎不具用冲击效应。总体上,先入债市的公开信息的主导下,两市的收益呈现微弱的负相关关系。
根据图 6,先入债市的私人信息对债市收益及其波动存在较显著的冲击影响,并且使两者之间表现出一定的负向关系;而对股市收益及其波动几乎不具有冲击效应。可见,先入债市的私人信息主要对债市具有冲击效应。
根据图 7与图 8,公共的私人信息冲击对两市的交易量具有显著的影响,且两市的交易量受公共私人信息冲击后总体呈现正相关关系。先入股市的私人信息对股票市场的交易量也有显著影响,而先入债市的私人信息冲击对债市交易量的影响不是很显著。
五、结论本文将中国股票市场与债券市场结合起来考虑,对市场信息冲击做了更细致的分解,首先将市场信息依次分解为公共的公开信息与私人信息、先入股票市场的公开信息与私人信息、先入债券市场的公开信息与私人信息6类。然后通过VMA模型的识别与分析,考察了中国股票市场与债券市场对于不同类型的信息冲击的动态关系。
实证结果表明:不同信息对两市的收益率、收益波动风险及交易量的冲击具有各自的特征。两市的变量关系受信息的冲击影响可能存在正相关,也可能存在负相关,这与文献[21]利用GARCH模型的研究结果有相同之处。不过,本文对信息做了更细致的分解,本文实证得出如下主要结论。
其一,公共信息(包括公开信息与私人信息)对股票市场与债券市场收益率的影响不是很显著,但对两市收益率波动风险的影响比较显著。
其二,先入股市信息对股票市场影响比较显著,对债券市场的影响不很显著,且收益率与风险受其影响总体呈现负相关关系。
其三,先入债市信息对债券市场影响比较显著,但对股票市场影响不够显著,且收益率与风险受其影响总体呈现负相关关系。
其四,私人信息(包括先入股市信息与先入债市信息)对收益率及其波动风险的影响比公开信息(包括先入股市信息与先入债市信息)对收益率及其波动的影响显著。
其五,两市交易量受相关的私人信息的影响(除先入债市信息对债券市场交易量的影响)总体上都比较显著。
总体上,这些信息对股票市场的影响比对债券市场的影响要显著,这与文献[21]的研究结果有相似性③。因此,从一定意义上讲,维护股票市场的稳定性对把握整个资本市场的良好运行具有更重要的作用。
③ Kwan从通过对同一公司发行的股票与债券的研究发现:当前的债券收益变化与公司股票的滞后期的收益有显著相关关系,而当前的股票收益变化与公司债券的滞后期的收益没有显著相关关系。
致谢 感谢在论文撰写过程中杨朝军老师在理论上的指导,感谢陈强同学在数据搜集及实证方面给予的帮助。
| [1] | SHILLER R J.Consumption, asset markets, and macroeconomic fluctuations[C].Carnegie Rochester Conference Series on Public Policy, 1982, 17:203-238. https://papers.ssrn.com/sol3/papers.cfm?abstract_id=351376 |
| [2] | BOSSAERTS P. Common nonstationy components of asset prices[J]. Journal of Economic Dynamics and Control, 1988, 12: 347–364. DOI: 10.1016/0165-1889(88)90045-0 |
| [3] | BARSKY R B. Why don't the prices of stocks and bonds move together?[J]. American Economic Review, 1989, 79: 1132–1145. |
| [4] | SHILER R J, BELTRATTI A E. Stock price and bond yields[J]. Journal of Monetary Economics, 1992, 20: 25–46. |
| [5] | CAMPBELL J Y, AMMER J. What moves the stock and bond markets? A variance decomposition for long-term asset returns[J]. The Journal of Finance, 1993, 48(1): 3–37. DOI: 10.1111/j.1540-6261.1993.tb04700.x |
| [6] | BARTOV E. Open-market stock repurchases as signals for earnings and risk changes[J]. Journal of Accounting and Economics, 1992, 14: 275–294. |
| [7] | DATTA S, DHILLON U S. Bond and stock market response to unexpected earnings announcements[J]. The Journal of Financial and Quantitative Analysis, 1993, 28(4): 565–577. DOI: 10.2307/2331166 |
| [8] | FLEMING J, KIRBY C, OSTDIEK B. Information and volatility linkages in the stock, bond, and money markets[J]. Journal of Financial Economics, 1998, 49: 111–137. DOI: 10.1016/S0304-405X(98)00019-1 |
| [9] | HOTCHKISS E S, RONEN T. The informational efficiency of the corporate bond market:An intraday analysis[J]. Review of Financial Studies, 2002, 15(5): 1325–1354. DOI: 10.1093/rfs/15.5.1325 |
| [10] | UNDERWOOD S. The cross-market information content of stock and bond order flow[J]. Journal of Financial Markets, 2009, 12: 268–289. DOI: 10.1016/j.finmar.2008.08.001 |
| [11] | 杨栋, 郭玉清. 指令驱动型市场, 非公开信息与中国证券收益率[J]. 南开经济研究, 2007(4): 105–117. |
| [12] | 王郧, 欧阳红兵. 公开信息和私人信息的识别与中国股市的过度自信研究[J]. 统计研究, 2009(10): 80–87. DOI: 10.3969/j.issn.1002-4565.2009.10.014 |
| [13] | 王璐. 中国股市和债市溢出效应影响因素的数量研究[J]. 金融理论与实践, 2008(8): 34–39. |
| [14] | 袁超, 张兵, 汪慧建. 债券市场与股票市场的动态相关性研究[J]. 金融研究, 2008(1): 63–75. |
| [15] | 曾志坚, 罗长青. 股票与债券市场流动性联动的实证研究[J]. 财经理论与实践, 2008(4): 45–49. |
| [16] | EASLEY D, KIEFER N M, HARA M O', et al. Liquidity information, and less-frequently traded stocks[J]. Journal of Finance, 1996, 51: 1405–1436. DOI: 10.1111/j.1540-6261.1996.tb04074.x |
| [17] | CHUANG W I, LEE B S. An empirical evaluation of the overconfidence hypothesis[J]. Journal of Banking & Finance, 2006, 30: 2489–2515. |
| [18] | KWAN S H. Firm-specific information and the correlation between individual stocks and bonds[J]. Journal of Financial Economics, 1996, 40: 63–80. DOI: 10.1016/0304-405X(95)00836-4 |
| [19] | GALLANT A R, PETER E R, GEORGE T. Stock price and volume[J]. Review of Financial Studies, 1992, 5: 199–242. DOI: 10.1093/rfs/5.2.199 |
| [20] | CHEN G, FIRTH M, RUI O M. The dynamic relation between stock returns, trading volume, and volatility[J]. The Financial Review, 2001, 38: 153–174. |
| [21] | DARBAR S M, PARTHA D. Cross-market correlations and transmission of information[J]. The Jourmal of Futures Markets, 2008, 22(11): 1059–1082. |
 2014, Vol. 20
2014, Vol. 20
