中小企业指在中华人民共和国境内依法设立的有利于满足社会需要,增加就业,符合国家产业政策,生产经营规模属于中小型的各种所有制和各种形式的企业[1]。现代经济活动中,随着中小企业队伍的不断壮大[2],企业之间的合作也愈来愈密切[3]。但是在这背后也隐藏了很多危机[4]。2008年以来, 由美国华尔街引发的金融风暴迅速波及全球,爆发了全球经济危机,冲击着各国的经济。在复杂严峻的国际经济环境和国内生产要素的制约下,越来越多的中小企业面临着生产经营困难、市场物价竞争压力大、销售难度增大等问题[5]。为了应对不稳定的经济环境,中小企业采取相互合作、抱成一团的态度来共同抵抗全球经济危机带来的冲击。同时伴随着信息网络的发展,政府对企业的监管力度也在不断加强,在上述市场背景下,中小企业之间的合作不再只是企业之间的问题,也涉及政府的监察与惩罚[6]。
用博弈论作为主要的分析工具来研究多个事物之间的关系已经成为一种趋势。博弈论的研究范围不再仅仅局限于经济学方面,也涉及了管理学、环境科学、生态学、社会学、食品安全、信息安全等多个领域[7]。其中演化博弈理论是从有限理性的角度,以群体为研究对象,提出博弈方是通过模仿学习和策略的不断调整,在受到少量干扰后仍能收敛到稳定状态的复制动态机制模拟[8]。
目前对中小企业诚信行为演化机制的研究不多。吴昊等应用演化博弈论的方法探讨了企业合作竞争博弈的演化模型, 分析了一个水平差异化产品的合作竞争博弈的演化均衡与稳定性, 及其演化过程中表现出来的复杂性[9]。朱小燕借助演化博弈的思想, 从企业竞合行为角度来分析中小企业集群的形成, 认为在有限理性和“满意利润”追逐的前提下, 中小企业竞争行为最终会演化成一种竞合行为, 竞合行为的组织表现就是企业集群[10]。曾江洪等利用演化博弈研究了中小企业贷款模式,发现抵押贷款在现实条件下无法达到最优均衡状态, 而互助担保贷款既可以增强中小企业的融资能力, 又规避了银行的贷款风险, 推动银行与企业动态博弈过程向最优均衡解演化, 达到互利双赢[11]。
所以研究如何正确引导中小企业诚信合作,实现企业双赢;如何协调博弈过程产生的矛盾;分析是什么影响了合作的中小企业之间的诚信机制,具有较强的研究价值。为了实现自身利益的最大化,中小企业重视短期利益,在合作过程中存在各自的利益诉求,并且这种矛盾愈演愈烈,在对双方共同的利益上可能更多采取消极态度[12]。只有准确地找到影响中小企业实现共赢的因素,规避风险,这样企业才能在云谲波诡的商场洪流中迎难直上,稳中求进,为中国创造更多的财富,以更强的实力走向世界。
一、中小企业诚信合作机制演化博弈模型假设博弈方企业Ⅰ和企业Ⅱ的策略空间都是{诚信、欺骗}。a为企业双方都选择诚信策略时,Ⅰ方的收益;b为企业双方都选择诚信策略时,Ⅱ方的收益;c为企业Ι选择诚信策略同时企业Ⅱ选择欺骗策略时,Ⅰ方的收益;d为企业Ⅰ选择诚信策略同时企业Ⅱ选择欺骗策略时,Ⅱ方的收益;e为企业Ι选择欺骗策略同时企业Ⅱ选择诚信策略时,Ⅰ方的收益;f为企业Ι选择欺骗策略同时企业Ⅱ选择诚信策略时,Ⅱ方的收益;g为博弈方均选择欺骗策略时,Ⅰ方的收益;h为博弈方都选择欺骗策略时,Ⅱ方的收益;θ为企业发生欺骗行为时,被监察部门检查到的概率;α为当欺骗行为被发现时,欺骗方支付给诚信方的违约金;η为监察部门对欺骗一方惩罚的罚款;r为欺骗方的造假成本。中小企业诚信机制演化博弈模型的得益矩阵如表 1所示。
| 表 1 中小企业诚信机制演化博弈模型的收益矩阵表 |
其中,当博弈双方同时采取{欺骗}策略时,博弈所得的收益(g-ηθ-r, h-ηθ-r)最小;如果只有一方采取{诚信}策略,则欺骗方的得益比诚信方多,即d-(η+α)θ-r>c+αθ, e-(η+α)θ-r>f+αθ,且比双方同时采用{欺骗}策略的得益有所提高,即c+αθ>g-ηθ-r,d-(η+α)θ-r>h-ηθ-r, e-(η+α)θ-r>g-ηθ-r,f+αθ>h-ηθ-r; 如果双方均采取{诚信}策略,双方的得益实现最大化,即(a, b)最大。则有a>c+αθ>g-ηθ-r, b>d-(η+α)θ-r>h-ηθ-r, a>e-(η+α)θ-r>g-ηθ-r, b>f+αθ>h-ηθ-r。我们还假设,博弈方在策略组合中只要采取{诚信}策略,就会给企业和社会带来一定的提高,即a-e-(η+α)θ-r]>c+αθ- g-ηθ-r],b-d-(η+α)θ-r]>f+αθ-h-ηθ-r],a-e-(η+α)θ-r]>f+αθ-h-ηθ-r], b-d-(η+α)θ-r]>c+αθ- g-ηθ-r]。
假设企业Ⅰ选择{诚信,欺骗}策略的概率分别是(x,1-x),企业Ⅱ选择{诚信,欺骗}策略的概率分别是(y,1-y)。其中x也可看作是群体博弈中选择{诚信}策略企业的比例或决策群体中支持{诚信}策略群体的比例,y亦然。
根据表 1中的得益矩阵,可得企业Ι选择{诚信}策略、{欺骗}策略的期望得益u11、u12和平均得益
| $ \left\{ \begin{array}{l} {u_{11}} = y \cdot a + (1 - {y}) \cdot ({c} + \alpha \theta )\\ {u_{12}} = y \cdot [{e}-(\eta + \alpha )\theta-r] + (1 - {y}) \cdot (g - \eta \theta - r)\\ \overline {{u_1}} = x \cdot {u_{11}} + (1 - {x}) \cdot {u_{12}} \end{array} \right. $ | (1) |
企业Ⅱ选择{诚信}策略、{欺骗}策略的期望得益u21、u22和平均得益
| $ \left\{ \begin{array}{l} {u_{21}} = x \cdot b + (1 - {x}) \cdot ({f} + \alpha \theta )\\ {u_{22}} = x \cdot [{d}-(\eta + \alpha )\theta-r] + (1 - {x}) \cdot (h - \eta \theta - r)\\ \overline {{u_2}} = y \cdot {u_{21}} + (1 - {y}) \cdot {u_{22}} \end{array} \right. $ | (2) |
所以,企业Ⅰ持{诚信}策略的比例x和企业Ⅱ持{诚信}策略的比例y的复制动态方程为:
| $ \left\{ \begin{gathered} F({x}) = \frac{{{\rm{d}}{x}}}{{{\rm{d}}t}}=x({u_{11}} - \overline {{{u}_1}} ) = {x}(1 - {x})\{ y({a} - {e} + {g} - {c}) + [(c + \alpha \theta )\\-(g-\eta \theta-r)]\} \hfill \\ F({y}) = \frac{{{\rm{d}}y}}{{{\rm{d}}t}}=y({{u}_{21}} - \overline {{{u}_2}} ) = {y}(1 - {y})\{ x({b} - {d} + {h} - {f}) + [(f + \alpha \theta )\\-(h-\eta \theta-r)]\} \hfill \\ \end{gathered} \right. $ | (3) |
由演化博弈理论[8]可知,系统演化的均衡点处必有F(x) =0且F(y) =0。由此可求得复制动态方程系统(3) 的均衡点有5个,分别是E1(x=0, y=0)、E2(x=0, y=1)、E3(x=1, y=0)、E4(x=1, y=1) 和
根据Friedman提出的方法,演化系统均衡点的稳定性是由该系统雅可比矩阵的局部稳定性求解得到[8]。对F(x)、F(y)分别关于x和y求偏导数,可得雅可比矩阵为
| $ F{(x)_x} = \frac{{{\rm{d}}F(x)}}{{{\rm{d}}x}} = (1 - 2x)\{ y{\rm{(}}a - e + g - c){\rm{ + }}[(c + \alpha \theta {\rm{) - (}}g{\rm{0}}\eta \theta - r)]\} $ |
| $ F{(x)_y} = \frac{{{\rm{d}}F(y)}}{{{\rm{d}}y}} = x(1 - x{\rm{)(}}a - e + g - c{\rm{)}} $ |
| $ F{(y)_x} = \frac{{{\rm{d}}F(y)}}{{{\rm{d}}x}} = y(1 - y{\rm{)(}}b - d + h - f{\rm{)}} $ |
| $ F{(y)_y} = \frac{{{\rm{d}}F(y)}}{{{\rm{d}}y}} = (1 - 2y)\{ x{\rm{(}}b - d + h - f){\rm{ + }}[(f + \alpha \theta {\rm{) - (}}h{\rm{-}}\eta \theta - r)]\} $ |
则有:
(1)
| $ \begin{array}{l} {{a}_{{\rm{11}}}}{\rm{ = (}}{c + }\alpha \theta {\rm{) - (}}{g - }\eta \theta - r{\rm{);}}{{a}_{{\rm{22}}}}{\rm{ = (}}{f + }\alpha \theta {\rm{) - (}}{h - }\eta \theta - r{\rm{)}}\\ {De}{{t}_{\rm{1}}}{\rm{(}}{J}{\rm{) = [}}{c}{\rm{ + }}\alpha \theta-{\rm{(}}{g-}\eta \theta-r{\rm{)][(}}{f + }\alpha \theta {\rm{)-(}}{h-}\eta \theta-r{\rm{)]}}\\ T{r_1}({J}) = [({c} + \alpha \theta )-{\rm{(}}{g-}\eta \theta-r{\rm{)}}] + {\rm{[(}}{f + }\alpha \theta {\rm{)-(}}{h-}\eta \theta-r{\rm{)]}} \end{array} $ |
(2)
| $ \begin{array}{l} {{a}_{{\rm{11}}}}{\rm{ = }}({a - e + g - c}) + [({c + }\alpha \theta )-{\rm{(}}{g}{\rm{-}}\eta \theta-r{\rm{)}}]\\ {{a}_{{\rm{22}}}} = - [({f + }\alpha \theta )-{\rm{(}}{h-}\eta \theta-r{\rm{)}}]\\ {De}{{t}_2}{\rm{(}}{J}{\rm{) = - \{ (}}{a - e + g - c}{\rm{) + [}}{c + }\alpha \theta {\rm{] - (}}{g - }\eta \theta - r{\rm{)\} }} \cdot {\rm{[(}}{f + }\alpha \theta {\rm{)-(}}{h-}\eta \theta-r{\rm{)]}}\\ T{r_2}({J}) = {\rm{\{ (}}{a - e + g - c}{\rm{) + [}}{c + }\alpha \theta {\rm{] - (}}{g - }\eta \theta - r{\rm{)\} }} - {\rm{[(}}{f + }\alpha \theta {\rm{)-(}}{h-}\eta \theta-r{\rm{)]}} \end{array} $ |
(3)
| $ \begin{array}{l} {{a}_{{\rm{11}}}}{\rm{ = -[(}}{c + }\alpha \theta {\rm{) - (}}{g - }\eta \theta - r{\rm{)]}}\\ {{a}_{{\rm{22}}}}{\rm{ = (}}b - d + h - f{\rm{) + [(}}{f + }\alpha \theta {\rm{)-(}}{h-}\eta \theta-r{\rm{)]}}\\ {De}{{t}_3}{\rm{(}}{J}{\rm{) = - [}}{c}{\rm{ + }}\alpha \theta-{\rm{(}}{g-}\eta \theta-r{\rm{)]}} \cdot \{ {\rm{(}}b - d + h - f{\rm{)}} + {\rm{[(}}{f + }\alpha \theta {\rm{)-(}}{h-}\eta \theta-r{\rm{)]}}\} \\ T{r_3}({J}) = {\rm{ - [}}{c}{\rm{ + }}\alpha \theta-{\rm{(}}{g-}\eta \theta-r{\rm{)]}} + \{ {\rm{(}}b - d + h - f{\rm{)}} + {\rm{[(}}{f + }\alpha \theta {\rm{)-(}}{h-}\eta \theta-r{\rm{)]}}\} \end{array} $ |
(4)
| $ \begin{array}{l} {{a}_{{\rm{11}}}}{\rm{ = }} - \{ (a - e + g - c) + [(c + \alpha \theta ) - (g{\rm{ - }}\eta \theta - r)]\} \\ {{a}_{{\rm{22}}}} = - {\rm{(}}b - d + h - f{\rm{) + [(}}{f + }\alpha \theta {\rm{)-(}}{h-}\eta \theta-r{\rm{)]}}\\ {De}{{t}_4}{\rm{(}}{J}{\rm{) = \{ (}}{a - e + g - c}{\rm{) + [}}{c + }\alpha \theta {\rm{] - (}}{g - }\eta \theta - r{\rm{)\} }} \cdot \{ {\rm{(}}b - d + h - f{\rm{)}} \\+ {\rm{[(}}{f + }\alpha \theta {\rm{)-(}}{h-}\eta \theta-r{\rm{)]}}\\ T{r_2}({J}) = - {\rm{\{ (}}{a - e + g - c}{\rm{) + [}}{c + }\alpha \theta {\rm{] - (}}{g - }\eta \theta - r{\rm{)\} }} - \{ {\rm{(}}b - d + h - f{\rm{)}} \\+ {\rm{[(}}{f + }\alpha \theta {\rm{)-(}}{h-}\eta \theta-r{\rm{)]}} \end{array} $ |
(5)
| $ {a_{{\rm{11}}}}{\rm{ = 0}};{{\rm{a}}_{{\rm{22}}}}{\rm{ = 0}};De{t_5}(J){\rm{ = 0}};T{r_5}(J) = 0。$ |
所以,根据前面博弈模型的假设容易得到:
| $ \begin{gathered} De{t_1}{\text{(}}{J}{\text{)}} > 0, T{r_1}{\text{(}}{J}{\text{)}} > 0;De{t_2}{\text{(}}{J}{\text{)}} < 0, T{r_2}{\text{(}}{J}{\text{)}} \\> 0;De{t_3}{\text{(}}{J}{\text{)}} < 0, T{r_3}{\text{(}}{J}{\text{)}} > 0;De{t_4}{\text{(}}{J}{\text{)}} > 0, T{r_4}{\text{(}}{J}{\text{)}} < \hfill \\ 0;De{t_5}{\text{(}}{J}{\text{) = }}0, T{r_5}{\text{(}}{J}{\text{) = }}0; \hfill \\ \end{gathered} $ |
基于复制动态方程计算出来均衡点,对其进行局部稳定性分析,可知当且仅当Det(J)>0、Tr(2) < 0时,该均衡点是ESS稳定的,其结果见表 2。
| 表 2 均衡点的局部稳定性 |
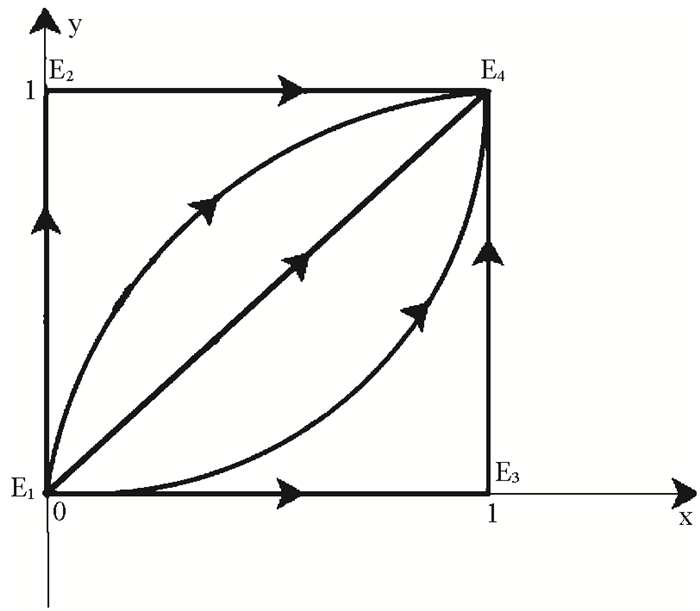
图 1给出了系统(3) 演化的相图,从图可知:(1)E1 (x=0, y=0) 是不稳定的,中小企业作为市场经济活动的参与者,具有市场投机性、机会主义行为。在企业的相互合作中,如果企业预测自己选择欺骗策略会获得较轻的惩罚或者被发现的概率较小时,博弈方就会倾向于“欺骗”战略。如果博弈方预测自己选择欺骗策略后获得的收益特别高或者成功避过监察的概率较大时,也会倾向于选择“欺骗”战略。说明市场经济的不确定性以及中小企业本身的投机性和机会主义倾向,会造成企业在策略的选择上有所偏差,在短时间内部分博弈方可能会为采取{欺骗, 欺骗}策略而得到甜头而感到沾沾自喜,但一段时间以后,博弈方要面对监察部门的监察约束和双方信任的缺失,该合作将难以继续。由此可见,该博弈的结果符合现实的规律,即企业双方长期选择{欺骗, 欺骗}策略是不可靠的。(2)E2(x=0, y=1) 和E3(x=1, y=0) 虽然是稳定的,但经过博弈方长期的学习和选择,最终都会收敛到E4(x=1, y=1)。而且我们可以看到当θ、η、α、r越大,即企业发生欺骗行为被监察部门检查到的概率越大、欺骗方支付给诚信方的违约金和监察部门对欺骗一方惩罚的罚款越多、欺骗方的造假成本越高,则系统收敛到{诚信, 诚信}策略(即收敛到E4(x=1, y=1) 的速度越快。(3)E4 x=1, y=1是局部稳定点,是博弈方长期选择后的结果。当企业的诚信得益大于欺骗得益时,即a- [e- η+αθ-r]>0、b-[d- η+αθ-r]>0这时系统将收敛到E4(x=1, y=1)。
|
图 1 中小企业诚信合作机制的动态过程图 |
综合上面对复制动态方程分析以及系统的局部稳定性分析可知:加大对不诚实企业的惩罚力度,或者采取有效的激励措施可以改变企业在欺诈和诚信这两个战略选择中的收益、成本和罚款,让企业能够在双方利益与单方收益的矛盾中获得均衡。
三、结论和总结本文在分析中小企业诚信合作机制的影响因素以及对演化博弈理论深入研究的基础上,对中小企业诚信合作机制进行了演化博弈应用研究。文中提出了影响中小企业诚信合作机制的三大因素:一是相关部门的监察力度对应于企业欺诈时被发现的概率;二是激励奖赏金额和罚款金额对应于中小企业在合作过程中的自觉性;三是中小企业在进行欺骗行为的造假成本。分析了合作企业形成演化博弈的原因:一方面是市场经济中中小企业具有机会主义倾向,有违约积极性和市场投机性;另一方面,如果博弈方预测到自己选择欺骗策略时获得的收益特别高或者成功避过监察的概率较大时,也会倾向于选择“欺骗”策略,造成企业在策略的选择上有所偏差。
本文根据分析结果,提出了针对性较强的对策建议:加强监察部门的监察力度;构建守信激励和失信惩戒机制;建设企业和个人联合征信平台,为失信惩戒机制的建立提供基础信息支撑;树立诚信企业的楷模,完善中小企业的激励奖赏机制,对诚信企业和模范个人给予表彰,营造守信光荣的舆论氛围。加强社会诚信建设,全面提升政府、企业和个人的诚信意识,形成“诚实守信”的市场环境和“普遍信任”的社会关系。在全社会广泛形成守信光荣、失信可耻的氛围,使诚信成为市场经济的一种文化,让诚信合作成为中小企业间的一种默契与双赢。
| [1] | 主席令9届第69号, 中华人民共和国中小企业促进法[S]. |
| [2] | 中华人民共和国国家统计局第二次全国基本单位普查领导小组办公室. 第二次全国基本单位普查主要数据公报[EB/OL]. (2003-01-17). [2013-04-20]. http://www.sdpc.gov.cn/zcfb/zcfbqt/zcfbqt2003/t20050614_7313.htm. |
| [3] | 中国经济信息网. 福建: 政策环境不断改善中小企业良性发展[OL]. (2004-10-15). [2013-04-20]. http://www.ndrc.gov.cn/xxfw/qyyb/t20050526_2059.htm. |
| [4] | 林鸿熙. 中小企业信用问题博弈研究[M]. 厦门: 厦门大学出版社, 2010: 167-173. |
| [5] | 吴群. 中小文化企业发展面临的困境及应对策略[J]. 经济纵横, 2012(11): 60–63. DOI: 10.3969/j.issn.1007-7685.2012.11.014 |
| [6] | 周斌, 张坚, 杜建国. 企业诚信机制形成的演化博弈分析[J]. 统计与决策, 2009, 15: 64–66. |
| [7] | 谢识予. 经济博弈论[M]. 上海: 复旦大学出版社, 2002: 115-119. |
| [8] | FRIEDMAN D. Evolutionary games in economics[J]. Econometrica, 1991, 59(3): 93–96. |
| [9] | 吴昊, 杨梅英, 陈良猷. 合作竞争博弈中的复杂性与演化均衡的稳定性分析[J]. 系统工程理论与实践, 2004(2): 90–94. |
| [10] | 朱小燕. 基于演化博弈的中小企业集群之形成机理分析[J]. 求索, 2011(1): 31–32. |
| [11] | 曾江洪, 肖涛, 王庄志. 基于演化博弈的中小企业贷款模式对比研究[J]. 数学的实践与认识, 2013, 17: 59–68. DOI: 10.3969/j.issn.1000-0984.2013.11.009 |
| [12] | 林鸿熙. 信息透明度对企业诚信行为影响的博弈分析[J]. 重庆大学学报:社会科学版, 2004(5): 23–25. |
 2014, Vol. 20
2014, Vol. 20

