当前,中国经济已经进入调整经济结构和转变增长方式的关键时期。随着要素成本的上升,过度依赖要素投入扩张来实现经济增长,从长期看不可持续,未来中国经济增长的可持续性更多地取决于全要素生产率(TFP)的提高,以及产业结构的转型升级。在此背景下,要求TFP增长与产业结构调整必须是健康、持续的,也就是TFP的提高必须要与产业结构的演进相互促进。尽管国内外关于这一问题的研究文献丰富,但对二者互动关系的关注却非常少,因此,对产业结构调整与TFP互动关系进行研究十分必要,对中国调整经济结构、转变增长方式具有重要的现实意义。
国内外学者对产业结构调整与TFP关系这一问题给予了高度关注,也提出了各种各样的观点。一方面,产业结构调整对TFP增长具有重要影响,Chenery等认为产业结构调整促进了生产要素在部门之间的流动从而导致了资源配置效率的改善,推动了经济的增长。Liang通过考虑产业结构调整所带来的投入要素质量的变化来测算TFP,重新评估了Krugman-Kim-Lau-Young的“投入驱动型经济增长”假说[1]。干春晖等指出产业结构不仅对经济规模有直接影响,还通过对生产要素的资源再配置作用间接影响经济增长。张学威认为安徽省产业结构变动对TFP具有显著影响,产业结构优化升级能够带动整体生产效率的提高,但这种带动效应远远低于东部地区[2]。张丽认为近10年来,全国产业结构演进效应对TFP贡献的下降趋势有所减缓,但新疆TFP的结构演进效应却达到峰值。另一方面,TFP也对产业结构调整产生推动作用。结构主义学派认为生产率增长的差异是产业结构变迁的一个重要动力。Galor和Weil通过数值模拟说明了技术进步在从马尔萨斯经济向索罗经济的产业结构变迁过程中的推动作用。Hansen和Prescott在此基础上提出了TFP是产业结构变迁的动力。胥爱欢将Hansen和Prescott模型中的TFP为外生变量修正为内生性假设,发现TFP对产业结构调整产生正向推动作用。
现有研究文献对产业结构变动和TFP的关系进行了较为深入的测度与分析,但仍存在值得进一步探讨之处,主要表现为:(1) 从研究对象看,多数研究集中在某类行业结构变化对TFP增长的影响或者是产业结构变动对单要素生产率增长的影响[3],而较少从中国整体上考查产业结构调整与TFP的互动关系;(2) 从研究时段看,已有文献主要集中在2008年之前,少有文献对2008年国际金融危机之后产业结构调整与TFP的关系进行分析;(3) 从变量选取看,在度量TFP时,对投入变量资本和劳动数据缺少最低限度的关注[4],采用资本存量和从业人数分别衡量资本投入和劳动投入的做法受到不少学者的质疑。
有鉴于此,本文基于永续盘存法(PIM)估算出具有物量和价格双重属性的资本服务物量指数,运用迭代比例拟合算法(IPF)将从业人数和劳动报酬按行业、性别、年龄、文化程度进行四维交叉分类测算出中国劳动投入指数,考虑资本和劳动投入数量变化的同时引入质量变化,在此基础上运用增长核算法对中国TFP进行更为谨慎的测度,并就中国1979-2013年的样本序列数据运用脉冲响应函数、方差分解法和格兰杰因果检验法实证分析产业结构调整与TFP的交互影响。
二、 模型设定为了分析产业结构调整与TFP之间的关系,本文借鉴Miller和Upadhyay的思路,引入Cobb-Douglas生产函数,两个生产函数分别如下所示:
| $ {Y_{\rm{t}}} = {A_{\rm{t}}}F\left( {{L_{{\rm{1t}}}},{L_{{\rm{2t}}}}, \cdots {L_{N{\rm{t}}}},{K_{{\rm{1t}}}},{K_{{\rm{2t}}}} \cdots {K_{M{\rm{t}}}}} \right) $ | (1) |
| $ {Y_{\rm{t}}} = {A_{\rm{t}}}F\left( {{L_{{\rm{1t}}}},{L_{{\rm{2t}}}}, \cdots {L_{N{\rm{t}}}},{K_{{\rm{1t}}}},{K_{{\rm{2t}}}} \cdots {K_{M{\rm{t}}}},I{S_{\rm{t}}}} \right) $ | (2) |
其中,方程(1)不包含产业结构调整,方程(2)包括产业结构调整;Yt表示国内生产总值,L1t, L2t, ...LNt和K1t, K2t, ...KMt分别表示N种不同类型的劳动投入和M种不同类型的资本投入,ISt表示产业结构调整,At表示希克斯中性的技术进步水平。对方程(1)和(2)两边取对数后微分,整理得到:
| $ \frac{{{\rm{d}}\ln Y}}{{{\rm{d}}t}} = \frac{{{\rm{d}}\ln A}}{{{\rm{d}}t}} + \sum\limits_{i = 1}^N {{\alpha _i}\frac{{{\rm{d}}\ln {L_i}}}{{{\rm{d}}t}}} + \sum\limits_{j = 1}^M {{\beta _j}\frac{{{\rm{d}}\ln {K_j}}}{{{\rm{d}}t}}} $ | (3) |
| $ \frac{{{\rm{d}}\ln Y}}{{{\rm{d}}t}} = \frac{{{\rm{d}}\ln A}}{{{\rm{d}}t}} + \sum\limits_{i = 1}^N {{\alpha _i}\frac{{{\rm{d}}\ln {L_i}}}{{{\rm{d}}t}}} + \sum\limits_{j = 1}^M {{\beta _j}\frac{{{\rm{d}}\ln {K_j}}}{{{\rm{d}}t}}} + \gamma \frac{{{\rm{d}}\ln IS}}{{{\rm{d}}t}} $ | (4) |
其中,αi、βj、γ分别表示第i种劳动投入、第j种资本投入和产业结构调整的产出弹性。考虑到不同质的资本和劳动投入,式(3)和(4)中允许多种类型的资本和劳动投入共同存在。一般来说,每种资本和劳动投入都有其特定的边际生产率,因而在加总资本和劳动投入的增长率时,可以根据不同类型要素投入的边际生产率进行加权求得,则式(3)和(4)可简化成:
| $ \frac{{{\rm{d}}\ln Y}}{{{\rm{d}}t}} = \frac{{{\rm{d}}\ln A}}{{{\rm{d}}t}} + \alpha \frac{{{\rm{d}}\ln L}}{{{\rm{d}}t}} + \beta \frac{{{\rm{d}}\ln K}}{{{\rm{d}}t}} $ | (5) |
| $ \frac{{{\rm{d}}\ln Y}}{{{\rm{d}}t}} = \frac{{{\rm{d}}\ln A}}{{{\rm{d}}t}} + \alpha \frac{{{\rm{d}}\ln L}}{{{\rm{d}}t}} + \beta \frac{{{\rm{d}}\ln K}}{{{\rm{d}}t}} + \gamma \frac{{{\rm{d}}\ln IS}}{{{\rm{d}}t}} $ | (6) |
其中,
| $ \ln \frac{{{Y_{\rm{t}}}}}{{{Y_{{\rm{t - 1}}}}}} = \ln \frac{{{A_{\rm{t}}}}}{{{A_{{\rm{t - 1}}}}}} + \alpha \ln \frac{{{L_{\rm{t}}}}}{{{L_{{\rm{t - 1}}}}}} + \beta \ln \frac{{{K_{\rm{t}}}}}{{{K_{{\rm{t - 1}}}}}} $ | (7) |
| $ \ln \frac{{{Y_{\rm{t}}}}}{{{Y_{{\rm{t - 1}}}}}} = \ln \frac{{{A_{\rm{t}}}}}{{{A_{{\rm{t - 1}}}}}} + \alpha \ln \frac{{{L_{\rm{t}}}}}{{{L_{{\rm{t - 1}}}}}} + \beta \ln \frac{{{K_{\rm{t}}}}}{{{K_{{\rm{t - 1}}}}}} + \lambda \ln \frac{{I{S_{\rm{t}}}}}{{I{S_{{\rm{t - 1}}}}}} $ | (8) |
其中,α、β、γ分别表示资本投入、劳动投入和产业结构调整的产出弹性。在完全竞争市场和规模报酬不变的假定下,要素产出弹性等于该要素报酬在总产出中的比重,且各要素的产出弹性之和为1,即α+β+γ=1。
考虑到本文的研究需要以及数据的可得性,在模型中加入贸易开放度和人力资本两个控制变量,同时以新增长理论为依据,借鉴Miller及Soderbom和Teal的思想,假定TFP由一国的产业结构调整度、贸易开放度、人力资本积累水平、ε共同决定,从而建立起用产业结构调整内生化全要素生产率的模型:
| $ \ln TFP = {\lambda _0} + {\lambda _1}\ln IS + {\lambda _2}\ln OPEN + {\lambda _3}\ln H + \varepsilon $ | (9) |
其中OPEN表示贸易开放度,H代表人力资本水平,λ0、λ1、λ2、λ3为弹性系数,ε表示随机干扰项。
三、 数据说明与研究方法 (一) 全要素生产率测算本文通过编制既可以反映数量变化又可以反映质量变化的资本服务物量指数和劳动投入指数,并根据Solow提出的新古典经济增长模型框架对中国1979-2013年的全要素生产率进行估算。要测算TFP的增长,必须已知资本和劳动投入的时间序列数据,下面就资本投入和劳动投入的测算进行说明。
1. 资本投入估算因为无法直接测算资本服务,资本服务的测量是以资本存量的估算为基础。本文估算资本服务的处理方法是:首先,采用1979-2013年中国固定资本形成总额和固定资本投资序列数据,运用永续盘存法(PIM)估算资本存量总额;其次,分别利用双曲线形态下的“年龄-效率”函数和“年龄-价格”函数以及二者的相关关系估算生产性资本存量;最后,以通过内生方法得到的资本租赁价格作为权数,用Tornqvist指数形式对不同类型资产进行加总,得出具有物量和价格双重属性的资本服务物量指数①。
① 详细的估算方法请参见:曹跃群,秦增强,齐倩.中国省际资本服务测量:概念、框架和指数构建[J].数量经济技术经济研究,2012(12)。
在PIM法的基础上,测算资本存量的公式为:
| $ {K_{\rm{t}}} = {K_{{\rm{t - 1}}}}\left( {1 - \delta } \right) + {I_{\rm{t}}} = {K_{{\rm{t - 1}}}} + {I_{\rm{t}}} - {R_{\rm{t}}} = \sum\limits_{\tau - 1}^\infty {{S_\tau }{I_{{\rm{t - }}\tau }}} $ | (10) |
其中K为资本存量,δ为折旧率,I为当年投资,S为各期资本品投资的残差率,由退役模式决定,本文选择常用的钟型退役模式。
为获得生产性资本存量,本文根据ABS和BLS资本服务估算的实践方法,通过双曲线形态下的“年龄-效率”函数将资本存量总额转化为标准效率单位的生产性资本存量。双曲线形态函数形式表示为:
| $ {V_{\rm{t}}} = {V_0}\left( {T - \left( {{\rm{t}} - {\rm{1}}} \right)} \right)/\left( {T - \beta \left( {{\rm{t}} - {\rm{1}}} \right)} \right) $ | (11) |
经过标准化处理,假设初始年份相对效率V0=1,Vt为第t年的相对效率,β为斜率,根据公式(10)、(11),在已知资本存量总额和“年龄-效率”函数的基础上,某一类资产的生产性资本存量可表示为:
| $ K_{\rm{t}}^p = \sum\limits_{\tau = 0}^L {{d_\tau }} \times {I_{{\rm{t - }}\tau }} \times {S_\tau } = \sum\limits_{\tau = 0}^L {{d_\tau }} \times {K_{\rm{t}}} $ | (12) |
资本租赁价格是资本品在核算期内提供服务的总成本。在竞争均衡条件下,资本品的当期购置价格等于它未来所有期望租赁收入的折现和,各年租赁收入由于折旧模式的递减和资本品的退役,是新资本品租赁价格的加权,权数和资本存量估算中的相对效率一致。
| $ {C_{\rm{t}}} = {q_{\rm{t}}}\left( {r + {\delta _{\rm{t}}}} \right) - \left( {{q_{\rm{t}}} - {q_{{\rm{t - 1}}}}} \right) $ | (13) |
δt为折旧率,r是资本报酬率,qt-qt-1是资本损益率。
假设资本报酬总额用C表示,则资本报酬总额、生产性资本存量、折旧和资本报酬率之间的关系可表示为:
| $ C = {C_{\rm{t}}} \times {K_{\rm{t}}} = {q_{\rm{t}}}\left[ {r + {\delta _{\rm{t}}} - \frac{{{q_{\rm{t}}} - {q_{{\rm{t - 1}}}}}}{{{q_{\rm{t}}}}}} \right] \times {K_{\rm{t}}} $ | (14) |
由此,可以得到资本报酬率为:
| $ r = \frac{{C - \left[ {{\delta _{\rm{t}}} \times {q_{\rm{t}}} - \left( {{q_{\rm{t}}} - {q_{{\rm{t - 1}}}}} \right)} \right] \times {K_{\rm{t}}}}}{{{q_{{\rm{t - 1}}}} \times {K_{\rm{t}}}}} $ | (15) |
在资本租赁价格作为权数的基础上,为了将不同类型资产的生产性资本存量进行加总,本文采用适用于离散经济数据的Tornqvist指数来测算总资本服务。资本服务的Tornqvist物量指数可表示为:
| $ {\prod\limits_i {\left( {\frac{{K_{i,{\rm{t}}}^p}}{{K_{i,{\rm{t - 1}}}^p}}} \right)} ^{{{\bar \omega }_i}}} $ | (16) |
其中ωi是相邻核算期内各类资产相对份额的算术平均,在超越对数函数形式下,可将式(16)变换为:
| $ \ln {K_{\rm{t}}} - \ln {K_{{\rm{t - 1}}}} = \sum\limits_i {{{\bar \omega }_i}\left( {\ln K_{i,{\rm{t}}}^p - \ln K_{i,{\rm{t - 1}}}^p} \right)} $ | (17) |
根据乔根森提供的方法论,经济活动中劳动投入总量可以表示为具有不同特征的劳动投入分量的函数,函数形式一般采用超越对数函数,则劳动投入表示为:
| $ \ln L = {\alpha _0} + \sum\limits_{i = 1}^n {{\alpha _i}\ln {L_i}} + \frac{1}{2}\sum\limits_{i = 1}^n {\sum\limits_{j = 1}^n {{\beta _{ij}}\ln {L_i}} } \times \ln {L_j} $ | (18) |
其中,i=1, 2, ..., n,j=1, 2, ..., n,α0、α1、βij为待估参数,Li、Lj分别表示i类和j类劳动投入分量。在超越对数函数形式下,度量劳动投入变化的公式可表示为:
| $ {g_{\rm{t}}} = \ln {L_{\rm{t}}} - \ln {L_{{\rm{t - 1}}}} = \sum\limits_{i = 1}^n {{{\bar V}_{i,{\rm{t}}}}\left[ {\ln {L_{i,{\rm{t}}}} - \ln {L_{i,{\rm{t - 1}}}}} \right]} = \sum\limits_{i = 1}^n {{{\bar V}_{i,{\rm{t}}}}} \times g_{{\rm{t,t - 1}}}^i $ | (19) |
其中Lt、Lt-1分别表示第t期、t-1期的劳动投入总量,gt, t-1i表示第i类劳动投入分量在t期和t-1期间的增长速度,权数Vi, t为t期和t-1期相应价值份额的均值。
而价值份额可以表示为:
| $ {V_{i,{\rm{t}}}} = \frac{{{w_{i,{\rm{t}}}}}}{{{W_{\rm{t}}}}} $ | (20) |
其中,wi, t为第t期第i类劳动投入分量的价格(劳动报酬),Wt为第t期劳动投入总量的价格(劳动报酬)。由式(19)可以看出,劳动投入变化指数等于不同种类劳动投入分量增长速度的加权和,权数为各种劳动投入分量劳动报酬比重在t期和t-1期之间的均值。
劳动投入分量可以表示为:
| $ {L_{i,{\rm{t}}}} = {e_{i,{\rm{t}}}}{G_{\rm{t}}}{H_{\rm{t}}} $ | (21) |
其中,Gt表示第t期从业人员总数,Ht为第t期每个从业人员平均工时数,ei, t表示第i类从业人员工时数占第t期总工时数的比例。假定Ht保持不变,则由式(19)、(21)可以得到:
| $ {g_{\rm{t}}} = \ln {L_{\rm{t}}} - \ln {L_{{\rm{t - 1}}}} = \left[ {\ln {G_{\rm{t}}} - \ln {G_{{\rm{t - 1}}}}} \right] + \sum\limits_{i = 1}^n {{{\bar V}_{i,{\rm{t}}}}\left[ {\ln {e_{i,{\rm{t}}}} - \ln {e_{i,{\rm{t - 1}}}}} \right]} $ | (22) |
式(22)右边第一项表示t期和t-1期间从业人数的变化,反映了劳动投入的数量变化;第二项表示第i类从业人员数所占比例变化的加权平均值,反映了劳动投入的结构变化,本文将其看作质量变化。可见,劳动投入变化指数gt同时考虑了劳动数量和劳动质量的改善。
由于统计资料的缺陷,很难直接获得多维交叉分组的从业人数及其劳动报酬的详细数据,因此本文参考任若恩、岳希明和郑海涛等的做法,运用迭代比例拟合算法(IPF)将从业人数和劳动报酬按行业、性别、年龄、文化程度进行四维交叉分类测算出中国劳动投入指数。
3. 产业结构调整指标学者对产业结构的分析,一般是停留在对三次产业结构变动的分析上。多数学者采用各产业占GDP比重来衡量产业结构调整程度。也有学者利用行业数据和工业企业数据构建工业内部的二位数产业结构调整指数和四位数的产业结构调整指数。为了考察产业结构调整与全要素生产率增长的互动关系,将产业结构调整分解为产业结构调整速度与产业结构调整方向两个指标。产业结构调整速度是用来动态衡量一国三大产业结构变动速度的指标,反映各产业波动程度,产业结构调整速度越快,各产业波动越剧烈;产业结构调整方向是用来考察产业结构从低水平状态向高水平状态发展的指标。
本文产业结构调整速度指标用K值衡量,产业结构调整方向用第三产业产值占GDP比重衡量。
其中K值指标是用报告期产业构成比与基期产业构成比差额绝对值的总和来度量,计算公式如下:
| $ K = \sum\limits_{i = 1}^n {\left| {{q_{i{\rm{t}}}} - {q_{i0}}} \right|} $ | (23) |
其中,qi0和qit分别表示第i产业在基期和即期的GDP比率。K值越大,表明产业结构调整的幅度越大。
4. 控制变量本文根据需要,加入贸易开放度和人力资本两个控制变量。其中贸易开放度用进出口总额比上GDP来衡量,进出口贸易总额用当年美元价折合成人民币表示;人力资本水平的测量一般包括劳动力成本法、教育年限法、在校学生比例法和教育经费法等,但是由于本文的数据追溯年份较早,收集较为困难,而在校学生数据的统计资料比较全面,因此本文借鉴干春晖等做法采用初中及以上在校学生人数占年底总人口的比重来衡量人力资本水平。
(二) 数据来源说明各变量的数据均来源于历年《中国劳动统计年鉴》、《中国国内生产总值核算历史资料:1952-1995》、《中国国内生产总值核算历史资料:1952-2004》、《中国固定资产投资统计数典:1952-2000》、《中国统计年鉴》(1983-2013),并以1979年不变价格进行换算,其中2013年数据用指数平滑法估算得来。
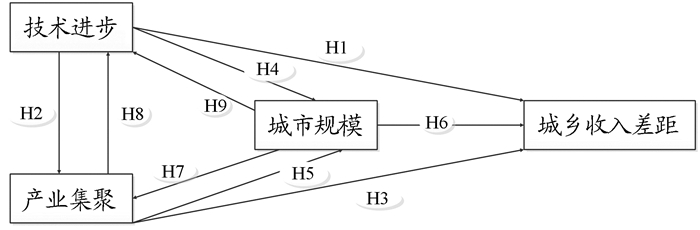
(三) 估算结果根据前文估算,得到中国资本服务指数、劳动投入指数、TFP增长以及产业结构调整速度的估算结果(图 1)。1979-2013年间,中国资本投入保持着11.23%的平均增长速度,整体增长趋势较为平稳;在考虑劳动投入质量的前提下,劳动投入平均增长率为2.99%,增长趋势平稳;TFP增长率波动幅度较大,但总体呈上升趋势,平均增长率为1.81%;产业结构调整速度趋势平稳,以平均-3.80%的速度调整产业结构。
|
图 1 资本服务、劳动投入指数、TFP增长及产业结构调整速度估算结果 |
在理论模型分析的基础上,我们首先对全要素生产率TFP、产业结构调整IS、贸易开放度OPEN和人力资本H的关系进行格兰杰因果检验。为了避免“伪回归”现象的出现,格兰杰因果关系检验要求所研究变量都是平稳的,因此我们需要对变量的单整性(ADF检验)进行检验。同时,为了消除数据的异方差,我们对各变量分别求取对数,即lnTFP、lnIS1、lnIS2、lnOPEN和lnH。接下来对5个变量进行ADF检验,以确定各变量的单整性和阶数。
根据表 1的检验结果可知,变量lnTFP、lnIS1是水平平稳的,而lnIS2、lnOPEN和lnH都是一阶单整的,服从I (1)过程。鉴于各变量不是同阶单整的,根据变量平稳性特征,需要将模型进行调整,修正过后的模型为:
| $ \ln TFP = {\lambda _0} + {\lambda _1}\ln IS1 + + {\lambda _2}\Delta \ln IS2 + {\lambda _3}\Delta \ln OPEN + {\lambda _3}\Delta \ln H + \varepsilon $ | (24) |
| 表 1 各变量的单位根检验 |
为了进一步确定变量之间的关系,检验过程中根据变量特征建立VAR模型,这就需要确定滞后期数。本文对最优滞后期数的选择按照AIC、SC信息准则, 如果AIC和SC的滞后期同时达到最小,则可以确定最优滞后期数,根据这两个原则,本文确定的最优滞后阶数为1,可以建立VAR (1)模型。
(二) 非限制性VAR模型平稳性判定如表 2所示,该VAR (1)模型的特征根的模全都比1小,均落在单位圆之外,因此该VAR (1)模型是稳定的,变量间具有短期均衡关系,可以做脉冲响应函数分析与方差分解分析。
| 表 2 VAR (1)过程的特征根列表 |
由于VAR模型存在高度参数化的特征,其拟合出来的方程组参数估计结果所代表的实际意义不是很大。而脉冲响应函数则是用来衡量随机扰动项的一个标准差冲击对内生变量当前和未来取值的影响,通过分析某因素对于其他因素突然变化的反馈可以更直接地反映在外部环境不断变化时各变量之间的动态交互作用和效应。
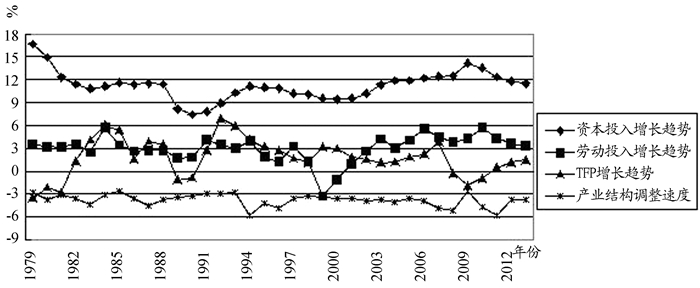
从图 2中可以看出,TFP对各变量的反馈基本属于正冲击(忽略人力资本微弱的负向冲击),都是先经历强弱变化期,然后图像又逐步呈现收敛,达到稳态均衡。具体来说,首先,外界环境对产业结构调整速度施加一个冲击对TFP的影响一直是正向的,影响程度先加强再减弱,在第2期到达顶点,即在第2期TFP对产业结构调整速度的响应是0.48。表明产业结构调整速度受到某一外部冲击之后,传递给TFP,在经历正向冲击加强过程之后达到最大值,然后正向冲击力度逐步下降,达到稳态均衡。其次,当产业结构调整方向受到外部经济环境的冲击之后,TFP的初始反应强度达到最大值,约为0.51,在第2期内迅速下降,之后小幅上升,并出现了一个短暂的平稳期,随后强度开始减弱,逐步收敛,趋于平衡。再次,人力资本对TFP的冲击初始状态强度最大,约为0.05,然后逐步减弱,仅仅维持了很短的时间后在第3期就转为负向关系,但这种反应强度比较微弱,随后就趋于平衡状态。最后,贸易开放度对TFP的反应初始状态是负向的,但只是一个非常短暂的过程就立刻变为正向关系,并且强度逐步增加,在第3期达到顶点,约为0.28,随后逐渐减弱,趋于平衡。
|
图 2 各变量对TFP脉冲响应函数图 |
综上,产业结构调整所带来的TFP增长过程比较缓慢,存在较长的滞后期。TFP对产业结构调整速度和产业结构调整方向的脉冲响应模式存在较大差异,这种差异不仅体现在冲击力度上,也体现在脉冲响应的时间轨迹上。产业结构调整方向的振荡幅度要大于产业结构调整速度的振荡幅度,在脉冲响应的1~11期上,TFP对于产业结构调整速度的平均脉冲响应值要高于产业结构调整方向,且TFP对产业结构调整速度的时滞更短。
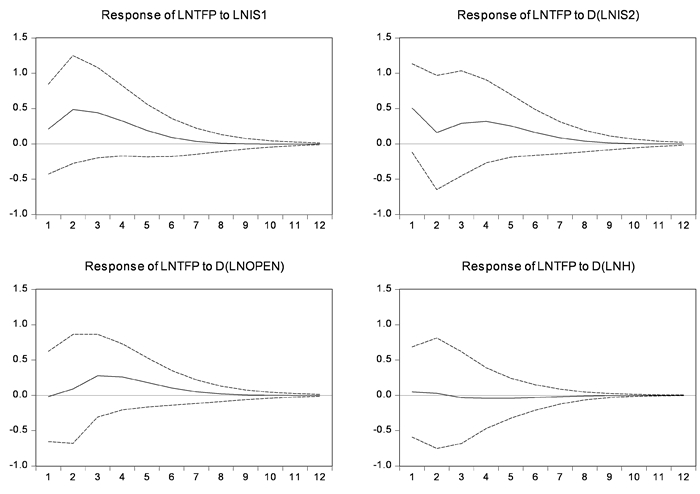
从图 3可以看出,产业结构调整速度对TFP冲击的反应强度初始状态达到最大,约为0.09,之后强度逐步减弱,到第3期开始进入平稳期,并逐步收敛,最终达到稳态均衡。同样的,产业结构调整方向对TFP冲击的影响初期达到最大值,即在第1期TFP对产业结构调整方向的响应是0.010 2,随后强度逐步下降,直至收敛。综观产业结构调整对TFP的脉冲响应函数可以发现,产业结构调整方向对TFP的振荡幅度要大于产业结构调整速度,但TFP对产业结构调整速度的平均冲击力度更大。同时,TFP对产业结构调整的冲击是非常迅速的,当一项新技术获得应用时,一国的产业结构会快速作出调整,并重新进行产业布局,因而技术进步对产业结构的冲击很明显,时效性非常显著。
|
图 3 TFP对产业结构调整脉冲响应函数图 |
采用Cholesky方法对产业结构调整速度、产业结构调整方向和TFP进行方差分解,得到表 3和表 4所示的结果。
| 表 3 TFP方差分解表 |
| 表 4 产业结构调整速度和方向方差分解表 |
从表 3可以发现,TFP本身对其波动的贡献度经历了逐步下降的过程,从第8期后趋于稳定, 贡献度在82.73%左右;其余各变量对TFP波动的贡献度都经历了先加速增大后增速趋缓最后趋于稳定的过程,其中TFP本身对其波动的贡献度始终最高,产业结构调整速度的贡献度也较大,贸易开放度和人力资本积累水平次之,贡献度最小的是产业结构调整方向。具体看,产业结构调整速度对TFP波动的贡献度前4期变化幅度较大,之后稳定在6.67%左右,在几个变量中是贡献值最大的。而产业结构调整方向一直比较稳定,波动幅度不是很大,保持在2.91%上下。人力资本对TFP的贡献前7期反应比较灵敏,从第8期开始,维持在3.66%的水平。贸易开放度对TFP变化的贡献度在前5期波动幅度较明显,随后趋于稳定,保持在4.03%左右的贡献度。
如表 4所示,产业结构调整速度对其本身波动的贡献程度始终在降低,且滞后前3期下降非常明显,之后稳定在78.23%的水平,而TFP对产业结构调整速度的影响在滞后初期最大,之后4期有所下降,随后又处于上升趋势,并稳定在1.18%的贡献度水平。产业结构调整方向对其本身波动的影响一直处于下降趋势,最后保持77.07%的水平,而TFP对产业结构调整方向的贡献度滞后前7期处于上升趋势,之后波动下降,最终稳定在10.65%的贡献水平。
(五) 格兰杰因果关系检验为了进一步验证产业结构调整速度、产业结构调整方向与TFP之间的关系,需要就各变量分别对TFP进行格兰杰因果关系检验。滞后期仍然根据AIC和SC信息准则进行选择,得到如表 5所示的结果。
| 表 5 各变量间的格兰杰因果关系检验 |
通过对表 5分析发现,在10%的显著性水平下,1979-2013年间TFP与产业结构调整速度和方向之间存在双向的因果关系,产业结构变动速度的加快以及产业结构的高度化都是TFP提高的格兰杰原因,而TFP的增加也是产业结构调整速度加快和产业结构高度化的格兰杰原因。贸易开放度和人力资本积累水平与TFP之间是单向的因果关系,贸易开放度以及人力资本水平的提高是TFP增加的格兰杰原因。格兰杰因果关系检验的结果也为前文的分析结论提供了有力支撑。
五、 研究结论与政策含义本文采用中国改革开放以来(1979-2013年)35年的样本序列数据,构建VAR模型,运用脉冲响应函数、方差分解以及格兰杰因果关系检验,实证分析了产业结构调整与全要素生产率之间的相互影响和相互作用。
研究认为:产业结构调整与全要素生产率之间存在着密切的相互作用关系。全要素生产率可以在较短时间内引起产业结构的调整,时效性显著,而产业结构调整则从更长的时期内对全要素生产率产生影响,存在较长的滞后期。尽管产业结构调整与全要素生产率互为影响因素,但其贡献度不同,产业结构调整速度、产业结构调整方向对TFP波动的贡献度约分别为6.67%和2.91%;反之,TFP对产业结构调整速度变动和产业结构调整方向的贡献度分别为1.18%和10.65%。此外,TFP与产业结构调整之间存在双向因果关系的结论也表明产业结构调整与TFP的交互影响不容忽视,可以实现良性互动。
实证分析结果所蕴含的启示是:从产业结构调整角度看,中国每5年或者更短时间的产业规划布局以及连续的产业结构调整是TFP提高、经济可持续发展的重要保障,同时政府根据全球经济形势和中国国情所作出的宏观产业结构调整也是经济稳定增长的重要条件。在经济转轨时期应该注重优化产业结构调整方向,促进产业结构向合理化和高度化发展,抓住全球产业转移和产业升级的机会,大力提升产业层次、技术水平和技术效率,促进产业结构的内生性发展,使产业结构调整的要素配置功能能够得到最大发挥,为TFP的提高提供源源不断的动力。从全要素生产率角度看,在更长的时期内,要借鉴发达国家的经验,顺应并利用TFP增长的基本规律,建立并完善科技创新制度,加强对技术创新的宏观调控,弱化技术进步带来的负效应,在深刻认识科技创新规律的基础上,强化TFP增长对产业结构调整的正向促进作用,实现TFP与产业结构调整之间的良性互动,从而促进中国经济结构的调整与增长方式的转变,实现稳增长的目标。
| [1] | LIANG C Y. Industrial structure changes and the measurement of total factor productivity growth:The Krugman-Kim-Lau-Young Hypothesis revisited[J]. Academic Economic Papers, 2009, 37: 307–333. |
| [2] | 张学威. 全要素生产率和产业结构优化的关系——基于1978-2008年安徽省和长三角地区面板数据的实证分析[J]. 中国软科学, 2010(S): 207–213. |
| [3] | 李小平, 卢现祥. 中国制造业的结构变动和生产率增长[J]. 世界经济, 2007(5): 52–67. |
| [4] | 岳希明, 任若恩. 测量中国经济的劳动投入: 1982-2000[J]. 经济研究, 2008(3): 16–28. |
 2015, Vol. 21
2015, Vol. 21
