2. 重庆大学 经济与工商管理学院, 重庆 400044
2. School of Economics and Business Administration, Chongqing University, Chongqing 400044, P. R. China
顺应产业竞争由企业之间的竞争转换为供应链之间竞争的态势,供应链金融应运而生。供应链金融被视为银行和物流企业共同提供的一种“金融与物流集成式的创新服务”[1],其实质是一种物流企业参与下的质押担保业务[2]。供应链金融的迅速发展,使现实中出现了多种创新模式,例如融通仓、保兑仓、应收账款融资、订单融资业务和进口全程货权质押授信业务等, 但因为存货是物流的基本元素,最能体现物流的特征,也是多数中小企业都拥有的资产,具有良好的流动性和变现性,所以国内外都将存货质押融资业务作为供应链金融的核心模式之一[3]。与传统的抵押贷款相比,存货质押融资不需要以固定资产和设备作为贷款抵押,只需向金融机构提供库存产品并将之送至其指定的3PL企业仓库监管,就可以从金融机构贷到所需款项[4]。而在质押过程中,融资企业只要按照合同约定,向金融机构支付所获贷款的本息和,即可将质押的全部存货解押出来。在一项关于粮食质押融资业务的调研中,我们发现粮食企业基本上都是选择在金融机构授信期末一次解押质押的所有粮食,并支付各项费用。实际上,授信期末一次解押存货往往会造成资金价值的“浪费”。在动态质押模式下,存货质押融资业务处理比较灵活方便,融资企业可选择任意时刻进行质押与解押活动。因此,如果融资企业在授信期内已经拥有足够解押存货的资金,那么其完全可以将质押给金融机构并在3PL企业仓库进行监管的存货提前解押出来,从而有可能减少贷款的成本支出。
尽管不同的解押方式会影响融资企业的融资成本,且存货质押业务实践中也的确存在这种现象,但这个问题还没有引起学者们的关注,尚没有相应的研究成果出现。现有的关于存货质押融资文献主要集中于风险控制管理方面。质押率作为风险控制的一个关键指标,其研究成果最为丰富。如Jokivuolle和Peura建立了担保物价值和企业违约概率相关风险债务模型,表明对贷款价值比率的限制可部分限制违约损失,使贷款的风险达标[5]。Cossin和Hricko等建立模型分析有担保物时信用风险的估值,模型证明了设定折扣率限值是有用的[6]。随后,Cossin和Huang等假设企业的违约概率外生给定,利用简化方法得出了与银行风险承受能力相一致的质押率[7]。李毅学和冯耕中等沿用Cossin和Huang等的研究思路,综合考虑外生的企业违约概率,针对价格随机波动的存货,应用“主体+债项”的风险评估策略分析了下侧风险规避的银行在质押存货的期末价格服从一般分布和几种具体分布时的质押率决策[4]。需要指出的是,上述文献均是以银行期望收益为目标函数基于数理优化方法建立定量模型得到质押率。而在实证分析方面,He等根据钢材质押中实际价格波动特征的大样本数据,研究了钢材质押贷款动态质押率设定的VaR方法[8-9]。陈云和刘喜等以钢材存货质押为例,从银行风险管理角度,建立简化式多周期动态质押率设定模型[10]。在存货质押融资业务实践中,当融资企业质押完一种存货所获得的融资额度尚不能满足生产(订货)需要时,便会考虑质押其他存货来弥补融资缺口,因此研究多存货组合质押具有重要的现实意义[11]。齐二石和马珊珊等考虑多品类质押商品价格变动率服从正态copula分布情形下,对银行在组合质押业务中以最小化贷款成本为目标函数的质押率决策进行了分析[12]。孙朝苑和韦燕假设静态质押模式下组合质押存货的价格变动相互独立且服从对数正态分布,构建了组合质押率决策模型[13]。实际上,文献[12-13]在计算组合质押率时,默认已经确定送去质押存货的种类,但这个前提是矛盾的,不同存货组合计算出的组合质押率是不同的,而不同的组合质押率又会影响对质押存货的选择,这相当于讨论先有“鸡”还是先有“蛋”的问题。基于此,匡海波和张一凡等在研究低碳港口物流质押贷款决策时,分别界定单笔港口货类质押贷款的VaR质押率[14-15]。张云丰和王勇以期望收益为目标函数,制定组合质押规则与循环置换规则,建立多存货组合质押与动态循环置换优化模型[16]。
综上所述可知,质押率的研究已比较成熟,因此在下文的讨论中将不再花费过多笔墨讨论质押率的设置,而将其假定为一已知常数。考虑到在存货质押期间,融资企业可采用授信期末一次解押、授信期内分批解押、授信期内提前解押三种方式解押存货,所以,本文将在系列假设的基础上,分别建立三种解押方式的总成本函数,通过求解函数得到每种解押方式的最优解押数量与最优解押批次,并根据数值算例对三种解押方式的适用情形进行说明,分析相关参数变化对解押总成本的影响方式。
二、 基本假设与参数说明本文建立的模型基于如下假设:(1) 考虑融资企业解押单一存货的情形;(2) 授信期内存货销售价格不发生变化;(3) 融资企业有足够资金解押全部质押存货;(4) 每次解押的时间间隔和存货数量相同;(5) 在3PL企业仓库中存储期间损耗的存货不发生运输成本;(6) 被解押的存货在授信期内被置于融资企业仓库存储而不是用于销售;(7) 在融资企业和3PL企业仓库中存储期间损耗的存货需考虑仓储成本。
本文所使用的主要数学符号及含义说明如下:Q为质押的存货数量(千克);T为金融机构的授信期限(月);T0为融资企业有足够资金解押存货的时间始点;P为存货的销售价格(元/千克);F为每次运输的固定成本(元/次);k为运输单位存货的变动成本(元/千克);C1为存货在3PL企业仓库的单位库存成本(元/月);C2为存货在融资企业仓库的单位库存成本(元/月);θ为存货在3PL企业仓库和融资企业仓库的自然损耗率(月),0≤θ < < 1;λ为存货的贷款价值比(质押率);σ1为融资企业向金融机构贷款的月利率;σ0为融资企业自有资金存入金融机构的月利率;q为每次解押的存货数量(千克);n为存货解押的批次(次);TCi为第i种解押方式的总成本函数,其中,i=1, 2, 3。
三、 模型与求解建立总成本函数需要考虑的成本影响因素主要包括:存货运输成本(包括固定成本及变动成本)、存货库存成本(包括在3PL企业仓库库存成本及在融资企业仓库库存成本)、融资企业的利息成本(包括支付给金融机构的利息及自有资金获得的利息收益)。
(一) 授信期末一次解押的总成本函数存货运输成本。存货在授信期内任意时刻t的数量满足微分方程dI(t)/dt=-θI(t),I(0)=Q,解此微分方程得I(t)=Qexp (-θt)。授信期末一次解押时,存货在3PL企业仓库存储时间为T,需运输的存货数量为I(T)=Qexp (-θT)。对指数函数进行泰勒展开,参考文献[17-19]的处理方式,取其前三项值,有I(T)=Qexp (-θT)=Q(1-θT+0.5θ2T2)。运输固定成本为F,运输变动成本为kQ(1-θT+0.5θ2T2),存货运输成本为F+kQ(1-θT+0.5θ2T2)。
存货库存成本。存货在整个授信期内始终存储在3PL企业仓库,因而存货在3PL企业仓库的库存成本为C1QT,在融资企业仓库的库存成本为0,存货总的库存成本为C1QT。
融资企业的利息成本。融资企业质押的存货总价值为PQ,从金融机构获得的资金额度为λPQ,在授信期末需要支付的利息为λPQσ1T。融资企业在T0时刻解押存货需支付给金融机构的资金为λPQ(1+σ1T0), 该资金如果不用于解押存货,则在授信期末可获得的利息收益为λPQ(1+σ1T0)σ0(T-T0)。融资企业的利息成本为λPQσ1T-λPQ(1+σ1T0)σ0(T-T0)。
综上所述,授信期末一次解押的总成本函数为:
| $T{C_1} = F + kQ\left( {1- \theta T + 0.5{\theta ^2}{T^2}} \right) + {C_1}QT + \left[{\lambda PQ{\sigma _1}T-\lambda PQ(1 + {\sigma _1}{T_0}){\sigma _0}(T-{T_0})} \right]$ | (1) |
式(1)中,所有参数均为外生变量,可直接计算TC1的值。此时,每次解押的存货数量q=Q,解押的批次n=1。
(二) 授信期内分批解押的总成本函数设存货解押的相邻批次间隔期为t,则3PL企业仓库中的存货库存水平如图 1所示。
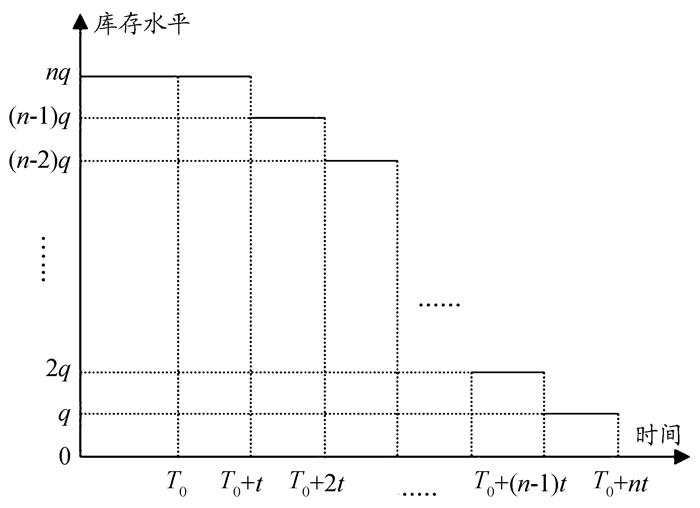
|
图 1 存货在3PL企业仓库的库存水平 |
由图 1可知,授信期内存货在3PL企业仓库的平均库存水平
| $\begin{array}{c} {{\hat I}_1}\left( q \right) = \frac{{nq \cdot {T_0} + nq \cdot t + \left( {n-1} \right)q \cdot t + \left( {n-2} \right)q \cdot t + \cdots + 2q \cdot t + q \cdot t}}{T} = \\ \frac{{nq \cdot {T_0} + 0.5\left( {n + 1} \right)q \cdot nt}}{T} \end{array}$ | (2) |
将nq=Q及nt=T-T0带入式(2),解得
存货运输成本为
存货在3PL企业仓库的库存成本为
融资企业将3PL企业仓库中所有存货解押所需的资金本息和为
综上所述,授信期内分批解押的总成本函数为:
| $T{C_2}\left( q \right) = \left[\begin{array}{l} F \cdot \frac{Q}{q} + k\left[{Q-\frac{1}{2}\left. {\left( {\left( {Q + q} \right)T + \left( {Q-q} \right){T_0}} \right)} \right)\left( {\theta-0.5{\theta ^2}T} \right)} \right] + \\ \frac{1}{2}\left[{\left( {{C_1} + {C_2}} \right)QT + \left( {{C_1}-{C_2}} \right)qT + \left( {{C_1}-{C_2}} \right)\left( {Q-q} \right){T_0}} \right] + \\ \frac{{\lambda P}}{2}\left[{\left( {Q + q} \right){\sigma _1}T + \left( {Q-q} \right){\sigma _1}{T_0}-\left( {Q + q} \right)\left( {1 + {\sigma _1}{T_0}} \right){\sigma _0}\left( {T-{T_0}} \right)} \right] \end{array} \right]$ | (3) |
将式(3)关于q分别求一阶、二阶导数得到
| $\frac{{{\rm{d}}T{C_2}\left( q \right)}}{{{\rm{d}}q}} = \frac{{FQ}}{{{q^2}}} + \left[{\left( {{C_1}-{C_2}} \right) + \lambda P\left( {{\sigma _1}-\left( {1 + {\sigma _1}{T_0}} \right){\sigma _0}} \right)-k\left( {\theta - 0.5{\theta ^2}T} \right)} \right] \cdot \frac{{T -{T_0}}}{2}$ | (4) |
| $\frac{{{{\rm{d}}^2}T{C_2}\left( q \right)}}{{{\rm{d}}{q^2}}} = \frac{{2FQ}}{{{q^3}}} > 0$ | (5) |
因此,TC2(q)存在最小值,令dTC2(q)/dq=0,解得
| ${q^*} = \sqrt {\frac{{2FQ}}{{\left[{\left( {{C_1}-{C_2}} \right) + \lambda P\left( {{\sigma _1}-\left( {1 + {\sigma _1}{T_0}} \right){\sigma _0}} \right)-k\left( {\theta - 0.5{\theta ^2}T} \right)} \right]\left( {T -{T_0}} \right)}}} $ | (6) |
将q*带入式(3),有
| $T{C_2} = \left[\begin{array}{l} KQ\left[{1 + \frac{1}{2}\left( {T + {T_0}} \right)\left( {\theta-0.5{\theta ^2}T} \right)} \right] + \frac{1}{2}Q\left[{\left( {{C_1} + {C_2}} \right)T + \left( {{C_1}-{C_2}} \right){T_0}} \right] + \\ \frac{1}{2}\lambda PQ\left[{{\sigma _1}\left( {T + {T_0}} \right) + {\sigma _0}\left( {1 + {\sigma _1}T} \right)\left( {T-{T_0}} \right)} \right]\\ \sqrt {2FQ\left[{\left( {{C_1}-{C_2}} \right) + \lambda P\left( {{\sigma _1}-{\sigma _0}\left( {1 + {\sigma _1}{T_0}} \right)} \right)-k\left( {\theta - .05{\theta ^2}T} \right)} \right]\left( {T -{T_0}} \right)} \end{array} \right]$ | (7) |
考虑到解押批次n取值的整数约束,应满足
设融资企业在时刻T′(T0≤T′≤T)正好将存货解押完毕。在0~T′期间,3PL企业仓库的平均库存水平为
综上所述,授信期内提前解押的总成本函数为:
| $T{C_3}\left( {T\prime, q} \right) = \left[\begin{array}{l} F\cdot\frac{Q}{q} + k\left[{Q-\frac{1}{2}\left( {\left( {Q + q} \right)T\prime + \left( {Q-q} \right){T_0}} \right)(\theta-0.5{\theta ^2}T\prime )} \right] + \\ \frac{1}{2}\left( {{C_1} - {C_2}} \right)\left( {\left( {Q + q} \right)T\prime + \left( {Q - q} \right){T_0}} \right) + 2{C_2}QT + \\ \frac{{\lambda P}}{2}\left[{\left( {Q + q} \right){\sigma _1}T\prime + \left( {Q-q} \right){\sigma _1}{T_0}-\left( {Q + q} \right)\left( {1 + {\sigma _1}{T_0}} \right){\sigma _0}\left( {T\prime-{T_0}} \right)} \right] \end{array} \right]$ | (8) |
命题1:在授信期内提前解押方式中,当满足
证明:TC3(T′, q)存在最小值需满足以下条件:(1)
在条件(1)和条件(2)中,分别有
| $\begin{array}{l} \frac{{{\partial ^2}T{C_3}\left( {T', q} \right)}}{{\partial T'\partial q}}.\frac{{{\partial ^2}T{C_3}\left( {T', q} \right)}}{{\partial q\partial T'}}- \frac{{{\partial ^2}T{C_3}\left( {T', q} \right)}}{{\partial {{T'}^2}}}.\frac{{{\partial ^2}T{C_3}\left( {T', q} \right)}}{{\partial {q^2}}} = \\ {\left[{-\frac{k}{2}\left( {\theta-{\theta ^2}T' + 0.5{\theta ^2}{T_0}} \right) + \frac{{{C_1}-{C_2}}}{2} + \frac{{\lambda P}}{2}\left( {{\sigma _1} - \left( {1 + {\sigma _1}{T_0}} \right){\sigma _0}} \right)} \right]^2} -\frac{{k{\theta ^2}FQ\left( {Q + q} \right)}}{{{q^3}}} > 0 \end{array}$ |
由下列式(9)可解得
| $T\prime = \frac{{k\theta-({C_1}-{C_2})-\lambda P\left( {{\sigma _1} - \left( {1 + {\sigma _1}{T_0}} \right){\sigma _0}} \right)}}{{k{\theta ^2}}} - \frac{{\left( {Q - q} \right){T_0}}}{{2\left( {Q + q} \right)}}$ |
将T′代入条件(3),知
| $\frac{{{\partial ^2}T{C_3}\left( {T\prime, q} \right)}}{{\partial T\prime \partial q}}\cdot\frac{{{\partial ^2}T{C_3}\left( {T\prime, q} \right)}}{{\partial q\partial T\prime }}-\frac{{{\partial ^2}T{C_3}\left( {T\prime, q} \right)}}{{\partial T{\prime ^2}}}\cdot\frac{{{\partial ^2}T{C_3}\left( {T\prime, q} \right)}}{{\partial {q^2}}} = \frac{{{\theta ^4}{T_0}^2}}{{16}}{\left( {k-\frac{{Q-q}}{{Q + q}}} \right)^2} - \frac{{k{\theta ^2}FQ\left( {Q + q} \right)}}{{{q^3}}} > 0.$ |
证毕。
因此,在授信期内提前解押方式中,总成本取得最小时的解押量q和解押终点时刻T′满足
| $\left\{ \begin{array}{l} \frac{{\partial T{C_3}\left( {T\prime ,q} \right)}}{{\partial T\prime }} = \frac{k}{2}\left[ {0.5{\theta ^2}\left( {Q - q} \right){T_0} - \left( {Q + q} \right)\left( {\theta - {\theta ^2}T\prime } \right)} \right]\\ + \frac{{\left( {Q + q} \right)({C_1} - {C_2})}}{2} + \frac{{\lambda P\left( {Q + q} \right)}}{2}\left[ {{\sigma _1} - (1 + {\sigma _1}{T_0}){\sigma _0}} \right] = 0\\ \frac{{\partial T{C_3}\left( {T\prime ,q} \right)}}{{\partial q}} = \frac{{ - FQ}}{{{q^2}}} - \frac{k}{2}(\theta - 0.5{\theta ^2}T\prime )(T\prime - {T_0}) + \frac{{({C_1} - {C_2})(T\prime - {T_0})}}{2}\\ + \frac{{\lambda P(T\prime - {T_0})}}{2}\left[ {{\sigma _1} - (1 + {\sigma _1}{T_0}){\sigma _0}} \right] = 0 \end{array} \right.$ | (9) |
从式(9)中解出的T′*与q*表达式是非常复杂的,下面给出一种比较简便的求解T′*与q*的方法。先写出T′*与q*的另一种表达形式
| $\left\{ \begin{array}{l} T{\prime ^*}\left( {{q^*}} \right) = \frac{{k\theta-\left( {{C_1}-{C_2}} \right)-\lambda P{\sigma _1} - \left( {1 + {\sigma _1}{T_0}} \right){\sigma _0}}}{{k{\theta ^2}}} - \frac{{\left( {Q - {q^*}\left( {T{\prime ^*}} \right)} \right){T_0}}}{{2\left( {Q + {q^*}\left( {T{\prime ^*}} \right)} \right)}}\\ {q^*}\left( {T{\prime ^*}} \right) = \sqrt {\frac{{2FQ}}{{\left( {{C_1} - {C_2}} \right) + \lambda P\left( {{\sigma _1} - \left( {1 + {\sigma _1}T} \right){\sigma _0}} \right) - k\left( {\theta - 0.5{\theta ^2}T{\prime ^*}\left( {{q^*}} \right)} \right)\left( {T{\prime ^*}\left( {{q^*}} \right) - {T_0}} \right)}}} \end{array} \right.$ | (10) |
在式(10)中,除T′*(q*)与q*(T′*)是内生变量外,其他参数皆为外生变量,将所有外生变量值代入T′*(q*),判断T′*(q*)的取值范围:若T0≤T′*(q*)≤T, 则联立求解T′*(q*)与q*(T′*)两式可解得T′*与q*;若T′*(q*) < T0,则T′*=T0,代入q*(T′*)可解得q*;若T′*(q*)>T,则T′*=T,代入q*(T′*)可解得q*。此时,授信期内提前解押的总成本函数表示为
| $T{C_3} = \left[\begin{array}{l} F\cdot\frac{Q}{{{q^*}}} + k\left[{Q-\frac{1}{2}\left( {\left( {Q + {q^*}} \right)T{\prime ^*} + \left( {Q-{q^*}} \right){T_0}} \right)\left( {\theta-0.5{\theta ^2}T{\prime ^*}} \right)} \right] + \\ \frac{1}{2}\left[{\left( {{C_1}-{C_2}} \right)\left( {\left( {Q + {q^*}} \right)T{\prime ^*} + \left( {Q-{q^*}} \right){T_0}} \right) + 2{C_2}QT} \right] + \\ \frac{{\lambda P}}{2}\left[{\left( {Q + {q^*}} \right){\sigma _1}T{\prime ^*} + \left( {Q-{q^*}} \right){\sigma _1}{T_0}-\left( {Q + {q^*}} \right)\left( {1 + {\sigma _1}{T_0}} \right){\sigma _0}\left( {T{\prime ^*}-{T_0}} \right)} \right] \end{array} \right]$ | (11) |
同样,考虑到解押批次n取值的整数约束,应满
从以上三种解押方式的总成本函数表达式可以看出,要直接比较其总成本大小是困难的,现给出如下决策方法。
命题2:给定外生变量,若TCi=Min{TC1, TC2, TC3},其中i=1, 2, 3,则TCi为融资企业解押存货的最低总成本函数值,第i种解押方式为最佳存货解押方式。
证明:由于融资企业将存货解押的总成本作为决策解押方式的唯一考虑因素,因此当TCi的值在三种解押方式中最小时,融资企业必选择第i种解押方式。
四、 数值算例融资企业面临着存货解押的决策问题,相关的参数如下:需要解押的存货数量为Q=60 000千克;金融机构授信期限T=10个月;融资企业在T0=4个月时获得一笔充足的资金,因此有能力去解押全部存货,当然融资企业也可以选择将这笔资金存入金融机构获取利息收益;存货的市场销售价格为P=10元/千克;每次运输的固定成本为2 000元,变动成本为k=0.5元/千克;金融机构按照存货市场价值的60%赋予融资企业贷款,即λ=0.6;存货在融资企业仓库及3PL企业仓库的自然损耗率皆为θ=0.01;存货在3PL企业仓库的单位存储成本为C1=0.10元/月,存货在融资企业仓库的单位存储成本为C2=0.08元/月;金融机构的贷款月利率为I1=0.6%,融资企业自有资金的存款月利率为I0=0.3%。
(一) 总成本计算将上述外生变量分别带入三种解押方式的总成本函数进行计算,求解过程如下:
授信期末一次解押时,有TC1=104 115元。
授信期内分批解押时,有最优解押数量q*=34 912千克,故n=1或n=2。取n=1时,TC2=104 115元;取n=2时,TC2=103 161元。故取TC2=103 161元。
授信期内提前解押时,解得
比较三种解押方式的总成本,可知TCi=Min{TC1, TC2, TC3}=92 264元,即授信期内提前解押的总成本最小,融资企业选择第3种存货解押方式。
(二) 敏感性分析上一节通过具体算例演示了三种解押方式的总成本求解过程并对其进行了比较,本节将进一步分析相关外生变量发生变化时对三种解押方式总成本的影响方式。图 2-图 9考察了相关外生变量值分别变化-50%、-25%、0%、+25%、+50%时三种解押方式的总成本变化情况。
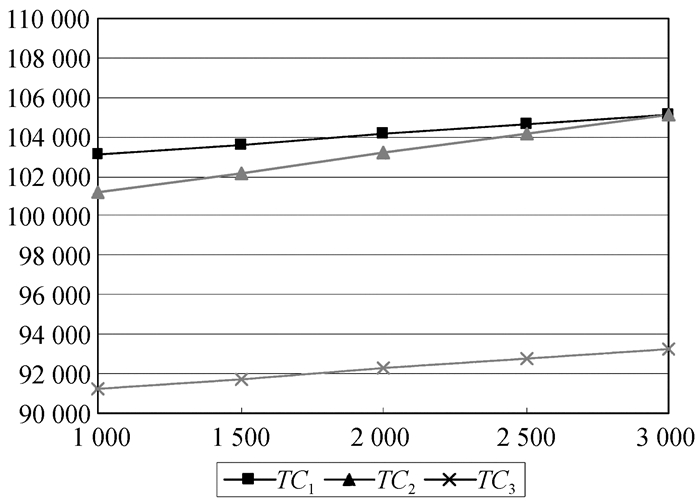
|
图 2 F对三种解押方式总成本的敏感性分析 |
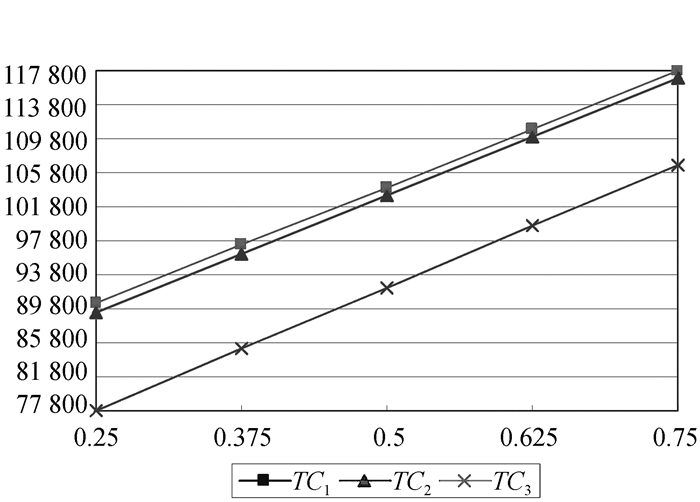
|
图 3 k对三种解押方式总成本的敏感性分析 |
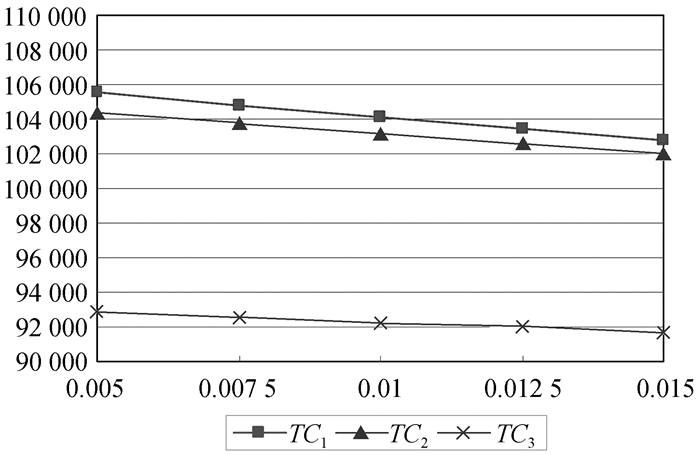
|
图 4 θ对三种解押方式总成本的敏感性分析 |
|
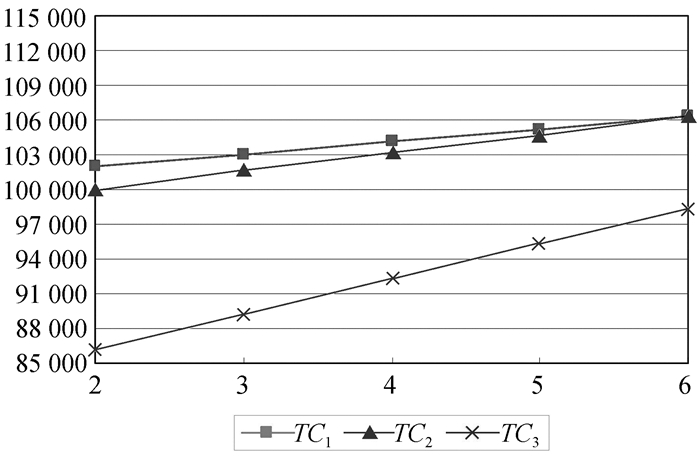
图 5 T0对三种解押方式总成本的敏感性分析 |
|
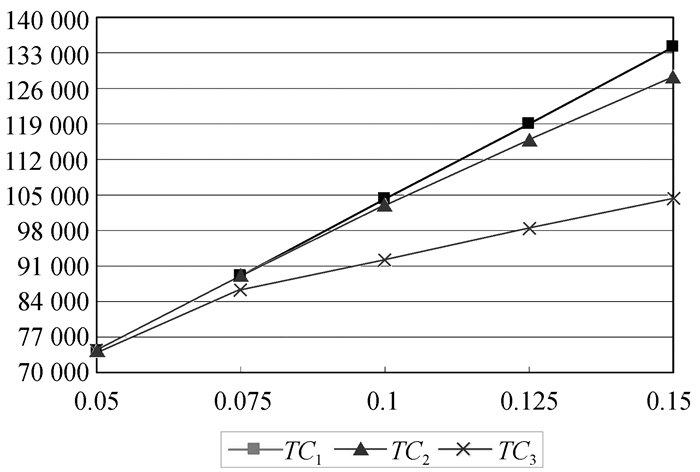
图 6 C1对三种解押方式总成本的敏感性分析 |
|
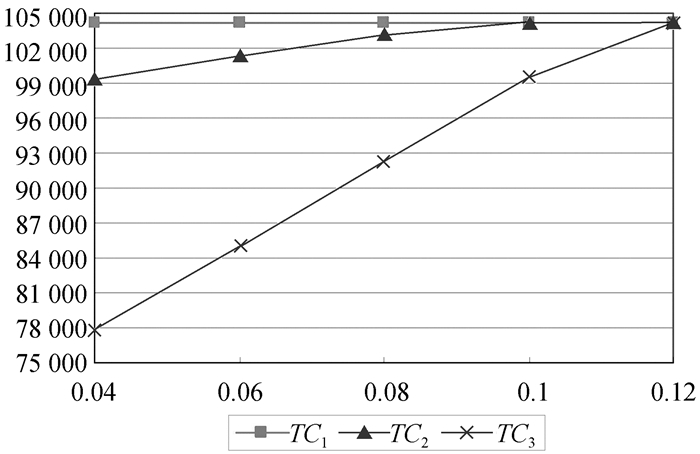
图 7 C2对三种解押方式总成本的敏感性分析 |
|
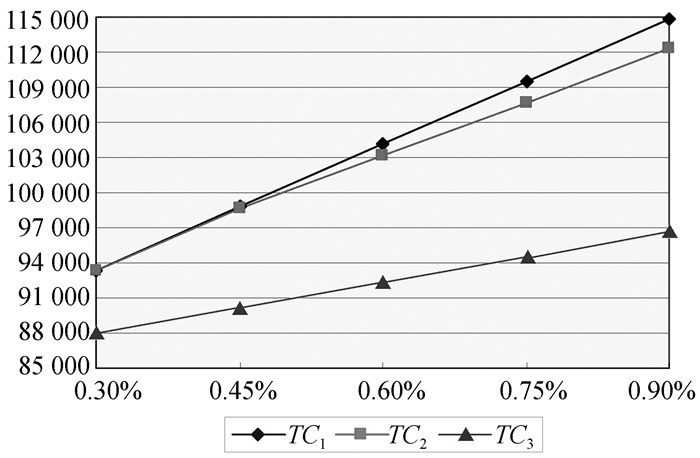
图 8 σ1对三种解押方式总成本的敏感性分析 |
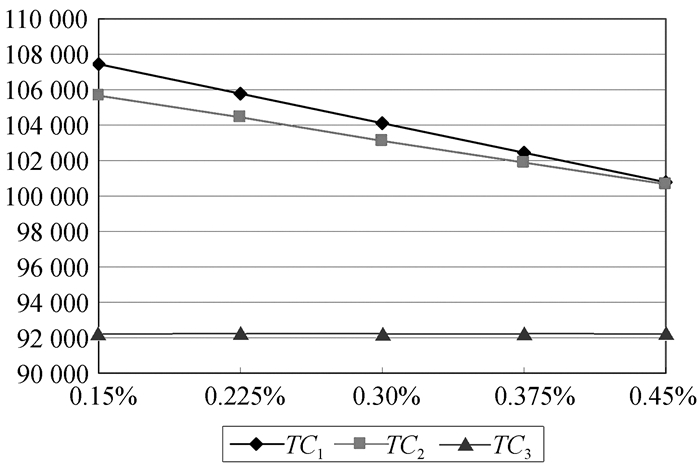
|
图 9 σ0对三种解押方式总成本的敏感性分析 |
从图 2中可以看出,随着每次运输的固定成本F的增加,三种解押方式的总成本都在增加,但是授信期内提前解押的总成本TC3远小于授信期末一次解押的总成本TC1和授信期内分批解押的总成本TC2;另外,由于每次运输固定成本F的增加,授信期内分批解押的最优解押数量也逐渐增加,在存货质押数量不变的条件下,解押的批次n不断减少,当F增加到一定值时,授信期内分批解押方式转化为授信期内一次解押方式。
从图 3中可以看出,随着存货运输单位变动成本k的增加,三种解押策略的总成本随之增加,授信期内提前解押的总成本TC3明显小于授信期末一次解押的总成本TC1和授信期内分批解押的总成本TC2,且差值基本上维持在12 000元左右。
从图 4中可以看出,随着存货的自然变质率θ的增加,三种解押方式的总成本都在逐渐减小,并且授信期内提前解押的总成本TC3远小于授信期末一次解押的总成本TC1和授信期内分批解押的总成本TC2,但其差值有逐渐变小的趋势。之所以三种解押方式的总成本发生下降,是因为随着自然变质率θ的增加,在3PL企业仓库存储期间发生损耗的存货增加,导致存货运输的总变动成本下降引起的。
从图 5中可以看出,随着融资企业有充足资金的时间始点T0的增加,三种解押方式的总成本都在增加,并且授信期内提前解押的总成本TC3随T0增加而增加的速度最快,三种解押方式的总成本差值逐渐变小,可以想象的是,当T0=T时,授信期内分批解押方式和授信期内提前解押方式完全蜕化为授信期内一次解押方式。
从图 6中可以看出,当存货在3PL企业仓库的单位库存成本C1较小时,三种解押方式的总成本并无区别,这是因为存货存储在3PL企业仓库具有优势,因此,即便融资企业有三种解押可供选择时,也会选择在授信期末一次解押存货。然而,随着C1的逐渐增加,三种解押方式的总成本也开始增加,但是授信期内提前解押的总成本上升速度较前两者要小,使得授信期内提前解押方式越来越优于前两者。
从图 7中可以看出,当存货在融资企业的单位库存成本C2较小时,存货存储在融资企业仓库的库存成本要小于存储在3PL企业仓库,因此,融资企业倾向于将存货提前解押存储于自己的仓库,这时授信期内提前解押方式的成本优势非常明显。随着C2的增加,这种成本优势逐渐丧失,当C2增加到某一特定值时,三种解押方式趋于一致,随后,提前解押方式的总成本将进一步增加,并超过其他两种解押方式的总成本。
从图 8中可以看出,当贷款月利率σ1较小时,授信期末一次解押方式与授信期内分批解押方式并无差异,而授信期内提前解押的总成本最小。随着σ1的增加,三种解押方式的总成本形成差值,且两两之间的差值越来越大。这是因为σ1值越大,存货在3PL企业仓库的平均存储量越多,融资企业支付给金融机构的利息就越多,因此,三种解押方式的总成本差值也就逐渐变大。
从图 9中可以看出,随着存款月利率σ0的增加,授信期末一次解押与授信期内分批解押的总成本逐渐下降并趋于一致,但是授信期内提前解押的总成本始终维持在一个较低的水平,而不受σ0变化的影响。这是由于在此种情形下,融资企业的最佳解押方式是在T0时刻解押所有的存货,因此并没有从金融机构获得任何存款利息。
五、 结束语不同的存货解押方式会产生不同的解押成本,因此融资企业需要决策最佳存货解押方式以最小化自己的融资成本。本文从融资企业的角度出发,考虑存货解押的总成本由运输成本、库存成本及利息成本三部分构成,分别建立融资企业在授信期末一次解押、授信期内分批解押、授信期内提前解押三种情形下的总成本函数,并给出每种解押方式的最优解押数量及最优解押批量表达式,通过数值算例对三种解押方式的总成本进行比较,敏感性分析呈现出相关外生变量的变化对三种解押方式总成本的影响方式。
自然损耗率θ可指存货重量、数量、效用及价值等的损耗,其取值可以体现不同类型存货的特点,如取θ=0,可视为没有存储损耗的一般物品;取θ < 0,可视为易变质品或易腐品;取θ>0,可视为存储期间改良效果大于变质影响的改良品。
通过敏感性分析可知,三种解押方式的总成本大小很大程度上取决于相关外生变量的取值,因此,融资企业在面临存货解押方式的选择问题时,应结合外生变量的取值情况,经过科学合理的计算,才能作出最佳决策。
| [1] | 陈祥峰, 石代伦, 朱道立. 融通仓与物流金融服务创新[J]. 科技导报, 2005, 23(9): 30–34. |
| [2] | 冯耕中. 物流金融业务创新分析[J]. 预测, 2007, 26(1): 49–54. |
| [3] | 李毅学, 冯耕中, 屠惠远. 供应链金融创新中下侧风险规避银行的贷款额度分析[J]. 系统科学与数学, 2009, 29(11): 1552–1558. |
| [4] | 李毅学, 冯耕中, 徐渝. 价格随机波动下存货质押融资业务质押率研究[J]. 系统工程理论与实践, 2007, 27(12): 42–48. |
| [5] | JOKIVUOLLE E, PEURA S. Incorporating collateral value uncertainty in loss given default estimates and loan-to-value ratios[J]. European Financial Management, 2003, 9(3): 299–314. DOI: 10.1111/eufm.2003.9.issue-3 |
| [6] | COSSIN D, HRICKO T. A structural analysis of credit risk with risky collateral:A methodology for haircut deter mination[J]. Ecomomic Notes, 2003, 32(2): 243–282. DOI: 10.1111/ecno.2003.32.issue-2 |
| [7] | COSSIN D, HUANG Z J, AUNON N D.A frame work for collateral risk control determination[R].Working paper, European central bank working paper series, 2003(1):1-47. |
| [8] | HE J, JIANG X L, WANG J, et al. VaR methods for the dynamic impawn rate of steel in inventory financing under auto-correlative return[J]. European Journal of Operational Research, 2012, 223(1): 106–115. DOI: 10.1016/j.ejor.2012.06.005 |
| [9] | 何娟, 蒋祥林, 朱道立, 等. 供应链融资业务中钢材质押贷款动态质押率设定的VaR方法[J]. 管理工程学报, 2012, 26(3): 129–135. |
| [10] | 陈云, 刘喜, 杨琴. 基于清算延迟和流动性风险的供应链存货质押率研究[J]. 管理评论, 2015, 27(4): 197–208. |
| [11] | 张云丰, 王勇. 损失额视角下多存货组合质押融资决策研究[J]. 金融理论与实践, 2014(8): 57–60. |
| [12] | 齐二石, 马珊珊, 韩铁. 组合仓单质押贷款质押率研究[J]. 西安电子科技大学(社会科学版), 2008, 18(6): 50–53. |
| [13] | 孙朝苑, 韦燕. 双品类存货组合的质押率研究[J]. 财经科学, 2011(10): 117–124. |
| [14] | 匡海波, 张一凡, 张连如. 低碳港口物流质押贷款组合优化决策模型[J]. 系统工程理论与实践, 2014, 34(6): 1468–1479. |
| [15] | 匡海波, 张一凡, 张连如. 低碳港口物流质押贷款利率定价理论和模型[J]. 中国管理科学, 2014, 22(12): 1–10. |
| [16] | 张云丰, 王勇. 统一授信模式下存货组合与循环质押融资决策[J]. 重庆大学学报(社会科学版), 2015, 21(2): 92–98. |
| [17] | HWANG H S. A study on inventory model for items with Weibull ameliorating[J]. Computers and Industrial Engineering, 1997, 33(3/4): 701–704. |
| [18] | GHARE P M, SCHRADER G H. A model for exponentially decaying inventory system[J]. International Journal of Production Research, 1963, 14(4): 238–243. |
| [19] | 张钦红, 骆建文. 不对称信息下易腐物品供应链最优数量折扣合同研究[J]. 系统工程理论与实践, 2007, 27(1): 23–28, 35. |
 2016, Vol. 22
2016, Vol. 22

