2. 济南大学 商学院, 山东 济南 250022
2. School of Business, University of Jinan, Jinan 250022, P. R. China
寻找关注城市和区域联动发展的经典理论,即中心—外围理论 (Core and Periphery Theory),发现中国区域与城市经济体系结构与世界格局相似,只不过是尺度空间范围可以缩小到城市,全国和局部都存在着中心城市。借助于经典理论解释中国城市体系格局演变捉襟见肘,要想建构本土理论必须找到分析对象。统一大国分治,既依赖于行政区,又分设不同行政层级的城市,副省级城市的增长模式和中心带动作用尤其不同,广深双城归属于这一类别又同属于广东下辖,广东省域经济已呈现出双中心内核经济增长驱动模式,广州市和深圳市两大中心城市发展并驾齐驱①。再有,政府推动的高铁建设进入红利收获阶段,高铁已经打破了两个城市之间的藩篱,逐渐成为影响区域经济社会发展的关键因素。综观而论,城市间联动发展关系的塑造是城市发展和高铁建设共同作用的结果。不断发达的高铁网络,逐步改变着人们的出行方式选择;不断缩短城市间的时间距离,增进了城市间的空间联动关系。城市群发展大变奏时代,唤起人们重视城市与高铁的关系识别难题。是福还是祸?通盘考虑权衡利弊之后的城市发展之路何处寻?
① 2015年3月,马兴瑞任职深圳市委书记,是15个副省级市中首个“中央委员”书记。
关注城市联动发展的研究始于19世纪末对城市群概念和发展理念开展的一系列研究[1]。中国从20世纪80年代开始对城市群进行探索,关于城市群的研究主要集中于城市群的定义[2]、城市群的联动路径[3]、城市群联动效应的影响因素[4-7],在城市联动效应的影响因素中政府、市场及制度的作用受到重视[8-10]。直至姚士谋和朱英明的研究发现完备的运输网络和现代化的交通工具,尤其是高铁已经成为城市与城市之间的联系紧密度与发展方向的重要影响因素,由此城市群呈现出“一个城市主导、多个城市协作”的发展特征[11]。此外,高铁通过影响人流、物流、信息流等要素的双向乃至多向的流动,实现城市经济要素重新聚集,引致城市群的经济格局发生着潜移默化的改变。高铁时代,城市群再聚将会是区域经济的重要内容,同时也必将带来新的城市格局体系变化。
讨论高速铁路等交通网络体系对区域和城市体系格局的影响,不得不提及“城市带”的概念,其最早由法国著名地理学家Jean Gottman提出,继而被学术界所认可与推崇[12]。交通方式对城市带的推动作用也越来越受到重视[13-15]。城市带内具有严格的等级体系、明确的地域分工、完备的交通建设以及敏捷的通讯工具等重要特质。城市交通方式的推动与创新引致要素集聚与扩散,形成了驱动城市带经济格局不断更迭的机理。还有研究认为,城市带是以现代化交通方式为发展驱动,包涵了经济、政治、社会等多方面、多层次、多领域相融合的带状连续城市实体[16]。
目前,国内外关于高速铁路空间效应的研究,主要从可达性角度[17-19]和从站点周边发展角度出发[20]。从城市经济发展角度,大部分学者注重研究高铁对区域内核心大城市与边缘中小城市发展的不同影响[21-22]。高铁促使区域极化发展还是平衡发展,一直以来都是争论的焦点。随着中国高铁时代到来,国内学者们对高铁对城市及区域、城市及城市群空间结构的影响进行了研究[23-25]。认为高铁是城市空间结构重构的重要原因[26-31]。
纵观现有研究,在高铁打通的城市格局中,过去和现在的竞争与合作关系可能走向破裂。中国未来城市发展及关系走向,很可能因高铁而进行人口与经济的空间重构。因此,哑铃双城共谋发展是大势所趋,城市将在竞争中走向整合。研究该城市带内各城市间的联动效应,对于评估区域中心城市的经济扩展方向、确定各城市的经济扩展方向及企业投资区位的选择都具有重要的实践意义和政策价值。为此,本文将以高铁带动城市区域发展为逻辑论证之起点,测度珠三角城市带广深双城及其对腹地城市的带动效应以及各城市间的联动关系。选题初衷和归宿,通过研究以期对制定城市空间的发展战略,构建合理的城市发展体系,提供理论依据和现实借鉴。
一、特征事实:珠三角城市竞争合作关系 (一) 珠三角城市竞争合作关系识别本文借鉴并修正引力模型,计算得出珠三角各城市之间的经济联系程度指数,以分析珠三角城市间的合作竞争关系。Reilly[32]最早运用引力模型分析地理学研究问题,在随后的研究中,Zipf[33]又运用该模型研究城市间的空间关系,并引起了相关学者的广泛关注。国内相关研究中,引力模型同样被应用于城市间的空间格局关系研究。以往研究中,广泛采用的引力模型为:
| ${{F}_{ij}}=\frac{\sqrt{{{P}_{i}}{{G}_{i}}}\sqrt{{{P}_{j}}{{G}_{j}}}}{D_{ij}^{2}}\frac{\delta y}{\delta x}$ | (1) |
其中,F代表城市间的经济联系量,i和j分别代表城市i和城市j,P为城市的人口规模,G代表城市的地区生产总值,D代表两城市之间的空间距离。
随着当今城市群和城市带的快速发展,传统的引力模型不能有效衡量交通联系紧密的现代化城市间的经济联系程度,因此本文对传统引力模型进行了修正。
由城市群和城市带发展的要素交互作用看,衡量城市与城市间的经济联系程度需考虑下列因素的作用:其一,城市间的交通便捷度,快捷高效的交通,缩短了城市间的空间距离。未来珠三角城际轨道交通布局对交通便捷度的影响更为显著②;其二,城市自身的发展空间,即城市的建成区面积;其三,城市发展的经济基础;其四,城市产业结构的差异性及升级程度。
② 参见:http://zwgk.gd.gov.cn/006939748/201008/P020100810397877969463.jpg。
在综合考量上述影响城市间经济联系程度的因素后,本研究对引力模型进行修正。首先,引入衡量交通发达程度的变量,即用城市间的铁路最快到达时间,来描述两城市的时间距离。用铁路到达时间进行衡量,主要基于以下两方面的原因:一方面,整个珠三角地区铁路里程数占了整个广东省的60%;另一方面,由于珠三角地区铁路的建设,尤其是2011年底高铁通车之后,人们的出行方式发生了显著变化,大部分珠三角居民的出行工具由原来的汽车转变为高铁列车。其次,引入城市建成区面积,以此来衡量城市未来的空间发展格局。再次,用“综合人口”变量,衡量城市人口受教育水平对城市经济联系程度的影响。最后,引入各城市每个产业就业人员占所有产业就业人员总量的比例变量,计算克鲁格曼指数,并将克鲁格曼指数代入引力模型中,以衡量产业优化升级程度对城市联系程度的影响。修正后的公式为:
| ${{F}_{ij}}={{K}_{ij}}\frac{\sqrt[3]{{{S}_{i}}{{P}_{i}}{{G}_{i}}}\sqrt[3]{{{S}_{j}}{{P}_{j}}{{G}_{j}}}}{{{D}_{ij}}{{d}_{ij}}}$ | (2) |
| ${{Z}_{ij}}=\frac{{{F}_{ij}}}{{{F}_{\min }}}$ | (3) |
其中,F代表城市间的经济密切度即联动效应,i和j分别表示城市i和城市j,K表示克鲁格曼指数,S表示城市建成区面积,P表示城市的“复合人口”数,G表示城市的GDP,
其中,克鲁格曼指数为:
| ${{K}_{ij}}=\sum\limits_{t=1}^{n}{\left| \frac{{{q}_{ic}}}{{{q}_{i}}}-\frac{{{q}_{jc}}}{{{q}_{j}}} \right|}$ | (4) |
式中,K表示克鲁格曼系数,i和j分别表示城市i和城市j,c表示城市的产业,qic和qjc表示城市i和城市j第c产业的从业人数,qi和qj表示城市i和城市j所有产业部门总的就业人数,n为全部的产业数。
“综合人口”公式设定为:
| $p=\sum\limits_{\alpha =1}^{n}{{{E}_{\alpha }}\times {{Q}_{\alpha }}}$ | (5) |
其中p为“综合人口数”。Eα是第α种学历的人口数,Qα为Eα的权重,n为总人口数,参照赵雪雁等[34]的做法,根据变异系数法并结合专家打分法,给不同学历程度的人口赋予权重,按照受教育程度由低到高分别将权重设置为0.23、0.21、0.23、0.33,以衡量小学及以下、初中、高中、大学及以上四个层次文化程度人口数对综合人口数的影响。
本文参照苗长虹和王海红[35]的做法,采用城市联动效应占所考察范围内全部城市联动效应之和的比例大小,来确定城市间的经济联系方向。设定经济联系隶属度公式为:
| ${{R}_{ij}}={{F}_{ij}}/\sum\limits_{j=1}^{n}{{{F}_{ij}}}$ | (6) |
上式中,R表示城市经济隶属度。
采用2014年度的不同层次的受教育人口数、地区生产总值、城市中各产业的从业人口数、市区建成面积等变量,分别利用公式 (3) 和公式 (6) 检验城市间的联动效应指数和经济隶属度,数据来源于《城市统计年鉴》和《中国城市发展报告》。结果分别如表 1和表 2所示。由表 1的结果可以得出珠三角城市间的联动效应指数最大的为广深之间,表明广州和深圳表现出显著的双城联动效应,其他城市之间的经济联系指数基本符合“广佛肇”“深莞惠”“珠中江”经济圈的特征。表 2展示了主要城市的隶属度关系值,此测算结果也验证了珠三角城市间的发展符合“广佛肇”“深莞惠”“珠中江”城市经济圈空间格局的存在性。此联系表还能够给出样本城市的位序特征描述,也即广州和深圳两市的中心地位。再就是,腹地城市与中心城市之间的联系性强弱排序,而且,联系强度与地理空间距离的远近高度相关。
| 表 1 珠三角城市间联动效应指数及高铁日班次数 |
| 表 2 2014年珠三角各城市间的经济隶属度 |
为对表 1的结果进行比较检验,本文参照周靖祥[25]的做法,通过“去哪儿”网站查询得到各个城市间的日发高铁班次,检验高铁的交通便利程度与城市之间联系强度的关系。经检验发现,城市间的经济联系强度和高铁日发班次之间的系数为0.86,表明城市之间的经济联系强度和日发班次是正向关系,证明本文修正后的模型能较准确地描述城市间的经济联系强度。由经济隶属度表可以得出这样的判断:城市群中的要素 (尤其是劳动力) 基本流向了广州、深圳这两个核心城市,它们的城市发展水平明显高于区域内其他城市;而处于边缘地位的惠州、中山、江门、肇庆等城市间的发展程度却处于相对较低水平。
(二) 广深双城腹地区域城市组展开识别需要找到理论基础,这就是城市边界的确立。1949年Converse在Reilly的“零售引力法则”的基础上,把相邻两城市间吸附力的平衡点定义为断裂点,提出“断裂点”理论。在此后的一系列研究中,“断裂点”理论被广泛应用于衡量城市的辐射能力。“断裂点”理论的公式为:
| ${{D}_{A}}=\frac{{{D}_{AB}}}{1+\sqrt{{{P}_{B}}/{{P}_{A}}}}或者{{D}_{B}}=\frac{{{D}_{AB}}}{1+\sqrt{{{P}_{A}}/{{P}_{B}}}}$ | (7) |
其中DA和DB分别表示断裂点到城市A和到城市B的距离,DAB是城市A与城市B之间的直线距离,PA和PB分别表示城市A和城市B的人口量。
然而,上述断裂点理论在衡量现代中心城市的辐射效应时存在一定的局限性。其一,现代社会中,发达的交通基础设施网络缩短了城市间的实际距离,尤其是高铁已经重塑中国城市体系格局,时间距离代替了空间距离③。因此,城市之间的距离不能再单纯地采用城市之间的直线距离表示。其二,单纯的城市人口规模也不能衡量一个城市的质量和经济辐射能力。
③ 中山大学地理科学与规划学院教授袁奇峰接受《华夏时报》记者采访时的观点。
鉴于上述两个方面的局限性,本文对“断裂点”理论的公式进行了修正:一方面,用时间距离替代城市间的空间距离,衡量时间距离对地理距离的缩短效应;另一方面,将采用上文公式 (2) 中的3SPG表示城市综合质量,即用城市面积、“复合人口”数和地区生产总值来衡量城市的综合质量。
修正后的公式为:
| ${{D}_{A}}=\frac{{{d}_{AB}}}{1+\sqrt{{{P}_{B}}/{{P}_{A}}}}或者{{D}_{B}}=\frac{{{d}_{AB}}}{1+\sqrt{{{P}_{A}}/{{P}_{B}}}}$ | (8) |
其中,dA和dB分别表示断裂点到城市A和到城市B的时间距离,dAB是城市A与城市B之间的时间距离,pA和pB分别表示城市A和城市B的综合质量。
本部分的宏观数据如2014年度的不同层次的受教育人口数、地区生产总值、城市中各产业的从业人口数、市区建成面积等均来自于各城市的《城市统计年鉴》或《中国城市发展报告》,城市间的直线距离为在电子地图上直接量取,其中高铁的发车车次、时间等信息均取自“去哪儿”网站。
根据修正的断裂点公式 (8),得出中心城市在不同方向上的断裂点的时间距离,并据此确定城市的辐射范围。广州和深圳的经济断裂点计算结果如表 3所示。
| 表 3 广州和深圳与珠三角其他城市的断裂点 |
由断裂点公式的计算结果得出,广州和深圳的时间距离最短,广深之间的断裂点离深圳的时间距离较短,表明广深之间的双城联动效应带动了城市联系平衡点向深圳方向移动。对于广州作为核心城市而言,其对佛山、东莞的辐射力最大,这三个城市可以被看成一个以广州为首的核心都市区。然而,以深圳作为核心城市而言,其对东莞、惠州的辐射力最大,因此,深圳、东莞、惠州也可以被看成一个以深圳为首的核心都市区。而珠海、中山、江门、肇庆等处于两大核心都市区的外围,两大核心城市对这些城市的辐射力均比较薄弱。
二、理论框架及计量模型 (一) 理论框架 1. 双核理论查阅中文文献发现,经济地理学家陆玉麒在1998年就已经提出了“双核理论”[36],其主要内容是指在某一区域内由区域中心城市和港口城市及其连线所组成的一种空间结构现象,或是由区域中心城市与边缘城市组合而形成的一种空间结构现象。“双核”空间结构结合了中心城市的中心性和港口城市的边缘性,在空间功能上为互补关系,逐渐成为众多空间结构模式中比较高效的类型。
近年来,广州和深圳两市的“双核”结构呈现出快速发展的趋势。2014年广州地区生产总值为1.66万亿元,增长速度达到8.5%。2014年,深圳市地区生产总值达1.6万亿元,继续居于内地大中城市第四位;2014年深圳市生产总值增长约10%,高于全国、全省平均增速,提前一年完成1.5万亿元的“十二五”规划目标;人均GDP约2.4万美元,比2009年增加1万美元,居内地副省级以上城市首位。广州市、深圳市创造的经济总量已占广东省的半壁江山,创造的财政收入接近广东省的60%,极化作用相当突出,成为领跑广东现代化建设名副其实的“领头羊”。这种“双核结构模式”符合区域经济发展的规律。用马克思主义哲学观点来看,就是抓主要矛盾。通过解决主要矛盾,带动次要矛盾的解决;通过一个重点地区的发展,带动一个片区的发展。
2. 双核理论的拓展双核城市结构最早出现于港口城市和中心城市,但随着现代化交通网络的发展,双核城市也出现于交通便捷的区域。归其原因:现代化的交通运输方式加强了城市间的联系,交通的便捷性成了形成双核结构的一个重要因素。在本文的研究中,随着中国高速铁路这一现代化快速交通方式的发展,广州和深圳作为高铁建设的重点城市,显著表现出双核城市的特点,高铁时代背景下,广深双城已经步入了资源快速共享,在竞争与合作中寻求发展,并对周围城市形成有效辐射效应,带动周边城市发展,加速了珠三角区域的一体化步伐。
3. 本文对双核理论的有益改进以往的双核结构的研究中往往对铁路交通的作用没有足够重视,广州和深圳两市之间的密切联系与高度发达的“高铁”网络有着不可分割的关系。因此,本文对传统的双核理论进行了拓展,并将给出高铁背景下的双核结构分析内容,重点关注高铁发展对广深双城联动效应,以及如何改变着珠三角地区城市的联动效应及其与广深双核的联系。
传统的双核结构早期更多地注重一个省会城市和一个港口城市的结合,而广州和深圳这个城市不仅满足一个为省会城市一个为港口城市的条件,重要的是广州和深圳也同时是国内的两大一线城市,两个一线城市的双核结构成为一个值得研究的问题。再就是,把省会城市定义为中心城市,而港口城市为边缘城市,注重中心城市对边缘城市的带动作用,忽略了两个城市的联动效应,而广州和深圳这两个城市的发展已经突破了一个是中心城市一个是边缘城市的范畴,且最近的相关研究报道指出,深圳大有超越广州的势头,未来中国一线城市的排名会变成为“北上深广”,因此研究广州和深圳这样两个具有特性的城市的联动效应对双核理论产生的影响,变得更有意义。
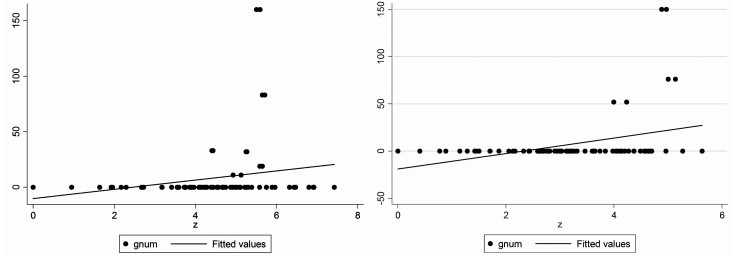
经改进之后,结合图 1的简单特征事实描述图,本文将作以下判断给以证明。
|
图 1 高铁和城市联系指数的关系 (左图为广州,右图为深圳) 资料来源:笔者绘制。 |
其一,高速铁路的开通强化了广州和深圳之间的双城联动效应。
其二,高速铁路对广深双城的腹地城市也起到极强的联动效应,尤其使得广州和深圳对腹地城市的辐射效应增强。
(二) 计量模型设定及数据说明 1. 计量模型构建为考察高铁对城市之间的联动效应,以引力模型为基准,作线性变换之后,根据面板数据结构特征将模型设定如下:
| $\begin{align} & \ln {{Z}_{\text{i}t}}={{\beta }_{0i}}+{{\beta }_{1}}\ln e{{m}_{\text{i}t}}+{{\beta }_{2}}\ln po{{p}_{\text{i}t}}+{{\beta }_{3}}\ln L.po{{p}_{\text{i}t}} \\ & +{{\beta }_{4}}\ln gd{{p}_{\text{i}t}}+{{\beta }_{5}}\ln inves{{t}_{\text{i}t}}+{{\beta }_{6}}\ln valu{{e}_{\text{i}t}}+ \\ & {{\beta }_{7}}{{X}_{\text{i}t}}+{{\beta }_{8}}ydu{{m}_{\text{i}t}}+{{\beta }_{9}}T+{{\varepsilon }_{\text{i}t}} \\ \end{align}$ | (9) |
在式 (9) 的城市联动效应方程中,i表示城市,包括了珠三角的广州、深圳、佛山、东莞、珠海、中山、江门、肇庆和惠州,t表示时间,本文的样本区间为1990-2014年。其中Z表示城市间的联动效应指数。模型的先决变量为em,代表第三产业就业人口。模型的内生变量包括:pop代表人口总量,gdp为城市的地区生产总值,invest代表城市的固定资产投资规模,value代表第二产业的增加值。其中X为方程的控制变量,包括了城市间的高铁班次数Gnum、普通铁路火车班次数Pnum以及城市间的高速公路里程数way。由于广州和深圳之间2011年12月26日高铁开始通车,为检验高铁对城市联动效应的影响,设置了年份虚拟变量ydum,将2011年之前无高铁的年份设置为0,2011年高铁开通后的年份设置为1。
在公式 (9) 中,若与城市联动效应相关的变量产生变动,如存在交通便利程度的外在冲击、投资规模的变化、人口和就业人员产生变动时,城市间的联动效应就会偏离稳态水平,为重新达到均衡状态,需要在计量方程中引入城市联系指数的滞后项。
由于数据具有横截面和时间序列因素,本文研究中的城市联动效应模型的一般动态预测方程形式为:
| $\begin{gathered} \ln {Z_{i{\text{t}}}} = {\beta _{0i}} + {\beta _1}\ln {Z_{i{\text{t}} - 1}} + {\beta _2}\ln e{m_{i{\text{t}}}} + {\beta _3}\ln po{p_{i{\text{t}}}} + {\beta _4}\ln L.po{p_{i{\text{t}}}} \hfill \\ + {\beta _5}\ln gd{p_{i{\text{t}}}} + {\beta _6}\ln inves{t_{i{\text{t}}}} + {\beta _7}\ln valu{e_{i{\text{t}}}} + {\beta _8}{X_{i{\text{t}}}} + {\beta _9}ydu{m_{i{\text{t}}}} \hfill \\ + {\beta _{10}}T + {\varepsilon _{i{\text{t}}}} \hfill \\ \end{gathered} $ | (10) |
需注意的是,该公式假定解释变量对不同城市的影响是相同的。为方便起见,将式 (10) 中估计方法简单说明如下:将模型中的全部变量去除时间均值,从而去除时间趋势项,城市联动效应方程进行差分以去除各地区的固定效应特征,动态方程变为:
| $\begin{gathered} \Delta \ln {Z_{i{\text{t}}}} = {\beta _1}\Delta \ln {Z_{i{\text{t}} - 1}} + {\beta _2}\Delta \ln e{m_{i{\text{t}}}} + {\beta _3}\Delta \ln po{p_{i{\text{t}}}} + {\beta _4}\Delta \ln L.po{p_{i{\text{t}}}} \hfill \\ + {\beta _5}\Delta \ln gd{p_{i{\text{t}}}} + {\beta _6}\Delta \ln inves{t_{i{\text{t}}}} + {\beta _7}\Delta \ln valu{e_{i{\text{t}}}} + {\beta _8}\Delta {X_{i{\text{t}}}} + {\beta _9}\Delta ydu{m_{i{\text{t}}}} \hfill \\ + {\varepsilon _{i{\text{t}}}} \hfill \\ \end{gathered} $ | (11) |
本文所用的城市面板数据变量如下:第三产业就业人口、人口总量、地区生产总值、固定资产投资规模、第二产业增加值。这些数据均取自各期《城市统计年鉴》和《城市统计公报》。其中,高铁和普特的车次信息根据“去哪儿”网站和中国铁路客户服务中心官方网站查询整理获得,本文所用城市实际客运车次数据均来自“去哪儿”网站和中国铁路客户服务中心官方网站,这两个网站提供了铁路客运车次的站点信息和线路信息④。站点信息包括车站的始发、途经和终到车次,线路信息在选择出发地和到达地后,可以显示两地之前所有的始发、过路和终到车次。在统计城市站点和城市间客运车次数据时,依据车类型 (G、C、D、Z、T、K和其他字母开头) 进行分类,以区分不同车次类型在城市联系中的重要程度。高速公路里程数根据广东省高速公路官方网站数据整理获得,各变量的基本统计量如表 4。
④ 数据查询时间:2015年4月20日至5月20日之间。
| 表 4 变量基本统计量 |
本部分中以公式 (11) 为初步分析的计量模型,采用面板动态差分方法进行检验,在运用面板动态差分方法进行回归时,由于滞后因变量和残差项中不可观测的固定效应具有相关性,滞后因变量的系数会因差分而产生有偏估计,因此,本文参照Arellano和Bond[37]的方法,用内生变量的滞后1期项和滞后2期项作为自身的工具变量。若差分方程的二阶和更高阶不存在序列相关问题,计量模型便可得出无偏一致估计结果。在初步回归分析阶段,运用一阶差分GMM方法估计模型,为检验工具变量是否存在过度识别问题,本文以Sargan/ Hansen检验来进行判定。为检验工具变量选择的合理性,因而进一步检验模型中差分后的残差项之间是否存在的二阶序列相关性。表 5分别报告了广州 (模型①) 和深圳 (模型②) 的城市联动效应估计结果,各模型估计结果中,Sargan/Hansen检验p值为1.000,不能拒绝工具变量选择满足过度识别约束条件,因此可以判定不存在工具变量的过度识别问题。残差项也不存在二阶自相关问题,表明模型中工具变量的选择具有合理性。表 5报告了方程 (11) 的估计结果。
| 表 5 一阶差分GMM (two-step) 估计结果 |
本文重点关注高速铁路对广州和深圳双城联动效应及广深对腹地城市的联动效应。模型①中高铁班次系数为0.022,模型②中高铁班次变量系数为0.037,且都在1%的显著性水平下显著。表明高速铁路的开通运营对广州和深圳的双城联动效应起到了显著的促进作用,且通过其中心城市的地位将这种联动效应辐射到其腹地城市。同样代表交通便捷因素的普通班次变量和高速公路里程变量对城市的联动效应均表现为显著正向影响。高铁开通年份虚拟变量的系数显著为正。通过高铁、普通列车班次变量、高速公路里程变量及高铁开通年份虚拟变量这一系列代表交通便捷度变量的检验,表明以高铁为先锋的便利交通运输网络,对广州和深圳的双城联动及其与腹地城市的联动效应起到了显著的推动作用,高铁作为一个推动城市体系格局重组的重要要素必须引起充分重视与关注。
由表 5的检验结果可知,上一期的城市联系指数的系数为正,且在1%的显著性水平下显著,前期联系越紧密的城市之间会有一个连续的惯性效应,从而当期的城市联动效应指数会增加。第三产业就业人口系数为正向显著,表明城市中第三产业的发展及就业人员的增加,提升了城市的联动效应。城市的人口总量和城市人口总量的滞后项对城市的联动效应均呈正向影响,这可能与广州和深圳的人口密度有关,广州和深圳都是中国人口密度较大的城市,前一期的人口总量对当期的城市联动效应产生正向的作用惯性,从而呈现为正向效应。地区生产总值和第二产业的增加值对城市的联动效应表现出显著的正向效应,表明经济发展水平越高,城市间的联动效应越强,城市间的联动效应呈现出强—强联合的发展趋势,第二产业的增加值的正向效应是由于在广州和深圳两个城市的经济发展中第二产业为占主导地位的产业,表现出强劲的拉动城市联动效应的作用。城市的投资规模对城市联动效应则表现为负向影响,这可能是由于城市的投资增加时,各城市会专注于自身的建设,对城市间的联动起到负向影响。
有两个问题会导致模型 (11) 在估计中产生有偏估计。其一是城市联动的惯性,这可能会引起一阶序列相关的误差。其二,人口、地区生产总值、固定资产投资和第二产业增加值都是潜在内生变量[38]。若采用OLS方法对包含因变量滞后项的面板模型进行估计,会产生有偏和不一致的结果。因此,为得出无偏一致估计结果,本文借鉴Blundell和Bond[39]的处理方法,运用系统GMM方法进行估计。为解决内生性问题,本文决定引用人口、地区生产总值、固定资产投资和第二产业增加值的一期、二期和三期滞后项分别作为人口、地区生产总值、固定资产投资和第二产业增加值的工具变量。系统GMM估计结果如表 6所示。
| 表 6 系统GMM (one-step) 估计结果 |
由表 6的系统GMM估计结果显示,变量的估计结果与表 5一阶差分估计时的基本估计结果在符号上保持一致,只是在系数的大小上略有差异。从本文重点关注的高铁变量系数看,高铁对广州联动效应的影响系数由表 5的0.022增加至0.026,可能由于表 5模型①中差分GMM的有偏估计造成了对估计系数的低估。而从深圳市高铁的变量系数看,系数由表 5的0.037增加至0.054,表明在表 5模型②中存在对高铁变量的低估。
(二) 稳健性讨论为检验上述计量估计结果的稳健性,依据客运车次数及相应权重构建城市联系指数,相应的指数的构建和具体测度方法参见周靖祥[25]的方法,沿用此方法计算广州和深圳与各城市之间的联动指数,并将其作为因变量进行检验。检验结果分别见表 7和表 8。
| 表 7 一阶差分GMM (two-step) 稳健性检验估计结果 |
| 表 8 系统GMM (one-step) 稳健性检验估计结果 |
依旧重点关注高铁变量结果的变化。从表 7的估计结果可知,由依据客运车次数及相应权重构建城市联系指数,带入模型 (11) 进行一阶差分GMM检验,得出的结果比表 5和表 6中依据修正引力模型得出的城市联系变量代入模型 (11) 时有显著增加。在表 7中,高铁变量系数在广州模型中为0.036,在深圳模型中为0.058,且均在1%的显著性水平下显著。表明在用交通衡量城市联动效应时,高铁的作用得到了充分体现。为增强城市间的联动效应,应加强交通网络的建设,尤其是高速铁路的建设。
由表 8中依据客运车次数及相应权重构建城市联系指数,带入模型 (11) 进行系统GMM检验,模型①和模型②高铁变量的系数分别由表 7中的0.036和0.058增加为表 8中的0.042和0.067,且均在1%的显著性水平下显著。表明表 7中一阶差分GMM估计方法下存在对变量的低估。
由稳健性检验结果看,其他各变量的符号均和基本检验时结果一致,只是系数的大小发生了变化,故表明本文的检验结果具有稳健性。
四、结论及启示中国高铁的发展改变了城市的格局,本文采用城市宏观数据与高铁微观数据考察了广州和深圳的双城联动效应及广深对其他城市的辐射效应,重点关注了高铁的作用。在修正引力模型的基础上,通过扩展双核和断裂点理论,借助城市经济数据测算广深双城的联动效应;并与基于铁路运行车次数据的测算结果进行比对,虽采取不同算法,城市关系及位序法则却保持着一致性。测算结果证实,中心城市的辐射效应表现为地域相邻指向性,各城市的联系方向表现为中心城市指向性。进一步地,将1990年至2014年城市面板数据与高铁通行微观数据进行匹配,重点考察广州和深圳的联动效应及广深双城的辐射效应,测度高铁开通带来的城市联动效应。结果表明:高铁强化了珠三角城市间的联动效应,并且使得广深的辐射效应逐步增强,普通铁路和高速公路的增长效应也十分明显,当使用铁路列车班次并赋予权重计算的城市联系指数进行再检验,该实证结果仍然稳健。其中,能够增强城市联动效应的其他因素包括:第三产业就业、人口规模、地区生产总值和第二产业的增加值,而齐头并进的城市投资规模扩张并不利于联动和协同发展格局的形塑。可见,以高铁为标志的现代交通网络的形成,促进了城市间的联动效应,增加了中心城市对周围城市的辐射力。
珠三角,广义上应该纳入香港和澳门;狭义上的界定,则应当是广东一省之辖域范围。如果劈开政治管辖、社会与经济发展区域属性之差异,有共通之处;然而,中国之大却不得不将其分离出来,这就是本研究所关注的城市样本选取缩小在一省范围之内的主要原因,结果只是选择广州和深圳两大中心及其腹地并属于广东管辖。虽不纳入政治因素,但是已经暗涵“省管”该区域的这一基本假设。将样本城市数放大到周边省区或是全国,会部分地改变双中心城市的影响范围,但不会改变腹地城市与中心城市的联动关系测度结果。如果将广深双城放置于全国城市体系进行考察,必然要触及政府与市场关系的甄别。在深圳调整之前,除非属于非常重要或特殊的城市,地级市的市委书记一般难以进入省委常委。然而,在最新一届省级党委中,广东省委常委有三位市委书记,分别来自广州、深圳和珠海。在中国政治体系格局下,市委书记兼任省委常委,为减少行政层级设置已经成为一种常态;城市经济发展道路上,这样的行政设置有助于城市获得资源和政策支持。与此同时,地级市一把手“高配”也体现出本土化和年轻化的新特点,新上任的深圳市市委书记还是中央委员,对城市体系空间格局会产生哪些有利或不利影响,这些都将在后续研究中不断丰富。一经给定国家和地方社会经济发展规划之约束,规划文本中的广东省城市体系格局,与本文的研究如出一辙。当然,此内容并非数据测度和战略制定的偶然和巧合,反过来侧影理论和实践融合的广泛区域。如表 9所示,纵向考察城市横向关联关系也证实了重塑广东城市体系新格局存有必然之因素,也有实现之可能。规划文件的出台,研究之发现所能给予的启示、借鉴意义已然呈现,关键在于城市政府当局如何采取具体行动。
| 表 9 按六个层次组织的广东省城镇职能等级结构表 |
立足于“诸侯”经济格局之假设,观摩区域与城市联动发展诸多思路与实践行动,广东省城市体系联动发展有自身之优势,但也并无太多特别之处。由于京津冀三地联动已经破题,并有现实有效之举措,借鉴其中,结合广东省域城市经济发展之优势,能够打破僵局开始新征途。在具体做法上有两点思考:其一,借势改革大格局,创新区域发展体制机制,推动省域范围内和近邻省市主要城市之间的联动。其二,有序推进广深双城协同发展、广深珠三城联动发展。构建城市布局和空间结构优化新机制,以广深双城为中心载体,统筹人口、产业、空间、土地利用等;充分利用现代化交通网络优势,以地面快速交通网络促成城市发展共谋新格局,撬动中国全域经济走向平衡的发展才是长久之计。
| [1] | 埃比尼泽·霍华德. 明日的田园城市[M]. 金经元, 译. 北京: 商务印书馆, 2000. |
| [2] | 宋家泰. 城市-区域与城市区域调查研究——城市发展的区域经济基础调查研究[J]. 地理学报, 1980, 35(4): 277–287. |
| [3] | VIJAY R, KORI C, KUMAR M, et al. Assessment of traffic noise on highway passing from urban agglomeration[J]. Fluctuation and Noise Letters, 2014, 13(4): 1450031, 12pages. |
| [4] | SCOTT A J. Regional motors of the global economy[J]. Future, 2001, 28(5): 391–411. |
| [5] | RAVIBABU M, SREE V P. Public transport for Indian urban agglomerations:A strong case for surface rail[J]. Economic & Political Weekly, 2014, 49(23): 105–116. |
| [6] | SUZ Y, WANG Y L, SHI R, et al. Optimal mass transport for shape matching and comparison[J]. IEEE Trans Pattern Anal Mach Intell, 2015, 37(11): 2246–2259. DOI: 10.1109/TPAMI.2015.2408346 |
| [7] | 张浩然, 衣保中. 基础设施、空间溢出与区域全要素生产率[J]. 经济学家, 2012(2): 61–67. |
| [8] | 国家发改委国地所课题组, 肖金成. 我国城市群的发展阶段与十大城市群的功能定位[J]. 改革, 2009(9): 5–23. |
| [9] | WEI Z M, ZOU X L, LI M, et al. Research on reliability of urban agglomeration transport system after a disaster[J]. Applied Mechanics and Materials, 2014, 496/500: 2989–2995. DOI: 10.4028/www.scientific.net/AMM.496-500 |
| [10] | 汪宇明, 刘高, 施加仓, 蔡萌. 中国城乡一体化水平的省区分异[J]. 中国人口·资源与环境, 2012, 22(4): 137–142. |
| [11] | 姚士谋, 朱英明. 中国城市群[M]. 第二版. 合肥: 中国科学技术大学出版社, 2001. |
| [12] | GOTTMANN J. Megalopolis or the urbanization of the Northeastern Seaboard[J]. Economic Geography, 1957, 33(7): 189–200. |
| [13] | 袁俊, 谭传凤, 常旭. 城市带及我国沿海城市带的培育[J]. 经济管理, 2007, 29(15): 85–90. |
| [14] | Oil Asia Group. First ever installation of deck by float over method in ONGC[J]. Oil Asia, 2013, 33(1): 1–5. |
| [15] | 任平, 王志良. 中国城市带:实践与理论模型研究[J]. 苏州大学学报 (哲学社会科学版), 1992(4): 23–27. |
| [16] | 韩会然, 焦华富, 李俊峰, 王荣荣. 皖江城市带空间经济联系变化特征的网络分析及机理研究[J]. 经济地理, 2011, 31(3): 384–389. |
| [17] | KIM K S. High-speed rail developments and spatial restructuring:A case study of the capital region in South Korea[J]. Cities, 2000, 17(4): 251–262. DOI: 10.1016/S0264-2751(00)00021-4 |
| [18] | COTO-MILLÁN P, INGLADA V, REY B. Effects of network economies in high-speed rail:The Spanish case[J]. Annals of Regional Science, 2007, 41(4): 911–925. DOI: 10.1007/s00168-007-0134-6 |
| [19] | GIVONI M. Development and impact of the modern high-speed train:A review[J]. Transport Reviews, 2012, 26(5): 593–611. |
| [20] | BERTOLINI L. Nodes and places:Complexities of railway station redevelopment[J]. European planning Studies, 2006, 4(3): 331–345. |
| [21] | PUGA D. European regional policies in light of recent location theories[J]. Journal of economic geography, 2002, 2(4): 373–406. DOI: 10.1093/jeg/2.4.373 |
| [22] | CHEN C, HALL P. The impacts of high-speed trains on British economic geography:A study of the UK's inter city 125/225 and its effects[J]. Journal of Transport Geography, 2011, 19(4): 689–704. DOI: 10.1016/j.jtrangeo.2010.08.010 |
| [23] | 王姣娥, 丁金学. 高速铁路对中国城市空间结构的影响研究[J]. 国际城市规划, 2011, 26(6): 49–54. |
| [24] | 王姣娥, 焦敬娟, 金凤君. 高速铁路对中国城市空间相互作用强度的影响[J]. 地理学报, 2014, 69(12): 1833–1846. DOI: 10.11821/dlxb201412009 |
| [25] | 周靖祥. 测度中国高铁的城市吸附能力[N]. 中国社会科学报, 2015-04-13. |
| [26] | 赵丹, 张京祥. 高速铁路影响下的长三角城市群通达度空间格局演变[J]. 长江流域资源与环境, 2012, 21(4): 391–398. |
| [27] | 张莉, 朱长宁, 曹莉娜. 沪宁城际高速铁路对区域通达度的影响研究[J]. 铁道运输与经济, 2013, 35(1): 82–87. |
| [28] | 姜博, 初楠臣, 王媛, 等. 高速铁路影响下的城市可达性测度及其空间格局模拟分析[J]. 经济地理, 2014, 34(11): 58–62. |
| [29] | 宋文杰, 朱青, 朱月梅, 等. 高铁对不同规模城市发展的影响[J]. 经济地理, 2015, 35(10): 57–63. |
| [30] | 方大春, 孙明月. 高铁时代下长三角城市群空间结构重构[J]. 经济地理, 2015, 35(10): 50–56. |
| [31] | 陈宏胜, 杨浩然, 王兴平. 新常态背景下高铁对我国城市空间的影响及规划应对[C]//新常态: 传承与变革-2015中国城市规划年会论文集, 2015, 12(1): 1-12. |
| [32] | REILLY WJ. Methods for the study of retail relationships[J]. University of Texas, Bulletin, 1929, 48(2944): 1–9. |
| [33] | ZIPF G K. Human behaviour and the principle of least effort:An introduction to human ecology[J]. Psychological Bulletin, 1949, 47(2): 180–183. |
| [34] | 赵雪雁, 侯成成, 李建豹, 等. 甘肃省县域经济增长与空间格局演变探析[J]. 西北师范大学学报 (自然科学版), 2011, 47(5): 104–109. |
| [35] | 苗长虹, 王海江. 河南省城市的经济联系方向与强度——兼论中原城市群的形成与对外联系[J]. 地理研究, 2006, 25(2): 222–232. |
| [36] | 陆玉麒. 双核型空间结构模式的探讨[J]. 地域研究与开发, 1998, 17(4): 44–48. |
| [37] | ARELLANO M, BOND S. Some tests of specification for panel data:Monte Carlo evidence and an application to employment equations[J]. Review of Economic Studies, 1991, 58(2): 277–297. DOI: 10.2307/2297968 |
| [38] | KIVIET J F. On bias, inconsistency, and efficiency of various estimators in dynamic panel data models[J]. Journal of Econometrics, 1995, 68(1): 53–78. DOI: 10.1016/0304-4076(94)01643-E |
| [39] | BLUNDELL R, BOND S. Initial conditions and moment restrictions in dynamic panel data models[J]. Journal of Econometrics, 1998, 87(1): 115–143. DOI: 10.1016/S0304-4076(98)00009-8 |
 2017, Vol. 23
2017, Vol. 23

