金融资产收益的波动率一直是现代经济金融研究的重要变量,波动率的精确估计和预测已经成为衍生资产定价、投资组合决策和风险评估管理的关键,也吸引了大量学者的关注。以往的研究对如何进行波动率的估计给出了很多模型,采用不同的方法和数据得到的结论不尽相同,在一定程度上也反映了各类模型自身可能存在的缺陷。
传统的GARCH族和SV族模型基于历史低频数据建模,其中日收益率的估计值和真实值之间的差异会给波动率的预测带来大量误差,同时模型设定的偏误也可能造成波动率估计的不一致。近年来,随着技术手段的发展和高频数据的广泛应用,金融市场高频时间序列的波动性逐渐成为研究热点。Andersen等基于等间隔时间序列分割提出已实现波动率的概念,并证明它是积分波动率的一致估计[1-2];该方法直接从当期高频数据中提取信息,从而避免了模型的设定和复杂的参数估计。收益的整体波动不仅具有连续性特征,还具有瞬时、高强度的跳跃行为特征。Barndorff-Nielsen和Shephard提出非参数的跳跃检验方法 (BNS),在将已实现波动率分解为连续路径变差和离散跳跃方差的基础上实现了对跳跃行为的直接测度[3-4]。高频数据采集周期短,信息损失相对较小,比低频数据包含更丰富的日内波动信息,基于高频数据的波动率和跳跃的估计在市场微观结构理论的实证研究中也表现出更好的预测能力。
在已实现波动率序列特征的研究基础上,许多学者提出基于高频数据的波动率建模方法。Corsi根据异质市场假说提出不同波动率驱动成分的简单叠加模型HAR-RV[5],Andersen等进一步将其扩展成HAR-RV-CJ模型,分别研究了跳跃成分和连续成分对波动率预测精度的影响[6]。Ghysels等的研究表明绝对幂变差可以有效地对波动率进行预测[7]。Brandt和Jones提出的高低极差能显著提高波动率的预测精度[8]。Engle和Gallo将已实现波动率应用于GARCH模型,利用高频数据中的日内波动信息提高了预测效果[9]。国内学者对基于高频数据的波动率的研究也有不少成果。张伟等对中国市场个股的已实现波动率进行了估计[10]。徐正国和张世英[11]、唐勇和刘峰涛[12]通过实证比较得出已实现波动率的预测能力优于GARCH模型和SV模型。陈国进和王占海对沪深300指数的分析表明A股市场波动的连续成分和跳跃成分均具有显著的滞后自相关性[13]。
大量实证研究表明,利空消息的冲击大于利好消息,即收益的大幅负向变动对未来波动率的影响要大于同等幅度的正向变动,这种现象称为波动的非对称性或杠杆效应。经验分析中,通常采用TARCH和EGARCH等经典模型来研究波动的非对称特征,但这样的设定可能无法解释极端的价格变化对股市波动的影响,而这样的极端情况通常伴随着跳跃行为的发生,跳跃因子的引入能够更准确地检验价格波动的非对称性,提高波动率的预测效果。Eraker等通过连续时间的随机波动率模型 (SVCJ) 的研究发现跳跃行为能很好地解释股市的异常波动[14]。孙坚强和陈浪南在对混合GARCH跳跃模型的研究中发现上证指数、纳斯达克指数等全球主要股指的跳跃行为具有时变特征,且跳跃与条件波动率之间也存在相互回馈效应[15]。左浩苗和刘振涛首次将基于非参数估计的跳跃风险指标应用到波动的非对称性检验中,并指出跳跃尤其是负向跳跃中还包含有能够预测波动率的其他信息[16],但并没有给出这些额外信息的具体特征。
上述研究仅反映了跳跃风险不同于连续性风险的定价特征,没有考虑跳跃中可能包含的额外预测因素;除了波动的非对称性研究之外,对不同性质的跳跃成分及其预测能力几乎没有加以区分。本文的创新之处在于将系统性和非系统性跳跃因子引入波动率的预测模型,考察具有不同风险特征的跳跃行为对未来波动率的影响。首先根据BNS方法估计波动率和各类跳跃风险指标,验证当期波动对上一期正向跳跃和负向跳跃的非对称性反应;在此基础上发现系统性跳跃行为对下一期波动率具有显著影响,大盘指数的跳跃能够为投资者提供更多预测信息,这与相关性分析的结果也是一致的,从而有效地改进了对波动率的预测。
本文第二部分根据非参数方法理论,在给定假设下构建了波动率和各类跳跃风险的测度指标;第三部分基于不同风险性质的跳跃成分对波动率的预测模型进行了改进;第四部分为由样本数据得到的实证分析结果;最后第五部分是主要结论与建议。
二、非参数方法理论框架非参数跳跃检测方法的两个核心指标是已实现波动率 (RV) 和已实现双幂次变差 (BV),这些指标之间的联系源于下述假设,即股票的对数价格服从满足零套利原则的半鞅过程:
| ${\rm{d}}p\left( {\rm{t}} \right) = \mu \left( {\rm{t}} \right){\rm{dt}} + \sigma \left( {\rm{t}} \right){\rm{d}}W\left( {\rm{t}} \right) + \kappa \left( {\rm{t}} \right){\rm{d}}N\left( {\rm{t}} \right)$ | (1) |
其中μ(t)是一个有限变差过程,称为瞬时漂移项;σ(t)为瞬时波动率,是cadlag随机波动过程;W(t)为标准布朗运动;N(t)是泊松计数过程;κ(t)代表瞬时跳跃幅度。基于一定的采样频率,设一天内共有M个日内收益率:
| ${r_{{\rm{t}},k}} = {p_{{\rm{t}},k}} - {p_{{\rm{t}},k - 1}},k = 1,2, \cdots ,M$ | (2) |
这里rt, k表示第t天的第k个收益。已实现方差由日内高频收益率的平方求和得:
| $R{V_{\rm{t}}} = \sum\limits_{k = 1}^M {r_{{\rm{t}},k}^2} $ | (3) |
Andersen等证明了RV依概率收敛于价格随机过程的二次变差 (QV)[6]。当不存在跳跃时,QV等于积分波动率 (IV),即:
| $\mathop {p\lim R{V_{\rm{t}}}}\limits_{M \to \infty } = Q{V_{\rm{t}}} = I{V_{\rm{t}}} = \int\limits_{{\rm{t}} - 1}^{\rm{t}} {{\sigma ^2}} \left( u \right){\rm{d}}u$ | (4) |
当跳跃存在时,则有
| $\mathop {p\lim R{V_{\rm{t}}}}\limits_{M \to \infty } = Q{V_{\rm{t}}} = I{V_{\rm{t}}} = \int\limits_{{\rm{t}} - 1}^{\rm{t}} {{\sigma ^2}} \left( u \right){\rm{d}}u + \sum\limits_{{\rm{t}} - 1 \le u \le {\rm{t}}} {{{\left( {\kappa \left( u \right)} \right)}^2}} $ | (5) |
由于RV对跳跃的稳健性较差,Barndorff-Nielsen和Shephard提出用BV来度量波动的连续成分,并证明了BV依概率收敛于积分波动率[3-4]:
| $B{V_{\rm{t}}} = \mu _1^{ - 2}\left( {\frac{M}{{M - 1}}} \right)\sum\limits_{k = 2}^M {\left| {{r_{{\rm{t}},k}}} \right|} \left| {{r_{{\rm{t}},k - 1}}} \right|$ | (6) |
其中μ1-2=(E[|u|])-2=π/2,u~N(0, 1),
| $\mathop {p\lim B{V_{\rm{t}}}}\limits_{M \to \infty } = I{V_{\rm{t}}} = \int\limits_{{\rm{t}} - 1}^{\rm{t}} {{\sigma ^2}} \left( u \right){\rm{d}}u$ | (7) |
即当不存在跳跃时,RV和BV都是积分波动率Ⅳ的一致估计;而当跳跃存在时,BV仍然是IV的一致估计。在分离出跳跃成分的基础上根据渐近分布性质可以构建跳跃的检验统计量。我们采用的是Barndorff-Nielsen和Shephard提出的对数形式的统计量,即在不存在跳跃的原假设下,如果满足
| $\log {Z_{BNS,{\rm{t}}}} = \frac{{\log \left( {R{V_{\rm{t}}}} \right) - \log \left( {B{V_{\rm{t}}}} \right)}}{{\sqrt {\left( {{{\left( {\frac{\pi }{2}} \right)}^2} + \pi - 5} \right)} \frac{1}{M}\max \left( {1,\frac{{TP{V_{\rm{t}}}}}{{BV_{\rm{t}}^2}}} \right)}} > \Phi _{1 - \alpha }^{ - 1}$ | (8) |
则认为第t天发生了跳跃,其中TPVt=Mμ4/3-3
设It为示性函数,定义若第t天发生了跳跃其取值为1,否则取值为0。这里我们假设每天最多发生一次日内跳跃,则跳跃的估计为
| ${J_{\rm{t}}} = {\rm{sign}}\left( {{r_{\rm{t}}}} \right){I_{\rm{t}}}\sqrt {R{V_{\rm{t}}} - B{V_{\rm{t}}}} $ | (9) |
定义RJt=It(RVt-BVt)为跳跃变差,则估计市场整体波动的已实现波动率RV可以分解为度量连续性波动部分的已实现双幂次变差BV和度量跳跃部分的已实现跳跃变差RJ, 通过后面的实证讨论表明这样的分解放松了系数相等的约束条件,增强了模型的解释效力。
三、实证模型的改进为反映一个持续时间段内的整体趋势,我们对上述基于高频数据估计的RV,BV和RJ等日度数据在月内求和,得到月度数据,用月度变量来建立模型,用下标t表示月度频率。
国内外学者对金融市场收益率的波动非对称性进行了大量的研究。陈浪南和黄杰鲲[17],陆蓉和徐龙炳[18],吴毅芳和彭丹[19]等借助GARCH族模型的分析表明中国股市波动具有显著的杠杆效应特征。同时也有很多结论相反的研究成果,如曹国华和何燕[20]同样利用ARCH模型对中国房地产上市公司个股收益率的波动情况进行了实证研究,却发现利好消息比同等程度利空消息引起的收益率波动幅度更大,一定程度上反映了目前中国房地产市场的不成熟属性。为了克服上述传统模型的不足,部分国外研究考虑利用更精确的高频数据对波动的非对称性问题进行建模。Bollerslev和Zhou基于已实现波动率对国外市场波动进行检验并得到了显著的非对称性[4]。Visser提出用向下绝对幂变差来改进GARCH模型的预测效果[21]。Barndorff-Nielse等在波动率预测的建模中引入已实现半方差度量下方风险并研究波动的非对称性[22]。本文基于高频收益数据,利用非参数方法直接进行已实现波动率的估计和跳跃的检验。类似于TARCH模型,首先考虑下述设定:
| $R{V_{\rm{t}}} = {\alpha _0} + \beta R{V_{{\rm{t}} - 1}} + {\gamma _1}\left| {{R_{{\rm{t}} - 1}}} \right| + {\gamma _2}\left| {{R_{{\rm{t}} - 1}}} \right|{d_{{\rm{t}} - 1}} + {\varepsilon _{\rm{t}}}$ | (10) |
其中Rt为月度收益率;dt是虚拟变量,当Rt<0时,dt=1,否则dt=0。γ2是波动非对称性的一个刻画指标,即若γ2显著为正,则利空消息的影响大于利好消息的影响。对RV进行分解可得:
| $R{V_{\rm{t}}} = {\alpha _0} + {\beta _1}R{V_{{\rm{t}} - 1}} + {\beta _2}R{J_{{\rm{t}} - 1}} + {\gamma _1}\left| {{R_{{\rm{t}} - 1}}} \right| + {\gamma _2}\left| {{R_{{\rm{t}} - 1}}} \right|{d_{{\rm{t}} - 1}} + {\varepsilon _{\rm{t}}}$ | (11) |
由于收益率考虑的是所有幅度的价格变动,而在杠杆效应的检验中我们更关心的是波动对大幅度极端价格冲击的非对称反应,模型 (11) 可能无法对非对称性作出准确的检验。大幅度的收益变动通常表现为价格的跳跃行为,Patton和Sheppard在将已实现波动率分解为正向波动和负向波动的基础上,通过构造符号跳跃估计量证明跳跃对波动有重要预测作用,且负向跳跃的影响持续更久[23]。因此,考虑将跳跃因子引入模型:
| $R{V_{\rm{t}}} = {\alpha _0} + {\beta _1}R{V_{{\rm{t}} - 1}} + {\beta _2}R{J_{{\rm{t}} - 1}} + {\gamma _1}\left| {{R_{{\rm{t}} - 1}}} \right| + {\gamma _2}\left| {{R_{{\rm{t}} - 1}}} \right|{d_{{\rm{t}} - 1}} + {\varphi _1}N{J_{{\rm{t}} - 1}} + {\varepsilon _{\rm{t}}}$ | (12) |
其中PJt表示第t月正向跳跃的月度变量;NJt表示第t月负向跳跃的月度变量。
左浩苗和刘振涛在波动的非对称性基础上指出跳跃尤其是负向跳跃中还包含可以预测波动率的因素,考虑这些额外因素可以有效提高对波动率的预测效力[16]。本文在此基础上对跳跃特征作了进一步描述。根据Gilder等的命名方法,若某次跳跃与大盘指数跳跃同时发生,则称之为系统性跳跃,否则称为非系统性跳跃[24]。当覆盖市场整体的政策或信息发布时,往往会引起大多数股票价格发生共同跳跃行为,并最终表现为整体大盘指数的跳跃现象。系统性跳跃行为一定程度上反映了市场风险因素,与度量整体波动风险的已实现波动率有关联;同时经验研究表明波动具有聚类效应,当期波动对下一期波动有影响。因此,系统性跳跃风险与未来股市波动率有一定关联,本文据此对模型 (11) 作了进一步拓展:
| $\begin{array}{l} R{V_{\rm{t}}} = {\alpha _0} + {\beta _1}R{V_{{\rm{t}} - 1}} + {\beta _2}R{J_{{\rm{t}} - 1}} + {\gamma _1}\left| {{R_{{\rm{t}} - 1}}} \right| + {\gamma _2}\left| {{R_{{\rm{t}} - 1}}} \right|{d_{{\rm{t}} - 1}} + {\varphi _1}P{J_{{\rm{t}} - 1}} + \\ {\rho _1}NS{J_{{\rm{t}} - 1}} + {\rho _2}NS{J_{{\rm{t}} - 1}} + {\varepsilon _{\rm{t}}} \end{array}$ | (13) |
这里NSJt表示负向系统性跳跃的月度数据;NNSJt表示负向非系统性跳跃的月度数据。
四、实证分析本文选取上证综指和6个上证行业指数2009年4月至2014年10月期间的高频交易数据进行经验分析,采样频率为五分钟,以减小市场微观结构噪声的干扰。其中日度数据的计算包含隔夜收益率;月度收益率采取对数收益率的形式,即对月末数据的对数进行差分计算:
| ${R_{\rm{t}}} = \ln {P_{\rm{t}}} - \ln {P_{{\rm{t}} - 1}},{\rm{t}} = 1,2, \cdots ,N{\rm{。}}$ |
所有样本数据均来自于标普永华高频数据库。
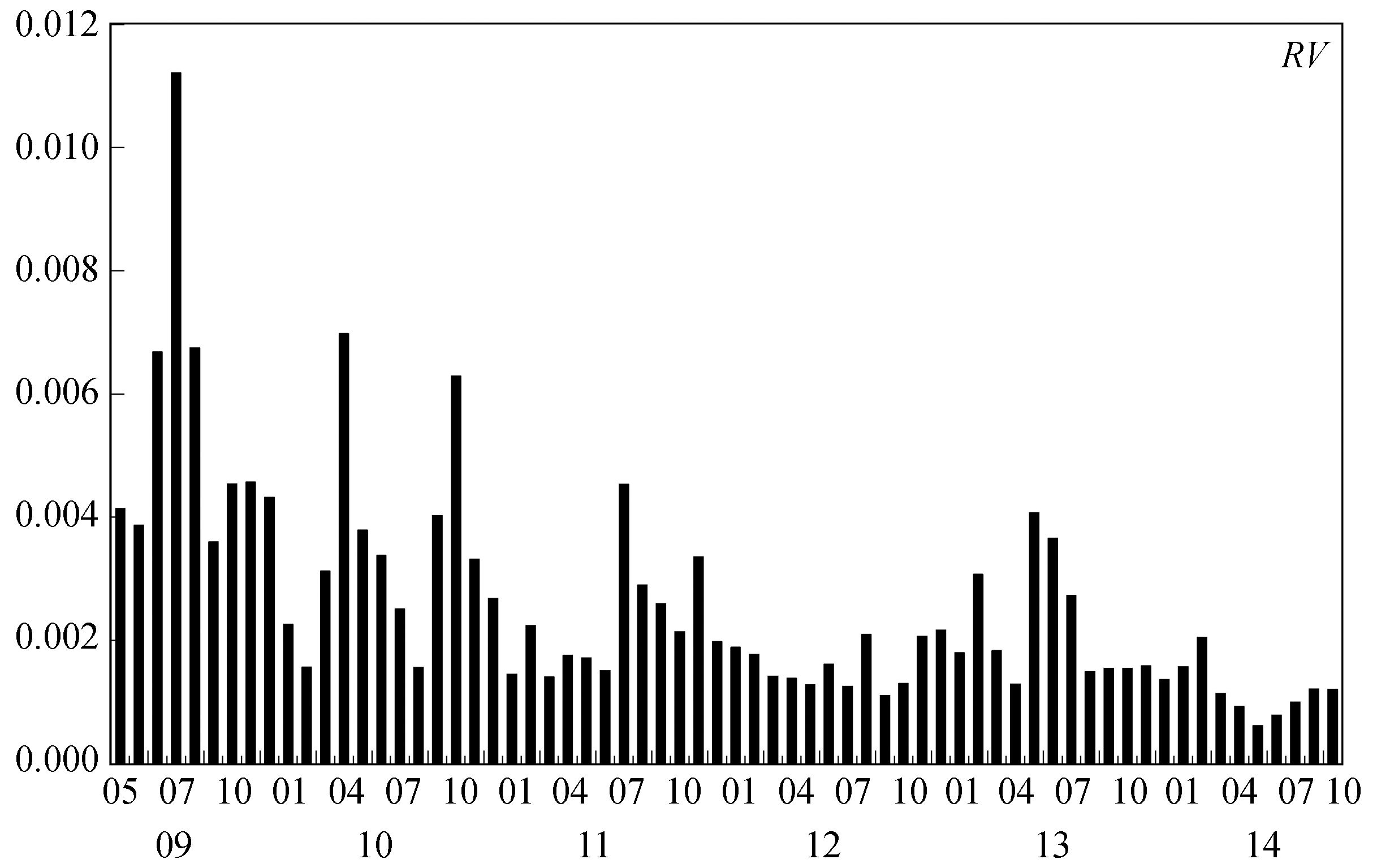
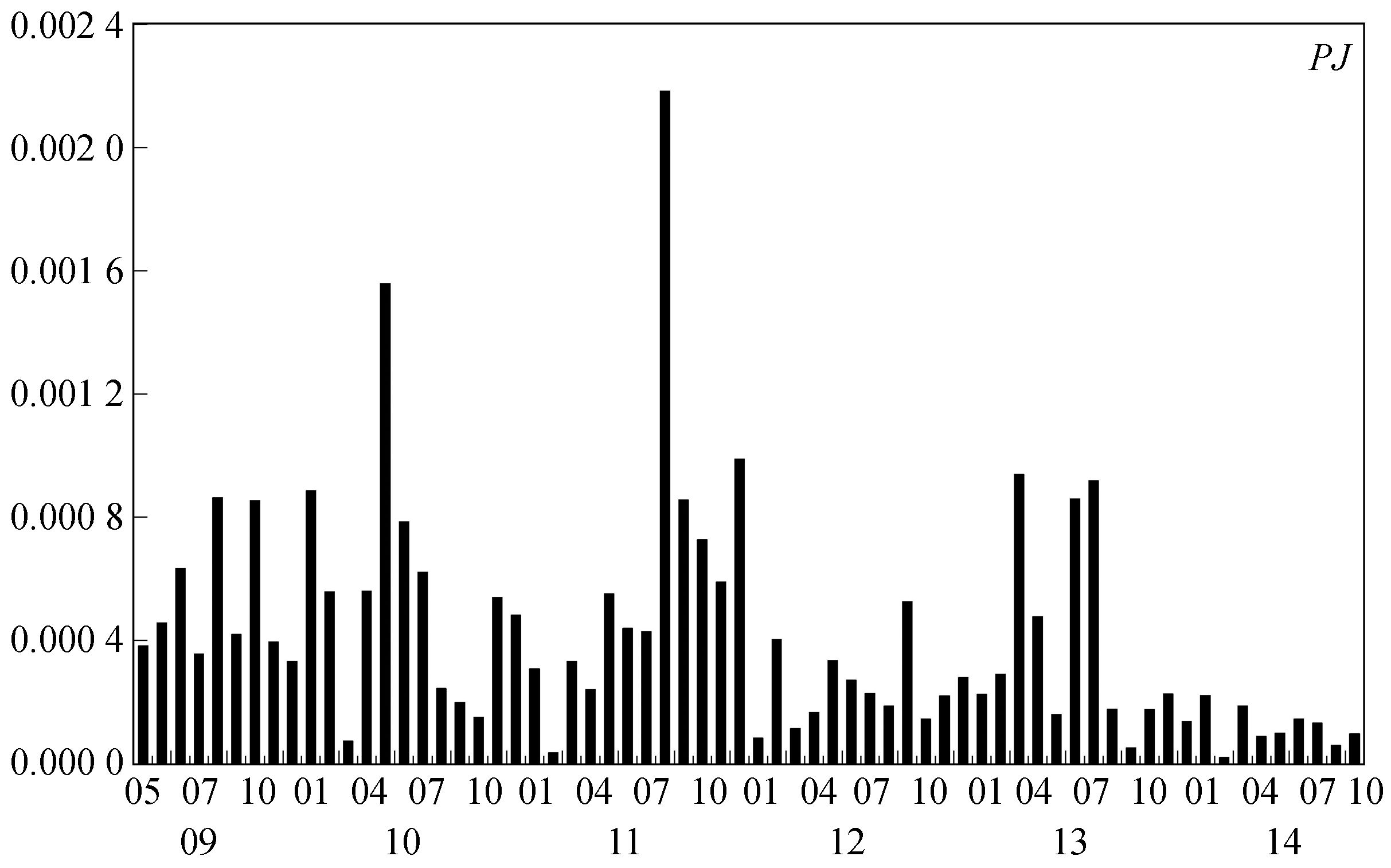
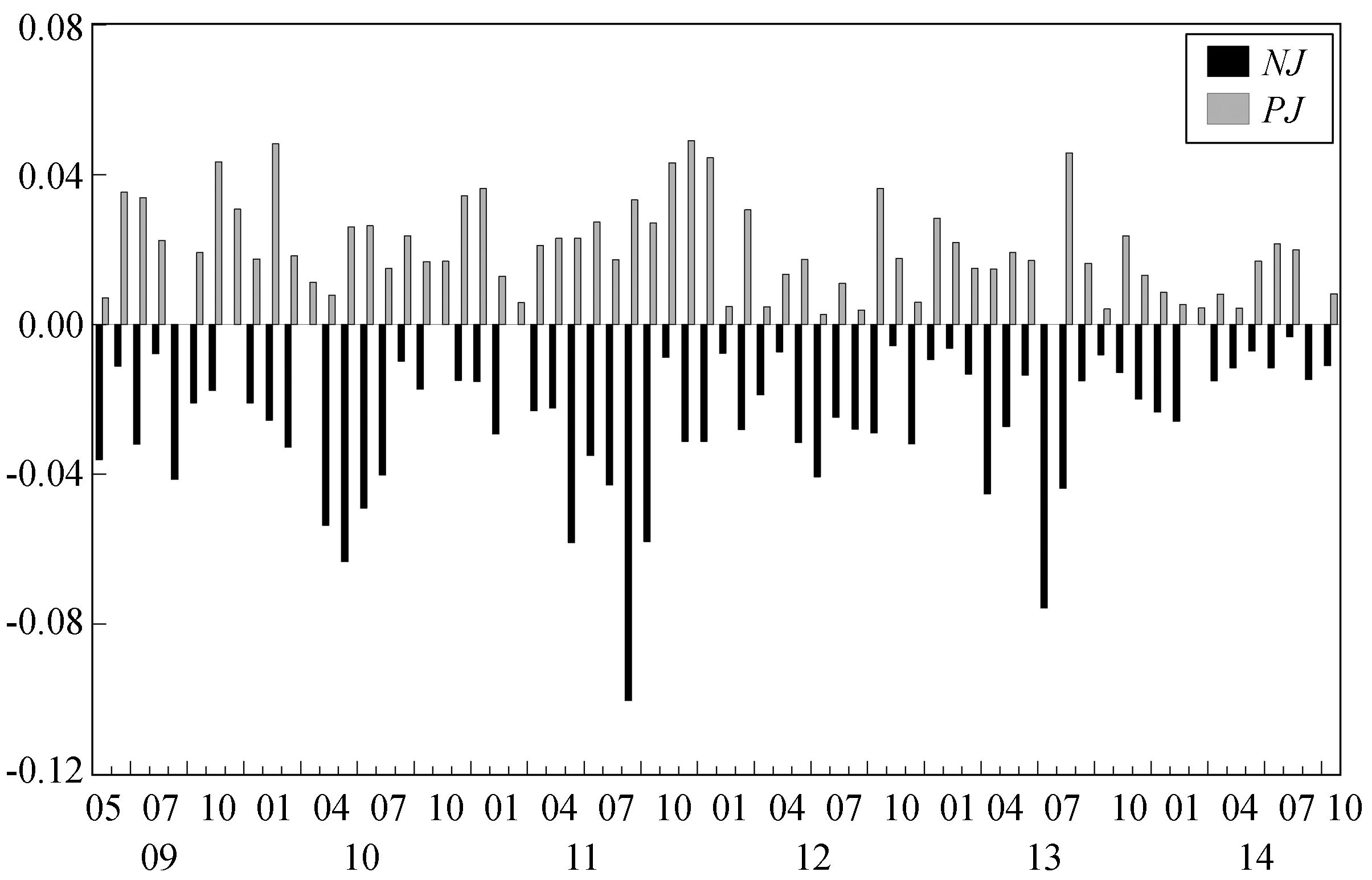
(一) 描述性统计特征 1. 相关系数与聚类特征图 1和图 2表明上证综指的波动率和跳跃指标均具有一定的持续性。其中包含连续性波动成分的RV和BV自相关系数高达0.65与0.70,跳跃变差RJ的自相关系数也达到0.31。同时,负向跳跃NJ的持续性 (自相关系数0.29) 也要强于正向跳跃PJ(0.18)。由图 3可以看出负向跳跃的聚类特征更明显,即股价的负向连续大幅下跌较之正向上升更容易发生,这跟实际金融活动中投资者的风险态度有关。大多数投资者属于风险厌恶者,股价大幅下跌时会出现恐慌性抛售以求减少损失的局面,这必将导致股市的进一步下跌;而股价处于大幅上升阶段时,有一部分投资者会放弃继续持有,选择卖出股票获取超额收益,从而在一定程度上制约了股市继续上扬的势头。
|
图 1 上证综指已实现波动率 (RV) 月度图 |
|
图 2 上证综指跳跃变差 (RJ) 月度图 |
|
图 3 上证综指正向跳跃 (PJ) 和负向跳跃 (NJ) 月度图 |
另外,上证各行业指数的系统性跳跃 (PSJ和NSJ) 自相关系数普遍高于非系统性跳跃 (PNSJ和NNSJ),意味着在系统性的大幅跳跃之后通常还伴随系统性跳跃的发生。这些描述性特征表明将波动率中的跳跃成分尤其是系统性负向跳跃成分进行分离并引入回归是有实际意义的。
| 表 1 上证行业指数的自相关系数 (AC) |
| 表 2 上证指数相关系数表 |
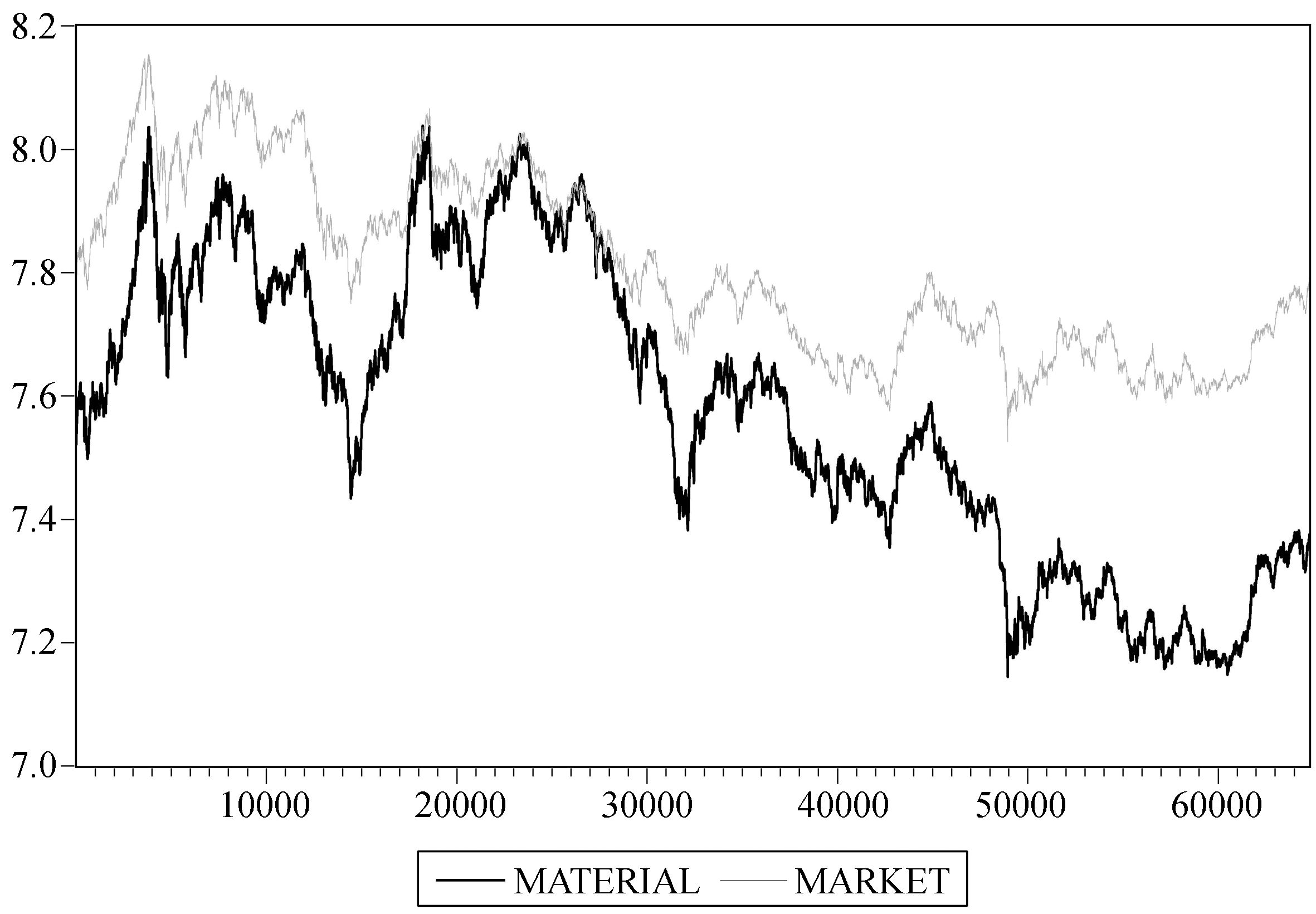
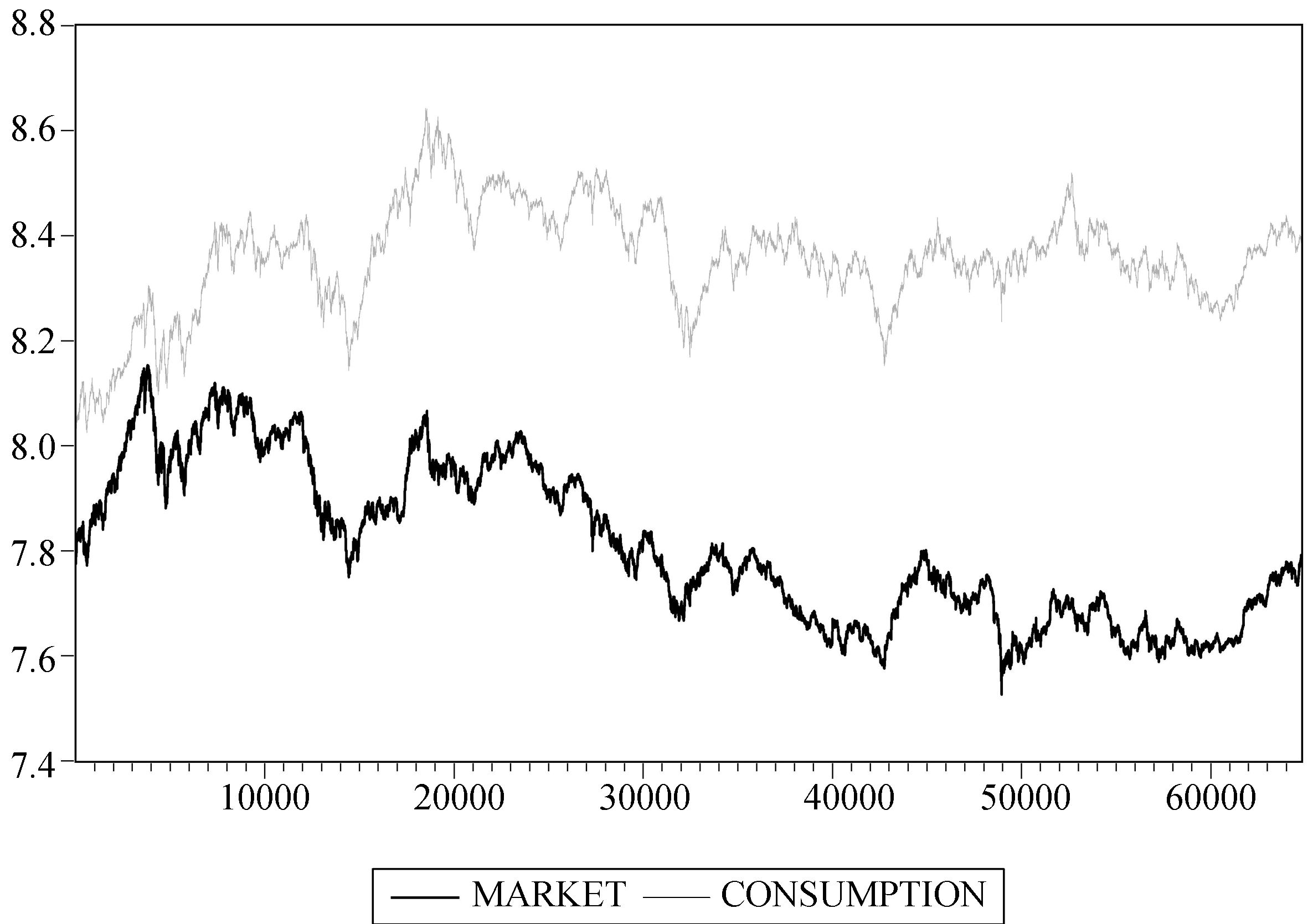
从各指数与上证综指的相关系数表可以看出,材料、电信、金融和能源这4个指数与综指的相关系数均达到了80%以上,其中材料指数高达91%,而消费指数和医药指数与大盘指数的关联程度相对较弱。以材料指数和消费指数为例,从图 4和图 5可以直观地观察到相关程度的差别。
|
图 4 上证综指 (MARKET) 和材料指数 (MATERIAL) 走势图 |
|
图 5 上证综指 (MARKET) 和消费指数 (CONSUMPTION) 走势图 |
跳跃对波动率的影响包含两个方面:一方面是考察正向和负向跳跃的影响,验证负向跳跃对下一期波动率具有更显著的影响,即波动的非对称性;另一方面,在此基础上提取负向跳跃中关于波动的进一步信息,即将跳跃按不同的风险性质分解为系统性跳跃与非系统性跳跃成分,并考察其对波动率的预测能力。
表 3对上证综指进行了波动的非对称性检验,其中回归3、回归4和回归6分别对应模型 (10)、模型 (11) 和模型 (12) 的估计结果,拟合优度均为调整后的R2(百分比)。从表中可以看出,回归2比回归1的调整后R2高出3%左右, 表明将RV分解为BV和RJ能够改进对已实现波动率的预测。回归6中正向跳跃的系数γ1为0.01,负向跳跃的系数γ2为-0.03且统计显著,说明无论是正向跳跃还是负向跳跃都会导致下一期波动风险的增加,且负向跳跃的影响大于正向跳跃,这正是波动非对称性的表现;而仅考虑一般收益率的回归3和回归4则无法准确地反映这一点,在未引入跳跃因素的情况下系数γ2甚至显著为负。
| 表 3 上证综指的波动非对称性检验 |
为了进一步考察系统性跳跃和非系统性跳跃对波动率的作用,本文选取上证材料、电信、金融、能源、消费和医药等6个不同行业的指数为研究对象,对模型 (11)-(13) 进行估计。基于数据特征,我们对样本区间作了分段考察。表 4和表 5分别报告了材料指数和电信指数2010年12月至2014年10月的OLS估计结果;表 6报告了能源指数2009年5月至2013年7月的OLS估计结果。回归2、回归3和回归4分别代表模型 (11)、模型 (12) 和模型 (13)。
| 表 4 上证材料指数 |
| 表 5 上证电信指数 |
| 表 6 上证能源指数 |
表 4至表 6的实证结果表明,回归2中的指征系数γ2均没有表现出显著为正的特征,能源指数甚至出现显著为负的结果,与Rabemananjara和Zakoian[25]一致,说明在价格变动幅度较小时存在正向价格变动对波动率的影响更大的可能;而在引入跳跃因素的回归3中,材料和能源等指数则一致表现出显著的杠杆效应,表明跳跃成分确实能够解释波动的非对称特征,提高模型的预测能力。需要注意的是表 5中系数φ1显著为正而φ2却不显著,即电信指数的正向跳跃对未来波动率的影响大于负向跳跃,表现出与其他指数相反的非对称性特征,这与电信行业的经济非周期性有关,因此考虑将模型 (13) 修正为如下形式:
| $\begin{array}{l} R{V_{\rm{t}}} = {\alpha _0} + {\beta _1}B{V_{{\rm{t}} - 1}} + {\beta _2}R{J_{{\rm{t}} - 1}} + {\gamma _1}\left| {{R_{{\rm{t}} - 1}}} \right| + {\gamma _2}\left| {{R_{{\rm{t}} - 1}}} \right|{d_{{\rm{t}} - 1}} + {\lambda _1}PS{J_{{\rm{t}} - 1}} + \\ {\lambda _2}PNS{J_{{\rm{t}} - 1}} + {\varphi _2}NS{J_{{\rm{t}} - 1}} + {\varepsilon _{\rm{t}}} \end{array}$ | (14) |
即表 5中的回归4代表模型 (14) 而不是模型 (13)。
行业指数的跳跃行为本质上是该行业内一定数量个股的共同跳跃。根据Gilder等的研究,系统性共同跳跃中所包含的个股数量显著高于非系统性共同跳跃,大盘指数的跳跃与其成分股的共同跳跃之间有很强的联系[24],行业指数的系统性跳跃对其波动率的影响要大于非系统性跳跃。可以看到,回归4中的系数ρ1和λ1均统计显著,表明大盘指数的跳跃行为对材料、能源和电信等行业指数的波动都具有较强的预测效力,这与它们在相关性分析 (表 2) 中的表现也是一致的。同时,调整后的R2也有不同程度的提高,尤其是材料指数,回归4的调整后R2比回归3高出了8%左右。
表 7报告了金融指数2009年12月至2012年12月的实证结论。由于数据在残差分析中存在不同程度的异方差特征,我们进一步给出了ARCH效应的回归结果。如表 7,回归1-3和回归4-6分别对应了模型 (11)-(13) 的OLS估计结果和ARCH估计结果。
| 表 7 上证金融指数 |
可以看到回归4-6中代表GARCH效应的ξ1和η1都是显著的,即存在GARCH效应。与OLS结果相比,金融指数的GARCH回归具有明显优势:第一,回归4已经表现出显著的波动非对称性特征,即月度负向收益变动对下月已实现波动率的影响大于正向收益变动,但回归1的结果并不显著;第二,考虑跳跃因素后,回归2依然不显著,但回归5中的系数φ2显著,即下月已实现波动率对当月跳跃有非对称反应;第三,回归3和回归6中的系数ρ2都显著,说明金融指数的非系统性跳跃对未来波动率的影响大于系统性跳跃,这一点与其他指数是不同的,这要归结于金融股的特殊性。中国市场的政策调控性比较强,金融股本身作为权重股,也是政策股,在维持价格理性和市场稳定方面有着重要地位,这样的特点决定了金融股在大盘强势涨跌期间经常处于“潜伏”状态,如2014年7月至2015年5月在各路题材全线大涨的环境下,银行板块表现疲软,银行股和券商股集体表现出滞后市场的反应。
表 8提示消费指数和医药指数均没有检验出波动的非对称性,大盘指数的跳跃行为对其波动也无显著作用,这是由行业的非周期性决定的。消费和医药行业属于典型的非周期性行业,提供的产品大都是生活必需品,其需求变动一般不受宏观经济走势的影响。在表 2中也可以看到,它们和大盘综指之间的相关系数也相对较低。
| 表 8 上证消费指数和上证医药指数 |
本文利用基于高频数据的非参数方法来估计已实现波动率和跳跃风险的月度指标,在此基础上进一步研究不同性质的跳跃成分对波动率的预测作用。
通过实证研究我们发现:首先,上证综指及各周期性行业指数在发生大幅跳跃行为时不同程度地具有杠杆效应的特征,这与国内外大多数关于波动的非对称性研究观点是相符的。其中电信指数的波动率呈现相反特征的非对称性,可能与行业的经济非周期性有关。其次,材料、电信和能源等指数的系统性跳跃行为对下一期波动率的影响普遍大于非系统跳跃行为,表现出与大盘较强的关联性,这与Gilder等[24]关于共同跳跃的结论一致。但金融指数的结果却与此相异,其非系统性跳跃反而表现出显著影响,造成这种差异的原因在于金融股自身的特殊性。最后,代表非周期性行业的消费指数和医药指数则表现不明显,与大盘走势也没有必然联系。
综上所述,股市跳跃行为对未来波动率普遍存在非对称的回馈效应,且系统性跳跃对下一期波动率具有显著影响,说明跳跃尤其是负向跳跃中确实包含可以预测波动率的额外信息,据此对预测模型进行的改进也是有效的。
在中国股市经常起伏不定的背景下,提取高频金融收益数据中的信息来识别波动中的各种跳跃成分,可以帮助投资者更准确地分析日内波动的典型特征并改进波动的预测,从而构造最优的投资组合,达到规避风险与提高收益的目的。同时,对波动规律的研究也是市场管理部门制定政策以促进证券市场健康发展和资本合理配置的有力依据。
| [1] | ANDERSEN T G, BOLLERSLEV T M, DIEBOLD F X, et al. The distribution of realized stock return volatility[J]. Joural of Financial Economics, 2001, 61(1): 43–76. DOI: 10.1016/S0304-405X(01)00055-1 |
| [2] | ANDERSEN T G, BOLLERSLEV T M, DIEBOLD F X, et al. Modelling and forecasting realized volatility[J]. Econometrica, 2003, 71(2): 579–625. DOI: 10.1111/ecta.2003.71.issue-2 |
| [3] | BARNDORFF-NIELSEN O, SHEPHARD N. Power and bipower variation with stochastic volatility and jumps[J]. Journal of Financial Econometrics, 2004, 2(1): 1–37. DOI: 10.1093/jjfinec/nbh001 |
| [4] | BARNDORFF-NIELSEN O, SHEPHARD N. Economics of testing for jumps in financial economics using bipower variation[J]. Journal of Financial Econometrics, 2006, 4(1): 1–30. |
| [5] | CORSI F.A simple long memory model of realized volatility[R].Working paper, University of Lugano, 2004:1-28. |
| [6] | ANDERSEN T G, BOLLERSLEV T M, DIEBOLD F X. Roughing it up:Including jump components in the measurement, modelling and forecasting of return volatility[J]. The Review of Economics and Statistics, 2007, 89(4): 701–720. DOI: 10.1162/rest.89.4.701 |
| [7] | GHYSELS E, SANTA-CLARA P, VALKANOV R. Predicting volatility:Getting the most out of return data sampled at different frequencies[J]. Journal of Econometrics, 2006, 131(1/2): 59–95. |
| [8] | BRANDT M W, JONES C S. Volatility forecasting with range-based EGARCH models[J]. Journal of Business and Economic Statistics, 2006, 24(4): 470–486. DOI: 10.1198/073500106000000206 |
| [9] | ENGLE R F, GALLO G M. A multiple indicators model for volatility using intra-daily data[J]. Journal of Econometrics, 2006, 131(1/2): 3–27. |
| [10] | 张伟, 李平, 曾勇. 中国股票市场个股已实现波动率估计[J]. 管理学报, 2008, 5(2): 269–273. |
| [11] | 徐正国, 张世英. 调整"已实现"波动率与GARCH及SV模型对波动的预测能力的比较研究[J]. 系统工程, 2004, 22(8): 60–63. |
| [12] | 唐勇, 刘峰涛. 金融市场波动测量方法新进展[J]. 华南农业大学学报 (社会科学版), 2005, 4(1): 48–53. |
| [13] | 陈国进, 王占海. 我国股票市场连续性波动与跳跃性波动实证研究[J]. 系统工程理论与实践, 2010, 30(9): 1554–1562. DOI: 10.12011/1000-6788(2010)9-1554 |
| [14] | ERAKER B, JOHANNES M, PLOSON N. The impact of jumps in volatility and returns[J]. Journal of Finance, 2003, 58(3): 1269–1300. DOI: 10.1111/1540-6261.00566 |
| [15] | 陈浪南, 孙坚强. 股票市场资产收益的跳跃行为研究[J]. 经济研究, 2010(4): 54–66. |
| [16] | 左浩苗, 刘振涛. 跳跃风险度量及其在风险-收益关系检验中的应用[J]. 金融研究, 2011(10): 170–184. |
| [17] | 陈浪南, 黄杰鲲. 中国股票市场波动非对称性的实证研究[J]. 金融研究, 2002(5): 67–73. |
| [18] | 陆蓉, 徐龙炳. "牛市"和"熊市"对信息的不平衡性反应研究[J]. 经济研究, 2004(3): 65–72. |
| [19] | 吴毅芳, 彭丹. 我国股票市场价格波动的非对称性及其国际比较[J]. 中南大学学报 (社会科学版), 2007, 13(5): 568–572. |
| [20] | 曹国华, 何燕. 中国房地产上市公司股票收益率波动实证研究[J]. 重庆大学学报 (社会科学版), 2011, 17(6): 39–46. |
| [21] | VISSER M P.Forecasting S & P 500 daily volatility using a proxy for downward price pressure[R].Working paper, University of Amsterdam, 2008:1-31. |
| [22] | BARNDORFF-NIELSEN O E, KINNERBROCK S, SHEPHARD N.Measuring downside risk-realised semivariance[C]//BOLLERSLEV T, RUSSELL J, WATSON M.Volatility and time series econometrics:Essays in honor of Robert F.Engle.New York:Oxford University Press, 2009:1-21. |
| [23] | PATTON A J, SHEPPARD K. Good volatility, bad volatility:Signed jumps and the persistence of volatility[J]. The Review of Economics and Statistics, 2015, 97(3): 683–697. DOI: 10.1162/REST_a_00503 |
| [24] | GILDER D, SHACKLETON M B, TAYLOR S J. Cojumps in stocks prices:Empirical evidence[J]. Journal of Banking & Finance, 2014, 40: 443–459. |
| [25] | RABEMANANJARA R, ZAKOIAN J M. Threshold arch models and asymmetries in volatility[J]. Journal of Applied Economics, 1993, 8(1): 31–49. DOI: 10.1002/(ISSN)1099-1255 |
 2017, Vol. 23
2017, Vol. 23

