2. 国网重庆市电力公司 电力科学研究院, 重庆 401120
2. Electric Power Research Institute of Chongqing Electric Power Company, State Grid Corporation of China, Chongqing 401120, P. R. China
电子商务技术和互联网技术的快速发展为企业带来了新的发展机遇[1]。在此环境下,双渠道销售模式作为一种发展趋势已经被越来越多的企业采用[2-3]。本文研究的双渠道销售模式是指制造商同时通过传统零售商线下渠道和自有线上渠道销售产品。在该双渠道供应链中,零售商线下渠道面临着制造商线上渠道入侵产生的直接竞争[4-5]。为了凸显竞争优势,零售商借助其线下实体店优势,通过提供渠道服务来吸引消费者以促进需求[6]。然而,零售商提供的服务同时也会对制造商线上渠道需求具有溢出效应,即部分消费者在线下体验服务之后转移至制造商线上渠道购买。调查数据显示,有45.9%的消费者在线上购买之前会先去线下实体店了解产品信息[7]。然而,服务溢出效应同时也会对线下渠道需求产生竞争效应,导致零售商提供的服务不能完全转化为线下渠道需求。这可能会加剧渠道竞争,不利于双渠道供应链的有效运作。因此,当线下渠道服务同时具有溢出和竞争效应时,零售商如何制定服务策略,制造商如何通过有效的合作机制激励零售商提高服务水平以提高双渠道供应链的整体绩效是值得研究的重要问题。
近年来,双渠道供应链领域的相关问题是学者们重点关注的研究对象。与本文直接相关的研究涉及两方面:一是制造商线上渠道与零售商线下渠道间的竞争以及如何通过有效的合作机制缓解渠道竞争;二是双渠道供应链中制造商线上渠道和零售商线下渠道服务的作用和影响。下面分别从这两个方面对研究现状进行梳理。
制造商线上渠道的引入将导致与零售商线下渠道之间的直接竞争与冲突。一些学者对该情形下的渠道竞争问题进行了研究。例如,孙燕红等建立了双渠道供应链渠道服务竞争模型,并对制造商网络渠道选择问题以及引入网络渠道后的影响进行了研究[8]。许民利等研究了供应链成员风险偏好对渠道价格竞争的影响[9]。范小军和刘艳研究了存在价格与服务竞争时制造商的渠道选择策略[10]。考虑到竞争带来的不利影响,一些学者对如何通过有效的合作机制来缓解制造商线上渠道和零售商线下渠道竞争并提高供应链绩效进行了研究。例如,Cai等分析了价格折扣机制对供应链成员竞争的影响。研究发现,该机制可以提高供应链成员绩效[11]。Ryan等研究了双渠道供应链中渠道价格竞争问题,并通过改进收益共享契约和收益损失共享契约提高供应链成员绩效[12]。Yan和Pei研究发现,合作广告可以作为一个有效的机制来缓解渠道竞争并提高供应链绩效[13]。Li等提出了一种改进的风险分担机制来协调由一个供应商和一个风险规避零售商组成的双渠道供应链[14]。王先甲等研究了生产规模不经济情形下双渠道供应链的协调问题[15]。以上研究主要从供应链成员合作角度出发,论证如何通过有效的合作机制来提高供应链绩效,获取更多利润。
另一个与本文研究相关的是双渠道供应链中制造商线上渠道和零售商线下渠道服务的作用和影响。在销售相同产品的双渠道供应链中,一个渠道的服务势必会对另一个渠道的需求产生溢出效应。一些学者对服务溢出效应的影响进行了研究。例如,Luo等针对零售商线下渠道服务对制造商线上渠道需求具有溢出效应时,设计了三部转移支付实现供应链协调[16]。艾兴政等在考虑制造商线上渠道和零售商线下渠道同时提供服务时产生双向服务溢出效应的基础上,结合数值算例,分析了服务溢出效应对制造商和零售商绩效的影响[17]。与艾兴政类似,罗美玲等研究了双向服务溢出效应下,溢出效应对供应链成员最优决策的影响[18]。以上研究主要关注了渠道服务对另一渠道需求具有溢出效应。然而,一个渠道的服务在对另一渠道需求产生溢出效应的同时,也会导致渠道服务提供方失去原本属于自己需求的竞争效应,使得渠道服务不能全部转化为自身渠道需求,进而影响渠道的服务决策。在同时考虑服务的溢出和竞争效应基础上,浦徐进和龚磊验证了成本分担机制对供应链绩效的影响。研究发现,该机制可以实现供应链成员的帕累托改进[19]。
鉴于此,本文在文献[19]的基础上,构建制造商和零售商的主从博弈模型,分析价格竞争程度、服务溢出效应对最优决策的影响,探讨服务溢出效应对价格竞争的调控作用机理。在此基础上,以集中式决策下的最优决策为基础,设计一种基于需求引导的线上与线下渠道合作机制并实现分散式双渠道供应链的完美协调。
二、问题描述考虑由一个制造商和一个独立传统零售商组成的双渠道供应链,制造商的产品同时通过传统零售商线下渠道和制造商自有线上渠道销售。制造商线上渠道销售价格为pm,并将产品以批发价格w销售给零售商,零售商再以价格pr将产品销售给终端消费者。为了促进线下渠道需求,零售商借助其线下实体店更接近消费者的便利性向消费者提供售前服务,如产品试用、功能体验以及现场专业销售人员解说。零售商提供的服务水平为e,服务成本为C(e),其中C(e)满足∂C(e)/∂e>0,∂2C(e)/∂e2>0[20-21]。不失一般性,我们假设
| $ {d_{\rm{m}}} = 1-\alpha-{p_{\rm{m}}} + \theta \left( {{p_{\rm{r}}}-{p_{\rm{m}}}} \right) + \lambda e $ | (1) |
| $ {d_{\rm{r}}} = \alpha-{p_{\rm{r}}} + \theta \left( {{p_{\rm{m}}}-{p_{\rm{r}}}} \right) + \left( {1-\lambda } \right)e $ | (2) |
其中,α (0 < α < 1)表示零售商线下渠道所占市场份额,相应地,1-α则表示制造商线上渠道占有的市场份额,θ反映了渠道间的价格竞争程度,λ (0 < λ < 1)表示零售商服务溢出效应程度系数。在本文中,上标C、D、F分别表示集中、分散和合作情形,下标m和r分别表示制造商和零售商。为了使研究有意义,需要满足pr>w、pm>w。因此,本文在条件R下进行研究,其中
| $ {\pi _{\rm{m}}} = {p_{\rm{m}}}{d_{\rm{m}}} + w{d_{\rm{r}}} $ | (3) |
| $ {\pi _{\rm{r}}} = \left( {{p_{\rm{r}}}-w} \right){d_{\rm{r}}}-C\left( e \right) $ | (4) |
集中式决策是一种用于与分散式决策进行对比的基准情形。在该情形下,供应链成员作为一个整体,以供应链系统利润最大化为目标制定最优pm、pr和e。根据式(3)和式(4),我们可以得到系统利润函数πC,其中πC=πm+πR。由此,我们得到集中式决策情形下供应链系统的决策问题为
| $ \mathop {\max }\limits_{{p_{\rm{m}}}, {p_{\rm{r}}}, e} {\pi ^{\rm{C}}} = {p_{\rm{m}}}{d_{\rm{m}}} + {p_{\rm{r}}}{d_{\rm{r}}}-\frac{1}{2}{e^2} $ | (5) |
定理1:集中式决策情形下,双渠道供应链系统存在唯一最优解为
证明:求解πC关于pm、pr和e的二阶偏导数,得到Hessian矩阵为:
| $ \begin{array}{l} H\left( {{p_{\rm{m}}}, {p_{\rm{r}}}, e} \right) = \\ \left( {\begin{array}{*{20}{c}} {{\partial ^2}{\pi ^{\rm{C}}}/\partial p_{\rm{r}}^2}&{{\partial ^2}{\pi ^{\rm{C}}}/\partial {p_{\rm{r}}}\partial {p_{\rm{m}}}}&{{\partial ^2}{\pi ^{\rm{C}}}/\partial {p_{\rm{r}}}\partial e}\\ {{\partial ^2}{\pi ^{\rm{C}}}/\partial {p_{\rm{m}}}\partial {p_{\rm{r}}}}&{{\partial ^2}{\pi ^{\rm{C}}}/\partial p_{\rm{m}}^2}&{{\partial ^2}{\pi ^{\rm{C}}}/\partial {p_{\rm{m}}}\partial e}\\ {{\partial ^2}{\pi ^{\rm{C}}}/\partial e\partial {p_{\rm{m}}}}&{{\partial ^2}{\pi ^{\rm{C}}}/\partial e\partial {p_{\rm{r}}}}&{{\partial ^2}{\pi ^{\rm{C}}}/\partial {e^2}} \end{array}} \right)\\ = \left( {\begin{array}{*{20}{c}} {-2\left( {1 + \theta } \right)}&{2\theta }&{1-\lambda }\\ {2\theta }&{-2\left( {1 + \theta } \right)}&\lambda \\ \lambda &{1 - \lambda }&{ - 1} \end{array}} \right) \end{array} $ |
易知,∂2πC/∂pr2 < 0,
分散式决策情形下,制造商和零售商作为独立的决策个体,分别以自身利益最大化为目标,进行Stackelberg主从博弈,博弈顺序为:制造商为主方,首先公布产品线上渠道销售价格pm和批发价格w,零售商观察到pm和w之后,制定线下渠道销售价格pr和服务水平e,即
| $ \left\{ \begin{array}{l} \mathop {\max }\limits_{w, {p_{\rm{m}}}} \pi _{\rm{m}}^{\rm{D}} = {p_{\rm{m}}}\left( {1-a-{p_{\rm{m}}} + \theta \left( {{p_{\rm{r}}}-{p_{\rm{m}}}} \right) + \lambda e} \right) + w\left( {a - {p_{\rm{r}}} + \theta \left( {{p_{\rm{m}}} - {p_{\rm{r}}}} \right) + \left( {1 - \lambda } \right)e} \right)\\ {\rm{s}}.{\rm{t}}\left( {{p_{\rm{r}}}, e} \right) = \arg \max \pi _{\rm{r}}^{\rm{D}}\\ \mathop {\max }\limits_{{p_{\rm{r}}}, e} \pi _{\rm{r}}^{\rm{D}} = \left( {{p_{\rm{r}}} - w} \right)\left( {a - {p_{\rm{r}}} + \theta \left( {{p_{\rm{m}}} - {p_{\rm{r}}}} \right) + \left( {1 - \lambda } \right)e} \right) - \frac{1}{2}{e^2} \end{array} \right. $ | (6) |
通过求解式(6),可以得到分散式决策情形下制造商和零售商的最优解。
定理2:分散式决策情形下,制造商和零售商存在唯一最优解,分别为
| $ {w^{\rm{D}}} = \frac{{\left( {{\lambda ^3} + \left( {4\theta + 2} \right){\lambda ^2} + \left( {-5\theta + {\theta ^2}-5} \right)\lambda-5{\theta ^2} - 7\theta - 2} \right)\alpha - \left( {{\lambda ^2} - 2\lambda - 2\theta - 1} \right)\left( {{\lambda ^2} + \theta \lambda - \lambda + 2{\theta ^2} + \theta } \right)}}{{{\lambda ^4} + \left( { - 2 + 2\theta } \right){\lambda ^3} + \left( {5 + 8\theta + 9{\theta ^2}} \right){\lambda ^2} + \left( { - 22\theta - 8 - 18{\theta ^2}} \right)\lambda - 4 - 20\theta - 31{\theta ^2} - 16{\theta ^3}}}, $ |
| $ p_{\rm{m}}^{\rm{D}} = \frac{{\left( {1 + \theta } \right)\left( {3\lambda + \theta \lambda + 3\theta + 2-{\lambda ^2}} \right)\alpha + 2{{\left( {1 + \theta } \right)}^2}\left( {{\lambda ^2}-2\theta-1 - 2\lambda } \right)}}{{{\lambda ^4} + \left( { - 2 + 2\theta } \right){\lambda ^3} + \left( {5 + 8\theta + 9{\theta ^2}} \right){\lambda ^2} + \left( { - 22\theta - 8 - 18{\theta ^2}} \right)\lambda - 4 - 20\theta - 31{\theta ^2} - 16{\theta ^3}}}, $ |
| $ p_{\rm{r}}^{\rm{D}} = \frac{{\left( {{\lambda ^3} + \left( {1 + 4\theta } \right){\lambda ^2} + \left( {{\theta ^2}-4-6\theta } \right)\lambda-12\theta - 4 - 9{\theta ^2}} \right)\alpha + {\lambda ^4} + \left( {\theta - 3} \right){\lambda ^3} + \left( { - 2\theta + 2 + 2{\theta ^2}} \right){\lambda ^2} + \left( { - 5{\theta ^2} - \theta } \right)\lambda - 5{\theta ^2} - 4{\theta ^3} - 2\theta }}{{{\lambda ^4} + \left( { - 2 + 2\theta } \right){\lambda ^3} + \left( {5 + 8\theta + 9{\theta ^2}} \right){\lambda ^2} + \left( { - 22\theta - 8 - 18{\theta ^2}} \right)\lambda - 4 - 20\theta - 31{\theta ^2} - 16{\theta ^3}}}, $ |
| $ {e^{\rm{D}}} = \frac{{\left( {1-\lambda } \right)\left( {\left( {\lambda-{\lambda ^2}-\theta \lambda - 4{\theta ^2} - 2 - 5\theta } \right)\alpha - \left( {1 + \theta } \right)\left( {1 - \lambda } \right)\left( {\lambda + \theta } \right)} \right)}}{{{\lambda ^4} + \left( { - 2 + 2\theta } \right){\lambda ^3} + \left( {5 + 8\theta + 9{\theta ^2}} \right){\lambda ^2} + \left( { - 22\theta - 8 - 18{\theta ^2}} \right)\lambda - 4 - 20\theta - 31{\theta ^2} - 16{\theta ^3}}} $ |
证明:采用逆向归纳法求解制造商和零售商的最优决策问题。首先,我们判定πrD关于线下渠道销售价格pr和服务水平e的联合凹性。πrD关于pr和e的Hessian矩阵为:
根据定理2中的结果,接下来,我们对服务溢出效应和竞争效应对制造商、零售商最优决策的影响进行分析,得到命题1。
命题1:随着服务溢出效应增加,线下渠道服务水平的变化趋势为:当0 < λ < 0.181且α < α1时,∂eD/∂λ>0;当0 < λ < 0.181且α>α1或0.181 < λ < 1时,∂eD/∂λ < 0。
证明:根据定理2,求解eD关于λ的一阶导数为
| $ \partial {e^{\rm{D}}}/\partial \lambda =-\frac{{{A_1}\left( {\theta, \lambda } \right)\alpha + {B_1}\left( {\theta, \lambda } \right)}}{{{{\left( {{\lambda ^4} + \left( {-2 + 2\theta } \right){\lambda ^3} + \left( {5 + 8\theta + 9{\theta ^2}} \right){\lambda ^2} + \left( {-22\theta - 8 - 18{\theta ^2}} \right)\lambda - 4 - 20\theta - 31{\theta ^2} - 16{\theta ^3}} \right)}^2}}} $ |
由前文假设易知,A1(θ, λ)>0。由此,对B1(θ, λ)的正负情况进行讨论:将B1(θ, λ)写为关于θ的一元四次函数B1(θ)=x1(λ)θ4+x2(λ)θ3+x3(λ)θ2+x4(λ)θ+x5(λ)。通过对θ前系数正负判定,易知,当0 < λ < 0.0659时,x1(λ)>0,x2(λ)>0,x3(λ)>0,x4(λ) < 0,x5(λ) < 0;当0.0659 < λ < 0.2696时,x1(λ)>0,x2(λ)>0,x3(λ)>0,x4(λ)>0,x5(λ) < 0;当0.2696 < λ < 1时,x1(λ)>0,x2(λ)>0,x3(λ)>0,x4(λ)>0,x5(λ)>0。接下来,我们分别讨论三个区间。易知,当0.2696 < λ < 1时,B1(θ)>0,此时∂eD/∂λ < 0。当0 < λ < 0.0659时,可以判定函数
命题1揭示了在不同情况下服务溢出效应对服务水平的影响方式。具体影响方式取决于服务溢出效应大小和线下渠道初始市场规模大小。具体地,当服务溢出效应小于一定值时,零售商会根据其线下渠道占有的初始市场规模大小来调节服务水平大小。在此情形下,我们发现当线下渠道市场规模较小时,零售商会随着服务溢出效应增强而提高服务水平。相反,当线下渠道市场规模较大时,零售商会随着服务溢出效应增强而降低服务水平。当服务溢出效应大于一定值时,无论线下渠道初始市场规模情况如何,零售商总会随着服务溢出效应增强而降低服务水平。
通过对命题1的阐述,对产生以上现象的原因进行分析。首先,一旦服务溢出效应大于一定值(λ>0.181)时,随着服务溢出效应增强,零售商总会通过降低服务水平来抑制服务对制造商线上渠道需求产生的促进作用。这是由于较大的服务溢出效应意味着服务对制造商线上渠道需求的促进作用也较大。此时,为了确保自身利益并防止制造商趁机降低线上渠道价格来凸显竞争优势,零售商只能通过降低服务水平来减少服务水平本身及其较大的溢出效应对制造商线上渠道需求的促进作用。然而,当服务溢出效应小于一定值(λ < 0.181)时,随着服务溢出效应增加,零售商如何调节其服务水平与线下渠道初始市场规模大小有关。为了揭示服务水平变化的原因,我们先考察渠道价格的变化情况。通过软件作图,我们发现,在该范围下,随着服务溢出效应增加,制造商会提高线上渠道价格来提高产品单位利润,而零售商会随之降低线下渠道价格来凸显竞争优势,使零售商线下渠道竞争优势增加,而制造商线上渠道竞争优势则减弱。此时,零售商将根据线下渠道初始规模的大小来调节服务水平。当线下渠道初始规模较小时,零售商会同时利用价格竞争优势和更高的服务水平去吸引更多的消费者。当线下渠道初始规模较大时,由于线下渠道已经具有较大的规模,零售商只利用价格竞争优势就能确保自身利益,因此零售商会降低服务水平。以上分析表明,为了确保自身利益并防止制造商趁机降低线上渠道价格来凸显竞争优势,在大多数情况下,零售商会随着服务溢出效应增强而降低服务水平;然而,当服务溢出效应很小时,由于服务溢出效应的作用有限,零售商会在线下渠道初始规模较小时,同时利用价格竞争优势和更高的服务水平来获取更多需求。在线下渠道初始规模较大时,只需通过价格优势和较低的服务水平来维持竞争优势以及抑制服务对线上需求的促进作用。
接下来,我们考察渠道间价格竞争程度和服务溢出效应对供应链成员最优定价的影响。
命题2:存在临界值α2:(1)当α < α2时,∂pmD/∂θ < 0,进一步,当max(0, α3) < α < α2时,∂2pmD/∂θ ∂λ < 0,否则,∂2pmD/∂θ ∂λ>0;(2)当α>α2时,∂pmD/∂θ>0,∂2pmD/∂θ ∂λ < 0。
证明:根据定理2,求解pmD关于θ的一阶导数为:
| $ \partial p_{\rm{m}}^{\rm{D}}/\partial \theta =-\frac{{{A_2}\left( {\theta, \lambda } \right)\alpha + {B_2}\left( {\theta, \lambda } \right)}}{{{{\left( {{\lambda ^4} + \left( {-2 + 2\theta } \right){\lambda ^3} + \left( {5 + 8\theta + 9{\theta ^2}} \right){\lambda ^2} + \left( {-22\theta - 8 - 18{\theta ^2}} \right)\lambda - 4 - 20\theta - 31{\theta ^2} - 16{\theta ^3}} \right)}^2}}} $ |
易知,A2(θ, λ) < 0,B2(θ, λ)>0。令∂pmD/∂θ=0,可得关于α的临界值α2,当α < α2时,∂pmD/∂θ < 0;反之,∂pmD/∂θ>0。进一步,求解∂pmD/∂θ关于λ的一阶导数为:
| $ {\partial ^2}p_{\rm{m}}^{\rm{D}}/\partial \theta \partial \lambda = \frac{{{A_3}\left( {\theta, \lambda } \right)\alpha + {B_3}\left( {\theta, \lambda } \right)}}{{{{\left( {{\lambda ^4} + \left( {-2 + 2\theta } \right){\lambda ^3} + \left( {5 + 8\theta + 9{\theta ^2}} \right){\lambda ^2} + \left( {-22\theta-8 - 18{\theta ^2}} \right)\lambda - 4 - 20\theta - 31{\theta ^2} - 16{\theta ^3}} \right)}^3}}} $ |
易知,(λ4+(-2+2θ)λ3+(5+8θ+9θ2)λ2+(-22θ-8-18θ2)λ-4-20θ-31θ2-16θ3)3 < 0。令g1(α)=A3(θ, λ)α+B3(θ, λ),可知g1(α)为关于α的单调增函数。由g1(α2)>0,可得当α>α2时,∂2pmD/∂θ ∂λ < 0。然而,当α < α2时,无法通过单调性判定g1(α)正负,因此,对B3(θ, λ)分情况进行讨论:当B3(θ, λ)>0时,对任意α,有∂2pmD/∂θ ∂λ < 0成立;当B3(θ, λ) < 0时,令∂2pmD/∂θ ∂λ=0,可得关于α的临界值α3,当α < α3时,∂2pmD/∂θ ∂λ>0;反之,∂2pmD/∂θ ∂λ < 0。证毕。
命题2揭示了制造商线上渠道价格对渠道间价格竞争程度变化而变化的灵敏性以及服务溢出效应对该灵敏性的影响。首先,渠道间价格竞争程度对制造商线上渠道价格的影响与渠道所占市场份额有关。当线下渠道市场份额小于一定规模时,随着渠道间价格竞争程度的增加,制造商会策略性地降低线上渠道价格以凸显其价格优势,吸引更多需求;当线下渠道市场规模较大时,随着渠道间价格竞争程度的增加,制造商反而会提高线上渠道价格以确保单位产品利润。同时,我们发现,线上价格对价格竞争程度的灵敏性进一步受到市场份额和服务溢出效应的共同影响。当线下渠道市场份额较小时,随着价格竞争程度的增加,线上渠道价格降低。此时,服务溢出效应的增加将会促使制造商趁机加快线上渠道价格的降低速度以吸引更多需求。当线下渠道市场份额进一步增加,服务溢出效应的增加能够抑制制造商价格降低的速度。这说明,一定条件下,服务溢出效应能够缓解渠道间价格竞争。当线下渠道市场份额较大时,随着价格竞争程度的增加,制造商会提高线上渠道价格来提高单位产品利润。此时,服务溢出效应的增加会减缓线上价格增加的速度,使制造商线上渠道在较高单位产品利润情况下获取较多需求。
命题3:存在临界值α4:(1)当α < α4时,∂prD/∂θ>0,进一步,当max(0, α5) < α < α4时,∂2prD/∂θ ∂λ>0,否则,∂2prD/∂θ ∂λ < 0;(2)当α>α4时,∂prD/∂θ < 0,∂2prD/∂θ ∂λ>0。
证明:根据定理2,求解prD关于θ的一阶导数为:
| $ \partial p_{\rm{r}}^{\rm{D}}/\partial \theta = \frac{{{A_4}\left( {\theta, \lambda } \right)\alpha + {B_4}\left( {\theta, \lambda } \right)}}{{{{\left( {{\lambda ^4} + \left( {-2 + 2\theta } \right){\lambda ^3} + \left( {5 + 8\theta + 9{\theta ^2}} \right){\lambda ^2} + \left( {-22\theta-8 - 18{\theta ^2}} \right)\lambda - 4 - 20\theta - 31{\theta ^2} - 16{\theta ^3}} \right)}^2}}} $ |
易知,A4(θ, λ) < 0,B4(θ, λ)>0。令∂prD/∂θ=0,可得关于α的临界值α4,当α < α4时,∂prD/∂θ>0;反之,∂prD/∂θ < 0。进一步,求解∂prD/∂θ关于λ的一阶导数为:
| $ {\partial ^2}p_{\rm{r}}^{\rm{D}}/\partial \theta \partial \lambda =-\frac{{{A_5}\left( {\theta, \lambda } \right)\alpha + {B_5}\left( {\theta, \lambda } \right)}}{{{{\left( {{\lambda ^4} + \left( {-2 + 2\theta } \right){\lambda ^3} + \left( {5 + 8\theta + 9{\theta ^2}} \right){\lambda ^2} + \left( {-22\theta - 8 - 18{\theta ^2}} \right)\lambda - 4 - 20\theta - 31{\theta ^2} - 16{\theta ^3}} \right)}^3}}} $ |
易知,(λ4+(-2+2θ)λ3+(5+8θ+9θ2)λ2+(-22θ-8-18θ2)λ-4-20θ-31θ2-16θ3)3 < 0。令g2(α)=A5(θ, λ)α+B5(θ, λ),可知g2(α)为关于α的单调增函数。由g2(α4)>0,可得当α>α4时,∂2prD/∂θ ∂λ>0。然而,当α < α4时,无法通过单调性判定g2(α)正负,因此,对B5(θ, λ)分情况进行讨论:当B5(θ, λ)>0时,对任意α,有∂2prD/∂θ ∂λ>0成立;当B5(θ, λ) < 0时,令∂2prD/∂θ ∂λ=0,可得关于α的临界值α5,当α < α5时,∂2prD/∂θ ∂λ < 0;反之,∂2prD/∂θ ∂λ>0。证毕。
命题3揭示了零售商线下渠道价格对渠道间价格竞争程度的灵敏性以及服务溢出效应对该灵敏性的影响。首先,零售商线下渠道价格对渠道间价格竞争程度变化而变化的灵敏性与线下渠道市场份额有关。当线下渠道市场规模较小时,随着价格竞争程度增加,零售商会提高线下渠道价格以确保单位产品利润。当线下渠道市场规模较大时,价格竞争程度的增加会促使零售商降低价格以吸引更多需求。线下价格对价格竞争程度的灵敏性也进一步受到市场份额和服务溢出效应的共同影响。当线下渠道市场份额较小时,服务溢出效应的增加会抑制零售商提高价格的增速以在确保产品单位利润情况下获取较多需求。随着线下渠道市场份额进一步增加,零售商线下渠道价格提高的速度随着服务溢出效应的增加而加快。当线下渠道市场份额较大时,服务溢出效应的增加会激励零售商加快价格降低速度以获取更多产品利润。
以上分析表明了服务溢出效应对服务水平的影响以及服务溢出效应如何影响渠道价格对价格竞争强度灵敏性的高低程度。在现实操作中,企业管理者可以根据渠道市场份额相对大小调节服务水平高低以使自身利益最大化。同时,结合渠道间价格竞争程度高低,发挥服务溢出效应对价格竞争的调节作用以保持适度的价格竞争。在命题2和命题3基础上,我们可以得到推论1。
推论1:通过命题2和命题3,我们得到α2>α4,即
(1) 当α < α4时,∂pmD/∂θ < 0,∂prD/∂θ>0;
(2) 当α4 < α < α2时,∂pmD/∂θ < 0,∂prD/∂θ < 0;
(3) 当α>α2时,∂pmD/∂θ>0,∂prD/∂θ < 0。
证明:在条件R下,易判定α2>α4。证毕。
推论1进一步表明了同一条件下,渠道间价格竞争强度变化对制造商和零售商最优渠道价格决策的影响情况。当线下渠道市场份额较小时,渠道间价格竞争强度的增强将驱使制造商降低线上销售价格以突显渠道价格优势,而零售商将被迫提高线下价格以确保产品单位利润。随着线下渠道市场份额进一步增加,制造商和零售商都会通过降低渠道价格来获取竞争优势。此时,渠道间价格竞争加剧。当线下渠道市场份额较大时,制造商提高线上价格以确保单位产品利润,而零售商会降低价格来吸引更多需求。推论1的分析表明,渠道间价格竞争强度一定程度上具有调节渠道定价的作用。渠道间价格竞争强度可以理解为产品替代程度。管理者可以根据市场份额情况,通过调节渠道产品的差异性程度来影响渠道定价进而保持适当的价格竞争。接下来,我们通过比较集中式决策模型和分散式决策模型,进一步揭示分散式决策模型下供应链失调的原因。由此,我们得到命题4。
命题4:(1) pmD < pmC;(2) eD < eC;当α < α6时,prD < prC,反之,prD>prC;(3) πD < πC。
证明:(1) pmD与pmC差值为:
| $ p_{\rm{m}}^{\rm{D}}-p_{\rm{m}}^{\rm{C}} =-\frac{{\left( {2\theta + 1} \right)\left( {{\lambda ^2}-2\lambda - 2\theta - 1} \right)\left( {{A_6}\left( {\theta, \lambda } \right)\alpha + {B_6}\left( {\theta, \lambda } \right)} \right)}}{{\left( {2{\lambda ^2} - 2\lambda - 3\theta - 1} \right)\left( {{\lambda ^4} + \left( { - 2 + 2\theta } \right){\lambda ^3} + \left( {5 + 8\theta + 9{\theta ^2}} \right){\lambda ^2} + \left( { - 22\theta - 8 - 18{\theta ^2}} \right)\lambda - 4 - 20\theta - 31{\theta ^2} - 16{\theta ^3}} \right)}} $ |
易知,λ4+(-2+2θ)λ3+(5+8θ+9θ2)λ2+(-22θ-8-18θ2)λ-4-20θ-31θ2-16θ3 < 0,λ2-2λ-2θ-1 < 0,2λ2-2λ-3θ-1 < 0,B6(θ, λ) < 0。现判定A6(θ, λ)的正负。A6=(5λ-1)θ+λ2+5λ-2为关于θ的一元一次函数。当0 < λ < 0.2时,5λ-1 < 0;当0.2 < λ < 1时,5λ-1>0;当0 < λ < 0.37时,λ2+5λ-2 < 0;当0.37 < λ < 1时,λ2+5λ-2>0。综上,可以得到:
1) 当0 < λ < 0.2时,5λ-1 < 0且λ2+5λ-2 < 0;
2) 当0.2 < λ < 0.37时,5λ-1>0且λ2+5λ-2 < 0;
3) 当0.37 < λ < 1时,5λ-1>0且λ2+5λ-2>0。
易知,在1)下,A6(θ, λ) < 0,可得pmD < pmC;在2)下,λ区间进一步可分为:当0.2 < λ < 0.35且0 < θ < θ时,A6(θ, λ) < 0,易知pmD < pmC;当0.35 < λ < 0.37且0 < θ < θ′时,A6(θ, λ) < 0,易知pmD < pmC;当0.35 < λ < 0.37且θ′ < θ < θ时,A6(θ, λ)>0,其中
(2) eD < eC的证明与命题4 (1)证明类似。现考察prD与prC差值为:
| $ p_{\rm{r}}^{\rm{D}}- p_{\rm{r}}^{\rm{C}} = \frac{{{A_7}\left( {\theta, \lambda } \right)\alpha + {B_7}\left( {\theta, \lambda } \right)}}{{2\left( {2{\lambda ^2}- 1- 3\theta - 2\lambda } \right)\left[{{\lambda ^4} + \left( {-2 + 2\theta } \right){\lambda ^3} + \left( {5 + 8\theta + 9{\theta ^2}} \right){\lambda ^2} + \left( {-22\theta-8 - 18{\theta ^2}} \right)\lambda - 4 - 20\theta - 31{\theta ^2} - 16{\theta ^3}} \right]}} $ |
易知,A7(θ, λ)>0,B7(θ, λ) < 0。令prD-prC=0,可得关于α的临界值α6,当α < α6时,prD < prC;反之,prD>prC。
(3) 由于πC存在唯一最优解,并且πC和πD的利润表达式相同。根据pmD≠pmC、prD≠prC以及eD≠eC,可得πD < πC。证毕。
命题4表明,相较于集中式决策模型,分散式决策模型下供应链系统不能达到最优状态。我们发现,与集中式决策模型相比,制造商在分散式决策模型下始终会制定一个更低的线上渠道价格来吸引更多消费者进行渠道转移。对于零售商来说,由于线下渠道提供的服务对制造商线上渠道需求的溢出效应,相较于集中式决策,为了防止过多的需求溢出效应,零售商在分散式决策下始终会提供一个更低的服务水平以确保自身利益不受损害。同时,根据线下渠道的市场份额情况,零售商进一步调节线下渠道价格水平。
从命题4的分析可以看出,相较于集中式决策模型,在分散式决策模型下,制造商线上渠道价格的降低将加剧渠道间价格竞争。同时,虽然零售商通过降低服务水平来控制服务溢出效应,然而服务水平的降低同时也将导致线下渠道需求的减少,进而迫使零售商在一定情况下通过降低线下渠道价格获取竞争优势。分散式决策情形下供应链成员基于自身利益最大化的决策行为将导致系统失调,不利于供应链实现协调运作。为了实现供应链系统的最优,有必要通过有效的合作机制对供应链成员行为进行约束。
四、基于需求引导的O2O渠道合作机制为了实现分散式供应链系统最优,我们设计一种基于需求引导的O2O线上与线下渠道合作机制。在该机制下,制造商激励零售商提高服务水平来引导消费者从线下转移至线上渠道,为了补偿零售商,制造商同时与零售商分享部分线上渠道收益。由此,我们得到制造商向零售商提供的转移支付机制f为:
| $ f = \varphi {p_{\rm{m}}}{d_{\rm{m}}} + tC\left( e \right)-w{d_{\rm{r}}} $ | (7) |
其中,φ表示制造商分享给零售商的收益比例,t表示制造商承担的零售商服务成本比例,w为批发价格。根据式(7),我们得到合作机制下制造商和零售商的利润函数分别为:
| $ \pi _{\rm{m}}^{\rm{F}} = {p_{\rm{m}}}{d_{\rm{m}}}-f $ | (8) |
| $ \pi _{\rm{r}}^{\rm{F}} = {p_{\rm{r}}}{d_{\rm{r}}}-C\left( e \right) + f $ | (9) |
与分散式决策模型相同,制造商和零售商以各自利润最大化为目标进行求解。当合作机制下的最优解与集中式决策下最优解一致时,供应链系统可以达到最优状态。由此,我们得到命题5。
命题5:当合作机制参数(t, φ, w)满足t=tF且w=wF时,分散式供应链系统能够实现系统最优。其中,
证明:与定理2的求解过程类似,可求得pmF、prF和eF。分别令pmF=pmC、prF=prC以及eF=eC,联立求解,可得到tF(φ)和wF(φ)。证毕。
命题5表明,当合作机制参数满足一定条件时,分散式供应链系统可以获取与集中式决策系统一致的最优系统利润。同时,我们发现,使供应链系统实现协调的机制参数之间存在线性函数关系,这意味着,所设计的合作机制具有柔性,实现供应链系统协调的参数组合有无穷多个。接下来,我们进一步考察服务溢出效应对机制参数的影响。
推论2:
证明:根据命题5,求解tF关于φ的一阶导数
推论2呈现了合作机制参数之间的线性关系以及服务溢出效应对合作机制参数的影响。首先,成本分摊比例和批发价格与收益分享比例之间都存在着单调递减的线性关系。同时,我们发现,服务溢出效应的增加能够激励制造商提高零售商服务成本的分担比例。为了确保自身利益,制造商会随之提高批发价格。虽然该合作机制能够实现供应链系统的最优,然而合作机制的顺利实施还取决于供应链成员是否实现了帕累托改进。由此,我们得到推论3。
推论3:合作机制实施后,当收益共享比例φ满足条件φL < φ < φH时,分散式供应链系统可以实现系统最优利润,各供应链成员能够实现帕累托改进,其中,φL=πrF-πrD,φH=πmF-πmD。
证明:将分散式决策下和合作机制下的最优解分别带入两种情形下的利润函数。联立求解πmF-πmD>0与πrF-πrD>0,可求得φH与φL。证毕。
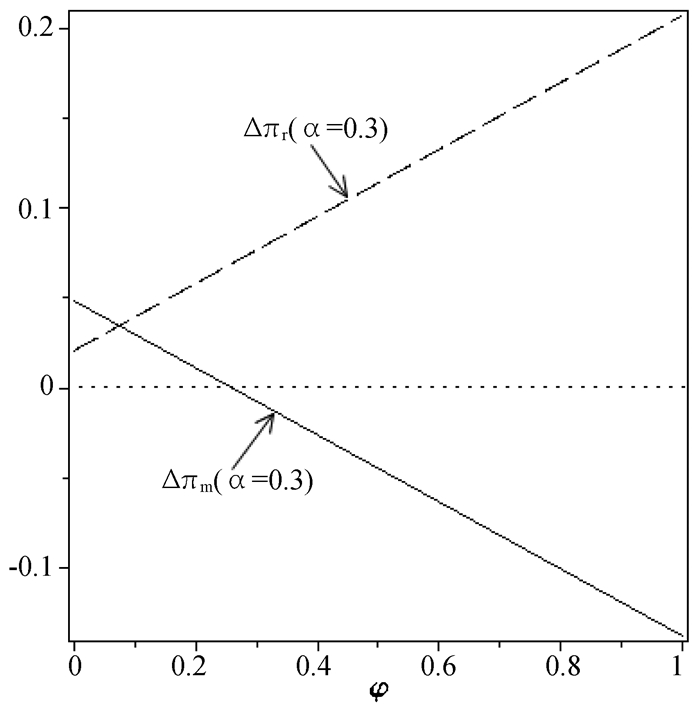
推论3表明在一定条件下,基于需求引导的线上与线下渠道合作机制可使分散式供应链实现完美协调。同时,通过调节收益共享比例,可以实现供应链利润在制造商和零售商之间的任意分配。为了更直观地呈现基于需求引导的渠道合作机制实施效果,令λ=0.8,θ=0.03,α分别取0.3,0.4,0.5,我们得到收益分享比例对制造商和零售商利润变化的影响情况,如图 1、图 2和图 3所示。
|
图 1 α=0.3时φ对供应链成员利润变化的影响情况 |
|
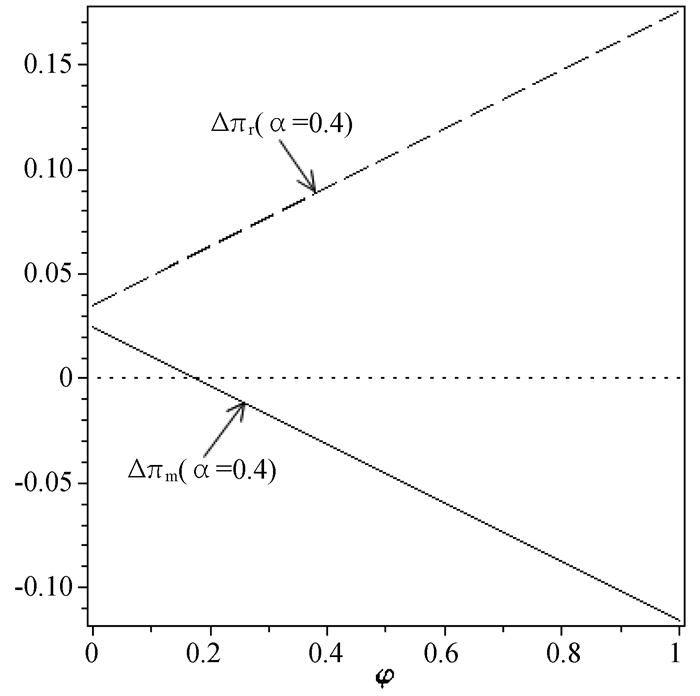
图 2 α=0.4时φ对供应链成员利润变化的影响情况 |
|
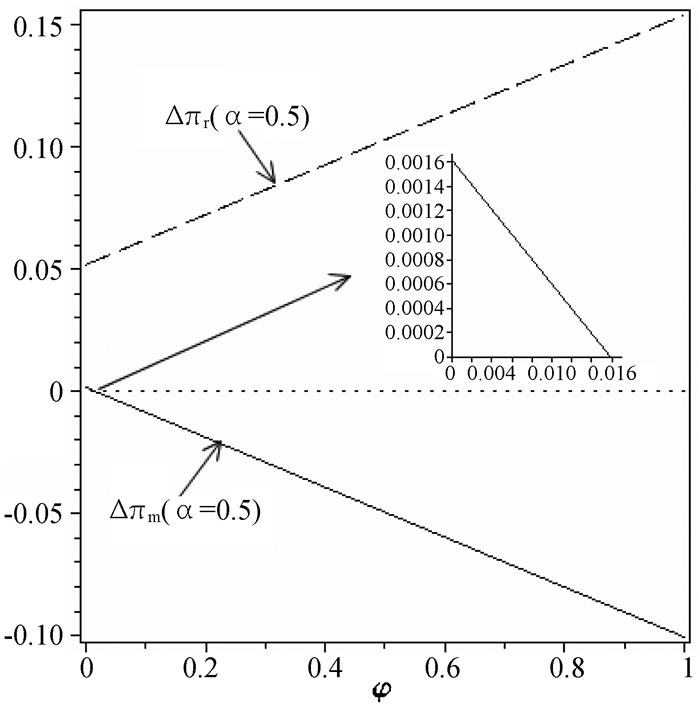
图 3 α=0.5时φ对供应链成员利润变化的影响情况 |
图 1—图 3展示了收益分享比例和市场份额对供应链成员利润变化的影响情况。对制造商来说,合作机制实施后,随着其收益分享比例的增加以及线上渠道市场份额的减少,制造商获取的利润增加量减少。而对零售商来说,随着收益分享比例增加,零售商能更大程度地从合作机制中获益。然而,只有在收益分享比例较小时,零售商才能更大程度受益于线下市场份额的增加。同时,我们发现,当收益分享比例满足一定条件时,合作机制能够实现制造商和零售商的帕累托改进,改进区间随着线下市场份额的增加而缩小。通过以上分析,我们可以看出,在一定条件下,基于需求引导的线上与线下渠道合作机制不仅能够实现分散式供应链决策系统的利润最大化,还能够实现制造商和零售商的帕累托改进。
五、结束语电子商务和互联网技术的快速发展使得制造商从传统单一销售模式向线上与线下渠道并存的双渠道供应链转变。在双渠道销售模式下,制造商线上渠道与零售商线下渠道存在直接竞争。面对线上渠道带来的威胁,零售商借助其线下渠道优势向消费者提供体验服务来吸引更多市场需求。然而,消费者在线下渠道体验服务之后可能转移至制造商线上渠道购买。此时,零售商提供的服务对线上渠道产生了服务溢出效应。同时,随着这种效应的增加,零售商也将失去更多原本属于线下渠道的需求。服务溢出效应的存在可能会抑制零售商提供服务的积极性,进而使供应链双方绩效受损。因此,本文在考虑零售商服务同时存在溢出效应和竞争效应背景下,建立了集中式决策模型和分散式决策模型,求解了不同模型下供应链系统和各成员的最优决策,分析了服务溢出效应对服务水平以及价格竞争的影响,通过对比集中与分散式决策模型,揭示了分散式供应链系统失调的原因。在此基础上,设计了基于需求引导的线上与线下渠道合作机制,实现了供应链系统的协调以及各成员的帕累托改进。通过分析,得到以下重要结论:(1)随着渠道间价格竞争程度增加,制造商和零售商都会借助其渠道市场份额优势降低渠道价格来获取更多产品销量;(2)服务溢出效应增加虽然对零售商线下渠道需求产生竞争效应,然而在一定条件下,这并不会抑制零售商提供服务的积极性。同时,根据渠道市场份额情况以及价格竞争程度大小,服务溢出效应具有调节渠道间价格竞争的作用;(3)分散式决策下供应链成员的自利性将导致供应链系统的失调。基于需求引导的线上与线下渠道合作机制能够改善分散供应链绩效并实现系统利润最大化。同时,该合作机制具有柔性,可以对系统利润进行任意分配以实现供应链各成员的帕累托改进。
| [1] | 邵兵家, 蒋飞, 宁蓓蓓. 网络渠道应用对中国零售业上市公司绩效的影响[J]. 重庆大学学报(社会科学版), 2015, 21(2): 48–57. |
| [2] | 李诗杨, 但斌. 药品连锁零售企业多渠道运营模式及其影响因素研究[J]. 重庆大学学报(社会科学版), 2016, 22(3): 82–88. |
| [3] | LU Q H, LIU N. Effects of e-commerce channel entry in a two-echelon supply chain:A comparative analysis of single-and dual-channel distribution systems[J]. International Journal of Production Economics, 2015, 165: 100–111. DOI: 10.1016/j.ijpe.2015.03.001 |
| [4] | XU G Y, DAN B, ZHANG X M, et al. Coordinating a dual-channel supply chain with risk-averse under a two-way revenue sharing contract[J]. International Journal of Production Economics, 2014, 147: 171–179. DOI: 10.1016/j.ijpe.2013.09.012 |
| [5] | LI Q H, LI B. Dual-channel supply chain equilibrium problems regarding retail services and fairness concerns[J]. Applied Mathematical Modelling, 2016, 40(15/16): 7349–7367. |
| [6] | HU W, LI Y J. Retail service for mixed retail and E-tail channels[J]. Annals of Operations Research, 2012, 192(1): 151–171. DOI: 10.1007/s10479-010-0818-7 |
| [7] | BALAKRISHNAN A, SUNDARESAN S, ZHANG B. Browse-and-switch:Retail-online competition under value uncertainty[J]. Production and Operations Management, 2014, 23(7): 1129–1145. DOI: 10.1111/poms.2014.23.issue-7 |
| [8] | 孙燕红, 涂燚鑑, 徐晓燕. 基于顾客渠道偏好的服务竞争模型[J]. 管理科学, 2011, 24(4): 62–70. |
| [9] | 许民利, 聂晓哲, 简惠云. 不同风险偏好下双渠道供应链定价决策[J]. 控制与决策, 2016, 31(1): 91–98. |
| [10] | 范小军, 刘艳. 制造商引入在线渠道的双渠道价格与服务竞争策略[J]. 中国管理科学, 2016, 24(7): 143–148. |
| [11] | CAI G S, ZHANG Z G, ZHANG M. Game theoretical perspectives on dual-channel supply chain competition with price discounts and pricing schemes[J]. International Journal of Production Economics, 2009, 117(1): 80–96. DOI: 10.1016/j.ijpe.2008.08.053 |
| [12] | RYAN J K, SUN D, ZHAO X Y. Coordinating a supply chain with a manufacturer-owned online channel:A dual channel model under price competition[J]. IEEE Transactions on Engineering Management, 2013, 60(2): 247–259. DOI: 10.1109/TEM.2012.2207903 |
| [13] | YAN R L, PEI Z. The strategic value of cooperative advertising in the dual-channel competition[J]. International Journal of Electronic Commerce, 2015, 19(3): 118–143. DOI: 10.1080/10864415.2015.1000225 |
| [14] | LI B, HOU P W, CHEN P, et al. Pricing strategy and coordination in a dual channel supply chain with a risk-averse retailer[J]. International Journal of Production Economics, 2016, 178: 154–168. DOI: 10.1016/j.ijpe.2016.05.010 |
| [15] | 王先甲, 周亚平, 钱桂生. 生产商规模不经济的双渠道供应链协调策略选择[J]. 管理科学学报, 2017, 20(1): 17–31. |
| [16] | LUO M L, LI G, CHENG T C E. Free riding and coordination in a dual-channel supply chain in e-commerce[J]. International Journal of Shipping and Transport Logistics, 2016, 8(3): 223–249. DOI: 10.1504/IJSTL.2016.076253 |
| [17] | 艾兴政, 马建华, 陈忠, 等. 服务搭便车的电子渠道与传统渠道协调机制[J]. 系统工程学报, 2011, 26(4): 507–514. |
| [18] | 罗美玲, 李刚, 张文杰. 双渠道供应链中双向搭便车研究[J]. 系统管理学报, 2014, 23(3): 314–323. |
| [19] | 浦徐进, 龚磊. 消费者"搭便车"行为影响下的双渠道供应链定价和促销策略研究[J]. 中国管理科学, 2016, 24(10): 86–94. |
| [20] | TAYLOR T A. Supply chain coordination under channel rebates with sales effort effects[J]. Management Science, 2002, 48(8): 992–1007. DOI: 10.1287/mnsc.48.8.992.168 |
| [21] | YAO D Q, LIU J J. Competitive pricing of mixed retail and e-tail distribution channels[J]. Omega, 2005, 33(3): 235–247. DOI: 10.1016/j.omega.2004.04.007 |
| [22] | Van BAAL S, DACH C. Free riding and customer retention across retailers' channels[J]. Journal of Interactive Marketing, 2005, 19(2): 75–85. DOI: 10.1002/dir.20036 |
 2018, Vol. 24
2018, Vol. 24

