2. 四川雪宝乳业集团有限公司, 四川 绵阳 621000
2. Sichuan Xuebao Dairy Group Co., Ltd., Mianyang 621000, P. R. China
截至2017年6月, 中国网民规模达到7.51亿, 互联网普及率达54.3%。互联网的普及为网民表达自己对事件的态度和看法提供了便捷途径, 这种对事件的态度和看法形成网络舆情, 网络舆情通过网络媒体的传播和扩散, 在一定程度上能够促进或阻碍事态发展。地震造成基础设施、人员和财产的巨大损失, 在各种因素作用下震灾舆情增加了震灾的应对难度, 甚至造成更为严重的次生或衍生灾害。
现行的各种舆情管控实践证明, 如果能够对震灾网络舆情风险进行科学评估, 一方面能够有效减轻震灾带来的灾害损失和社会危害, 另一方面能够为应急管理部门掌握灾区需求信息和制定舆情管控预案提供支持。目前相关研究主要集中于网络舆情的热度、传播规律、风险管控等方面。在网络舆情热度研究方面, 王慧军等[1]为降低舆情热度负面影响, 依据优化理论, 研究了政府对舆情热度监控问题; 柳虹[2]提出了舆情热点发现模型, 对均值聚类和支持向量机两种算法在网络舆情发现作用方面进行了比较; 方倩等[3]认为微信公众号文章热度与主题、推送时间、标题特征相关, 与推送频率弱相关; 焦超等[4]提出了独立网络突发事件热度分布的泊松分布模型; 翟晓芳等[5]通过分析微博提出了新的热度指标计算方法; 曹学艳等[6]研究了突发事件网络舆情热度等级与突发事件风险等级之间的对应关系, 根据对应关系的“一致”或“不一致”提出突发事件应对策略; 张一文等[7]研究了非常规突发事件网络舆情热度评估指标和权重; 魏德志等[8]将新闻网页内容的相似度和页面链接分析作为话题热度的计算依据, 提出一种基于时间序列的热点话题发现模型; Fu等分别采用不同聚类算法和仿真模型对网络热点时间进行发现和模拟[9-12]。在网络舆情传播研究方面, 王治莹等[13]研究了政府干预下突发事件舆情传播规律与管控决策问题; Huo等[14]建立了突发事件下官方行为与舆情传播的交互作用模型; Lebensztayn等[15]构建了群众谣言传播的马尔科夫模型; Zhao等[16]研究了突发事件演化与舆情传播及官方媒介的交互作用; 齐佳音等[17]研究了突发公共事件网络舆情的耦合机制, 认为网络舆情的耦合协调度与社会影响力呈正比; 康伟[18]研究了网络舆情传播结构对信息的传播路径、速度和范围的影响。在网络舆情风险管控方面的研究, 张玉亮[19]依据突发事件发生周期系统提出网络舆情风险评估指标; 路枝芳等[20]以舆情热点事件为验证对象, 采用因子聚类分析方法研究了2015年中国第一季度各类热点舆情事件的风险程度。
综上, 现有研究主要有两方面需要继续深入:一是在指标构建上, 现有研究更多考虑事件的外因, 即社会属性, 如舆情转载量、评论量及发文量等, 较少考虑事件本身的物理属性, 如事件自身导致舆情演化的动因、敏感性、促进因素等。对外因的考虑也多从定量角度提取指标, 较少关注一些定性指标, 尤其是面对突发灾害背景下网络舆情监测所涉及的关键不确定性指标; 二是针对震灾网络舆情综合风险评估问题较少涉及, 已有研究更多围绕舆情热点的分布、线性拟合及预测等方面, 少量成果针对突发事件风险提出监测指标与评估方法, 但监测指标更多突出舆情风险的社会属性, 很少涉及导致舆情风险的物理属性, 而且评估方法较为单一, 往往忽略突发灾害网络舆情指标数据的非线性、高维度和非正态问题, 评估结果与实际偏差较大。基于以上原因, 本研究的不同之处在于:从突发灾害网络舆情的物理属性和社会属性两方面提出适应性强、能够覆盖整个舆情演化周期的风险监测指标; 将BP神经网络运用于突发灾害网络舆情综合风险评估之中, 并用AGA对BP神经网络进行改进, 提出基于AGABP的震灾网络舆情风险评估方法。
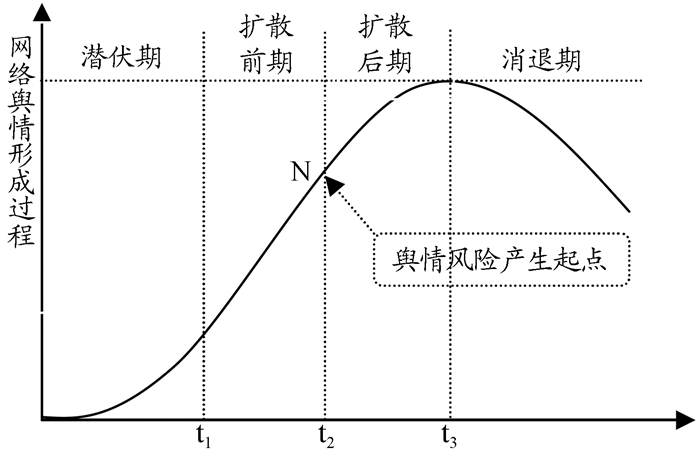
二、震灾网络舆情风险监测指标 (一) 指标构建网络舆情主要有潜伏、扩散和消退三个阶段, 其传播曲线呈“S”型(如图 1), 其风险点一般处于传播中的扩散前期和扩散后期的转折处, 如图 1中的N点, N点也是舆情高涨转折点。
|
图 1 网络舆情传播过程 |
在图 1中, 网络舆情传播风险的产生和高涨的出现主要由载体、主体和事件本身共同推动完成。网络媒体是震灾舆情产生的载体, 属条件因素; 网民是震灾舆情产生的主体, 属推动因素; 震灾是舆情事件的本身, 属舆情产生的诱导因素。条件因素和推动因素是震灾网络舆情扩散和传播的社会属性, 诱导因素是震灾网络舆情的物理属性, 敏感性对舆情的产生起诱导作用。在风险监测指标设计上, 本研究围绕震灾网络舆情产生的物理属性和社会属性两个维度的作用力设计风险监测指标。
其一, 震灾网络舆情产生的物理属性。这由震灾本身的危害程度决定, 一般来讲, 震灾危害程度越大, 社会影响力就越高, 诱发网络舆情扩散的能力也会越强。可采用震灾危害等级、受灾程度等二级指标予以衡量, 其中震灾危害等级主要包括地震震级和震中烈度2个三级指标, 受灾程度主要包括伤亡人数、受灾范围、财产损失3个三级指标。
其二, 震灾网络舆情产生的社会属性。可采用震灾应急能力、网络媒体作用力、舆情扩散能力3个二级指标予以衡量, 其中震灾应急能力对减轻灾害损失、缓解网民负面情绪有直接影响, 主要包括应急资源满足能力、政府部门反应能力、监测预警能力3个三级指标; 网络媒体作用力主要包括各主要网络平台的发文量、评论数及转发量3个三级指标; 舆情扩散能力主要包括点击数与回复数之比、原发文数变化率2个三级指标。
综上所述, 本研究围绕物理属性和社会属性两个维度提出5个二级指标和13个三级指标的震灾网络舆情风险监测评估指标, 进一步通过文献调查、专家问询等方式, 在震灾危害等级中增加1个次生灾害发生概率的三级指标, 在震灾应急能力中增加1个灾民综合满意度的三级指标, 删除舆情扩散能力指标, 形成4个二级指标和13个三级初选指标。为验证初选指标之间相对独立性、与评估目标的相关性及代表性, 本研究采取专家计分的方式获取了13个初选指标的初始数据, 并采用Cronbach
| 表 1 震灾网络舆情风险监测指标体系 |
表 1中的震灾应急能力所属的三级指标采取专家计分方式确定; 网络作用力所属三级指标采用北京清博大数据科技有限公司开发的“清博大数据舆情系统”平台中的数据, 通过统计微信、微博、网页、报刊、客户端和论坛6个舆情传播平台上地震网络舆情的发文量、评论数和转发量数据。
(二) 建立风险等级标准建立震灾网络舆情风险等级标准包括两部分内容:设定风险等级数和确定各风险等级下每个指标的标准区间值。在设定震灾网络舆情风险等级数上, 本研究参考国际惯例及国内相关学者研究, 将震灾网络舆情风险等级划分为4级, 即v={Ⅳ, Ⅲ, Ⅱ, Ⅰ}={极高风险, 高风险, 一般风险, 低风险}, 并赋值:“极高风险”为4、“高风险”为3、“一般风险”为2、“低风险”为1。在确定各风险等级下每个指标的标准区间上, 以上海交通大学舆情研究实验室“中国公共事件数据库”为依托, 从500多起震灾案例中挑选出2000年以来震级在3~9之间的150起案例作为研究样本, 针对定性指标按表 1赋值后采取问卷方式获取数据; 针对定量指标, 以特定期间客观数据为准, 其中, 地震震级、伤亡人数和财产损失风险标准依据《国家地震应急预案》确定, 其余指标的风险等级划分借鉴蒋金才等[21]对水旱灾害风险等级划分方法, 对获取的指标数据采用聚类方法进行修正后得到震灾网络舆情风险等级标准值。由于震灾背景下的网络舆情风险指标数据往往具有不确定性, 各指标的风险等级标准难以用确切数据划分, 故采用模糊区间数表示各指标的风险等级更为合理。鉴于此, 本研究以150起案例为依据, 采用四分位风险划分方法来确定震灾网络舆情风险等级标准。具体做法是:首先, 将各个指标的专家建议值Z(i)进行升序排列, 设定Z(i)max为极高风险上限值, Z(i)min为最低风险下限值, 中位数Z(i)med为一般风险值; 然后, 找出Z(i)min和Z(i)med序列中的中位数Z*(i)med、Z(i)med和Z(i)max序列的中位数Z**(i)med, 其风险等级划分方法如表 2。
| 表 2 震灾网络舆情风险等级标准 |
最后, 依据表 2方法, 计算各个风险等级下每个指标的标准区间值, 如表 3。
| 表 3 震灾网络舆情风险等级标准 |
BP神经网络是一种负梯度优化算法, 具有自适应、自组织、容错性和鲁棒性强的优点, 而且易于在计算机上实现编译。将BP神经网络用于震灾舆情网络风险评估点评估中, 能够有效解决多指标非线性、高维度和非正态评估问题的局限性, 有利于评估系统以任意均方差的精度逼近任意平方可积非线性连续函数, 保证评估结果的可靠。但BP神经网络学习速度较慢、存在局部最小问题, 会在很大程度上影响网络的外推能力。为解决这个问题, 采用AGA对常规BP神经网络进行改进, 在BP算法训练评估网络出现收敛速度缓慢时启动AGA来优化网络参数, 把优化的参数作为BP算法的初始值。通过这样的改进, 能够有效增强BP网络的外推能力, 防止训练网络进入局部循环。
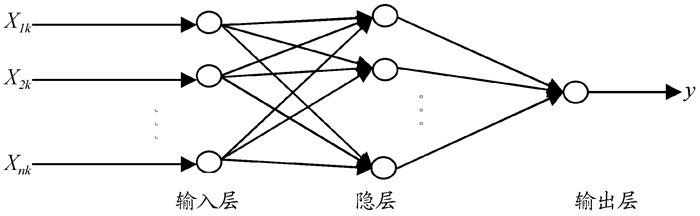
(一) 构建步骤由于存在一个三层BP神经网络可以任意精度逼近从输入层到输出层的映射, 对输出层节点n和隐层节点m的大小没有严格限制。根据经验, 隐层的节点数m一般不宜过大, m较大, BP网络的概括能力和训练速度都会降低, 在能达到期望精度条件下, m的取值范围一般控制在[n, 2n+1]内且尽可能小。本研究构建一个三层BP神经网络(如图 2), 其拓扑结构为n :n :1, n取3。
|
图 2 三层BP神经网络拓扑结构 |
记输入层神经元为h, 隐层神经元为i, 输出神经元为j, 隐层节点i和输出层节点j的阈值分别为θi、θj, 输入层节点h与隐层节点i间以及输出层节点j与隐层节点i间的连线权值分别为whi、wij, 各点的输入、输出分别为x、y。基于AGA的BP网络算法设计如下。
步骤1:指标随机样本点获取。在后续的BP神经网络训练中, 首先需要随机生成无量纲的震灾网络舆情风险等级样本数据, 通过随机样本训练得到最优参数后, 再用实际样本数据进行测试。在随机样本数据获取上, 本研究参考王硕等[22]的研究成果, 用均匀随机数在各级指标变化区间范围内随机产生nu个指标样本值x*(k, j), 相应的震灾网络舆情风险标准等级值为y(k)=i。为充分反映评估指标中各指标的边界值的信息, 取各指标边界值各1次, 风险等级值取与该边界值有关的两个风险等级值的算术平均值, 这样就可得震灾网络舆情风险评估标准样本系列{x*(k, j), y(k)}, k=1~nk, j=1~nj, 其中nk为样本数目。为消除指标量纲, 使本研究评估模型具有一般性, 各指标的无量纲化处理采取以下式子进行:
| $ x\left( {k, j} \right) = {x^*}\left( {k, j} \right)/{X_{{\rm{max}}}}\left( j \right)\;\;\;\;\;\;\;\;\;\left( {k = 1 \sim nk, j = 1 \sim nj} \right) $ | (1) |
| $ a\left( {i, j} \right) = {a^*}\left( {k, j} \right)/{x_{{\rm{max}}}}\left( j \right)\;\;\;\;\;\;\;\;\;\;\;\left( {i = 1\sim ni, j = 1\sim nj} \right) $ | (2) |
| $ b\left( {i, j} \right) = {b^*}\left( {k, j} \right)/{x_{{\rm{max}}}}\left( j \right)\;\;\;\;\;\;\;\;\;\;\;\;\left( {i = 1\sim ni, j = 1\sim nj} \right) $ | (3) |
步骤2:初始化。设用于机器学习的已做归一化处理后的震灾舆情网络样本值的输入、输出样本对为{xhk, dk|h=1, 2, …, n; k=1, 2, …, N}, 给各节点间的连接权值、阈值赋予(-1, 1)区间上的随机值。
步骤3:置k=1。把各层输入、输出样本对{xhk, dk}提供给网络, (h=1, 2, …, n; k=1, 2, …, N)。
步骤4:计算隐层各节点的输入xi、输出yi, 输出层节点的输入xj、输出yj, 则有:
| $ {x_i} = \sum\limits_{h = 1}^n {{w_{hi}}{x_{hk}}} + {\theta _i}, {y_i} = 1/\left( {1 + {e^{-{x_i}}}} \right), \;(i = 1, 2, \ldots, n) $ | (4) |
| $ {x_j} = \sum\limits_{i = 1}^n {{w_{ij}}{y_i}} + {\theta _j}, {y_j} = 1/(1 + {e^{-{x_j}}}) $ | (5) |
步骤5:计算输出层节点所收到的总输入变化时单样本点误差Ek=0.5(yj-dk)2的变化率以及隐层节点所收到的总输入变化时单样本点误差Ek的变化率。
| $ \frac{{\partial {E_k}}}{{\partial {x_j}}} = {y_i}\left( {1-{y_i}} \right)\left( {{y_i}-{d_k}} \right) $ | (6) |
| $ \frac{{\partial {E_k}}}{{\partial {x_i}}} = {y_i}\left( {1-{y_i}} \right)(\frac{{\partial {E_k}}}{{\partial {x_j}}}{w_{ij}}), \left( {i = 1, 2, \ldots, n} \right) $ | (7) |
步骤6:修正各连接的权值和阈值。
| $ {w_{ij}}^{m + 1} = {w_{ij}}^m-\eta {y_i}\frac{{\partial {E_k}}}{{\partial {x_j}}} + a\left( {{w_{ij}}^m-{w_{ij}}^{m-1}} \right), {\theta _j}^{m + 1} = {\theta _j}^m - \eta \frac{{\partial {E_k}}}{{\partial {x_j}}} + a\left( {{\theta _j}^m - {\theta _j}^{m - 1}} \right) $ | (8) |
| $ {w_{hi}}^{m + 1} = {w_{hi}}^m-\eta {x_{hk}}\frac{{\partial {E_k}}}{{\partial {x_i}}} + a\left( {{w_{hi}}^m-{w_{hi}}^{m-1}} \right), {\theta _i}^{m + 1} = {\theta _i}^m - \eta \frac{{\partial {E_k}}}{{\partial {x_i}}} + a\left( {{\theta _i}^m - {\theta _i}^{m - 1}} \right) $ | (9) |
其中, m为修正次数, η为学习速率且η∈(0, 1), a为动量因子且a∈(0, 1)。
步骤7:置k=k+1, 转步骤3, 直至全部N个样本点训练完毕, 转步骤9。
步骤8:转步骤2, 进行新一轮的学习, 直至网络全局误差函数小于预先设定的一个较小值或学习次数大于预先设定的值, 结束学习。
| $ E = \sum\limits_{k = 1}^N {{E_k}} = \sum\limits_{k = 1}^N {{{\left( {{y_j}-{d_k}} \right)}^2}/2} $ | (10) |
为使式(10)的全局误差函数极小化, 需要确定BP网络中θi、θj、whi和wij的最优值, 以促使各层级网络连接的权值和阈值达到稳定。标准BP神经网络在训练参数过程中容易出现局部最小问题, 且训练后的参数在学习后期收敛速度过于缓慢, 在较大程度上影响评估结果的可靠性。本研究采用AGA对BP网络参数进行优化, 将优化后的参数作为BP网络的初始值, 避免标准BP网络的不足。其优化步骤如下[23]。
(1) BP网络参数变化区间构造。设cj是BP算法训练网络出现收敛速度缓慢时网络的任一参数的值, 则它的变化区间构造为[aj, bj], 其中, aj=cj-d|cj|, bj=cj+d|cj|, d为一正的常数。
(2) BP网络参数编码。设编码长度为e, 把区间[aj, bj]等分成2e-1个子区间, 于是整个网络参数变化空间被离散成(2e)p个网格点。其中, p=2n2+n+1。每个网格点称为个体, 它对应网络p个参数的一种可能取值状态, 并用p个e位二进制数表示。于是, p个网络参数、网格点、个体、二进制数予以一一对应。
(3) 初始父代群体的随机生成与父代个体适应度的评估。从上述(2e)p个网格点中均匀随机选取n个点作为初始父代群体。把第i个个体代入式(7)中, 得到相应的网络全局误差函数值Ei, Ei越小则个体的适应能力越强。
(4) 父代个体的选择与杂交。把父代个体按优化准则函数值Ei从小到大排序, 排序后最前面几个个体称为优秀个体。构造与Ei成反比的函数pi, pi>0, p1+p2+…, +pn=1, 从这些父代个体中以概率pi选择i个个体。于是共选择两组各为n个的个体, 然后将两组个体随机两两配对n对双亲, 将双亲的二进制数组的任意一段值互换, 得到两组子代个体。
(5) 子代个体的变异。任取步骤父代个体杂交中的一组子代个体, 将它们的二进制数组的任意两值以变异率pm进行翻转, 即将原值为0的变为1, 原值为1的变为0。
(6) 迭代。由步骤(6)得到的n个子代个体作为新的父代, 算法转入父代个体适应度评估步骤, 进入下一代进化过程。
(7) 加速循环。用第一次、第二次进化迭代所产生的优秀个体参数的变化范围, 作为参数新的初始变化区间, 算法进入网络参数编码步骤, 即上述步骤(2);如此循环往复, 优秀个体的参数变化区间将逐步收缩, 与最优的距离越来越近, 直至达到给定加速次数, 结束运行。
步骤9:把待测的第k期对应各单项评估模型的评估值作为输入样本, 输入已学习完毕的网络, 其网络输出值经过与归一化对应的逆处理即为组合评估值Fk。
(二) 控制参数配置在AGA-BP算法中, 根据经验, 控制参数预先设定为:(1)设定BP网络中的学习因子η=0.1, 动量系数a=0.1;(2)设定AGA中的编码长度e=10, 变异率pm=1.0, 父代个体数目q=300, 优秀个体数目s=10。
四、实例应用 (一) 验证数据选取计算机运行环境为:Core(TM) 2 CPU 2.29GHZ、内存为2.00GB, 仿真工具:Matlab_R2012a。本研究从《中国震例》中选取2005年以来国内发生的6次地震作为AGABP评估模型的验证数据, 数据获取途径包括定性指标专家评分、清博大数据舆情系统、《中国震例》及官方网站(如表 4)。其中, 网络舆情转发量、发文量及评论量的统计期间规定为震灾发生当日后30日的数据量; 震级、死伤人数及财产损失以震灾发生地官方网站公布为准。评估方法应用分为两个阶段:第一阶段采用随机样本数据训练AGABP网络以获得最优参数, 并与BP神经网络、逻辑斯蒂曲线对比, 以观察AGABP评估模型的训练精度; 第二阶段将6次地震网络舆情数据装入训练后的AGABP模型中, 对6次震灾网络舆情的风险性进行评估, 并提出政策建议。
| 表 4 2005年以来6次震灾网络舆情风险监测指标数据 |
根据表 3的震灾网络舆情风险等级标准和步骤1, 随机生成1~31组震灾网络舆情风险等级标准样本数据, 如表 5所示。
| 表 5 震灾网络舆情风险评估随机样本数据及AGABP计算对比 |
对样本数据按式(1)至式(3)进行无量纲处理后输入AGABP网络学习训练, 取训练次数10 000次, AGABP加速寻优4次, 计算结果如表 5。进一步, 将随机样本数据输入BP神经网络、逻辑斯蒂曲线, 其训练精度对比如图 3。

|
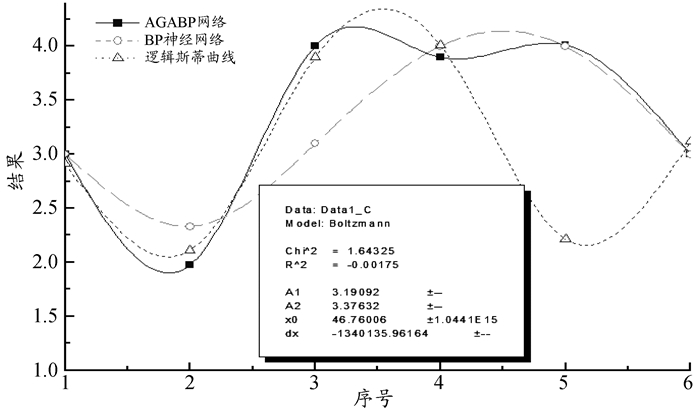
图 3 AGABP与BP神经网络、逻辑斯蒂曲线训练精度对比 |
从图 3可知, 经过10 000次训练后, AGABP网络全局误差为0.000 712, 达到收敛要求; BP网络的全局误差为0.001 671;逻辑斯蒂曲线的拟合误差为0.001 011。与实际风险等级值相比, AGABP网络的精度明显高于BP神经网络和逻辑斯蒂曲线; 此时, AGABP网络的稳定权值和阈值见表 6。
| 表 6 随机样本数据训练AGABP网络10 000次后的稳定权值和阈值 |
经过10 000次训练后, AGABP网络的阈值和各层的权值达到稳定, 训练精度符合要求, 说明训练后的AGABP网络能够用于震灾网络舆情风险评估中。分别运用AGABP网络、BP神经网络和逻辑斯蒂曲线对表 4中6个案例进行评估。设定AGABP网络和BP神经网络各自训练次数15 000、加速寻优4次, 其他参数不变; 逻辑斯蒂曲线仍采取拟合方式进行风险评估。三种方法得到结果如表 7、图 4所示。
| 表 7 三种方法的评估结果 |
|
图 4 AGABP、BP和逻辑斯蒂的评估曲线 |
采用AGABP模型对6次震灾网络舆情风险评估结果表明:(1)地震震级、伤亡人数、财产损失、发文量、评论数和转发量等6个指标是影响震灾网络舆情风险等级的关键性指标。通过观察随机数据训练结果, 次生灾害发生率、应急资源满足能力、监测预警能力和灾民综合满意度这4个指标对震灾网络舆情风险等级的影响程度低于其余6个指标。(2)AGABP模型评价结果与实际基本一致, 可信度高于BP神经网络和逻辑斯蒂曲线。表 7中, BP神经网络将汶川地震网络舆情风险评估为低风险, 这与实际不符, 实际上汶川地震后网络舆情迅速扩散, 谣言四起, 经过政府、专家的正确引导和管控才杜绝众多负面舆情的膨胀。逻辑斯蒂曲线将雅安地震评估为一般风险, 这也与实际不符。
五、结论科学构建震灾网络舆情风险评估体系是制定网络舆情应对预案、提升震灾应急效率和增加灾害应急能力的基础工作。本研究得出如下结论。
第一, 提出具有高度代表性特征的震灾网络舆情风险监测指标。依据网络舆情传播规律和震灾网络舆情产生特征, 从事件的物理属性和社会属性两方面设置风险监测粗选指标。通过指标信度、效度检验后, 采用主成分分析和累计贡献率方法对粗选指标筛选后, 提出2个维度、4个二级指标、10个三级指标所构成的震灾网络舆情风险监测指标体系。模型验证结果表明, 本研究所构建的指标体系能够有效对震灾网络舆情进行评估。
第二, 训练后的AGABP模型, 在收敛速度、参数优化和预防过早收敛上明显优越于BP神经网络, 能够用于震灾网络舆情风险管理实践。
第三, AGABP模型的精度高于BP神经网络和逻辑斯蒂曲线。样本训练和实例验证表明, BP神经网络容易陷入局部最优, 精度低于AGABP模型, 训练时间也长于AGABP模型; 逻辑斯蒂曲线在众多非线性拟合中精度较高, 从图 3、图 4也可以看出, 两次拟合结果表明逻辑斯蒂曲线对非线性数据的拟合结果十分稳定, 但与AGABP模型相比, 逻辑斯蒂曲线的拟合精度仍然较差。
| [1] | 王慧军, 石岩, 胡明礼, 等. 舆情热度的最优监控问题研究[J]. 情报杂志, 2012, 31(1): 71–75. DOI: 10.3969/j.issn.1002-1965.2012.01.014 |
| [2] | 柳虹, 徐金华. 网络舆情热点发现研究[J]. 科技通报, 2011, 27(3): 421–425. DOI: 10.3969/j.issn.1001-7119.2011.03.022 |
| [3] | 方倩, 陆伟. 微信公众号信息传播热度的影响因素实证研究[J]. 情报杂志, 2016, 35(2): 157–162. DOI: 10.3969/j.issn.1002-1965.2016.02.028 |
| [4] | 焦超, 刘功申. 网络突发热点事件的热度分布[J]. 通信技术, 2012, 4(4): 58–60. DOI: 10.3969/j.issn.1003-8329.2012.04.014 |
| [5] | 翟晓芳, 刘全明, 程耀东, 等. 基于转发层次分析的新浪微博热度评估研究[J]. 计算机工程, 2015, 41(7): 31–35. DOI: 10.3969/j.issn.1000-3428.2015.07.006 |
| [6] | 曹学艳, 张仙, 刘樑, 等. 基于应对等级的突发事件网络舆情热度分析[J]. 中国管理科学, 2014, 22(3): 82–89. DOI: 10.3969/j.issn.1003-207X.2014.03.011 |
| [7] | 张一文, 齐佳音, 方滨兴, 等. 非常规突发事件网络舆情热度指标评估体系构建[J]. 情报杂志, 2010, 29(11): 71–75. DOI: 10.3969/j.issn.1002-1965.2010.11.016 |
| [8] | 魏德志, 陈福集, 林丽娜. 一种基于时间序列的热点话题发现模型和算法[J]. 情报科学, 2017, 35(10): 142–146. |
| [9] | FU X H, LI J Q, YANG K, et al. Dynamic Online HDP model for discovering evolutionary topics from Chinese social texts[J]. Neuroncomputing, 2016, 171(1): 412–424. |
| [10] | KHAN K, BAHARUDIN B, KHAN A, et al. Mining opinion components from unstructured reviews:A review[J]. Journal of King Saud University-Computer and Information Sciences, 2014, 26(3): 258–275. DOI: 10.1016/j.jksuci.2014.03.009 |
| [11] | HUANG S H, LIU Y, DANG D P. Burst topic discovery and trend tracing based on Storm[J]. Physical A:Statistical Mechanics and its Applications, 2014, 416(15): 331–339. |
| [12] | MA B J, ZHANG N, LIU G N, et al. Semantic search for public opinions on urban affairs:A probabilistic topic modeling-based approach[J]. Information Processing & Management, 2016, 52(3): 430–445. |
| [13] | 王治莹, 李勇健. 政府干预下突发事件舆情传播规律与控制决策[J]. 管理科学学报, 2017, 20(2): 43–52. DOI: 10.3969/j.issn.1007-9807.2017.02.005 |
| [14] | HUO L A, HUANG P Q, FANG X. Interplay model for authorities' media and rumor spreading in emergency event[J]. Physical A:Statistical Mechanics and its Applications, 2011, 390(20): 3267–3274. DOI: 10.1016/j.physa.2011.05.008 |
| [15] | LEBENSZTAYN E, RODRIGUEZ P M. A connection between a system of random walks and rumor transmission[J]. Physical A:Statistical Mechanics and its Applications, 2013, 392(23): 5793–5800. DOI: 10.1016/j.physa.2013.07.073 |
| [16] | ZHAO L J, WANG Q, CHENG J J, et al. The impact of authorities' media and rumor dissemination on the evolution of emergency[J]. Physical A:Statistical Mechanics and its Applications, 2012, 391(15): 3978–3987. DOI: 10.1016/j.physa.2012.02.004 |
| [17] | 齐佳音, 刘慧丽, 张一文. 突发公共危机事件网络舆情耦合机制研究[J]. 情报科学, 2017, 35(9): 102–108. |
| [18] | 康伟. 突发事件舆情传播的社会网络结构测度与分析—基于"11.16"校车事故的实证研究[J]. 中国软科学, 2012, 7(7): 169–178. DOI: 10.3969/j.issn.1002-9753.2012.07.018 |
| [19] | 张玉亮. 基于发生周期的突发事件网络舆情风险评估指标体系[J]. 情报科学, 2012, 30(7): 1034–1037. |
| [20] | 路枝芳, 薛耀文. 基于因子聚类分析的舆情风险研究[J]. 情报科学, 2016, 34(7): 76–80. |
| [21] | 蒋金才, 季新菊, 刘良, 等. 河南省1950~1990年水旱灾害分析[J]. 灾害学, 1996(4): 69–73. |
| [22] | 王硕, 张礼兵, 金菊良. 系统预测与综合评价方法[M]. 合肥: 合肥工业大学出版社, 2006: 186-191. |
| [23] | 王思艳.自适应遗传算法的研究[D].保定: 华北电力大学, 2009. |
 2018, Vol. 24
2018, Vol. 24

