纵观人类的经济发展历程,从史前时代到公元纪年,物质生活匮乏的局面一直没有显著改观;1800年以前,就全人类平均而言,生活水准从来没有较大进步,一直在“马尔萨斯陷阱”中徘徊;直到发生“工业革命”,人均收入才呈持续快速增长趋势。但许多经济体发展到一定阶段以后,很可能又会陷入另一个“中等收入陷阱”中。
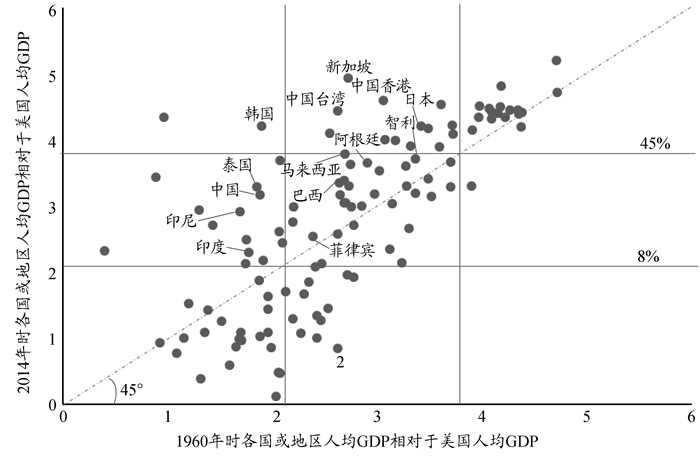
从图 1可以看出,在所考察的113个国家或地区中,1960年时处于中等收入组①的共有58个国家或地区,到2014年时,其中有13个国家或地区已步入高收入组,12个国家或地区却跌入低收入组,其余33个国家或地区仍处于中等收入组。可见当步入中等收入国家或地区后,其发展差距很大,只有少数国家或地区人均收入进一步相对增长,步入了高收入国家或地区的行列,其余大部分仍在原地徘徊甚至下跌。
① 本文依据各国以美元计价的人均收入占美国人均收入的百分比来定义收入分组(图 1再将此百分比取自然对数):“低收入国家或地区”:≤8%(ln8=2.08);“中等收入国家或地区”:8% < ~≤45%(ln45=3.81);“高收入国家或地区”:>45%。
|
图 1 中等收入陷阱图② 数据来源:Penn World Table 9.0(http:// www.ggdc.net/pwt) |
② 在由横纵两组ln8和ln45直线划分的三行三列中,首先,处于中间列的国家或地区表示的是1960年时处于中等收入国家或地区组;然后,再将此中间列细分:处于上行的是2014年时已步入高收入组的国家或地区(13个)、处于中间行的是仍处于中等收入组的国家或地区(33个)、处于下行的是跌入低收入组的国家或地区(12个)。另外,就所有113个国家或地区整体而言,收入相对下降(即处于45度线以下)的国家或地区共有45个。
诞生于21世纪初并且目前正处于蓬勃发展阶段的统一增长理论旨在将整个人类历史统一起来,从而为整个人类历史发展提供解释。Galor认为“统一”有双重含义:一是宏观经济增长模型与其微观基础的统一;二是将长期经济发展不同阶段的内生转型过程统一在同一理论框架中[1]171-293。统一增长理论主要从技术进步、人力资本积累、人口转型等角度来解释经济发展转型,在人类发展早期,人口规模引致技术进步;随着社会经济的发展,人力资本积累开始成为技术进步及促进经济增长的重要原因。发挥作用的机制可以概括为三类:第一,从物质资本和人力资本回报率的相对关系角度,Galor和Moav提出,经济发展初期物质资本匮乏,物质资本回报率高于人力资本回报率,经济增长主要由物质资本驱动。随着经济发展,物质资本存量增加,人力资本回报率逐渐上升,这激励了人力资本投资,并使其逐渐成为推进经济增长的重要原因[2]1001-1026。第二,人口转型影响居民养育子女数量及质量决策的角度,生育率[3]481-501、预期寿命[4]401-418、子女成活率和营养状况[5]114-144、死亡率[6]1058-1104这些影响人口结构的因素发生变化会影响居民养育子女数量及对其进行人力资本投资数量的决策,进而影响经济增长。第三,从人口规模扩大带来的外溢性角度,Goodfriend和Mcdermott[7]116-133、Jones[8]1-45以及Voigtländer和Voth[9]319-361说明人口规模扩大使得思想交流更便利,这种外部性会促进技术进步进而摆脱“马氏陷阱”。
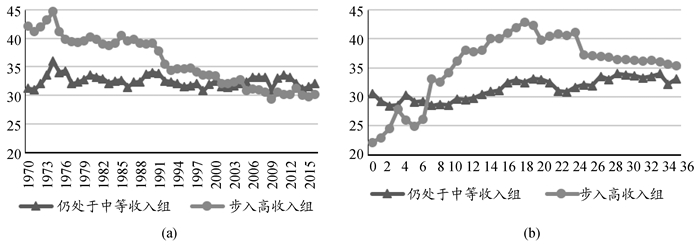
不同产业部门对技术水平及人力资本规模的需求是不同的,在经济发展的不同阶段发挥着不同的作用,从世界主要经济体的产业结构变迁来看,工业部门的发展在经济体步入快速增长阶段中发挥了重要的先导作用。接续图 1对1960年时的中等收入国家或地区进行产业结构变迁分析,按2014年时的相对收入水平分为:仍处于中等收入组(33个国家或地区)和步入高收入组(13个国家或地区),分别计算组内国家或地区工业产值占GDP比重的均值。从图 2可以看出,步入高收入组国家或地区的均值显著高于仍处于中等收入组国家或地区的均值,尤其是从(b)图(初始时刻设定为各经济体工业化起始的年份③)看,这些成功跳跃“中等收入陷阱”的国家或地区都有一个工业部门产值占比显著提升的过程,工业部门高度发达后,才有逐渐下降的趋势。这说明工业的发展不仅直接增加国民收入,而且基于其强大的上下游产业“联动效应”能有效带动其他产业的发展,不仅能有效提升农业的生产效率,也能使服务业建立在更高的发展平台之上,否则只能发展低附加值的劳动密集型低端服务业。
③ 步入高收入组的国家或地区工业化起始年份:中国香港、爱尔兰、葡萄牙,1950;塞浦路斯、西班牙、希腊、意大利、日本、马耳他、新加坡、塞舌尔,1960;中国台湾,1970;特立尼达和多巴哥,1980。仍处于中等收入组的国家或地区工业产值占GDP比重计算的起点取以上年份的中位值1965年。
|
图 2 中等收入国家或地区工业产值占GDP比重图(%) 数据来源:根据CEIC数据库—全球数据库(China Economic & Industry Data Database,https://insights.ceicdata.com/insight/34dfa752-27ba-46b3-b2fb-080864cffd89/data)相关数据计算而得 |
本文的理论探索在于试图从三大产业的关联发展、人口规模扩大、人口质量提高角度来解释跨越“马尔萨斯陷阱”及寻求跨越“中等收入陷阱”的途径。从公元前8 000年的新石器革命到工业革命之前,人类一直受马尔萨斯人口理论的制约,随着农业部门生产率的提高和人口规模逐渐扩大,市场也逐步扩张,工业企业能承担更大的创新成本,技术水平显著提升,人类就此跨越了“马氏陷阱”;但是随着人均收入水平的提高,人口增速逐渐放缓,一方面作为生产要素市场的要素供给者,投入增速放慢,另一方面作为商品市场的需求者,市场规模扩大也受到限制,这时通过提升人口素质,积累人力资本,降低工业企业的创新(固定)成本,能够使生产技术进一步发展,这是跨越“中等收入陷阱”的可能路径之一。具体而言,首先,从微观经济主体的最优化行为及人口增长规律出发推导出经济增长的内生转型机制,使该增长理论建立在微观基础之上,也为探讨有助于跨越“中等收入陷阱”的微观经济政策寻找切入点;其次,建模描述了经济体中各部门的相互作用,以及强调了工业发展在经济转型中的重要作用,突出了差异化产品种类与垄断定价的相互关系及其对技术进步的作用,很好地拟合了经济现实;然后,在拟合经济现实的基础上,通过数值模拟,使各变量的作用方向更明晰,及作用大小可比较;最后,探索了能激励微观经济主体增加有效劳动总规模进而摆脱陷阱的微观经济政策。
本文以下的安排是:首先建立一个四部门增长模型,阐释产业间关联发展、人口增长与人力资本积累使经济体相继跨越“马氏陷阱”和“中等收入陷阱”的机制;然后进行量化分析,拟基于经济发展事实进行参数赋值,然后通过数值模拟分析经济增长率关于人口转型参数及主要经济决策相关变量的弹性;最后总结全文并得出政策启示。
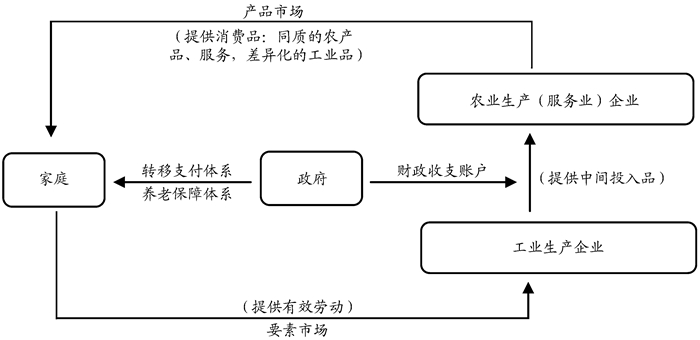
二、模型该模型包含四个部门:农业生产(服务业)部门、工业生产部门、家庭部门和政府。
假设农业生产(服务业)部门在产品市场上是完全竞争的,生产单一同质不可储存的消费品(服务),所需投入的生产要素包括劳动和土地(代表广义的自然资源)。该部门有自身外生的技术进步率,同时也受工业部门技术水平提高的影响。
工业生产部门在产品市场上是垄断竞争性的,生产一系列差异化产品,能够根据产品需求弹性进行成本加成定价,在非长期均衡点处能获得垄断利润,而这样的非长期均衡抑或是经济体的常态。正是由于垄断利润的存在,工业生产企业才有激励进行产品种类创新和提高生产效率的生产过程创新。工业部门的创新不仅能提高本部门的生产效率,还因为大部分工业产品可以作为中间投入品应用到农业生产(服务业)部门中,因此可以带动其他部门生产效率的提高。
家庭部门中的代表性个人生存两期,获得效用的来源是消费同质的农产品(服务)、差别化的工业品,以及闲暇。对于工业品的消费,每个家庭有特定的偏好类型。时间分配是接受教育获取人力资本、在农业生产(服务业)或工业生产部门劳动获取收入,以及退休后享受闲暇。家庭接受教育的时间分配决策是人力资本积累速度的决定因素之一。
政府部门经营即收即付制的养老保障体系、通过遗产税将死去人的财富进行再分配的转移支付体系和财政收支账户。政府可以通过前两个体系影响家庭的劳动供给和人力资本积累决策,即影响有效劳动总量;通过财政收支账户制定有效的财政政策。
这四个部门有各自的行为模式,又相互关联,最终共同决定了经济增长率。政府可以在了解这些决策机制的基础上,寻找政策相关变量,最终影响经济增长路径。
|
图 3 模型框架图 |
假定经济体中的代表性个人生存两期:青年期和老年期,每一时期的时间总量都被单位化为1。
青年期接受教育,积累人力资本,时间比例为et(0 < et < 1);其余时间用于工作,时间比例即为1-et。获得的工资收入在缴纳养老保险后,一部分用于本期消费,一部分储蓄留待下期消费。
老年期只将全部时间中lt(0 < lt < 1)比例的部分用于工作,获得工资收入;其余时间退休,领取养老金。
1. 人口结构Nt, i(其中i=0或1)表示生存在第t期的年轻人(i=0时)或生存第t期的老年人(i=1时) ④,则第t期的总人口量自然是年轻人和老年人数量之和:Nt=Nt, 0+Nt, 1。
④ 即第一个下标表示生存的时期,第二个下标表示处于青年期(取0值)或老年期(取1值)。以下类似的二维下标都有同样的含义。
假定人口增长率是n(n>0),则Nt, 0=(1+n)Nt-1, 0。
假定存活率是s(0 < s < 1),则Nt, 1=sNt-1, 0。
因此老年人的扶养比=
进一步内生化人口增长率n。为了刻画人口增长率的变动,我们分析一下人类经济和人口发展的历史:在摆脱“马氏陷阱”之前,人口增长始终被有限的生产力水平所压抑,增长缓慢;工业革命之后,人口增长率显著提高;经济发展到现代,随着人力资本在生产过程中发挥越来越重要的作用,个人对教育的投资也越来越多,这意味着抚养子女的成本也逐渐提高,抑或是随着产品和服务逐渐丰富,人们认为未来的生活更有保障,对养育子女的需求逐渐降低,人口增长率逐步放缓。为了描述人口增长率的这种变动趋势,我们在马氏人口增长理论的基础上进一步引入了人力资本的因素,将人口增长率函数设定为以下形式:
| $ {n_{\rm{t}}} = \beta \left( {{w_{\rm{t}}} - \bar w} \right) - \tau \left( {{H_{\rm{t}}}} \right) $ | (1) |
其中,wt表示人均收入,w表示维持基本生存的最低人均收入,β>0,第一项基于马氏人口理论,即只有当人均收入在维持基本生存后还有剩余时,人口才开始增长;Ht表示人力资本规模,τ′(H)t >0表示抚养子女的成本随着人力资本规模扩大而提高,进而人口增长率下降。很显然,在人类经济发展初期,人力资本规模很低,主要是第一项发挥作用;随后,随着人力资本积累,第二项对人口增长的抑制作用逐渐显露;发展到现代,第二项发挥着主导作用。
2. 政府影响的财富转移支付体系假设经济体中存在这样一种财富转移支付体系:由于我们考虑了死亡率(或称预期寿命),即有些年轻人的生命不能延续至老年期,又没有直接引入遗赠动机,因此存在一种将不能存活至老年期的年轻人的遗产转移给存活老年人的转移支付体系,以便抵消死亡风险对财产浪费的影响,使“沉淀”的资产重新回流到经济体中。联系经济现实,这种转移支付体系也具有遗赠的性质,虽然在现实中大多是代际间的遗赠,但从整个经济体的特定一期看,死去人的财富终究是分配给了存活的人,并且该体系与遗赠有非常重要的一点相似性质——直接增加了接受者的终生可支配收入。因此可以将该财富转移支付体系理解为一种简化形式的遗赠。
通过这种方式可以分析人口死亡和财富转移支付体系的财富再分配作用:假定t期年轻人的财产(即储蓄)量是st,暂时不考虑利率,单纯考虑转移支付体系的影响,则到了t+1期已变为老年人时的财产量是
(1) 效用函数。
代表性居民终生总效用是青年期和老年期效用的贴现值之和,并且采用离散形式。第t期出生的一代人终生效用函数用Ut表示,它是关于在每一期所获效用的函数。青年期将全部时间用于人力资本投资或工作,没有闲暇,仅从消费中获得效用;老年期部分时间工作,部分退休,从闲暇和消费中获得效用。消费品包括同质的农业消费品(服务),以及差异化的工业产品。效用函数采用C-D型,具体形式是:
| $ {U_{\rm{t}}} = U\left( {{u_{{\rm{t}},0}},{u_{{\rm{t}} + {\rm{1}},1}}} \right) = {\left[ {{{\left( {{C^A}} \right)}^{1 - \alpha }} \cdot {{\left( {{C^M}} \right)}^\alpha }} \right]^\mu }{\left[ {\beta s\left( {1 - {l_{{\rm{t}} + 1,1}}} \right)} \right]^{1 - \mu }} $ | (2) |
其中,lt+1, 1表示老年期的劳动时间比例,则1-lt+1, 1即表示退休时间比例;CA表示一生中对农产品(服务)消费的贴现值,即CA= Β·Ca;Β为主观时间偏好行向量,Β = [1, βs], β表示主观时间偏好率,其与存活率s的乘积可理解为考虑死亡风险后的“综合主观时间偏好率”;Ca=[ca, t, ca, t+1]T表示消费列向量;同理,CM= Β · Cm,Cm= [g(cm, t), g(cm, t+1)]T,其中cn, i(n=a, m; i=t, t+1)表示第i期对农产品(或服务)(当n=a时)或工业品(当n=m时)的消费量。
Gautschi和Lancaster为考虑差异化工业品种类与价格的关系提供了很好的理论分析框架[10]403-405,本文在此基础上将居民对工业品的消费作出进一步的设定:假定在t期所有工业产品的种类是Vt,并且所有这些种类均匀地分布在一个虚拟的“种类环”上,该环形的周长设为χ,先考虑χ是外生恒定的情形。每位居民对工业品有其特定的偏好类型,并且该种类偏好也均匀地分布在“种类环”χ上。假设理想的消费种类是
| $ g\left( {{c_{m,{\rm{t}}}}} \right) = \mathop {\max }\limits_{m \in {V_{\rm{t}}}} \left( {\frac{{{c_{m,{\rm{t}}}}}}{{1 + d_{m\tilde m}^\gamma }}} \right) $ | (3) |
等式右侧括号内表达式的含义是,与消费1单位理想种类
(2) 预算约束。
我们考虑了两种消费品,需要确定它们的价格,简化起见,设农产品(服务)的价格为1,工业品的价格为pm, t,该价格有相对价格的含义。
假设工资收入需要按照τt的贡献率向养老保障账户缴费,并且在退休后领取退休金Pt+1。
| $ \begin{array}{l} \mathit{\boldsymbol{R}} \cdot {\mathit{\boldsymbol{C}}_a} + \mathit{\boldsymbol{P}} \cdot {\mathit{\boldsymbol{C}}_m} \le \\ \left( {1 - {e_{\rm{t}}}} \right){h_0}{w_{\rm{t}}}\left( {1 - {\tau _{\rm{t}}}} \right) + \frac{s}{{\left( {1 + {r_{{\rm{t}} + 1}}} \right)\xi }}\left[ {{l_{{\rm{t}} + {\rm{1}},1}}{h_{{\rm{t}} + {\rm{1}},1}}{w_{{\rm{t}} + {\rm{1}}}}\left( {1 - {\tau _{{\rm{t}} + {\rm{1}}}}} \right) + \left( {1 - {l_{{\rm{t}} + {\rm{1}},1}}} \right){P_{{\rm{t}} + {\rm{1}}}}} \right] = {y_{\rm{t}}} \end{array} $ |
其中,R表示农产品(服务)消费支出的折现向量,
(3) 教育技术。
| $ {h_{{\rm{t}} + {\rm{1}},1}} = \left( {1 + h\left( {{e_{\rm{t}}}} \right)} \right){h_0} $ | (4) |
其中h(et)是描述将接受教育的时间投入转化为人力资本的函数,其函数值表示人力资本的增长率。h′(et) >0,h″(et) < 0,并且满足稻田条件之一:
为了使模型得出解析解,我们进一步具体化人力资本生产函数的形式:
| $ h\left( {{e_{\rm{t}}}} \right) = Ae_{\rm{t}}^\varphi $ | (5) |
其中,A>0,表示技术参数;0 < φ < 1,表示该人力资本生产函数具有规模报酬递减的性质。由此可得有效劳动总规模:Ht= 1-eth0Nt, 0+lt, 1ht, 1Nt, 1,即以人力资本为权重的青年人和老年人劳动供给量的加权总和。
(4) 最优化行为。
| $ \begin{array}{l} \mathop {\max }\limits_{{C_{a,{\rm{t}}}},{C_{m,{\rm{t}}}},{e_{\rm{t}}},{l_{{\rm{t}} + 1,1}}} {U_{\rm{t}}} = {\left[ {{{\left( {{C^A}} \right)}^{1 - \alpha }} \cdot {{\left( {{C^M}} \right)}^\alpha }} \right]^\mu }{\left[ {\beta s\left( {1 - {l_{{\rm{t}} + 1,1}}} \right)} \right]^{1 - \mu }}\\ {\rm{s}}.{\rm{t}}.\;\;\;\;\mathit{\boldsymbol{R}} \cdot {\mathit{\boldsymbol{C}}_\mathit{\boldsymbol{a}}} + \mathit{\boldsymbol{P}} \cdot {\mathit{\boldsymbol{C}}_m} \le {y_{\rm{t}}} \end{array} $ |
构建拉格朗日函数解此最优化问题:
| $ L\left( {{C_{a,{\rm{t}}}},{C_{m,{\rm{t}}}},{e_{\rm{t}}},{l_{{\rm{t}} + 1,1}},\lambda } \right) = {\left( {{C_{a,{\rm{t}}}}^{1 - \alpha } \cdot C_{m,{\rm{t}}}^\alpha } \right)^\mu }{\left[ {\beta s\left( {1 - {l_{{\rm{t}} + 1,1}}} \right)} \right]^{1 - \mu }} + \lambda \left( {{C_{a,{\rm{t}}}} + {p_{m,{\rm{t}}}}{C_{m,{\rm{t}}}} - {y_{\rm{t}}}} \right) $ |
一阶条件:
| $ \left\{ \begin{array}{l} \mathit{\boldsymbol{R}} \cdot {\mathit{\boldsymbol{C}}_a} = \left( {1 - \alpha } \right){y_{\rm{t}}}\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left( {6{\rm{i}}} \right)\\ \mathit{\boldsymbol{P}} \cdot {\mathit{\boldsymbol{C}}_m} = \alpha {y_{\rm{t}}}\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left( {6{\rm{ii}}} \right)\\ h'\left( {{e_{\rm{t}}}} \right) = \frac{{\left( {1 + {r_{{\rm{t}} + 1}}} \right)\xi }}{s}\frac{{{w_{\rm{t}}}\left( {1 - {\tau _{\rm{t}}}} \right)}}{{{l_{{\rm{t}} + 1,1}}{w_{{\rm{t}} + 1}}\left( {1 - {\tau _{{\rm{t + 1}}}}} \right)}}\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left( {6{\rm{iii}}} \right)\\ {l_{{\rm{t}} + 1,1}} = 1 - \frac{1}{{\frac{1}{{s\beta }} + 2}}\frac{{\frac{{\left( {1 + {r_{{\rm{t}} + 1}}} \right)\xi }}{s}\left( {1 - {e_{\rm{t}}}} \right){h_0}{w_{\rm{t}}}\left( {1 - {\tau _{\rm{t}}}} \right) + {h_{{\rm{t}} + 1,1}}{w_{{\rm{t}} + 1}}\left( {1 - {\tau _{{\rm{t + 1}}}}} \right)}}{{{h_{{\rm{t}} + 1,1}}{w_{{\rm{t}} + 1}}\left( {1 - {\tau _{{\rm{t + 1}}}}} \right) - {P_{{\rm{t + 1}}}}}}\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left( {6{\rm{iv}}} \right) \end{array} \right. $ |
式(6iii)的含义是教育的边际回报=相对于综合利率的净工资收益。将g′(et) =Aφetφ-1的具体形式代入,得到最优人力资本投资量:
| $ e_{\rm{t}}^ * = {\left[ {A\varphi {l_{{\rm{t}} + 1,1}}\frac{s}{{\left( {1 + {r_{{\rm{t}} + 1}}} \right)\xi }}\frac{{{w_{{\rm{t}} + 1}}\left( {1 - {\tau _{{\rm{t + 1}}}}} \right)}}{{{w_{\rm{t}}}\left( {1 - {\tau _{\rm{t}}}} \right)}}} \right]^{\frac{1}{{1 - \varphi }}}} $ | (7) |
从以上表达式可以看出影响人力资本投资量的因素如下。
第一,扣除向养老保障账户缴费后的净工资增长率:
第二,物资资本收益率:rt+1。人力资本投资量与该收益率反相关。
综合以上两因素可发现,一些外生冲击,例如人口变迁带来原始劳动力缺乏时,会使w上升和r下降,会随之带来人力资本投资量et*上升。
第三,人力资本生产效率,由参数A和φ表示。人力资本生产越有效率,居民更倾向于进行人力资本投资。
第四,老年期的工作时间:lt+1, 1。老年期的工作时间延长,延长了积累的人力资本发挥作用的时间,自然居民更倾向于投资人力资本。
第五,转移支付因子ξ及存活率s,
从式(6iv)可以看出影响老年期工作时间的因素如下。
其一,主观时间偏好率,或“综合主观时间偏好率”βs:老年期工作时间与该偏好率负相关。从效用函数中可以看出,βs越大,劳动带来的负效用也越大。
其二,终生劳动收入,即减数的第二个分式的分子部分:终生劳动收入越大,劳动时间越短,这说明工资上升带来的收入效应占主导。
其三,老年期工资收入与退休金的差额,即减数的第二个分式的分母部分:老年期工作时间与该差额正相关。工资收入相对越高,越倾向于工作;反之,领取退休金。
(二) 农业生产(服务业)部门 1. 生产函数首先考虑农业生产部门,假设需要两种投入要素:土地和劳动。为了避免代际继承问题,假定土地供给量单位化为1,被农民所有。生产函数采用如下形式:
| $ {Y_{a,{\rm{t}}}} = {A_{a,{\rm{t}}}}H_{a,{\rm{t}}}^\theta $ | (8) |
其中,Ya, t表示农业部门总产量;Ha, t表示有效劳动投入量;θ(0 < θ < 1)表示该部门存在着边际报酬递减,这如实刻画了农业部门的生产效率,否则,农业部门足以维持人口增长并摆脱“马氏陷阱”;Aa, t表示农业部门的技术水平,模型为了简化分析,省略了资本投入要素,但也可以理解为资本被包含在Aa, t中,因为技术与物质资本具有不可分性,需要其作为物质载体。
工业品有大部分可以作为中间投入品被用于其他生产部门,工业生产部门发展对其他部门生产效率提高的联动效应反映在技术水平提高函数中:
| $ {A_{a,{\rm{t}} + {\rm{1}}}} = {A_{a,{\rm{t}}}}\left( {1 + \lambda _{\rm{t}}^a} \right) $ | (9) |
其中, λta=max {ra, λtm},ra表示恒定的外生增长率,λtm表示内生决定的工业部门的技术进步率。
2. 利润最大化该生产部门的利润最大化问题是:
| $ \mathop {\max }\limits_{{H_{a,{\rm{t}}}}} {\Pi _{a,{\rm{t}}}} = {A_{a,{\rm{t}}}}H_{a,{\rm{t}}}^\theta - {w_{a,{\rm{t}}}}{H_{a,{\rm{t}}}} $ |
其中wa, t表示农业部门的工资率。该优化问题得到一阶条件:
| $ {w_{a,{\rm{t}}}} = \theta {A_{a,{\rm{t}}}}H_{a,{\rm{t}}}^{\theta - 1} $ | (10) |
部门总利润(地租):Π
a, t= (1-θ) Aa, tHa, tθ;每单位有效劳动获得的利润:
以上描述的是农业部门。在人类经济发展的初期,主要是农业部门的率先发展为工业部门的发展提供物质基础,然后工业部门的崛起又促进了农业部门的发展,最终跳跃了“马氏陷阱”。随着经济发展,农业部门的产值占比逐渐下降并趋于稳定,服务业产值占比逐渐提高。工业部门对其他部门的“联动效应”也主要体现为其对服务业部门的作用,这种作用又为跨越“中等收入陷阱”提供了可能的路径。
(三) 工业生产部门 1. 生产函数假设工业生产部门的投入要素仅有有效劳动,固定成本(也以有效劳动的形式存在)的存在使生产具有了规模报酬递增的性质。与农业生产部门的生产函数类似,也可以理解为资本被隐含在技术参数中。生产函数形式如下:
| $ {Y_{m,{\rm{t}}}} = {A_{m,{\rm{t}}}}\left( {{H_{m,{\rm{t}}}} - {F_{m,{\rm{t}}}}} \right) $ | (11) |
其中,Ym, t表示种类为m的工业品产量;Hm, t表示有效劳动投入量。
Fm, t表示固定成本,具体形式是
Am, t表示技术水平,Am, t= (1+λtm) Ax, t,所有企业在t期初始的基础技术水平是t-1期所有工业企业技术水平的均值:
| $ {A_{x,{\rm{t}}}} = \sum\limits_{m \in {V_{{\rm{t}} - 1}}} {\frac{1}{{{x_{{\rm{t}} - 1}}}}{A_{m,{\rm{t}} - {\rm{1}}}}} $ | (12) |
其中xt-1表示t-1期工业品的种类数。
综合以上函数,则工业部门生产函数的具体形式是:
| $ {Y_{m,{\rm{t}}}} = \left( {1 + \lambda _{\rm{t}}^m} \right){A_{x,{\rm{t}}}}\left( {{H_{m,{\rm{t}}}} - f \cdot {e^{\frac{{\lambda _{\rm{t}}^m}}{H}}}} \right) $ | (13) |
可见,技术进步率λtm对产量Ym, t有正反两个方向的作用:正向作用,λtm越大,技术水平越高;反向作用,λtm越大,固定成本也越大。
2. 利润最大化由于每个工业企业都生产的是有差别的产品,并且存在固定成本,所以每一类产品都只由一个企业生产。每个垄断竞争企业对自己的产品具有一定的定价权,利润最大化决定的变量包括:单价、销售量、有效劳动投入量和采用的技术水平。
| $ \max {\Pi _{m,{\rm{t}}}} = {p_{m,{\rm{t}}}}{c_{m,{\rm{t}}}} - {w_{m,{\rm{t}}}}{H_{m,{\rm{t}}}} $ |
将
| $ \mathop {\max }\limits_{{p_{m,{\rm{t}}}},\lambda _{\rm{t}}^m} {\Pi _{m,{\rm{t}}}} = {p_{m,{\rm{t}}}} \cdot {c_{m,{\rm{t}}}}\left( {{p_{m,{\rm{t}}}}} \right) - {w_{m,{\rm{t}}}}\left[ {\frac{{{c_{m,{\rm{t}}}}\left( {{p_{m,{\rm{t}}}}} \right)}}{{\left( {1 + \lambda _{\rm{t}}^m} \right){A_{x,{\rm{t}}}}}} + f \cdot {e^{\frac{{\lambda _{\rm{t}}^m}}{H}}}} \right] $ |
一阶条件:
| $ \left\{ \begin{array}{l} {p_{m,{\rm{t}}}} = \frac{{{w_{m,{\rm{t}}}}}}{{\left( {1 + \lambda _{\rm{t}}^m} \right){A_{x,{\rm{t}}}}}}\frac{{{e_{m,{\rm{t}}}}}}{{{e_{m,{\rm{t}}}} - 1}}\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left( {14{\rm{i}}} \right)\\ \frac{{{c_{m,{\rm{t}}}}}}{{{{\left( {1 + \lambda _{\rm{t}}^m} \right)}^2}{A_{x,{\rm{t}}}}}} - \frac{f}{H}{e^{\frac{{\lambda _{\rm{t}}^m}}{H}}} = 0\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left( {14{\rm{ii}}} \right) \end{array} \right. $ |
其中em, t表示种类m工业品的需求价格弹性,
政府经营即收即付制的养老保障体系、通过遗产税将死去人的财富进行再分配的转移支付体系和财政收支账户。
即收即付制的养老保障体系,该账户的预算约束是:
| $ {\tau _{\rm{t}}}{w_{\rm{t}}}\left[ {\left( {1 - {e_{\rm{t}}}} \right){h_0}{N_{{\rm{t,0}}}} + {l_{{\rm{t,1}}}}{h_{{\rm{t,1}}}}{N_{{\rm{t,1}}}}} \right] = \left( {1 - {l_{{\rm{t,1}}}}} \right){P_{\rm{t}}}{N_{{\rm{t,1}}}} $ | (15) |
将老年人的扶养比
| $ {\tau _{\rm{t}}}{w_{\rm{t}}}\left[ {\left( {1 - {e_{\rm{t}}}} \right){h_0}{N_{{\rm{t,0}}}} + {l_{{\rm{t,1}}}}{h_{{\rm{t,1}}}}\frac{s}{{1 + n}}} \right] = \left( {1 - {l_{{\rm{t,1}}}}} \right){P_{\rm{t}}}\frac{s}{{1 + n}} $ | (16) |
以下集中分析这样一种“对称性均衡”的状态,也是一种长期均衡的状态:工业品的种类在虚拟的“种类环”上均匀分布,所有工业企业都采用相同的技术,产品定价也相同。暂时不考虑产品种类增加的情形。另外假定“种类环”的周长χ外生恒定,稍后再考虑其影响因素。
1. 总需求种类m工业品的总需求仅取决于其位置及“左邻右舍”产品的定价。两个相邻种类的距离:
假设居民偏好也在“种类环”上均匀分布,为了得出种类m工业品的总需求,首先需要确定哪些居民会购买种类为m的工业品。居民选择种类的原则是理想种类(
| $ {p_{c,{\rm{t}}}}\left[ {1 + {{\left( {{d_{\rm{t}}} - {d_{m,{\rm{t}}}}} \right)}^\gamma }} \right] = {p_{m,{\rm{t}}}}\left( {1 + d_{m,{\rm{t}}}^\gamma } \right) $ | (17) |
其中,pm, t表示种类m的工业品单价,pc, t表示种类m竞争者的单价。考虑到不区分“左邻”与“右舍”,并且产品定价相同,因此得dt=2dm, t,“偏好环”上一段
由家庭效用最大化一阶条件式(6ii)知,每个家庭一生中将其全部收入的α比例部分用于工业品消费,这是从单个人一生的纵向角度分析;根据结构的对称性,从t期经济体整体而言,也会将经济体总产出Yt的α比例部分用于工业品消费:
| $ {c_{m,{\rm{t}}}} = \frac{{{d_{\rm{t}}}}}{\chi }\frac{{\alpha {Y_{\rm{t}}}}}{{{p_{m,{\rm{t}}}}}} $ | (18) |
从上式可得:
| $ - \frac{{{p_{m,{\rm{t}}}}}}{{{c_{m,{\rm{t}}}}}}\frac{{\partial {c_{m,{\rm{t}}}}}}{{\partial {p_{m,{\rm{t}}}}}} = 1 - \frac{{{p_{m,{\rm{t}}}}}}{{{d_{m,{\rm{t}}}}}}\frac{{\partial {d_{m,{\rm{t}}}}}}{{\partial {p_{m,{\rm{t}}}}}} $ | (19) |
将式(17)关于pm, t求全微分,解出
| $ {e_{m,{\rm{t}}}} = 1 + \frac{{\left( {1 + d_{m,{\rm{t}}}^\gamma } \right){p_{m,{\rm{t}}}}}}{{\left[ {{p_{m,{\rm{t}}}}\gamma d_{m,{\rm{t}}}^{\gamma - 1} + {p_{c,{\rm{t}}}}\gamma {{\left( {{d_{\rm{t}}} - {d_{m,{\rm{t}}}}} \right)}^{\gamma - 1}}} \right]{d_{m,{\rm{t}}}}}} $ | (20) |
再引入对称性:pm, t=pc, t,dt=2dm, t,得:
| $ {e_{m,{\rm{t}}}} = 1 + \frac{1}{{2\gamma }}{\left( {\frac{2}{{{d_{\rm{t}}}}}} \right)^\gamma } + \frac{1}{{2\gamma }} $ | (21) |
该弹性表达式背后的经济学含义是直观的:当工业品的种类数(xt)增加时,种类间距(dt)缩小,则具体种类m的需求弹性提高,即单个垄断竞争企业对其产品的垄断能力降低,定价的成本加成也会下降。
2. 对称性均衡动态均衡是由人口增长运动方程、工业部门的基础技术进步率,以及相关的农业(服务业)部门技术进步率共同决定的一系列静态均衡点的轨迹。
从以下三个公式中可以得出人类经济发展跳跃“马氏陷阱”的原因以及寻求摆脱“中等收入陷阱”的可能途径。
垄断竞争企业在长期均衡点处,垄断利润为零,因此存在零利润约束:
| $ {\Pi _{m,{\rm{t}}}} = {p_{m,{\rm{t}}}} \cdot {c_{m,{\rm{t}}}} - {w_{m,{\rm{t}}}}\left[ {\frac{{{c_{m,{\rm{t}}}}}}{{\left( {1 + \lambda _{\rm{t}}^m} \right){A_{x,{\rm{t}}}}}} + f \cdot {e^{\frac{{\lambda _{\rm{t}}^m}}{H}}}} \right] = 0 $ | (22i) |
垄断竞争企业的成本加成定价公式:
| $ {p_{m,{\rm{t}}}} = \frac{{{w_{m,{\rm{t}}}}}}{{\left( {1 + \lambda _{\rm{t}}^m} \right){A_{x,{\rm{t}}}}}}\frac{{{e_{m,{\rm{t}}}}}}{{{e_{m,{\rm{t}}}} - 1}} $ | (22ii) |
工业品需求关于价格的弹性公式:
| $ {e_{m,{\rm{t}}}} = 1 + \frac{1}{{2\gamma }}{\left( {\frac{2}{{{d_{\rm{t}}}}}} \right)^\gamma } + \frac{1}{{2\gamma }} $ | (22iii) |
从式(22iii)可以看出,当产品种类增加时,“种类环”变得更拥挤,相邻种类的替代性提高,产品需求的价格弹性提高;进一步从式(22ii)知,企业间竞争加剧,价格的成本加成下降;最后从式(22i)可知,在既定的固定成本下,销量必须提高才能维持盈亏平衡。并且规模更大的企业能承担更大的创新固定成本,市场规模扩大有利于生产创新。
在人类经济发展的起步阶段,农业部门的技术水平提高非常缓慢,工业企业的规模也很小,人口增长缓慢,人均收入很低,因此工业企业的销量也有限,无力承担创新成本,技术发展缓慢,人类陷入了“马氏陷阱”。
随着农业部门的技术逐渐积累,收入和人口规模逐渐提高,经济逐渐接近了起飞的临界点,工业企业的市场规模扩大,认为创新有利可图,创新也就此启动,人类经济步入飞速发展的轨道。
但是当经济发展到一定阶段后,主要由于人口增长带来的市场规模扩大对技术进步的诱导作用逐渐减弱,又面临着“中等收入陷阱”。此时人口增长率已逐渐降低,单纯靠人口数量增长来增加生产要素投入以及扩大市场规模已经收效甚微,可行的途径是通过提高人力资本规模(H)来降低创新的固定成本(
(1) 工业生产部门有恒定的技术进步率(λm)。
假设总有效劳动规模是H,分配在农业和服务业部门的是Ha,分配在工业部门的是Hm,H=Ha+Hm;w表示每单位有效劳动的工资率。两部门的总收入=总支出,即:
| $ w{H^a} = \left( {1 - \alpha } \right){Y_{\rm{t}}} $ | (23i) |
| $ w{H^m} = \alpha {Y_{\rm{t}}} $ | (23ii) |
以上两式相除,得:
由零利润条件知:
| $ {c_m} = \frac{{{w_m}f{e^{\frac{{{\lambda ^m}}}{H}}}}}{{{p_m} - \frac{{{w_m}}}{{\left( {1 + {\lambda ^m}} \right){A_x}}}}} $ | (24) |
将价格的成本加成公式(22ii)代入上式,得:
| $ {c_m} = f{e^{\frac{{{\lambda ^m}}}{H}}}\left( {1 + {\lambda ^m}} \right){A_x}\left( {{e_m} - 1} \right) $ | (25) |
将最优技术水平的一阶条件
| $ {c_m} = \frac{{H{c_m}}}{{{{\left( {1 + {\lambda ^m}} \right)}^2}{A_x}}}\left( {1 + {\lambda ^m}} \right){A_x}\left( {{e_m} - 1} \right) $ | (26) |
即得技术进步率关于需求价格弹性的函数:
| $ {\lambda ^m} = H\left( {{e_m} - 1} \right) - 1 $ | (27) |
可见技术进步率(λm)关于需求价格弹性(em)递增。
将每个企业产量的表达式(式(25))与工业企业生产函数(式(11))联立,得到每个工业企业雇佣的有效劳动时长:
| $ {H_m} = \frac{{{Y_m}}}{{{A_m}}} + {F_m} = \frac{{f{e^{\frac{{{\lambda ^m}}}{H}}}\left( {1 + {\lambda ^m}} \right){A_x}\left( {{e_m} - 1} \right)}}{{\left( {1 + {\lambda ^m}} \right){A_x}}} + f{e^{\frac{{{\lambda ^m}}}{H}}} = f{e^{\frac{{{\lambda ^m}}}{H}}}{e_m} $ | (28) |
工业部门有效劳动的总时长是Hm,因此企业的数量是
| $ {e_m} = 1 + \frac{1}{{2\gamma }}{\left( {\frac{{2{H^m}}}{{f{e^{\frac{{{\lambda ^m}}}{H}}}{e_m}\chi }}} \right)^\gamma } + \frac{1}{{2\gamma }} $ | (29) |
上式整理后,得:
| $ 2\gamma e_m^{\gamma + 1} - \left( {2\gamma + 1} \right)e_m^\gamma - {\left( {\frac{{2{H^m}}}{{f{e^{\frac{{{\lambda ^m}}}{H}}}\chi }}} \right)^\gamma } = 0 $ | (30) |
为了得到需求价格弹性(em)关于技术进步率(λm)的增减性,将上式关于λm求全微分,得:
| $ \frac{{\partial {e_m}}}{{\partial {\lambda ^m}}} = - \frac{{\gamma {{\left( {2{H^m}} \right)}^\gamma }{{\left( {f\chi } \right)}^{ - \gamma }}{e^{ - \frac{{{\lambda ^m}\gamma }}{H}}}}}{{H\left[ {2\gamma \left( {\gamma + 1} \right)e_m^\gamma - 2\gamma \left( {\gamma + 1} \right)e_m^{\gamma - 1}} \right]}} $ | (31) |
因为已知em>1,所以上式严格< 0,即em关于λm递减。
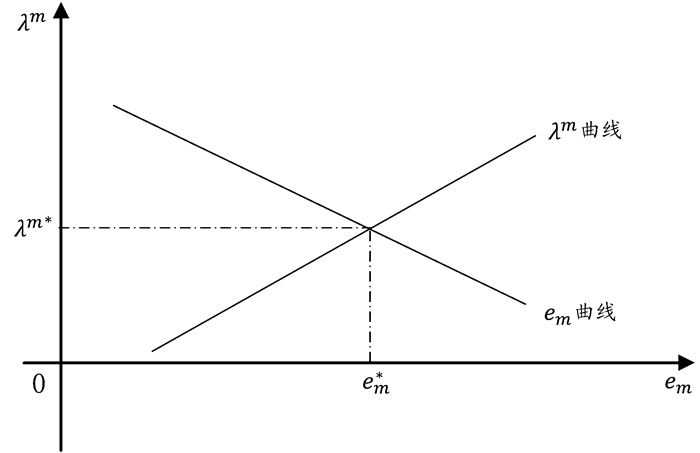
由式(27)和式(29)构成的关于λm和em的二元联立方程组中,技术进步率(λm)关于需求价格弹性(em)递增,而em关于λm递减,所以两条直线必有唯一的交点,即有唯一且恒定的一组em和λm值,也即经济体趋向于工业部门有恒定技术进步率的平衡增长路径。
(2) 在平衡增长路径上,技术进步率(λm)是关于有效劳动规模(H)的增函数。
由式(29)em的表达式可以看出,同时含有作为工业部门有效劳动投入量的Hm(该Hm占H的固定比例)和作为创新成本参数的总有效劳动规模H。为了简化分析,暂时将这两个变量单独考虑,再合并分析。
|
图 4 em与λm均衡图 |
将式(30)关于Hm求全微分,得:
| $ \frac{{\partial {e_m}}}{{\partial {H^m}}} = \frac{{{{\left( {\frac{2}{{f{e^{\frac{{{\lambda ^m}}}{H}}}\chi }}} \right)}^\gamma }\gamma {{\left( {{H^m}} \right)}^{\gamma - 1}}}}{{2\gamma \left( {\gamma + 1} \right)e_m^\gamma - \left( {2\gamma + 1} \right)\gamma e_m^{\gamma - 1}}} > 0 $ | (32) |
说明工业部门有效劳动投入量(Hm)增加,需求价格弹性(em)提高,技术进步率(λm)相应提高。而Hm占H的固定比例,所以即H提高,技术进步加快。
| $ \frac{{\partial {e_m}}}{{\partial H}} = \frac{{\gamma {{\left( {\frac{{2{H^m}}}{{f{e^{\frac{{{\lambda ^m}}}{H}}}\chi }}} \right)}^\gamma }{\lambda ^m}}}{{{H^2}\left[ {2\gamma \left( {\gamma + 1} \right)e_m^\gamma - \left( {2\gamma + 1} \right)\gamma e_m^{\gamma - 1}} \right]}} > 0 $ | (33) |
需求价格弹性(em)关于作为创新成本参数的总有效劳动规模(H)仍然递增,则H对于λm仍然有促进作用。
可见扩大经济体的有效劳动总量时,通过相应增加工业部门的有效劳动投入量和降低创新成本两种途径提高了技术进步率。
三、数值模拟 (一) 参数赋值模型数值模拟涉及的参数名称、含义和赋值见表 1。
| 表 1 参数赋值 |
⑤ 数据来源:根据CEIC数据库(China Economic & Industry Data Database,https://insights.ceicdata.com/insight/34dfa752-27ba-46b3-b2fb-080864cffd89/data)相关数据计算而得。
其他一些诸如在模型中虚拟设定的、在现实经济中不能直接找到对应指标的变量(例如γ、f、χ等),以及为变量赋予的初始值(例如h0、Nt, 1)并不会显著影响对变量之间弹性的分析。
(二) 模拟结果模拟主要分析人口结构变化(包括预期寿命和人口增长率变化)及政策变量(包括政府规定的劳动者退休年龄、养老保障账户缴费贡献率及政府影响的遗赠程度)对经济增长率的影响程度。分以下三种情形分析。
(1) 基准情形:人力资本生产效率φ=0.6,此时人力资本生产函数有较高凸性。
(2) 人力资本生产函数较低凸性的情形:人力资本生产效率φ=0.3。
(3) 人力资本的更高平均生产率的情形:A=16,相对于基准情形中A=6.3,说明人力资本生产函数有更高的平均生产效率。
1. 人口结构变化(1) 预期寿命变化。
分析存活率(s,即预期寿命)的变化对经济增长率的影响,本文分析的预期寿命的范围是60~85岁,对应s的取值范围是0~0.625。当分析该变量变化的影响时,需要固定其他变量,转移支付因子ξ=1,此时有完全转移支付体系(遗赠);人口自然增长率取值0.05。
从图 5可以得出以下结论。
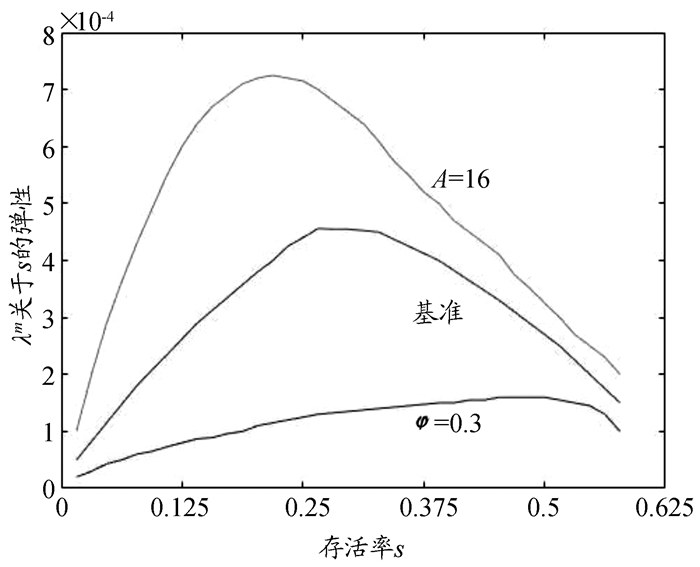
|
图 5 工业生产部门技术进步率(λm)关于存活率(s)的弹性 |
第一,三条曲线大致呈抛物线形状,背后的经济含义是当预期寿命开始延长时,一方面有利于提高老年期的劳动时间比例,另一方面也激励人力资本投资,这两种力量都有效提高了有效劳动总量,进而提高了经济增长率,该弹性也呈现逐渐上升趋势。但是当预期寿命进一步延长时,随着终生收入的增加,居民的劳动和人力资本投资意愿又逐渐降低,倾向于享受更多的闲暇,因此对有效劳动总量及经济增长率的提升作用逐渐降低,表现为该弹性又逐步下降。
第二,当人力资本生产函数有较低凸性时(φ=0.3),相对于基准情形,整体而言有较低的弹性,且一直呈缓慢上升的趋势,最后才呈下降趋势,背后的经济含义是当人力资本生产效率较低时,即使延长预期寿命,也不会促使居民进行更多的人力资本投资,因而有效劳动总量增加有限,对技术进步的贡献也较小。
第三,当人力资本有更高的平均生产率时(A=16),该弹性迅速达到最大值(约s=0.2(对应预期寿命为68)时达到峰值),且显著高于前两种情形(基准情形中,约s=0.25(对应预期寿命为70)时达到峰值),但随后迅速下降,背后的经济含义是当人力资本投资的平均收益较高时,同等条件下会增加居民的终生收入水平,从而促使居民在老年期消费更多的闲暇,使得λm关于s的弹性达到最大值时的预期寿命降低。
(2) 人口自然增长率变化。
分析人口自然增长率(n)的变化对经济增长率的影响,本文分析的人口自然增长率的范围是0~5.5(%)。当分析该变量变化的影响时,需要固定其他变量,转移支付因子ξ=1,此时有完全转移支付体系(遗赠);存活率s取值0.4(对应现阶段中国人口的预期寿命为76岁⑥)。
⑥ 数据来源:中国经济与社会发展统计数据库(http://tongji.cnki.net/kns55/index.aspx。)
从图 6看,技术进步率关于人口增长率的弹性随着人口增长率的降低呈递增趋势,这是因为随着人口增长率降低,老年人的扶养比
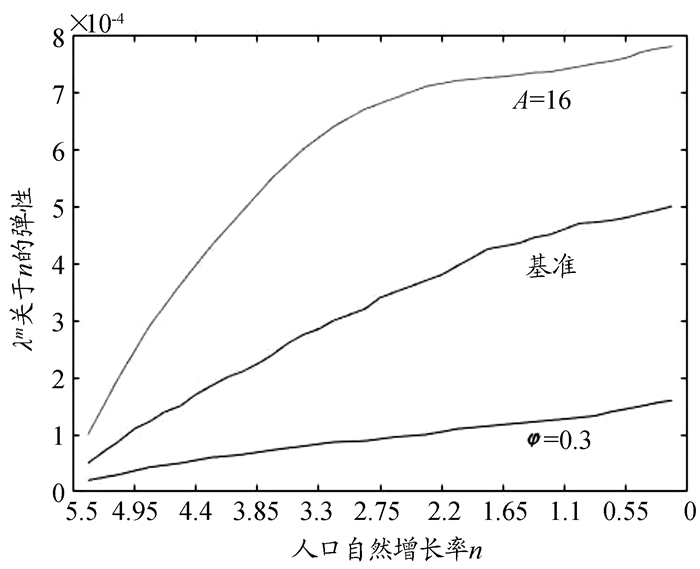
|
图 6 工业生产部门技术进步率(λm)关于人口自然增长率(n)的弹性 |
在理解以上变量基本作用机制的基础上,开始引入对政策变量的分析。
(1) 法定退休年龄。
在本文的模型中,老年期工作时间比例(l)是由居民最优化行为内生决定的,但在现实中,退休年龄多是由政府外生设定的,分析不同老年期工作时间比例上λm关于l的弹性,有利于确定最有利于经济增长的退休年龄。以下分析的老年期工作时间比例的范围是0.1~0.9⑦,同时固定其他参数(s=0.4,n=0.05,ξ=1)。
⑦ 老年期的劳动时间比例
从图 7可以得出以下发现。
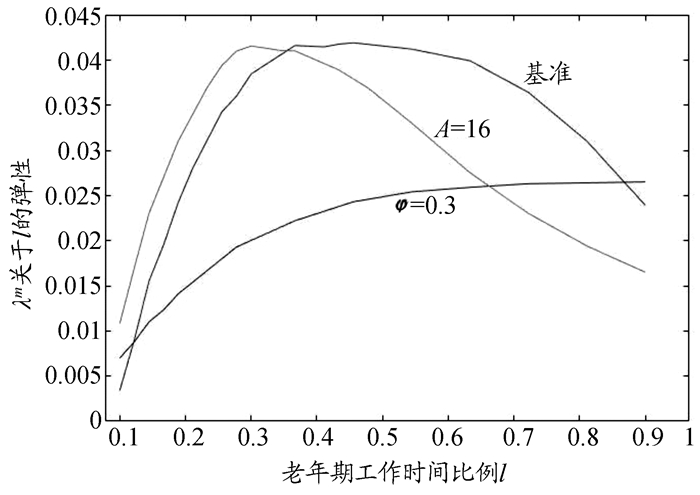
|
图 7 工业生产部门技术进步率(λm)关于老年期劳动时间比例(l)的弹性 |
第一,在基准情形中,当老年期的工作时间比例lt+1, 1=0.3时(此时对应约65岁退休),λm关于l的弹性达到最大值,然后缓慢下降。这说明适度延长老年期工作时间时,所积累的人力资本能获得更高的收入,从而有利于激励人力资本投资,并促进技术进步;但是过度延长劳动时间所导致的过高人力资本投资使得人力资本生产终将面临边际报酬递减规律的约束,最终有效劳动总量增加有限,对技术进步的贡献也逐渐变小。
第二,当人力资本生产函数有较低凸性时(φ=0.3),人力资本生产效率较低,所以整体而言有较低的弹性,并且该较低的凸性也减缓了边际报酬递减的速度,因此该弹性一直呈缓慢上升的趋势。
第三,当人力资本有更高平均生产率时(A=16),相对于基准情形,该弹性更快达到最大值,且高于前两种情形。对比三条曲线发现决定该弹性下降起点更重要的因素是人力资本投资的边际收益及其递减的速度(主要由参数φ决定),而非平均收益(主要由参数A决定)。
(2) 养老保障账户缴费贡献率。
以上的分析没有考虑养老保障账户缴费贡献率(τt)的影响,从上文的式(7)可知青年期和老年期向养老保障账户缴费的贡献率都会影响人力资本投资量,进而影响有效劳动总量及经济增长率。降低老年期的贡献率τt+1可以提高老年期相对青年期的相对工资(扣除养老保障账户缴费贡献率之后的),有利于激励人力资本投资,以便在老年期获得更高的收入。假设青年期的贡献率τt=0.3(对应现实工资收入中养老保险缴纳比例:个人8%,单位20%的情形),通过不同程度地降低老年期的贡献率τt+1,可以分析该政策对人力资本积累及经济增长的作用。以下分析中τt+1的范围是0.1~0.3,同时固定其他参数(s=0.4,n=0.05,ξ=1)。
图 8中曲线的形状及相对位置关系可从以下角度理解:降低老年期养老保障账户缴费贡献率的替代效应和收入效应的相对大小决定了每条曲线基本呈抛物线形状,适度降低该贡献率时替代效应占主导,因此会激励人力资本投资,以便在老年期获得更高的相对劳动收入;但是过度降低该贡献率后,收入效应又会占主导,居民更倾向于享受更多的闲暇,从而对增加有效劳动总量及提升技术进步的作用降低。进一步观察发现,当人力资本生产函数有更高的平均生产效率时(A=16),会提高收入效应占主导时贡献率的临界值,因此A=16对应的曲线峰值相对基准曲线峰值靠左。同理当人力资本生产函数有更低的边际生产效率时(φ=0.3),会降低收入效应占主导时贡献率的临界值,因此φ=0.3对应的曲线峰值相对基准曲线峰值靠右。
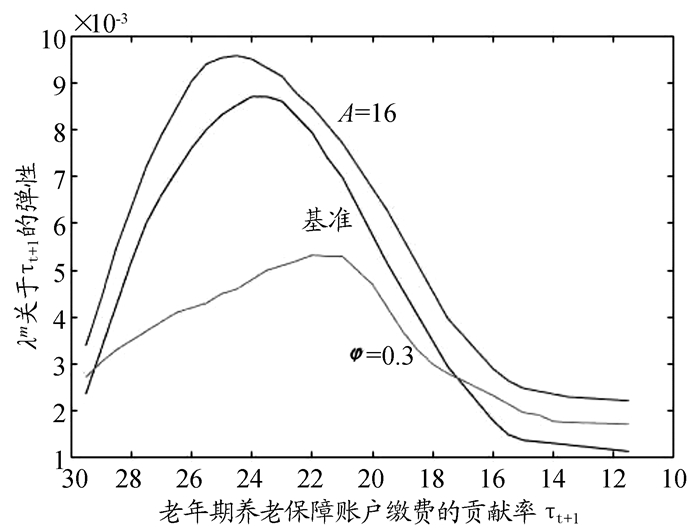
|
图 8 工业生产部门技术进步率(λm)关于老年期养老保障账户缴费贡献率(τt+1)的弹性 |
(3) 遗赠程度。
上文指出转移支付体系具有遗赠的性质,而政府可以通过征收遗产税的方式影响居民的遗赠程度,因此衡量转移支付体系完善程度(或遗赠程度)的因子ξ也是重要的决策变量。随着ξ从1下降到s(存活率),表明遗赠程度逐渐下降。以下分析的ξ的范围是1~0.4,同时固定其他参数(s=0.4,n=0.05,τt=τt+1=0)。
从图 9可以发现该弹性是负值,即降低遗赠程度会提高技术进步率。从上文的式(6iv)老年期劳动时间比例(lt+1, 1)的表达式及式(7)最优人力资本投资量(et*)的表达式可以看出,这两个变量都关于遗赠程度ξ递增。这背后的经济学含义是直观的,降低居民获得的遗赠即降低了其终生财富,这会激励居民延长劳动时间以及进行更多的人力资本投资。另外当人力资本生产函数有更高的平均或边际生产效率时会放大该效应对技术进步率的影响。
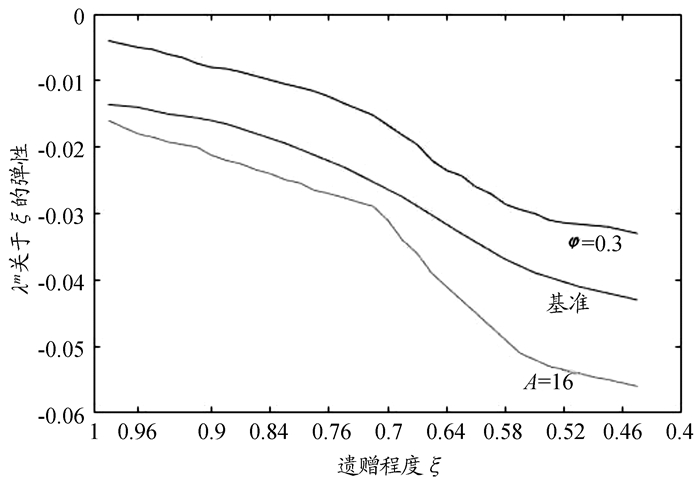
|
图 9 工业生产部门技术进步率(λm)关于遗赠程度ξ的弹性 |
本文从统一增长理论的人口规模(或有效劳动规模)和技术进步的关系角度解释经济发展不同阶段的内生转型,并在此基础上探索跨越“中等收入陷阱”的途径。人口规模在经济转型中发挥了重要作用,在“马氏陷阱”阶段,农业生产技术缓慢提高,伴随着人口逐渐增长,市场也逐步扩大,使得工业企业能承担更大的固定(创新)成本,生产创新就此启动,技术的显著提升带动了人均收入和人口规模的快速增长,经济体由此步入良性循环;但经济发展到一定阶段后,又面临人口转型,人口增长率下降,预期寿命延长,可能会陷入“中等收入陷阱”,此时不能再依靠单纯的人口数量增长,而是依赖人力资本积累才能增加有效劳动规模,进一步促进工业企业的创新,从而为摆脱“中等收入陷阱”奠定基础。有效劳动规模的扩大不再仅通过正向外溢性促进技术进步,而是通过降低工业企业的创新成本直接加快技术进步。
面对这样的人口增长规律变化引发的经济增长内生转型机制,财政政策具有推进经济体摆脱增长陷阱发挥作用的空间。首先,延长劳动者的劳动年限有利于促使劳动者接受更多的教育,积累人力资本,从而增加有效劳动的总规模。就中国而言,目前平均退休年龄不到55岁⑦,从图 10显示的不同年龄段收入指数看,中国劳动者收入最高的年龄段是36~40,然后逐渐下降;而相比之下,美国和澳大利亚劳动者收入最高的年龄段则分别是35~44、45~54,明显晚于中国。这说明中国劳动者劳动年限过短,也限制了人力资本积累,造成了人力资源的浪费。其次,适度降低老年期养老保障账户缴费贡献率也有利于激励居民积累人力资本以及延长终生的最优劳动时间。最后,通过降低遗赠程度的方式可以减少“不劳而获”的财富,有效激发居民的人力资本投资及劳动意愿。这也有助于在老年人扶养比提高的情形下改善养老保障账户收支状况。值得注意的是当人力资本积累效率更高时,以上政策效果会更显著,因此科教仍然是未来需要增加财政支出的重点领域。
⑦ 2015年10月14日,人社部部长尹蔚民介绍了“十二五”以来就业和社会保障工作成就,称中国是目前世界上退休年龄最早的国家,平均退休年龄不到55岁。(http://epaper.bjnews.com.cn/html/2015-10/15/content_602796.htm?div=-1)。
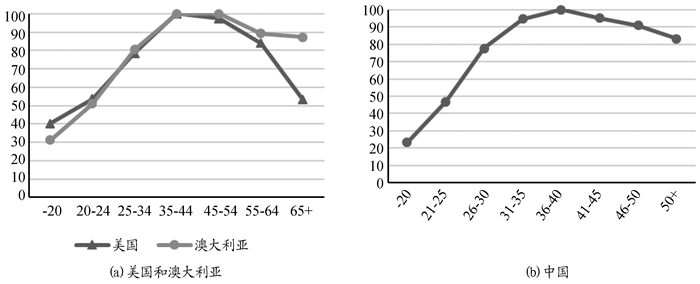
|
图 10 不同年龄段收入指数图⑧(%) 数据来源:根据美国劳工统计局(https://www.bls.gov/)、澳大利亚统计局(http://www.abs.gov.au/)和北京大学中国社会科学调查中心—中国家庭追踪调查(http://www.isss.edu.cn/cfps/)相关数据计算而得 |
⑧ 将最高年龄段的收入设为100,计算其他年龄段的收入占其比重而得。
| [1] |
GALOR O.From stagnation to growth: Unified growth theory[M]//Handbook of Economic Growth. Amsterdam: Elsevier B.V, 2005.
|
| [2] |
GALOR O, MOAV O. From physical to human capital accumulation:Inequality and the process of development[J]. Review of Economic Studies, 2004, 71(4): 1001-1026. |
| [3] |
BARRO R J, BECKER G S. Fertility choice in a model of economic growth[J]. Econometrica, 1989, 57(2): 481-501. |
| [4] |
BOUCEKKINE R, DE LA CROIX D, LICANDRO O. Early mortality declines at the dawn of modern growth[J]. Scandinavian Journal of Economics, 2003, 105(3): 401-418. DOI:10.1111/sjoe.2003.105.issue-3 |
| [5] |
STRULIK H, WEISDORF J. How child costs and survival shaped the Industrial Revolution and the demographic transition:A theoretical inquiry[J]. Macroeconomic Dynamics, 2014, 18(1): 114-144. |
| [6] |
SOARES R R.The demographic transition and the sexual division of labor[C]//Meeting Papers. Society for Economic Dynamics, 2015.
|
| [7] |
GOODFRIEND M, MCDERMOTT J. Early development[J]. American Economic Review, 1995, 85(1): 116-133. |
| [8] |
JONES C I.Was an industrial revolution inevitable? Economic growth over the very long run[C]//National Bureau of Economic Research, Inc, 2001.
|
| [9] |
VOIGTLÄNDER N, VOTH H J. Why England? Demographic factors, structural change and physical capital accumulation during the Industrial Revolution[J]. Journal of Economic Growth, 2006, 11(4): 319-361. DOI:10.1007/s10887-006-9007-6 |
| [10] |
GAUTSCHI D A, LANCASTER K. Variety, equity, and efficiency[J]. Journal of Marketing Research, 1980, 17(3): 403. |
| [11] |
ATTANASIO O P.Chapter 11 Consumption[M]//Handbook of Macroeconomics, 1999, 1(Part B). Amsterdam: Elsevier, 1999.
|
| [12] |
JAIMOVICH N, FLOETOTTO M. Firm dynamics, markup variations, and the business cycle[J]. Journal of Monetary Economics, 2008, 55(7): 1238-1252. DOI:10.1016/j.jmoneco.2008.08.008 |
| [13] |
BERMAN E, BOUND J, GRILICHES Z. Changes in the demand for skilled labor within U. S. manufacturing:Evidence from the annual survey of manufactures[J]. The Quarterly Journal of Economics, 1994, 109(2): 367-397. |
| [14] |
DESMET K, PARENTE S L. The evolution of markets and the revolution of industry:a unified theory of growth[J]. Journal of Economic Growth, 2012, 17(3): 205-234. DOI:10.1007/s10887-012-9080-y |
 2019, Vol. 25
2019, Vol. 25


