b. 华南师范大学 公共管理学院, 广东 广州 510631
b. School of Public Administration, South China Normal University, Guangzhou 510631, P. R. China
国内外学者对科技创新能力的研究是从探讨其评价指标体系开始的,直到1972年美国第一份《科学指标》出版,才标志着科技创新能力评价指标体系的诞生。随后,随着计算机技术的发展和信息技术的普及,学者从评价指标体系、评价方法、评价原则、影响因素等方面进行了大量研究,特定区域以及区域间科技创新能力的评价也引起了学者的广泛关注[1-6]。
与此同时,科技创新效率问题也渐渐成为研究热点。Farrell在1957年提出了效率评价的具体意义和概念,对实际生产单位投入产出的数据进行分析,评价不同生产步骤的技术效率。1975年,Rhodes等人基于分段线性函数的基础,引入了DEA方法对效率进行测算。经过多年的探索,美国国会于1993年通过了《政府绩效与结果法案》,效率评价的概念、制度和范围首次以法律形式得到了明确。同样,学者们对科技创新效率评价指标、评价方法、影响要素,以及区域创新效率等问题开展了大量研究[7-9]。
约瑟夫·熊彼特于1912年出版其著作《经济发展理论》,提出“创新”的概念,首次明确地将经济发展与创新结合起来,认为只有当它应用于经济活动并产生利益的时候才称得上是创新,即创新具有经济性的特征[10]。测定科技进步对经济增长的作用,成了科技进步分析工作的重要任务之一,众多学者开始研究经济增长中是否有技术进步、技术进步对经济增长的贡献度等问题[11-12]。
发展经济学认为,经济增长的主要源泉是科技创新,而科技创新能力与效率共同决定了科技创新的质与量,它们通过促进生产关系调整和经济结构变化,推动区域经济的发展和社会的进步[13]。高校作为科技创新、人才培养的主要基地,是推动科技进步与创新、促进经济发展的动力源泉和贡献主体[14]。高校创新能力和效率的提高与国民经济的健康快速发展之间具有重要联系[15]。学界对高校科技创新能力、效率、经济贡献率某一维度问题的研究,取得了丰硕成果和广泛共识,并在此基础上把某两个维度进行结合探讨[16-19]。已有评价研究中,对科技创新服务人才培养、国际化等创新辐射方面的重视不够,把三个维度问题结合在一起进行综合分析的研究尚未出现。可见,高校科技创新能力、效率、经济贡献率的综合评价研究,是一个尚未形成一致认识的难题。
基于此,本研究从科技创新能力、科技创新效率、科技创新经济贡献率三个维度,以2004—2016年有关数据为依据,综合评价中国高校的发展状况,以期为高校实施供给侧结构性改革、“双一流”建设和国家创新驱动发展战略等提供参考。需要说明的是,研究数据截至2016年,这是目前能搜集到的最新数据,研究中的“省域”是指中国行政规划中的省份,“省域高校”为教育部出版的《高等学校科技统计资料汇编》中某个省份地域内的全部高等学校。为确保评价数据前后的一致性和相关性,三个维度评价指标涉及的数据均采用同一出处、同一口径,评价科技创新效率和经济贡献率的指标,同时也是科技创新能力的指标。涉及经费指标用价格指数进行可比化平减[20]。
科技创新能力评价数据来源是:(1)2004—2016年全国科技经费投入统计公报(http://www.most.gov.cn/kjtj/);(2)中国科技统计年鉴(2005-2017)[21];(3)高等学校科技统计资料汇编(2005—2017年)(http://www.moe.gov.cn/s78/A16/A16_tjdc/);(4)“全省对创新的重视程度”一项由项目团队根据各省份每年政府工作报告整理。科技创新效率评价数据来源是:高等学校科技统计资料汇编(2005—2017年)。科技创新经济贡献率评价数据来源是:(1)中国科技统计年鉴(2005—2017);(2)高等学校科技统计资料汇编(2005—2017年);(3)国民经济和社会发展统计公报(http://www.stats.gov.cn/tjsj/tjgb/ndtjgb/)。根据数据科学性和可得性要求,青海、宁夏、西藏3个省份和港澳台地区未作评价。
二、科技创新能力分析 (一) 评价指标体系根据高校科技创新能力的内涵特点,以及评价的科学性、可比性、系统性、可行性等原则要求[5, 22],项目团队通过专家咨询和指标测算,确定表 1为高校科技创新能力评价指标体系。
| 表 1 高校科技创新能力评价指标体系 |
借助SPSS22.0统计工具,采用主成分分析法进行评价。主要理论步骤包括五步[23-24]。
1.对指标的原始数据无量纲化
设有n个样本,p项指标,可得数据矩阵X=(Xij)nxp,i=1, 2, …,n表示n个样本,j=1, 2, …,p表示p个指标,Xij表示第i个样本的第j项指标值。用Z-score法对数据进行标准化变换,得出:
| $ {Z_{ij}} = \left( {{x_{ij}} - \overline {{x_j}} } \right)/{S_j}。$ |
式中,
2.计算其相关系数矩阵
R=(rjk)pXp,j=1, 2, …, p,k=1, 2, …, p,rjk为指标j与指标k的相关系数。
| $ {r_{jk}} = \frac{1}{{n - 1}}\sum\limits_{i = 1}^n {\left[ {\frac{{{{\left( {{x_{ij}} - \overline {{x_j}} } \right)}^2}}}{{{S_j}}}} \right]} [{({X_{ik}} - \overline {{X_j}} )^2}/{S_k}]{\text{,即}}:{r_{jk}} = \frac{1}{{n - 1}}\sum\limits_{i = 1}^n {{Z_{ij}}{Z_{jk}}} 。$ |
有rii=1,rjk=rkj,i=1, 2…, n,j=1, 2…, p,k=1, 2, …,p。
3.求出各特征向量
由特征方程|λIp-R|=0,可求得p个特征根λg(g=1, 2, …, p),λ1将其按大小顺序排列为λ1≥λ2≥…≥λp≥0,它是主成分的方差,它的大小描述了各个主成分在描述被评价对象上所起作用的大小。由特征方程,每一个特征根对应一个特征向量Lg(Lg=lg1, lg2, …, lgp),g=1, 2, …, p。
将标准化后的指标变量转换为主成分:
| $ {F_g} = {l_{g1}}{Z_1} + {l_{g2}}{Z_2} + \cdots + {l_{gp}}{Z_p}\left( {g = 1, 2, \cdots , p} \right)。$ |
F1称为第一主成分,F2称为第二主成分,…,Fp称为第p主成分。
4.根据因子累积方差贡献率选出主成分
一般主成分个数等于原始指标个数,如果原始指标个数较多,进行综合评价时就比较麻烦。主成分分析法就是选取尽量少的k个主成分(k < p)来进行综合评价,同时还要使损失的信息量尽可能少。
k值由方差贡献率
5.以各主成分的方差贡献率为权数,将所选取的主成分进行综合评价
先求每一个主成分的线性加权值
最终评价值为:
根据以上步骤,分别对二级指标和一级指标进行主成分分析。在此,仅以创新投入能力(设为A)二级指标为例进行推演说明。
对创新投入能力二级指标的6个三级指标(设为A1,A2,…,A6)的原始数据进行标准化,并计算特征值、贡献率和累积贡献率,确定如表 2所示的主成分情况。
| 表 2 主成分分析各主成分的特征值和贡献率 |
从表 2可以看出,前2个主成分的累积贡献率达到了84.803%,说明这3个主成分所包含的信息占84.803%。选用斜交旋转法,得到因子得分系数矩阵和模型,如表 3和表 4。
| 表 3 因子分析的因子旋转结果 |
| 表 4 主成分得分函数的系数 |
F1=0.448A1+0.001A2+0.292A3-0.129A4+0.385A5-0.014A6。
F2=-0.242A1+0.021A2+0.194A3+0.618A4+0.009A5+0.455A6。
F3=0.000A1+0.992A2-0.037A3-0.059A4+0.030A5+0.086A6。
根据因子得分系数矩阵和各个主成分的贡献率可以确定创新基础能力的综合评分函数:
A=0.39259F1+0.25815F2+0.16728F3。
根据组合模型统计,考察期各省份高校科技创新能力得分如表 5所示,全国平均得分为0.063。高于平均值的有江苏、北京、广东、上海、山东、辽宁、浙江、湖北、陕西、四川、河南和安徽等12个省份,说明省域高校之间科技创新能力存在东部高、西部低的区域不均衡性。
| 表 5 各省高校科技创新能力情况 |
通过对科技创新能力排名前3的江苏、北京、广东高校的36项指标原始值分析可知,这3个省份高校有9项评价指标均排名在全国各省份前5名(表 6)。从表 6可以发现,创新支撑能力方面,全省R & D人员、全省R & D经费支出、全省对创新的重视程度3项指标对科技创新能力影响较大,各地政府应该高度重视创新工作,在人员和经费方面提供保障。创新投入能力方面,高校研究与发展全时人员、固定资产购置费2项指标对科技创新能力影响较大,各省、高校应该增加科研人力投入,加强实验仪器设备购置等基础平台建设工作。创新服务能力方面,高校研究与发展项目、培养学生数指标对科技创新能力影响较大,各省、高校应该支持和发展研究生教育,引导研究生积极参与科研项目创新研究工作。创新辐射能力方面,高校平均出席国际学术会议情况、人均提交国际学术会议特邀报告情况、高校主办国际学术会议情况3项指标对科技创新能力影响较大,各省、高校应该更加重视科技国际交流合作工作,注重“走出去”参加国际学术会议,了解国际学术前沿,也要通过主办国际学术会议“请进来”现场指导交流,同时重视通过提交国际学术会议特邀报告,在国际学术同行中提高学术知名度和影响力。
| 表 6 江苏、北京、广东3省份高校评价指标排名情况 |
在分析高校科技创新能力的基础上,项目组采用数据包络分析(DEA)模型构建评价指标体系[25]。数据包络分析(DEA)将每一个被评价的经济系统或生产过程视为一个决策单元(DMU),由决策单元组(DMUS)构成评价群体,处于同一评价群体的每个决策单元都具有同样种类的资源消耗,即各决策单元具有相同的投入项指标和相同的产出项指标,在指标项和决策单元组确定以后,采用数学规划模型比较决策单元之间的相对效率,进行投入与产出比率的综合分析,得到每一决策单元综合效率的量化指标值,从而确定有效的决策单元,指明其他决策单元非有效的程度。
本项目研究认为,高校科技创新过程具有复杂的阶段特征,主要包括产出创新成果和创新成果转化两个阶段。即:在第一阶段,将创新投入要素转化成知识创新产出成果;在第二阶段,将知识创新产出成果投入生产,进行技术创新成果转化,带来经济效益,促进经济发展。具体评价指标可参见表 7。第一阶段投入指标包括人力、财力和物力投入,研究与发展全时人员反映了人力资源投入的情况,研究与发展经费反映了财力资源投入的情况,固定资产购置费反映了物力资源投入的情况。第一阶段产出指标(第二阶段投入指标)包括研究、开发、知识产出(投入),发表学术论文数反映科学研究水平,专利授权数反映技术开发水平,出版科技著作数反映知识传承水平。第二阶段产出指标包括转让、出售和委托产出,技术转让、专利出售实际收入代表开发技术、专利技术的市场应用程度,企事业单位委托经费代表创新对社会经济发展的促进程度。
| 表 7 高校科技创新效率评价指标体系 |
根据DEA模型构建的评价指标体系,采用基于DEA的Malmquist指数计算方法,分别考察各省高校两个阶段科技创新全要素生产效率(Total Factor Productivity),第一、第二阶段时滞均为1年[21]。
基于DEA的Malmquist全要素生产效率指数是通过距离函数来定义的[26-27],可以定义投入距离函数和产出距离函数。本项目研究采用产出距离函数来定义Malmquist生产率指数。假定向量x表示投入量,x=(x1,x2,…,xm);y表示产出量,y=(y1,y2,…,yn);p(x)代表使用投入向量x所能生产的所有产出向量的集合。即:
产出距离函数可定义为:
| $ {\mathit{d}_0}\left( {y, x} \right) = {\text{min}}\left\{ {\varphi :\left( {y/\varphi } \right) \in p\left( x \right)} \right\} $ | (1) |
以时期t的技术T为参照,基于产出角度的Malmquist指数可以表示为:
| $ M_0^t({x_{t + 1}}, {y_{t + 1}}, {x_t}, {y_t} )= d_0^t\left( {{x_{t + 1}}, {y_{t + 1}}} \right)/d_0^t\left( {{x_t}, {y_t}} \right) $ | (2) |
以时期t+1的技术T+1为参照,基于产出角度的Malmquist指数可以表示为:
| $ M_0^{t + 1}({x_{t + 1}}, {y_{t + 1}}, {x_t}, {y_t} )= d_0^{t + 1}\left( {{x_{t + 1}}, {y_{t + 1}}} \right)/d_0^{t + 1}\left( {{x_t}, {y_t}} \right) $ | (3) |
从t到t+1时期,度量全要素生产率指数增长的Malmquist指数可以分解为不变规模报酬假定下技术效率指数(EC)和技术进步指数(TP),其中技术效率变化指数还可进一步分解为纯技术效率指数(PC)和规模效率指数(SC),其分解过程如下:
| $ \begin{gathered} M_0^t({x_{t + 1}},{y_{t + 1}},{x_t},{y_t}) \hfill \\ = \frac{{d_0^{t + 1}({x_{t + 1}},{y_{t + 1}})}}{{d_0^t({x_t},{y_t})}} \times \left[ {\frac{{d_0^t({x_{t + 1}},{y_{t + 1}})}}{{d_0^{t + 1}({x_{t + 1}},{y_{t + 1}})}} \times \frac{{d_0^t({x_t},{y_t})}}{{d_0^{t + 1}({x_t},{y_t})}}} \right] \hfill \\ = {\text{EC}} \times {\text{TP = TP}} \times {\text{PC}} \times {\text{SC}} \hfill \\ \end{gathered} $ | (4) |
式(4)中,(xt,yt)和(xt+1,yt+1)分别表示时期t和时期t+1的投入产出量,d0t和d0t+1分别表示以时期t的技术T为参照时期t和时期t+1的距离函数。
全要素生产率是指全部生产要素(包括资本、劳动、土地,但通常分析时都略去土地不计)的投入量都不变时,而生产量仍能增加的部分[28]。根据组合模型和函数进行统计,得分如表 8所示,全国平均得分为1.084。高于平均值的有辽宁、江西、吉林、山东、海南、内蒙古、广西、贵州、新疆、云南、江苏、浙江、福建、广东和陕西等15个省份,说明省域之间高校科技创新效率相对比较均衡。
| 表 8 各省高校科技创新效率情况 |
图 1分析发现,由于受国家供给侧结构性改革、东北老工业基地振兴等各项政策影响,高校科技创新效率排名前3的辽宁、江西和吉林,科技创新投入不足,如2016年全省研究与试验发展经费投入强度,辽宁、江西和吉林分别为1.69%、0.94%和1.13%,均低于全国平均的2.11%。但他们通过加强科技创新管理、优化创新政策等方式,在投入相对不足的情况下,实现了创新效率的良好效果,吉林2011年实施了创新型吉林建设科技行动计划、江西2013年实施了科技创新“六个一”工程、辽宁2014年出台了自主创新促进条例,确保了创新效率的提升。
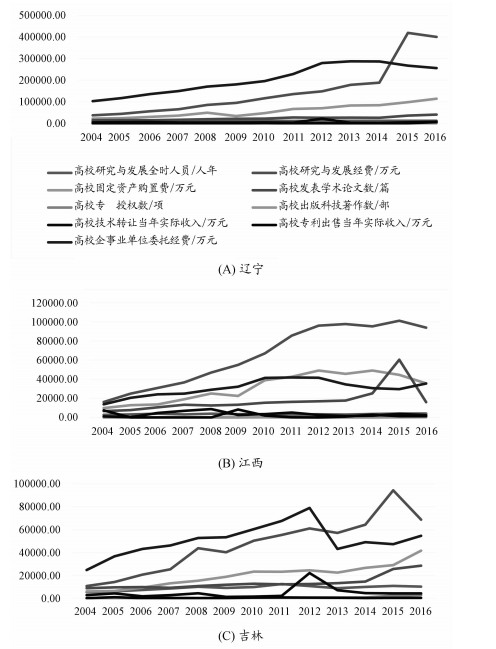
|
图 1 辽宁、江西和吉林三省高校科技创新效率评价指标情况 |
在上述分析基础上,借鉴“柯布-道格拉斯(C-D)生产函数”和索洛“增长速度方程”,推导出科技进步速度:
| $ a = y - \alpha k - \beta l $ |
式中,y表示产出(GDP)的年平均增长速度,k表示资金(固定资产)投入的年平均增长速度,l表示劳动力投入的年平均增长速度。则科技进步的经济贡献率为:
| $ a/y*100\% $ |
根据GDP增长与全省研究与试验发展(R & D)人员全时当量的相关性校验结果,采用高校R & D全时人员增加量与全省R & D全时人员增加量的比重,来对应衡量高校科技创新进步对经济的贡献率[29]。参照国家统计局推荐值,α=0.3,β=0.7[30]。
(二) 实证分析根据评价指标和公式模型,考察周期各省份高校科技创新经济贡献率平均得分如表 9所示,全国平均得分为5.15%。高于平均值的有广西、贵州、吉林、云南、湖南、湖北、上海、内蒙古、陕西、重庆、北京、海南、辽宁、安徽、山东和天津等16个省份。
| 表 9 各省高校科技创新经济贡献率情况 |
从对高校科技创新经济贡献率排前3名的广西、贵州、吉林的测算指标(表 10)分析发现,3个省的平均GDP总量增长幅度分别为15.6%、17.4%和14.8%,均高于全国平均增幅的11.6%。全省固定资产投资总额增幅与全国增长较大(22.5%)类似,分别增长27.8%、31.5%和19.3%。而全社会从业(就业)人员增幅远低于全国平均的3.12%,分别为0.67%、0.66%和1.70%,“全省高校R & D人员全时当量/全省R & D人员全时当量”则高于全国平均值的0.1,分别为0.33、0.18和0.34,科技进步对经济的贡献率也高于全国平均水平的18.7%,分别为45.2%、68.9%和32.1%。可见,广西、贵州和吉林GDP总量保持较快增长,主要原因是科技进步对经济的贡献率较高,全省高校R & D人员所占比重也较大。因此,各省应该高度重视科技创新工作,让经济发展更多依靠科技创新驱动,各高校应该注重科技人才引进和培养工作,增加或增强创新人才队伍数量与质量。
| 表 10 广西、贵州、吉林高校科技创新经济贡献率测算指标平均情况 |
根据上述分析,将高校科技创新能力、效率和经济贡献率三项指标分别取平均值,高于平均值的数界定为“高”(H),低于平均值的数界定为“低”(L),得出以下研究发现。
第一,三项指标评价结果和省份之间有8种对应关系。表现为H-H-H的是地处经济发展水平较好的辽宁、陕西和山东3个省份;表现为H-H-L的是地处经济最发达地区的江苏、广东和浙江3个省份;表现为H-L-H的是地处经济发达及发展水平较好的北京、上海、湖北和安徽4个省份;表现为L-H-H的是地处经济欠发达地区的吉林、广西、云南、内蒙古、贵州和海南6个省份;表现为H-L-L的是地处经济欠发达地区的四川和河南2个省份;表现为L-H-L的是地处经济欠发达地区的江西、福建和新疆3个省份;表现为L-L-H的是湖南、天津和重庆3个省份;表现为L-L-L的是地处经济欠发达地区的黑龙江、河北、山西和甘肃4个省份。
可以认为,地处经济发达地区省份的高校,在科技创新能力方面表现更为突出,地处经济欠发达地区省份科技创新效率更高,科技创新对经济发展的贡献率也更大。
第二,从图 2表现为H-H-H的辽宁、陕西和山东高校近5年情况可以看出,辽宁高校科技创新能力逐年平缓增长,创新效率波动较大,经济贡献率比较平缓,陕西高校科技创新能力在波动中增长,创新效率在波动中有所下降,经济贡献率也在波动中下降,山东高校科技创新能力略微上涨,创新效率在波动中有所下降,经济贡献率也有所下降。根据图 2中3个省域高校实证结果来看,高校科技创新能力、科技创新效率和GDP增长率之间,并无明显一致的线性关系,而经济贡献率和GDP增长率之间有较为明显的趋势一致的线性相关性,拟合指数R2=0.3114。
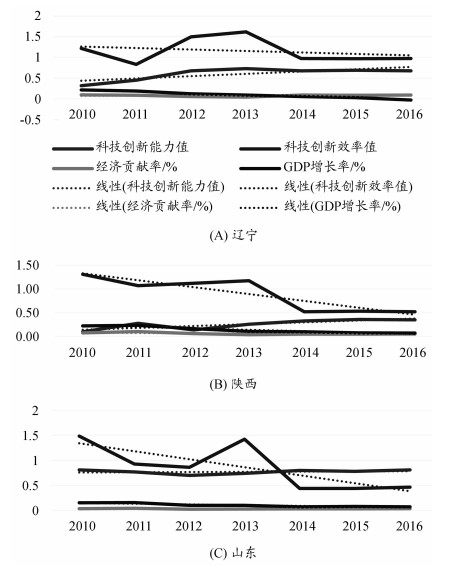
|
图 2 辽宁、陕西和山东三省高校科技创新能力、效率、经济贡献率和GDP增长情况(2010—2016年) |
由此说明,高校科技创新能力、科技创新效率并不能直接影响经济增长,而只有将高校科技创新有效转化为促进经济贡献率提升时,才对经济发展具有促进作用。因此,高校应该更加注重产学研结合,让科技创新向生产力进行有效转化,更加深入服务社会经济发展。由此也可以发现,科技创新效率的波动幅度比较大,说明效率受各方面综合因素影响较大,将在后续研究中进一步进行验证。
第三,从公布的国家“双一流”建设高校及建设学科名单来看[31],三项指标中其中两项为H的省份高校“双一流”建设情况如图 3所示。从图 3可以看出,表现为H-H-H的陕西有3所高校被列为世界一流大学建设行列,高校数量排在北京(8所)、上海(4所)之后,辽宁和山东分别有2所高校,并列排在北京、上海和陕西之后。表现为H-H-L的江苏、广东和浙江3个省份,分别有43个、18个和20个学科进入国家“双一流”建设行列。表现为H-L-H的北京、上海、湖北和安徽4个省份,分别有153个、57个、29个和13个学科进入国家“双一流”建设行列。表现为L-H-H的除广西、内蒙古、贵州和海南外,吉林有1所高校和12个学科、云南有1所高校和2个学科进入国家“双一流”建设行列。
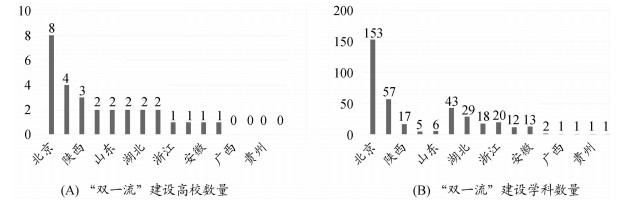
|
图 3 三项指标中有其中两项为H的省份“双一流”建设情况 |
由此也从另一个侧面反映出,科技创新能力、效率、经济贡献率三者的协调发展,有利于提升高校学科建设水平和整体竞争实力,也将有利于促进国家“双一流”建设。
第四,由于中国省域之间经济发展水平差异较大,政府部门应该出台相应政策,加大对经济欠发地区高校的科技创新投入,提高经济发达地区科技创新效率,促进地区之间科技创新资源的有效流动,促进区域间科技和经济健康、持续、协同发展。
回顾本研究对高校科技创新能力、科技创新效率、科技创新经济贡献率的综合分析可以发现,这项研究仅仅是一个探索性的研究,所以对评价指标构建、测算方法选取、参考数据来源等也只是试探性研究。不足之处以及影响因素、作用机理等将在今后的研究中进行弥补和深化。
| [1] |
TÖDTLING F, KAUFMANN A. Innovation systems in regions of Europe-a comparative perspective[J]. European Planning Studies, 1999, 7(6): 699-717. DOI:10.1080/09654319908720549 |
| [2] |
KERSSENS-VAN DRONGELEN I C, COOKE A. Design principles for the development of measurement systems for research and development processes[J]. R and D Management, 1997, 27(4): 345-357. DOI:10.1111/radm.1997.27.issue-4 |
| [3] |
ZABALA-ITURRIAGAGOITIA J M, VOIGT P, GUTIERREZ-GRACIA A. Regional innovation systems:How to assess performance[J]. Regional Studies, 2007, 41(5): 661-672. DOI:10.1080/00343400601120270 |
| [4] |
FREEMAN C. The 'National System of Innovation' in historical perspective[J]. Cambridge Journal of Economics, 1995, 19(1): 5-24. |
| [5] |
王章豹, 徐枞巍. 高校科技创新能力综合评价:原则、指标、模型与方法[J]. 中国科技论坛, 2005(2): 55-59. DOI:10.3969/j.issn.1002-6711.2005.02.014 |
| [6] |
谭恒.河南省科技创新能力评价研究[D].武汉: 武汉大学, 2010.
|
| [7] |
WANG E C, HUANG W. Relative efficiency of R & D activities:A cross-country study accounting for environmental factors in the DEA approach[J]. Research Policy, 2007, 36(2): 260-273. DOI:10.1016/j.respol.2006.11.004 |
| [8] |
JAYANTHI S, WITT E C, SINGH V. Evaluation of potential of innovations:A DEA-based application to US photovoltaic industry[J]. IEEE Transactions on Engineering Management, 2009, 56(3): 478-493. DOI:10.1109/TEM.2009.2013833 |
| [9] |
刘玲利.科技资源配置理论与配置效率研究[D].长春: 吉林大学, 2007.
|
| [10] |
熊彼特. 经济发展理论[M]. .
|
| [11] |
GRILICHES Z. R & D and the productivity slowdown[J]. National Bureau of Economic Research, 1980, 343-348. |
| [12] |
赵喜鸟, 钱燕云, 薛明慧. 技术进步对经济增长的贡献度分析——基于长三角和珠三角5个地区的实证分析[J]. 科技进步与对策, 2012(2): 23-26. |
| [13] |
史英慧.辽宁省科技创新能力及效率评价[D].沈阳: 辽宁大学, 2015.
|
| [14] |
周国华. 高校科技创新能力对江苏区域经济影响的实证研究[J]. 中国商贸, 2014(10): 174-176. |
| [15] |
赵绪胜.山东省高校科技创新效率的评价研究[D].济南: 山东大学, 2016.
|
| [16] |
范斐, 杜德斌, 李恒, 等. 中国地级以上城市科技资源配置效率的时空格局[J]. 地理学报, 2013(10): 1331-1343. DOI:10.11821/dlxb201310003 |
| [17] |
张静.我国农业科技创新能力与效率研究[D].杨凌: 西北农林科技大学, 2011.
|
| [18] |
盛彦文, 马延吉. 东北三省科技资源产出效率及经济贡献——基于34个地级城市的面板数据[J]. 中国科学院大学学报, 2016(5): 632-640. |
| [19] |
王青, 潘桔. 高校科技创新能力对地区经济增长贡献率研究——以辽宁省为例[J]. 沈阳工业大学学报(社会科学版), 2017(2): 129-133. |
| [20] |
林卓玲, 黄英, 贺浪萍. 不同类型高等学校科技创新效率变化分析[J]. 华南师范大学学报(自然科学版), 2014(4): 116-123. |
| [21] |
国家统计局社会科技和文化产业统计司, 科学技术部创新发展司. 中国科技统计年鉴(2005-2017)[M]. 北京: 中国统计出版社, 2005.
|
| [22] |
李文辉, 林卓玲. 地方高校科技创新能力评价指标体系构建思考[J]. 技术与创新管理, 2011(4): 325-327, 353. DOI:10.3969/j.issn.1672-7312.2011.04.001 |
| [23] |
李艳双, 曾珍香, 张闽, 等. 主成分分析法在多指标综合评价方法中的应用[J]. 河北工业大学学报, 1999(1): 94-97. DOI:10.3969/j.issn.1007-2373.1999.01.022 |
| [24] |
陈运平.高校科技创新体系、能力及其对经济增长的贡献研究[D].南昌: 南昌大学, 2007.
|
| [25] |
魏权龄. 数据包络分析[M]. 北京: 科学出版社, 2004.
|
| [26] |
陈国生, 杨凤鸣, 陈晓亮, 等. 基于Bootstrap-DEA方法的中国科技资源配置效率空间差异研究[J]. 经济地理, 2014(11): 36-42. |
| [27] |
刘为.大学科技园创新效率评价研究——基于两阶段共同边界DEA模型[D].苏州: 苏州大学, 2015.
|
| [28] |
石枕. 怎样理解和计算"全要素生产率"的增长——评一个具体技术经济问题的计量分析[J]. 数量经济技术经济研究, 1988(12): 68-71. |
| [29] |
齐艳杰.高校科技创新对河北省经济发展的贡献作用的实证研究[D].石家庄: 河北师范大学, 2012.
|
| [30] |
姜均露. 经济增长中科技进步作用测算:理论与实践[M]. 北京: 中国计划出版社, 1998.
|
| [31] |
赵蓉英, 张心源. "双一流"建设背景下中国高校人才与大学排名相关性分析[J]. 重庆大学学报(社会科学版), 2018(3): 117-127. |
 2019, Vol. 25
2019, Vol. 25


