长江经济带包含四川、重庆、贵州、云南、湖北、湖南、江西、安徽、浙江、江苏和上海等11个省市,占全国经济总量的四成。在十九大报告中,习近平同志两次提到了“长江经济带”,指出“长江经济带发展成效显著”。种种迹象表明长江经济带早已被视为“中国经济的脊梁”。近年来,长江经济带沿线各省市经济增长明显,人们生活水平有了质的提高,同时一些新的特点又逐渐显露出来,板块化发展模式就是其中之一,即当前长江经济带发展已然分成了上中下游三大板块,下游板块包括上海、江苏和浙江,中游板块包括安徽、江西、湖北和湖南,上游板块包括四川、重庆、云南和贵州。
长江经济带是新时期中国经济发展的一个重要战略选择,要始终如一地贯彻习近平总书记所提出“共抓大保护,不搞大开发”的发展理念。那么当前区域板块化模式和区域经济一体化模式哪种更适合长江经济带高质量发展?对此学术界并没有形成统一认识。有些学者认为,长江经济带上中下游的板块化发展,有利于形成不同产业分工,打造差异化产业集聚,进而带动长江经济带整体经济的发展[1-2];另一些学者则认为,长江经济带发展必须从全局出发,通过11个省市的区域经济一体化,实现要素重新配置,进而推动产业布局优化与结构升级,提高长江经济带经济增长效率[3-4]。
板块化模式是指,受地方政府“以邻为壑”的发展政策影响,经济要素在各省市之间流动存在较大限制,导致当前长江经济带上中下游之间存在产业发展梯度,互相之间经济往来相对较少,呈现出不同的板块化发展模式。区域经济一体化模式是指,长江经济带的各级地方政府打破“各自为政、以自我为中心”的分治模式,从更高的视野进行整体规划设计,保证经济要素能够相对自由地在各省市之间往来,实现区域间协调、有序、健康地发展[5-9]。
要解决区域板块化模式和区域经济一体化模式究竟哪一个更好的争论,笔者认为关键就在于何种发展模式能够真正推动长江经济带的高质量发展。即如果某个模式能够促使长江经济带自发实现内部产业空间布局优化,进而形成“产业集聚—区域创新—经济发展”的内在驱动链条,提高整体经济发展效率,那么该模式就是长江经济带高质量发展的最优选择。
鉴于以上分析,本文基于长江经济带发展特点,通过修正传统空间“中心—外围”模型,得到多元空间主体区位模型,将长江经济带11省市进行理论空间建模,并运用SBM-undesirable模型进行实证检验,以系统性分析区域板块化模式与区域经济一体化模式哪一种更加适合长江经济带高质量发展,并以此提出相关政策建议。
一、国内外相关文献综述长江经济带研究最早可以追溯到20世纪80年代[10],至今已有30余年,学术文献积累丰富,其相关研究可划分为区域差异和协调发展、重点省份与城市发展、相关产业问题研究等三个方面。关于长江经济带区域差异和协调发展的研究则主要侧重于生态环境、资源承载以及城市群发展等视角,其中关于长江经济带城市群发展的研究主要集中于空间分布格局优化[11]、组织优化[12]、梯度发展[13]、新型城镇化发展[14]、投入—产出效率[15]、劳动力市场一体化[16]、创新投入[17]、城市群内部经济联系[18]等方面。本文则主要从城市群空间优化布局视角来研究长江经济带高质量发展模式选择问题。
城市群范围识别和基于“中心—外围”模型的圈层划分是研究长江经济带空间优化布局的基础。“中心—外围”源自于Krugman的空间经济学理论,是指城市经济圈由中心城市和外围城市构成,以中心城市为中心,带动外围城市的经济发展模式。基于以上理论,国内外学者开展了大量研究。陈修颖等从要素相互作用的视角分析了长江经济带产业空间结构的形成与演化,然后又基于空间计量方法研究长江经济带空间分异特征,发现经过四个阶段的发展,长江经济带已逐步形成了特殊的条形“中心—外围—边缘”结构[19-20];于涛方等基于“中心—外围”理论,定量分析了长江经济带区域结构演化的特征与规律,认为2000年来长江经济带各地域之间的扩散和集聚开始强化,逐渐呈现梯度格局[5];赵琳等对长江经济带经济演进分析发现,经济带内部有两极分化趋势,以低于平均水平的区域为主,发达地区呈现组团状延伸和零星点状分布[21];张超等研究表明长江经济带城市体系空间分布呈现明显的片段化特征,各城市群空间演化存在显著差异,总体呈现东部较为密集、中西部相对稀疏的“中心—外围”结构[7];丁黄艳[22]、任毅等[23]也从不同视角对长江经济带空间发展问题进行了研究,得出了类似的结论。
梳理已有研究发现:(1)目前对于长江经济带空间优化布局研究的空间尺度选择并不统一。新时期中央提出“推动长江经济带协同发展”的指导意见,现有相关研究范围有待修订;(2)现有研究对于长江经济带“中心—外围”圈定识别有待深入。长江经济带是国务院依托长江黄金水道打造的中国经济新支撑带,沿江分布的大中小城市在空间形态上具有典型的连绵区多中心带状分布特征[24],笼统的“中心—外围”空间结构识别实有不妥之处。
基于此, 笔者将参考国外学者近年来对传统“中心—外围”模型修正及更新的相关经验[25-27],打破模型只能研究两个经济主体的限制,将其扩展为N个空间经济主体,以此进行系统互动分析。需要说明的是,长江经济带沿线11省市基本符合“中心—外围”理论建模结构,即省会周边属于中心城市圈,省内其余地区属于外围城市结构[28]。因此,笔者将在完成多元空间经济模型修正后,分别对沿线11省市进行数理建模,将其一并带入统一的空间经济模型中,分别研究在板块化发展模式以及区域经济一体化发展模式下,各个经济主体之间的相互作用,并通过SBM模型进行实证检验,以比较何种发展模式更能促使长江经济带经济高质量发展。
二、多元空间经济模型的构建 (一) 模型的基本假设及框架由于多元空间经济模型是基于传统“中心—外围”模型的进一步修正,因此本文基本假设基于传统“中心—外围”模型给出。
假设1:整个空间区域中存在θ个城市群体,城市群范围是有限的,任意两城市之间进行经济活动均存在成本。
假设2:整个空间区域内只存在两种产业,一种为制造业,其集中于城市范围中,另一种为农业,其分布在城市群以外区域。
假设3:在整个空间区域内,制造业属于不完全竞争性质,假定存在大量工业制成品,且生产存在规模报酬递增特性。农业属于完全竞争性质,生产同质、单一化产品。
假设4:在整个空间区域内,城市居民既是消费者又是制成品的生产者,其对两种产品有着相同偏好。城市居民可以在各城市主体间自由往来,他们的流动将导致消费及生产活动的转移,其中当地消费无成本,而跨区域消费则存在成本。
假定θ1为θ个城市群体中的任意一个成员城市,根据假设4,可基于C-D函数定义出该经济体中居民的效用函数:
| $ U = {M^\mu }{A^{1 - \mu }} $ | (1) |
其中:M与A分别表示制成品、农产品各自的消费量综合指数;μ是小于1大于0的常数,表示制成品的支出份额,1-μ则表示农产品的支出份额。根据假设3,假定M符合CES函数:
| $ M = {\left[ {\int_0^n m {{\left( i \right)}^{\frac{{\sigma - 1}}{\sigma }}}{\rm{d}}i} \right]^{\frac{\sigma }{{\sigma - 1}}}},\sigma > 1 $ | (2) |
上式中σ为制成品不变替代弹性,n表示制成品种类,m(i)表示第i种制成品的消费量。令ρ=
为得到θ1地区居民预算约束条件,给定第i种制成品价格为p(i),农产品价格为pA,居民收入为Y,可得:
| $ {p^A}A + \int_0^n p \left( i \right)m\left( i \right){\rm{d}}i = Y $ | (3) |
就制成品消费而言,需要选定每一个m(i),使得M组合的成本最低。
| $ \min \int_0^n p \left( i \right)m\left( i \right){\rm{d}}i\;\;\;\;\;{\rm{s}}.{\rm{t}}.{\left[ {\int_0^n m {{\left( i \right)}^\rho }{\rm{d}}i} \right]^{\frac{1}{\rho }}} = M $ | (4) |
由均衡公式求解可得,m(i)=m(j)(p(i)/p(j))1/(ρ-1),其中i和j表示任意一对制成品组合。将其带入约束条件可得:
| $ m\left( j \right) = \frac{{p{{\left( j \right)}^{1/\left( {\rho - 1} \right)}}}}{{{{\left[ {\int_0^n p {{\left( i \right)}^{\rho /\left( {\rho - 1} \right)}}{\rm{d}}i} \right]}^{1/\rho }}}}M $ | (5) |
根据上式,则可以得出θ1地区居民M消费的最低成本:
| $ \int_0^n p \left( j \right)m\left( j \right){\rm{d}}j = {\left[ {\int_0^n p {{\left( i \right)}^{\rho /\left( {\rho - 1} \right)}}{\rm{d}}i} \right]^{\frac{{\rho - 1}}{\rho }}}M = {\left[ {\int_0^n p {{\left( i \right)}^{1 - \sigma }}{\rm{d}}i} \right]^{1/\left( {1 - \sigma } \right)}}M = GM $ | (6) |
| $ G = {\left[ {\int_0^n p {{\left( i \right)}^{1 - \sigma }}{\rm{d}}i} \right]^{1/\left( {1 - \sigma } \right)}} $ | (7) |
上式中,G为制成品价格指数。
| $ \max U = {M^\mu }{A^{1 - \mu }}\;\;\;{\rm{ s}}{\rm{.t}}{\rm{.}}\;\;\;\;GM + {p^A}A = Y $ | (8) |
同样根据均衡求解公式可得,θ1地区居民制成品最优消费数量和农产品最优消费数量分别为:M=μY/G且A=(1-μ)Y/pA。进一步展开可得:
| $ A = \left( {1 - \mu } \right)Y/{p^A} $ | (9) |
| $ m\left( i \right) = \mu Y\frac{{p{{\left( j \right)}^{ - \sigma }}}}{{{G^{ - \left( {\sigma - 1} \right)}}}},i \in \left[ {0,n} \right] $ | (10) |
| $ U = {\mu ^\mu }{\left( {1 - \mu } \right)^{1 - \mu }}Y{G^{ - \mu }}{\left( {{p^A}} \right)^{ - \left( {1 - \mu } \right)}} $ | (11) |
其中:式(9)为θ1地区居民农产品需求函数,式(10)为单一制成品需求函数,式(11)为居民间接效用函数,G-μ(pA)-(1-μ)则表示θ1地区生活物价指数。
(二) 引入贸易互通变量在完成了单一地区经济主体模型构建后,本文进而引入贸易互通变量来将这θ个城市群体中的各个地区联系起来,以构建多元空间经济模型。借鉴“冰山成本”概念[29],①,在已有模型基础上引入贸易互通参数T,其具体表达式为:
① 所谓“冰山成本”,即如果把一单位产品(农产品或制成品)从地区r运到地区s,那么从地区r运出的产品只会有一部分可以到达地区s(即1/IrsA或者1/IrsM),而其余部分的产品就像冰雪一样“融化”掉了。因此要想有1单位农产品或制造业产品完整地运送到目的地,那么在原产地就必须装运IrsA或者IrsM的对应产品。
| $ T = 1/I,T \in \left[ {0,1} \right],I \in \left[ {1, + \infty } \right] $ |
上式中I为冰山成本,当T=0(I→+∞)时,表示各城市地区之间贸易成本无穷大,即存在绝对的贸易壁垒,各地区经济发展完全独立,互相之间没有任何经贸往来;当T=1(I=1)时,表示地区间不存在任何贸易壁垒,生产资料、物质资源和劳动力等可以在各地区间自由流动。为了便于后文分析,本文给出第五个假设。
假设5:整个城市群空间区域内部均存在经济活动。一方面,涉及农产品的经济活动在整个区间内均无成本;另一方面,涉及制成品的经济活动,在城市区域内无成本,城市之间存在“冰山成本”。
下面引入另一个城市经济主体θ2,使其与θ1建立空间经济联系。我们用nθ1表示θ1地区制成品种类。定义pMθ1表示θ1地区制成品当地出厂价格,pMθ1θ2表示θ1地区制成品运到θ2地区的到岸价,具体形式为:
| $ p_{{\theta _1}{\theta _2}}^M = \frac{{P_{{\theta _1}}^M}}{{T_{{\theta _1}{\theta _2}}^M}} $ | (12) |
记θ2地区价格指数为Gθ2,于是利用式(7)可写出引入贸易互通要素后θ2地区的价格指数:
| $ {G_{{\theta _2}}} = {\left[ {\sum\limits_{\alpha = {\theta _1}}^R {{n_\alpha }} {{\left( {\frac{{p_\alpha ^M}}{{T_{\alpha {\theta _2}}^M}}} \right)}^{1 - \sigma }}} \right]^{1/\left( {1 - \sigma } \right)}},R = \theta $ | (13) |
利用式(10)可以得θ2地区对θ1地区任一制成品的需求量:
| $ \mu {Y_{{\theta _2}}}{\left( {\frac{{p_{{\theta _{\rm{1}}}}^M}}{{T_{{\theta _1}{\theta _{\rm{2}}}}^M}}} \right)^{ - \sigma }}G_{{\theta _2}}^{\sigma - 1} $ | (14) |
上式中,Yθ2是θ2地区居民的收入。基于式(14),可得出θ1地区制成品在整个城市群的销售总量qMθ1:
| $ q_{{\theta _1}}^M = \mu \sum\limits_{\alpha = {\theta _1}}^R {{Y_\alpha }} {\left( {\frac{{p_{{\theta _{\rm{1}}}}^M}}{{T_{{\theta _1}{\theta _{\rm{2}}}}^M}}} \right)^{ - \sigma }}\frac{{G_\alpha ^{\sigma - 1}}}{{T_{{\theta _1}\alpha }^M}},R = \theta $ | (15) |
由式(15)可知,多元空间经济模型中,任一地区经济主体的制成品销量取决于地区收入、价格指数、出厂价格以及贸易互通条件,与各经济主体之间的具体空间分布无关,自此多元空间经济模型构建工作基本完成。
(三) 多元空间经济模型的完善为便于后文分析,假定所有地区制成品生产函数只包含劳动力这单一自变量且生产技术相同,且基于假设3,则生产数量qM与劳动力lM之间的关系可写为:
| $ {l^M} = F + {c^M}{q^M} $ | (16) |
上式中,F、cM分别为固定劳动力投入和边际劳动力投入。同样基于假设3,可推导产品种类数目等于厂商数目。对于θ1地区而言,假定产品出厂价为pMθ1,制造业工人名义工资为wMθ1,则利润πθ1为:
| $ {\pi _{{\theta _1}}} = p_{{\theta _1}}^Mq_{{\theta _1}}^M - w_{{\theta _1}}^M\left( {F + c_{{\theta _1}}^Mq_{{\theta _1}}^M} \right) $ | (17) |
根据利润最大化原则,可得:
| $ p_B^M = \left( {1 - 1/\sigma } \right) = {c^M}w_B^M $ | (18) |
由于厂商可以自由进出市场,如果定价原则给定,则利润方程变为:
| $ {\pi _B} = w_B^M\left[ {\frac{{q_B^M{c^M}}}{{\sigma - 1}} - F} \right] $ | (19) |
所以,零利润均衡产出为:q*≡F(σ-1)/cM,代入式(16)可得均衡劳动投入l*=Fσ。定义nθ1表示θ1地区厂商数目,LMθ1表示当地工人数量,则nθ1=LMθ1/l*
代入式(15)和式(18),基于厂商零利润条件可得:
| $ w_{{\theta _1}}^M = \left( {\frac{{\sigma - 1}}{{\sigma {c^M}}}} \right){\left[ {\frac{\mu }{{{q^*}}}\sum\limits_{\alpha = 1}^R {{Y_\alpha }} {{\left( {T_{{\theta _1}\alpha }^M{G_\alpha }} \right)}^{\sigma - 1}}} \right]^{1/\sigma }} $ | (20) |
由式(20)可知,θ1地区居民工资水平同收入水平及贸易互通条件成正比。由此θ1地区居民的实际工资ωMθ1为:
| $ \omega _{{\theta _1}}^M = w_{{\theta _1}}^MG_{{\theta _1}}^{ - \mu }{\left( {p_{{\theta _1}}^A} \right)^{ - \left( {1 - \mu } \right)}} $ | (21) |
下面开始参数简化推导。设cM=(σ-1)/σ,则式(18)可化简为pMθ1=wMθ1,可得q*=l*;设F=μ/σ,则均衡产量方程可以改写为nθ1=LMθ1/μ,可得厂商零利润产出为q*=l*=μ,进而可得到以下两式:
| $ {G_{{\theta _1}}} = {\left[ {\frac{1}{\mu }\sum\limits_{\alpha = 1}^R {L_\alpha ^M} {{\left( {\frac{{w_\alpha ^M}}{{T_{{\theta _1}\alpha }^M}}} \right)}^{1 - \sigma }}} \right]^{1/\left( {1 - \sigma } \right)}} $ | (22) |
| $ w_{{\theta _1}}^M = {\left[ {\sum\limits_{\alpha = 1}^R {{Y_\alpha }} {{\left( {T_{{\theta _1}\alpha }^M{G_\alpha }} \right)}^{\sigma - 1}}} \right]^{1/\sigma }} $ | (23) |
其中式(22)为θ1地区简化版价格指数,式(23)为θ1地区简化版名义工资方程。
下面开始进行多元空间经济模型组合构建。给定θ个城市群总的制造业人口为LM,农业劳动人口为LA。用λθ1、λθ2、…、λθn分别表示在任何一时间点上θ1地区、θ2地区、…、θn地区对应制造业劳动力比例,ψθ1、ψθ2、…、ψθn表示在任何一时间点上θ1地区、θ2地区、…、θn地区对应的农业劳动力比例。设LA+LM=1,则LM=μ,LA=1-μ。基于长江经济带大部分地区农业劳动力收入差距远小于城市劳动力收入差距的现实情况,同时结合前文假设,给定wAθ1=wAθ2=…=wAθn=1,且由于农业贸易成本为0,因此令T=TM。
假定地区工资差距是各城市地区制造业人口流动的主要原因,即倘若θ1地区工资高于θ2地区,那么θ2地区的制造业人口就会流向θ1地区,本文定义
综上所述,可以构建多元空间经济模型方程组,其中式(24)、式(25)、式(26)和式(27)分别表示多元空间经济模型的收入方程组、价格指数方程组、名义工资方程组和实际工资方程组:
| $ \left\{ \begin{array}{l} {Y_{{\theta _1}}} = \mu {\lambda _{{\theta _1}}}w_{{\theta _1}}^M + \left( {1 - \mu } \right){\psi _{{\theta _1}}}\\ {Y_{{\theta _2}}} = \mu {\lambda _{{\theta _2}}}w_{{\theta _2}}^M + \left( {1 - \mu } \right){\psi _{{\theta _2}}}\\ \cdots \\ {Y_{{\theta _n}}} = \mu {\lambda _{{\theta _n}}}w_{{\theta _n}}^M + \left( {1 - \mu } \right){\psi _{{\theta _n}}} \end{array} \right. $ | (24) |
| $ \left\{ \begin{array}{l} {G_{{\theta _1}}} = {\left[ {{\lambda _{{\theta _1}}}{{\left( {w_{{\theta _1}}^M} \right)}^{1 - \sigma }} + {\lambda _{{\theta _2}}}{{\left( {\frac{{w_{{\theta _2}}^M}}{T}} \right)}^{1 - \sigma }} + \cdots + {\lambda _{{\theta _n}}}{{\left( {\frac{{w_{{\theta _n}}^M}}{T}} \right)}^{1 - \sigma }}} \right]^{1/1 - \sigma }}\\ {G_{{\theta _2}}} = {\left[ {{\lambda _{{\theta _1}}}{{\left( {\frac{{w_{{\theta _1}}^M}}{T}} \right)}^{1 - \sigma }} + {\lambda _{{\theta _2}}}{{\left( {w_{{\theta _2}}^M} \right)}^{1 - \sigma }} + \cdots + {\lambda _{{\theta _n}}}{{\left( {\frac{{w_{{\theta _n}}^M}}{T}} \right)}^{1 - \sigma }}} \right]^{1/1 - \sigma }}\\ \cdots \\ {G_{{\theta _n}}} = {\left[ {{\lambda _{{\theta _1}}}{{\left( {\frac{{w_{{\theta _1}}^M}}{T}} \right)}^{1 - \sigma }} + {\lambda _{{\theta _2}}}{{\left( {\frac{{w_{{\theta _2}}^M}}{T}} \right)}^{1 - \sigma }} + \cdots + {\lambda _{{\theta _n}}}{{\left( {w_{{\theta _n}}^M} \right)}^{1 - \sigma }}} \right]^{1/1 - \sigma }} \end{array} \right. $ | (25) |
| $ \left\{ \begin{array}{l} {w_{{\theta _1}}} = {\left[ {{Y_{{\theta _1}}}G_{{\theta _1}}^{\sigma - 1} + {Y_{{\theta _2}}}{{\left( {T{G_{{\theta _2}}}} \right)}^{1 - \sigma }} + \cdots + {Y_{{\theta _n}}}{{\left( {T{G_{{\theta _n}}}} \right)}^{\sigma - 1}}} \right]^{1 - \sigma }}\\ {w_{{\theta _2}}} = {\left[ {{Y_{{\theta _1}}}\left( {TG_{{\theta _1}}^{\sigma - 1}} \right) + {Y_{{\theta _2}}}G_{{\theta _2}}^{\sigma - 1} + \cdots + {Y_{{\theta _n}}}{{\left( {T{G_{{\theta _n}}}} \right)}^{\sigma - 1}}} \right]^{1 - \sigma }}\\ \cdots \\ {w_{{\theta _n}}} = {\left[ {{Y_{{\theta _1}}}\left( {TG_{{\theta _1}}^{\sigma - 1}} \right) + {Y_{{\theta _2}}}{{\left( {T{G_{{\theta _2}}}} \right)}^{\sigma - 1}} + \cdots + {Y_{{\theta _n}}}G_{{\theta _n}}^{\sigma - 1}} \right]^{1/\sigma }} \end{array} \right. $ | (26) |
| $ \left\{ \begin{array}{l} {\omega _{{\theta _1}}} = {w_{{\theta _1}}}G_{{\theta _1}}^{ - \mu }\\ {\omega _{{\theta _2}}} = {w_{{\theta _2}}}G_{{\theta _2}}^{ - \mu }\\ \cdots \\ {\omega _{{\theta _n}}} = {w_{{\theta _n}}}G_{{\theta _n}}^{ - \mu } \end{array} \right. $ | (27) |
为了更好地讨论多元空间经济模型运行机制,首先令θ=3②。以克鲁格曼等学者及相关统计数据为参考依据,本文设σ=5, μ=0.4。定义农业在三地区间平均分布即
② 若θ=2,该模型则变成了克鲁格曼已经讨论过的传统“中心—外围”模型,且地区间要素流动方向过于单一,这里就不再讨论。
| $ \left\{ {\begin{array}{*{20}{c}} {{Y_{{\theta _1}}} = 0.4{\lambda _{{\theta _1}}}w_{{\theta _1}}^M + 0.2}\\ {{Y_{{\theta _2}}} = 0.4{\lambda _{{\theta _2}}}w_{{\theta _2}}^M + 0.2}\\ {{Y_{{\theta _3}}} = 0.4{\lambda _{{\theta _3}}}w_{{\theta _3}}^M + 0.2} \end{array}} \right\} $ | (28) |
| $ \left\{ \begin{array}{l} {G_{{\theta _1}}} = {\left[ {{\lambda _{{\theta _1}}}{{\left( {w_{{\theta _1}}^M} \right)}^{ - 4}} + {\lambda _{{\theta _2}}}{{\left( {\frac{{w_{{\theta _2}}^M}}{T}} \right)}^{ - 4}} + {\lambda _{{\theta _3}}}{{\left( {\frac{{w_{{\theta _3}}^M}}{T}} \right)}^{ - 4}}} \right]^{ - 1/4}}\\ {G_{{\theta _2}}} = {\left[ {{\lambda _{{\theta _1}}}{{\left( {\frac{{w_{{\theta _1}}^M}}{T}} \right)}^{ - 4}} + {\lambda _{{\theta _2}}}{{\left( {w_{{\theta _2}}^M} \right)}^{ - 4}} + {\lambda _{{\theta _3}}}{{\left( {\frac{{w_{{\theta _3}}^M}}{T}} \right)}^{ - 4}}} \right]^{ - 1/4}}\\ {G_{{\theta _3}}} = {\left[ {{\lambda _{{\theta _1}}}{{\left( {\frac{{w_{{\theta _1}}^M}}{T}} \right)}^{ - 4}} + {\lambda _{{\theta _2}}}{{\left( {\frac{{w_{{\theta _2}}^M}}{T}} \right)}^{ - 4}} + {\lambda _{{\theta _3}}}{{\left( {w_{{\theta _3}}^M} \right)}^{ - 4}}} \right]^{ - 1/4}} \end{array} \right. $ | (29) |
| $ \left\{ {\begin{array}{*{20}{l}} {{w_{{\theta _1}}} = {{\left[ {{Y_{{\theta _1}}}G_{{\theta _1}}^4 + {Y_{{\theta _2}}}{{\left( {T{G_{{\theta _2}}}} \right)}^4} + {Y_{{\theta _3}}}{{\left( {T{G_{{\theta _3}}}} \right)}^4}} \right]}^{1/5}}}\\ {{w_{{\theta _2}}} = {{\left[ {{Y_{{\theta _1}}}{{\left( {T{G_{{\theta _1}}}} \right)}^4} + {Y_{{\theta _2}}}G_{{\theta _2}}^4 + {Y_{{\theta _3}}}{{\left( {T{G_{{\theta _3}}}} \right)}^4}} \right]}^{1/5}}}\\ {{w_{{\theta _3}}} = {{\left[ {{Y_{{\theta _1}}}{{\left( {T{G_{{\theta _1}}}} \right)}^4} + {Y_{{\theta _2}}}{{\left( {T{G_{{\theta _2}}}} \right)}^4} + {Y_{{\theta _3}}}G_{{\theta _3}}^4} \right]}^{1/5}}} \end{array}} \right. $ | (30) |
| $ \left\{ {\begin{array}{*{20}{l}} {{\omega _{{\theta _1}}} = {w_{{\theta _1}}}G_{{\theta _1}}^{ - 0.4}}\\ {{\omega _{{\theta _2}}} = {w_{{\theta _2}}}G_{{\theta _2}}^{ - 0.4}}\\ {{\omega _{{\theta _3}}} = {w_{{\theta _3}}}G_{{\theta _3}}^{ - 0.4}} \end{array}} \right. $ | (31) |
下面论文以式(28)、式(29)、式(30)和式(31)为基础,运用matlab7.0仿真分析三地区贸易互通条件变动对整个空间经济体运作的影响机理。
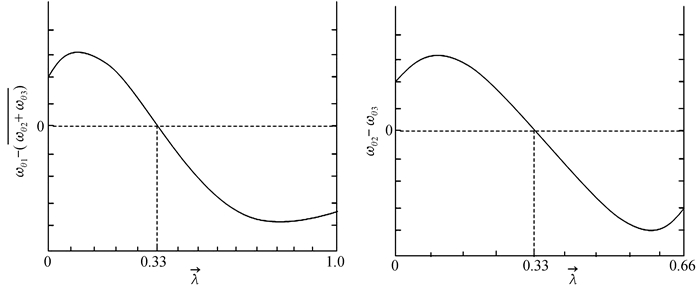
情况一:地区间贸易互通条件较差时(即区域板块化发展),要素在各经济主体间自由流通难度较大,定义T=0.2,可得到图 1。
|
图 1 地区间贸易互通条件较差(区域板块化发展) |
图 1中,横坐标
结论1:在地区间贸易互通条件较差的情况下(即区域板块化发展),三地区空间经济体在
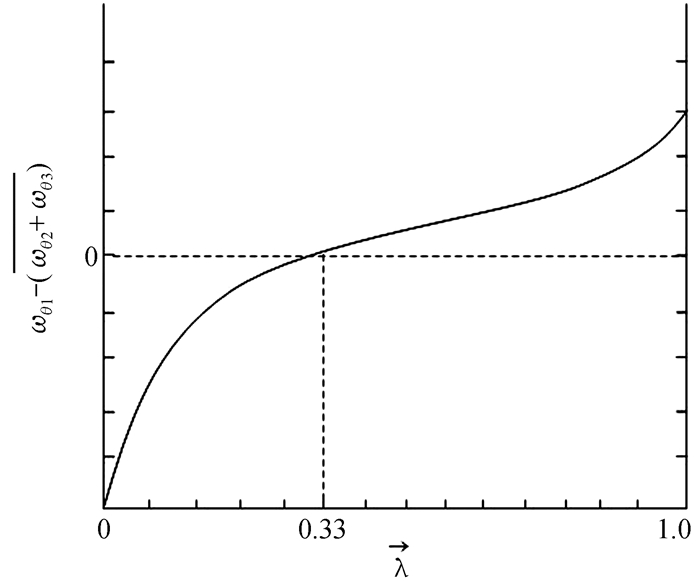
情况二:地区间贸易互通条件较好时(即区域经济一体化发展),要素在各经济主体间自由流通较为容易,令T=0.9,可得到图 2。
|
图 2 地区间贸易互通条件较好(区域经济一体化发展) |
由图 2可知,就同一制造业而言,当
结论2:在地区间贸易互通条件较好时(即区域经济一体化发展),三地区空间经济体将在市场推动下打破同一制造业的平均化,进而自发形成该制造业的集聚。其中该制造业集聚形成经济主体的选择,取决于最初θ1、θ2和θ3地区之间该制造业的比较优势。
(二) 贸易互通条件对长江经济带(多元空间经济体)发展的影响机制分析由克鲁格曼“中心—外围”模型结论可知,两地区空间经济模型在地区间贸易成本较高时,会存在地区经济平均化发展均衡,在贸易成本较低时会形成地区集聚化均衡。该结论与前文推导结论近乎一致,因此可进一步得出以下结论。
结论3:在地区间贸易互通条件较差情况下(即区域板块化发展),多元空间经济体将形成平均化均衡。
结论4:在地区间贸易互通条件较好情况下(即区域经济一体化发展),多元空间经济体将形成集聚化均衡。
结论3结果显示,长江经济带(多元空间经济体)如果采取区域板块化发展模式,流域各省市间行政壁垒影响将非常显著,导致经济要素在各主体之间流动存在较大难度,最终会使得多元空间经济体发展出现平均化均衡。平均化均衡即多元空间经济体内部各城市的各种制造业份额将趋于一致,使得整个区域形成制造业平均分布均衡,这一现象就是产业同构。很显然产业同构将使得区域内竞争激烈,影响资源配置效率,严重限制多元空间经济体的发展活力。
结论4结果显示,长江经济带(多元空间经济体)如果采取区域经济一体化发展模式,流域各省市间行政壁垒影响将不断削弱,区域内部贸易互通条件不断改善,进而激发经济要素在各主体之间流动速度,最终促使多元空间经济体有效转变地区经济增长方式,自发形成集聚化均衡。多元空间经济体集聚化均衡的形成,一方面,会进一步引发前向关联效应和后向关联效应,扩大各省市集聚经济辐射范围,从而提高整体经济发展活力;另一方面,会加快经济主体内部各项要素、资源自发地进行区位流动,优化相关资源的配置,改善多元空间经济体内部各主体产业结构,激发区域创新动力,提高多元空间经济体发展效率,从质的层面拉动长江经济带高质量发展。
综上所述,贸易互通条件视角的研究结果表明,对于长江经济带(多元空间经济体)而言,区域经济一体化发展模式要更优于区域板块化发展模式。
四、长江经济带发展模式比较分析:集聚化转型门槛视角 (一) 集聚化转型门槛理论推导本文进一步讨论当贸易互通条件改善到何种程度时,多元空间经济体平均化均衡会转化为集聚化均衡。
基于结论3,可定义多元空间经济体平均化均衡下各经济体内生变量值为:
| $ {\lambda _{{\theta _1}}} = {\lambda _{{\theta _2}}} = \cdots = {\lambda _{{\theta _n}}} = \frac{1}{n}; $ |
| $ {Y_{{\theta _1}}} = {Y_{{\theta _2}}} = \cdots = {Y_{{\theta _n}}} = \frac{1}{n}; $ |
| $ {w_{{\theta _1}}} = {w_{{\theta _2}}} = \cdots = {w_{{\theta _n}}} = 1; $ |
| $ G_{{\theta _1}}^{1 - \sigma } = G_{{\theta _2}}^{1 - \sigma } = \cdots = G_{{\theta _n}}^{1 - \sigma } = \frac{{1 + (n - 1){T^{\sigma - 1}}}}{n} $ |
显然,在平均化均衡下,当多元空间经济体其中某一地区内生变量发生变化,必定会使得其他地区同一变量产生相应变化,而且前后两者变化幅度相同,但符号相反。由此本文将多元空间经济体划分为两大群体,分别为θ1和θ2, ..., θn,定义:
| $ {\rm{d}}\lambda = {\rm{d}}{\lambda _{{\theta _{\rm{1}}}}} = - {\rm{d}}{\lambda _{{\theta _{\rm{2}}}, \cdots ,{\theta _{\rm{n}}}}} = - \left( {{\rm{d}}{\lambda _{{\theta _{\rm{2}}}}} + \cdots + {\rm{d}}{\lambda _{{\theta _n}}}} \right) $ |
| $ {\rm{d}}Y = {\rm{d}}{Y_{{\theta _{\rm{1}}}}} = - {\rm{d}}{Y_{{\theta _{\rm{2}}}, \cdots ,{\theta _n}}} = - \left( {{\rm{d}}{Y_{{\theta _{\rm{2}}}}} + \cdots + {\rm{d}}{Y_{{\theta _n}}}} \right) $ |
| $ {\rm{d}}w = {\rm{d}}{w_{{\theta _1}}} = - {\rm{d}}{w_{{\theta _2}, \cdots ,{\theta _n}}} = - \left( {{\rm{d}}{w_{{\theta _2}}} + \cdots + {\rm{d}}{w_{{\theta _n}}}} \right) $ |
| $ {\rm{d}}G = {\rm{d}}{G_{{\theta _{\rm{1}}}}} = - {\rm{d}}{G_{{\theta _{\rm{2}}} \ldots ,{\theta _n}}} = - \left( {{\rm{d}}{G_{{\theta _{\rm{2}}}}} + \cdots + {\rm{d}}{G_{{\theta _n}}}} \right) $ |
| $ {\rm{d}}\omega = {\rm{d}}{w_{{\theta _{\rm{1}}}}} = - {\rm{d}}{\omega _{{\theta _{\rm{2}}} \ldots ,{\theta _n}}} = - \left( {{\rm{d}}{\omega _{{\theta _{\rm{2}}}}} + \cdots + {\rm{d}}{\omega _{{\theta _n}}}} \right) $ |
则原方程组式(24)—式(27)可改写为:
| $ \left\{ {\begin{array}{*{20}{l}} {{Y_{{\theta _1}}} = {Y_{{\theta _1}}}}\\ {{Y_{{\theta _2}, \cdots ,{\theta _n}}} = {Y_{{\theta _2}}} + \cdots + {Y_{{\theta _n}}}} \end{array}} \right. $ | (32) |
| $ \left\{ {\begin{array}{*{20}{l}} {{G_{{\theta _1}}} = {G_{{\theta _1}}}}\\ {{G_{{\theta _2}, \cdots ,{\theta _2}}} = {G_{{\theta _2}}} + \cdots + {G_{{\theta _n}}}} \end{array}} \right. $ | (33) |
| $ \left\{ {\begin{array}{*{20}{l}} {{w_{{\theta _1}}} = {w_{{\theta _1}}}}\\ {{w_{{\theta _2}, \cdots ,{\theta _n}}} = {w_{{\theta _2}}} + \cdots + {w_{{\theta _n}}}} \end{array}} \right. $ | (34) |
| $ \left\{ {\begin{array}{*{20}{l}} {{\omega _{{\theta _1}}} = {\omega _{{\theta _1}}}}\\ {{\omega _{{\theta _2}, \cdots ,{\theta _n}}} = {\omega _{{\theta _2}}} + \cdots + {\omega _{{\theta _n}}}} \end{array}} \right. $ | (35) |
对式(32)求全微分可得:
| $ \left\{ {\begin{array}{*{20}{l}} {{\rm{d}}{Y_{{\theta _1}}} = \mu {w_{{\theta _1}}}{\rm{d}}{\lambda _{{\theta _1}}} + \mu {\lambda _{{\theta _1}}}{\rm{d}}{w_{{\theta _1}}}}\\ {{\rm{d}}{Y_{{\theta _2}, \ldots ,{\theta _n}}} = \mu {w_{{\theta _2}}}{\rm{d}}{\lambda _{{\theta _2}}} + \mu {\lambda _{{\theta _2}}}{\rm{d}}{w_{{\theta _2}}} + \cdots + \mu {w_{{\theta _n}}}{\rm{d}}{\lambda _{{\theta _n}}} + \mu {\lambda _{{\theta _n}}}{\rm{d}}{w_{{\theta _n}}}} \end{array}} \right. $ | (36) |
假设在整个空间区域内,各城市主体之间存在较大的贸易障碍,即贸易互通条件非常差,因此可以认为当前n地区制造业处于平均分布均衡附近,以上两式则可简化为一个式子:
| $ {\rm{d}}Y = \mu {\rm{d}}\lambda + \frac{\mu }{n}{\rm{d}}w $ | (37) |
同理可对式(33)、式(34)和式(35)求全微分,进而得出以下方程:
| $ \frac{{{\rm{d}}G}}{G} = \frac{{\left( {1 - {T^{\sigma - 1}}} \right)}}{{(1 - \sigma ){G^{1 - \sigma }}}}\left( {{\rm{d}}\lambda + \frac{{(1 - \sigma )}}{n}{\rm{d}}w} \right) $ | (38) |
| $ {\rm{d}}w = \frac{{\left( {1 - {T^{\sigma - 1}}} \right)}}{{\sigma {G^{1 - \sigma }}}}\left( {{\rm{d}}Y + \frac{{(\sigma - 1)}}{{nG}}{\rm{d}}G} \right) $ | (39) |
| $ {\rm{d}}\omega = {G^{ - \mu }}\left( {{\rm{d}}w - \frac{{\mu {\rm{d}}G}}{G}} \right) $ | (40) |
将式(37)带入式(39)中消除dY,然后将消除dY后的式(39)与式(38)联立变形可得以下两个式子:
| $ \frac{{{\rm{d}}G}}{G} = \frac{{n\sigma \left( {\frac{{1 - {T^{\sigma - 1}}}}{{1 + \left( {n - 1} \right){T^{\sigma - 1}}}}} \right)\left( {\frac{{\mu - \mu {T^{\sigma - 1}}}}{{1 + \left( {n - 1} \right){T^{\sigma - 1}}}}} \right)}}{{\left( {1 - \sigma } \right)\left( {{{\left( {\frac{{1 - {T^{\sigma - 1}}}}{{1 + \left( {n - 1} \right){T^{\sigma - 1}}}}} \right)}^2}\sigma - {{\left( {\frac{{1 - {T^{\sigma - 1}}}}{{1 + \left( {n - 1} \right){T^{\sigma - 1}}}}} \right)}^2} + \frac{{\mu - \mu {T^{\sigma - 1}}}}{{1 + \left( {n - 1} \right){T^{\sigma - 1}}}} - \sigma } \right)}}{\rm{d}}\lambda $ | (41) |
| $ {\rm{d}}w = \frac{{n\left( {\frac{{1 - {T^{\sigma - 1}}}}{{1 + (n - 1){T^{\sigma - 1}}}}} \right)\left( {\frac{{1 - {T^{\sigma - 1}}}}{{1 + (n - 1){T^{\sigma - 1}}}} - \mu } \right)}}{{{{\left( {\frac{{1 - {T^{\sigma - 1}}}}{{1 + \left( {n - 1} \right){T^{\sigma - 1}}}}} \right)}^2}\sigma - {{\left( {\frac{{1 - {T^{\sigma - 1}}}}{{1 + \left( {n - 1} \right){T^{\sigma - 1}}}}} \right)}^2} + \frac{{\mu - \mu {T^{\sigma - 1}}}}{{1 + \left( {n - 1} \right){T^{\sigma - 1}}}} - \sigma }}{\rm{d}}\lambda $ | (42) |
定义
将X带入式(41)和式(42)将方程进行简化,然后将简化后的两个方程带入式(40)整理后可得:
| $ \frac{{{\rm{d}}\omega }}{{{\rm{d}}\lambda }} = \frac{{nX{G^{ - \mu }}}}{{\sigma - 1}}\left( {\frac{{\left. {\mu \left( {2\sigma - 1} \right) - X\left( {\sigma \left( {1 + {\mu ^2}} \right) - 1} \right)} \right)}}{{{X^2} - {X^2}\sigma - X\mu + \sigma }}} \right) $ | (43) |
将
| $ \frac{{{\rm{d}}\omega }}{{{\rm{d}}\lambda }} = \frac{{nX{G^{ - \mu }}(1 - \rho )}}{\rho }\left( {\frac{{\mu (1 + \rho ) - X\left( {\rho + {\mu ^2}} \right)}}{{1 - \mu X + \mu X\rho - \rho {X^2}}}} \right) $ | (44) |
下面要讨论
在多元空间经济体内部几乎不存在任何贸易互通的情况下(即T=0),此时分子项变为(1-μ)(μ-ρ);由于克鲁格曼定义“中心—外围”模型必须要满足“非黑洞条件”(即ρ>μ),同时μ, ρ∈[0, 1],因此分子项(1-μ)(μ-ρ)符号为负。该结果表明,当贸易互通条件较差时,多元空间经济体内部任何一地区制造业实际工资都会因为人口增加而减少,因此平均化均衡是稳定的。
当多元空间经济体内部贸易互通条件接近于理想状态时(即T→1),此时μ(1+ρ)-X(ρ+μ2)符号显然为正,且随着X值增加而下降。该结果表明,当贸易互通条件较好时,多元空间经济体内部任一地区制造业实际工资都会因为人口增加而增加,此时平均化均衡将被集聚化均衡替代。
综述所述,当贸易互通条件T从0→1时(即不断改善),
结论5:多元空间经济体内部贸易互通条件只要未能够超过临界值点T*,那么平均化均衡始终是稳定的;一旦多元空间经济体内部贸易互通条件超过了临界点T*,那么平均化均衡将自发转变为集聚化均衡。
令式(44)中的
| $ {T^ * } = {\left[ {\frac{{\left( {{\mu ^2} + \rho } \right) - \mu (1 + \rho )}}{{\left( {{\mu ^2} + \rho } \right) + \mu (n - 1)(1 + \rho )}}} \right]^{\frac{{1 - \rho }}{\rho }}} $ | (45) |
基于前文定义,当n=2时,则表示是克鲁格曼等人构建的传统“中心—外围”两地区空间经济模型的贸易互通条件临界值方程;当n=3时,则变为了三地区空间经济模型的贸易互通条件临界值方程。在σ=5, μ=0.4时,两地区的贸易互通条件转变临界值T2*为0.614 8,而三地区贸易互通条件转变临界值T3*为0.562 3。显然,同样在σ=5, μ=0.4条件下,三地区贸易互通条件临界点值明显低于两地区的临界值。同时由式(45)分母可知,随着n的增大,贸易互通条件临界点值将越来越低,该结果则意味着,区域内参与经济主体越多,越容易形成集聚化发展模式。
结论6:贸易互通条件临界值与多元空间经济体内部参与主体个数呈现显著的负相关关系,即在同一空间区域内部,参与经济主体越多,随着贸易互通条件的不断改善,该区域空间越容易打破地区间制造业的平均分布均衡,进而在各经济城市主体之间形成稳定的集聚化均衡。
(二) 集聚化转型门槛对长江经济带(多元空间经济体)发展的影响机制分析当前经济数据显示,长江经济带上中下游三大板块之间经济差距较为明显,板块内部各地区产业结构也存在一定的同构性。基于前文理论,可将长江经济带分解为一个三地区空间经济模型(下游板块)和两个四地区空间经济模型(上、中游板块)。
以长江经济带下游板块为例,其属于三地区空间经济模型。虽然在该区域内,已出现一定的产业专业化集聚,例如,上海、江苏、浙江三省近年来制造业集聚化发展势头强劲,但是产业同构问题仍然存在[30-31],因此可认为该板块并没有跨越过T3*=0.562 3的门槛,仍处于产业平均化均衡。对于长江经济带上、中游两板块而言,其内部各地区产业结构的同构性更加明显,因此同样可认为这两板块也处于产业平均化均衡。
但是T*门槛的突破是存在明显难度的。以长江经济带下游板块为例,该区域实施长江三角洲城市群发展战略已然有些年份,各方资金投入和政策配套力度也十分之大,但是目前仍然没有能够使整个板块有效突破T3*=0.562 3这一门槛,进而形成区域集聚化发展模式。这一现实也进一步说明,T的改善不但需要在硬件上进行投入,即改善城市间互联互通基础设施条件,在软件上各城市主体也需要加大政策配套的扶持,而且需要长时间保持这一投入趋势。虽然上、中游地区属于四地区空间经济体,其门槛T4*=0.526 6要低于下游地区的T3*=0.562 3,但是相对于下游地区而言其板块内部经济环境、生产技术等优势并不明显。倘若未来的时间里,长江经济带发展仍然按照上中下游三大板块各自发展的模式进行,那么整个经济带生产力将在很长一段时间里得不到质的提升,因为产业平均发展均衡是很难得到有效改变的。只有一举突破T*门槛,才能使整个区域生产力实现从量到质的转变,而且这一转变一旦开始,地区不同产业之间就会自发地在市场引导下进行集聚转移,最终实现整个长江经济带产业结构的优化布局。
那么如何才能够尽快改变当前长江经济带产业同构发展局面?基于结论6可知,区域内部参与主体越多,T*门槛就越低。T*门槛越低就意味着,从平均发展均衡转变为集聚发展均衡的难度就越低,换句话讲,区域内部各城市前期用于改善贸易互通条件的经济成本、时间成本及政治成本就越低。显然选择区域经济一体化模式来替换当前的板块化发展模式,能够有效打破长江经济带内部各经济主体之间的板块壁垒。把11个省市同时作为一个区域整体的经济成员,该空间区域的集聚均衡突破门槛值就变为了T11*=0.414 1,远低于三地区门槛T3*=0.562 3及四地区门槛T4*=0.526 6。这样整个长江经济带就能够更早、更容易地实现产业集聚化发展均衡,从而优化资源配置,激发区域创新活力,提高整体经济效率。
综上所述,集聚化转型门槛值的研究结果表明,长江经济带选择区域经济一体化发展模式,将降低经济转型的门槛值,使整个区域更加容易形成集聚化发展均衡,这是区域板块化发展模式所不具备的。
五、长江经济带发展模式比较分析:经济发展效率视角基于“共抓大保护,不搞大开发”的发展理念,长江经济带经济发展效率必须是考虑了资源和环境约束的地区投入产出效率,然而传统DEA模型无法将经济活动中所排放出的废水、废气、固废等非期望产出纳入效率测算体系,因此本文将采用Tone提出的非径向非角度SBM-undesirable模型来对2010—2017年长江经济带经济发展效率进行测算,以此对区域板块化发展模式与区域经济一体化发展模式进行比较分析。需要说明的是,2014年中国成立推动长江经济带发展领导小组,推动长江经济带统筹协调发展,因此笔者定义从2014年开始长江经济带宏观上进入了区域经济一体化发展,而2014年以前长江经济带仍属于区域板块化发展。
首先构建长江经济带经济发展效率测算SBM-undesirable模型。假定生产决策系统中有n个DUM单元,使用投入要素为m种,期望产出为s1种,非期望产出为s2种,对应的向量分别为x∈Rm、yg∈Rs1、yb∈Rs2,定义矩阵X=(xij)∈Rm*n,Yg=(yijg)∈Rs1*n,Yb=(yijb)∈Rs2*n,假定X>0, Yg>0, Yb>0,且生产可能性集合为封闭集合与有界集合,投入及产出可自由处置,同时假设期望产出与非期望产出为零结合及产出联合弱可处置性,则模型表达为:
| $ \mathit{\boldsymbol{G}} = \left\{ {\left( {\mathit{\boldsymbol{x}},{\mathit{\boldsymbol{y}}^g},{\mathit{\boldsymbol{y}}^b}} \right)|\mathit{\boldsymbol{x}} \ge \mathit{\boldsymbol{X}}\lambda ,{\mathit{\boldsymbol{y}}^g} \le {\mathit{\boldsymbol{Y}}^g}\lambda ,{\mathit{\boldsymbol{y}}^b} = {\mathit{\boldsymbol{Y}}^b}\lambda ,\sum\limits_{i = 1}^n \lambda ,\lambda \ge 0} \right\} $ | (46) |
上式即为包含投入、期望产出、非期望产出的不等式预算约束模型,进一步可得到同时包含期望产出与非期望产出的SBM-undesirable模型:
| $ \begin{array}{l} \min {\rho ^ * } = \frac{{1 - \frac{1}{m}\sum\limits_{i = 1}^m {\frac{{s_i^ - }}{{{x_{i0}}}}} }}{{1 + \frac{1}{{{s_1} + {s_2}}}\left( {\sum\limits_{r = 1}^{{s_1}} {\frac{{s_r^{g + }}}{{y_{{r_0}}^g}}} + \sum\limits_{r = 1}^{{s_2}} {\frac{{s_r^{b + }}}{{y_{{r_0}}^b}}} } \right)}}\\ {\rm{s}}.{\rm{t}}.\left\{ \begin{array}{l} {x_0} = \mathit{\boldsymbol{X}}\lambda + {s^ - }\\ y_0^g = {\mathit{\boldsymbol{Y}}^g}\lambda - {s^{g + }}\\ y_0^b = {\mathit{\boldsymbol{Y}}^b}\lambda + {s^{b + }}\\ \lambda ,{s^ - },{s^{g + }},{s^{b + }} \ge 0 \end{array} \right. \end{array} $ | (47) |
式中,λ为权重,s-表示投入松弛变量,sg+表示期望产出松弛变量,sb+表示非期望产出松弛变量,ρ*为考虑了非期望产出时各DUM的生产效率。
(一) 指标体系构建基于长江经济带发展现状及数据的可获得性,本文选取上海、江苏、浙江、安徽、江西、湖北、湖南、重庆、四川、云南、贵州等11省市作为研究对象,以2010—2017年作为时间样本区间,运用SBM-undesirable模型对长江经济带经济发展效率值进行测算。具体投入产出指标名称与内涵阐释见表 1。为了更好地去除价格变动影响,以下指标涉及价格的均以2005年为基期进行了不变价格处理。所有数据均来自于《中国统计年鉴》《中国环境统计年鉴》《中国能源统计年鉴》以及各省统计年鉴。
| 表 1 SBM-undesirable模型指标体系 |
需要说明的是,本研究数据采集期间,由于上海、湖南及四川2018年统计年鉴尚未公开发行,因此2017年对应三省劳动力数据采取趋势法进行补齐。
(二) 测算结果及分析本文利用Max dea7.0 pro软件,基于2010—2017年长江经济带沿线11省市投入产出数据,运用SBM-undesirable模型进行经济效率测算,结果如表 2所示。
| 表 2 长江经济带经济发展效率:SBM-undesirable模型测算结果 |
测算结果显示,2010—2017年长江经济带沿线省市经济发展效率普遍不高(平均值仅为0.474 6),除了上海市在考察期间持续位于效率有效前沿面外,其余省市均为经济发展效率无效。11省市经济效率排名从高到低依次为:上海、江苏、浙江、重庆、湖北、湖南、四川、江西、贵州、云南、安徽。该结果表明,在未来的很长一段时间里长江经济带沿线各省市仍需坚持走生态优先、绿色发展之路,倒逼地区产业结构转型升级,努力推动长江经济带高质量发展。
如图 3所示,就长江经济带整体经济发展效率而言,2010—2017年间总体呈现阶梯上升状态。第一梯度为2010—2013年,长江经济带整体经济效率波动范围处于(0.442 1~0.466 4)区间,均值为0.459 4;第二梯度为2014—2017年,长江经济带整体经济效率波动范围处于(0.472 0~0.497 2)区间,均值为0.489 6。该结果表明,自2014年建立推动长江经济带发展领导小组,统筹长江经济带协调发展以来,长江经济带经济发展效率有了明显的提升,虽然受集聚化转型门槛的影响,2016年整体经济效率有了一定程度下滑,但是2014—2017年(区域经济一体化发展阶段)长江经济带经济发展效率明显要高于2010—2013年(区域板块化发展阶段)。

|
图 3 2010—2017年长江经济带经济发展效率折线图 |
综上所述,长江经济带经济发展效率视角研究结果表明,区域经济一体化发展模式比区域板块化发展模式更能够提高整体经济发展效率,有利于经济高质量增长。
六、结论及建议本文根据空间经济学的基本原理,在“中心—外围”模型基础上修正得到多元空间经济模型,以此对长江经济带11省市进行空间数理建模,并基于SBM-undesirable进行实证检验,进而系统性地分析区域板块化模式和区域经济一体化模式哪种更适合长江经济带经济高质量发展。研究结果如下。
第一,区域板块化发展模式由于存在显著的行政壁垒影响,将导致经济要素在各主体之间流动存在较大难度,最终会使得长江经济带发展出现平均化均衡。平均化均衡即长江经济带内部各城市的各种制造业份额将趋于一致,使得整个区域形成制造业平均分布均衡,这一现象就是产业同构。很显然产业同构将使得区域内竞争激烈,影响资源配置效率,导致资源大量浪费,严重限制区域内部经济活力,不利于长江经济带高质量发展。
第二,区域经济一体化发展模式将不断削弱长江经济带内部各省市行政壁垒影响,改善区域内部贸易互通条件,进而提升经济要素在各省市之间的流动速度,最终促使长江经济带有效转变地区经济增长方式,自发形成集聚化均衡。长江经济带集聚化均衡的形成,一方面,会进一步引发前向关联效应和后向关联效应,扩大各省市集聚经济辐射范围,从而提高整体经济发展活力;另一方面,会加快经济主体内部各项要素、资源自发的区位流动,优化相关资源的配置,改善长江经济带内部各主体产业结构,激发区域创新动力,提高多元空间经济体发展效率,从质的层面拉动长江经济带高质量发展。
第三,集聚化转型门槛值的研究结果表明,在区域板块化发展模式下,直接通过加大长江经济带人力、资金投入等方式来打破平均化均衡难度很大且成本很高,与长江发展要“共抓大保护,不搞大开发”理念不符合。长江经济带发展只有采用区域经济一体化模式,才能够有效降低集聚化转型的经济成本和时间成本,提升整体经济发展效率。
此外,基于SBM-undesirable模型对2010—2017年长江经济带经济发展效率测算的结果也显示,区域经济一体化发展模式比区域板块化发展模式更能够提高整体经济发展效率,有利于经济高质量增长。
基于以上结论,本文认为区域经济一体化发展模式更适用于长江经济带经济高质量发展,应当尽快全面落实,因此提出以下四点建议。
其一,在贸易互通层面,建议优先加快交通基础设施互联互通,这是推动长江经济带高质量发展的先手棋。只有将长江全流域打造成黄金水道,不断扩大长江经济带交通网络规模,最大限度发挥出长江的综合运输效益,才能够有力支撑整体区域经济发展的转型。
其二,在制度层面,应探索建立一系列跨区域协调发展机制,包括健全全国土地空间开发机制,健全跨区域合作协调机制,建立横向区域利益分配机制,深化生态文明建设机制等,以统筹安排协同长江经济带发展,主动引导各省市加强合作交流,改变各自为政、各图其利的发展态势,为长江经济带经济发展模式转型升级奠定基础。
其三,在管理机构层面,可积极借鉴美国田纳西河流域管理机构及中国(泛)长三角地区政府间合作的成功经验,在“推动长江经济带发展领导小组”的基础上,进一步完善长江经济带政府协调机构,建立统一、高效、顺畅的政府协调协商、交流沟通机制。
其四,在产业布局层面,长江经济带沿线各级政府应该严格按照《依托黄金水道推动长江经济带发展的指导意见》《加强长江经济带工业绿色发展的指导意见》等指导性文件的政策配套实施方案规定,有意识地进行地区优势产业培养,防止“羊群效应”及“产业同构效应”的再次出现。
| [1] |
黄庆华, 周志波, 刘晗. 长江经济带产业结构演变及政策取向[J]. 经济理论与经济管理, 2014(6): 92-101. DOI:10.3969/j.issn.1000-596X.2014.06.008 |
| [2] |
陆玉麒, 董平. 新时期推进长江经济带发展的三大新思路[J]. 地理研究, 2017, 36(4): 605-615. |
| [3] |
艾红如.长江经济带区域经济时空分异及其驱动机制[D].武汉: 华中师范大学, 2016. http://cdmd.cnki.com.cn/Article/CDMD-10511-1016271131.htm
|
| [4] |
李雪松, 张雨迪, 孙博文. 区域一体化促进了经济增长效率吗?:基于长江经济带的实证分析[J]. 中国人口·资源与环境, 2017, 27(1): 10-19. |
| [5] |
于涛方, 甄峰, 吴泓. 长江经济带区域结构:"核心-边缘"视角[J]. 城市规划学刊, 2007(3): 41-48. DOI:10.3969/j.issn.1000-3363.2007.03.009 |
| [6] |
于文静.长江经济带区域经济发展差异及协调度的定量分析[D].上海: 华东师范大学, 2009. http://kns.cnki.net/KCMS/detail/detail.aspx?dbcode=CMFD&filename=2009187773.nh
|
| [7] |
张超, 王春杨, 吕永强, 等. 长江经济带城市体系空间结构:基于夜间灯光数据的研究[J]. 城市发展研究, 2015, 22(3): 19-27. DOI:10.3969/j.issn.1006-3862.2015.03.003 |
| [8] |
徐廷廷.长江经济带产业分工合作演化研究[D].上海: 华东师范大学, 2015. http://cdmd.cnki.com.cn/Article/CDMD-10269-1016016863.htm
|
| [9] |
王振, 孙克强, 王晓娟. 长江经济带蓝皮书:长江经济带发展报告(2011~2015)[M]. 北京: 社科文献出版社, 2016.
|
| [10] |
陆大道. 二〇〇〇年我国工业生产力布局总图的科学基础[J]. 地理科学, 1986, 6(2): 110-118. |
| [11] |
李嬛, 宁越敏, 魏也华, 等. 长江经济带沿江城市群空间分布格局与联动机理研究[J]. 长江流域资源与环境, 2016, 25(12): 1797-1806. DOI:10.11870/cjlyzyyhj201612002 |
| [12] |
戢晓峰, 张玲, 陈方. 物流一体化视角下城市群空间组织优化研究:以长江经济带城市群为例[J]. 地域研究与开发, 2015, 34(5): 24-28, 41. DOI:10.3969/j.issn.1003-2363.2015.05.005 |
| [13] |
方创琳, 周成虎, 王振波. 长江经济带城市群可持续发展战略问题与分级梯度发展重点[J]. 地理科学进展, 2015, 34(11): 1398-1408. |
| [14] |
吴传清, 万庆. 长江经济带城镇化发展的时空格局与驱动机制研究:基于九大城市群2004-2013年数据的实证分析[J]. 武汉大学学报(哲学社会科学版), 2015, 68(5): 44-51. |
| [15] |
孙倩倩. 长江经济带城市群投入产出效率及竞争力研究[J]. 北方经贸, 2015(1): 76-78. DOI:10.3969/j.issn.1005-913X.2015.01.038 |
| [16] |
陈立泰, 李金林, 叶长华. 长江经济带城市群劳动力市场一体化测度及影响因素:基于劳动力工资视角的分析[J]. 华东经济管理, 2017, 31(3): 5-12. DOI:10.3969/j.issn.1007-5097.2017.03.001 |
| [17] |
肖泽磊, 朱威鹏, 范斐, 等. 城市群创新投入的空间格局与创新绩效研究:以长江经济带所辖城市群为例[J]. 人文地理, 2017, 32(3): 61-67, 130. |
| [18] |
吴培培, 朱小川, 王伟. 长江经济带十大城市群内部城市间产业联系对经济产出影响研究:基于行业间投入产出引力模型方法[J]. 城市发展研究, 2017, 24(7): 49-55. DOI:10.3969/j.issn.1006-3862.2017.07.007 |
| [19] |
陈修颖, 陆林. 长江经济带空间结构形成基础及优化研究[J]. 经济地理, 2004, 24(3): 326-329. DOI:10.3969/j.issn.1000-8462.2004.03.009 |
| [20] |
陈修颖. 长江经济带空间结构演化及重组[J]. 地理学报, 2007, 62(12): 1265-1276. |
| [21] |
赵琳, 徐廷廷, 徐长乐. 长江经济带经济演进的时空分析[J]. 长江流域资源与环境, 2013, 22(7): 846-851. |
| [22] |
丁黄艳. 长江经济带基础设施发展与经济增长的空间特征:基于空间计量与面板门槛模型的实证研究[J]. 统计与信息论坛, 2016, 31(1): 24-32. DOI:10.3969/j.issn.1007-3116.2016.01.004 |
| [23] |
任毅, 丁黄艳, 任雪. 长江经济带工业能源效率空间差异化特征与发展趋势:基于三阶段DEA模型的实证研究[J]. 经济问题探索, 2016(3): 93-100. |
| [24] |
潘鑫, 宁越敏. 长江三角洲都市连绵区城市规模结构演变研究[J]. 人文地理, 2008, 23(3): 17-21. DOI:10.3969/j.issn.1003-2398.2008.03.004 |
| [25] |
OTTAVIANO G I P. Monopolistic competition, trade, and endogenous spatial fluctuations[J]. Regional Science and Urban Economics, 2001, 31(1): 51-77. |
| [26] |
FORSLID R, OTTAVIANO G I P. An analytically solvable core-periphery model[J]. Journal of Economic Geography, 2003, 3(3): 229-240. DOI:10.1093/jeg/3.3.229 |
| [27] |
ROBERT-NICOUD F.A simple geography model with vertical linkages and capital mobility[R].Mimeo, London School of Economics, 2002.
|
| [28] |
藤田昌久, 保罗·克鲁格曼, 安东尼.J.维纳布尔斯.空间经济学[M].梁琦, 译.北京: 中国人民大学出版社, 2005.
|
| [29] |
保罗·萨缪尔森, 威廉·诺德豪斯.经济学[M].萧琛, 译.北京: 人民邮电出版社, 2008.
|
| [30] |
郝良峰, 邱斌. 基于同城化与产业同构效应的城市层级体系研究:以长三角城市群为例[J]. 重庆大学学报(社会科学版), 2016, 22(1): 22-32. |
| [31] |
谢浩, 张明之. 长三角地区产业同构合意性研究:基于产业中类制造业数据的分析[J]. 世界经济与政治论坛, 2016(4): 156-168. DOI:10.3969/j.issn.1007-1369.2016.04.010 |
 2020, Vol. 26
2020, Vol. 26


