改革开放以来我国经济迅速发展,传统能源消耗逐年膨胀,生态环境问题日益突出。2006年我国碳排放量首次超过美国,成为世界第一大碳排放国家。2013年我国人均碳排放量为7.2吨,超过欧盟人均排放量的6.8吨。全球碳项目(GCP)发布排放数据表明,2017年中国碳排放量排名世界第一。为有效解决碳排放问题,推动经济社会可持续发展,我国政府自“十八大”以来做了大量工作。十八大报告提出建设小康社会要“把生态文明建设放在突出地位”,要努力实现“二氧化碳排放大幅下降”的新要求,要积极开展碳排放权交易试点。十九大报告提出“推进绿色发展”等重要举措,强调要“积极参与全球环境治理,落实减排承诺”,进一步提出“创新是引领发展的第一动力,是建设现代化经济体系的战略支撑”。中央环保督察组用了3年时间,对全国31个省(区、市)存在的环境问题进行了一次全覆盖式的督察,此次督查是我国环境保护有史以来国家层面直接组织的最大规模行动,有力地推动了各地区各部门落实生态文明建设目标。当前,中国经济发展面临的不确定因素进一步增加,外部贸易争端不断加剧,内部环境规制不断强化,创新型国家建设不断深入,中国经济能否实现创新驱动发展,经济增长与环境保护是否可以实现双赢格局等问题越发突出。如何构建一个合理的模型来分析中国环境治理、技术创新、经济增长以及二氧化碳减排之间的影响关系,考察环境治理与经济增长之间的协调性成为当前环境经济领域研究的热点,具有重要政策意义,有利于进一步厘清创新型国家建设、环境治理投资对碳减排的影响机制,健全我国低碳发展政策体系。在此背景下,本文将技术创新、环境规制中的碳税税率等因素纳入包括居民、企业和政府三个部门的动态随机一般均衡模型中,研究了环保政策、技术创新对经济增长与二氧化碳排放影响的问题,是对经济增长与环境保护能否实现双赢目标的有益探索。
一、相关文献回顾动态随机一般均衡模型(DSGE)已经成为当代宏观经济分析的一个基本工具[1]。在一般均衡框架下,DSGE模型采用动态最优化方法考察经济系统中行为主体决策,能够很好地刻画经济系统中个体行为及个体效用最大化准则下经济系统所体现的整体特性。由于DSGE模型专长于刻画经济系统的具体结构,便于进行各种类型的冲击模拟,而自下而上的建模原则又赋予其逻辑清晰的解释能力,非常适合于冲击传导研究和政策模拟[2]。DSGE模型已经在财政政策、货币政策、环境政策等方面得到了广泛应用。一些学者将宏观经济学中的DSGE建模应用到生态环境领域[3]。Fischer和Springborn利用RBC模型研究了排放强度、碳税、碳排放限额和碳排放目标的关系,发现限额和碳税会抑制经济体中生产率冲击的效果[4]。Angelopoulos等利用DSGE模型研究了最优减排政策,发现碳税政策优于碳排放规则政策[5]。Bukowsk和Kowal利用DSGE模型对欧洲碳排放政策进行评估,发现节能减排对生态环境和经济结构改善起到推进作用[6]。Heutel利用DSGE模型,通过社会福利函数的分析,研究了最优减排政策问题[7]。Fischer和Heutel对纳入污染和环境政策的真实周期模型、考虑内生技术进步的宏观经济模型在环境政策方面的研究进行了比较[8]。Annicchiarico和Di Dio利用DSGE模型对碳排放强度、碳排放上限和碳税三种环境政策进行了比较,发现当存在价格粘性时,碳税政策更能增加社会福利[9]。Dissou和Karnizova利用多部门DSGE模型研究了技术冲击下的碳减排政策,发现当冲击来自于非能源部门时碳排放配额政策与碳税政策无明显差异[10]。
杨翱等对DSGE模型在环境和能源领域的研究做了三个方面的分析[11]。朱智洺和方培利用DSGE模型研究了能源价格与碳排放的动态影响关系,发现能源价格波动对碳排放的作用为负向的[12]。杨翱等构建了引入工资粘性的动态随机一般均衡(DSGE)模型,研究发现五种外生冲击中,货币冲击持续的时间最长,能源价格冲击影响的强度最大[13]。刘建华等构建区域创新体系DSGE模型,形成由30个模型组成的河南创新体系DSGE模型体系,运用贝叶斯方法和计量经济学方法等进行参数估计,分析了城镇化、工业化、信息化等的波动对河南创新体系状态变量和控制变量的作用效果[14]。武晓利通过构建包含环保政策因素的三部门动态随机一般均衡(DSGE)模型,研究发现征收碳税以及提升环境消费偏好均能够显著改善环境质量,但对经济增长存在一定的负效应[15]。高超平等围绕居民、企业、环境三者关系构建DSGE模型,研究发现碳配额的总量目标不变时,调整免费配额比例只能影响有偿发放配额的均衡价格[3]。肖红叶和程郁泰构建环境DSGE模型,发现环境政策对我国经济系统稳定性没有产生特别强烈的负面冲击[16]。武晓利通过构建三部门双系统DSGE模型,发现生产技术对产出、非能源与能源消费、投资和就业具有正效应,但长期内导致碳排放量上升;环保技术对产出、非能源与能源消费、投资和就业具有正效应,同时有效降低碳排放,且环保技术冲击对各变量的影响均有较强的持续性[17]。
上述利用DSGE模型研究碳减排的相关研究中,多数情况下是讨论技术冲击(通常用全要素生产率冲击来衡量)、减排政策冲击(常见的有碳排放强度、碳排放上限和碳税等冲击)对碳排放的影响,较少涉及技术创新因素(如R & D投入、专有技术设备投资等)以及环保政策(如碳税、环境治理等)对碳排放影响的综合研究。因此,本文在前人研究的基础上,以Klima等[18]的研究为基础,以Klimat等的垄断竞争的RBC模型为框架,将专有技术设备投资纳入居民资本积累过程中①,将技术创新(R & D投入)、碳税等因素纳入企业生产过程中,将环境治理纳入政府行为中,构建一个包括居民、企业和政府三个部门的动态随机一般均衡模型,以分析环保政策、技术创新对社会产出和二氧化碳排放的影响。
① 在DSGE模型中,资本存量的所有者可以是居民或者是厂商,托雷斯(2015)详细进行了论述。本模型假定资本为居民所有。
二、研究模型构建 (一). 居民假定经济体中存在着无数个无限生命期限的同质居民,居民的偏好是时间可分离的,居民效用函数采用对数形式,居民在每一期规划其消费与劳动供给以最大化一生的效用。借鉴Jerger和Röhe[19]、武晓利和晁江锋[20]、托雷斯[1]、徐文成等[21]研究中的居民效用函数设定形式,模型中代表性居民面临着如式(1)的最优化问题:
| $ \max {{E}_{0}}\sum\limits_{\text{t}=0}^{\square }{{{\beta }^{\text{t}}}\left[ \gamma \ln {{C}_{\text{t}}}+\left( 1-\gamma \right)\ln \left( 1-\text{L}{{\text{s}}_{\text{t}}} \right)-\tau \ln {{H}_{\text{t}}} \right]} $ | (1) |
式(1)中,E0表示条件期望算子,β表示居民消费贴现因子,γ表示居民闲暇比重,τ表示环境污染(本文指二氧化碳排放量)给居民带来的负效用权重,Ct表示第t期实际居民消费支出,Lst表示居民劳动供给时间,1-Lst表示居民闲暇时间,Ht表示中间品厂商二氧化碳排放量。
代表性居民的预算约束为:
| $ {{P}_{\text{Ft}}}{{C}_{\text{t}}}+{{P}_{\text{Ft}}}{{I}_{\text{t}}}={{W}_{\text{t}}}\text{L}{{\text{s}}_{\text{t}}}+{{R}_{\text{t}}}\text{K}{{\text{s}}_{\text{t}-1}}+\text{p}{{\text{i}}_{\text{t}}}+\text{pi}\_p{{s}_{t}}-{{T}_{t}} $ | (2) |
式(2)中,PFt表示t期最终产品价格水平,It为t期实际居民投资,Wt为t期名义劳动价格,Rt为t期名义资本价格,pit和pi_pst表示企业利润(对应式(9)、(17)中的利润)②,Tt表示居民每期向政府交纳的定量税。
② 居民约束条件设定参考了托雷斯(2015)、刘斌(2010)、Klima(2015)等人的研究。
假定居民t期的资本存量为Kst,资本以名义价格Rt出租给厂商用于生产,居民资本积累按照以下运动方程:
| $ \text{K}{{\text{s}}_{\text{t}}}\text{=}\left( 1-{{\delta }_{K}} \right)\text{K}{{\text{s}}_{\text{t-1}}}+\text{I}{{\text{I}}_{\text{t}}}{{I}_{\text{t}}}\left[ \left( 1-\frac{{{\varphi }_{1}}}{2} \right){{\left( \frac{{{I}_{\text{t}}}}{{{I}_{\text{t-1}}}}-1 \right)}^{2}} \right] $ | (3) |
式(3)中,δK表示资本折旧率,Ⅱt表示投资专有技术冲击[22-23],
假定投资专有技术冲击Ⅱt的对数服从如下AR(1)过程:
| $ \ln \left( \text{I}{{\text{I}}_{\text{t}}} \right)={{\rho }_{\text{II}}}\ln \left( \text{I}{{\text{I}}_{\text{t-1}}} \right)+\varepsilon _{\text{t}}^{\text{II}} $ | (4) |
式(4)中,随机冲击项εtⅡ为序列不相关且服从均值为零、标准差为σⅡ的正态分布,0≤ρⅡ<1。
(二). 厂商模型中厂商分为最终品厂商和中间品厂商[25]。中间品厂商在垄断竞争的市场上把中间品销售给最终品厂商,最终品厂商将中间品组装以后在完全竞争产品市场上出售给居民。模型中劳动和资本由居民提供,假定生产要素市场处于完全竞争状态。厂商设定参考了朱柏松[26]、Klima等[18]、吴智华和杨秀云[27]等人的研究。
1.最终品厂商
最终品厂商通过对连续分布的中间产品进行组装来生产最终产品,按照DSGE模型中Dixit-Stiglitz的加总方法有:
| $ {{Y}_{F\text{t}}}={{\left[ \int_{0}^{1}{{{Y}_{\text{MONt}}}{}^{{}^{\frac{\rho -1}{\rho }}}{{\text{d}}_{\text{MON}}}} \right]}^{\frac{\rho }{\rho -1}}} $ | (5) |
式(5)中:YFt表示最终产品;YMONt表示中间产品;ρ表示不同中间产品之间的替代弹性,用来衡量中间品厂商垄断程度[28],ρ越小,则任意两个中间产品的可替代弹性也越小,这就意味着中间产品生产商的垄断能力越强[29]。
最终品厂商在约束条件(5)下面临如下最优化问题:
| $ \text{Max}{{\prod }_{\text{t}}}={{P}_{F\text{t}}}{{Y}_{F\text{t}}}-\int_{0}^{1}{{{P}_{\text{MONt}}}}{{Y}_{\text{MONt}}}{{\text{d}}_{\text{MON}}} $ | (6) |
式(6)中,PMONt表示中间产品垄断价格,求解该最优化问题,可得最终品厂商与中间品厂商的产出水平有如下关系:
| $ {{Y}_{\text{MONt}}}=\left( \frac{{{P}_{\text{MONt}}}}{{{P}_{F\text{t}}}} \right){}^{-\rho }{{Y}_{F\text{t}}} $ | (7) |
在完全竞争的最终产品市场上,最终品厂商的利润为零,则有:
| $ {{P}_{\text{Ft}}}={{\left[ \int_{0}^{1}{{{P}_{\text{MONt}}}{}^{\left( 1-\rho \right)}{{\text{d}}_{\text{MON}}}} \right]}^{\frac{1}{1-\rho }}} $ | (8) |
2.中间品厂商
中间品厂商在完全竞争的要素市场上购买劳动Ldt和资本Kdt,投入RDt的费用用于企业技术创新活动,企业在生产过程中每单位二氧化碳排放被政府征收Pht单位的碳税。中间品生产商第一阶段面临如下最优化问题:
| $ \text{Maxp}{{\text{i}}_{\text{t}}}={{E}_{0}}\sum\limits_{\text{t}=0}^{\square }{{{\beta }^{\text{t}}}\frac{{{\lambda }_{\text{t}+1}}}{{{\lambda }_{\text{t}}}}\left[ {{P}_{\text{t}}}{{Y}_{\text{t}}}-{{R}_{\text{t}}}\text{K}{{\text{d}}_{\text{t}}}-{{W}_{\text{t}}}\text{L}{{\text{d}}_{\text{t}}}-\text{P}{{\text{h}}_{\text{t}}}{{H}_{\text{t}}}-\text{R}{{\text{D}}_{\text{t}}} \right]} $ | (9) |
式(9)中,λt表示居民的边际效用[30],Pt表示中间产品Yt的出厂价格,Ht表示中间产品生产企业二氧化碳排放量。
中间品生产商在这一阶段面临的约束条件如下:
| $ {{Y}_{\text{t}}}={{A}_{\text{t}}}\text{K}{{\text{d}}_{\text{t}}}{}^{{}^{\alpha }K}\text{L}{{\text{d}}_{\text{t}}}{}^{{}^{\alpha }L}\text{SR}{{\text{D}}_{\text{t-1}}}^{{}^{\alpha }\text{SRD}} $ | (10) |
| $ {{H}_{\text{t}}}={{n}_{1}}Y_{\text{t}}^{{{n}_{2}}}\text{SRD}_{\text{t-1}}^{{{n}_{3}}}\text{HJZL}_{\text{t}}^{{{n}_{4}}} $ | (11) |
| $ \text{SR}{{\text{D}}_{\text{t}}}\text{=(1- }{{\delta }_{\text{SRD}}}\text{)SR}{{\text{D}}_{\text{t-1}}}\text{+RR}{{\text{S}}_{\text{t}}}\text{R}{{\text{D}}_{\text{t}}} $ | (12) |
式(10)是中间品厂商生产函数,At表示技术进步即全要素生产率[31],其对数服从AR(1)过程。αK、αL、αSRD分别表示实物资本Kdt、劳动Ldt、研发资本SRDt的产出弹性,δSRD表示研发资本折旧率。HJZLt表示环境治理投资,RDt表示企业技术创新投入。Pht、HJZLt和RRSt分别表示碳税税率冲击、环境治理投资冲击和研发投入冲击,对数服从AR(1)过程。
| $ \ln ({{A}_{\text{t}}})=\text{ }{{\rho }_{A}}\ln ({{A}_{\text{t-1}}} $ | (13) |
| $ \ln (\text{HJZ}{{\text{L}}_{\text{t}}})=\text{ }{{\rho }_{\text{HJZL}}}\ln (\text{HJZ}{{\text{L}}_{\text{t-1}}})+\text{ }\varepsilon _{\text{t}}^{\text{HJZL}} $ | (14) |
| $ \ln ({{\begin{array}{*{35}{l}} \text{RRS} \\ \end{array}}_{\text{t}}})=\text{ }{{\rho }_{\text{RRS}}}\ln (\text{RR}{{\text{S}}_{\text{t-1}}})+\text{ }\varepsilon _{\text{t}}^{\text{RRS}} $ | (15) |
| $ \ln ({{\begin{array}{*{35}{l}} \text{Ph} \\ \end{array}}_{\text{t}}})=\text{ }{{\rho }_{\text{Ph}}}\ln (\text{P}{{\text{h}}_{\text{t-1}}})+\text{ }\varepsilon _{\text{t}}^{\text{Ph}} $ | (16) |
式(13)至(16)中随机冲击εtA、εtHJZL、εtRRS、εtPh分别为序列不相关且服从均值为零,标准差为σA、σHJZL、σRRS、σPh的正态分布,ρA为自相关系数,0≤ρA<1,其余自相关系数取值类似。
由于假设中间品厂商是垄断竞争的,厂商在市场上具有一定的定价权。中间品厂商在垄断竞争市场上以垄断价格PMONt把中间品卖给最终品厂商,最终品生产商在完全竞争的市场上把中间品组装以后出售给消费者[26-27]。中间品厂商在给定产品需求YMONt和中间品出厂价格Pt的情况下,选择垄断价格PMONt实现利润最大化,中间品厂商在第二阶段面临如下优化问题:
| $ \text{Maxpi }\!\!\_\!\!\text{ p}{{\text{s}}_{\text{t}}}={{E}_{0}}\sum\limits_{\text{t}=0}^{\square }{\left\{ \frac{{{\lambda }_{\text{t+1}}}{}^{U}{{\lambda }_{\text{t+1}}}}{{{\lambda }_{\text{t}}}}\left[ \left( {{P}_{\text{MONt}}}-{{P}_{\text{t}}} \right){{Y}_{\text{MONt}}}-\frac{{{\varphi }_{2}}}{2}{{\left( \frac{{{P}_{\text{MONt}}}}{\text{PPI}\cdot {{P}_{\text{MONt-1}}}}-1 \right)}^{2}}{{Y}_{F\text{t}}}{{P}_{Ft}} \right] \right\}} $ | (17) |
式(17)中,贴现率
政府部门从居民收取定量税Tt,同时向中间品厂商征收碳税PhtHt。政府所有税收等于其治污支出Gt,政府治污支出用于环境治理投资HJZLt。对政府部门而言,有如下条件:
| $ {{T}_{\text{t}}}+\text{P}{{\text{h}}_{\text{t}}}{{H}_{\text{t}}}=\text{ }{{P}_{F\text{t}}}G $ | (18) |
| $ \text{HJZ}{{\text{L}}_{\text{t}}}=\text{ }{{n}_{5}}G_{\text{t}}^{{{n}_{6}}} $ | (19) |
式(18)中政府支出Gt的对数序列服从不相关,均值为零、标准差为σG的正态分布。
三、参数校准与估计根据刘斌[35]、李建强[36]的研究,DSGE模型中的参数可以分为两大类:一类是反映模型稳态特性的有关参数,通常采用校准(calibration)的方法来设定;另一类是反映模型动态特性的有关参数,通常采用估计的方法来确定。孙宁华论述了DSGE模型中校准方法使用的必要性[37],本文对反映模型动态特性的部分参数也采用校准的方法③。
③ 校准法虽然不是严格意义上的统计估计方法,但校准法得到的参数源于现实经济数据,是对稳态时变量间长期关系的良好近似替代,能较好地解决卢卡斯批判问题。参见:王胜华.政府支出经济增长效应区域异质性研究[D].中国财政科学研究院,2018.
根据本文DSGE模型设定形式,需要校准的静态参数包括:居民消费贴现因子β,居民闲暇比重γ,环境污染给居民带来的负效用权重τ,投资调整成本的变动程度φ1,资本折旧率δK,中间品厂商研发资本折旧率δSRD,中间品之间的替代弹性ρ,中间品价格调整成本系数φ2。
环境污染给居民带来的负效用权重τ:该参数在DSGE文献中并不多见,武晓利[15]、朱智洺和方培[12]将此参数取值为1,郑丽琳和朱启贵将此参数取值为2[38]。考虑到“十三五”及以后更长的一段时期我国经济社会要实现又好又快发展、居民对环境质量要求进一步提高、生态文明建设目标的进一步实现等情况,所以将该参数校准为3④。
④ 限于篇幅,本文未对静态参数进行稳健性分析。
投资调整成本的变动程度φ1:张佐敏根据季度数据采用贝叶斯方法得到此参数估计值为2.105[39],武彦民和竹志奇也采用了这一取值[40],刘金全等根据季度数据采用贝叶斯方法得到此参数估计值为1.897 6[41]。本文在参数估计时使用年度数据,将张佐敏[39]和刘金全等[41]的此参数取值平均以后按复利再折算,取整后将此参数校准为8。
研发资本折旧率δSRD:吴延兵认为该参数的确定有三种方法[42],一是根据经验直接将折旧率δSRD设为15%;二是通过计算专利净收益来估计;三是假定δSRD值是专利产生收益时间长度的反函数来估计。文献中广泛使用的研发资本存量的年度折旧率一般设为15%,本文也照此取值。
价格调整成本系数φ2:徐文成等研究中利用国内宏观数据得到的估计值为20.9[21],郭立甫等用贝叶斯估计方法得到该参数设为28.932[34]。在采用Rotemberg[32]价格调整的文献中,该参数取值一般都在20以上,文中将参数设为22。
模型其他静态参数的设置,即居民消费贴现因子β、居民闲暇比重γ、资本折旧率δK、中间品之间的替代弹性ρ等4个参数的取值,文献中对此类参数的讨论结果比较一致[22]。本文对此4个参数的校准主要参考了蒋颖[43]、孙宁华[37]等的研究。模型全部静态参数如表 1。
| 表 1 模型静态参数 |
反映模型动态特性的有关参数利用1992—2014年的年度数据进行校准。数据来自《中国统计年鉴1993—2015》《中国环境统计年鉴1993—2015》及《中国统计摘要1993—2015》各期,采用国内生产总值代表Y,资本存量K的测算参考了单豪杰[44]的方法,R & D资本存量SRD的测算参考了吴延兵[45]的方法,年末从业人员用L来表示,碳排放量H的测算利用中国1992—2014年能源消费标准量数据,环境治理投资HJZL在1992—2000年数据来自董文福等[46],2001—2014年数据来自《中国环境统计年鉴》。所有价值型数据使用GDP缩减指数进行平减(1992=100)。
参数ρⅡ和σⅡ的校准参考华昱[22]、易小丽[47]的研究⑤。根据中国设备工器具购置价格指数(INDEX92)得到一阶自回归模型为式(20):
⑤ 专有技术投资进步的重要表现是设备投资价格的下降以及同时设备投资在经济总量中的比重上升,参见文献[22]。
| $ \text{LN}\left( \text{INDEX92} \right)\text{= 2}\text{. 2951+0}\text{. 5264LN}\left( \text{INDEX92}\left( \text{ -1} \right) \right)\text{ +}\left[ \text{AR}\left( \text{1} \right)\text{= 0}\text{. 9676} \right] $ | (20) |
根据式(20),得到参数ρⅡ的估计值为0.526 4,标准差σⅡ为0.015 3。易小丽利用1990—2011的年度数据得到参数ρⅡ估计值为0.540 0[47]。综合考虑,文中采用易小丽[47]的取值。n1和n2取值参考了武晓利[15],在此基础上利用样本数据估算出n3和n4。参考杨翱和刘纪显[48]的研究,ρPh和σPh分别取值为0.465和2.688。借鉴徐舒等[49]的做法,式(10)、式(11)以及随机冲击序列中部分可估计参数通过校准方法得到。张军等估算1992—1998年间我国劳动产出弹性为0.391[50]。资本的产出弹性,国内文献一般将其设为0.33~0.5之间[48]。进一步参考朱智洺和方培[12]、孙宁华[37]的生产函数的设定形式,将式(10)中αK、αL分别校准为0.493和0.349。吴延兵在C-D生产函数框架下估算我国R & D存量的产出弹性为0.1~0.3[45],本文取其平均值,故将αSRD校准为0.2。将αK、αL、αSRD代入式(10),利用样本数据可计算出ln(At)序列,利用式(10)得到⑥:
| $ \begin{matrix} \begin{array}{*{35}{l}} \text{ln(}{{A}_{t}}\text{)=0}\text{.5484+0}\text{.7473ln(}{{A}_{\text{t}}}\text{(-1))} \\ \end{array} \\ \begin{array}{*{35}{l}} \left( 0.\text{ }0728 \right)\text{ }\left( 0.\text{ }003 \right) \\ \end{array} \\ \end{matrix} $ | (21) |
⑥ 模型(21)满足计量经济学相关假定,相关过程略去,其他一阶自回归模型处理过程一致。
式(21)中,括号中的数据表示系数为0的概率,用于变量的显著性检验。由式(20)可知ρA=0.747 3,由EVIEWS软件回归结果可得回归标准差即σA=0.050 5。同理可得ρRRs和ρHJZL,如表 2所示。
| 表 2 反映模型动态特性的有关参数 |
由于模型涉及居民消费、投资、劳动供求、企业利润、研发资本存量、总产出等多个宏观经济变量和技术进步冲击、专有技术设备投资冲击、研发投资冲击等技术创新因素,以及碳税税率冲击、环境治理投资冲击、政府治污支出冲击等环保政策因素,模拟结果较多,所以下文仅对各类冲击对总产出、居民消费、研发资本存量、碳排放量、碳排放强度的动态效应及传导机制进行分析。
随机冲击对变量影响的动态效应主要是通过脉冲分析来完成的。脉冲响应分析有两个目的:一是考察随机冲击是否能够导致经济变量之间的共动性;二是揭示随机冲击导致的变量之间的影响机制[31]。图 1至图 6展示了各类随机冲击对主要宏观经济变量的动态影响⑦。
⑦ 图 1至图 6中纵坐标表示变量相对于其稳态值的变化率,其单位为“%”,即一个百分点。变量稳态值是指随机冲击项取其均值(通常为零)时变量的取值,模型求解采用线性对数的形式。参考文献[35]。
|
图 1 技术进步冲击的脉冲响应 |
|
图 2 专有技术设备投资冲击的脉冲响应 |
|
图 3 碳税税率冲击的脉冲响应 |
|
图 4 环境治理投资冲击的脉冲响应 |
|
图 5 研发投入冲击的脉冲响应 |
|
图 6 政府治污支出冲击的脉冲响应 |
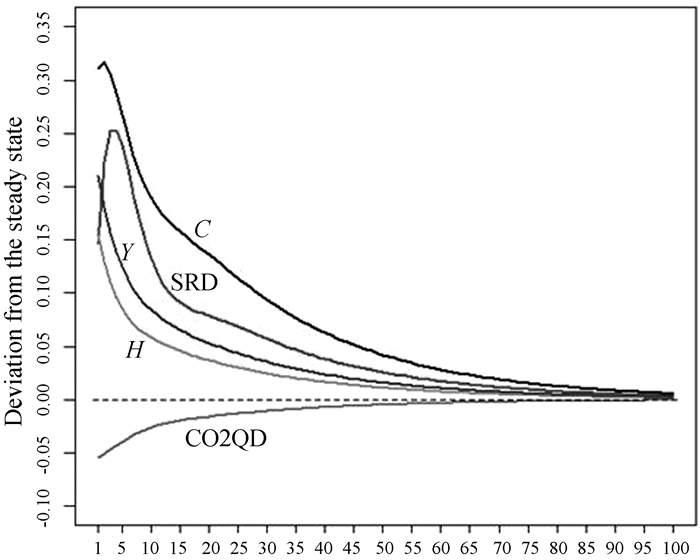
在受到一个标准差的技术进步冲击后(图 1),居民消费C、研发资本存量SRD、总产出Y和碳排放量H相对于系统稳态值的偏离显现正向变动趋势,二氧化碳排放强度CO2QD显现负向变动趋势。居民消费在第2期达到正向峰值,达到0.316 5个百分点。研发资本存量在第4期达到正向峰值,达到0.253 5个百分点。总产出和碳排放量都在第1期达到正向峰值,分别为0.209 6和0.154 6个百分点。碳排放强度在第1期达到负向峰值0.055 0个百分点。各变量在达到峰值以后逐步向稳态值逼近。
分析模拟结果可知,当期技术进步促进企业产出增加,企业利润增加,引起居民消费水平增加。企业利润增加的同时引起企业研发投入增加导致研发资本存量增加。居民消费和技术进步最终导致总产出增加,碳排放量也增加。碳排放量的增加不及总产出的增加,因而引进碳排放强度下降。随着时间的推移,技术进步引起的总产出逐步下降,居民消费、研发资本存量、碳排放量也逐步下降向稳态逼近,碳排放强度也呈下降趋势(相对于稳态)并逐步向稳态逼近。
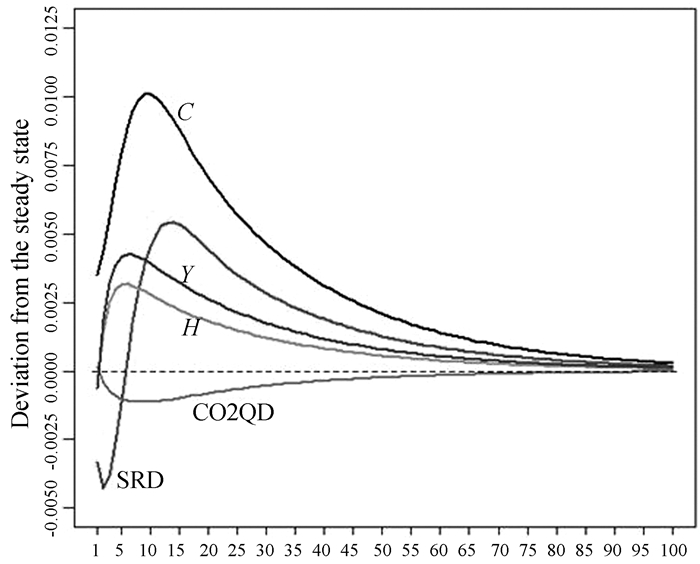
(二). 专有技术设备投资冲击在受到一个标准差的专有技术设备投资冲击后(图 2),居民消费C相对于系统稳态值的偏离显现正向的驼峰变动趋势,在第10期达到正向峰值,达到0.010 1个百分点,其变动趋势与华昱[22]研究结论相似。总产出Y相对于系统稳态值的偏离在第1期出现负值,随后上升,在第6期达到正向峰值,其值为0.004 3个百分点,随后往稳态逐步下降。碳排放H变动也出现类似情形,在第6期达到正向峰值0.003 2个百分点。研发资本存量SRD相对于系统稳态值的偏离情况比较复杂,在6期之前是负向变动,在第2期达到负向峰值0.004 3个百分点,在7期以后呈驼峰形波动,在14期达到正向峰值0.005 4个百分点后往稳态逐步下降。碳排放强度CO2QD第1期正向变化,然后开始负向变化,在第9期达到-0.001 1个百分点,之后逐步向稳态逼近。
分析模拟结果可知,当期设备投资增加需要一段时间才能转化为生产资本,所以当期设备投资增加以后总产出有个短暂的下降进而引起当期碳排放强度的增加。由于居民当期没有预期到设备投资增加,所以他们的当期消费仍然维持在较高水平。但随着时间推移,设备投资转换为生产资本,增加了资本存量,增加了企业利润,因此后期居民消费呈增加趋势。随着总产出增加,碳排放量也显现增加趋势。进一步分析可知,短期内设备投资增加挤压了研发投资。长期来看,设备投资对研发投资的挤出效应逐步减弱,总产出的增加逐步引起研发资本存量大幅度的增加,从而导至碳排放强度显现下降趋势并逐渐趋近于稳态水平。
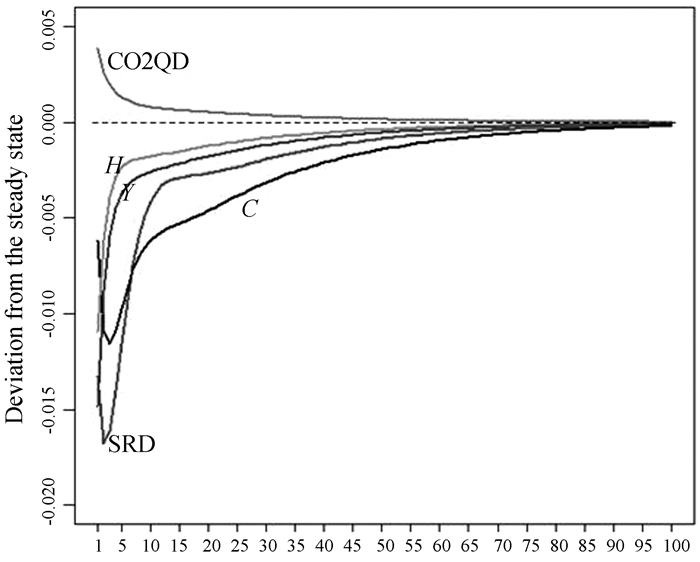
(三). 碳税税率冲击在受到一个标准差的碳税税率冲击后(图 3),居民消费C、研发资本存量SRD、总产出Y和碳排放量H相对于系统稳态值的偏离显现负向变动趋势,碳排放强度的变化率显现正向变动趋势。征收碳税将影响企业研发,结论与杨翱和刘纪显[48]基本类似。居民消费在第3期达到负向峰值,达到0.011 6个百分点。研发资本存量在第4期达到负向峰值,达到0.014 0个百分点。总产出和碳排放量都在第1期达到负向峰值,分别为0.014 8和0.011 0个百分点。碳排放强度CO2QD在第1期达到正向峰值0.003 9个百分点。各变量在达到峰值以后逐步向稳态值逼近。
分析模拟结果可知,当期碳税税率冲击较大地减少了企业利润,引起居民收入降低,导致居民消费降低。企业利润降低引进居民收入下降,从而引起居民投资减少,投资下降进而影响资本存量减少,企业产出也相应减少。由于研发资本存量减少的幅度大于总产出的幅度,引起碳排放量的变化率大于总产出的变动,进而引起碳排放强度的正向变动,但碳排放强度也显现下降趋势。
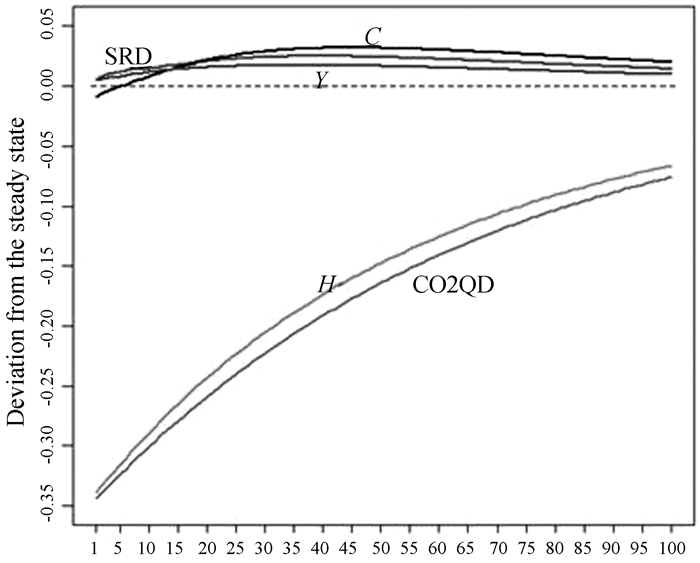
(四). 环境治理投资冲击在受到一个标准差的环境治理投资冲击后(图 4),居民消费C相对于系统稳态值的偏离显现从负向变动到正向变动然后逼近稳态的趋势,居民消费在第1期达到负向峰值,达到0.008 5个百分点,在第46期达到正向峰值0.032 0个百分点。研发资本存量SRD、总产出Y相对于系统稳态值的偏离显现正向变动达到峰值并逐步逼近稳态的趋势,研发资本存量在第2期达到正向峰值0.008 0个百分点,总产出在第36期达到正向峰值0.017 6个百分点。碳排放H及碳排放强度CO2QD相对于系统稳态值的偏离显现负向增加趋势。
分析模拟结果可知,当期环境治理投资的增加,意味着当期居民定量税增加(图 4中没有表示出来),当期居民可支配收入下降引起当期居民消费下降。由于资本生产的惯性,企业当期产出、研发投入未受影响,因此总产出、研发资本存量仍保持较高水平。当期环境治理投资的增加直接引起当期碳排放量减少进而引起碳排放强度下降。随着时间的推移,环境治理投资对碳排放量的抑制作用益发明显,企业碳税减少,企业利润增加,民居收入增加,引起后期居民消费、总产出、研发资本存量的增加。
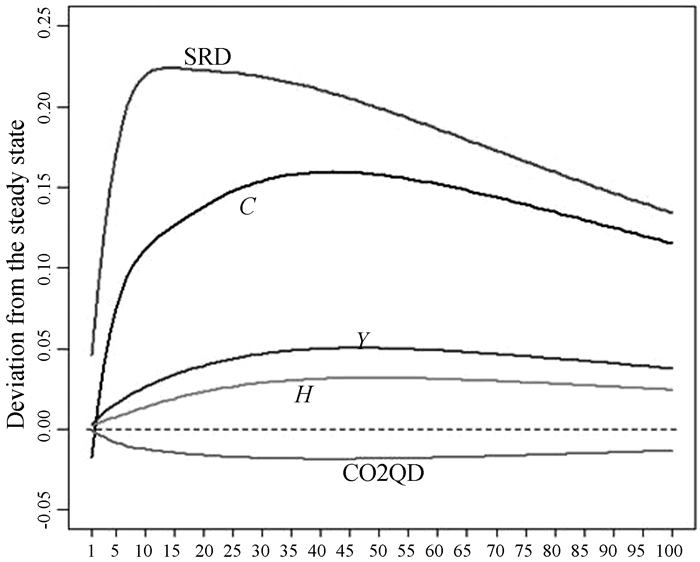
(五). 研发投入冲击在受到一个标准差的研发投入冲击后(图 5),居民消费C、研发资本存量SRD、总产出Y、碳排放量H相对于系统稳态值的偏离均显现正向驼峰型变动趋势,碳排放强度CO2QD相对于系统稳态值的偏离显现负向变动趋势。居民消费在第1期偏离稳态-0.017 1个百分点,居民消费在第42期达到正向峰值,达到0.159 4个百分点。研发资本存量在第28期达到正向峰值,达到0.219 7个百分点。总产出在第46期达到正向峰值,达到0.050 2个百分点。碳排放强度在第42期达到负向峰值0.018 6个百分点。各变量在达到峰值以后逐步向稳态值逼近。
分析模拟结果可知,当期研发投入增加引起研发资本存量的增加,进而引进总产出的增加,总产出增加以后碳排放量也增加,但碳排放量增加不及总产出增加,所以碳排放强度下降。当期研发投入增加以后,当期企业利润减少,居民可支配收入相应减少,所以当期居民消费减少。随着时间的推移,研发投入的产出效应越来越明显,引起总产出水平、居民消费、碳排放量的增加及碳排放强度的下降。
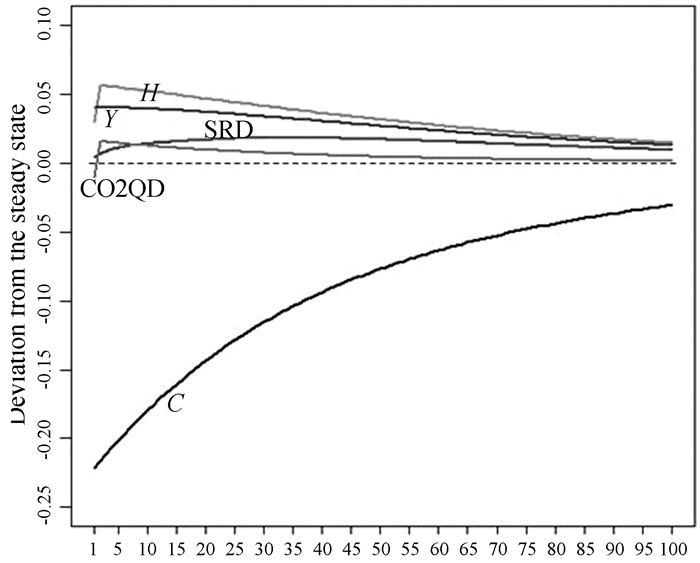
(六). 政府治污支出冲击在受到一个标准差的政府治污支出冲击后(图 6),研发资本存量SRD、总产出Y、碳排放量H相对于系统稳态值的偏离均显现正向的变动趋势,碳排放强度CO2QD相对于系统稳态值的偏离显现负向到正向然后逐步逼近稳态的变动趋势。居民消费相对于系统稳态值的偏离显现负向变动趋势。
分析模拟结果可知,企业当期未预期到政府支出增加,企业生产未受影响,因此总产出和研发资本存量维持在较高水平上。当期总产出增加、政府治污支出增加,引进企业当期碳排放量的增加量比较小,碳排放强度因此偏离稳态显现负向趋势。当期政府治污支出的增加,对居民消费造成了较大挤出,居民消费变动在第1期达到负向峰值0.222 1个百分点。由于居民消费减少幅度过大造成总需求的减少,因此随着时间的推移,总产出显现下降趋势,研发资本存量也随之显现下降趋势。政府治污支出增加、研发资本存量增量较小,二者最终引进碳排放量在第2期增加到正向峰值。由于产出变动幅度不大,引起碳排放强度在第2期也达到其正向峰值。从第3期开始,各变量显现常规的合理变动趋势。总体来看,政府治污支出增加挤出了居民消费,同时会引起碳排放强度下降。
五、方差分析以上分析了各类随机冲击对主要宏观经济变量的动态效应及影响机制。为了进一步考察各类冲击对宏观经济变量波动的影响程度,表 3列出了方差分析的结果。以表 3中数据第一行为例,对于居民消费的波动,技术进步冲击能够解释53.05%,政府支出冲击能够解释40.93%,其他冲击的影响均比较小。通过分析可以发现,环境治理投资冲击对碳排放及碳排放强度波动的影响比较大,分别达到72.99%和99.34%。
| 表 3 方差分析(%) |
本文将技术创新(R & D投入)、碳税税率等因素纳入包括居民、企业和政府三个部门的动态随机一般均衡模型中,通过脉冲响应和方差分析得到如下结论。
第一,技术进步、研发投入、专有技术设备投资、环境治理投资可以有效地降低碳排放强度,总体上可以实现经济增长与环境改善的双赢目标。比较四类冲击对总产值正向峰值和碳排放强度负向峰值影响可知,技术进步对其作用最大,环境治理投资其次,研发投入再次,专有技术设备投资排在最后。碳税税率冲击对总产出的负向影响特别明显,环境治理投资的后期正向效应比较明显,政府治污支出的当期效果比较明显。同时发现,设备投资短期将会挤出研发投资,政府治污支出将会挤出居民消费。
第二,总体来看,专有技术设备投资冲击对碳排放、碳排放强度波动贡献最小,环境治理投资冲击对碳排放、碳排放强度波动的影响比较大。随机冲击对碳排放波动贡献大小排序为:环境治理投资冲击、技术进步冲击、碳税税率冲击、政府支出冲击、研发投入和专有技术设备投资冲击。随机冲击对碳排放强度波动贡献大小排序为:环境治理投资冲击、政府支出冲击、技术进步冲击、研发和碳税税率冲击。
上述结论对我们进一步认识环境保护、技术创新和经济增长之间的关系具有重要启示,对进一步完善碳减排政策、优化环保政策体系具有重要指导意义。从宏观层面看,在我国经济进入新常态的时代特征下,在我国生态文明建设目标不断强化的现实背景下,通过加大环境治理投入,加强环境保护监督,关停并转一批高耗能、高污染企业,切实提高生态环境质量,优化企业技术创新环境,加强企业创新创业资助政策落实,达到既要金山银山、又要绿水青山的发展格局是能够实现的。从微观层面看,根据本文研究结论,可以着手完善以下四个方面的制度体系:其一,完善企业碳排放内部治理及外部监督机制。一方面,要建立碳减排与创新资助之间的激励机制,鼓励企业通过加强自身技术创新来减少企业碳排放水平;另一方面,环境监管部门也要加强碳排放监管力度,惩罚型机制与激励型机制共同发力,确保企业碳排放保持在红线范围之内。其二,成立协调管理机构,保证重大政策目标的协调性。环境保护及环保相关政策的制定要考虑到多个部门相关政策的协调性。环境保护是一项系统性工程,需要环保部门、科技部门、工业信息化部门等多个部门的协同,才能从环境治理、科技投入、企业技术改造等多个方面推进环境质量提升,建议成立相应的协调管理机构,对环保、科技、工业信息化等部门的低碳、技术创新资助等相关文件进行清理,对不一致的内容进行调整。其三,逐步建立碳税试点机制。要进一步突出科技政策在环境保护中的导向作用,要不断加强工业企业碳排放清单编制工作。在北京市、天津市、上海市、重庆市、湖北省、广东省及深圳市开展碳排放权交易试点的基础上,利用碳排放清单,对碳排放强度大、大气排放污染问题突出的企业建立碳税试点机制。其四,要进一步落实国家各项政策,完善创新政策体系。从模拟结果可以明显看到,由技术创新带来的二氧化碳碳排放强度下降非常明显。进一步加强基础研究,集成创新,特别是引进消化吸收再创新,切实提高整个社会的全要素生产率。进一步落实《关于提高研究开发费用税前加计扣除比例的通知(财税〔2018〕99号)》等政策要求,进一步激励企业加大研发投入,支持科技创新,落实《技术改造国产设备投资抵免企业所得税暂行办法》的各项要求,加强对各类企业的技术改造力度,推进企业设备更新改造,加大企业技术装备投资。落实《中华人民共和国清洁生产促进法》的各项要求,推广先进适用清洁生产技术工艺及装备,推进重点行业清洁生产水平显著提高,切实改善生态环境质量。
| [1] |
何塞·路易斯·托雷斯.动态宏观经济一般均衡模型入门[M].刘斌, 译.北京: 中国金融出版社, 2015.
|
| [2] |
杨晓光. 轻松走进宏观经济分析的高大上:《动态随机一般均衡模型及其应用》评述[J]. 全国新书目, 2014(5): 12-13. |
| [3] |
高超平, 刘纪显, 赖小东. 基于DSGE模型的碳交易管理制度研究[J]. 科技与经济, 2017, 30(2): 86-90, 100. DOI:10.3969/j.issn.1007-6921.2017.02.042 |
| [4] |
FISCHER C, SPRINGBORN M. Emissions targets and the real business cycle:Intensity targets versus caps or taxes[J]. Journal of Environmental Economics and Management, 2011, 62(3): 352-366. |
| [5] |
ANGELOPOULOS K, ECONOMIDES G, PHILIPPOPOULOS A.What is the best environmental policy? Taxes, permits and rules under economic and environmental uncertainty[R].CESIFO Working Paper, NO.2980, 2010.3
|
| [6] |
BUKOWSKI M, KOWAL P.Large scale, multi-sector DSGE model as a climate policy assessment tool: Macroeconomic Mitigation Options (MEMO) model for Poland[R].IBS Working Paper, 2010.
|
| [7] |
HEUTEL G. How should environmental policy respond to business cycles? Optimal policy under persistent productivity shocks[J]. Review of Economic Dynamics, 2012, 15(2): 244-264. DOI:10.1016/j.red.2011.05.002 |
| [8] |
FISCHER C, HEUTEL G. Environmental macroeconomics:environmental policy, business cycles, and directed technical change[J]. Annual Review of Resource Economics, 2013, 5(1): 197-210. DOI:10.1146/annurev-resource-091912-151819 |
| [9] |
ANNICCHIARICO B, DI DIO F. Environmental policy and macroeconomic dynamics in a new Keynesian model[J]. Journal of Environmental Economics and Management, 2015, 69: 1-21. DOI:10.1016/j.jeem.2014.10.002 |
| [10] |
DISSOU Y, KARNIZOVA L. Emissions cap or emissions tax? A multi-sector business cycle analysis[J]. Journal of Environmental Economics and Management, 2016, 79: 169-188. DOI:10.1016/j.jeem.2016.05.002 |
| [11] |
杨翱, 刘纪显, 吴兴弈. 基于DSGE模型的碳减排目标和碳排放政策效应研究[J]. 资源科学, 2014, 36(7): 1452-1461. |
| [12] |
朱智洺, 方培. 能源价格与碳排放动态影响关系研究:基于DSGE模型的实证分析[J]. 价格理论与实践, 2015(5): 54-56. |
| [13] |
杨翱, 刘纪显, 吴兴弈. 能源价格波动对中国经济的影响:基于DSGE模型的分析[J]. 系统工程, 2016, 34(11): 147-153. |
| [14] |
刘建华, 王姝琪, 姜照华. 区域创新体系模拟与预测:多主体DSGE建模分析[J]. 科技进步与对策, 2016, 33(14): 33-40. DOI:10.6049/kjjbydc.2015120198 |
| [15] |
武晓利. 环保政策、治污努力程度与生态环境质量:基于三部门DSGE模型的数值分析[J]. 财经论丛(浙江财经学院学报), 2017(4): 101-112. DOI:10.3969/j.issn.1004-4892.2017.04.012 |
| [16] |
肖红叶, 程郁泰. E-DSGE模型构建及我国碳减排政策效应测度[J]. 商业经济与管理, 2017(7): 73-86. |
| [17] |
武晓利. 能源价格、环保技术与生态环境质量:基于包含碳排放DSGE模型的分析[J]. 软科学, 2017, 31(7): 116-120. DOI:10.3969/j.issn.1002-9753.2017.07.011 |
| [18] |
KLIMA G, PODEMSKI K, RETKIEWICZ-WIJTIWIAK K, et al.Smets-Wouters'03 model revisited-an implementation in gEcon[R].MPRA Working Paper, 2015.
|
| [19] |
JERGER J, RÖHE O. Testing for parameter stability in DSGE models.The cases of France, Germany, Italy, and Spain[J]. International Economics and Economic Policy, 2014, 11(3): 329-351. |
| [20] |
武晓利, 晁江锋. 财政支出结构对居民消费率影响及传导机制研究:基于三部门动态随机一般均衡模型的模拟分析[J]. 财经研究, 2014, 40(6): 4-15. |
| [21] |
徐文成, 薛建宏, 毛彦军. 宏观经济动态性视角下的环境政策选择:基于新凯恩斯DSGE模型的分析[J]. 中国人口·资源与环境, 2015, 25(4): 101-109. DOI:10.3969/j.issn.1002-2104.2015.04.013 |
| [22] |
华昱. 设备投资专有技术冲击与宏观经济波动:基于贝叶斯估计的新凯恩斯动态随机一般均衡的研究[J]. 产业经济研究, 2016(6): 67-77. |
| [23] |
王国静, 田国强. 政府支出乘数[J]. 经济研究, 2014, 49(9): 4-19. |
| [24] |
张伟进, 胡春田, 方振瑞. 农民工迁移、户籍制度改革与城乡居民生活差距[J]. 南开经济研究, 2014(2): 30-53. |
| [25] |
CHRISTIANO L J, EICHENBAUM M, EVANS C L. Nominal rigidities and the dynamic effects of a shock to monetary policy[J]. Journal of Political Economy, 2005, 113(1): 1-45. DOI:10.1086/426038 |
| [26] |
朱柏松.基于DSGE模型的货币政策和财政政策联动机制研究[D].武汉: 华中科技大学, 2013.
|
| [27] |
吴智华, 杨秀云. 信贷结构摩擦、住房市场波动与货币政策[J]. 财经科学, 2017(10): 1-16. |
| [28] |
盛芳芳.调整成本约束下的中国经济波动数量分析[D].杭州: 浙江工商大学, 2017.
|
| [29] |
蔡文娟.劳动调整成本、货币政策与中国经济波动[D].武汉: 华中师范大学, 2016.
|
| [30] |
毛彦军, 王晓芳, 徐文成. 消费约束与货币政策的宏观经济效应:基于动态随机一般均衡模型的分析[J]. 南开经济研究, 2013(1): 53-67. |
| [31] |
庄子罐, 崔小勇, 龚六堂, 等. 预期与经济波动:预期冲击是驱动中国经济波动的主要力量吗?[J]. 经济研究, 2012(6): 46-59. |
| [32] |
ROTEMBERG J J. Sticky prices in the United States[J]. Journal of Political Economy, 1982, 90(6): 1187-1211. DOI:10.1086/261117 |
| [33] |
简志宏, 朱柏松, 李霜. 动态通胀目标、货币供应机制与中国经济波动:基于动态随机一般均衡的分析[J]. 中国管理科学, 2012, 20(1): 30-42. |
| [34] |
郭立甫, 姚坚, 高铁梅. 基于新凯恩斯DSGE模型的中国经济波动分析[J]. 上海经济研究, 2013, 25(1): 3-12. |
| [35] |
刘斌. 动态随机一般均衡模型及其应用[M]. 北京: 中国金融出版社, 2010.
|
| [36] |
李建强. 我国财政支出结构与居民消费异质性动态关系[J]. 山西财经大学学报, 2012, 34(1): 9-21. DOI:10.3969/j.issn.2095-106X.2012.01.002 |
| [37] |
孙宁华. 中国宏观经济动态模型与校准分析[M]. 南京: 南京大学出版社, 2015.
|
| [38] |
郑丽琳, 朱启贵. 技术冲击、二氧化碳排放与中国经济波动:基于DSGE模型的数值模拟[J]. 财经研究, 2012, 38(7): 37-48, 100. |
| [39] |
张佐敏. 中国存在财政规则吗?[J]. 管理世界, 2014(5): 23-35. |
| [40] |
武彦民, 竹志奇. 地方政府债务置换的宏观效应分析[J]. 财贸经济, 2017, 38(3): 21-37. DOI:10.3969/j.issn.1005-913X.2017.03.007 |
| [41] |
刘金全, 王译兴, 刘子玉. 新常态下的中国经济周期波动:基于金融摩擦视角的实证研究[J]. 商业研究, 2017(6): 107-114. |
| [42] |
吴延兵. R & D存量、知识函数与生产效率[J]. 经济学(季刊), 2006, 5(3): 1129-1156. |
| [43] |
蒋颖.DSGE视角下我国金融加速器效应的地区差异分析[D].广州: 广东财经大学, 2015.
|
| [44] |
单豪杰. 中国资本存量K的再估算:1952~2006年[J]. 数量经济技术经济研究, 2008(10): 17-31. |
| [45] |
吴延兵. 中国工业R & D产出弹性测算(1993-2002)[J]. 经济学(季刊), 2008, 7(3): 869-890. |
| [46] |
董文福, 傅德黔, 努丽亚. 我国环境污染治理投资的发展及存在问题[J]. 中国环境监测, 2008, 24(4): 87-89. DOI:10.3969/j.issn.1002-6002.2008.04.023 |
| [47] |
易小丽. 投资专有技术冲击、货币冲击与中国宏观经济波动[J]. 福建师范大学学报(哲学社会科学版), 2014(4): 36-45, 66. |
| [48] |
杨翱, 刘纪显. 模拟征收碳税对我国经济的影响:基于DSGE模型的研究[J]. 经济科学, 2014(6): 53-66. |
| [49] |
徐舒, 左萌, 姜凌. 技术扩散、内生技术转化与中国经济波动:一个动态随机一般均衡模型[J]. 管理世界, 2011(3): 22-31, 187. |
| [50] |
张军, 施少华, 陈诗一. 中国的工业改革与效率变化:方法、数据、文献和现有的结果[J]. 经济学(季刊), 2003, 2(4): 1-38. |
 2020, Vol. 26
2020, Vol. 26

