降低人民币汇率风险,尤其是降低人民币汇率异常波动风险,是“稳外贸”的重要举措。汇率市场化改革、人民币入篮以及外资股比放宽等因素促使人民币汇率波动幅度及频率扩大,人民币汇率高估或低估现象时有发生。根据国际货币基金组织(International Monetary Fund, IMF)公布的数据,1994年1月至2018年12月,人民币实际有效汇率累计升值61.96%,月度最大波幅为5.08%。近年来,人民币汇率波动幅度及频率进一步扩大,汇率风险进一步凸显。在“8.11汇改”之时,人民币一次性贬值2%引发市场恐慌;2018年受中美贸易摩擦等内外部因素的影响,人民币兑美元汇率出现9.8%的较大幅度波动,合理均衡下的人民币汇率或出现失调现象。
改革开放以来,我国已成为最大的货物贸易国。海关总署统计数据显示,2018年我国国际贸易出现了以下新特征:第一,进出口总值达30.51万亿元,增速较2017年下降1.7个百分点;第二,农产品进口开始从发达国家转向发展中国家,机械及电子信息产品的出口开始从周边国家及地区转向“一带一路”沿线国家及地区;第三,食品类行业进口较上一年增加了36.44%,出口较上一年增加了32.4%,而木制品类行业进口较上一年增长了5.4%,出口却较上一年减少了0.54%。由于汇率是影响进出口的重要因素,那么由汇率波动引起的汇率失调会对进出口贸易产生影响吗?汇率失调对各行业进出口的影响存在异质性吗?因此,本文基于国际贸易标准分类(Standard International Trade Classification, SITC),研究汇率失调对我国10类进出口行业的影响,这对于实施差异化的行业进出口发展策略和企业汇率风险管理策略,进而“稳外贸”具有重要的现实意义。
一、文献综述1976年牙买加协议的签订正式宣告了黄金非货币化和浮动汇率合法化。伴随着汇率的波动,学者开始探讨均衡汇率,由此形成均衡汇率理论。均衡汇率的概念最早由Williamson[1]提出,并进一步提出均衡汇率的测算方法——基本因素均衡汇率(Fundamental Equilibrium Exchange Rate, FEER)模型,不过该模型只分析了中长期基本面因素对汇率的影响,而没有考虑短期周期性因素和随机干扰因素的影响。随后MacDonald和Clark[2]提出行为均衡汇率(Behavioral Equilibrium Exchange Rate, BEER)模型,克服了FEER模型的上述缺陷。由于该方法可操作性较强,对于一个特定国家纵向汇率分析具有优势,因此被学者广泛应用。国内学者周源和唐晓婕[3]、严太华和程欢[4]、姚宇惠和王育森[5]都运用BEER模型对均衡汇率和汇率失调进行了研究,研究结果皆表明,人民币实际有效汇率高估与低估交替出现,并非持续低估或高估。然后是购买力平价(Purchasing Power Parity, PPP)均衡汇率模型,在实证研究中大都采用拓展的PPP方法,如Cheung等[6]。国内学者刘阳[7]、王磊和范超[8]也运用该模型进行了相关研究。基于购买力平价的均衡汇率模型最为简单和直接,但购买力平价成立的条件太为苛刻,制约了该模型的实际有效性。
浮动汇率制及全球经济一体化加剧了人民币汇率波动,使国际贸易汇率风险凸显[9]。王全意和张澜基于人民币实际有效汇率进行研究,结果表明实际有效汇率的波动对经常账户余额具有负向影响[10]。汇率失调是汇率风险的一种表现形式,也被称为汇率错位,是指实际汇率相对于均衡汇率的偏离,存在高估和低估两种情况。关于汇率失调对进出口影响,国内外学者还没有形成统一的意见。大部分研究认为汇率失调的影响是负向的,如Obstfeld和Rogoff[11]研究指出新兴市场货币低估是导致全球经济失衡的根本原因。国内学者韩国高认为实际汇率错位对中美出口贸易产生了显著的负向影响[12]。宫旭红和曹云祥研究显示汇率失衡程度决定经常账户失衡惯性,当汇率偏离均衡汇率值超过一定的阈值时,汇率失衡将加剧经常账户失衡持续性[13]。王铮等指出人民币大幅贬值不利于我国产业结构优化和技术创新[14]。同样持有负向观点的还有金祥义和张文菲[15]、吴丽华和王锋[16]。但也有研究表明汇率失调对进出口贸易具有正向作用,如Mckenzie[17]。Krugman和Obstfeld[18]、巴曙松和王群[19]、李利[20]进一步指出汇率升值能够使贸易结构得到优化。现有研究很少从行业层面对汇率失调的效应进行对比分析,只有少部分的文献从商品角度和产业角度进行分析,如王宇雯[21]发现中国不同商品的出口部门受到汇率错位及波动的影响不同,而李腊生和高书丽[22]研究制造业发现,无论在中短期,汇率错位及波动都将对其造成显著的负面影响。从行业角度的方面,普遍研究的是汇率波动对进出口的影响,如马君潞等[23]、袁申国和郑雯[24]从行业角度研究了人民币实际汇率波动对外向型企业进出口的影响。
本文基于已有的研究成果,综合借鉴学者对汇率失调及汇率波动对行业影响的研究,基于国际贸易标准分类(SITC),分析汇率失调对10类进出口行业影响的异质性,并基于此提出汇率管理及行业差异化发展的对策建议。
二、汇率失调程度测度 (一) 理论模型行为均衡汇率(BEER)模型由MacDonald和Clark[2]提出,该模型的关键是识别出影响人民币实际有效汇率的中长期基本面因素和短期随机因素,在时间分析框架内证明协整关系存在的情况下导出均衡汇率,进而得到汇率失调。其基础的模型形式可以表示如下:
| $ {Y_{\rm{t}}} = {\mathit{\boldsymbol{\beta }}_1}{\mathit{\boldsymbol{X}}_{{\rm{1t}}}} + {\mathit{\boldsymbol{\beta }}_2}{\mathit{\boldsymbol{X}}_{{\rm{2t}}}} + {\mathit{\boldsymbol{\beta }}_3}{\mathit{\boldsymbol{X}}_{{\rm{3t}}}} + {\mu _{\rm{t}}} $ | (1) |
其中Yt表示实际有效汇率,X1t、X2t和X3t分别表示长期、中期和短期的汇率影响因素对应的经济变量组成的向量,β1、β2、β3表示系数矩阵,μt表示随机扰动项。
不包括随机扰动项μt时可得式(2),(2)式中的Yt*表示用经济变量当前数据计算得出的当前均衡汇率。式(1)与式(2)之差为当前汇率失调(Current Misalignment, CMT)。
| $ Y_{\rm{t}}^* = {\mathit{\boldsymbol{\beta }}_1}{\mathit{\boldsymbol{X}}_{{\rm{1t}}}} + {\mathit{\boldsymbol{\beta }}_2}{\mathit{\boldsymbol{X}}_{{\rm{2t}}}} + {\mathit{\boldsymbol{\beta }}_3}{\mathit{\boldsymbol{X}}_{{\rm{3t}}}} $ | (2) |
运用滤波技术可以得到变量的长期均衡值LFX1t、LFX2t和LFX3t,则有式(3)。式(1)与式(3)之差为长期汇率失调(Long-term Misalignment, TMT)。
| $ {\rm{LF}}{{\rm{Y}}_{\rm{t}}} = {\beta _1}{\rm{LF}}{{\rm{X}}_{{\rm{1t}}}} + {\beta _2}{\rm{LF}}{{\rm{X}}_{{\rm{2t}}}} + {\beta _3}{\rm{LF}}{{\rm{X}}_{{\rm{3t}}}} $ | (3) |
本文综合参考MacDonald和Clark[2]、严太华和程欢[4],姚宇惠和王育森[5]等关于人民币实际有效汇率失调的研究,选取人民币实际有效汇率(Real Effective Exchange Rate, REER)作为被解释变量,选取劳动生产率(Labour Productivity, LP)、贸易条件(Terms of Trade, TOT)、贸易开放度(Trade openness, TO)、国外净资产(Net Foreign Assets, NFA)、政府支出(Government Expenditure, GE)、广义货币供应量(Money Supply, MS)作为解释变量。因此本文的BEER模型可以具体表示为:
| $ {\rm{REER}} = \alpha + {\beta _1}{\rm{LP}} + {\beta _2}{\rm{TOT}} + {\beta _3}{\rm{TO}} + {\beta _4}{\rm{NFA}} + {\beta _5}{\rm{GE}} + {\beta _6}{\rm{MS}} + \mu $ | (4) |
模型中有关变量的指标选取与数据来源如表 1。
| 表 1 指标选取与数据来源 |
为了增加数据的平稳性,对较大的数据项REER、NFA、GE、MS进行对数处理,则BEER模型为:
| $ {\rm{LnREER}} = \alpha + {\beta _1}{\rm{LP}} + {\beta _2}{\rm{TOT}} + {\beta _3}{\rm{TO}} + {\beta _4}{\rm{LnNFA}} + {\beta _5}{\rm{LnGE}} + {\beta _6}{\rm{LnMS}} + \mu $ | (5) |
本文采用的样本区间为1994—2018年,为了避免“伪回归”问题,对经过处理后的样本数据进行ADF检验,检验结果如表 2所示。
| 表 2 各变量ADF检验结果 |
根据上述检验结果可知,TOT、LnGE为Ⅰ(0),为平稳时间序列,其余各变量均为Ⅰ(1),即一阶单整序列。接着采用EngleandGranger检验变量间是否存在协整关系,分两步进行。首先用Eviews9.0对各变量样本数据进行协整回归,估计结果如表 3所示。
| 表 3 协整回归结果 |
然后对回归残差序列进行ADF检验,结果如表 4。
| 表 4 回归残差序列ADF检验结果 |
由表 4可以看出,残差序列的ADF统计量低于1%显著水平的临界值,说明残差序列是一个平稳序列,各变量之间存在长期均衡关系,协整方程的估计结果为:
| $ \begin{array}{*{20}{l}} { {\rm{LnREER}} = 0.9599 - 0.7935{\rm{LP}} + 0.1066{\rm{TOT}} - 0.4123{\rm{TO}} - }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 0.1105{\rm{LnNFA}} - 0.0004{\rm{LnGE}} + 0.3905{\rm{LnMS}}} \end{array} $ | (6) |
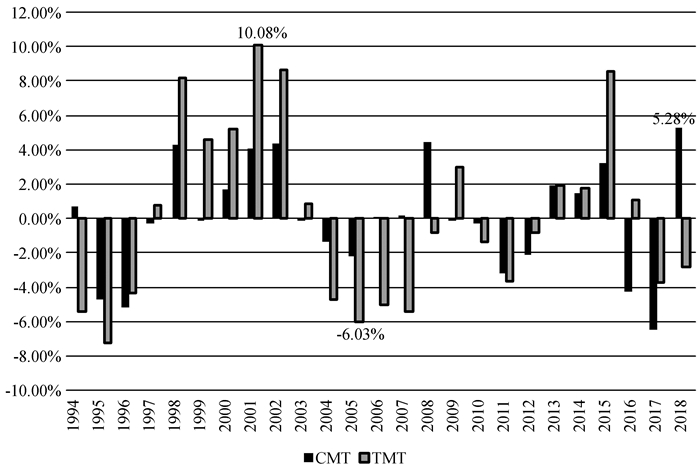
将解释变量的当前值代入式(6)可得当期均衡汇率(Current Equilibrium Exchange Rate, CEER)的对数值,换算得到当期均衡汇率CEER。则人民币实际汇率的当前汇率失调CMT=(REER-CEER)/REER×100%;采用提取长期均衡值常用的HP滤波方法得到各变量的长期均衡值,再将长期均衡值代入式(6)可得长期均衡汇率(Long-term Equilibrium Exchange Rate, LEER)的对数值,再换算得到长期均衡汇率LEER。则人民币实际汇率的长期汇率失调TMT=(REER-LEER)/REER×100%,具体如图 1。
|
图 1 人民币汇率的当前失调程度(CMT)和长期失调程度(TMT) |
由图 1可以直观地看出人民币实际有效汇率失调在高估与低估间循环往复,这与周源和唐晓婕[3]、严太华和程欢[4]、姚宇惠和王育森[5]等的研究结果具有一致性。具体分析如下。
由图 1和表 5可得,当前人民币实际有效汇率有轻微失调,近年来,失调程度均在10%以内。当前汇率失调和长期汇率失调总体一致,且具有周期性特征。大多数情况下长期汇率失调程度略高于当前汇率失调程度。1994—2018年期间,对其中15年,当前汇率失调与长期汇率失调符号相同,即具有方向一致性;对另外10年,当前汇率失调与长期汇率失调具有方向相反性。
| 表 5 人民币实际有效汇率失调情况分析 |
Kenen和Rodrik[25]提出了一个适用于讨论行业分类层面的模型,可以反映各变量间的长期动态关系,袁申国和郑雯[23]运用该模型研究了汇率波动对外向型企业进出口的影响。本文借鉴袁申国和郑雯[23]的研究,基于国际贸易标准分类(SITC)层面研究人民币实际有效汇率失调对我国10类进口行业影响的异质性研究。本文将汇率失调作为主要变量,由于该模型研究的是长期动态关系,故汇率失调用长期汇率失调(TMT)表示,同时引入收入水平和实际有效汇率水平作为控制变量。需要说明的是这里没有选用汇率波动作为控制变量是因为在后面的数据处理过程中发现汇率波动与汇率失调存在较强的共线性。为了避免时间序列数据可能存在的“异方差”问题,有关变量采用对数形式,由于汇率失调有正负交叉项,不进行对数变换,最终建立如下的实证模型:
| $ {\rm{Ln}} {M_{i{\rm{t}}}} = \alpha + {\beta _1} {\rm{Ln}} Y_{\rm{t}}^c + {\beta _2} {\rm{Ln}} {( {\rm{REER}} )_{\rm{t}}} + {\beta _3}{\rm{TM}}{{\rm{T}}_{\rm{t}}} + {\mu _{\rm{t}}} $ | (7) |
其中Mit表示t时期我国第i个行业的进口额,Ytc表示t时期我国收入水平,REERt表示t时期人民币实际有效汇率,TMTt表示t时期人民币实际有效汇率的长期失调,μt表示随机误差项。
式(7)反映的是变量间的长期协整关系,而短期动态分析则需要进一步建立误差修正(ECM)模型,此时汇率失调应用短期汇率失调(即当前汇率失调(CMT))表示。式(7)对应的ECM模型为:
| $ \begin{array}{l} \Delta {\rm{Ln}}{M_{i{\rm{t}}}} = {c_0} + \sum\limits_{k = 1}^{n1} {{c_{1k}}} \Delta {\rm{Ln}}{M_{i,{\rm{t}} - k}} + \sum\limits_{k = 0}^{n2} {{c_{2k}}} \Delta {\rm{Ln}}Y_{{\rm{t}} - k}^c + \sum\limits_{k = 0}^{n3} {{c_{3k}}} \Delta {\rm{Ln}}{( {\rm{REER}} )_{{\rm{t}} - k}} + \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \sum\limits_{k = 0}^{n4} {{c_{4k}}} \Delta {\rm{CM}}{T_{{\rm{t}} - k}} + \tau {\mu _{{\rm{t}} - 1}} + {\varepsilon _{\rm{t}}} \end{array} $ | (8) |
其中μt-1表示误差修正项的一阶滞后项,可以通过其系数确定该模型在受到短期冲击后向长期均衡状态调整的情况,并可以量化调整的速度。如果系数τ在统计上显著为负,τ绝对值越大,则表示调整速度越快。
但用方程(7)研究变量的长期动态关系有一定局限,即各变量必须为同阶单整过程。基于此,Pesaran等[26]应用自回归分布滞后(Autoregressive Distribution Lag, ARDL)模型来检验变量间是否存在长期协整关系,克服了方程(7)的缺陷,不要求变量同为Ⅰ(0)或Ⅰ(1)过程,并提出了对应的ECM模型。具体做法为,从方程(7)中解出μt的线性表达式,并代入方程(8)中μt-1的线性组合中,参考袁申国和郑雯的做法,模型同时考虑各变量的差分项和滞后水平项,则式(8)对应的ARDL模型如下:
| $ \begin{array}{l} \Delta {\rm{Ln}}{M_{i{\rm{t}}}} = {c_0} + \sum\limits_{k = 1}^{n1} {{c_{1k}}} \Delta {\rm{Ln}}{M_{i,{\rm{t}} - k}} + \sum\limits_{k = 0}^{n2} {{c_{2k}}} \Delta {\rm{Ln}}Y_{{\rm{t}} - k}^c + \sum\limits_{k = 0}^{n3} {{c_{3k}}} \Delta {\rm{Ln}}{({\rm{REER}})_{{\rm{t}} - k}} + \sum\limits_{k = 0}^{n4} {{c_{4k}}} \Delta {\rm{CM}}{T_{{\rm{t}} - k}} + \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \theta {\rm{Ln}}{M_{i,{\rm{t}} - 1}} + {\omega _1}{\rm{Ln}}Y_{{\rm{t}} - 1}^c + {\omega _2}{\rm{Ln}}{({\rm{REER}})_{{\rm{t}} - 1}} + {\omega _3}{\rm{TM}}{{\rm{T}}_{{\rm{t}} - 1}} + {\mu _{\rm{t}}} \end{array} $ | (9) |
式(9)中差分项的滞后期数由AIC原则确定,使AIC值最小的滞后阶数即为差分项的滞后阶数。根据Pesaran的做法,可采用F检验及辅助检验判断变量间是否存在长期稳定关系。如果F统计量大于临界值的上界,即可认为存在协整关系;如果F统计量小于临界值的下界,则认为不存在协整关系;而如果F统计量介于临界值的上界和下界之间,则无法确定是否存在协整关系,应进一步通过辅助检验来确定。辅助检验需要借助于误差修正模型(Error Correction Model, ECM),如果τ显著为负,则认为存在长期协整关系。进一步,CMT对进口的影响由C4k的估计值来反映,而TMT对进口的影响由ω3的估计值来反映。
2. 出口方向用Xit表示t时期我国第i个行业的出口额,Ytw表示t时期世界收入水平,其他变量的选取同进出口方向。同理,出口方向的模型为:
| $ {\rm{Ln}}{X_{i{\rm{t}}}} = \alpha + {\beta _1}{\rm{Ln}}Y_{\rm{t}}^w + {\beta _2}{\rm{Ln}}{({\rm{REER}})_{\rm{t}}} + {\beta _3}{\rm{LnTM}}{{\rm{T}}_{\rm{t}}} + {\mu _{\rm{t}}} $ | (10) |
为了联合检验实际短期汇率失调和长期汇率失调对出口的影响,同理可将方程(4)改写成如下ARDL模型:
| $ \begin{array}{l} \Delta {\rm{Ln}}{X_{i{\rm{t}}}} = {\gamma _0} + \sum\limits_{k = 1}^{n1} {{\gamma _{1k}}} \Delta {\rm{Ln}}{X_{i,{\rm{t}} - k}} + \sum\limits_{k = 0}^{n2} {{\gamma _{2k}}} \Delta {\rm{Ln}}Y_{{\rm{t}} - k}^w + \sum\limits_{k = 0}^{n3} {{\gamma _{3k}}} \Delta {\rm{Ln}}{({\rm{REER}})_{{\rm{t}} - k}} + \sum\limits_{k = 0}^{n4} {{\gamma _{4k}}} \Delta {\rm{CM}}{{\rm{T}}_{{\rm{t}} - k}} + \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \lambda {\rm{Ln}}{X_{i,{\rm{t}} - 1}} + {\lambda _1}{\rm{Ln}}Y_{{\rm{t}} - 1}^w + {\lambda _2}{\rm{Ln}}{({\rm{REER}})_{{\rm{t}} - 1}} + {\lambda _3}{\rm{TM}}{{\rm{T}}_{{\rm{t}} - 1}} + {\mu _{\rm{t}}} \end{array} $ | (11) |
采用F检验及辅助检验来验证长期协整关系是否成立,进一步,短期汇率失调对出口的影响由γ4k的估计值来反映,长期汇率失调对出口的影响由λ3的估计值来反映。
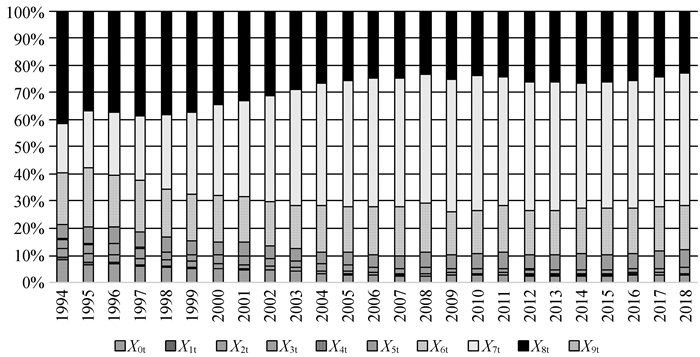
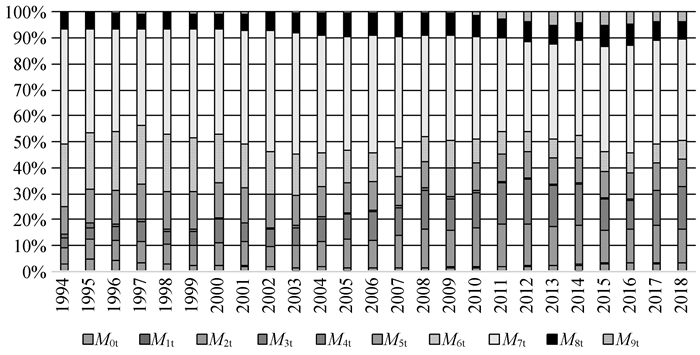
(二) 变量及描述性统计本文选取相关变量1994—2018年的年度数据作为样本数据,基于国际贸易标准分类(SITC)国际贸易标准分类(SITC)①的10类进出口行业层面,研究汇率失调、收入水平及人民币实际汇率对我国进出口行业影响的异质性。为使分析更为全面,也对总的进口、出口进行相应分析。各变量对应的指标选取与数据来源见表 6,变量的描述性统计见表 7,各行业的进出口情况如图 2和图 3。
① 将国际贸易行业分为了10类,第0类(食品及活动物),第1类(饮料及烟类),第2类(非食用原料(燃料除外)),第3类(矿物燃料、润滑油及有关原料),第4类(动植物油、脂及蜡),第5类(化学成品及有关产品),第6类(按原料分类的制成品),第7类(机械及运输设备),第8类(杂项制品),第9类(未分类的商品)。
| 表 6 指标选取与数据来源 |
| 表 7 相关变量数据描述性统计分析 |
|
图 2 1994—2018年10类行业的进口情况 |
|
图 3 1994—2018年10类行业的出口情况 |
如式(9)和式(11)所示,对除汇率失调以外的变量对应的时间序列数据进行自然对数变换。
(三) 实证分析由于解释变量汇率及汇率失调在10类进出口行业中是相同的,不便于建立面板模型,因此针对各行业的方程分别进行估计。本文用Eviews9.0进行实证检验,估计了出口和进口方向总计22个方程,各行业进出口方向的实证结果如表 8—表 11。
| 表 8 1994—2018我国10类进口行业的估计结果 |
| 表 9 进口模型中短期汇率失调与长期汇率失调对应系数的显著性 |
| 表 10 1994—2018我国10类出口行业的估计结果 |
| 表 11 出口模型中短期汇率失调与长期汇率失调对应系数的显著性 |
对于所选样本而言(解释变量个数m=3,自由度n-m-1=21),取置信度为90%时,F统计量临界值的上界为4.87,下界为3.07。如表 8所示,总进口和其中8类行业的F统计量大于4.87,可判定为存在长期协整关系。而另外第0类和第3类行业的F统计量介于上界和下界之间无法肯定变量间是否存在协整关系,需要进一步进行辅助检验。第0类和第3类行业对应的ARDL模型中,ECMt-1项系数显著为负数。综上,样本总进口和10类行业的进口与解释变量间都存在长期协整关系。接下来,分析包括长期汇率失调在内的各个变量对进口行业长期效应的异质性,并对短期汇率失调的效应进行分析。
(1) 各解释变量对行业进口长期效应的异质性分析。
首先,在总进口和10类行业进口模型中,Ytc的系数都显著为正,说明随着我国收入水平的提高,从长期看各类行业的进口都有所扩大,但是对比可发现,收入变动对第1类和第9类行业的进口影响最大;然后,在第0类、第1类、第9类行业的进口模型中,LnREER的系数显著为正,在总进口和其他行业进口模型中显著为负,说明人民币贬值不利于总进口和大多数行业的进口,这与我们的一般认知是一致的,但是汇率贬值对其中3类行业的影响却是正向的,人民币贬值反而会促进这3类行业进口的增加;最后,TMT系数在第0类、第1类、第9类行业进口模型中显著为负,在总进口和其他行业进口模型中显著为正。当TMT对应的系数为正时,如果TMT为正,即人民币实际有效汇率相对于长期均衡汇率低估阶段(见表 5),汇率失调程度的扩大会促使总进口和大多数行业的进口增加,使第0类行业等个别行业的进口减少;而TMT为负,即人民币实际有效汇率相对于长期均衡汇率高估阶段(见表 5),汇率失调程度的扩大会促使总进口和大多数行业的进口减少,使第0类行业等个别行业的进口增加。当TMT对应的系数为负时,与以上情况相反。同时,由“模型设定”部分可知,在ECMt-1对应系数显著为负的情况下,系数绝对值越大表示经济模型受到冲击后向长期均衡状态调整的速度越快; 因此,根据表 8可得,在受到同样的经济冲击后,总进口模型向均衡状态调整的速度最快,其次是第4类、第3类、第8类行业进口模型,调整速度最慢的是第5类行业进口模型。
(2) 短期汇率失调对各行业进口影响的异质性分析。
由“模型设定”部分可知,在进口模型中长期汇率失调对进口的影响由ω3表示,短期汇率失调对进口的影响由C4k表示。ω3的分析见第(1)部分。为了考察短期汇率失调对各行业进口影响的异质性,以及短期汇率失调对各行业进口影响与长期汇率失调对各行业进口影响有无关系,两者关系在各行业的进口模型是否相同,接下来对C4k与ω3进行对比分析。
由表 9可知,在总进口和其中7类行业的进口模型中,CMT及其滞后项的系数至少有一个在统计上是显著的。对大部分行业而言,CMT及其滞后项对应的系数方向是正向的,那么当CMT为正时,即在人民币实际有效汇率相对于当期均衡汇率低估阶段(见表 5),汇率失调程度的扩大会促使总进口和大多数行业的进口增加,而在人民币实际有效汇率相对于当前均衡汇率高估阶段(见表 5),汇率失调程度的扩大会促使总进口和大多数行业的进口减少。但CMT及其滞后项对应的系数也有负向的,如第4类行业,其进口受短期汇率失调程度的影响与以上情况相反。同时,只有在第0类、第4类、第7类行业进口模型中,CMT滞后项对应的系数存在显著的情况,即CMT只有在这3类行业的进口模型中存在滞后效应。
值得注意的是,CMT的系数与TMT的系数在大多数情况下方向是一致的,但CMT的系数也可能与TMT的系数方向相反。如第0行业,CMT及其滞后2期、滞后3期的系数显著为正,但TMT的系数显著为负。又如第4类行业,CMT滞后3期的系数显著为负,但是TMT的系数显著为正。结合表 5进一步分析,在CMT与TMT方向一致的阶段,总进口和大多数行业的进口受CMT和TMT的影响具有方向一致性,而第0类行业和第4类行业进口受CMT与TMT的影响具有方向相反性;在CMT与TMT方向相反的阶段,总进口和大多数行业的进口受CMT和TMT的影响具有方向相反性,而第0类行业和第4类行业进口受CMT和TMT的影响具有方向一致性。同时,由表 9可知,短期汇率失调的显著性不能推定长期汇率失调的显著性,短期汇率失调不会显著影响第1类、第3类、第9类行业的进口,但长期汇率失调对这几个行业的进口均有显著影响。
2. 10类行业出口方向的整体分析出口方面,如表 10所示,总出口和第0类、第2类、第4类等6类行业的F统计量均大于临界值上界4.87,第9类行业对应F统计量小于临界值下界3.07,意味着不能拒绝该行业的解释变量不是长期协整的假设,不存在长期协整关系,剩余3类行业的F统计量落在临界值范围内,不好判断,需进一步通过辅助检验来确认。辅助检验显示,第1类行业对应的ARDL模型中,ECMt-1项系数显著为负数。综上,样本总出口和其中7类行业的出口与解释变量存在长期协整关系。接下来,对存在长期协整关系的行业分析各解释变量的长期效应,以及对所有行业分析短期汇率失调的效应。
(1) 各解释变量对行业出口长期效应的异质性分析。
对存在长期协整关系的总出口模型和8类行业出口模型进行分析。首先,对于变量Ytw,结果显示只有总出口和3类行业出口模型中对应系数的符号为正,包括总出口、第6类、第7类、第9类,而第2类、第5类行业的Ytw系数不显著,其他3类行业出口模型中Ytw的系数显著为负。由此可以看出,并非所有行业的出口与世界收入水平正向增加。随着收入的增加,人们的消费水平会提高,消费结构会产生变化,对于一些具有替代效应的商品,收入增加,人们更倾向消费质量更高的商品,被替代的商品呈现出吉芬商品的特征,随着世界收入水平的提高而呈现下降的趋势。然后,对于变量LnREER,大部分行业该变量对应系数的符号与预期一致,显著为正,即人民币贬值有利于出口,只有第0类行业LnREER的系数显著为负。最后,长期汇率失调对第3类、第8类、第9类行业的进口无显著影响。在总出口和第1类行业等6类行业出口模型中,变量TMT对应的系数显著为负,当TMT为正时,即人民币实际有效汇率相对于长期均衡汇率低估阶段(见表 5),汇率失调程度扩大会抑制出口,而当TMT为负时,即人民币实际有效汇率相对于长期均衡汇率高估阶段(见表 5),汇率失调程度的扩大会促进出口。在第0类行业出口模型中,变量TMT对应的系数显著为正,其出口受汇率失调的影响与以上情况相反。同时,由表 10可知,在ECMt-1系数显著为负的出口模型中,第4类行业的出口模型受冲击后向均衡水平调整的速度最快,其次是第1类、第2类、第0类行业出口模型,调整速度最慢的是第7类行业出口模型,而总出口和其他4类行业出口模型的调整速度此处无法得知。
(2) 短期汇率失调对各行业出口影响的异质性分析。
由“模型设定”部分可知,在出口模型中长期汇率失调对进口影响由λ3表示,短期汇率失调对出口的影响由γ4k表示。λ3的分析见第(1)部分。为了考察短期汇率失调对各行业出口影响的异质性,以及短期汇率失调对各行业出口影响与长期汇率失调对各行业出口影响有无关系,两者关系在各行业的出口模型是否相同,接下来对γ4k与λ3进行对比分析。
由表 11可知,在7类行业的出口模型中CMT及其滞后项的系数在统计上是不显著的,即短期汇率失调对大多数行业的出口不会产生影响。只有总出口、第2类、第6类、第7类行业的出口会受到短期汇率失调的影响,同时只有在第6类行业的出口模型中,短期汇率失调对出口的影响存在滞后效应,其滞后1期和滞后3期对应的系数显著为正,而对总出口、第2类、第7类行业出口的影响主要体现在当期,对应的系数也显著为正。如果CMT为正,即在人民币实际有效汇率相对于当前均衡汇率低估阶段(见表 5),汇率失调程度的扩大会促使总出口和这几类行业的出口增加,而在人民币实际有效汇率相对于当前均衡汇率高估阶段(见表 5),汇率失调程度的扩大会促使总出口和这几类行业的出口减少。
对于受CMT影响的总出口、第2类、第6类、第7类行业的出口而言,CMT及其滞后项对应的系数与TMT的系数方向相反。结合表 5进一步分析,在CMT与TMT方向一致的阶段,总出口和这几类行业受CMT与TMT的影响具有方向相反性; 在CMT与TMT方向相反的阶段,总出口和这几类行业受CMT与TMT的影响具有方向一致性。其他行业由于CMT及其滞后项的系数不具有显著性,此处无从探讨。同时,与进口模型类似,在出口模型中,仍然不能由短期汇率失调对应系数的显著性推定长期汇率失调对应系数的显著性,短期汇率失调不会显著影响第0类、第1类、第4类、第5类行业的出口,但长期汇率失调对应的系数在第0类行业出口模型中显著为正,在第1类、第4类、第5类行业出口模型中显著为负。
3. 汇率失调对进出口行业影响的异质性整体分析(1) 人民币实际有效汇率长期失调对9类行业的进口均有影响,对7类行业的出口有影响。进口方面,如果人民币实际有效汇率相对于长期均衡汇率低估,则会对第0类、第1类、第9类行业的进口产生负向影响,反之则反是,其中又以第9类行业所受影响最大。而人民币实际有效汇率相对于长期均衡汇率低估对总进口和其他行业的进口产生正向影响,反之则反是,其中以第3类行业所受影响最大。另外,各进口模型在受到同样的冲击时,总进口模型向均衡状态调整的速度最快,其次是第4类、第3类、第8类行业进口模型,调整速度最慢的是第5类行业进口模型。
出口方面,长期汇率失调对第3类、第8类、第9类行业长期的出口无显著影响,而对于总出口和第1类等6类行业的出口行业,如果人民币实际有效汇率相对于长期均衡汇率低估,则汇率失调程度扩大会抑制出口,反之则反是,其中又以第4类、第5类行业所受影响最大。而人民币实际有效汇率相对于长期均衡汇率低估对总出口和第0类行业的出口产生正向影响,反之则反是。另外,在ECMt-1的系数显著为负的出口模型中,在受到同样的冲击时,第4类行业的出口模型向均衡水平调整的速度最快,其次是第1类、第2类、第0类行业出口模型,调整速度最慢的是第7类行业出口模型,无法判断总出口和其他4类行业出口模型的调整速度。
(2) 短期汇率失调对大多数行业的进口有影响,对大多数行业的出口无显著影响。进口方面,短期汇率失调对第1类、第3类、第9类行业的进口无显著影响,对总进口和第2类、第5类、第6类、第8类行业的当期进口有影响,但不存在滞后效应,但对第0类、第4类、第7类行业的进口存在滞后效应;出口方面,短期汇率失调只对总出口、第2类、第6类和第7类行业的出口有影响,同时只对第6类行业的出口存在滞后效应。
(3) 综合来看,长期汇率失调对于进出口的影响强于短期汇率失调的影响,且方向上在不同的时段及不同行业间也并非全部一致。因此,汇率失调对于进出口贸易的影响不能一概而论,要结合短期汇率失调与长期汇率失调,结合汇率失调的方向,结合不同行业具体分析,这是区别于韩国高[12]、金祥义和张文菲[15]、吴丽华和王锋[16]等现有大多数研究的地方。具体来看,长期汇率失调会影响总进口及全部行业的进口,会影响总出口和7类行业的出口,而短期汇率失调会影响总进口及7类行业的进口,会影响总出口及3类行业的出口;汇率失调对进出口的影响的方向性由CMT和TMT本身的符号及其对应的系数的符号共同决定,因此二者对进出口是促进还是抑制作用在不同的时段、不同的行业间也并非全部一致。
四、结论及对策建议关于人民币汇率失调对我国进出口额的影响效应,有研究从产业及某个行业进行研究。本文选取1994—2018年中国不同行业年度数据作为样本,运用BEER对人民币实际有效汇率的失调进行度量;同时,基于国际贸易标准分类(SITC),选取我国同期的10类进出口行业年度数据,运用自回归分布滞后(ARDL)模型与误差修正(ECM)模型分析人民币实际有效汇率失调、国内外收入水平及人民币实际汇率对10类行业进口额与出口额的影响,并进一步对比分析短期汇率失调和长期汇率失调对各行业进出口额的影响。实证结果显示:当前人民币实际有效汇率有轻微失调,近年的失调程度均在10%以内。长期汇率失调与短期汇率失调变动趋势基本一致,但是总体上长期汇率失调比短期汇率失调幅度高。人民币汇率失调对进出口行业的影响存在异质性,且具有不同的时滞效应。整体上,汇率失调对进口的影响比对出口的影响大,长期汇率失调对进出口的影响比短期汇率失调对进出口的影响大,且二者对进出口影响的方向在不同时段、不同行业间并非全部一致。基于本文的研究,提出如下对策建议。
第一,持续推进人民币汇率市场化改革,构建和完善人民币汇率管理长效机制和应急机制。
在现有汇率管理及形成机制下,汇率失调程度较小,不存在严重失调,因此在内外部环境相对平稳时,应该继续推进人民币汇率形成机制市场化改革;长期汇率失调对于进出口的影响较短期汇率失调更大,因此应更注重对汇率的长期管理,形成汇率管理长效机制,同时要对汇率的大幅度或者异常的波动进行有效管理,完善汇率管理应急机制,避免汇率的大幅波动和严重失调。
第二,开发多元化工具对冲汇率风险,提高市场效率,降低汇率风险对冲成本。
目前国内企业在进行汇率风险对冲时,有的找不到适合自己的金融工具,有的认为管理成本过高,对于某些小的业务来说,企业运用金融工具进行对冲的成本甚至可能比其风险头寸还要大。因此既要从市场的效率和降成本方面入手,也要在丰富对冲汇率风险的工具方面下功夫,以适应不同行业内有关进出口企业的需求。
第三,实施差异化的进出口行业发展策略。
由于汇率失调对不同行业进出口的影响存在异质性,同时还会对部分行业产生不同程度的滞后效应,因此应实施差异化的进出口行业发展策略。从相关部门角度,一是在人民币汇率政策制定时,除了关注总量分析外,还应根据现有行业结构从行业层面综合考虑,除了考虑汇率管理当前的有效性外,还要考虑汇率传递的滞后效应;二是要做好有关的汇率风险知识普及和宣传工作,必要时进行风险提示;三是要通过信贷政策、税收政策等方面的支持和优惠引导企业转型升级,促进我国进出口行业结构优化。
从企业角度而言,要擅打“组合拳”,根据自身特征制定行之有效的外汇风险管理方案。一是对于受汇率失调影响小、国际竞争力具有显著优势、议价能力较强的企业,在谈判时争取采用人民币结算。二是对于外汇风险头寸大、汇率失调影响较大的企业,可综合运用远期合同、期货合约、期权合约和掉期交易管理汇率风险。三是对于主要从事进出口业务的企业,出口企业若自身经营产品所属行业受汇率失调的影响较大,应该考虑在主要出口地建立分公司进行生产经营活动;进口企业将进口市场多样化,提高自己的谈判优势,提高自己的议价能力。四是,从长期发展而言,企业应该加快转型升级,改进管理模式,提高自身的核心竞争力。当一个企业的产品替代性较小时,其议价能力就会很强,市场占有率就会较稳定,因此汇率及汇率失调对其的影响就会微乎其微。
| [1] |
WILLIAMSON J. The exchange rate system[M]. Washington: MIT Press, 1983: 85.
|
| [2] |
MACDONALD R, CLARK P B.Exchange rates and economic fundamentals: A methodological comparison of BEERs and FEERs[R].IMF Working Papers, 1998, 67: 1-38.
|
| [3] |
周源, 唐晓婕. 人口年龄结构对均衡汇率的影响研究[J]. 金融研究, 2014(6): 132-145. |
| [4] |
严太华, 程欢. 1997~2013年人民币均衡汇率失调程度的实证研究[J]. 经济问题, 2015(1): 50-54. |
| [5] |
姚宇惠, 王育森. 人民币均衡汇率的再研究:1998—2015[J]. 国际金融研究, 2016(12): 23-32. |
| [6] |
CHEUNG Y, CHINN M, NONG X.Estimating currency misalignment using the Penn effect: it's not as simple as it looks[R].National Bureau of Economic Research, 2016.DOI: 10.3386/w22539.
|
| [7] |
刘阳. 相对购买力平价与人民币均衡汇率[J]. 世界经济研究, 2004(10): 45-51. |
| [8] |
王磊, 范超. 购买力平价与汇率背离原因研究[J]. 数量经济技术经济研究, 2013, 30(11): 125-143. |
| [9] |
谢非, 阳华. 外汇衍生品对外汇风险暴露的影响研究:基于中国跨国公司的实证分析[J]. 重庆大学学报(社会科学版), 2017, 23(6): 21-29. |
| [10] |
王全意, 张澜. 人民币实际有效汇率的变动能否有效调节中国国际收支:基于11国面板数据的实证检验[J]. 重庆理工大学学报(社会科学), 2019, 33(1): 40-47. |
| [11] |
OBSTFELD M, ROGOFF K.The unsustainable US current account position revisited[M]//G7 Current Account Imbalances.Chicago: University of Chicago Press, 2007: 339-376.DOI: 10.7208/chicago/9780226107288.003.0010.
|
| [12] |
韩国高. 人民币实际汇率错位、汇率波动对中美出口贸易影响的实证分析[J]. 南方金融, 2010(4): 8-11. |
| [13] |
宫旭红, 曹云祥. 汇率失调与经常账户失衡的非线性关系研究[J]. 新金融, 2017(8): 14-17. |
| [14] |
王铮, 王宇, 胡敏, 等. 全球视角下汇率变动对产业结构影响的分析[J]. 世界经济研究, 2016(8): 3-14, 135. |
| [15] |
金祥义, 张文菲. 人民币汇率错位及波动对中国机电行业的进口影响[J]. 经济与管理评论, 2017, 33(6): 137-143. |
| [16] |
吴丽华, 王锋. 人民币实际汇率错位的经济效应实证研究[J]. 经济研究, 2006, 41(7): 15-28. |
| [17] |
MCKENZIE M D. The impact of exchange rate volatility on international trade flows[J]. Journal of Economic Surveys, 1999, 13(1): 71-106. |
| [18] |
KRUGMAN P R, OBSTFELD M. International economics:Theory and policy[M]. London: Pearson Education Limited, 2008.
|
| [19] |
巴曙松, 王群. 人民币实际有效汇率对我国产业、就业结构影响的实证分析[J]. 财经理论与实践, 2009, 30(3): 2-7. |
| [20] |
李利. 人民币汇率与区域产业结构关系实证研究[J]. 经济地理, 2012, 32(3): 36-39. |
| [21] |
王宇雯. 人民币实际有效汇率及其波动对我国出口结构的影响:基于ARDL-ECM模型的实证研究[J]. 数量经济技术经济研究, 2009, 26(6): 53-63. |
| [22] |
李腊生, 高书丽. 人民币实际汇率波动、汇率错位对中国制造业出口的影响[J]. 当代财经, 2012(11): 90-100. |
| [23] |
马君潞, 王博, 杨新铭. 人民币汇率变动对我国出口贸易结构的影响研究:基于SITC标准产业数据的实证分析[J]. 国际金融研究, 2010(12): 21-28. |
| [24] |
袁申国, 郑雯. 人民币实际汇率波动对外向型企业进出口影响实证分析:基于行业层面比较[J]. 国际经贸探索, 2015, 31(11): 88-103. |
| [25] |
KENEN P B, RODRIK D. Measuring and analyzing the effects of short-term volatility in real exchange rates[J]. The Review of Economics and Statistics, 1986, 68(2): 311-315. |
| [26] |
PESARAN M H, SHIN Y, SMITH R J. Bounds testing approaches to the analysis of level relationships[J]. Journal of Applied Econometrics, 2001, 16(3): 289-326. |
 2020, Vol. 26
2020, Vol. 26

