制造业在一个国家的地位举足轻重,靠工业革命崛起的发达国家都非常重视制造业的发展。作为世界制造业的主要集聚地区,中国已经建立了一个种类齐全、规模庞大的制造业体系,与美国、日本等其他大国相比,中国整体的资本回报率和投资率更高[1-3]。但制造业的投资增速明显低于全国的平均增速,制造业生产率低下,作为一个制造业大国,中国的制造业总产值位居世界第一,但生产率只有发达国家的1/4。金融危机以后,美国、英国、德国等发达国家相继推行“再工业化”,希望通过制造业的结构调整和转型升级巩固其世界强国地位,中美贸易摩擦的本质即是美国意图拖慢中国向先进制造业转型升级的速度。同时,印度、越南等发展中国家也凭借其低廉的劳动力成本,采取措施发展制造业,试图成为第二个“世界工厂”。一方面受到发达国家和新兴经济体的双重挤压,另一方面劳动力成本优势锐减而新的竞争优势尚未形成,中国制造业仍然处于价值链的低端;因此,中国制造业如何提质增效,如何从“中国制造”走向“中国智造”,成为学术界及政府关注的一大议题。在此背景下,研究中国制造业的资本回报率有重要意义,一方面,只有制造业生产率提高,中国才有可能成为世界制造强国,而以资本回报率的收敛性为标志的资本配置效率的提高是生产率提高的一个重要途径;另一方面,资本回报率的高低决定了投资的流向,投资不仅是当前的需求, 更是未来的供给, 因此,资本回报率的高低以及区域差异对制造业未来的发展和空间布局有重要影响。
目前测算资本回报率的方法可以分为非模型化方法和模型化方法。非模型化方法主要采用企业的财务会计等微观数据测算,并不使用复杂的模型[4-6],比如用GDP减去劳动者工资总额度量资本收益,用资本收益与资本存量的比值度量资本回报率。模型化方法主要采用GDP、资本存量等宏观数据测算,测算时使用的模型有生产函数模型以及Jorgenson和Hall的资本租金公式[7-11];如果采用生产函数模型,则根据资本的边际产出计算资本回报率[12-20]。
根据资本的边际产出度量资本回报率时,最常用的生产函数是CD型、CES型、超越对数型。目前的文献存在的问题是:多数文献假定技术进步是外生给定的,这会导致测算的资本回报率低于实际值。其实,人们越来越认识到技术进步并非外生,从理论上看,内生增长理论认为,长期增长率是由内生因素决定的,资本积累本身就融合了新技术,因此,技术进步包含在物质资本投资中,从而内生于物质资本[21-23]。从实证上看,Bernanke等认为,实际的经济增长路径并不符合技术进步外生的特征,新技术附着于新增资本之上,物质资本与技术进步是相互融合、相互包含的[24-25]。赵志耘等也认为中国经济的增长过程体现了新投入资本包含新技术的特征,资本不断扩大的过程本身就蕴含着技术进步的不断增加[26]。所以,改革开放以来中国的高储蓄和高投入在驱动经济增长的同时, 本身就蕴含着大幅度的嵌入式技术进步,带来中国生产率的提升。以上分析表明,在建立生产函数时,技术进步不应该是外生给定而应该是内生于资本,这就意味着资本增加既包括直接方式带来产出的增加——即技术进步不变时,由于资本本身增加而带来的产出的增加,又包括间接方式带来产出的增加——也就是由于新增资本本身蕴含着新技术,而新技术也会带来产出的增加。因此,如果假定生产函数是技术进步外生的,则测算的资本回报率只包含了资本增加而带来的产出的直接增加部分,而忽略了蕴含在资本本身中的新技术带来的产出的增加,从而会导致测算的资本回报率低于实际值。
尽管也有文献考虑了技术进步的内生性,但这些文献只是假定技术进步与资本投入的内生关系满足一个特定的方程,并没有对二者的关系作一般性的假定[3, 19]。可能的原因是,如果不假定技术进步与资本投入的关系满足一个特定的方程,不仅会较难估计回归系数,也较难估计资本本身蕴含的新技术带来的产出的增加。另外一个问题在于数据类型上,根据边际产出法测算资本回报率时,文献上都是利用宏观数据建立生产函数,较少有文献建立微观生产函数测算资本回报率。随着微观计量的发展及微观数据的完善,人们开始用微观数据研究宏观问题。Olley和Pakes在1996年建立了微观生产函数测算TFP,被人们称为OP模型[27]。该模型不仅考虑了技术进步内生于资本,而且不用设定技术进步与资本的特定函数形式。Olley和Pakes根据OP模型提出了估计参数的方法——半参数OP方法,近年来,该模型和方法被广泛应用并成为估计全要素生产率的一种主要方法。但查阅文献发现,OP模型及OP方法尚未用于估计资本回报率。其实,可以先利用OP模型及OP方法估计出全要素生产率,然后根据非参数方法估计出在资本投入不变的情况下,仅仅由于技术水平的提高而带来的产出增加,也即资本的增加通过间接途径带来的产出的增加,从而测算资本回报率。
为了更准确地测算制造业的资本回报率,本文对边际产出法的以上不足之处进行改进。具体说来,本文的主要内容如下:首先构建了一般性的技术进步内生的生产函数,而且认为资本产出弹性和劳动产出弹性不仅依赖于行业,也依赖于企业的所有制性质,并提出了一种估计资本回报率的新方法。然后结合《中国工业企业数据库》中制造业企业的数据,先运用OP方法估计参数和全要素生产率,再利用修正的边际产出法估计出资本的增加通过直接途径和间接途径带来的产出增加之和,从而避免了资本回报率的低估。最后从全国层面和区域层面测算了制造业的资本回报率,分析了其差异、收敛性和影响因素。
与以往的文献相比,本文有如下特点与创新:第一,本文提出的非参数方法是测算资本回报率是一种新方法。第二,本文构造的技术进步内生的生产函数可以避免资本回报率的低估,使测算结果尽可能准确。
二、模型设计、数据来源与样本处理 (一) 模型设计1.生产函数模型
根据资本的边际产出测算资本的回报率时,要先设定生产函数,本文假设企业的生产函数与行业i和所有制j都有关,形式如下:
| $Y=A(K, I) K^{\alpha_{i j}} L^{\beta_{i j}} $ | (i) |
此处的技术进步内生于资本,并且要素产出弹性与i和j都有关。
则资本回报率的计算公式是:
| $r=\frac{\partial Y}{\partial K}=\alpha_{i j} A K^{\alpha_{i j}-1} L^{\beta_{i j}}+K^{\alpha_{i j}} L^{\beta_{i j}} \frac{\partial A}{\partial K} $ | (2) |
公式(2)也可以写成:
| $r=\alpha_{i j} \frac{Y}{K}+K^{\alpha_{i j}} L^{\beta_{i j}} \frac{\partial A}{\partial K} $ | (3) |
其中:公式(3)的第一项表示技术进步不变时,由于资本使用量增加而带来的总产出的增加;第二项表示资本使用量不变时,由于生产技术的进步而带来的总产出增加;
只要求出公式(3)中的αij、βij、
模型(1)两边取对数得到:
| $Y^{*}=A^{*}\left(K^{*}, I^{*}\right)+\alpha_{i j} K^{*}+\beta_{i j} L^{*} $ | (4) |
对于模型(4),先利用OP方法求出αij和βij,再利用索罗余值法求出技术进步A,然后利用非参数方法求出
2.收敛模型
σ收敛是指随着时间增长,不同经济体的水平值越来越集中,其差距越来越小。σ收敛系数的计算公式是资本回报率的标准差与资本回报率均值的比值:
| $V_{\mathrm{t}}=\frac{S_{\mathrm{t}}}{r_{\mathrm{t}}} $ | (5) |
β收敛是指不同经济体的增长率与其水平值负相关,只有存在β收敛才有可能存在σ收敛性。β收敛又分为绝对β收敛和条件β收敛。条件β收敛模型如下:
| $\mathrm{d} r_{i \mathrm{t}}=\alpha+\beta_{1} \mathrm{l} \cdot \mathrm{r}_{i \mathrm{t}}+\beta_{2} \mathrm{d} \mathrm{tfp}_{i \mathrm{t}}+\beta_{3} \mathrm{d} k_{i \mathrm{t}}+\beta_{4} \mathrm{d} p_{i \mathrm{t}}+\mu_{i \mathrm{t}} $ | (6) |
如果模型(6)中系数β1显著小于0,即认为存在β收敛。各个符号的含义见表 1。
| 表 1 各个变量的符号及含义 |
当模型(6)中解释变量只有l.r时,即是绝对β收敛模型,绝对β收敛模型研究所有经济体之间,是否具有资本回报率越高,资本回报率的增长率越低的特征。模型(6)中引入的企业规模(s)和企业所处的外部环境(o)是两个控制变量,用来检验收敛结果的稳健性。
(二) 数据来源与样本处理本文采用“中国工业企业数据库”中的制造业企业数据,共包括三维度:行业、地区和所有制,其中行业包括制造业的30个行业,地区包括中国的港澳台以外的31个省、自治区和直辖市,所有制包括国有、集体所有、私营等共7种。产出采用工业增加值,投入采用固定资本存量和从业人员数。对数据进行平减的方式为:根据《中国城市(镇)生活与价格年鉴》,采用工业生产者出厂价格指数对工业增加值平减,采用固定资产投资价格指数对固定资本存量平减,且都以2001年为基期。
样本处理过程如下:先采用序贯匹配法对样本企业进行匹配,再删除投入或产出指标缺失的样本,对余下的样本根据模型(4)估计参数及全要素生产率。由于企业的错误报表造成一些样本极端异常,这一部分样本需要剔除。本文认为,如果根据模型(4)估计的全要素生产率的增长率位于区间(-100%,100%)以外,则该样本予以剔除,经过这一步处理后仍然存在离群值,再根据箱形图原理剔除离群值,本文的后续研究所用到的样本都是经过这一步处理后余下的样本。为了保证模型参数估计的准确性,利用余下的样本重新估计模型(4)的参数及全要素生产率,再根据非参数法求出
1.资本回报率的变化趋势分析
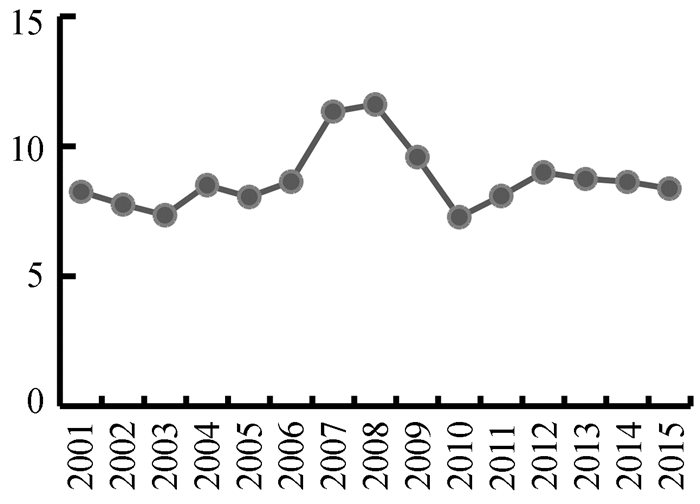
求出制造业整体的资本回报率,见图 1。从中看出,从2001年到2015年,制造业平均资本回报率是8.79%,2007年和2008年最高,都在11%以上,分别高于平均值2.54和2.82个百分点,原因是这两年中国经济异常繁荣,旺盛的需求带来资本的充分使用。但随后的金融危机使资本回报率大幅下降,在2009年和2010年分别降到9.58%和7.27%,2011年以后有所上升。除了2007年和2008年,其他年份资本回报率都在7%~10%之间。多数研究者的测算结果认为中国宏观资本回报率也在金融危机爆发后有大幅下降,所以制造业的资本回报率变化与中国宏观趋势相同。
|
图 1 制造业整体的资本回报率(单位:%) |
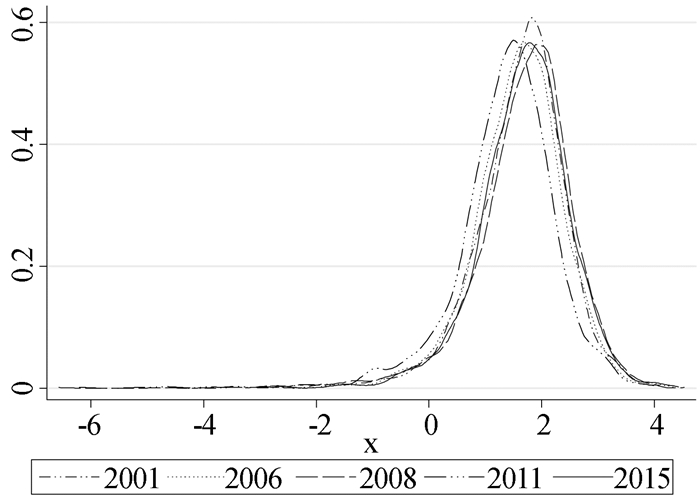
绘制出资本回报率对数值的核密度曲线,见图 2。从中可以看出,相比于2001年和2006年,2008年密度曲线整体向右移动,说明各类企业的资本回报率都有所增加,同时密度曲线左尾部下方的面积减小,右尾部下方的面积增大,说明资本回报率本来就高的企业提高得更多。相比于2008年,2011年密度曲线整体向左移动,但是右尾部移动的幅度较小,说明资本回报率高的企业受金融危机的影响要小一些。2015年密度曲线整体右移,各类企业的资本回报率都有所回升。
|
图 2 制造业资本回报率对数值的核密度函数 |
2.资本回报率的区域差异性分析
计算出各地区各年的资本回报率,结果见表 2。
| 表 2 制造业各地区各年资本回报率(单位:%) |
从表 2可以看出,在多数年份,东部省份的资本回报率要高于西部省份,各个省、自治区、直辖市的平均资本回报率从高到低分别是:浙江(9.61%)、福建(9.54%)、江苏(9.16%)、山东(9.14%)、广东(8.96%)、海南(8.85%)、新疆(8.82%)、安徽(8.68%)、河南(8.55%)、上海(8.55%)、天津(8.51%)、河北(8.50%)、内蒙古(8.45%)、黑龙江(8.41%)、广西(8.35%)、湖北(8.32%)、宁夏(8.29%)、江西(8.29%)、辽宁(8.27%)、北京(8.26%)、湖南(8.16%)、四川(8.11%)、云南(7.86%)、吉林(7.84%)、陕西(7.80%)、重庆(7.72%)、山西(7.64%)、甘肃(7.62%)、青海(7.46%)、贵州(7.19%)、西藏(6.89%)。再把全国分为东部、中部、西部、东北4个区域,计算出各个区域的资本回报率,见图 3。
|
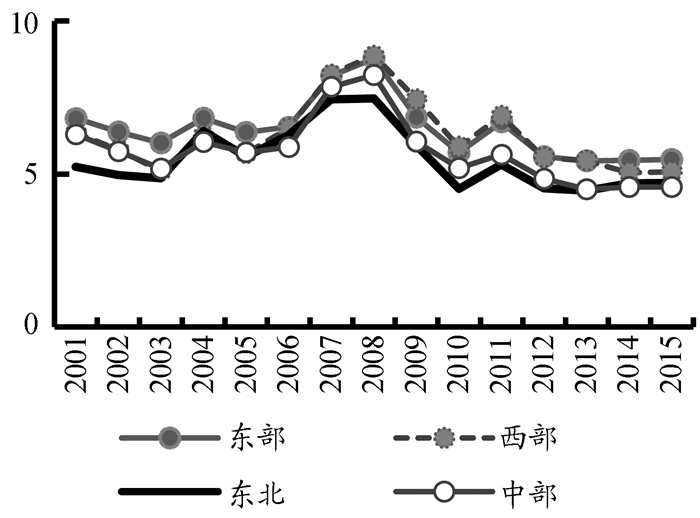
图 3 各个区域制造业的资本回报率 |
从图 3中看出,资本回报率从高到低依次是东部、西部、中部、东北,资本回报率分别是6.47%、6.28%、5.75%、5.49%;而且东部区域不仅平均值高,几乎每年都是最高的,东北区域不仅平均值低,几乎每年都是最低的。单从4大区域看,资本回报率并没有呈现出与人均资本负相关的特征,样本期内,东部、西部、中部、东北的人均资本分别是633.45亿元、454亿元、585亿元、519亿元,西部区域人均资本最低,其资本回报率却不是最高的,东部区域的人均资本最高,但由于东部区域是制造业企业的聚集地,有着较高的技术水平及管理水平,其资本回报率仍然是最高的。区域间资本回报率的差异使越来越多的资本流向东部沿海地区,而西部地区资本增加较慢,甚至是负增长。
在资本自由流动下,如果一个区域的资本回报率较高,会导致下一期资本向该区域流动。计算出区域资本增加量与资本回报率的一期滞后值的相关系数,结果显著为正,说明整体来看,资本是向着高回报的区域流动,资本回报率越高,资本增加量也就越多,配置效率是增加的。需要注意的是,西部区域的回报率不是最低的,但其资本增加量却是最低的,并且资本占比在下降,从2001年到2015年,东部、中部、西部、东北的资本分别增加1 803.89亿元、430.6亿元、344.59亿元、186.3亿元,资本占比分别从2001年的57.99%、15.4%、14.79%、11.42%变化到2015年的63.68%、15.55%、13%、7.8%,西部区域资本占比的降低会在一定程度上降低全国层面资本配置的改善程度,影响整体资本回报率的提高。
(二) 资本回报率的收敛性分析1.σ收敛结果分析
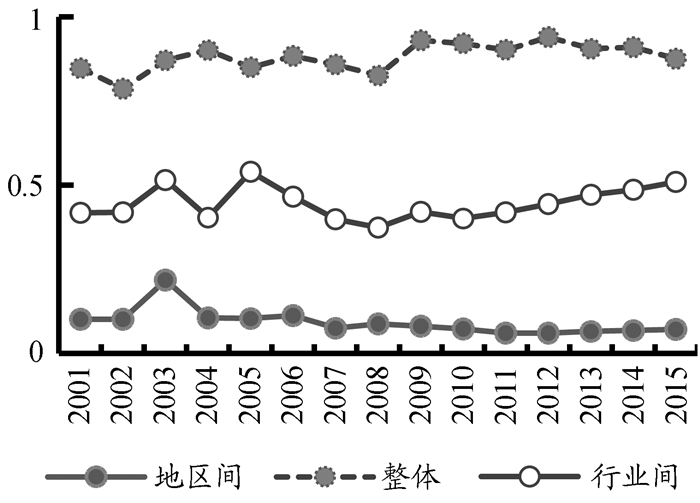
根据公式(5)可以得到资本回报率的省际间、行业间以及整体的σ收敛系数,见图 4。
|
图 4 资本回报率的σ收敛系数 |
从图 4中可以看出,制造业资本回报率在不同省际之间的差异最小,在不同行业之间的差异居中,而整体的差异最大。从2009年开始,行业间和整体的σ收敛系数都有明显上升,但省际间的σ收敛系数略有下降,这意味着金融危机发生后,行业间和整体的资本回报率差异增大、资本配置效率明显下降,低于金融危机前的水平,但省际间资本回报率差异减小、资本配置效率略有提高。
2.β收敛结果分析
表 3中的各个模型用以判断省际间资本回报率是否存在β收敛,采用的数据是各个微观样本的数据,模型都控制了地区以外的两个维度,即行业和所有制,且分别采用随机效应模型和固定效应模型估计参数,其中第1列至第3列是随机效应模型,第4列至第6列是固定效应模型。第1列和第4列用以检验绝对β收敛性,第2列和第5列用以检验条件β收敛性,第3列和第6列用以判断收敛结果的稳定性。
| 表 3 β收敛分析结果 |
在进行回归之前,需要先做内生性检验。以第2列为例,最可能的内生解释变量是dtfp,考虑到dtfp的一期滞后值与l.r相关,因此,用dtfp的二期滞后值作为dtfp的工具变量。首先采用Cragg-Donald检验,结果通过弱工具变量检验,因此认为用dtfp的二期滞后值作为工具变量是合理的;然后采用Durbin-Wu-Hausman内生性检验,结果认为dtfp是内生变量,因此,模型2可以用dtfp的滞后二期值作为dtfp的工具变量。类似的,对于其他模型,都采用dtfp的滞后二期值作为dtfp的工具变量。
从表 3的回归结果可以看出,所有模型的l.r的系数都显著为负,说明省际间资本回报率同时存在条件β收敛和绝对β收敛,而且结果稳健,这与Bai等[8]、陈培钦[17]、贾润崧和张四灿[28]等的结论一致。他们的研究也表明资本回报率的省际差异逐渐缩小,呈现收敛趋势,省际间资本配置效率在逐渐提高。同时,表 3中dk和dp的系数都为负且显著,说明房价和人均资本的增长对资本回报率有显著负影响;全要素生产率增长率的系数显著为正且绝对值比其他解释变量要大得多,说明其对资本回报率增长有显著正影响,且是影响资本回报率的主要因素。从资本回报率的影响因素看,本文与方文全[9]、黄伟力[14]、黄先海等[19]的结论一致。他们也认为全要素生产率是影响资本回报率的最主要因素,是资本回报率没有随资本—劳动比的提高而下降的重要原因,而资本—劳动比对资本回报率的影响要小于技术进步的影响。另外,本文的研究结果意味着技术进步与资本回报率相互促进,较高的资本回报率带来较高的投资,由于技术进步内生于资本,进而会带来较快的技术进步,而技术进步的加快会进一步带来资本回报率的提高。
本文对资本回报率的省际间差异性和收敛性分析表明,省际间存在绝对β收敛、条件β收敛和σ收敛性,地区之间的资本回报率差异减小;这意味着东部省市的资本回报率逐渐下降,中西部地区逐渐上升,开始向东部地区靠拢;除了东部地区较高的房价以及逐渐增加的资本—劳动比外,一个主要的原因是技术进步速度的差异。本文还分析了全要素生产率增长的地区差异,发现中西部地区明显高于东部地区。
本文还测算了各行业的资本回报率,结果是烟草业的资本回报率最低,这与邵挺[15]的结论不同。邵挺认为,烟草业的资本回报率明显高于其他行业。导致这种差异的原因除了样本不同外,还有一个原因是,尽管邵挺也是用边际产出法,但其假设劳动力市场是完全竞争的,从而认为工资等于劳动的边际产出。本文与蔡真[6]的结论也不同,蔡真用资本收益与资本存量的比值度量资本回报率,用GDP减去劳动者工资总额度量资本收益,这意味着也要承认劳动力市场的完全竞争性,工资等于劳动的边际产出。但事实上,许多行业都存在着进入壁垒,劳动力市场并不是完全竞争的,从而导致工资并不等于劳动的边际产出。本文测算了各个行业劳动的边际产出,发现烟草业劳动的边际产出明显高于其从业人员的工资,如果仍然用GDP减去劳动者报酬表示烟草业的资本收益,或者认为工资等于边际产出,显然会造成烟草业资本回报率的高估。
四、结论及启示本文首先构建了一般性的技术进步内生的生产函数,考虑了资本增加带来技术进步增加,进而带来产出增加的过程,并提出了一种估计资本回报率的新方法——非参数法。然后结合《中国工业企业数据库》中制造业企业的微观面板数据测算了制造业的资本回报率。结果显示:从资本回报率的水平值看,2001—2015年全国层面制造业资本回报率的平均值是8.79%;从区域看,资本回报率从高到低依次是东部、西部、中部、东北;从省际间资本回报率的收敛性看,资本回报率的增长率与水平值都负相关,资本回报率的差距有所减小;从资本回报率的影响因素看,全要素生产率是影响资本回报率的主要因素,此外,房价和人均资本量对资本回报率有显著负影响;较高的资本回报率带来较高的投资,由于新增投资蕴含着新技术,而技术水平的提高会使资本回报率通过间接途径增加产出,提高资本回报率,从而技术进步与资本回报率相互促进,具有良性互动。
本文的研究也意味着要促进制造业的高质量发展,可以考虑从以下几个方面着手:第一,鼓励企业创新,使中国制造向全球价值链高端攀升。中国尽管在制造业的总量上处于世界第一,但制造业资本回报率与生产率水平都较低,主要原因是产品质量不高,低附加值产品比重过大,重要行业缺乏核心技术,缺乏具有自主知识产权的国际知名品牌,缺少国际顶级制造企业。而中国要成为世界制造强国,必须要制定相应的政策鼓励企业创新并做好知识产权保护,采取各种措施提高技术水平,掌握关键技术,使中国制造向全球价值链高端攀升。第二,促进制造业向西部转移,建立新的制造业产业集聚区。要达到制造业的高质量发展,向全球价值链高端迈进,除了靠技术进步外,另外一种力量就是结构优化,即生产要素的再配置,使生产要素从生产率较低的部门或地区向生产率较高的部门或地区流动,进而促进社会整体效率的提高,由此带来的“结构红利”促进经济的持续增长。目前制造业空间分布不均衡,主要集中在东部沿海地区,较高的劳动力成本和土地成本会加重企业负担,束缚制造业发展,促进制造业向西部转移,建立新的制造业产业集聚区,不仅会降低企业成本,减轻企业负担,也会促进区域经济协调发展。第三,合理引导人们预期,抑制房价过快上涨。正如本文所示,房价对资本回报率有显著负影响,抑制房价过快上涨,一方面可以避免投机动机导致的资金向房地产市场的流动,增强企业向制造业投资的意愿;另一方面,也可以减少制造业的租金成本,提高利润,为制造业高质量发展营造良好的环境,引导资金“脱虚向实”。
| [1] |
孙文凯, 肖耿, 杨秀科. 资本回报率对投资率的影响:中美日对比研究[J]. 世界经济, 2010, 33(6): 3-24. |
| [2] |
张勋, 徐建国. 中国资本回报率的再测算[J]. 世界经济, 2014, 37(8): 3-23. |
| [3] |
刘晓光, 卢锋. 中国资本回报率上升之谜[J]. 经济学(季刊), 2014, 13(3): 817-836. |
| [4] |
CCER"中国经济观察"研究组. 我国资本回报率估测(1978-2006):新一轮投资增长和经济景气微观基础[J]. 经济学(季刊), 2007, 6(3): 723-758. |
| [5] |
辛清泉, 林斌, 杨德明. 中国资本投资回报率的估算和影响因素分析:1999-2004年上市公司的经验[J]. 经济学(季刊), 2007, 6(4): 1143-1164. |
| [6] |
蔡真. 中国的资本回报率、实际利率与投资:基于行业数据的分析[J]. 金融评论, 2013, 5(6): 39-58,122. |
| [7] |
HALL R E, JORGENSON D. Tax policy and investment behaviour[J]. American Economic Review, 1967, 57: 391-414. |
| [8] |
BAI C E, HSIEH C T, QIAN Y Y.The return to capital in China[R].National Bureau of Economic Research, 2006.DOI: 10.3386/w12755.
|
| [9] |
方文全. 中国的资本回报率有多高:年份资本视角的宏观数据再估测[J]. 经济学(季刊), 2012, 11(2): 521-540. |
| [10] |
白重恩, 张琼. 中国的资本回报率及其影响因素分析[J]. 世界经济, 2014, 37(10): 3-30. |
| [11] |
张慕濒. 中国地区资本回报率的变动及其影响因素分析[J]. 当代财经, 2016(4): 3-11. |
| [12] |
LUCAS R E. Why doesn't capital flow from rich to poor countries?[J]. The American Economic Review, 1990, 80(2): 92-96. |
| [13] |
龚六堂, 谢丹阳. 我国省份之间的要素流动和边际生产率的差异分析[J]. 经济研究, 2004, 39(1): 45-53. |
| [14] |
黄伟力. 中国资本利润率的变动趋势及其影响因素[J]. 山西财经大学学报, 2007, 29(8): 15-21. |
| [15] |
邵挺. 金融错配、所有制结构与资本回报率:来自1999~2007年我国工业企业的研究[J]. 金融研究, 2010(9): 51-68. |
| [16] |
胡凯. 中国省际资本回报率的地区差距[J]. 湖北经济学院学报, 2012, 10(3): 80-86. |
| [17] |
陈培钦. 生产率、资本回报率和增长率的良性互动:"中国奇迹"的一种新解释[J]. 华中科技大学学报(社会科学版), 2013, 27(3): 59-67. |
| [18] |
孟望生, 林军. 我国省份资本存量及其回报率估算[J]. 东北财经大学学报, 2015(1): 81-88. |
| [19] |
黄先海, 杨君, 肖明月. 资本深化、技术进步与资本回报率:基于美国的经验分析[J]. 世界经济, 2012, 35(9): 3-20. |
| [20] |
刘晓光, 苟琴. 劳动力转移、技术进步与资本回报率变动[J]. 产业经济研究, 2017(2): 76-87. |
| [21] |
ARROW K J. The economic implications of learning by doing[J]. The Review of Economic Studies, 1962, 29(3): 155-173. DOI:10.2307/2295952 |
| [22] |
ROMER P M. Increasing returns and long-Run growth[J]. Journal of Political Economy, 1986, 94(5): 1002-1037. DOI:10.1086/261420 |
| [23] |
BARRO R J, SALA-I-MARTIN X I. Economic growth[M]. Cambridge: Massachusetts Institute of Technology Press, 2004.
|
| [24] |
BERNANKE B, GURKAYNAK R.Is growth exogenous? Taking Mankiw, Romer and Weil seriously[R].National Bureau of Economic Research, 2001.DOI: 10.3386/w8365.
|
| [25] |
REBUCCI A. Is growth exogenous?Evidence from the 1970s and 1980s[J]. Applied Economics, 2010, 42(5): 535-543. |
| [26] |
赵志耘, 吕冰洋, 郭庆旺, 等. 资本积累与技术进步的动态融合:中国经济增长的一个典型事实[J]. 经济研究, 2007, 42(11): 18-31. |
| [27] |
OLLEY G S, PAKES A. The dynamics of productivity in the telecommunications equipment industry[J]. Econometrica, 1996, 64(6): 1263-1297. DOI:10.2307/2171831 |
| [28] |
贾润崧, 张四灿. 中国省际资本存量与资本回报率[J]. 统计研究, 2014, 31(11): 35-42. |
 2020, Vol. 26
2020, Vol. 26

