2. 南京大学 博士后流动站, 江苏 南京 210093
2. Postdoctoral Mobile Station, Nanjing University, Nanjing 210093, P. R. China
长江经济带是中国跨越三个主要经济圈,连接中国东部、中部、西部的唯一经济带[1-3]。其区域内的11个省市,无论是人口数量还是经济总量均超过我国的40%。由此可以看出,长江经济带对于国家地区经济水平和社会协作机制的发展进步具有关键作用[4-5]。基于我国经济战略发展视角可以得知长江经济带的重要性,长江经济带发展战略已经成为我国新时代发展进程中的三大发展战略之一,国家各级党政机关与相关部门对其予以高度关注。目前长江经济带三维开发的顶层设计已投入实践阶段,国家正逐步实行整改和过渡,但仍然面临着地区开发差别化、产业改革和改善两难等诸多问题[6]。对此,习近平总书记提出应将长江经济带纳入创新主导开发区。2016年《长江经济带发展规划纲要》指出,长江经济带的开发是向改革创新和新动能开发上进行深化推进,并始终致力于将这一经济地带构建成兼具良好生态文化与创新文化的经济推动区域[7]。长江经济带的开发需要深入推行五大发展理念,要特别重视依靠科技创新推进长江沿岸地区的飞跃性开发。为此,文章以长江经济带区域内11个省市为研究对象,基于其科技创新现状及地理区位对长江经济带科技创新效率的动态和影响因素进行详细分析,解明和预测长江经济带区域科技创新成效,以探索长江经济带科技创新效率的有效推动渠道,从而推动长江经济带沿线区域的创新主导型开发。
吴传清和黄磊在创新效率的概念定义基础上指出,创新效率性就是在同一水平的创新输入中获得更多的创新产品,或者是在同一水平的创新输入中投入更少的资源,即在创新投入和产出之间,定义的比率产生动态变化[8]。根据当前相关理论研究,地域科学技术创新的效率性定义为地域科技创新活动的投入与产出之间的关系。这不仅显著表明了在一定区域范围内创新体系的资源应用水平与资源应用成效,而且反映了这一体系对资源的配备实践。国内外学者对一定区域范围内科技创新效率的检测方法主要有数据包络分析(DEA)、成分因素分析(PCA)、随机前沿分析(SFA)以及分析层次过程(AFP)等[9-11]。
数据包络分析(DEA)是一种用于测量科学技术创新的检测方法,通常将其用于效率性的学术研究[12]。随着时代的发展,这种测量方法已经分化为传统型与改良型。国内众多学者利用经典的DEA方法对我国31个省份(地区和城市)的科技创新效率进行了测定计算和分析。也有一部分学者[13]运用传统类型的DEA法针对我国具体省市地区的科技创新效率现状以及历史发展沿革进行了调查研究。在改良的DEA方法应用方面,文献[14]利用两个不同类型的DEA模型,对国内各省份的科技创新效率进行了定量检测分析。此外,主成分分析(PCA)方法也被用于测定科技创新的效率。文献[15]就根据PCA模型对我国31个省份的科技创新效率进行了检测分析。文献[16]则采用PCA方法,定量研究了长江经济带11个省市的科技创新效率与实践成效。
综合相关研究,从研究方法视角看,DEA、PCA、SFA、AHP等分析方法均曾被用于科技创新效率的测定,其中,传统DEA模型更被广泛地使用[17]。从空间尺度视角看,目前,对科技创新效率的研究主要集中在国内31个省份或市、镇、村的测量和比较上,而对长江经济带的专题研究比较少见。从研究视角看,当前大部分研究普遍聚焦在科技创新效率上,再进一步开展深化价值计算、动态进化规律研究并探讨影响科技创新效率的因素[18]。本研究在此基础上,使用改进的DEA分析法以及PCA法搭建了PCA-SE-DEA组合模型,分析长江经济带区域内11个省市的科技创新效率以及发展进程,并对其影响要素进行研判。
一、科技创新效率测度 (一) 模型设定本文使用的SE-DEA模型是在CCR模型基础上建立形成,但同CCR模型有所差异,其是从DMU模型“前沿”中分离出来的,能够使科技创新效率的测定结果超过1,进而可以对相关决策指标进行单位排序[18]。因此,“前沿平面”指的就是在各种投入与产出的组合当中,寻求最大组合值而构成的多维空间平面。本文基于一定输入方向的回馈比例选择SE-DEA模型。设定DUM数量为n个,并且每个DUM有m个输入和s个输出;xij代表输入有i种,yrj表示输出有r种,λj代表第n个DUM的输入输出指标权重。
| $ \begin{array}{*{20}{c}} {\min \left[ {\theta - \varepsilon \left( {\sum\limits_{i = 1}^{\rm{m}} {S_i^ - } - \sum\limits_{i = 1}^s {S_i^ + } } \right)} \right]}\\ {\sum\limits_{j = 1}^m {{x_{ij}}} {\lambda _j} + S_i^ - = \theta {x_{ij}}, i \in (1, 2, \ldots , m)}\\ {\sum\limits_{j = 1}^m {{y_{rj}}} {\lambda _j} + S_i^ + = {y_{ij}}, r \in (1, 2, \ldots , s)}\\ {{\lambda _j} \ge 0, i = 1, 2, \ldots , n}\\ {S_i^ - \ge 0}\\ {S_{\rm{i}}^ + \ge 0} \end{array} $ | (1) |
在式(1)里,0代表相对效率,Si-和Si+代表缓和变量,ε代表非阿基米德无限小,在一般情况下这一取值为ε=0.000 001。设定式(1)有最佳的解决方案,θ*则是科技创新效率的值。
运用PCA法提炼出与长江经济带技术创新效率密切相关的公共因素。现有研究对区域科技创新效率的选取因素主要来自人力、物力以及生态环境方面的输入情况。在这项科技创新测定指标体系中,共有两大类指标,分别为投入指标和产出指标。其中投入指标又分为四大方面指标要素,主要是政策环境、人力要素、资金运用情况以及社会环境条件。产出指标要素也分为四大主要具体指标,即产品销售额、市场交易份额、科技企业数量以及专利数量。具体指标要素情况见表 1。
| 表 1 科技创新效率测度指标 |
从上述可知,PCA-SE-DEA组合模型不仅可以保持各输入输出指示指标的完整信息,还能降低指示指标之间的相关水平。从另一层面看,其可以更好地显示SE-DEA模型对决策单元的评价比较成效,极大地提升了测算环节的精确性水平,在对我国长江经济带各省市的创新效率进行定量测定的时候能够提升准确性保障。
(二) 科技创新效率收敛性检验为了具体实证把握我国长江经济带11个省市科技创新效率的发展现状和动态进展成果,现运用下列两种方法进行收敛性检验测算,即σ收敛法和绝对β收敛法[19]。在测试科技创新效率的收敛过程中,首先,长江经济带技术创新效率σ收敛性测试公式如下:
| $ \sigma_{t}=\left\{N^{-1} \sum\limits_{i=1}^{n}\left[\mathrm{IE}_{i}(t)-\left(N^{-1} \sum\limits_{i=1}^{n} \mathrm{IE}_{i}(t)\right)\right]^{2}\right\}^{+} $ | (2) |
在式(2)中,IEi(t)是第i个区域的技术创新效率,N是省市的数量。在本文中N的取值为11。在σt+1 < σt的情况下,各省市技术创新效率的离散系数会减少,即有σ收敛存在;在σt+1>σt的情况下,各省市技术创新效率的离散系数呈现上涨态势,表示σ具备发散现象。
其次,长江经济带区域内科技创新效率的绝对β收敛回归公式如下所示:
| $ \frac{\ln \left(\mathrm{IE}_{i, T}\right)-\ln \left(\mathrm{IE}_{i, 0}\right)}{T}=\alpha+\beta \ln \left(\mathrm{IE}_{i, 0}\right)+\varepsilon $ | (3) |
在式(3)中,IEi, T表示在T时间单位内科技创新效率,IEi, 0表示在一定时间单位内第i个省市的科技创新效率,[ln(IEi, T)-ln(IEi, 0)]/T代表第i个省市在1=T之前拥有科技创新效率的平均增长率,α、β、ε分别代表常数项、系数和误差项。在β<0的情况下,有绝对的β收敛,各地区技术创新效率的增长率与初始水平成反比,即技术创新效率与初期值成反比,显示出发展中地区追赶先进地区的倾向。在β>0的情况下,各区域不会收敛,即发展中地区追赶先进地区的倾向还不明显。
(三) Tobit模型基于11个省市在长江经济带的科技创新效率计算,将技术创新效率(IE)定义为响应变量,其余的影响要素则定义为控制变量。通过应用2阶段分析,在其中构建模型进行研究,并从中寻找科技创新效率的影响要素。由于IE取值范围受到限制,如果还使用通常的最小二乘法,则回归参数的估计值就会产生偏颇。鉴于此,本文运用Tobit模型实现对变量建模环节当中的有限性限制解决,如式(4)所示。
| $ Y_{k}=\left\{\begin{array}{l} \beta X_{k}+\mu k, \beta X_{k}+\mu K>0 \\ 0, \beta X_{k}+\mu k <0 \end{array}\right. $ | (4) |
在这个公式中,Yk是带限制的从属变量,Xk是控制变量,β是参数集。根据相关文献资料得知,区域开发水平、经济结构及政策环境对区域技术创新的效率性存在关键影响效应。为了进一步分析科技创新效率性的相关影响因素,本文在影响要素体系中纳入表 2当中的各项变量,并实施Tobit分析。
| 表 2 长江经济带科技创新效率影响因子 |
在研究中,首先使用KMO和Bartlett的数据值进行样本数据共同要素分析的适应性测定,随后运用SPSS 22.0软件进行输入指示器的主要构成要素分析。由于要优化数据测定结果,满足模型数据测定运行系统的要求,因此追加建立了具有4个输出和输入指示器的SE-DEA模型,最大标准模型被用于数据的无量纲处理,避免了主成分分析过程中共同因子为负值情形的出现,详细的测算模式在公式(5)当中显示。
| $ F_{i j}^{\prime}=0.1+\frac{0.9\left(F_{i j}-\min F_{i j}\right)}{\max F_{i j}-\min F_{i j}} $ | (5) |
式中,Fij代表未经处理的数值,F′ij代表经过处置之后的数值,maxFij代表数值的最大化,minFij代表数值的最小化。数据转换结束后,所得出的数据结果都会在一定的区域数值范围内。
在输入数据和输出数据无量纲处理后,使用PCA-SE-DEA结合模型,测量2008—2019年中国本土30个省份的科技创新效率。表 3显示的是长江经济带11个省市科技创新效率的测定结果。从国家整体的角度看,北京、上海和江苏呈现出最高的科技创新效率水平,基本上每年都超过一级,居国内领先地位。基于长江经济带进行分析,江苏和上海在科技创新效率上处于优势领先地位,浙江和湖北处于中等水平以上,云南和贵州处于相对落后的水平。从区域分布的角度看,江苏、上海、浙江位于长江下游地带,在长江经济带的11个省市中具有最高的科技创新效率。安徽、江西、湖北、湖南是位于长江经济带中游地带的省份,只有湖北呈现出良好的科技创新效率水平。位于上游地区的四川、重庆、云南和贵州其科技创新效率水平较为落后。基于数据平均数值视角进行分析,本研究选取的11个省市在2008—2019年这段时间的总体效率数值低于全国平均水平。由此可以看出,我国长江经济带各省市在科技创新方面具有巨大的发展潜力,长江经济带下游区域的各省份具备的科技创新环境条件较好,其相应的科技创新效率水平处于较为优势的地位,同时在创新主导的产业结构变革和升级方面具有较强的竞争优势。
| 表 3 长江经济带11省市科技创新效率测度结果(2008—2019) |
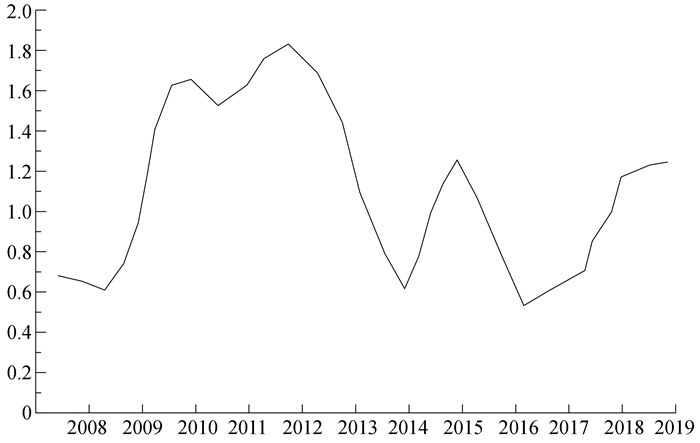
综上,长江经济带科技创新效率的地域差异非常显著。鉴于此,为准确掌握地区差异的发展趋势,必须对相关数据进行深化处理,进而对各省份科技创新效率的收敛性作出预测。其中首要预测步骤就是在长江经济带进行科技创新效率的σ收敛分析。结合公式(2)进行测算,图 1为2008—2019年11个省市科技创新效率的σ收敛结果。根据数据显示得知,长江经济带11个省市的科技创新效率σ收敛结果数值在2012年达到顶峰;2012年以前,11个省市的科技创新效率的地域差距持续扩大;2012年到2016年,11个省市的科技创新效率的收敛率σ发生了变化,各省市科技创新效率的地域差距逐年缩小;2016年以后,11个省市的科技创新效率的收敛率σ又发生了明显变化,其具体体现为各省市的科技创新效率地区差异又趋显著。在全球金融危机之前,我国长江经济带下游区域各省市纷纷开启国际化发展进程,并在这一发展进程中深入落实科技创新战略,由此导致了与上中游地区省份在科技创新效率上的初步地区差异化现象。在全球金融危机爆发以后,长江经济带下游地区各省市的经济发展受到了金融危机影响,从而对科技创新活动造成了不利影响。此时,上中游省市地区的科技创新开发呈现出快速发展的趋势,出现了小范围小幅度的区域效率差异现象。这是由于该地区经过前几年经济良好发展的累积,在科学技术以及创新实践方面具有了一定的优势地位,因此在危机面前没有产生效率水平大幅下降的现象。
|
图 1 长江经济带11省市2008—2019年科技创新效率σ收敛结果 |
本研究继续对我国长江经济带实施绝对收敛分析,测试科技创新效率低的省市能否有效赶上科技创新效率高的省市。测试结果显示回归系数是正值(见表 4),因此后开发地区对占主导地位的地区没有明显的追赶成效,且区域间的科学技术创新效率差正在不断扩大,这个结论与σ测试分析的结果一致。长江经济带的11个省市在经济、社会、技术发展状况等方面均不同,特别是位于上游和中游地区的省市一般不擅长科技创新。由于各方面要素的投资与下游省市之间的差异水平较大,所以上游省份的科技创新捕捉效果不显著。
| 表 4 长江经济带11省市2008—2019年科技创新效率β收敛检验结果 |
结合以上检测成果,本文深入建构一个面板经验模型,其中具体涵盖各省市的科技创新效率以及相关影响要素的变量体系。运用二阶分析法,对科技创新影响机制以及组成要素进行分析探索。其中采用的影响要素具体体现在公式(6)中,使用Tobit面板来测量回归模型,解决科技创新效率的限制从属变量问题。
| $ \begin{array}{l} \mathrm{IE}_{\mathrm{it}}=\beta_{0}+\beta_{1} \mathrm{LNGDP}_{i {\rm{t}}}+\beta_{2} \mathrm{INEUS}_{i {\rm{t}}}+\beta_{3} \mathrm{LNPOPU}_{i {\rm{t}}}+\beta_{4} \mathrm{URBAN}_{i {\rm{t}}}+\beta_{5} \mathrm{FORIN}_{i {\rm{t}}}+ \\ \;\;\;\; \beta_{6} \mathrm{R} \& \mathrm{D}_{i {\rm{t}}}+\varepsilon_{i} \end{array} $ | (6) |
式中,IEit是长江经济带i省市t年的科技创新效率,βj(j=1,2,…,11)是参数,εi是误差项。根据最大似然法则,由Statia12.0测算得到的Tobit模型回归数据成果在表 5当中进行显示。
| 表 5 长江经济带11省市2008—2019年科技创新效率影响因素回归结果 |
根据回归结果得知,各变量在5%的水平下通过了有效性测试。在变量体系中除了产业结构和区域科技创新效率之间为负相关外,所有其他各项变量在与科技创新效率的关联性方面均呈现出正相关关系,其中,研发资金对科技创新效率影响最大。可见,投资科研是提升科技创新效率的关键实施基点,其对我国各省市区的科技创新效率提升产生直接促进效应。同时,区域GDP与科学技术创新效率有很大关联,区域科学技术创新效率和经济发展水平之间具有显著的一致性。区域生产总值的增长,不仅有助于改善实施科学技术创新的基础设施,而且有利于科学技术的实践运用,最终实现科技创新效率的提升。此外,区域的就业水平与科技创新效率正相关,这可能是因为就业人口数量的提升有利于人力资源产生较高水平的积累,这不仅有利于优化人力资源体量,而且有利于更多人力资源进行创新实践。城市化水平与科技创新效率之间存在正相关关系,这是因为城市化发展涵盖了城市基础设施条件优化完善和其他软件与硬件改进等,其对于地区科技创新效率提升展现出显著的促进作用。外国投资与科技创新效率正相关,表明在积极引进外资和产业转移的过程中,各地区正在向发达国家积极学习有效利用科学技术创新的先进经验。通过在地区产业结构的动态转变与科技创新效率之间的负相关关系可知,科技的创新实践能够对产业结构的变革发展产生推进作用,同时提示在经济发展中提高第三产业的比例,能够对科技创新效率水平的提升产生有效作用。
二、科技创新对长江经济带经济发展的影响作用总体看,科学技术创新在经济发展质量和效益的水平提升过程中具有关键的导向性影响。长江经济带跨越我国东、中、西部的主要地区,是国家发展战略的关键引领区域,其中蕴藏了巨大的发展可能性。自我国创新驱动战略提出并纳入实践运行以来,位于我国长江经济带的地区在科技创新水平上逐步呈现出阶梯状分布,并且各省份间的科技创新能力逐步呈现出明显的相关性。2019年,我国长江经济带科研经费将近7 030亿元,约为国内GDP的2.49%,相较于2018年实现了0.07%的增长。由此可以看出我国政府重视科技创新的程度。长江经济带的经济增长水平高于全国平均经济增长水平,但仍然存在一些问题,即尚未实现协调性的经济发展,与我国倡导的高质量经济发展模式尚有一定的距离。
我国学术界众多学者对科技创新与经济发展之间的关联性进行了广泛的研究。文献[20]在研究中运用广义定义上的生产函数模型,针对国内经济投资所产生的经济发展成效进行了研究分析,提出科技投资能够显著推动经济水平的提升。文献[21]利用研发资源指标体系对我国吉林省的科技创新投资规模和强度进行了分析论证。文献[22]基于创新科研驱动链,针对我国地区科研创新体系的分布格局进行了分析研究,认为国内科研创新体系现阶段整体开发水平不高,各地区之间的协调发展不足。文献[23]基于体系发展视角,提出国内科研创新对国内经济发展的推动成效不是非常显著,这一领域还有很大的提升空间,具体要依靠优化创新资源的配置来实现。文献[24]研究了以投资和出口为导向的经济主导区域开发模式的基本特性,得出了科学技术创新能力的地域差距高于目前经济发展水平地域差距的结论。文献[25]通过生产函数模型验证了科技创新对地区经济发展水平的贡献度,认为科学技术创新投资对经济发展的贡献率正在上升,并使用耦合协调度模型对科技创新和经济发展之间关系的进化进行了研究。
基于以往学术研究成果,本文从科学技术投入力、科技生产力、科技创新环境三个方面研究科技创新对长江经济带经济发展的影响,深入分析科学技术创新对经济发展水平的影响,并提出了相应政策建议。
(一) 模型设定与数据说明为进一步研究科技创新与经济发展之间影响效应,本文采用通用的Cob-Douglass生产函数实施研究分析。C-D生产函数是美国的Cobb和Douglas用于计算技术对经济发展水平产生贡献成效的模型。传统典型公式如下:
| $ Y_{i {\rm{t}}}=A\left(C_{i {\rm{t}}}\right)^{\alpha}\left(L_{i {\rm{t}}}\right)^{\beta}\left(T_{i {\rm{t}}}\right)^{\chi} $ | (7) |
其中,Yit是生产的合计值,Cit、Tit、Lit分别表示资本投入、科技创新投入和劳动投入。α、χ、β分别表示各自的弹性系数。
以典型传统Cob-Douglas生产函数为研究基础,本文采用自然对数构建法对公式进行两侧取值实施,由此构建回归公式如下:
| $ \ln Y_{i \mathrm{t}}=\ln A+\alpha \ln C_{i \mathrm{t}}+\beta \ln L_{i {\rm{t}}}+\chi \ln T_{i {\rm{t}}}+\mu_{i {\rm{t}}} $ | (8) |
在公式中,μit是随机误差项,变量Y、C、L和T的测量指标是地区GDP、固定资本投资、总就业人数和科技创新。研究将从三方面对科技创新与地区经济发展水平之间的影响效应进行分析:(1)科技投资强度,用R&D资金内部支出与地区GDP的比例衡量;(2)科技生产能力,用国内三项专利授权量衡量;(3)科技创新环境,用技术市场合同周转率衡量。
(二) 实证检验与结果分析使用基于C-D生产函数的测算模型,并运用stata12.0软件,针对2008—2019年长江经济带各省市进行相关数据的定量实证研究分析。首先,根据模型的内部数学处置,各变量成为自然对数,不均匀分散的影响被大幅度排除。其次,变量的分散扩展系数VIF值小于10,表示没有多重共线性。最后,面板设置F检定的P值为0,由此显示个体效果非常明显。使用Hausman检验对固定效应模型和随机效应模型进行适当性比较时,P值在5%的水平上被排除应用固定效应模型。鉴于此,本文在研究分析中采用随机效应模型。表 6显示了上述数据的定量实证分析结果。模型1—模型3分别研究了科技投入水平、科技生产能力、科技创新环境对经济发展的影响。模型4是对影响经济发展三个因素综合效果的综合考察。回归分析的结果表明,经济发展受科学技术创新的影响很大,但如果科技创新的指标不同,则对经济发展的影响也不同。
| 表 6 长江经济带科技创新对经济发展的影响回归结果 |
第一,科技创新投资促进了长江经济带经济的发展。科技创新投资的弹性模量为0.338 8,即科技投资每增加1%,经济增长率增加0.34%。科技创新投资水平表现为研究开发资金运用,研究开发资金的内部支出主要用于该地区的基础科学研究。资金集中度越高,对经济发展越有贡献,在1%的水平上越显著。
第二,科技生产能力对经济发展有积极影响,且存在显著的正向关系。现阶段,科技创新投入的弹性模量为0.287 7,这表明科技生产能力每增强1%,经济增长率就增加0.28%。
第三,科技创新环境对经济发展有积极影响,但不显著。目前,科技创新投资的弹性模量为0.033 4,表明科技创新环境每改善1%,经济增长率就增加0.03%。科技创新环境用技术市场合同的交易量来表示,相关数据表明,技术市场契约周转率越高,科技创新环境越活跃,对于经济水平的发展就愈加有益。但是,其结果显示,影响成效并不大,由此说明长江经济带的科技创新环境还不是十分成熟,仍有改善的余地。
三、结语本文基于超高效数据包络分析法和主成分分析法,进行了PCA-SE-DEA组合模型的建构。通过分析和研究长江经济带11个省市科技创新效率的进化规律和影响因素,得出相关结论:第一,长江经济带11个省市的平均科技创新效率略低于全国平均水平。其中,江苏、上海、浙江等省市科技创新效率最高,云南和贵州的科技创新效率较低。第二,长江经济带科技创新效率在2016年以后表现出显著的发散趋势,区域科技创新的一般低效性进一步显现,长江中游及上游省市科技创新的追赶效果明显,为了缩小与长江下游科技创新效率的差距,在未来的发展进程中仍然需要进一步强化创新导向。第三,经济发展水平、就业人数、城市化率、外国投资、研究开发费用等要素会给科技创新效率提升带来巨大的正面效果,但是产业结构变化会对科技创新的效率产生负面影响。
为了积极推进长江经济带创新主导建设,全方位提升长江经济带科技创新成效,长江经济带沿线省市可以采取以下专项优化发展措施:第一,提高科技创新资源的输入输出比例,促进产业结构不断优化和升级。第二,全面改革和创新,深化落实推进创新经济建设,加大产业转移实施力度,最大限度地利用科技创新成果。第三,长江经济带11个省市应全面加强协调,打破行政区域限制和地区保护主义的制约。第四,通过建立跨地区科技创新治理机制、跨行业合作创新机制等,在整体流域上打造良好创新创业氛围,最终实现长江经济带科学科技创新效率的总体改善。
基于以上结论,本文对相关政策的制定提出以下建议以供参考。
一是提升长江经济带的科技创新能力。首先,扩大对上海的支持,建设具有世界影响力的综合性科学中心,发挥东部地区的主导作用。其次,加强城市科技创新基础,有效促进合肥综合性国家科学中心建设,强化城市辐射运行功能。再者,充分发挥西部地区在共建“一带一路”中的科技创新合作主导作用,开掘创新资源,提高创新能力。最后,长江经济带的所有地区应加强创新资源流动,打破区域系统和机制壁垒,实现东部、中部、西部地区的协调开发,缩小区域差距,促进区域整体创新水平的高品质改善。
二是全面深化科技系统改革和经济社会改革,依靠科学技术推进经济发展。第一,加强相关经济建设法律法规的有效实施,确保科学技术成果的有效应用推广;第二,建立高质量的“创新链”,加强各类创新项目之间的合作;第三,加强产学研结合,促进科技创新与高质量经济发展的深度融合。
三是改进科技创新系统,支持高质量经济发展。首先,基于国家科技创新计划,改进相关创新体系;其次,应注重人才资源体系建设,支持科技人才培养;再次,应加强学科基础研究和应用基础研究;最后,要增加科技创新投资,提高创新资源分配效率,激活科技创新和创业精神,改进科技创新和经济发展支持。
| [1] |
吴传清, 黄磊, 文传浩. 长江经济带技术创新效率及其影响因素研究[J]. 中国软科学, 2017(5): 160-170. DOI:10.3969/j.issn.1002-9753.2017.05.016 |
| [2] |
黄磊, 吴传清. 长江经济带工业绿色创新发展效率及其协同效应[J]. 重庆大学学报(社会科学版), 2019, 25(3): 1-13. |
| [3] |
吴传清, 董旭. 环境约束下长江经济带全要素能源效率研究[J]. 中国软科学, 2016(3): 73-83. DOI:10.3969/j.issn.1002-9753.2016.03.007 |
| [4] |
路小静, 时朋飞, 邓志伟, 等. 长江经济带旅游业绿色生产率测算与时空演变分析[J]. 中国人口·资源与环境, 2019, 29(7): 19-30. |
| [5] |
习明明. 长江经济带创新环境对科技创新效率影响的实证研究[J]. 江西财经大学学报, 2019(3): 19-29. |
| [6] |
卢丽文, 宋德勇, 李小帆. 长江经济带城市发展绿色效率研究[J]. 中国人口·资源与环境, 2016, 26(6): 35-42. DOI:10.3969/j.issn.1002-2104.2016.06.005 |
| [7] |
刘明玉, 袁宝龙. 环境规制与绿色创新效率的空间异质效应:基于长江经济带工业企业数据[J]. 财会月刊, 2018(24): 144-153. |
| [8] |
吴传清, 黄磊. 长江经济带工业绿色发展效率及其影响因素研究[J]. 江西师范大学学报(哲学社会科学版), 2018, 51(3): 91-99. DOI:10.3969/j.issn.1000-579X.2018.03.014 |
| [9] |
易明, 程晓曼. 长江经济带城市绿色创新效率时空分异及其影响因素[J]. 城市问题, 2018(8): 31-39. |
| [10] |
杜宇, 黄成. 长江经济带高技术制造业创新效率时空格局演变研究[J]. 科技进步与对策, 2019, 36(21): 35-42. |
| [11] |
黄磊, 吴传清. 长江经济带城市工业绿色发展效率及其空间驱动机制研究[J]. 中国人口·资源与环境, 2019, 29(8): 40-49. |
| [12] |
廖继胜, 刘志虹, 郑也夫. 文化制造业的科技金融支持效率及其影响因素研究:基于长江经济带省际面板数据[J]. 江西社会科学, 2019, 39(10): 37-49, 254. |
| [13] |
杨仁发, 杨超. 长江经济带高质量发展测度及时空演变[J]. 华中师范大学学报(自然科学版), 2019, 53(5): 631-642. |
| [14] |
黄庆华, 时培豪, 胡江峰. 产业集聚与经济高质量发展:长江经济带107个地级市例证[J]. 改革, 2020(1): 87-99. |
| [15] |
袁茜, 吴利华, 张平. 长江经济带一体化发展与高技术产业研发效率[J]. 数量经济技术经济研究, 2019, 36(4): 45-60. |
| [16] |
王圣云, 林玉娟, 罗玉婷. 长江经济带科技创新效率变化的指数分解及聚类分析[J]. 华东经济管理, 2018, 32(9): 66-72. |
| [17] |
胡艳, 汪徐. 长江经济带产业结构优化对区域创新绩效的影响差异分析[J]. 科技管理研究, 2019, 39(14): 86-93. |
| [18] |
余淑均, 李雪松, 彭哲远. 环境规制模式与长江经济带绿色创新效率研究:基于38个城市的实证分析[J]. 江海学刊, 2017(3): 209-214. |
| [19] |
李雪松, 张雨迪, 孙博文. 区域一体化促进了经济增长效率吗:基于长江经济带的实证分析[J]. 中国人口·资源与环境, 2017, 27(1): 10-19. |
| [20] |
龚艳, 张阳, 唐承财. 长江经济带旅游业效率测度及影响因素研究[J]. 华东经济管理, 2016, 30(9): 66-74. |
| [21] |
高红贵, 赵路. 长江经济带产业绿色发展水平测度及空间差异分析[J]. 科技进步与对策, 2019, 36(12): 46-53. |
| [22] |
汪克亮, 刘悦, 史利娟, 等. 长江经济带工业绿色水资源效率的时空分异与影响因素:基于EBM-Tobit模型的两阶段分析[J]. 资源科学, 2017, 39(8): 1522-1534. |
| [23] |
周杰文, 蒋正云, 李凤. 长江经济带绿色经济发展及影响因素研究[J]. 生态经济, 2018, 34(12): 47-53, 69. |
| [24] |
崔学海, 王崇举, 曾波. 基于DEA-Tobit的长江经济带技术转移金融支持效率研究[J]. 统计与信息论坛, 2019, 34(9): 77-84. |
| [25] |
游达明, 黄曦子. 长江经济带省际工业生态技术创新效率评价[J]. 经济地理, 2016, 36(9): 128-134. |
 2021, Vol. 27
2021, Vol. 27

