2. 重庆大学 经济与工商管理学院, 重庆 400044
2. School of Economics and Business Administration, Chongqing University, Chongqing 400044, P. R. China
2020年中国GDP总量突破100万亿元,和1978年比绝对数增长了276倍,改革开放40多年来经济增长取得了举世瞩目的成就。伴随着高增长,资源耗竭和环境污染成为制约中国经济可持续发展的重要阻力,尤其是资源分布不均、利用方式粗放等一系列问题凸显,现阶段中国经济由高速增长阶段转向高质量发展,环保、资源节约、循环经济等概念被纳入“生态文明”,同时提出节约资源是保护生态环境的根本之策。不少学者对资源与经济发展之间的关系以及产生悖论的原因从不同的角度给予了解释。然而中国地域广阔,同时影响经济发展的因素复杂,使得中国地区之间经济发展水平差异较大,而且呈现出自然资源较丰富的中西部地区的发展落后于自然资源较为贫乏的东部地区的特征。那么如何在兼顾经济增长的同时尽可能实现资源节约,协调好资源对经济增长的数量控制型约束和质量控制型约束,使资源与经济增长实现可持续发展是本文研究的重点。
资源对经济增长是“诅咒”还是“福音”,不同学者有不同的看法。Corden和Neary发现了“荷兰病”(Dutch disease)现象,使人们开始关注资源对经济发展的双向因果关系[1];Auty在研究影响产矿国经济发展的因素时注意到“丰富的自然资源非但没有促进经济的增长反而有可能会阻碍经济的发展”[2];徐康宁和王剑是国内较早系统关注资源对经济增长的影响的学者,他们认为丰裕的自然资源在经济发展中未能发挥优势的主要原因是过度开采引发的制造业衰退和制度问题[3];李天籽研究了资源丰裕度对经济产生影响的传导机制[4];邵帅等发表一列文章从不同角度和研究对象入手论证了自然资源对经济发展存在某些挤出效应,从而影响了经济的增长[5-7];其他有代表性的学者包括于立和于左[8]、谢波和陈仲常[9]、孙永平和叶初升[10]、董利红和严太华[11]、李虹和邹庆[12]、周黎和李程宇[13]。已有研究多从“荷兰病”与反工业化假说、制度质量与寻租、自然资源对知识的挤出效应等视角研究资源与经济增长之间的关系。本文利用1997—2017年除西藏外的30个省际面板数据,采用非线性平滑转换回归模型,针对中国不同区域的经济特征对资源与经济增长之间的传导机制进行深入分析,期望更清楚地展现传导机制对资源和经济增长之间的影响路径与程度。本文在以下两个方面区别于已有文献:(1)采用非线性面板平滑转换回归模型(PRST),考虑了模型中不可观测的异质性,能够更丰富地刻画经济体的行为特征,揭示资源制约中国不同区域经济发展的深层次原因。(2)全面考察了不同省份技术投入、人力资本、产业结构、制造业的投入与对外开放度等经济因素在资源依赖与经济增长关系中的内在传导机制,并深入分析了不同经济因素水平下资源依赖对经济增长影响的差异程度。在资源约束下针对中国区域经济的发展现状分析资源诅咒现象产生的机理以及深层次原因,不仅是研究资源配置微观方面的重要内容,而且对中国经济的长远发展与制度优化改革具有借鉴意义。
一、研究设计 (一) 模型设定与检验 1. 面板平滑转换模型的设定本文借鉴Granger和TerTeräsvirta[14]、Teräsvirta[15]提出的面板平滑转换模型(The Panel Smooth Transition Regression,PSTR)来揭示资源、经济增长以及中间传导因素之间的非线性关系。那么,含有一个转换函数的PSTR可表示为:
| $ {y_{i{\rm{t}}}} = {\mu _i} + {\beta '_0}{x_{i{\rm{t}}}} + {\beta '_1}{x_{i{\rm{t}}}} \cdot g({q_{i{\rm{t}}}}, \gamma , \mathit{c}{\rm{) + }}{\varepsilon _{i{\rm{t}}}}, i = 1, \cdots , N;{\rm{t}} = 1 \cdots {\rm{T}} $ | (1) |
其中,i表示截面个体,t表示时间维度。g(qit, γ, c)为取值介于0~1之间连续变化的转换函数;转换变量qit是导致yit由一种变化转变为另一种变化的变量;参数γ决定了转换速度;c为转换发生的位置参数,c=(c1, …, cm)且c1≤…≤cm;μi为个体固定效应;εit为残差项。依据Granger和Teräsvirta[14]、Teräsvirta[15]假设转化函数为一个广义logistic函数即对数转换函数:
| $ g({q_{i{\rm{t}}}}, \gamma , c) = {\left( {1 + \exp \left\{ { - \gamma \prod\limits_{j = 1}^m {\left( {{q_{i{\rm{t}}}} - {c_j}} \right)} } \right\}} \right)^{ - 1}}, {c_1} \le \cdots \le {c_m}, \gamma > 0 $ | (2) |
当m=1,γ=1,转换函数的形式为对数平滑转化,且当转换函数g(qit, γ, c)=0时,对应的模型退化为线性面板模型,表现为低体制;当g(qit, γ, c)=1时,对应的模型退化为一个多元面板回归模型,表现为高体制;当g(qit, γ, c)的值在0与1之间平滑转换,则体现了式(1)的系数以c为中心随着qit的变化在β0和β0+β1间平滑转换,研究的变量在高低两种不同体制β0和β0+β1间平滑转换。对于m>1,如m=2,γ=1时,转换函数的形式为指数平滑转化,当转换函数值为1时,称为外机制;当qit=(c1+c2)/2时,转换函数值达到最小值,称对应的机制为中间机制。
可以将基本的两体制模型进一步推广为多体制PSTR模型:
| $ {y_{i{\rm{t}}}} = {\mu _i} + {\beta '_0}{x_{i{\rm{t}}}} + \sum\limits_{j = 1}^r {{{\beta '}_j}{x_{i{\rm{t}}}} \cdot {g_j}\left( {q_{i{\rm{t}}}^j, {\gamma _j}, {c_j}} \right) + {\varepsilon _{i{\rm{t}}}}, i = 1, \cdots , N;{\rm{t = 1, }} \cdots {\rm{, }}\mathit{T}{\rm{;j = 1, }} \cdots {\rm{, }}\mathit{r}} $ | (3) |
其中,转换函数为gj(qitj, γj, cj)为式(2)所示的logistic函数。
2. 面板平滑转换模型的同质性检验由于面板平滑转换回归模型要求数据存在个体异质性,因此需要先对数据进行同质性检验。借鉴前人研究,可以通过检验H0:γ=0是否成立来确定数据是否存在个体异质性。同时该检验还可以进一步用于确定每个模型对应的m值。借鉴前人将g(qit, γ, c)在γ=0处进行一阶泰勒展开,得到辅助回归方程:
| $ {y_{i{\rm{t}}}} = {\mu _i} + {\beta }{_0^{' *} }{x_{i{\rm{t}}}} + {\beta }{_1^{' *} }{x_{i{\rm{t}}}}{q_{i{\rm{t}}}} + \cdots + {\beta }{_m^{' *} }{x_{i{\rm{t}}}}q_{i{\rm{t}}}^m + \varepsilon _{i{\rm{t}}}^ * $ | (4) |
其中
| $ {\rm{L}}{{\rm{M}}_{{x^2}}} = \frac{{TN({\rm{SS}}{{\rm{R}}_0} - {\rm{SS}}{{\rm{R}}_1})}}{{{\rm{SS}}{{\rm{R}}_0}}} $ | (5) |
| $ {\rm{L}}{{\rm{M}}_F} = \frac{{TN({\rm{SS}}{{\rm{R}}_0} - {\rm{SS}}{{\rm{R}}_1})/\mathit{mk}}}{{{\rm{SS}}{{\rm{R}}_1}/(TN - N - mk)}} $ | (6) |
当面板数据存在异质性时,则考虑建立一个面板平滑转换模型,其转换速度为γ和位置参数为c,通常利用网格搜索法进行估计,通过迭代使得残差平方和最小时即为最优估计:
| $ {\left( {\gamma , c} \right)^\prime } = \arg \mathop {\min }\limits_{\left( {\gamma , c} \right)} \frac{1}{{NT}}\sum\limits_{i = 1}^N {\sum\limits_{{\rm{t = 1}}}^T {{{\left( {y_{i{\rm{t}}}^ * - {\beta ^{'\left( j \right)}}x_{i{\rm{t}}}^ * \left( {\gamma , c} \right)} \right)}^2}} } $ | (7) |
考虑数据的可得性和样本容量的充足性,本文利用中国大陆除西藏外的30个省、直辖市、自治区1997—2017年面板数据为考察对象,数据主要来源于中国统计年鉴、中国工业经济统计年鉴、中国能源统计年鉴等。涉及的指标有人均gdp、资源依赖度rd、资源丰裕度ra、技术创新tech、人力资本h、产业结构is、制造业的投入水平manu、对外开放度open等(具体含义见表 1)。
| 表 1 变量的定义 |
将技术投入水平tech、人力资本h、产业结构is、制造业的投入水平manu、对外开放度open等考虑为“资源诅咒”产生的内在机制,在模型中作为转换函数的转换变量qit,检验如何通过转换函数影响资源与经济增长的关系。
二、数据分析与结果 (一) 变量的描述性统计中国经济发展不均衡,资源丰裕度和资源依赖度的地区差异严重。在各传导因素中,各地区技术投入水平、人力资本、产业结构、制造业投入水平、对外开放程度差异均较大。利用同时处理组内自相关与组间同期相关的可行广义最小二乘法(FGLS),先分别估计资源依赖度和资源丰裕度对经济增长的影响;再估计二者同时作用于经济增长的情况;最后添加影响经济增长的其他变量,进行“资源诅咒”效应的存在性检验。估计结果见表 2。
| 表 2 “资源诅咒”效应的存在性检验 |
由表 2可知,资源依赖度与经济增长负相关,资源丰裕与经济增长正相关。在二者同时作用的情况下,资源依赖度与经济增长在1%显著性水平上负相关,阻碍作用进一步增强;在各经济影响因素的共同作用下,资源依赖系数为-0.003 7,变得不再具有显著性。这说明资源依赖度仍然是阻碍经济增长的原因,“资源诅咒”效应存在而且在一定程度上通过技术投入水平、人力资本、产业结构、制造业的投入水平、对外开放程度等传导机制发挥作用。
(二) 单因素PSTR模型分析结合客观经济环境,为了考察各个传导因素在资源与经济增长关系中的影响程度,分别设定技术投入水平tech、人力资本h、产业结构is、制造业的投入水平manu、对外开放度open等5个影响资源依赖度的中间传导因素作为模型转换变量的面板平滑转换模型。资源依赖度rd为解释变量,人均gdp为被解释变量。那么相对应单因素PSTR模型构建如下:
| $ {\rm{gd}}{{\rm{p}}_{i{\rm{t}}}} = {\mu _i} + {\beta _0}{\rm{r}}{{\rm{d}}_{i{\rm{t}}}} + {\beta _1}{\rm{r}}{{\rm{d}}_{i{\rm{t}}}} \cdot g\left( {{\rm{tec}}{{\rm{h}}_{i{\rm{t}}}}, \gamma , c} \right) + {\varepsilon _{i{\rm{t}}}} $ | (8) |
| $ {\rm{gd}}{{\rm{p}}_{i{\rm{t}}}} = {\mu _i} + {\beta _0}{\rm{r}}{{\rm{d}}_{i{\rm{t}}}} + {\beta _1}{\rm{r}}{{\rm{d}}_{i{\rm{t}}}} \cdot g\left( {{{\rm{h}}_{i{\rm{t}}}}, \gamma , c} \right) + {\varepsilon _{i{\rm{t}}}} $ | (9) |
| $ {\rm{gd}}{{\rm{p}}_{i{\rm{t}}}} = {\mu _i} + {\beta _0}{\rm{r}}{{\rm{d}}_{i{\rm{t}}}} + {\beta _1}{\rm{r}}{{\rm{d}}_{i{\rm{t}}}} \cdot g\left( {i{s_{i{\rm{t}}}}, \gamma , c} \right) + {\varepsilon _{i{\rm{t}}}} $ | (10) |
| $ {\rm{gd}}{{\rm{p}}_{i{\rm{t}}}} = {\mu _i} + {\beta _0}{\rm{r}}{{\rm{d}}_{i{\rm{t}}}} + {\beta _1}{\rm{r}}{{\rm{d}}_{i{\rm{t}}}} \cdot g\left( {{\rm{man}}{{\rm{u}}_{i{\rm{t}}}}, \gamma , c} \right) + {\varepsilon _{i{\rm{t}}}} $ | (11) |
| $ {\rm{gd}}{{\rm{p}}_{i{\rm{t}}}} = {\mu _i} + {\beta _0}{\rm{r}}{{\rm{d}}_{i{\rm{t}}}} + {\beta _1}{\rm{r}}{{\rm{d}}_{i{\rm{t}}}} \cdot g\left( {{\rm{ope}}{{\rm{n}}_{i{\rm{t}}}}, \gamma , c} \right) + {\varepsilon _{i{\rm{t}}}} $ | (12) |
就本文而言,这种平滑转换的经济意义可表述为:转换变量在较低水平区间和较高水平区间分别对应着两种不同的资源依赖度对经济发展水平的影响程度,随着“转换变量”从较低阶段向较高阶段的发展,资源依赖度对经济发展水平的影响表现出非线性的结构变化。
1. 模型的非线性检验首先对模型进行线性检验,只有当变量之间存在一种非线性关系时,面板平滑转换模型才是可识别的。检验的原假设H0:面板数据模型是不存在异质性的线性模型(r=0);备择假设H1:面板数据模型是至少存在一个转换函数的非线性模型(r=1)。若原假设H0被拒绝,则说明γ≠0,模型(1)为非线性模型。检验结果见表 3
| 表 3 模型1—5非线性检验 |
由非线性检验结果可知:模型1—模型5对应的LM、LMF统计量均在1%的显著性水平下拒绝原假设,表明分析的数据有较强的截面异质性,即资源依赖通过传导机制的作用对经济增长效应具有明显的非线性特征。
2. 序贯检验确定m值根据序贯检验的结果确定m值。设定原假设:H0*: β1*=β2*=β3*=0;H03*: β3*=0;H02*: β2*=0/β3*=0;H01*: β1*=0/β3*=β2*=0。如果H02*被最强拒绝,对应的p值最小,则选取m=2,否则选取m=1。通过序贯检验可知,以转换变量制度质量、产业结构、制造业投入水平对应的模型中的转换函数的m值取2,技术投入水平、人力资本投入、对外开放度对应的模型中的转换函数的m值取1,如表 4。
| 表 4 模型1—5序贯检验确定m值 |
尽管两体制的PSTR模型基本上反映了资源依赖对经济增长的非线性影响,为了提高对模型的评估效果,在两体制PSTR模型的基础上进一步建立多体制的PSTR模型。需要先进行非保留异质性检验,确定r的取值。当r=1时,为两体制PSTR模型;r=2时,为三体制PSTR模型,如表 5。
| 表 5 模型1—5非保留异质性检验 |
由表 5可知,模型1、3、4选用两体制的PSTR模型是合适的,但是模型2、5需要选用具有两个转换变量的三体制PSTR模型。
4. PSTR模型估计结果通过PSTR模型在参数估计过程中,运用Matlab 2010统计软件,采用网格搜索法,反复抽样10 000次,模型1的最优位置参数为1个,模型2、3、4、5的最优位置参数为2个。估计结果见表 6。
| 表 6 模型1—5最终估计结果 |
由表 6可知,各传导因素在不同阶段对资源依赖与经济增长效应的影响显著不同。图 1—图 5比较直观地反映了各因素的传导效应。
|
图 1 技术投入水平 |
|
图 2 人力资本 |
|
图 3 产业结构 |
|
图 4 制造业投入水平 |
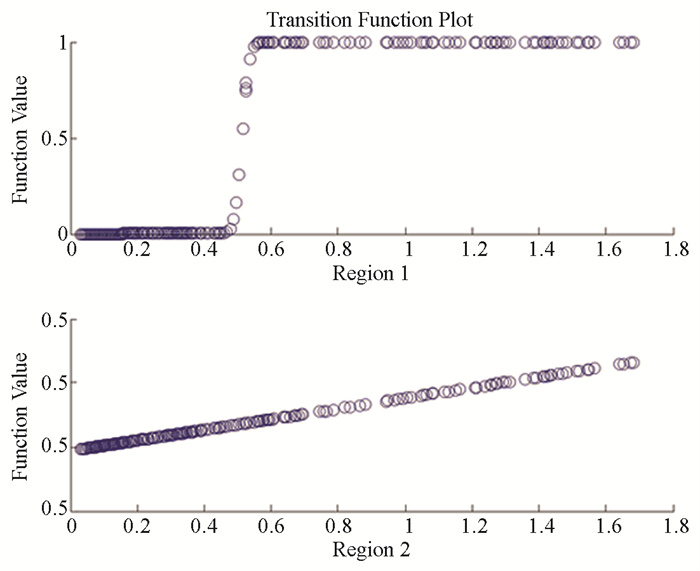
|
图 5 对外开放程度 |
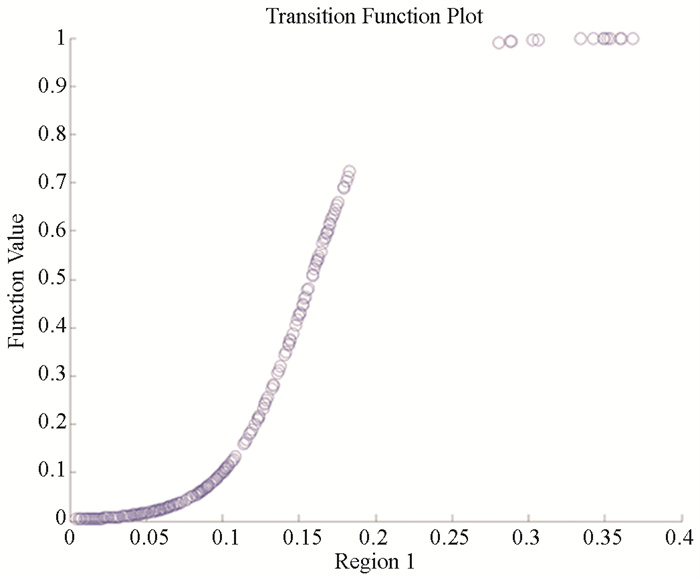
第一,模型1是以技术投入水平为转换变量的两体制模型。模型含有一个位置参数,技术投入水平和经济增长正相关。当技术投入水平tech>0.158时,模型趋于高体制;当tech<0.158时,模型趋于低体制。位于门限值之上的观测值有61个,位于门限值之下的观测值有569个,分别占观测值的9.68%和90.32%。大部分观测值位于门限值以下,随着技术投入水平的变换,资源对经济增长的作用在高低体制之间平滑转换。此外,转换函数对应的平滑参数为37.816,表明模型在门限值前后转换速度较慢,呈现平滑渐进的变化趋势。模型1表明在技术水平投入较高的地区,资源依赖对经济增长的阻碍作用小,而在技术水平投入较低的地区,资源依赖对经济增长的阻碍作用大。技术投入水平较高的地区有北京、天津、上海、江苏、浙江、山东、广东等地,而在资源诅咒现象较严重的地区技术投入水平普遍较低。
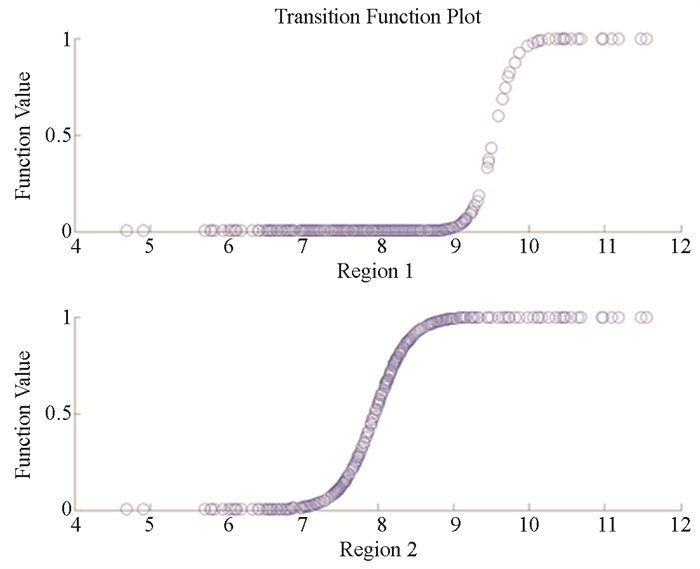
第二,模型2是以人力资本为转换变量相对复杂的三体制模型。包含了两个转换函数,每个转换函数对应一个位置参数和转换速度。第一个转换函数的位置参数为9.539 6,转换速率为7.284 4;第二个转换函数的位置参数为7.966 4,转换速率为4.43。所以当7.966 4<h<9.539 6时,模型处于中间体制。当h<7.966 4或者h>9.539 6时,模型处于外体制。第一个转换函数的系数β1=20.007 3,第二个转换函数的系数β2=2.182。当h<7.966 4时,处于外体制,转换函数g(hit, γ, c)≈1,对应的资源依赖的经济增长系数为β0+β2;当h>9.539 6时,模型亦处于外体制,转换函数g(hit, γ, c)≈1,对应的资源依赖的经济增长系数为β0+β1;当7.9664<h<9.539 6,模型处于中间体制,对应的资源依赖的经济增长系数为β0。参数β1和β2的系数均为正,说明人力资本的投入与经济增长的效应正相关,即人力资本的投入越高经济增长对资源依赖的作用越小,人力资本的投入越低经济增长对资源的依赖作用越强。在630个观测值中,h<7.966 4的观测值有216个,占全部观测值的34.29%;7.966 4<h<9.539 6的观测值有369个,占全部观测值的58.57%;h>9.539 6的观测值有45个,占全部观测值的7.14%,而且主要集中在北京、上海、天津。结合图 2可知,模型在两个门槛值前后的转换均呈现平滑渐进变化的趋势,第一个门槛值7.966 4附近较第二个门槛值9.539 6附近的转换速度稍慢。说明人力资本结构大于9.539 6时,对经济增长的影响效果更加明显。
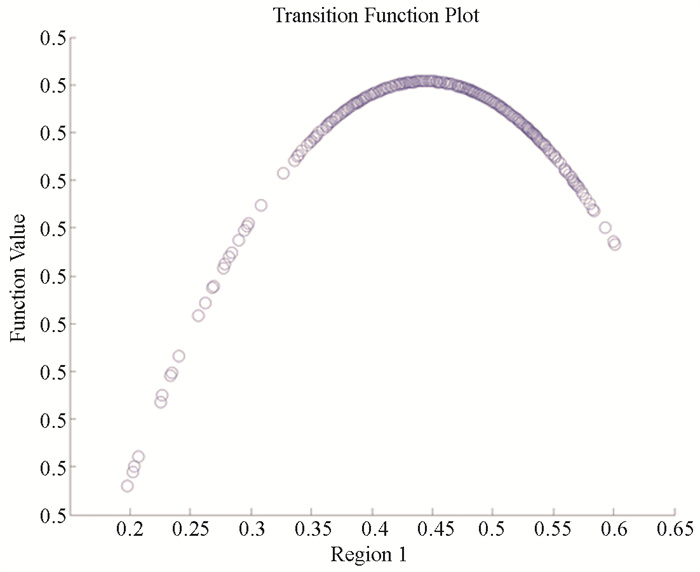
第三,模型3是以产业结构为转换变量的两体制模型。产业结构对经济增长的影响表现出趋于对称的双门限特征。当产业结构is<0.421 1及is>0.467 8,处于外体制,转换函数g(instit, γ, c)≈1,从而对应的资源依赖的经济增长系数为β0+β1。当0.421 1<is<0.467 8时,处于中间体制,转换函数g(instit, γ, c)≈0,那么对应的资源依赖的经济增长系数为β0。参数β1的系数为负,说明在外体制时会形成一个替代效应。在630个观测之中,中间体制的样本观测量只有20个,仅占全部观测值的3.17%,外体制的样本观测量有610个,其中is>0.467 8的有432个,占全部观测量的68.54%。由模型的分析可知,在其他条件一定的情况下,第二产业产值越大的地区,资源依赖对经济增长会有一个替代效应,即依靠资源依赖而形成的第二产业产值大对经济的增长会有消极的作用。这就说明了,资源依赖性地区应该调整产业结构,减少资源依赖对经济产生的阻碍作用。
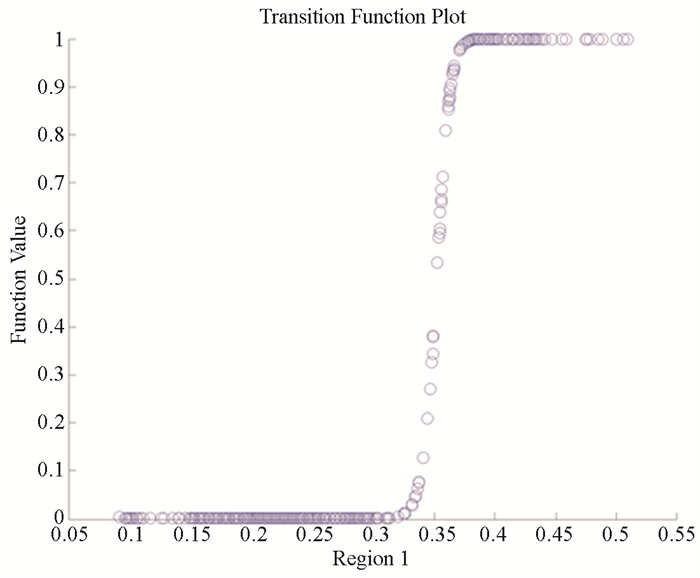
第四,模型4是以制造业投入水平为转换变量的两体制模型。制造业投入水平对经济增长的影响具有双门限特征并且是非对称的,包含了一个转换函数和两个位置参数。当制造业投入水平manu<0.056 3及manu>0.352 1,处于外体制,转换函数g(instit, γ, c)≈1,从而对应的资源依赖的经济增长系数为β0+β1。当0.056 3<manu<0.352 1时,处于中间体制,转换函数g(instit, γ, c)≈0,那么对应的资源依赖的经济增长系数为β0。在630个观测之中,中间体制的样本观测量有495个,占全部观测值的78.54%,外体制的样本观测量有135个,占全部观测量的21.46%,其中manu<0.056 3的观测个数为0,因此制造业投入水平对经济增长的影响可视为正相关。此外,模型转换函数对应的转换斜率为625.554 7,表明模型在门槛值前后转换的速度非常快。模型4说明,在其他条件不变的情况下,资源对经济增长的促进在制造业投入水平较高的地区更为突出。
第五,模型5是以对外开放水平为转换变量的三体制模型。包含了两个转换函数,每个转换函数对应一个位置参数和转换速度。第一个转换函数的位置参数为0.513 5,转换速率为103.132 5;第二个转换函数的位置参数为0.076 1,转换速率为0.003 4。所以当0.076 1<open<0.513 5时,模型处于中间体制。当open<0.076 1或者open>0.513 5时,模型处于外体制。当0.076 1<open<0.513 5时,对于其中一个转换函数来说是外体制,而对于另一个转换函数来说是中间体制,受到两个转换函数的交错影响。在630个观测值中,open<0.076 1的观测值有103个,占全部观测值的16.34%;0.076 1<open<0.513 5的观测值有404个,占全部观测值的64.12%;open>0.513 5的观测值有123个,占全部观测值的19.58%。对外开放水平较高的主要是福建、江苏、浙江、天津、上海、北京、广东。模型转换函数1对应的转换斜率为103.132 5,表明模型在门槛值前后转换的速度非常快。而转换函数2对应的平滑参数为0.003 4,模型呈现平滑渐进的转换趋势。同时参数β1和β2的系数均为正,说明对外开放水平与经济增长的效应正相关,即对外开放的水平越高经济增长对资源依赖的作用越小,对外开放的水平越低经济增长对资源的依赖作用越强。
(三) 多因素PSTR模型分析根据相关模型选择准则,最强地拒绝线性原假设的模型为最优。模型5中对外开放度(Wald Tests值为254.413)作为转换变量时和其他模型相比对应的Wald Tests最大,最强拒绝原假设,而且残差平方和最小,所以在5个转换变量中,对外开放度是资源依赖与经济增长关系中非线性效应最强的转换变量,模型5最优。在现实经济中,资源依赖度的诅咒效应受地区综合经济条件的影响。故在本节中考虑技术投入水平tech表示、人力资本h、产业结构is、制造业的投入水平manu、对外开放度open等5个影响因素作为解释变量建模,以对外开放度构建多因素PSTR模型6如下:
| $ \begin{array}{c} {\rm{gd}}{{\rm{p}}_{i{\rm{t}}}} = {\mu _i} + {\beta _0}{\rm{r}}{{\rm{d}}_{i{\rm{t}}}} + {\beta _1}{\rm{tec}}{{\rm{h}}_{i{\rm{t}}}} + {\beta _2}{h_{i{\rm{t}}}} + {\beta _3}{\rm{i}}{{\rm{s}}_{i{\rm{t}}}} + {\beta _4}{\rm{man}}{{\rm{u}}_{i{\rm{t}}}} + {\beta _5}{\rm{ope}}{{\rm{n}}_{i{\rm{t}}}} + \left( {{{\beta '}_0}{\rm{r}}{{\rm{d}}_{i{\rm{t}}}} + } \right.\\ \left. {{{\beta '}_1}{\rm{tec}}{{\rm{h}}_{i{\rm{t}}}} + {{\beta '}_2}{{\rm{h}}_{i{\rm{t}}}}{{\beta '}_3}{\rm{i}}{{\rm{s}}_{i{\rm{t}}}} + {{\beta '}_4}{\rm{man}}{{\rm{u}}_{i{\rm{t}}}} + {{\beta '}_5}{\rm{ope}}{{\rm{n}}_{i{\rm{t}}}}} \right)g\left( {{\rm{ope}}{{\rm{n}}_{i{\rm{t}}}}, \gamma , c} \right) + {\varepsilon _{i{\rm{t}}}} \end{array} $ | (13) |
| 表 7 模型6非线性检验 |
| 表 8 模型6序贯检验确定m值 |
| 表 9 模型6非保留异质性检验 |
对模型依次进行非线性检验、序贯检验和非保留异质性检验可知:在包含多个影响因素的模型中,制度质量作为转换变量,显著拒绝同质性原假设具有截面异质性,制度质量仍然是资源依赖影响经济增长的内在机制,可以用面板平滑转换模型来分析。
通过PSTR模型在参数估计过程中,运用Matlab 2010统计软件,采用网格搜索法,反复抽样10 000次,得到模型的最优位置参数为1个。最终估计结果如表 10和图 6。
| 表 10 模型6最终估计结果 |
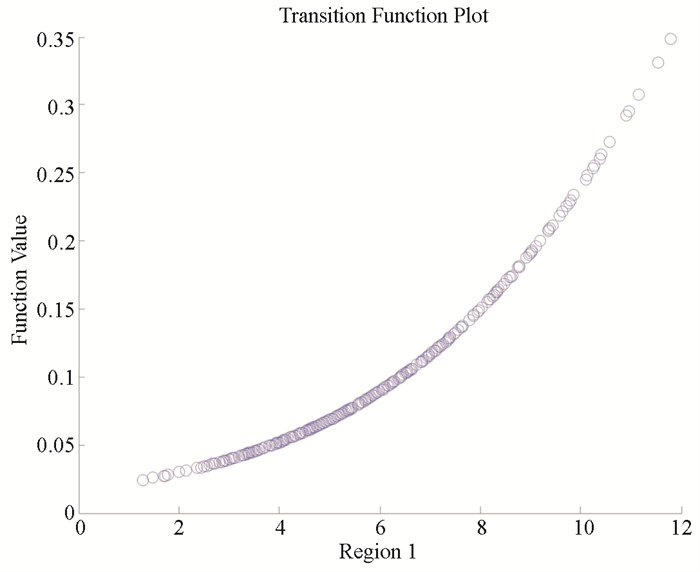
|
图 6 多因素 |
根据表 10的最终估计结果,这里可以发现估计系数大多数是显著的;相对于单因素模型,AIC、BIC值均有不同程度的降低且残差平方和SSR也大幅度降低,由此可知多因素面板平滑转换模型能够更好地解释模型所包含的经济含义。选取对外开放度作为转换变量反映资源依赖通过对外开放度作为传导机制对经济增长效应表现出的非线性特征。其中,技术投入水平、人力资本、产业结构、制造业的投入水平和对外开放度均显著影响了经济增长效应。以对外开放度的门限值1.694 5为界,模型将地区的经济增长效应分为高体制和低体制,并在二者之间平滑转换。在多因素共同的作用下,技术投入水平、人力资本、制造业投入水平以及对外开放度在地区处于高体制时表现为更好的经济增长效应。
三、结论与建议本文采用面板平滑转换模型,利用1997—2017年各省级面板数据,分析了技术投入水平、人力资本、产业结构、制造业投入水平、对外开放程度5个传导因素在资源依赖与经济增长效应中的非线性关系。在单变量的模型中,对资源和经济增长产生相对重要作用的传导机制是对外开放水平,多因素的面板平滑转换模型较单因素的模型更加优化,对经济现象的解释更加合理。结论与建议:(1)资源依赖对经济增长的效应随着各省份技术投入水平、人力资本、产业结构、制造业投入水平、对外开放程度的不同而明显不同,总的来说,在技术投入水平较高、人力资本水平较高、制造业投入和对外开放程度较高的地区,资源依赖对经济增长的阻碍作用较小,反之,资源依赖对经济增长的阻碍作用较大。(2)在其他条件一定的情况下,依靠资源依赖而形成的第二产业产值大对经济增长有一定的制约作用;在资源依赖较高的地区更应该注重调整产业结构,适应“新常态”,减少由于资源依赖而对经济产生的阻碍作用。(3)对外开放度是典型的影响资源依赖与经济增长的中间传导机制。由于资源行业的特殊性,各地区应该扩大对外开放的程度,加强交流,发挥资源在利用中通过后向关联和前向关联发挥联动优势,规避“资源诅咒”,促进经济的长期高质量增长。
由于数据的可获得性,本文仅研究了技术、人力资本、产业结构、制造业投入以及对外开放程度在资源依赖与经济增长效应中的影响,未能将研究范围延伸至资源利用效率、资源的生产结构和消费结构与经济增长的关系。对这方面的深入研究有利于全面把握资源约束下经济的长期可持续发展,将是进一步探索的重要方向。
| [1] |
CORDEN W M, NEARY J P. Booming sector and de-industrialisation in a small open economy[J]. The Economic Journal, 1982, 92(368): 825-848. DOI:10.2307/2232670 |
| [2] |
AUTY R M. Sustaining development in mineral economics: The resource curse thesis[M]. London: Routledge, 1993.
|
| [3] |
徐康宁, 王剑. 自然资源丰裕程度与经济发展水平关系的研究[J]. 经济研究, 2006(1): 78-89. |
| [4] |
李天籽. 自然资源丰裕度对中国地区经济增长的影响及其传导机制研究[J]. 经济科学, 2007(6): 66-76. |
| [5] |
邵帅, 齐中英. 西部地区的能源开发与经济增长: 基于"资源诅咒"假说的实证分析[J]. 经济研究, 2008(4): 147-160. DOI:10.3969/j.issn.1005-913X.2008.04.065 |
| [6] |
邵帅, 杨莉莉. 自然资源丰裕、资源产业依赖与中国区域经济增长[J]. 管理世界, 2010(9): 26-44. |
| [7] |
邵帅, 范美婷, 杨莉莉. 资源产业依赖如何影响经济发展效率: 有条件资源诅咒假说的检验及解释[J]. 管理世界, 2013(2): 32-63. |
| [8] |
于立, 于左. 资源枯竭型城市产业转型与社会稳定的关联度[J]. 改革, 2009(1): 37-42. |
| [9] |
谢波, 陈仲常. 自然资源、人力资本异质性与区域经济增长: 基于省际面板数据的经验分析[J]. 人口与经济, 2011(4): 35-44. |
| [10] |
孙永平, 叶初升. 自然资源丰裕与产业结构扭曲: 影响机制与多维测度[J]. 南京社会科学, 2012(6): 1-8. DOI:10.3969/j.issn.1001-8263.2012.06.001 |
| [11] |
董利红, 严太华. 制度质量、技术和人力资本投入与"资源诅咒": 基于我国省际面板数据的实证机理分析[J]. 管理工程学报, 2016(4): 18-24. |
| [12] |
李虹, 邹庆. 环境规制、资源禀赋与城市产业转型研究: 基于资源型城市与非资源型城市的对比分析[J]. 经济研究, 2018(11): 182-198. |
| [13] |
周黎, 李程宇. 分阶段视角下资源强度与地区经济的关系及其演变: 基于37个国家的实证分析[J]. 中国人口·资源与环境, 2019(12): 138-148. |
| [14] |
GRANGER C W, TERÄSVIRTA T. Modelling non-linear economic relationships[M]. Oxford, UK: Oxford University Press, 1993.
|
| [15] |
TERÄSVIRTA T. Specification, estimation, and evaluation of smooth transition autoregressive models[J]. Journal of the American Statistical Association, 1994, 89(425): 208-218. |
 2021, Vol. 27
2021, Vol. 27

