习近平总书记多次明确提出了我国要通过提升全要素生产率推动经济发展动力变革和效率变革的总体目标，并指出“以城市群为主体构建大中小城市和小城镇协调发展的城镇格局”，要通过优化城市体系结构来释放空间效率。事实上，从1992年党的十四大报告确立社会主义市场经济体制以来，我国生产要素的流动性得到了极大程度的释放，并在跨区域的流动过程中形成了“东高西低”的要素分配格局^[1]。生产部门在市场作用下的“重新洗牌”，使得不同地区的城市体系结构和产业集聚水平均在悄然发生演变，进而作用于生产率的变化过程^[2]。然而，值得注意的是，不同区位的城市体系结构表现出了明显的空间异质性特征^[3]。例如，长三角城市群形成了以上海为中心，南京和杭州为两翼，其他节点城市网络分布的多中心层级体系结构^[4]，而成渝城市群的经济重心则集中在成都和重庆，形成了典型的双中心空间结构^[5]。那么，究竟何种结构更有利于我国地区生产率的提升？考虑到产业集聚对地区生产率增长的重要性，在探讨城市体系的空间效率时能否忽略产业集聚过程的动态变化？城市体系结构的演变与产业动态集聚又如何作用于城市生产率的增长？回答上述问题，在现阶段我国优化区域空间结构与提升地区生产率的战略背景下显得尤为重要。

国内外并不缺乏围绕城市体系空间效率的研究。Glaeser等在理论上系统阐述了单中心和多中心城市体系结构的形成原理与外部影响^[6]。然而，究竟何种结构具有更高的空间效率，现有的研究结论莫衷一是。Bailey和Turok认为单中心结构通过发挥集聚优势而呈现更高的空间效率^[7]。Brezzi和Veneri研究发现OECD(Organization for Economic Cooperation and Development，OECD)国家单中心的城市体系结构与人均GDP具有较高的关联度，而多中心结构则呈现出效率的劣势^[3]。Veneri和Burgalassi就发现在意大利单中心结构对劳动生产率表现出更积极的影响^[8]。Burger等强调了多中心城市体系形成的自然条件和过程复杂性，并且对荷兰兰斯塔德地区分析后发现单中心结构更有效率^[9]。在国内研究中，张浩然和衣保中认为在我国城市群中，单中心结构对生产率的提升作用更明显^[10]。孙斌栋和李琬发现单中心结构对应更高的劳动生产率，但仅限于2010年的数据^[11]。与上述研究相对应的，同时存在大量文献认为多中心结构更具效率优势和合理性，其理论依据源于Alonso^[12]首次提出的“借用规模”理论。Glaeser等通过构建理论模型指出，多中心城市体系所形成的空间网络更有助于促进城市间的分工和要素流动，从而具有更高的空间效率^[6]。Meijers和Burger研究认为美国大都市区的多中心结构效率更高，但同时指出单中心结构所拥有的规模优势仍然是无法取代的^[13]。相对于亚洲和美洲等国家，多中心结构在欧洲的城市体系中更为常见。Camagni等则通过欧洲136个城市样本研究发现“借用规模”在城市之间普遍存在^[14]。就我国而言，在广阔的地理范围内多中心结构更有利于地区生产率提升^[15]，但也表现出一定的空间异质性^[11]。值得注意的是，判别单中心还是多中心城市体系结构的效率更高，还取决于所考察区域的空间尺度。刘修岩等发现在单个城市内部单中心空间结构更有效率，而在省域层面则多中心结构更具有优越性^[15]。

根据以上典型事实不难发现，在不同区位或者时间段，城市体系结构呈现差异化的空间效率。然而，需要指出的是，现有研究在解释城市体系结构与生产率之间关系时，通常忽略了产城融合的过程。事实上，城市体系结构的形成和演变是生产要素重新配置和产业在空间动态集聚的结果，该过程不仅决定了城市体系结构的演变方向，而且可以更直接地解释地区生产率的变化。也就是说，对于一个产业流入或者流出的地区，其城市体系结构并不是导致生产率提升或者损失的直接原因，因此忽略产业的集聚过程而单纯评价城市体系结构的效率问题是片面的，也无法解释其中的影响机制。基于此，本文将企业进入和退出某地区的过程引入集聚指标构建，以体现城市集聚水平的动态变化。同时，构建城市体系结构评价指数，选择空间计量模型检验城市体系结构演变、产业动态集聚对地区生产率的影响，并对三者之间的影响机制进行解释。

新经济地理理论指出，如果某个城市在区位禀赋推动下成为区域的中心，则会通过循环累积因果规律而得到自我强化，并很难在其他地区形成新的中心，从而构成了单中心的城市体系结构。然而，单中心结构并非长期稳定，它建立在人口规模低于某临界值的前提条件下。当整个城市体系的人口规模超过临界点时，则会产生新的中心城市。此外，根据集聚效应的非线性特点也可以看出，当某个城市的人口规模越过一定门槛时，则拥挤效应“占据上风”，从而导致生产要素的退出或者转移，进而形成了产业的分散化布局。该过程其实也构成了从单中心结构向多中心结构演变的理论解释。

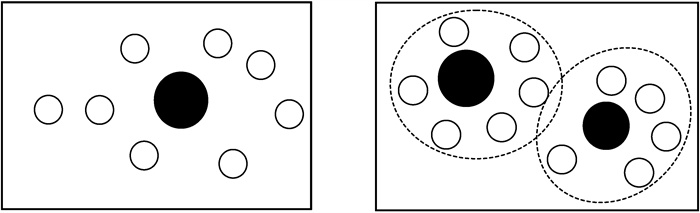
单中心和多中心城市体系具有不同的空间结构特征，如图 1所示。其中，左图为单中心结构，右图为多中心结构。可以看出，单中心结构形成了以某个大城市为核心的空间分布，其它卫星城市均环绕在中心城市周围。然而，对于距离中心城市较远的地区，其接受中心城市的辐射效应将大幅缩减。而多中心结构在一定程度上克服了围绕单中心城市建设的空间局限性，它可以通过构造多个次中心城市来形成层级分布的体系结构，而且多中心结构通常具有更多的城市数量和更广的空间范围。

图 1(Figure 1)

图 1 单中心和多中心城市体系结构分布特征示意图

究竟何种城市体系结构更有利于地区生产率的提升取决于区域内部的城市规模分布和功能联系。支持单中心结构具有更高空间效率的内在逻辑在于，其增强了生产要素的紧凑度，同时降低了通勤成本^[16]。Rosenthal和Strange认为集聚效应随着空间半径的增加而呈现指数式的衰减，由此推断多中心结构可能使集聚效应的发挥“大打折扣”，而单中心结构可以在某种程度克服空间距离的障碍^[17]。如果区域内部不同等级城市之间形成了功能互补、分工合理的多中心城市体系结构，那么其可以有效避免由单中心结构易形成的“城市病”，并构建一个“1+1>2”的城市综合体。特别是当大都市区出现集聚不经济现象时，可以通过产业转移促进要素的重新配置，改善地区资源配置效率。Meijers等认为多中心结构所形成的空间网络可以通过“借用规模”而释放更强的集聚效应^[18]。同时，由于多中心结构形成了一种相对均衡的空间分布，因此对缩小区域差异也表现出积极影响^[19-20]。如前文所言，多中心的空间结构促进生产率提升的内在机制源于Alonso早期提出的“借用规模”理论。“借用规模”可以增强大城市对中小城市的正向外部溢出，同时，降低超大规模城市的负外部性^[21]。

综上所述，单中心城市体系结构可能会通过提高生产要素的空间聚集度而有利于生产率改进。然而，从长期来看，随着城市数量的增加和区域规模的扩张，多中心结构可能会有效缓解由于资源过度集中所导致的效率损失。同时可以发现，在探讨城市体系结构的空间效率时，重点阐述了如何更大程度地优化要素配置和释放集聚效应。因此，可以从理论上推断，对于产业整体流失的地区，其单中心或者多中心城市体系结构的表现可能均是缺乏效率的。相反，对于产业流入的区域，如果要素向中心城市过度集聚而形成单中心结构，则可能产生中心城市生产率远高于周边城市的结果。而如果通过要素配置形成多中心结构，则可以通过“借用规模”缩小地区间生产率差异，而空间效率获得整体提升的概率也更高。

现有研究形成了多个对城市体系结构评价的指标，而用来评价多中心结构的帕累托指数得到了广泛的应用，其测算公式为：

其中，Pop_ct表示城市c在t时期的人口数量，R_ct表示城市c在t时期人口数量排序，Poly_pt为省级层面的多中心结构指数。其中，Poly_pt如果小于1，则表现为单中心结构；相反，如果大于1，则为多中心结构。因此，本文采用帕累托指数对城市体系结构进行评价。需要指出的是，城市人口数量的统计口径在各年并不一致，特别是近年来我国对城市人口的统计口径从户籍人口转变为常住人口，统计口径的变化预计将对指数的估计造成一定偏差。此外，行政区划的调整更增加了对人口数量统计的挑战。为克服上述困难，本文借鉴刘修岩等^[15]的做法，采用全球夜间灯光数据对城市规模进行替代。目前，美国国家海洋和大气管理局公布了1992—2013年的夜间影像，但由于夜间灯光数据具有较大的不稳定性，而且在个别年份存在两组灯光数据，同时考虑到观测卫星的老化和切换可能会降低不同年份数据的可比性，需要对原始数据进行校正。同时需要强调的是，在计算各省多中心指数时，为了降低各省份间城市体系结构不同所带来的偏差，借鉴Meijers和Burger^[13]的方法，将各省排名前四位、前三位和前两位的城市分别进行回归，并将各条件下测算得到的多中心指数取平均值，从而得到各省在不同时期的多中心指数。

关于产业集聚水平的衡量，现有研究已形成了丰富的测度方法，包括空间基尼指数、E-G指数等，但这些集聚指标并未充分消除城市地理面积的影响，更重要的是，也并未充分反映集聚效应的动态特征。事实上，大多数指标衡量的是产业的静态地理集中度，即侧重于反映产业集聚的绝对规模，而产业集聚效应的衡量和发挥还应在资源动态配置的过程中得到体现^[22]。目前，用来测算产业动态集聚水平的方法多采用Duranton和Overman^[23]提出的DO指数，其通过定位企业的位置并通过k-density函数来度量企业间距离，进而评价产业在全局或者局部的集聚动态。需要指出的是，本文拟在全国城市范围测算产业的动态集聚水平，而DO指数的复杂性和对数据的高要求限制了其在更广空间的运用。基于上述考虑，该部分在王永进和盛丹^[24]方法构建的基础上，借鉴Duranton和Overman的思路，将企业进入和退出某地区的过程融入集聚指标构建，并具体包括以下四个步骤。

第一，由于行政区划面积并不能反映城市“真实”的经济活动空间，我们借鉴李松林和刘修岩^[25]的处理方法，采用夜间灯光来提取城市的活动空间。其中，对城市活动空间的提取参照Jiang等^[26]的“两步法”：首先，对城市栅格的灯光值进行加总平均，并保留大于均值的栅格；然后，对保留栅格进行再平均，并保留高于平均值的栅格，同时将其保留的城市栅格面积总和作为城市的“真实”活动空间。

第二，将城市c企业f的劳动力数量、资本和产出规模加总至城市×行业层面，然后除以步骤1中提取的城市地理面积，用area_c来表示，从而得到城市c行业i在劳动、资本和产出的地理密集度，具体计算公式可表示为：$\mathrm{do}_{c i \mathrm{t}}=\sum_f \text { output }_{f c i \mathrm{t}} / \text { area }_{\mathrm{c}}, \mathrm{da}_{c i \mathrm{t}}=\sum_f \operatorname{asset}_{f c i \mathrm{t}} / \text { area }_c$和$\mathrm{de}_{c i \mathrm{t}}=\sum_f \text { employment }_{c i \mathrm{t}} / \text { area }_c$。

第三，为评价企业进入和退出对地区产业集聚水平的影响，我们借鉴毛其淋和盛斌^[2]的处理方法对进出某地区的企业进行识别，并采用(1+p_cit)对地理密集度进行加权。其中，p_cit表示城市c行业i在t时期的净增份额。由于当企业退出规模大于新进入企业时，p_cit为负值，因此这里采用(1+p_cit)进行修正。在劳动、资本和产出的加权公式分别表示为：$\mathrm{ade}_{c i \mathrm{t}}=\left(1+p_{\mathrm{c i t e}}\right) \times \mathrm{de}_{c i \mathrm{t}-1}, \mathrm{ada}_{c i \mathrm{t}}=(1+\left.p_{c i \mathrm{t} a}\right) \times \mathrm{da}_{c i \mathrm{t}-1}$和$\mathrm{ado}_{c i \mathrm{t}}=\left(1+p_{c i \mathrm{t} o}\right) \times \mathrm{do}_{c i \mathrm{t}-1}$。

第四，由于不同城市间的产业构成存在较大差异，为增加城市间集聚水平的可比性，进一步以城市c行业i的劳动、资本和产出份额为权重，对ade_cit、ada_cit以及ado_cit进行加总，具体表示为：$\text { density_ade }_{c \mathrm{t}}=\sum_i \text { ade }_{c i \mathrm{t}} \times \mathrm{se}_{c i \mathrm{t}}, \text { density_ada }{ }_{c \mathrm{t}}=\sum_i \text { ada }_{c i \mathrm{t}} \times \mathrm{sa}_{c i \mathrm{t}}$以及$\text { density_ado }{ }_{c \mathrm{t}}=\sum_i \mathrm{ado}_{c i \mathrm{t}} \times \mathrm{so}_{c i \mathrm{t}}$。se_cit、sa_cit和so_cit分别表示行业i在t时期占城市c的劳动、资本和产出份额。

目前，关于生产率的测算和分解多采用随机前沿法和数据包络法。由于随机前沿模型放松了数据包络法中关于固定生产前沿面的设定，而且放松了生产要素不变替代弹性假设，可以区别无效率项和随机误差项，在一定程度克服了模型的内生性问题。因此，我们选用随机前沿模型对生产率进行测算，其超越对数生产函数可表示为：

其中，Y表示城市产出，L为劳动力，K表示城市资本存量。由于城市资本存量的数据并不能直接获取，参照现有研究采用永续盘存法进行测算，并具体表示为：

其中，K_ct表示城市c在t时期的资本存量，δ_c为折旧率，I_ct表示城市c在t时期的固定资产投资。对于投资额I而言，借鉴柯善咨和向娟^[27]的做法，采用新增固定资产进行衡量，并将固定资产的平均建设周期设置为3年，表示为I=(I_ct+I_ct-1+I_ct-2)/3。对于折旧率而言，现有研究多采用张军等^[28]或者单豪杰^[29]测算得到的折旧率，然而，所有城市采用同一折旧率并不恰当，更何况折旧率所覆盖的时期可能并不适用于当期资本存量的测算。考虑到数据的可得性，这里对各个省份的折旧率进行测算，进而估算所辖城市折旧率，其结果如表 1所示。

表 1(Table 1)

表 1 我国不同地区折旧率的测算结果 地区 加权总折旧率 地区 加权总折旧率 北京 9.90% 河南 10.85% 天津 10.10% 湖北 10.38% 河北 10.66% 湖南 9.58% 山西 10.28% 广东 10.08% 内蒙古 10.37% 广西 10.49% 辽宁 10.46% 海南 9.36% 吉林 11.49% 重庆 9.19% 黑龙江 10.46% 四川 9.53% 上海 10.06% 贵州 9.57% 江苏 11.49% 云南 9.29% 浙江 10.33% 陕西 9.50% 安徽 10.38% 甘肃 9.95% 福建 10.14% 青海 9.46% 江西 10.78% 宁夏 10.36% 山东 10.93% 平均 10.19%

表 1 我国不同地区折旧率的测算结果

此外，采用永续盘存法还需要确定初始资本存量，计算公式为：K_co=

其中，g_c为固定资产投资I′_co的增长率，I′_co表示初始年份的投资额。由于根据式(4)可以对前期的资本存量进行倒推，因此在选择基期时具有一定的自由度，该部分以2000年作为基期。

基于随机前沿模型对超越对数生产函数系数的回归，并参照Kumbhakar和Lovell^[30]的分解方法，可计算出各城市全要素生产率及其分解指标的变化率，包括规模效率、技术进步率和技术效率。

基于城市体系结构、产业动态集聚和城市生产率等相关指标的构建，本文进一步通过选择合适的计量模型开展实证检验。考虑到地区间可能存在空间相关性，本文通过Moran指数对城市生产率的空间相关性进行检验，结果如表 2所示。其中，Moran指数的测算基于经济距离空间权重矩阵，结果表明地区间存在显著的空间关联性。采用常用的OLS回归模型来进行实证分析可能存在偏误，于是本文通过选择合适的空间计量模型进行检验。

表 2(Table 2)

表 2 城市全要素生产率空间相关性检验 年份 Moran’s I值 年份 Moran’s I值 2004 0.176***(3.127) 2011 0.267*(1.928) 2005 0.211**(2.090) 2012 0.256**(2.016) 2006 0.228***(3.902) 2013 0.245***(4.448) 2007 0.236***(2.617) 2014 0.245***(3.897) 2008 0.311***(7.903) 2015 0.236(1.457) 2009 0.326***(8.448) 2016 0.236*(1.668) 2010 0.257***(4.698) 2017 0.224***(3.834) 注：1. * **，**，*分别表示变量在1%，5%和10%的水平下通过显著性检验；2.回归系数括号内为z值。

表 2 城市全要素生产率空间相关性检验

一般而言，通常被采用的空间计量模型主要包括空间自相关模型(Spatial Autoregressive Model，SAR)和空间误差模型(Spatial Error Model，SEM)。由于空间杜宾模型(Spatial Dubin Model，SDM)同时嵌套了空间滞后模型和空间误差模型，可以有效衡量空间溢出的直接效应和间接效应^[31]，因此也逐渐成为主要的空间计量分析方法之一。对于模型的选取，空间计量经济学提供了丰富的识别方法，结果如表 3所示。

表 3(Table 3)

表 3 空间计量模型的识别结果 空间权重矩阵 SAR与SDM SEM与SDM SAR SEM Wald Test LR Test Robust LM Test Robust LM Test 邻接空间权重矩阵 2.186 (0.702) 1.984 (0.723) 0.491 (0.483) 10.813*** (0.001) 物理距离空间权重矩阵 3.074 (0.546) 3.621 (0.398) 0.025 (0.873) 11.642*** (0.001) 经济距离空间权重矩阵 7.295 (0.121) 5.023 (0.269) 1.359 (0.244) 8.323*** (0.004) 注：1. * **，**，*分别表示变量在1%，5%和10%的水平下通过显著性检验；2.回归系数括号内为p值。

表 3 空间计量模型的识别结果

以SDM为母体的Wald检验和LR检验结果表明，在三种空间权重矩阵交互作用下的SDM模型均不优于SAR模型或者SEM模型，因此应直接采用SAR模型或者SEM模型。通过对比稳健LM检验的统计值可以发现，采用SEM模型为更优选择，并将空间计量模型设定为：

其中，△TFP表示城市生产率增长率，Poly为省级层面的城市体系结构指数，Agg表示城市产业动态集聚指数，X为其他控制变量。同时，κ_c和v_t分别表示地区和时间的固定效应，ε_ct为随机扰动项，λ为空间误差系数，μ_ct为随机误差项。此外，W_n为空间权重矩阵。需要强调的是，考虑到区域空间结构的复杂性，很难找到能够准确衡量地区间实际依赖关系的权重矩阵，而空间权重矩阵的误用很可能产生计量结果的偏差。因此，模型(5)中的空间权重矩阵 W_n同时嵌套了邻接空间权重矩阵、物理距离空间权重矩阵和经济距离空间权重矩阵，从而增加回归结果的准确度和稳健性。其中，邻接空间权重矩阵由城市间位置关系决定，相邻则权重设置为1，否则为0。物理距离空间权重矩阵的元素ω_ij表示城市i与j的最短公路里程的倒数，而经济距离空间权重矩阵则在物理距离空间权重矩阵的基础上加城市的经济权重，这里采用的是城市人均GDP。

需要说明的是，由于随机前沿模型测算的是地区生产率的增长率，其可能存在负值，因此，在取对数时应当进行相应调整。此外，城市体系结构演进和产业动态集聚水平可能对地区生产率的影响产生一定时期的滞后，参照魏守华等^[32]的做法，我们将两个变量统一滞后四期。同时，还对可能影响地区生产率的变量进行控制，包括固定资产投资占比(pinvest)、外商直接投资规模(fdi)和每万人大学生数(pedu)等。表 4为主要变量的描述性统计，其中，△SE表示城市规模效率增长率，△FTP为技术进步率，△TE表示技术效率增长率。

表 4(Table 4)

表 4 主要变量描述性统计 变量 样本量 均值 最大值 最小值 标准差 ln(1+ΔTFP) 3 696 0.008 0.034 -0.148 0.006 ln(1+ΔSE) 3 696 -0.004 0.354 -0.907 0.042 ln(1+ΔFTP) 3 696 0.338 0.819 -0.386 0.200 ln(1+ΔTE) 3 696 0.276 0.647 0.040 0.065 lnpoly 3 696 -0.363 0.683 -2.669 0.758 lnagg 3 696 5.476 10.454 0.026 1.667 lnpinvest 3 696 -0.585 0.764 -10.246 0.457 lnfdi 3 696 8.110 14.333 0.653 3.213 lnpedu 3 696 -3.579 -1.416 -8.682 1.107

表 4 主要变量描述性统计

本文采用的数据库主要包括全球夜间灯光数据^①。、中国工业企业数据库、《中国城市统计年鉴》和《中国统计年鉴》等，综合考虑数据库可获取的时限性，将时间区间设置为2000年至2013年。其中，测算城市体系结构指数采用的是由美国国家海洋和大气管理局公布的城市夜间灯光数据，计算结果为省级层面的多中心空间结构指数，时间范围为2000年至2013年。测算城市层面的产业动态集聚指数主要采用2000年至2013年中国工业企业数据库和全球夜间灯光数据，而测算城市生产率和其他控制变量的数据主要来自2005年至2018年《中国城市统计年鉴》和《中国统计年鉴》。为减小计量模型的回归误差，本文剔除了样本缺失和存在异常值的城市，同时对行政区划调整的城市进行数据整合，样本覆盖264个地级及以上城市。

① 夜间灯光数据的下载地址为：https://ngdc.noaa.gov/eog/dmsp/downloadV4composites.html

表 5为在城市体系结构演进和产业动态集聚作用下城市生产率的变动结果。为对比在引入空间相关性前后对结果产生的影响，我们同时采用了无空间权重矩阵的OLS方法。首先，用来表示城市间空间相关性的λ值显著为正，表示在城市间存在正向的空间关联性。同时，在总体上，采用OLS模型与空间计量模型的回归结果存在一定的差异，说明忽略城市间的空间溢出效应会导致结果的偏差。具体而言，在三种空间权重矩阵作用下，多中心的城市体系结构对城市生产率的影响并不显著。然而，在加入包含产业动态集聚指数的交互项后则显著为正，表明在产业动态调整与城市体系结构演变的共同作用下，对城市生产率增长的影响显著为正。基准回归模型所反映出的经济现象可以解释为，多中心空间结构本身的演变对城市生产率的促进效应并不显著，反而需要在空间溢出效应作用下，通过城市间产业集聚的动态调整来释放多中心城市体系结构的效率。而且，对于无空间权重矩阵的结果而言，ln agg_c(t-4) × lnpoly_p(t-4)交互项的绝对值明显偏小，进一步表明在城市空间溢出效应的作用下，多中心结构与产业动态集聚对生产率的影响得到了强化，而且表现出积极的影响。

表 5(Table 5)

表 5 基准回归 解释变量 OLS 邻接空间权重矩阵 物理距离空间权重矩阵 经济距离空间权重矩阵 lnpolyp(t-4) -0.003*** (-5.50) -0.004 (-1.47) -0.004 (-1.45) -0.001 (-0.46) ln aggc(t-4) -0.000 1* (-1.69) 0.003*** (14.96) 0.003*** (11.87) 0.003*** (16.08) ln aggc(t-4) × ln polyp(t-4) 0.000 1*** (5.67) 0.001*** (3.35) 0.001*** (3.20) 0.001*** (2.65) λ 0.345*** (14.24) 0.487*** (18.88) 0.263*** (7.37) 其他变量 控制 控制 控制 控制 时间和地区固定效应 控制 控制 控制 控制 样本量 3 696 3 696 3 696 3 696 R2 0.612 0.316 0.428 0.384 注：* **，**，*分别表示变量在1%，5%和10%的水平下通过显著性检验；回归系数括号内为z值。

表 5 基准回归

为进一步明确城市体系结构对地区生产率的影响机制，该部分对生产率的分解指标进行检验，结果如表 6所示。可以发现，多中心结构与产业集聚均显著提升了城市的规模效率，而且两者的交互作用也产生了积极影响。该结果表明城市的产业聚集有利于规模效率的改善，而且多中心结构也可以同时优化区域的规模效率。然而，对技术进步率和技术效率而言，则表现出差异化的结果。具体而言，产业集聚本身并未显著促进技术进步，而且其与多中心结构的交互项显著为负，反映出在多中心结构下的产业集聚并不利于技术进步。同时，对于技术效率而言，其回归结果与技术进步率相似，也反映出多中心的空间结构与产业集聚并未显著提升技术效率，反而表现出一定的抑制作用。由此可以推断，多中心结构的“借用规模”可能对地区的规模效率更加有效，但要素的分散化配置反而不利于技术进步和技术效率的改善。

表 6(Table 6)

表 6 基于生产率分解指标的检验 解释变量 规模效率 技术进步率 技术效率 lnpolyp(t-4) 0.025* (1.67) -0.006 (-0.24) 0.008*** (2.76) ln aggc(t-4) 0.013*** (8.26) -0.026*** (-4.90) -0.000 3 (-0.49) ln aggc(t-4) × ln polyp(t-4) 0.017*** (2.59) -0.017*** (-6.29) -0.002*** (-7.88) λ 0.405*** (14.40) 0.970*** (195.95) 0.963*** (157.63) 其他变量 控制 控制 控制 时间和地区固定效应 控制 控制 控制 样本量 3 696 3 696 3 696 R2 0.222 0.410 0.911 注：1. * **，**，*分别表示变量在1%，5%和10%的水平下通过显著性检验；2.回归系数括号内为z值。

表 6 基于生产率分解指标的检验

现有研究在讨论单中心和多中心结构的空间效率时并未得到一致结论，其较大程度源于空间的异质性特征。目前，我国已形成包括京津冀、长三角、珠三角、长江中游和成渝等在内的发展较为成熟的五大国家级城市群，而且由于自然禀赋和历史文化的不同，又形成了各具特色的城市体系结构。根据城市体系结构指数的测算，五大国家级城市群的Poly_ut值均大于1，即表现为多中心的空间结构(表 7)。然而，需要指出的是，京津冀城市群的多中心特征正逐年减弱。

表 7(Table 7)

表 7 基于不同城市群的空间异质性检验 城市群 京津冀城市群 长三角城市群 珠三角城市群 长江中游城市群 成渝城市群 ln polyu(t-4) -0.032** (-2.32) -0.006 (-1.09) -0.038* (-1.76) 0.001 (0.93) -0.028 (-1.56) ln aggc(t-4) -0.004 (-1.34) 0.002* (1.70) 0.008 (1.33) -0.000 1 (-0.76) -0.002* (-1.77) ln aggc(t-4)× ln polyu(t-4) -0.002** (-2.05) 0.001*** (2.76) 0.003* (1.73) -0.000 2* (-1.72) 0.009** (2.34) λ 0.372*** (6.98) 0.530*** (8.03) 0.440* (1.69) 0.665*** (7.99) 0.374*** (4.41) 其他变量 控制 控制 控制 控制 控制 时间和地区固定效应 控制 控制 控制 控制 控制 样本量 196 378 210 420 224 R2 0.486 0.297 0.398 0.336 0.590 注：1. * **，**，*分别表示变量在1%，5%和10%的水平下通过显著性检验；2.回归系数括号内为z值。

表 7 基于不同城市群的空间异质性检验

对于京津冀城市群而言，多中心结构与产业集聚的交互项显著为负，表明产业在京津冀城市群布局的过程中，其形成的城市体系结构并未有效提升生产率。产生该现象的原因可能在于，京津冀城市群内部存在明显的要素非均衡化配置，形成了以北京和天津为中心的空间结构，但周围节点城市“借用”中心城市规模的效果并不理想。相比而言，长三角城市群呈现出更显著的多中心特征，形成了以上海为中心，南京、杭州为次中心，其他节点城市星罗棋布的层级城市体系结构^[4]。回归结果显示，在生产率提升方面，长三角城市群的多中心结构与产业集聚之间形成了良好的协同效应。珠三角城市群的回归结果与长三角城市群相似，但从珠三角内部的经济构成来看，其与长三角城市群存在较大差异。对比发现，珠三角城市群的经济重心集中分布在珠江口大湾区，同时也是生产率水平相对较高的区域，但外围地区的生产率水平相对较低。同时，珠三角城市群整体的空间关联性相对偏弱。值得注意的是，由于长三角城市群和珠三角城市群均为产业净流入较高的地区，其多中心结构效率的释放更依赖于融入产业集聚的动态变化过程。

就长江中游城市群而言，其位于长江经济带中间环节，属于覆盖城市数量和空间范围最广的特大型城市群。然而，结果表明，多中心结构与产业集聚的协同效应显著为负，表明长江中游城市群尚未形成富有效率的城市体系结构。其原因可能在于，长江中游城市群内部要素过度聚集在武汉、长沙、南昌等省会城市，而周边城市与中心城市之间形成了悬殊的经济差异^②。同时，由于长江中游城市群地跨四省，其庞大的空间范围和合作机制的不成熟势必会增加城市群的协调难度。成渝城市群是典型的以成都和重庆为双核的城市体系结构，回归结果表明，多中心结构和产业集聚本身并不利于生产率的提升，但在两者的协同作用下显著改善了地区生产率。

② 以湖北省为例，根据2019年湖北省统计数据，在湖北12个地级市中，武汉市GDP占湖北省的比重达35%，而人口占比也达到24%，其他城市经济和人口占比相对较低。通过测算多中心指数平均为0.58(小于1)，表明湖北省形成了以武汉为核心的单中心结构。

尽管空间计量模型可以通过引入不同的空间权重矩阵来减小内生性偏误，但核心解释变量与地区生产率之间仍然可能存在因果联系。为进一步校正内生性问题，该部分采用广义空间二阶段最小二乘法进行处理。关于工具变量的选取，主要包括两个方面：第一，参照刘修岩^[1]的思路，将城市地表粗糙度作为产业集聚的工具变量。Ramcharan也通过研究表明，城市地表越不平坦，则修建和维护道路的成本越高，在该区域形成聚集状态的概率则越高^[33]。第二，考虑到自然禀赋在空间经济学中的重要性，借鉴刘修岩等^[15]的思路，将区域的河流密度作为多中心结构的工具变量。Bosker和Buringh考察欧洲城市的历史也发现，是否靠近水源与城市规模之间存在内在联系，并发现河流沿岸通常是城市和人口分布的集中地^[34]。需要强调的是，地表粗糙度与河流密度并不随时间发生变化，因此不能充分反映被替代变量的动态特征。历史证明，对外开放一直是我国经济增长和要素聚集的内在动力，且汇率是随时间波动的可以影响对外开放度的变量，因此这里将汇率作为变动因子对地表粗糙度和河流密度进行加权^③。回归结果如表 8所示，模型一和模型二分别对多中心结构和产业集聚指标进行内生性处理，而模型三对两个变量进行双重处理。结果表明，模型一和模型二所对应的交互项结果与基准模型并不一致，即对生产率的影响反而为负。然而，值得注意的是，在模型三的双重处理结果中，与基准模型保持一致。分析其原因可能在于，仅对某一经济变量进行内生性处理可能是片面的，而且增加了对经济现象的解释难度。而同时采用自然禀赋指标进行替代后，一方面较大程度地降低了模型可能由因果联系而产生的内生性偏误，另一方面可以仅从自然地理特征的角度对结果进行解释。因此，我们认为，模型三对应的回归结果更具有参考价值。

③ 这里的汇率是指人民币兑换美元的比率。

表 8(Table 8)

表 8 内生性处理 解释变量 模型一(河流密度) 模型二(地表粗糙度) 模型三(双重处理) ln polyp(t-4) 0.002* (1.77) 0.028*** (5.47) -0.009*** (-3.56) ln aggc(t-4) -0.002 (-1.35) 0.001 (1.09) 0.010* (1.77) ln aggc(t-4)× ln polyp(t-4) -0.001** (-2.09) -0.001*** (-3.86) 0.003*** (3.42) λ 0.997*** (10.57) 0.893*** (9.47) 0.996*** (10.98) 其他变量 控制 控制 控制 时间和地区固定效应 控制 控制 控制 样本量 3 696 3 696 3 696 R2 0.475 0.332 0.280 注：1. * **，**，*分别表示变量在1%，5%和10%的水平下通过显著性检验；2.回归系数括号内为z值。

表 8 内生性处理

为保证回归结果的稳健性，本文通过变换评价指标的方法进行检验。其中，模型一和模型二通过构建不同指标对城市体系结构进行评价，包括调整的赫芬达尔指数和变换的首位度指数。其中，赫芬达尔指数的构建参照Al-Marhubi^[35]的方法，具体表示为：

在式(6)中，H_pt表示省级层面的赫芬达尔指数，l_ct为城市c在时期t的夜间灯光亮度，L_pt表示省份p在t时期的平均夜间灯光亮度，n表示各省地级市的数量。H_pt的值介于(0，1)之间，且越趋近于1，则表明越趋向于单中心结构。为保持与基准模型结果的可比性，本文采用1/H_pt作为poly指数的代理变量。同时，用1减去首位城市规模比例来代替poly指数，其中首位城市为各省份灯光亮度最高的城市。根据表 9回归结果，多中心结构与产业集聚协同促进生产率提升的结论是稳健的。同时，考虑到评价地区生产率的指标是多样的，本文进一步借鉴Fallah等^[36]的方法，将劳均实际GDP作为生产率的替代指标，其中劳均实际GDP以各市辖区实际GDP除以非农就业人数得到，模型三对应的结果进一步支持了基准模型的回归结果。

表 9(Table 9)

表 9 稳健性检验 解释变量 模型一(调整赫芬达尔指数) 模型二(变换首位度指数) 模型三(人均GDP) ln polyp(t-4) -0.014*** (-3.95) -0.032*** (-5.23) -0.011*** (-3.21) ln aggc(t-4) 0.005*** (8.90) 0.006*** (-9.50) 0.026* (1.71) ln aggc(t-4)× ln polyp(t-4) 0.002*** (7.89) 0.002*** (7.99) 0.003* (1.87) λ 0.915*** (135.03) 0.915*** (135.04) 0.581*** (10.32) 其他变量 控制 控制 控制 时间和地区固定效应 控制 控制 控制 样本量 3 696 3 696 3 696 R2 0.933 0.932 0.541 注：1. * **，**，*分别表示变量在1%，5%和10%的水平下通过显著性检验；2.回归系数括号内为z值。

表 9 稳健性检验

Glaeser等^[6]曾指出多中心空间结构所形成的城市网络有助于促进要素流动和专业分工，那么，由多中心结构所带来的要素分散化配置能否促进区域生产率的收敛？为进一步探讨区域生产率的协同性，该部分将方程(5)进一步拓展为：

表 10中模型一至模型四分别为逐步引入多中心结构指数、产业动态集聚指数以及两者交互项的回归结果。通过表 10可以看出，在不同情形下，ln (1+△TFP_ct-1)的系数均显著为负，表明地区间生产率存在收敛的趋势。通过对比加入控制变量前后的结果不难发现，模型二在引入多中心结构指数后，ln (1+△TFP_ct-1)的系数绝对值有所增加，表明多中心结构有利于地区生产率的协同。同时，模型三在引入产业动态集聚指数后，ln (1+△TFP_ct-1)的系数绝对值同样增加，表明产业集聚动态调整的过程也促进了生产率的协同。在同时引入多中心指数和产业集聚指数后，ln (1+△TFP_ct-1)的绝对值进一步增加，表明在两者的共同作用下，可以促进生产率的协同。分析其原因可能在于，多中心的城市体系结构更利于资源的分散化配置，而产业集聚动态的调整也使资源得到更加均衡化的配置。

表 10(Table 10)

表 10 对地区生产率协同性的影响 解释变量 模型一 模型二 模型三 模型四 ln (1+△TFPct-1) -0.009** (-2.43) -0.012** (-2.56) -0.061*** (-2.94) -0.073*** (-3.48) ln polyp(t-4) 0.005*** (3.30) -0.003 (-1.30) ln aggc(t-4) 0.002*** (10.75) 0.003*** (11.68) ln aggc(t-4)× ln polyp(t-4) 0.001*** (3.98) λ 0.392*** (15.71) 0.402*** (16.19) 0.285*** (10.50) 0.283*** (10.46) 其他变量 控制 控制 控制 时间和地区固定效应 控制 控制 控制 样本量 3 696 3 696 3 696 3 696 R2 0.189 0.191 0.264 0.276 注：1. * **，**，*分别表示变量在1%，5%和10%的水平下通过显著性检验；2.回归系数括号内为z值。

表 10 对地区生产率协同性的影响

由于单中心或者多中心城市体系结构是由不同规模城市构成，城市间空间溢出效应的非对称性可能导致在相同的空间框架下对不同规模城市产生差异化影响。因此，有必要基于不同规模城市进行分样本检验，回归结果如表 11所示。具体而言，模型一和模型二为对大规模城市的影响，分别以省会城市和省内前三大城市来衡量。可以看出，多中心结构本身对生产率影响为负，但加入产业集聚指数后的交互项显著为正，表明产业集聚对大规模城市产生了积极影响。而且，尽管多中心结构可能通过扩大要素的配置空间而分散了大规模城市的利益，但在产业动态集聚的过程中依然有利于大规模城市的发展。相比之下，多中心结构和产业集聚对小规模城市的影响恰好相反，即尽管多中心结构对小城市生产率产生了积极影响，但考虑产业集聚动态调整的影响后却抑制了地区生产率的提升。其原因可能在于，多中心结构可以通过“借用规模”助力小规模城市发展，但大规模城市对生产要素的吸引力可能同时对中小城市的要素集聚形成一定的“极化效应”，从而导致在产业动态集聚的过程中更有利于大规模城市。此外，通过对比模型一和模型二，以及模型三和模型四可以看出，对于规模越大的城市，两者对生产率的提升作用越明显。相反，对于规模越小的城市，其对生产率的抑制作用也更显著。

表 11(Table 11)

表 11 对不同规模城市生产率的影响 解释变量 模型一(省会城市) 模型二(前三位大城市) 模型三(后三位小城市) 模型四(最小城市) ln polyp(t-4) -0.709** (-2.48) -0.403** (-2.03) 0.896** (2.08) 1.757*** (4.85) ln aggc(t-4) 0.123*** (2.69) 0.103 (1.23) -0.530*** (-3.21) -0.634*** (-10.55) ln aggc(t-4)× ln polyp(t-4) 0.096*** (2.82) 0.019* (1.89) -0.109* (-1.94) -0.358*** (-7.62) 其他变量 控制 控制 控制 控制 时间和地区固定效应 控制 控制 控制 控制 样本量 364 1 092 1 092 364 R2 0.207 0.509 0.660 0.611 注：1. * **，**，*分别表示变量在1%，5%和10%的水平下通过显著性检验；2.回归系数括号内为z值。

表 11 对不同规模城市生产率的影响

根据理论机制部分的描述，城市体系结构的演进与产业集聚的过程密不可分，而且不同城市体系结构对地区生产率的影响也与集聚外部效应的释放紧密相关。基于上述逻辑，将影响机制检验方程设置为：

其中，方程(8)中被解释变量为多中心城市体系结构指数，产业动态集聚为核心解释变量；而方程(9)中多中心城市体系结构指数为核心解释变量，地区生产率增长为被解释变量，回归结果如表 12所示。由于城市体系结构的形成与城市的空间分布有关，因此，在方程(8)中引入地理距离distance，用来表示各省内部城市间的平均距离。方程(8)对应模型一的回归结果，可以看出，城市间平均距离越远，则更有利于多中心结构的形成。由于集聚更倾向于在某一空间范围的集中，根据lnagg_ct为负值可以推断产业集聚并不利于多中心结构的形成。然而，产业集聚与地理距离的交互项为正，说明对于城市位置分布相对分散的省份，产业集聚的过程加速了多中心结构的形成。

表 12(Table 12)

表 12 影响机制的检验 解释变量 模型一 模型二 ln aggct -0.009* (-1.77) ln distance 0.096 (1.60) ln aggct×ln distance 0.011* (1.92) ln polyp(t-4) 1.572* (1.69) ln marketc(t-4) -0.109 (-0.56) ln polyp(t-4)×ln marketc(t-4) 3.051*** (3.88) 其他变量 控制 控制 样本量 3 696 3 696 R2 0.328 0.405 注：1. * **，**，*分别表示变量在1%，5%和10%的水平下通过显著性检验；2.回归系数括号内为z值。

表 12 影响机制的检验

根据理论分析，多中心结构可以通过“借用规模”促进生产率提升，但需要建立在要素充分流动和分工协作的基础上。因此，在方程(9)中引入了市场一体化指数，用来反映城市体系内部要素的自由流动程度。模型二对应方程(9)的回归结果，发现建立在市场一体化基础上的多中心结构具有更高的空间效率。综合以上两步回归结果可以看出，我国城市的产业集聚促进了多中心城市体系结构的形成，而市场一体化进程又充分释放了多中心结构空间效率，进而加速了地区生产率的提升。

随着城市化水平提升和城市集群化发展，围绕城市体系空间效率的研究不断呈现。然而，究竟单中心结构还是多中心结构具有更高的空间效率，相关文献并未得到一致结论。需要指出的是，城市体系结构的演化和地区生产率的提升与产业集聚的过程密不可分，忽略产业集聚过程而探讨城市体系的效率问题是片面的。本文从城市体系结构演化、产业动态集聚与地区生产率提升的逻辑关系出发，对三者之间的作用机制进行阐释，并选择合适的空间计量模型进行检验。

研究发现，多中心结构与产业集聚共同推动了地区生产率的提升，而且同时有利于城市规模效率的改善，但损失了技术进步率和技术效率。通过对我国不同区位国家级城市群进行对比分析后发现，长三角、珠三角和成渝城市群具有较高的空间效率，但京津冀和长江中游城市群则恰好相反。为降低模型内生性偏误，分别采用河流密度和地表粗糙度作为多中心指数和产业集聚指数的工具变量，并采用调整的赫芬达尔指数和变换的首位度指数进行稳健性检验，其结果并未呈现明显差异。通过进一步分析发现，多中心空间结构与产业动态集聚均显著促进了区域生产率的协同。同时，多中心结构可以促进小规模城市的生产率提升，但由于在产业集聚的过程中处于劣势地位，因此在两者的交互作用下依然损失了小城市的空间效率。相反，该过程有力推动了大规模城市生产率的提升。通过影响机制的检验可以看出，产业集聚加速了多中心空间结构的形成，而多中心结构在市场一体化的推动下又改进了地区生产率。

基于丰富的研究结论，本文具有较强的政策导向性，主要体现在以下三个方面。

第一，深化城市体系结构演进与产业动态集聚的耦合关系，进一步释放生产率增长潜能。尽管实证结果表明，多中心结构与产业集聚的交互作用推动了地区生产率的提升，然而，从更深层次的角度，两者对技术进步率和技术效率却呈现消极影响。因此，还应当在释放城市规模效益的同时，提升产业集聚的技术含量，将技术进步作为未来推动我国生产率提升的核心力量。同时，加强城市间的产业合作和技术共享，探索实现跨区域一体化发展的机制和路径，以“一盘棋”的思维统筹推进区域生产率的提升。

第二，以城市群为载体打造兼顾效率与公平的城市综合体。研究发现，我国五大国家级城市群呈现了各具特征的城市体系结构和空间效率。值得注意的是，究竟何种城市体系结构更有效率，很难通过对比不同城市群得到确切答案。然而，由于京津冀和长江中游城市群内部存在相对明显的“中心—外围”特征，形成了优质资源向中心城市过度聚集的情形，该过程不仅损害了小城市的生产率，而且不利于区域的协同发展。因此，应当立足于城市群各城市的空间分布特征，着力打造大中小城市和小城镇协调发展的空间格局。也就是说，对于要素资源集中流向某一个或者少数中心城市时，应当注重不同规模城市的职能分工和功能互补，避免成为中心城市的“独角戏”。事实上，雄安新区的设立将较大程度地缓解京津冀城市群内部要素非均衡分布的问题。

第三，应当在突出中心城市主导地位的同时，更加注重中小城市的发展。《中华人民共和国国民经济和社会发展第十四个五年规划和2035年远景目标纲要》明确指出，“要发展壮大城市群和都市圈，分类引导大中小城市发展方向和建设重点，形成疏密有致、分工协作、功能完善的城镇化空间格局”。然而，研究表明，在多中心结构与产业集聚共同作用下其实更有利于中心城市，而对中小城市形成了一定的“挤出效应”。因此，应当在发挥中心城市辐射带动作用的同时，引导非核心部门向周边城市转移，积极承接中心城市的外部溢出。同时，加强城市间的分工协作，例如，生产性服务业倾向于向大城市聚集，而专业化的制造业企业则倾向于向小城市集聚，如何在不同规模城市之间形成良性互动的关系，是下一步释放空间效率的重点。此外，对影响机制的分析结果也表明，需要进一步提升市场一体化水平，加强区域内部的要素流动，打造一个中心城市拉动中小城市、中小城市反哺中心城市的良性循环体系。