风能是一种最具开发利用前景的清洁能源和可再生能源。随着环境保护意识及要求的提高，近年来，风能已成为新能源的重要组成部分，是水电和火电的有力补充。

由于风电机组出力具有随机性、间歇性，部分电力运行部门将风力发电视为一种完全不可靠的发电形式，其只能提供能源，而不能替代一定量的发电容量。实际上，风力发电和传统发电方式只是出力的随机性、可用率等方面有数量上的差异，并没有本质区别^[1]。因此，估计风电场的容量可信度(capacity credit,CC)具有重要的意义。容量可信度是风电场提供的等值发电容量能力的重要指标，它的计算是含风电的电力系统规划、设计和分析的重要内容之一。

元件故障及负荷变化等不确定因素都会影响电力系统的可靠性和输电能力，造成系统阻塞。将一定容量的风电场接入电力系统可以缓解电力系统的阻塞状况。

目前，在评估含风电场的电力系统可靠性和风电场的发电容量可靠性方面有不少研究成果。文献[2, 3]主要集中在对发输电系统、发输配电系统的可靠性评估。考虑到风电场配置适当的储能容量可以有效改善因风速变化而造成的输出功率波动，文献[4]探讨了风电场及含储能装置对发输电系统的可靠性的影响，文献[5]还对风电场储能容量合理取值范围进行了研究。风电场的发电容量可靠性主要集中在对风电场发电容量充裕度及容量可信度的研究，包括多种风速模型(如滑动平均模型MA、自回归滑动平均模型ARMA、正态分布模型等)对风电场发电容量充裕度指标的影响^[6]、风电场容量可信度的定义和计算方法^{[7, 8]}，含储能装置的风电场容量可信度模型及求解算法^[9]。已有的风电场容量可信度研究提出了多种风电场容量可信度的定义和衡量准则。这些准则都有一个共同的前提：维持原有系统可靠性水平，即这些研究都是基于电力系统可靠性而提出的。但从输电阻塞角度研究风电场容量可信度还很鲜见。

风电场接入电力系统对缓解系统输电阻塞具有一定的贡献，对于如何刻画风电场缓解系统输电阻塞程度的贡献文献[10]提出了计及元件故障的电力系统输电阻塞Monte Carlo评估方法，给出了刻画输电阻塞程度的指标体系，这些指标能够反映整个系统的输电阻塞水平，但不能直接显示风电场对电力系统输电阻塞缓解程度的贡献。

针对以上问题，笔者在已有研究成果的基础上，提出基于输电阻塞指标的风电场容量可信度的定义、可信度计算模型及其求解算法。

文献[10]给出了系统输电阻塞指标体系及算法，如表 1所示。

表1(Table 1)

表1 系统输电阻塞评估指标体系Table 1 System congestion evaluation indices system 指 标 定 义 Psc 系统阻塞概率(Psc)：给定时段内，系统出现输电阻塞的概率为${{P}_{\text{sc}}}=\sum\limits_{j\in S}{{{P}_{j}}}$，式中：S为系统出现输电阻塞状态全集，Pj为第j个系统状态下的概率。 Fsc(times/a) 系统阻塞频率(Fsc)：给定时段内，系统发生阻塞次数为${{F}_{\text{sc}}}=\sum\limits_{j\in S}{{{F}_{j}}}=\sum\limits_{j\in S}{{{P}_{j}}}\sum\limits_{k=1}^{N}{{{\lambda }_{k}}}$，式中：Fj为第j个系统状态的发生频率；N为系统元件数；λk为元件k从状态j离开的转移率。如果元件k在工作，则λk是失效率；如果元件k处于停运，则λk是修复率。 Csc(MV·A) 系统阻塞容量(Csc)：给定时段内，系统在某一状态发生阻塞时的阻塞容量为${{C}_{\text{s}{{\text{c}}_{j}}}}=\sum\limits_{i=1}^{l}{{{C}_{\text{TL}{{\text{C}}_{ij}}}}}$，式中：l 为在第j个系统状态下出现阻塞的输电线路数。CTLCij为第j个系统状态下第i条输电线路的阻塞容量。(注：系统中任意一条线路发生阻塞，则判定系统发生阻塞。出现阻塞的线路，其阻塞容量为其实际传输的容量与额定容量之差。) Esc(MW·h/a) 系统受阻电量(Esc)：给定时段内(这里取1年)，系统受阻电量为${{E}_{\text{sc}}}=\sum\limits_{j\in S}{{{P}_{j}}\times {{C}_{\text{s}{{\text{c}}_{j}}}}}\times 8760$。

表1 系统输电阻塞评估指标体系 Table 1 System congestion evaluation indices system

该指标体系能够反映电力系统整体输电阻塞水平，但不能刻画风电场并入电力系统后对缓解系统阻塞的贡献。因此，笔者在文献[10]的基础上，进一步提出如下风电阻塞指标。

1)风电场对系统阻塞概率贡献指标(B_SCP)。

2)风电场对系统阻塞频率贡献指标(B_SCF)。

3)风电场对系统受阻电量贡献指标(B_SCE)。

由于风速的随机性和波动性，WTG(wind turbine generation)出力随时间变化，导致其出力不同于传统发电机组，即常用风机出力概率来描述其可靠性模型^[11]。

已有文献提出用多状态概率模型来描述风机出力随风速随机变化的特征^{[11, 12]}。基于风速时间序列法模型和功率曲线，分别求出风机的风速和输出功率，从而得到风机出力(即输出功率)的多状态概率表^[12]。该过程简要描述如下：

1)定义风机出力状态数；

2)统计风机各级出力状态的时点数；

3)各级出力状态的时点数除以总时点数，估算各级出力状态的概率。

理论上出力状态数越多，精度越高，但同时也会大大地增加计算量。文献[12]指出5状态概率模型已能满足工程计算精度的要求，为此，本文风电场可靠性模型也采用5状态概率模型。

如前所述，目前已有多种风电场容量可信度的定义和衡量标准，但归纳起来主要有两种：有效载荷能力(effective load carrying capability，ELCC)和有效固定容量(equivalent firm capacity，EFC)^{[13, 14, 15]} 。这里借鉴第二种方法定义基于系统阻塞指标的风电场容量可信度。

基于输电阻塞指标的风电场的容量可信度(β_CC)是指：保持系统输电阻塞指标水平不变的前提下风电场能替代的常规机组容量与风电场装机容量的比值。它直接反映了风电场建设后可节省的常规机组容量。

从表 1中系统受阻电量E_sc的计算公式可以看出：在系统阻塞指标体系中，该指标能综合反映系统阻塞程度，在计算风电场容量可信度时可选择E_sc指标。当然，其他指标可依此进行定义。

由定义知，风电场容量可信度为：

根据前述基于系统输电阻塞指标的风电场容量可信度的定义，其计算过程如下：

首先，不考虑并网风电场(即初始系统)的情况下计算电力系统的系统阻塞指标——E_sc，记作E_sc0。然后，计入风电场后重新计算E_sc，记作E_scr；去掉风电场，恢复到初始系统(即系统受阻电量为E_sc0)，用常规机组代替风电场，调整新增常规机组容量，直至E_sc等于E_scr。此时，新增常规机组容量与风电场容量之比即为β_CC，新增常规机组容量也称为等效传统机组容量。

含风电场的电力系统和用等效传统机组替代风电场的电力系统，其阻塞指标E_sc与系统总发电容量分别存在以下关系：

由于f并不存在一个精确表达式，已知ΔC_w或ΔC_c求E_sc可通过Monte Carlo仿真计算实现。反过来，已知E_sc求对应的ΔC_w或ΔC_c却是一件极其复杂的工作。

在某电力系统中，因元件故障、负荷变化等因素引起系统输电阻塞，若在某一缺电母线上并入风电场，一定范围内，随着风电场容量的增加，系统阻塞状况会逐渐缓解，但当风电场容量过大时，由于风电场的实际出力由风速决定，不能随意调度，在低水平负荷情况下反而可能导致系统阻塞状况恶化。在同一母线，若用常规机组替换风电场，与风电机组不同，常规机组可降额运行，其实际出力可以根据负荷大小进行调度，因此，随着常规机组总容量增加，系统阻塞状况缓解越明显，即新增等效传统机组容量与阻塞指标E_sc之间呈现明显的非线性、连续、单调递减关系。

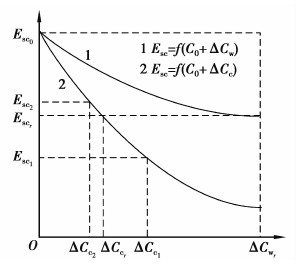
鉴于此，笔者采用二分搜索法求解风电场容量可信度。图 1为风电场容量可信度二分法几何示意图，曲线1、2分别为系统并入风电场容量和加入等效传统机组容量与E_sc关系曲线。初始系统时输电阻塞指标为E_sc0，当系统并入风电场容量ΔC_w=ΔC_wr时，E_sc=E_scr，要计算风电场容量可信度，必须求出系统的E_sc=E_scr时对应的等效传统机组容量，即图 1中的ΔC_cr。由风电特点可知，等效传统机组容量位于0和风电场装机容量之间，即ΔC_c∈(0,ΔC_wr)。

图1(Figure 1)

图1 风电场容量可信度二分法几何示意图 Fig. 1 Calculating wind farm capacitycredit using the bisection method

风电场容量可信度的求解步骤如下：

1)给定收敛精度，用Monte Carlo法计算系统并入装机容量为ΔC_wr风电场后系统阻塞指标E_scr；

2)令等效传统机组初始边界为[a,b]=[0,ΔC_wr]；

3)确定等效传统机组装机容量d=(a+b)/2；形成新的系统，并计算E_scn；

4)比较新的系统E_sc指标与E_scr指标，计算误差e=E_scn-E_scr；判断是否收敛。如不收敛，且e>0，则令a=d，返回第3步；如e < 0，则令b=d，返回第3步；直到收敛结束计算，输出d即为所求风电场等效传统机组容量ΔC_cr。

图 1中，等效传统机组容量初始范围为[0,ΔC_wr]，精确解为ΔC_cr。曲线2呈单调递减特性。由前述算法知，第1次二分可得到等效传统机组容量区间为[0,ΔC_C1]，其对应阻塞指标为E_sc1；第2次二分得到区间为[ΔC_C2,ΔC_C1]，对应的阻塞指标为E_sc2。重复以上过程，可使E_sc计算值不断逼近E_scr直至达到收敛解。此时对应的等效传统机组容量ΔC_cr即为满足阻塞指标E_scr要求的等效传统机组容量。

风电场容量可信度：

利用IEEE-RTS系统^[16]进行算例分析。该系统包括230 kV和138 kV 2个电压等级，有24条母线、33条交流输电线路、5台变压器及32台发电机组，总发电容量3 405 MW，系统峰荷2 850 MW。

为突出系统阻塞特性，对IEEE-RTS进行了修改：将负荷峰值增至原系统的1.1倍。Bus6、Bus10间的电缆容量增至原系统的1.1倍，将原系统Bus1上的2台76 MW机组移至Bus18，将原系统Bus7上1台100 MW的机组移至Bus22。修改后的系统总发电容量仍保持3 405 MW，系统负荷峰值达到3 135 MW。其他系统电气参数、可靠性参数见文献[16]。

利用非时序Monte Carlo法在Matlab7.3上编制相应的程序，仿真次数为100万次；采用交流潮流，以负荷峰值作为恒定负荷的负荷模型；所有元件(发电机组、输电线路和变压器)只有两种状态，即正常和故障；当负荷总量大于机组总容量时，采用就近削减负荷策略。

本文风电场的风速历史数据源于Canada Saskatchewan风场，额定风速为19.46 km/h，标准方差为9.7 km/h^[12]，单台风电机组装机容量为2 MW。其5状态风电机组概率模型见表 2。

表2(Table 2)

表2 5状态风电机组概率模型Table 2 5-state WTG probability model 风电机组容量水平 0 0.25 0.50 0.75 1.00 概率 0.058 98 0.063 54 0.114 66 0.244 07 0.518 75

表2 5状态风电机组概率模型 Table 2 5-state WTG probability model

对修改的IEEE-RTS，原系统受阻电量E_sc0为82.27 MW·h/a。

分别在修改的IEEE-RTS的4个位置并入一定容量的风电场，其余电气参数不变。为简化计算和分析，假设如下：

方案1：Bus1并入100 MW风电场;

方案2：Bus7并入100 MW风电场;

方案3：Bus8并入100 MW风电场;

方案4：Bus13并入100 MW风电场;

方案5：Bus1并入120 MW风电场。

需要说明的是，在修改的IEEE-RTS中，相对于原系统，Bus1和Bus7上均有常规机组移至北部，而Bus1上移至北部的常规机组总容量大于Bus7，Bus1相对缺电一些，故在实验中，增加方案5，即在Bus1并入120 MW风电场。由于风电场容量可信度β_CC是一个相对值，并入风电场容量的大小不会影响对结果的分析。

针对这5个方案，分别计算系统阻塞指标E_sc、风电阻塞指标B_SCE，利用二分搜索法求解等效传统机组容量和风电场容量可信度，计算结果如表 3所示。

表3(Table 3)

表3 风电场经不同母线并网的系统阻塞指标、风电阻塞指标及容量可信度Table 3 System congestion indices, wind power congestion indices, and capacity credit under different incorporation buses 方案号 并入母线 Esc/(MW·h·a-1) Δ Cw/MW Δ Cc/MW βCC BSCE/(h·a-1) 1 Bus1 57.46 100 34 0.34 0.248 1 2 Bus7 36.87 100 35 0.35 0.454 0 3 Bus8 33.03 100 31 0.31 0.492 4 4 Bus13 64.43 100 26 0.26 0.178 4 5 Bus1 49.98 120 43 0.36 0.269 1

表3 风电场经不同母线并网的系统阻塞指标、风电阻塞指标及容量可信度 Table 3 System congestion indices, wind power congestion indices, and capacity credit under different incorporation buses

从表 3可以看出，相对于原系统，5个方案的系统受阻电量E_sc指标均减小，表明它们的系统阻塞都得到不同程度的缓解。可见，将一定容量的风电场并入电网，可减轻系统阻塞程度。从5个方案可以看出，系统在不同阻塞水平E_sc下，其风电场容量可信度不一样，即β_CC与E_sc水平相关。容量可信度还与风电场并入位置有关，同样容量为100 MW的风电场，方案1、2、3、4由于并入位置不同，它们的E_sc、β_CC、B_SCE存在较大差异，尤其是方案3和方案4。这是因为各母线和系统联系的输电线容量有差异，使得相同容量的风电场并入不同位置缓解系统阻塞的效果不一样。5个方案中，方案4的E_sc、β_CC、B_SCE指标均最差，说明在4个位置中，Bus13并入风电场效果最不理想。

从表 3还可以看出，与方案1相比，由于方案5在Bus1接入的风电场容量由100 MW增至120 MW，其E_sc、β_CC、B_SCE均好转。5个方案中，方案5的β_CC指标最好，但其E_sc、B_SCE指标明显不如方案2和方案3。可见单纯评价β_CC指标具有片面性，这是由于β_CC虽能较好地反映在某水平系统阻塞指标下风电场与常规机组改善阻塞的贡献的相对值，但是在考虑输电网络元件故障以后，风电场和传统机组的阻塞指标都受到网络的影响，相对值就不能反映风电场对缓解阻塞程度贡献的影响，但B_SCE恰恰是它的补充。因此，综合考虑β_CC和B_SCE指标才能更好地评价风电场并入大电网对系统阻塞状况改善的有效性和经济性。

通过对修改的IEEE-RTS实验系统进行算例分析，得出以下结论：

1)装机容量相同的风电场并入大电网的不同位置，系统阻塞状况的缓解程度可能不一样。

2)风电场容量可信度β_CC反映了风电场与传统机组缓解阻塞状况贡献的相对值，风电出力对输电阻塞的贡献指标B_SCE反映了风电场缓解阻塞贡献的大小。将β_CC和B_SCE相结合可以更好地评价风电场并网对系统阻塞状况改善的有效性和经济性。本研究有助于拓展风电场规划理论，风电场并网时既要考虑系统可靠性又要考虑系统阻塞状况。这为系统规划人员和风电投资者在风电场的选址、风电场建设规模等方面科学决策提供了更丰富的信息。这里仅考虑单个风电场并入电网的情形，下一步将对多个风电场并入电网的情形进行研究。