2. 中国矿业大学(北京) 煤炭资源与安全开采国家重点实验室, 北京 100083
2. State Key Laboratory for Coal Resources and Safe Mining, China University of Mining and Technology(Beijing), Beijing 100083, P. R. China
岩石单轴抗压强度(uniaxial/unconfined compressive strength,UCS)既是反映岩石力学性能的基本指标,又是岩石力学与工程领域应用最为广泛的强度指标[1, 2, 3, 4],被广泛应用于岩体分类、岩石地下工程开挖与支护、岩石边坡工程稳定性分析、岩石地基工程地基承载力计算等领域的工程设计与计算中。
目前,岩石力学与工程中单轴抗压强度仍广泛采用国际岩石力学学会(ISRM)建议的方法[5],即取几组岩样的平均值(下文简称“单值点指标”或传统值)为单轴抗压强度。由于岩样数量的有限性与岩石强度分布的随机性,以及试验过程中产生的系统误差等多种不确定性因素的影响,导致岩样强度呈现出较明显的离散性。现有的“单值点指标”方法没能给出数据的精确程度及误差范围,即给出的数据“信息不足”,致使获得的强度指标值可能存在较大误差甚至失真,且不同试验条件下得到的各组试验数据之间的横向比较的可靠性得不到保证。Yamaguchi[6]用统计学方法研究了测定岩石强度所需的岩样数量问题,发现测定岩样强度需要至少10个岩样等规律;Kostak等[7]对420个Matinenda砂岩岩样进行试验,依据岩样中原始裂纹对其影响造成的破坏形式,将岩样划分为完整岩样(sound core)与缺陷岩样(defective core),发现了320个完整岩样与100个缺陷岩样的单轴抗压强度均分别服从相应的正态分布,且岩样强度具有很强的离散性等规律;Pretorius[8]认为岩样强度的差异大小与取样空间位置有关,岩石力学参数具有区域(空间)分布随机特性;Gill等[9]用统计学方法中的小样本理论分析了岩样数量与岩石力学参数值之间的关系,认为所需最小岩样数量随岩石类型、试验方法等改变而改变;Ruffol等[10]研究了岩样数量对单轴抗压强度的影响,得到了为获得岩石强度所需最小岩样数量与所选统计方法及允许偏差等有关的结论;黄志全等[11]基于随机模糊概率理论提出了相应的置信度分析模型;董陇军等[12]用区间分析、未确知数学理论分析了区间内不同强度代表值的可信度,且认为不能排除区间强度可能存在非真实信息的可能。
由于室内试验需要系统的对大量岩样(可能达上百个)进行采集、加工与试验,具有成本高、耗时长、干扰因素多等缺点,往往无法系统实施并取得理想效果。因此,笔者以文献[7, 10]中的数据为例,系统研究岩石单轴抗压强度的置信区间、置信度、最大相对偏差、允许偏差、岩样强度分布的随机性等之间的关系。
1 岩样单轴抗压强度的“区间估计指标”由于岩样单轴抗压强度近似服从正态分布(normal(Gaussian)distribution)[7, 9, 10],故在下文中的理论计算中假设岩样单轴抗压强度服从正态分布,依据数理统计知识[13],将在置信度为1-α下岩样单轴抗压强总体均值μσc的置信区间定义为
| ${\mu _{{\sigma _c}}} = \left[{{\sigma _{{\text{c - lower}}}},{\sigma _{c - upper}}} \right]$ | (1) |
根据选取区间估计的要求,取
| $T = \frac{{{{\bar \sigma }_{\text{c}}} - {\mu _{{\sigma _c}}}}}{{\frac{S}{{\sqrt n }}}}~t\left( {n - 1} \right)$ | (2) |
由t分布的分位数定义知
| $P\left\{ {\left| T \right|{\text{ < }}{t_{1 - \frac{a}{2}}}\left( {n - 1} \right)} \right\} = 1 - a$ | (3) |
| $P\left\{ {{{\bar \sigma }_c} - \frac{S}{{\sqrt n }}{t_{1 - \frac{a}{2}}}\left( {n - 1} \right){\text{ < }}{\mu _{{\sigma _c}}}{\text{ < }}{{\bar \sigma }_c} + \frac{S}{{\sqrt n }}{t_{1 - \frac{a}{2}}}\left( {n - 1} \right)} \right\} = 1 - a$ | (4) |
单轴抗压强度总体均值的置信下限σc-lower与置信上限σc-upper分别为
| $ {\sigma _{{\text{c - lower}}}} = {\bar \sigma _c} - \frac{S}{{\sqrt n }}{t_{1 - \frac{a}{2}}}\left( {n - 1} \right)$ | (5) |
| ${\sigma _{{\text{c - upper}}}} = {\bar \sigma _c} - \frac{S}{{\sqrt n }}{t_{1 - \frac{a}{2}}}\left( {n - 1} \right)$ | (6) |
样本标准差S与样本相对标准标差(变异系数)cv由式(7)确定
| $S = \sqrt {\frac{1}{{n - 1}}\sum\limits_{i = 1}^n {{{\left( {{\sigma _i} - {{\bar \sigma }_{\text{c}}}} \right)}^2}} } $ | (7) |
| ${c_{\text{v}}} = \frac{S}{{{{\bar \sigma }_{\text{c}}}}} \times 100\% $ | (8) |
式中:${{{\bar \sigma }_{\text{c}}}}$为岩样单轴抗压强度样本均值;t1-α/2(n-1)为自由度为(n-1)的t分布的分位数。
同理,将在置信度为1-α下岩样单轴抗压强总体标准差Δσc的置信区间定义为
| ${\delta _{{\sigma _{\text{c}}}}} = \left[{{\delta _{{\text{lower}}}},{\delta _{{\text{upper}}}}} \right]$ | (9) |
根据选取区间估计的要求,取
| ${\chi ^2} = \frac{{\left( {n - 1} \right){S^2}}}{{{\delta ^2}}}~{\chi ^2}\left( {n - 1} \right)$ | (10) |
由χ2分布的分位数定义知
| $P\left\{ {\chi _{\alpha /2}^2\left( {n - 1} \right){\text{ < }}\frac{{\left( {n - 1} \right){S^2}}}{{{\delta ^2}}}{\text{ < }}\chi _{\alpha /2}^2\left( {n - 1} \right)} \right\} = 1 - \alpha$ | (11) |
| $P\left\{ {\frac{{\left( {n - 1} \right){S^2}}}{{\chi _{1 - \alpha /2}^2\left( {n - 1} \right)}}{\text{ < }}{\delta ^{\text{2}}}{\text{ < }}\frac{{\left( {n - 1} \right){S^2}}}{{\chi _{\alpha /2}^2\left( {n - 1} \right)}}} \right\} = 1 - \alpha $ | (12) |
单轴抗压强度总体标准差的置信下限Δlower与置信上限Δupper分别为:
| ${\delta _{{\text{lower}}}} = \sqrt {\frac{{\left( {n - 1} \right){S^2}}}{{\chi _{1 - \alpha /2}^2\left( {n - 1} \right)}}} ,$ | (13) |
| ${\delta _{{\text{upper}}}} = \sqrt {\frac{{\left( {n - 1} \right){S^2}}}{{\chi _{\alpha /2}^2\left( {n - 1} \right)}}} $ | (14) |
式中:χα/22(n-1)与χ1-α/22(n-1)为自由度为(n-1)的χ2分布的分位数。
上述系统计算方法就构成了确定岩样单轴抗压强度的“区间估计指标”体系,该体系通过置信区间和置信度等参数,克服了“单值点指标”给出的数据“信息不足”的缺陷,给出了数据的精确程度及误差范围,且包含更丰富的信息并便于不同试验条件下得到的各组试验数据之间的横向比较,是现有“单值点指标”方法的补充。
值得注意的是,以上理论推导均建立在岩石单轴抗压强度服从正态分布假设的基础上,但也有学者发现极少数种类岩石的强度服从其他分布,如Pincus[14]发现一些岩石的单轴抗压强度用对数正态分布表示更为合适。岩石单轴抗压强度的具体分布形式对岩样强度平均值等的估计有一定的影响,由于岩样强度不可能为负值,所以采用正态分布计算出的岩样强度值可能偏低,趋于保守,而采用Weibull分布得到的计算结果可能更趋于准确,但是Weibull分布与正态分布极其相似,从工程安全的角度分析,采用正态分布进行计算是合适的,同时也是简单可行的。此外,文献[1]对上万个岩样(天然及饱和抗压强度的总有效试验数据8 958×2个)进行统计发现其强度服从正态分布,也为假设岩样单轴抗压强度服从正态分布提供了佐证。
2 实例验证应用与分析 2.1 试验方法 2.1.1 岩样采集、加工与试验[7, 10]在Rio Algom Nordic Mine采集Matinenda砂岩,分两排共20个孔钻取岩芯,从每个钻孔中加工出21个岩样,总共420个岩样,依据岩样中原始裂纹对其影响造成的破坏形式,将岩样划分为完整岩样与缺陷岩样,完整岩样为320个(均值为239.1 MPa,标准差为35.4 MPa),缺陷岩样为100个(均值为144.4 MPa,标准差为65.8 MPa),岩样直径为54 mm,高径比为2左右,具体信息详见文献[7];从某地采集Milbank花岗岩,共加工成50个岩样,岩样直径为54 mm,高径比为2~2.5,具体信息详见文献[10]。
2.1.2 数据处理与分析步骤借助Excel分别对Matinenda砂岩中的320个完整岩样、100个缺陷岩样与Milbank花岗岩中的50个完整岩样进行随机抽样,并借助Excel的统计功能计算单轴抗压强度的置信区间等值。
具体试验方案:
1)从Matinenda砂岩的320个完整岩样中分别随机抽取3,4,…,15,20,25,30,35,40,50个岩样,岩样数量为3~10时,抽取10次;岩样数量为11~15时,抽取5次;其余抽取3次。
2)从Matinenda砂岩的320个完整岩样中随机抽取10个岩样。
3)分别从Matinenda砂岩的320个完整岩样、Matinenda砂岩的100个缺陷岩样、Milbank花岗岩的50个完整岩样中随机抽取10个岩样。
4)从Matinenda砂岩的100个缺陷岩样中分3次随机抽取5个岩样。
2.2 岩样数量对“单值点指标”样本均值、样本标准差的影响320个Matinenda砂岩完整岩样的单轴抗压强度平均值、标准差分别为239.1 MPa与35.4 MPa,现以239.1 MPa与35.4 MPa分别代表名义总体均值与名义总体标准差。按照试验方案1)操作后,对数据进行处理,得到不同岩样数量下样本均值、样本标准差的值。
2.2.1 岩样数量对样本均值的影响不同样本数量下得到的样本均值及样本均值最大相对偏差如图 1所示。从图 1(a)可以看出,当样本数量较小时,岩样单轴抗压强度样本均值呈现较明显的离散性,随岩样数量的增加,样本均值越来越趋于名义总体均值。从图 1(b)可以看出,当样本数量≥5时,样本均值相对偏差在±11.3%内;当样本数量>10时,样本均值相对偏差在±7.2%内;当样本数量>20时,样本均值相对偏差在±5.5%内,样本均值相对偏差绝对值大体上随岩样数量的增加而减小,但并不是严格的减小,这可能是由于岩样强度分布的随机性造成的,下文2.6节将详细介绍,不再敖述。

|
图1 岩样数量对岩样单轴抗压强度样本均值的影响 Fig. 1 Effect of the number of test samples on sample average of uniaxial compressive strength of rock specimen |
不同样本数量下得到的样本标准差如图 2所示。从图 2可以看出,当样本数量较小时,岩样单轴抗压强度样本标准差波动性很高,可达数十倍,远高于样本均值的波动性,比样本均值的波动性约高一个数量级,且随岩样数量的增加,样本标准差越来越趋于名义总体标准差,当岩样数量≥20时,样本标准差才趋于稳定,这与Spiegel的“只有当样本数量大于30时,才可用样本标准差代替总体标准差”的结论相似[15],岩样数量为20与30的差别是由于岩石种类、加工与试验精度等差异造成的。通常岩样单轴抗压强度的总体标准差是不知道的,所以得到的样本标准差在使用时应慎重,只有岩样数量足够大时,才可用样本标准差表示总体标准差,而通常的试验岩样数量是小于20或30的,因此,得到的样本标准差具有很大的随机性,只可供参考使用。

|
图2 岩样数量对岩样单轴抗压强度样本标准差的影响 Fig. 2 Effect of the number of test samples on sample standard deviation of uniaxial compressive strength of rock specimen |
定义单轴抗压强度总体均值最大相对偏差η为最大偏差Δσc与样本均值σc之比,即
| $\eta = \frac{{\Delta {\sigma _{\text{c}}}}}{{{{\bar \sigma }_{\text{c}}}}} = \frac{{\frac{{\left( {{\sigma _{{\text{c - upper}}}} - {\sigma _{{\text{c - lower}}}}} \right)}}{2}}}{{{{\bar \sigma }_{\text{c}}}}} \times 100\%$ | (15) |
式(1)可改写成
| ${\bar \sigma _{\text{c}}} - \eta {\bar \sigma _{\text{c}}} \leqslant \mu {\sigma _{\text{c}}} \leqslant {\bar \sigma _{\text{c}}} + \eta {\bar \sigma _{\text{c}}}$ | (16) |
亦可得到
| $1 - \eta \leqslant \frac{{{\mu _{{\sigma _c}}}}}{{{{\bar \sigma }_c}}} \leqslant 1 + \eta $ | (17) |
将式(5)与(6)带入式(15),得到
| $\eta = \frac{{\frac{S}{{\sqrt n }}{t_{1 - \frac{\alpha }{2}}}\left( {n - 1} \right)}}{{{{\bar \sigma }_{\text{c}}}}}$ | (18) |
把式(8)中cv带入式(18),得到
| $ \eta = \frac{{{c_{\text{v}}}}}{\eta }{t_{1 - \frac{\alpha }{2}}}\left( {n - 1} \right)$ | (19) |
可求出岩样数量n,
| $n = {\left[{\frac{{{c_{\text{v}}}}}{\eta }{t_{1 - \frac{\alpha }{2}}}\left( {n - 1} \right)} \right]^2}$ | (20) |
定义η0为单轴抗压强度总体均值允许最大相对偏差,计算公式为:
| ${\eta _0} = \frac{{\Delta {\mu _{{\sigma _c}}}}}{{{\mu _{{\sigma _c}}}}} \times 100\% $ | (21) |
由于n为整数,所以求出的与n相对应的η要满足式(22),即
| $\eta \leqslant {\eta _0}$ | (22) |
由式(22)可以看出,理论上η与总体均值置信区间宽度均随岩样数量的增加而减小,且随cv的增大而增大。
2.3.1 岩样数量对总体均值置信区间的影响同上,按照试验方案1)操作后,对数据进行处理,得到在置信度1-α=95%的情况下的岩样数量对置信区间的影响,如图 3所示。从图 3(a)可以看出一些统计规律:当岩样数量较小时,置信下限与置信上限均呈现较显著的离散性;随岩样数量的增大,置信下限与置信上限均向名义总体均值“靠拢”,且当岩样数量增大到一定程度时,均分别趋于稳定值;置信下限与置信上限近似呈对称关系,但两者并不是严格的完全对称;置信区间宽度随岩样数量的增加呈负幂函数关系不断减小。

|
图3 岩样数量对总体均值置信区间的影响 Fig. 3 Effect of the number of test samples on confidence interval for population mean |
图 3(b)指分别在不同岩样数量下得到的置信下限最小值、置信上限最大值的连线,需要说明的是,由于样本均值并不等同于总体均值,所以,同一岩样数量下的置信下限最小值与置信上限最大值并不一定来自于同一组数据。从图 3(b)可以看出,总体均值置信下限最小值与置信上限最大值均随岩样数量的增加而逐渐向名义总体均值“靠拢”,但并不是随岩样数量的增加而逐渐严格“靠拢”,这是由于岩石强度分布的随机性造成的,下文2.6节将详细介绍。
从图 3(c)可以看出,总体均值最大允许相对偏差越大,所需的岩样数量就越小。当η0=±25%时,需要的岩样数量n≥5;当η0=±20%时,需要的岩样数量n>10;当η0=±15%时,需要的岩样数量n>15;当η0=±10%时,需要的岩样数量n>25。需要说明的是,当总体均值最大允许相对偏差一定时,所需最小岩样数量还与岩石种类、试验方法等有关,对于同一种岩石,非均质性越大,所需的最小岩样数量就会越大,对于岩石非均质性与置信区间的关系,下文2.5节将详细介绍。
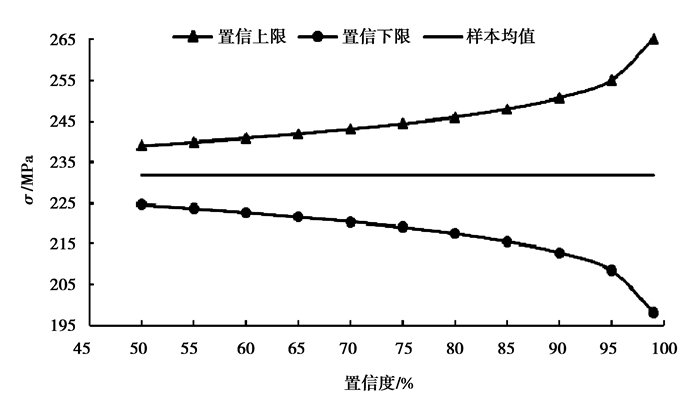
2.3.2 置信度对总体均值置信区间的影响按照试验方案2)操作后,抽样得到岩样单轴抗压强度值如表 1所示,对表 1中数据进行处理,分别得到在置信度1-α=50%~99%的情况下的岩样置信度与置信区间的关系,如图 4所示。从图 4可以看出,当岩样数量保持一定时,总体均值的置信下限与置信上限均随置信度的增加呈指数函数偏离样本均值,偏离幅度越来越大。由于当置信度超过95%时,置信区间宽度增幅明显增大,而置信区间宽度的增大就意味着偏差的增大,所以文中的其他数据处理时的置信度均是95%。同理,我们也能推测出,当岩样的置信区间宽度保持不变时,对应的置信度随着岩样数量的增加而增大,且增幅越来越小。
| 表1 岩样单轴抗压强度分布 Table 1 Uniaxial compressive strength of rock specimen distribution |
|
图4 岩样总体均值置信度与置信区间的关系 Fig. 4 The relationship between confidence level and confidence interval for population mean of rock specimen |
将式(9)改写成
| $AS \leqslant {\delta _{{\sigma _c}}} \leqslant BS$ | (23) |
其中,参数A与B为
| $A = \sqrt {\frac{{\left( {n - 1} \right)}}{{\chi _{1 - \alpha /2}^2\left( {n - 1} \right)}}} $ | (24) |
| $B = \sqrt {\frac{{\left( {n - 1} \right)}}{{\chi _{\alpha /2}^2\left( {n - 1} \right)}}} $ | (25) |
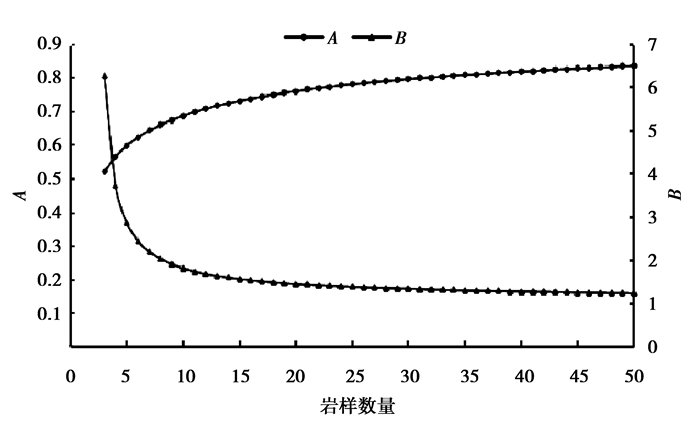
由上节2.2知,只有当岩样数量足够大时,才可用样本标准差代替总体均值标准差,样本标准差应慎重使用,因此,本节仅从理论上分析总体标准差的置信区间比上样本标准差的值与岩样数量的关系,其参数A、B与岩样数量的关系如图 5所示。从图 5可以看出,参数A随岩样数量的增加呈对数函数关系不断增大,增幅越来越小,当岩样数量>10时,参数A无限趋近于稳定值;参数B随岩样数量的增加呈倒指数函数关系不断较小,减幅越来越小,当岩样数量>10时,参数B无限趋近于稳定值。由上式可知,当岩样数量趋于无穷大时,A与B值均为1;需要说明的是,当岩样数量为50时,A的值为0.835,B的值为1.246,A的偏差为-16.5%,B的偏差为+24.6%,B的偏差绝对值较大于A的绝偏差对值,尽可能的将总体标准差值估计较大一些,这也是区间估计较保守的一个体现。
|
图5 置信度为95%时岩样数量与参数A、B的关系 Fig. 5 Variation of parameters (A) and (B) as a function of the sample size with 95% confidence level |
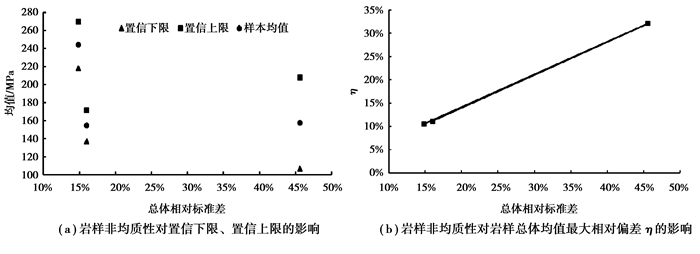
假定岩样单轴抗压强度的相对标准差越大,岩样非均质性就越强,岩样非均质性用岩样的总体相对标准差来定量表示,经计算,Matinenda砂岩的320个完整岩样、Matinenda砂岩的100个缺陷岩样、Milbank花岗岩的50个完整岩样的总体相对标准差分别为14.8%、45.6%、16.0%。按照试验方案3)操作后,得到在置信度1-α=0.95的情况下的岩样非均质性对置信区间的影响,如图 6所示。从图 6(a)可以看出,当岩样数量保持一定时,Matinenda砂岩岩样单轴抗压强度的总体均值置信区间宽度随岩样非均质性的增大而增大,而Matinenda砂岩完整岩样的总体均值置信区间宽度比Milbank花岗岩岩样的总体均值置信区间宽度大,这是由于岩石种类不同造成的。从图 6(b)可以看出,η随岩样非均质性的增大而呈线性增大。同理,也可说明对于非均质性较强的岩样,在岩样数量与置信区间一定时,其置信度低于同种非均质性较小的岩样的置信度。
|
图6 岩样非均质性对置信区间的影响 Fig. 6 Effect of heterogeneous of test samples on confidence interval of uniaxial compressive strength of rock specimens |
岩样单轴抗压强度的平均值等(包含区间估计指标)及其所需最小岩样数量均随岩石种类、试验方法等改变而改变,为得到上述指标必须通过一定数量的试验,即岩石的非均质性、非连续性、各向异性等本质属性决定了具体试验结果随岩石种类改变而不同,但整体规律是一致的。本文的研究结果仍具有广泛的指导意义,即运用本文研究结果可在一定程度上在其他条件不变时提高岩样单轴抗压强度估计值的精确程度(降低误差范围),或在满足同样的精确程度条件下可降低试验岩样的数量,总之,本文研究结果在其他种类岩石试验前虽不能对其进行精确定量分析,但对于获得丰富的试验信息及降低试验成本仍具有一定的指导作用。
2.6 岩样单轴抗压强度分布的随机性尽管岩样单轴抗压强度近似服从正态分布,但是,值得注意的是,并不是意味着随着岩样数量的增加,置信下限与置信上限逐渐严格向总体均值“靠拢”及置信区间宽度逐渐严格较小,例如在图 1(b)中,岩样数量为10时的“置信下限”比岩样数量为6,7,8,9时的还要小,这可能是由于岩样单轴抗压强度分布具有较大的随机性所造成的。
表 3所示。从表 3中可以看出:单轴抗压强度分布具有很大的随机性,3组岩样之间以及每组岩样之内的单轴抗压强度均呈现较大的离散性;由于强度分布的随机性,3组岩样的“单值点指标”样本均值、样本标准差与“区间估计指标”置信下限、置信上限等并不相同,甚至相差较大,但是整体统计规律相似。
| 表2 岩样数量为5时的单轴抗压强度分布 Table 2 Uniaxial compressive strength of rock specimen distribution when the number of test samples is 5 |
1)现有“单值点指标”方法没能给出数据的精确程度及误差范围,即给出的数据“信息不足”,不同试验操作人员、不同试验设备、不同加工精度等试验条件下,各试验组数据之间的横向比较的可靠性得不到保证。“区间估计指标”可克服其不足,包含更丰富的信息并便于不同组试验数据之间的横向比较,是现有方法的补充,且“区间估计指标”在岩样数量较小时仍可使用,只是其置信度会较低(置信区间宽度会较大)。
2)当岩样数量较小时,岩样单轴抗压强度样本均值、样本标准差均具有波动性,但样本标准差的波动性远高于样本均值的波动性,定量而言约高一个数量级,样本标准差的随机性与离散性更大且达到收敛稳定所需的岩样数量也更大。
3)岩样单轴抗压强度的“区间估计指标”置信区间、置信度等与岩样数量、岩样非均质性、岩样强度分布的随机性等有关。当置信度一定时,置信区间长度随岩样数量的增加近似呈负幂函数关系减小,且最终趋于稳定值;当置信区间长度一定时,置信度随岩样数量的增加而增大;一定置信度下的置信区间长度随着岩样非均质性的增加近似线性增大。
| [1] | 陈小平.重庆沙溪庙组地层岩石单轴抗压强度研究[J].岩土力学,2014,35(10):2994-2999. CHEN Xiaoping. Study of uniaxial compressive strength of Shaximiao formation rock in Chongqing urban area[J]. Rock and Soil Mechanics,2014,35(10):2994-2999.(in Chinese)( 2) 2) |
| [2] | Goodman R E. Introduction to rock mechanics[M]. New York:John wiley & Sons,1989.( 1) 1) |
| [3] | Jaeger J C, Cook N G W, Zimmerman R W. Fundamentals of rock mechanics[M]. New York:Wiley-Blackwell,2007.( 1) 1) |
| [4] | 蔡美峰,何满潮,刘东燕.岩石力学与工程(第二版)[M].北京:科学出版社,2013. CAI Meifeng, HE Manchao, LIU Dongyan. Rock mechanics and engineering(2nd edition)[M]. Beijing:Science Publishing House,2013.(in Chinese)( 1) 1) |
| [5] | International Society for Rock Mechanics, Commission on Standardization of Laboratory and Field Tests. Suggested methods for determining the uniaxial compressive strength and deformability of rock materials[J]. International Journal Rock Mechanics and Mining Sciences & Geomechanics Abstracts,1979,16(2):135-140.( 1) 1) |
| [6] | Yamaguchi U. The number of test-pieces required to determine the strength of rock[J]. International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts,1970,7(2):209-227.( 1) 1) |
| [7] | Kostak B, Bielenstein H U. Strength distribution in hard rock[J]. International Journal of Rock Mechanics and Mining Sciences,1971,8(4):501-521.( 5) 5) |
| [8] | Pretorius J P G. The estimation of the experimental and basic components of the observed variance of rock stren-gth[J]. Rock mechanics, 1980,13(2):119-130.( 1) 1) |
| [9] | Gill D E, Corthesy R, Leite M H. Determining the minimal number of specimens for laboratory testing of rock prop-erties[J]. Engineering geology, 2005, 78(1):29-51.( 2) 2) |
| [10] | Ruffolo R M, Shakoor A. Variability of unconfined compressive strength in relation to number of test samples[J]. Engineering Geology, 2009, 108(1):16-23.( 5) 5) |
| [11] | 黄志全, 王思敬, 李华晔, 等. 岩体力学参数取值的置信度及其可靠性[J]. 岩石力学与工程学报, 1999, 18(1):33-35. HUANG Zhiquan, WANG Sijing, LI Huaye, et al. The believable degree of mechanical parameters of rockmass and its reliability[J]. Chinese Journal of Rock Mechanics and Engineering, 1999, 18(1):33-35.(in Chinese)( 1) 1) |
| [12] | 董陇军, 李夕兵. 岩石试验抗压、抗拉区间强度及代表值可信度研究[J]. 岩土工程学报, 2010, 32(12):1969-1974. DONG Longjun, LI Xibing. Interval parameters and credibility of representative values of tensile and compression strength tests on rock[J]. Chinese Journal of Geotechnical Engineering, 2010, 32(12):1969-1974.(in Chinese)( 1) 1) |
| [13] | 盛骤, 谢式千, 潘承毅. 概率论和数理统计[M]. 北京:高等教育出版社, 2001. SHENG Zhou, XIE Shiqian, PAN Chengyi. Probability theory and mathematical statictics[M]. Beijing:Higher Education Press, 2001.(in Chinese)( 1) 1) |
| [14] | Pincus H J. Goodness-of-fit of six probability functions to some commonly used properties of rock[C]//Proceedings of the 12th Pan-American Conference on Soil Mechanics and Geotechnical Engineering and the 39th U.S. Rock Mechanics Symposium. Massachusetts:MIT, 2003:2757-2764.( 1) 1) |
| [15] | Spiegel M R. Schaum's outline of theory and problems of statistics[M]. New York:McGraw-Hill, 1961.( 1) 1) |
 2016, Vol. 39
2016, Vol. 39

