风力发电是中国发展最迅速的可再生能源产业[1]。风电机组是资金与技术密集型产品,它结构复杂,常年运行于高温、高海拔、强沙尘、台风等恶劣环境下,故障停机时间长、维修成本高。对于企业而言,设备的维修费用往往占到其总支出的15%以上[2]。因此需要通过科学的运维策略采取合理的维修活动,减少风电机组故障停机时间,提高风电机组生命周期的可用度。
系统或部件的故障往往不是瞬时发生的,通过规划检测发现故障征兆并采取维修活动,可以避免设备发生重大故障[3]。当前国内外学者对设备维修策略进行了研究,并提出了一些维修模型。在维修策略方面,苏春等[4]考虑各部件维修之间的经济相关性,以可用度为约束建立了维修模型,研究了预防性检测周期对于维修成本的影响;Cao等[5]提出了一种选择性维修方法,在规定时间内,对各部件安排不同维修活动,从而提高维修资源利用率。在维修模型方面,延迟时间(Delay-time)理论运用较广,Andrawus[6]对风电机组全生命周期的维修优化进行了详细介绍,并基于延迟时间模型制定了预防性维修方案,以成本为目标优化了检测周期;Kerres等[7]综合可用度和经济性等指标,对比多种维修策略,得出延迟时间模型对分析风电机组维修策略具有明显优势。
传统的预防性维修策略根据检测到的故障立即展开维修,中断设备正常运行,在提高设备可靠性的同时,也增加了企业的维修费用。Nakagawa等[8-10]指出在检测到系统故障的周期,立即采取维修活动是不合理的;Zhang等[11]指出:对于风电机组,常常存在多个部件在某一时间段内相继出现故障,应考虑机会维修策略,将多个部件同时维修以减少停机损失。因此可以基于延迟时间模型,推迟维修有潜在故障的部件,推迟维修具有以下优势:潜在故障未发展成为功能故障前风电机组继续运行工作,延长了部件使用时间,避免其维修过度;此时提前准备必要维修资源,或在维修推迟时间内与其他部件联合实施机会维修以减少停机时间和故障损失。
笔者通过推迟维修,利用某个部件的潜在故障延迟时间,以其他部件的随机故障为维修机会,提出了一种多部件风电机组机会维修策略,并基于延迟时间理论,建立了维修模型,结合实际故障数据求解模型。以可用度和维修成本为评价指标,动态制定了风电机组最佳维修方案。
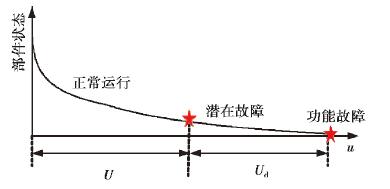
1 风电机组机会维修策略 1.1 延迟时间理论产品(部件或系统)丧失规定功能称之为故障,在故障发生之前往往能够检测到征兆,如齿轮箱振动过度,噪音、温度异常,发电机功率降低,油液成分改变等,通过维修可以及时将其消除。为了研究检测对于设备维修的重要性,延迟时间模型起到了很好的作用。延迟时间理论将故障分为两个阶段,第1阶段为新部件从开始运行至可以探测到故障征兆时的潜在故障点,称为设备正常运行阶段;第2阶段为潜在故障点到进一步发展成为功能故障,称为延迟时间阶段,由潜在故障起始点到发展成为功能故障的时间称为延迟时间Ud(见图 1)。应当说明,延迟时间与部件种类、故障类别、检测方式都有很大的关系,例如风电机组电气系统、控制系统中的电子元件在功能故障前可能没有任何征兆,故不存在潜在故障状态。延迟时间模型的关键在于确定U,Ud的分布F(u)和Fd(u),不同的分布函数对结果有很大的影响[12]。
|
图 1 延迟时间模型 Fig. 1 Delay-time module |
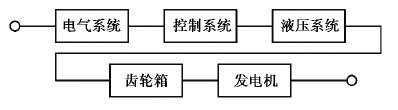
假设风电机组系统由5个关键部件串联组成,如图 2所示,任一部件发生功能故障且未及时维修时,风电机组将进入停机状态。齿轮箱和发电机的故障停机时间长、维修成本高,其故障采用延迟时间模型描述,其余部件则仅考虑正常、功能故障两种状态。笔者用随机变量U来描述各部件的故障发生时间,其密度函数为f(u),累积概率函数为F(u),即
|
图 2 风电机组可靠性框图 Fig. 2 Reliability diagram of wind turbine |
部件的可靠度为
| $ R\left( t \right) = 1F\left( t \right) = 1-\int_0^t {f\left( u \right){\rm d}u, t \ge 0} 。$ | (1) |
不同于马尔可夫(Markov)模型只能使用指数分布[13],延迟时间模型可以采用任意分布进行描述。威布尔(Weibull)分布是可靠性中广泛使用的连续型分布,这里选用两参数威布尔分布,并通过平均故障间隔时间(MTBF)进行参数估计[14]。
将风电机组的MTBF数据从小到大进行排序,对应F(ui)用中位秩法计算公式为[15]
| $ F({u_i}) = \frac{{{u_i}}}{{\left( {N + 1} \right) + 0.4}},i = 1, 2, \ldots , N。$ | (2) |
式中:ui为排序后的第i个故障数据;N为故障总数。已知威布尔分布的累积函数为
| $ F({u_i}) = 1-{{\rm e}^{ - (\frac{{{ui}}}{\alpha })}}^{^\beta }。$ | (3) |
可写成如下形式:
| $ - \beta {\rm{ln}}({u_i}) + \beta {\rm{ln}}\left( \alpha \right) = {\rm{ln}}({\rm{ln}}(1-F({u_i})))或A\left( i \right) = B\left( i \right) + k,$ | (4) |
其中
| $ \left\{ {\begin{array}{*{20}{l}} {A(\mathit{i}) = {\rm ln}({\rm ln}(1 - \mathit{F}({\mathit{u}_i}))),}\\ {B(\mathit{i}) = - \beta {\rm ln}({\mathit{u}_i}),}\\ {k = \beta {\rm ln}(\alpha )}。\end{array}} \right. $ | (5) |
β,α分别为威布尔分布的形状参数和尺度参数,通过最小二乘法对各部件分布进行参数估计,得到其故障模型。
1.2 建立机会维修模型 1.2.1 模型假设为了更好描述机会维修触发条件并简化计算,模型假设如下:1)各部件的威布尔分布相互独立,且风电机组全生命周期内故障规律不发生改变;2)周期性检测能够准确获得部件状态,发生潜在故障后,系统仍可正常运行;3)将风电机组简化为关键部件串联系统,其中齿轮箱和发电机采用延迟时间模型描述,且齿轮箱故障损失最大,推迟其维修时间,推迟期间不再进行检测;d)任一部件功能故障会引起系统停机,必须立即维修,维修方式仅考虑更换,更换后部件概率属性不变,维修时间相对于风电机组运行时间忽略不计。
1.2.2 模型建立风电机组设计生命周期为20 a,每间隔周期T检测各部件状态。X, Y分别表示其潜在故障发生和延迟时间,对应概率密度函数为fX(x)和fY(y),其余R个部件的故障发生时间Zr服从分布FZr(zr),r=1, 2, …, R。建立维修模型如下。
1) 未检测到潜在故障。
潜在故障延迟时间过短,与功能故障发生在同一检测周期内,即X和X+Y均在周期((i-1)T, iT)内。对应概率为
| $ P({F_i}) = \int_{(\mathit{i} - 1)\mathit{T}}^{iT} {{f_X}\left( x \right)} \int_0^{iT - x} {{f_Y}\left( y \right){\rm{d}}y{\rm{d}}x} , $ | (6) |
风电机组全生命周期概率为
| $ {P_{\rm{F}}} = \sum\limits_{i = 1}^N {P({F_i})}, N = \frac{{20}}{T}, $ | (7) |
式中N为全生命周期内的检测总次数。该情况下只能立即采用事后维修,所需停机时间最长,计算公式为
| $ {t_{{\rm{down}}}} = {t_{{\rm{ins}}}} + {t_{\rm{d}}} + {t_{{\rm{wait}}}} + {t_{{\rm{spar}}}} + {t_{{\rm{fix}}}}。$ | (8) |
式中:tdown表示风电机组系统累计停机时间;twait表示维修团队响应时间,响应时间服从均匀分布;td则表示维修团队通勤时间;tins则表示每次停机检测所需时间;tspar为维修资源准备时间,包括备件预定、到货及准备维修设备等;tfix表示维修固定停机时间。
2) 检测到潜在故障后采用机会维修。
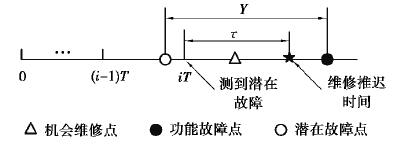
已经假设检测是完善的,设备在发生功能故障之前的一次检测周期iT一定可以发现潜在故障,且系统可继续运行至采取维修活动或发生功能故障之前。如图 3所示推迟维修潜在故障,在推迟时间τ内待其余部件发生故障再共同进行维修。此时潜在故障发生在(i-1)T, iT)内,且机会维修点在延迟时间Y和推迟维修时间τ内,即Zr < X+Y, Zr < X+τ。故在第i个检测周期采用机会维修的概率为
| $ {P_r}\left( {{O_i}} \right) = \int_{(\mathit{i} - 1)\mathit{T}}^{iT} {{f_X}\left( x \right)} \int_{\mathit{iT}}^{iT + \tau } {{f_{{Z_r}}}\left( {{z_r}} \right)} \int_{z - x}^\infty {{f_Y}\left( y \right)} {\rm{d}}y{\rm{d}}z{\rm{d}}x。$ | (9) |
|
图 3 周期性检测示意图 Fig. 3 Schematic diagram of inspection |
在推迟维修期间,其余任何部件随机故障可触发机会维修,故风电机组全生命周期概率为:
| $ \left\{ {\begin{array}{*{20}{L}} {{B_{\rm{r}}}({O_i}) = {P_{\rm{r}}}({O_i})\mathop \Pi \limits_m^s (1 - {P_{\rm{m}}}({O_i})),\mathit{r},\mathit{m = }{\rm{1,2,}} \ldots ,R,\mathit{m} \in S,\mathit{r} \notin \mathit{S,}}\\ {{P_{\rm{O}}} = \sum\limits_{i = 1}^N {P(\bigcup\limits_{r = 1}^R {{B_{\rm{r}}}({O_i})} )} }。\end{array}} \right. $ | (10) |
式中Br(Oi)表示除齿轮箱外的R个部件中,仅部件r采用机会维修,其余部件m正常运行的概率,集合S为除部件r以外的所有部件。式(10)可通过Boole不等式展开计算:
| $ P(\bigcup\limits_{r = 1}^R {{B_{\rm{r}}}} ) = \sum\limits_{r = 1}^R {P({B_{\rm{r}}}) - } \sum\limits_{r = 1}^R {P(\mathop \cup \limits_{n < r} ({B_{\rm{r}}} \cap {B_n}))}。$ | (11) |
机会维修通过将两个部件一起维修,减少固定停机时间tfix,采取维修活动前若备件未到货则需等待备件到达。
3) 检测到潜在故障后采用预防性维修。
部件潜在故障发生时间和延迟时间与上一种情况相同,由于推迟期间未触发机会维修,为避免系统发生功能故障导致停机,将在推迟维修时间τ后进行预防性维修。故在第i个检测周期采用预防性维修的概率为
| $ {P_{\rm{r}}}({P_i}) = \int_{(\mathit{i} - 1)\mathit{T}}^{iT} {{f_X}\left( x \right)} \int_{iT + \tau }^\infty {{f_{{Z_r}}}\left( {{z_r}} \right)} \int_{iT + \tau - x}^\infty {{f_Y}\left( y \right)} {\rm{d}}y{\rm{d}}z{\rm{d}}x, $ | (12) |
| $ {P_{\rm P}} = \sum\limits_{i = 1}^N {P(\bigcup\limits_{r = 1}^R {{P_\mathit{r}}({\mathit{P}_i})} )} 。$ | (13) |
4) 测到潜在故障后用事后维修。
若推迟时间过长,潜在故障未及时维修并发展为功能故障,风电机组进入停机状态,需要立即采取事后维修,并反馈给抢修团队做出维修响应。对应概率为
| $ {P_{\rm{r}}}({D_i}) = \int_{(\mathit{i} - 1)\mathit{T}}^{iT} {{f_X}\left( x \right)} \int_{iT - x}^{iT + \tau - x} {{f_Y}\left( y \right)} \int_{y - x}^\infty {{f_{{Z_r}}}\left( {{z_r}} \right)} {\rm{d}}\mathit{z}{\rm{d}}\mathit{y}{\rm{d}}x, $ | (14) |
| $ {P_{\rm{D}}} = \sum\limits_{i = 1}^N {P(\bigcup\limits_{r = 1}^R {{P_\mathit{r}}({\mathit{D}_i})} )} 。$ | (15) |
通过蒙特卡洛法模拟各检测周期内部件状态以及故障发生时间,求解该模型,获得风电机组服役20 a内所有停机时间tdown,计算可用度A(T, τ)。求解模型方程得到各维修方式的概率,并计算经济评价指标E(T, τ)。在保证可用度最大的前提下,尽可能降低维修成本,从而制定合理的维修方案。各指标计算公式为
| $ \left\{ {\begin{array}{*{20}{l}} {A\left( {T, \tau } \right) = 1-\frac{{{t_{{\rm{down}}}}}}{{8 760}}},\\ {E\left( {T, \tau } \right) = {C_{\rm{O}}}·{P_{\rm{O}}} + {C_{\rm{P}}}·{P_{\rm{P}}} + {C_{\rm{f}}}·({P_{\rm{F}}} + {P_{\rm{D}}})}。\end{array}} \right. $ | (16) |
式中CO,CP,Cf分别为采用机会维修、预防性维修和事后维修的单位成本。
2 模型求解蒙特卡洛法求解风电机组可用度流程如图 4所示,其中zr,x,y为新更换部件的故障时间,Zr,X,Y为部件累计运行时间,tO,tf,tP为部件每次维修的停机时间。

|
图 4 可用度计算流程 Fig. 4 Block diagram of wind turbine availability computation |
求解的步骤描述如下:
步骤1 初始化仿真并定义仿真中需要检测和维修的部件,指定所有数据,包括各部件服从的威布尔分布参数、维修参数、预定仿真次数、检测周期及推迟维修时间等。部件累计运行时间、系统累积停机时间初始值为零。
步骤2 重新生成各部件故障时间,可通过式(3)随机抽样获得,比较各部件故障顺序和检测周期,依次进行维修。
步骤3 根据部件故障情况采取维修活动,并计算对应的维修用时tO,tf,tP,更新系统总停机时间和累计运行时间。重复步骤2,待所有部件累计运行时间超过20 a后,计算可用度A(T, τ),并进行下次仿真。
步骤4 重复步骤1到3,直到迭代次数达到预设最大值后,计算所有A(T, τ)的平均值,输出结果。
3 算例分析以某工程技术公司的2 MW风电机组为研究对象,通过现场实测故障数据MTBF,根据式(4)拟合各部件威布尔分布参数,得到其故障模型。图 5为该型号风电机组的控制系统参数拟合结果,其余部件的MTBF拟合结果及所有维修参数如表 1所示。关于延迟时间模型,准确获得潜在故障延迟时间Ud十分困难[16],通常由经验确定,其威布尔分布参数α,β须大于0.2,且β须小于0.4,这里均取0.4。

|
图 5 控制系统X和Y的数据散点图 Fig. 5 Scatter plot of control system X and Y |
| 表 1 风电机组维修参数 Table 1 Maintenance parameters of wind turbines |
利用表 1参数初始化仿真,对模型进行求解。图 6为检测间隔3个月,不考虑推迟维修时风电机组可用度随仿真次数的变化规律。该情况下仅考虑预防性维修和事后维修,检测到潜在故障,待备件物流准备完毕后立即维修。此时可用度随着蒙特卡洛仿真次数的增加趋于97.71%,并在正负0.02%内波动,后续计算取最大迭代次数为100 000。图 7为重复100 000次蒙特卡洛仿真时可用度的频数分布,从图形可以看出,该采样近似服从正态分布,并且峰值也位于97.71%附近,说明模型结果可靠。

|
图 6 T=3/月,τ=0时的可用度 Fig. 6 Availability when T=3, τ=0 |

|
图 7 T=3/月,τ=0时的可用度分布 Fig. 7 Availability distribution when T=3, τ=0 |
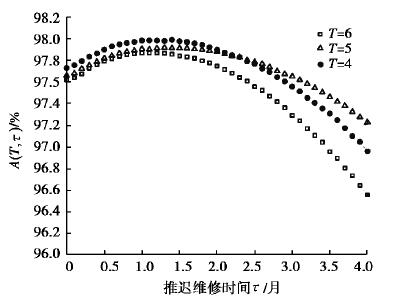
图 8为可用度曲线,从图中看出,相较于传统预防性维修,通过推迟维修(τ>0)提出的机会维修策略,可以将风电机组可用度提升至98%。由结果可知,降低间隔TT以增加检测频率,能够更好发现部件的潜在故障,但检测本身也需要将风电机组停机,间隔时间过短反而会造成系统频繁启停机。与此同时推迟维修能够延长部件使用周期,增加系统可用度,且推迟期间若其余部件发生随机故障,将通过机会维修的方式一并处理,进一步减少系统的停机时间和运维成本。但推迟维修时间过长,可用度反而降低,此时相较于传统预防性维修,机会维修不再存在优势。
|
图 8 可用度曲线 Fig. 8 Availability curve |
为了更好比较不同的方案,必须综合经济指标对风电机组维修策略进行评价。由于维修成本取决于维修方式,求解模型对应的方程,可以得到风电机组故障时采用不同维修方式的概率,取CO=10 000元、CP=18 000元、Cf=38 000元,计算风电机组一次故障的维修成本E(T, τ),结果如下。
由图 9可知,当τ=0时,PO=0,此时模型退化为不触发机会维修,随着推迟维修时间(τ>0)的增加,其余部件相继发生随机故障获得维修机会,机会维修概率逐渐增加至10%~20%。如图 10所示,尽管延长维修推迟时间τ能增加触发机会维修的概率,但也增加了部件发生功能故障导致系统停机的风险,采用事后维修的概率迅速增加至60%。由于预防性维修需在推迟维修时间τ处展开,图 11表明预防性维修概率随着推迟时间τ的增加显著降低。与此同时,若检测周期小于部件潜在故障的延迟时间,就能够有效避免发生功能故障,因此减小周期间隔T能够增加采用预防性维修和机会维修的概率,且检测周期越短效果越显著。

|
图 9 机会维修概率 Fig. 9 Probability of opportunistic maintenance |

|
图 10 事后维修概率 Fig. 10 Probability of corrective maintenance |

|
图 11 预防性维修概率 Fig. 11 Probability of preventive maintenance |
由表 2对比所得,周期性检测可提前发现潜在故障,利用延迟时间提前准备维修资源,能够提高风电机组可用度,降低维修成本。计划检测周期在3.5月,推迟维修时间在1月时的维修方案最佳。
| 表 2 风电机组维修方案 Table 2 Scheme of wind turbine maintenance |
笔者引入推迟维修的概念来描述机会维修,建立了基于延迟时间的风电机组机会维修模型。该模型可以考虑备件物流、团队响应及停机损失等因素,也能够有效描述各部件之间的维修相关性,解决了因检测周期和决策响应安排不合理造成的维修不足和维修过度。算例表明,该方法相较于传统的维修方法具有明显优势,在保证风电机组运行可用度和维修经济性的前提下,能够确定最佳检测间隔和推迟维修时间,并制定最优维修方案。
维修活动广义上不止更换部件一种,后续研究可通过不同措施如修复来扩展该模型,也可将维修对象细分到零部件来进行扩展,从而满足工程实际中对于该模型的不同应用。
| [1] |
王晓阳, 郑迪, 杨国生, 等. 混合风电场中双馈风电机组三相短路电流分析[J]. 重庆大学学报, 2018, 41(9): 19-29. WANG Xiaoyang, ZHENG Di, YANG Guosheng, et al. Analysis of three-phase short-circuit currents contributed by DFIG in hybrid wind farm[J]. Journal of Chongqing University, 2018, 41(9): 19-29. (in Chinese) |
| [2] |
Bevilacqua M, Braglia M. The analytic hierarchy process applied to maintenance strategy selection[J]. Reliability Engineering & System Safety, 2000, 70(1): 71-83. |
| [3] |
赵庆海, 赵玮, 石玉霞. 现代故障诊断技术研究现状与趋势[J]. 包装工程, 2018, 39(15): 159-165. ZHAO Qinghai, ZHAO Wei, SHI Yuxia. Present situation and trend of modern fault diagnosis technology[J]. Packaging Engineering, 2018, 39(15): 159-165. (in Chinese) |
| [4] |
苏春, 胡照勇, 郑玉巧. 基于可用度约束的风力机单部件顺序维修优化[J]. 东南大学学报(自然科学版), 2019, 49(1): 110-115. SU Chun, HU Zhaoyong, ZHENG Yuqiao. Single part sequential maintenance optimization for wind turbines based on availability constraint[J]. Journal of Southeast University (Natural Science Edition), 2019, 49(1): 110-115. (in Chinese) |
| [5] |
Cao W B, Jia X S, Liu Y, et al. Selective maintenance optimisation considering random common cause failures and imperfect maintenance[J]. Proceedings of the Institution of Mechanical Engineers, Part O: Journal of Risk and Reliability, 2019, 233(3): 427-443. DOI:10.1177/1748006X18799907 |
| [6] |
Andrawus J. Maintenance Optimization for Wind Turbine [D].Aberdeen, UK: The Robert Gordon University, 2008.
|
| [7] |
Kerres B, Fischer K, Madlener R. Economic evaluation of maintenance strategies for wind turbines: a stochastic analysis[J]. IET renewable power generation, 2015, 9(7): 766-774. DOI:10.1049/iet-rpg.2014.0260 |
| [8] |
Nakagawa T, Zhao X F. Maintenance overtime police in reliability theory: model with random working cycles[M]. London, UA: Spring-Verlag, 2015.
|
| [9] |
Nakagawa T, Zhao X. Which is better for replacement policies with continuous or discrete scheduled times?[J]. European Journal of Operational Research, 2015, 242(2): 477-486. DOI:10.1016/j.ejor.2014.11.018 |
| [10] |
Zhao X F, Nakagawa T. Over-time and over-level replacement policies with random working cycles[J]. Annals of Operations Research, 2016, 244(1): 103-116. |
| [11] |
Zhang C, Gao W, Guo S, et al. Opportunistic maintenance for wind turbines considering imperfect, reliability-based maintenance[J]. Renewable Energy, 2017, 103: 606-612. DOI:10.1016/j.renene.2016.10.072 |
| [12] |
Scheu M N, Kolios A, Fischer T, et al. Influence of statistical uncertainty of component reliability estimations on offshore wind farm availability[J]. Reliability Engineering & System Safety, 2017, 168: 28-39. |
| [13] |
Li Y, Coolen F P. Time-dependent reliability analysis of wind turbines considering load-sharing using fault tree analysis and Markov chains[J]. Proceedings of the Institution of Mechanical Engineers, Part O: Journal of Risk and Reliability, 2019, 233(6): 1074-1085. DOI:10.1177/1748006X19859690 |
| [14] |
张根保, 金传喜, 冉琰, 等. 基于FMA分解的关键质量特性映射变换技术[J]. 重庆大学学报, 2019, 42(3): 1-14. ZHANG Genbao, JIN Chuanxi, RAN Yan, et al. Mapping technique of key quality characteristics based on FMA decomposition[J]. Journal of Chongqing University, 2019, 42(3): 1-14. (in Chinese) |
| [15] |
张志春.双馈风力发电机组运行可靠性建模及若干相关问题研究[D].天津: 天津大学, 2017. ZHANG Zhichun. Research on Operational Reliability Modeling of Doubly-fed Wind Turbine and Several Related Issues[D]. Tianjin: Tianjin University, 2017. (in Chinese) |
| [16] |
Berrade M D, Scarf P A, Cavalcante V A V. A study of postponed replacement in a delay time model[J]. Reliability Engineering & System Safety, 2017, 168: 70-79. |
 2020, Vol. 43
2020, Vol. 43


