渐开线圆柱蜗杆斜齿轮传动副作为一种传递交错轴之间运动的传动形式,因其具有结构紧凑、传动平稳及振动噪声小及制造成本低等优点[1]被广泛应用于汽车和家电等轻载传动领域。
目前,国内外大量学者从啮合传动理论[2]、误差敏感性[3]及承载能力[4]等角度出发,对渐开线圆柱蜗杆斜齿轮传动副进行了研究。Sohn等[5-6]对蜗杆传动副啮合承载能力和接触区域进行了研究,分析了使用增径滚刀加工对蜗杆传动副啮合区域的影响。Nomura等[7]对不同类型的蜗杆与塑料斜齿轮进行了分析研究,给出了一种疲劳寿命的预测方法。李传闪等[8]分析了塑料蜗杆与钢制斜齿轮传动副的接触强度,得到了塑料蜗杆与钢制斜齿轮啮合的动态接触强度。赵超飞等[9]建立了直廓环面蜗杆斜齿轮传动的三维模型,分析得出了运用内凹修形方法能够减小齿面接触应力及位移量, 从而提高齿轮副的承载能力。上述对渐开线圆柱蜗杆斜齿轮传动副的研究,集中于啮合状态、加工方法以及承载能力等方面,并没有对其啮合过程中的接触特性进行分析和讨论,这使得在运动过程中无法对齿面接触位置进行合理有效的控制,增加了传动副出现疲劳失效的可能,降低了传动副使用寿命。
笔者基于齿轮啮合原理和微分几何,建立了渐开线圆柱蜗杆斜齿轮传动副的齿面接触数学模型,利用MATLAB软件进行了啮合副的运动模拟分析,系统分析了法向压力角、模数、螺旋角及传动比等几何参数对理论接触轨迹与接触面积的影响,进行了灵敏度分析并得出了几何参数对传动副接触特性的影响规律。最后以某型汽车座椅水平调节器中渐开线圆柱蜗杆斜齿轮传动副为例,进行了啮合齿面接触实验,验证其理论数学模型和分析结果的正确性。
1 齿面接触分析 1.1 齿面几何模型渐开线圆柱蜗杆斜齿轮传动副由一渐开线圆柱蜗杆和一渐开线斜齿啮合形成,其轴线呈交错形式,夹角通常为90°。
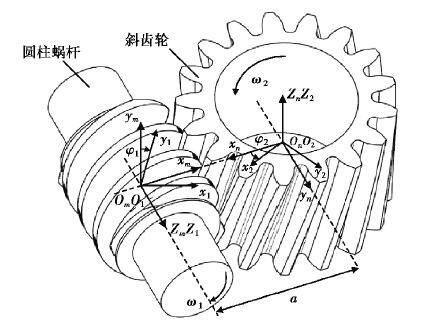
根据渐开线圆柱蜗杆斜齿轮传动副啮合传动过程,建立两构件啮合接触分析坐标系,如图 1所示。图中σm(om-xm, ym, zm)和σn(on-xn, yn, zn)为空间固定坐标系,σ1(o1-x1, y1, z1)和σ2(o2-x2, y2, z2)为2个空间运动坐标系,其中渐开线圆柱蜗杆与坐标系σ1固定连接,绕Z1轴以角速度为ω1转动,渐开线斜齿轮与坐标系σ2固定连接,绕Z2轴以角速度为ω2转动,Z1轴和Z2轴的距离a为传动副中心距。设某时刻渐开线圆柱蜗杆的角位移为φ1,渐开线斜齿轮的角位移为φ2,由传动关系可知,角位移与传动比以及两齿轮转速间的关系为
| $ \frac{{{\varphi _1}}}{{{\varphi _2}}} = \frac{{{\omega _1}}}{{{\omega _2}}} = \frac{{{z_2}}}{{{z_1}}} = {i_{21}}, $ | (1) |
|
图 1 传动副接触分析坐标系 Fig. 1 The contact analysis coordinate system of transmission pair |
式中:z1和z2分别代表渐开线圆柱蜗杆的头数和渐开线斜齿轮的齿数;i21表示传动副的传动比。
根据渐开线圆柱蜗杆加工成形原理,可得其齿面
| $ \left\{ {\begin{array}{*{20}{l}} {{\mathit{\boldsymbol{r}}_1} = {x_1}{\mathit{\boldsymbol{i}}_1} + {y_1}{\mathit{\boldsymbol{j}}_1} + {z_1}{\mathit{\boldsymbol{k}}_1}, }\\ {{x_1} = {r_{{\rm{b}}1}}{\rm{cos}}{u_1} + {\theta _1}{\rm{cos}}{\delta _1}{\rm{sin}}{u_1}, }\\ {{y_1} = {r_{{\rm{b}}1}}{\rm{sin}}{u_1} - {\theta _1}{\rm{cos}}{\delta _1}{\rm{sin}}{u_1}, }\\ {{z_1} = {p_1}{u_1} - {\theta _1}{\rm{sin}}{\delta _1}}。\end{array}} \right. $ | (2) |
式中:u1为蜗杆渐开线参数;p1为蜗杆螺旋参数;θ1为蜗杆齿面参数;rb1为蜗杆基圆半径;δ1为蜗杆基圆柱螺旋升角。
斜齿轮齿面是端面渐开线做螺旋运动的结果,可得在坐标系σ2(o2-x2, y2, z2)的齿面
| $ \left\{ {\begin{array}{*{20}{l}} {{\mathit{\boldsymbol{r}}_2} = {x_2}{\mathit{\boldsymbol{i}}_2} + {y_2}{\mathit{\boldsymbol{j}}_2} + {z_2}{\mathit{\boldsymbol{k}}_2}, }\\ {{x_2} = {r_{{\rm{b}}2}}{\rm{cos}}({u_2} + {\theta _2}) + {r_{{\rm{b}}2}}{u_2}{\rm{sin}}({u_2} + {\theta _2}), }\\ {{y_2} = {r_{{\rm{b}}2}}{\rm{sin}}({u_2} + {\theta _2}){r_{{\rm{b}}2}}{u_2}{\rm{sin}}({u_2} + {\theta _2}), }\\ {{z_2} = {p_2}{\theta _2}}。\end{array}} \right. $ | (3) |
式中:u2为斜齿轮渐开线参数;p2为斜齿轮螺旋参数;θ2为斜齿轮齿面参数;rb2为斜齿轮基圆半径。
为确定渐开线圆柱蜗杆和斜齿轮啮合时的接触轨迹,需求得蜗杆和斜齿轮在固定坐标系σm(om-xm, ym, zm)下的位置矢量和单位法矢量,利用坐标变换方法,可将坐标系σ1和σ2中的位置矢量转换到固定坐标系σm(om-xm, ym, zm)中,可得蜗杆位置矢量r1m和斜齿轮位置矢量r2m为[12]
| $ \left\{ {\begin{array}{*{20}{l}} {\mathit{\boldsymbol{r}}_1^\mathit{m} = {x_1}{\mathit{\boldsymbol{i}}_1} + {y_1}{\mathit{\boldsymbol{j}}_1} + {z_1}{\mathit{\boldsymbol{k}}_1}},\\ {{x_1} = {r_{{\rm{b1}}}}{\rm{cos}}({u_1} + {\theta _1} + {\varphi _1}) + {r_{{\rm{b1}}}}{u_1}{\rm{sin}}({u_1} + {\theta _1} + {\varphi _1})},\\ {{y_1} = {r_{{\rm{b1}}}}{\rm{sin}}({u_1} + {\theta _1} + {\varphi _1})-{r_{{\rm{b1}}}}{u_1}{\rm{cos}}({u_1} + {\theta _1} + {\varphi _1})},\\ {{z_1} = {p_1}{\theta _1}}。\end{array}} \right. $ | (4) |
| $ \left\{ {\begin{array}{*{20}{l}} {\mathit{\boldsymbol{r}}_2^m = {x_2}{\mathit{\boldsymbol{i}}_1} + {y_2}{\mathit{\boldsymbol{j}}_1} + {z_2}{\mathit{\boldsymbol{k}}_1}},\\ {{x_2} = {r_{{\rm{b2}}}}{\rm{cos}}({u_2} + {\theta _2} + {\varphi _2}) + {r_{{\rm{b2}}}}{u_2}{\rm{sin}}({u_2} + {\theta _2} + {\varphi _2})},\\ {{y_2} = {p_2}{\theta _2}},\\ {{z_2} = {r_{{\rm{b2}}}}{\rm{sin}}({u_2} + {\theta _2} + {\varphi _2})-{r_{{\rm{b2}}}}{u_2}{\rm{cos}}({u_2} + {\theta _2} + {\varphi _2})}。\end{array}} \right. $ | (5) |
同理,可得固定坐标系σm(om-xm, ym, zm)中蜗杆齿面
| $ {\rm{ }}\mathit{\boldsymbol{n}}_1^m = \frac{1}{{\sqrt {r_{{\rm{b1}}}^{\rm{2}} + p_{\rm{1}}^{\rm{2}}} }}\left[ {\begin{array}{*{20}{c}} \;\;\;{{p_1}{\rm{sin}}\left( {{u_1} + {\theta _1} + {\varphi _1}} \right)}\\ {-{p_1}cos({u_1} + {\theta _1} + {\varphi _1})}\\ {{r_{{\rm{b1}}}}} \end{array}} \right],$ | (6) |
| $ {\rm{ }}\mathit{\boldsymbol{n}}_2^m = \frac{1}{{\sqrt {r_{{\rm{b2}}}^{\rm{2}} + p_2^{\rm{2}}} }}\left[ {\begin{array}{*{20}{c}} \;\;\;{{p_2}{\rm{sin}}\left( {{u_2} + {\theta _2} + {\varphi _2}} \right)}\\ { - {r_{{\rm{b2}}}}}\\ { - {p_2}{\rm{sin}}\left( {{u_2} + {\theta _2} + {\varphi _2}} \right)} \end{array}} \right]。$ | (7) |
根据齿轮啮合原理可知,渐开线圆柱蜗杆斜齿轮传动为单自由度传动,共轭齿面每一瞬时接触为点接触,在啮合过程中,一系列瞬时接触点在齿轮齿面上形成的轨迹线为传动副的接触迹。为实现配对齿轮副正常啮合传动,蜗杆齿面
| $ \left\{ {\begin{array}{*{20}{l}} {\mathit{\boldsymbol{r}}_1^m + a = \mathit{\boldsymbol{r}}_2^m, }\\ {\mathit{\boldsymbol{n}}_1^m = \mathit{\boldsymbol{n}}_2^m}。\end{array}} \right. $ | (8) |
式(8)具有6个表达式,含有u1,u2,θ1,θ2,φ1,φ26个未知量,但实际只有5个独立方程,在求解时给定多个圆柱蜗杆初始转角φ1值,就可计算出具有5个未知量的非线性方程组,并根据解出的渐开线参数u和齿面位置参数θ可得瞬时接触点在两齿面上的具体位置。其中通过u1,θ1可得渐开线圆柱蜗杆啮合齿面的接触点位置,通过u2,θ2可得斜齿轮啮合齿面接触点的位置。
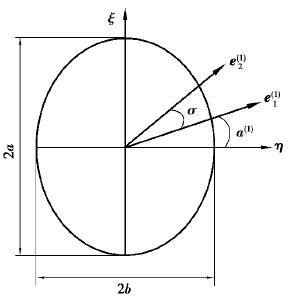
1.3 接触区域面积求解渐开线圆柱蜗杆斜齿轮传动副受载接触时,由于两配对轮齿在材料、刚度等方面存在不同,在瞬时接触点会发生弹性变形,瞬时接触点会变成瞬时接触面,理论接触面近似于椭圆形[15],如图 2所示。e1(1)和e2(1)分别为圆柱蜗杆和斜齿轮的主方向的单位矢量,a(1)为接触点处齿面主方向上的单位矢量与接触椭圆短轴的夹角,σ为向量e1(1)和e2(1)之间的夹角。a(1)和σ的关系为
| $ {\mathit{\boldsymbol{a}}^{(1)}} = \frac{1}{2}{\rm{arctan}}\left( {\frac{{{g_2}{\rm{sin}}2\sigma }}{{{g_1}-{g_2}{\rm{cos}}2\sigma }}} \right),$ | (9) |
|
图 2 瞬时接触椭 Fig. 2 Instantaneous contact ellipse |
则接触椭圆长轴长度和短轴长度分别为
| $ \left\{ {\begin{array}{*{20}{l}} {a = \sqrt {\left| {\frac{\gamma }{A}} \right|} ,b = \sqrt {\left| {\frac{\gamma }{B}} \right|} },\\ {A = \frac{1}{4}[K_\mathit{\Sigma }^{(1)}-K_\mathit{\Sigma }^{(2)}-{{(g_1^2-2{g_1}{g_2}{\rm{cos}}2\sigma + g_2^2)}^{\frac{1}{2}}}]},\\ {B = \frac{1}{4}[K_\mathit{\Sigma }^{(1)}-K_\mathit{\Sigma }^{(2)}+{{(g_1^2+2{g_1}{g_2}{\rm{cos}}2\sigma + g_2^2)}^{\frac{1}{2}}}]}。\end{array}} \right. $ | (10) |
式中:γ为相对变形量,常取0.006 35 mm,
上述推导可得接触椭圆长短轴分别为a和b,故接触区域面积:
| $ S = {\rm{ \mathsf{ π} }}ab。$ | (11) |
根据上述渐开线圆柱蜗杆与斜齿轮的接触分析模型,选取某型汽车电动座椅调节器中渐开线圆柱蜗杆斜齿轮传动副为例进行计算,其主要几何参数如表 1所示。
| 表 1 渐开线圆柱蜗杆与斜齿轮传动副几何参数 Table 1 Structure parameters of involute cylindrical worm and helical gear |
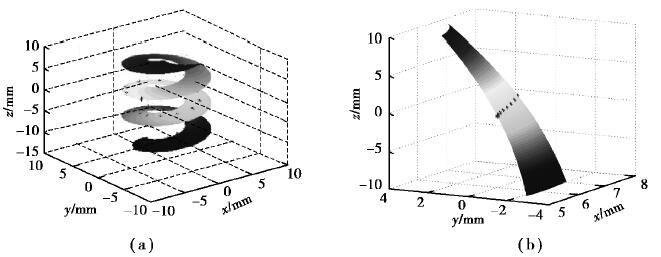
将上述几何参数代入渐开线圆柱蜗杆与斜齿轮接触分析模型中,可得渐开线圆柱蜗杆齿面瞬时接触点的分布情况如图 3(a)所示,斜齿轮齿面瞬时接触点的分布情况如图 3(b)所示。
|
图 3 蜗杆斜齿轮啮合齿面接触迹分布 Fig. 3 The contact trajectory distribution of worm and helical gear |
图 3所示两齿轮接触时,圆柱蜗杆齿面接触轨迹从基圆处出发绕蜗杆轴向旋转延伸至齿顶圆处,斜齿轮齿面接触轨迹从齿宽中部出发,成某一角度向齿顶部延伸。
2.2 接触特性规律根据上文提出的基于空间啮合理论的渐开线圆柱蜗杆斜齿轮接触几何学模型,分别考察螺旋角β、法向模数mn、法向压力角an和传动比i等因素对渐开线圆柱蜗杆斜齿轮传动副接触区域面积以及接触迹分布的影响规律。
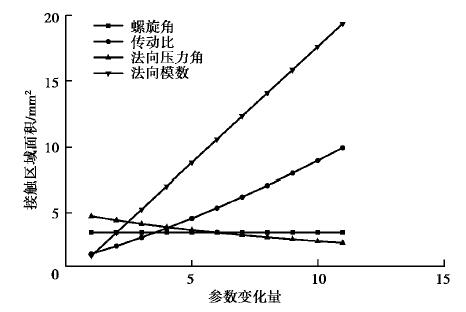
2.2.1 多种因素对接触区面积的影响规律以表 1实例中具体几何参数为基础,斜齿轮螺旋角取β∈(10°, 30°),传动比取i∈(5, 15),法向模数取mn∈(0.5, 5.5),法向压力角取其an∈(15°, 25°)。在改变上述某一影响因素的参数值时,保持其余参数不变,则可得到该影响因素对接触区面积的影响规律如图 4所示。
|
图 4 不同因素对接触区面积的影响 Fig. 4 Influence of different factors on the contact area |
由图 4可以看出在给定参数变化范围内,随着斜齿轮螺旋角β的逐渐增大,接触区面积基本不受影响,可见螺旋角的取值不影响接触区面积的大小;法向模数mn以及传动比i逐渐增大时,会使接触区面积明显增大,二者与接触面积成正相关关系;法向压力角an的增大会导致接触区面积减小,降低齿轮副的承载能力。
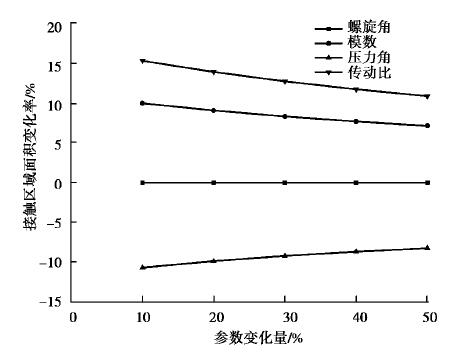
为了更为准确分析上述几何参数对接触区面积的影响规律,运用灵敏度分析方法,找出影响接触区面积的最重要参数。以表 1的几何参数为例,设置参数改变量为10%,求解基础椭圆面积的增长率如图 5所示。从图 5可以看出,接触区面积对传动比i变化最为敏感,法向模数mn与法面压力角an次之,对螺旋角β最不敏感。
|
图 5 参数改变量对接触面积增长率的影响 Fig. 5 Influence of parameter change on growth rate of contact area |
因此在进行蜗杆斜齿轮传动副设计时,若以接触区面积大小和提高承载能力为优化目标,应优先考虑对传动比i进行合理设置,适当放宽螺旋角β取值范围,并综合考虑法向模数mn和法面压力角an取值。
2.2.2 多种因素对接触迹位置的影响规律接触迹分布情况是衡量齿轮副正确啮合与否的关键因素。因此需要对接触迹分布进行合理有效的控制。根据上述模型,接触迹轨迹点位置受螺旋角β、法向模数mn、法向压力角an和传动比i等参数的影响。为了更合理地描述接触迹的位置情况,将三维空间的接触点投影到二维齿面上,二维齿面以齿宽中点为零点,齿宽长度为横坐标,齿高为纵坐标,以接触点坐标值来衡量接触迹位置,并设定用接触迹倾斜角α来衡量接触迹的偏斜情况。用μ近似表示齿面接触迹的长度。
| $ \alpha = {\rm{arctan}}\frac{{\left| {{h_{{\rm{out}}}}-{h_{{\rm{in}}}}} \right|}}{\left|{{x_{{\rm{out}}}}-{x_{{\rm{in}}}}}\right|},$ | (12) |
| $ \mu = \sqrt {{{({h_{{\rm{out}}}}-{h_{{\rm{in}}}})}^2} + {{({x_{{\rm{out}}}}-{x_{{\rm{in}}}})}^2}} ,$ | (13) |
式中:hout为退出啮合时的最后一个接触点在二维齿面上的纵坐标;hin为进入啮合时的初始接触点在二维齿面上的纵坐标;xout为退出啮合时的最后一个接触点在二维齿面上的横坐标;xin为进入啮合时的初始接触点在二维齿面上的横坐标。
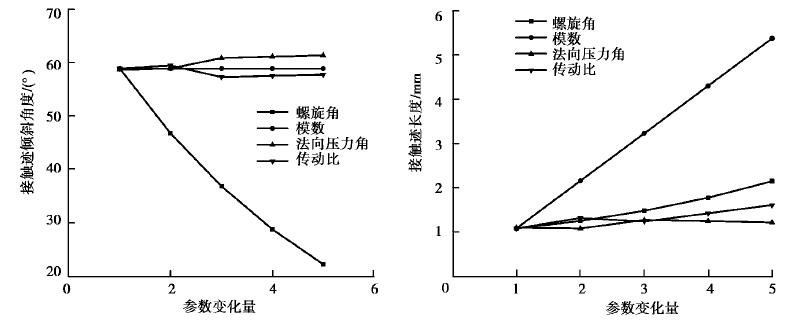
以表 1中的几何参数为标准,以斜齿轮齿面为例,具体分析螺旋角β∈(10°, 30°)、法向模数mn∈(1, 5)、法向压力角an∈(15°, 25°)和齿轮副传动比i∈(5, 10)等因素数对接触迹位置的影响规律,如图 6所示。
|
图 6 不同因素对接触迹位置的影响 Fig. 6 Influence of different factors on the positon of contact trajectory |
如图 6所示,接触迹倾斜角α随螺旋角β的增大而逐渐减小,接触迹不集中在齿宽中部初始接触点位置,其逐渐偏向一端齿廓,且接触迹长度不断变长;随着法向模数mn的增大,接触迹倾斜角α保持不变,但初始接触点会超出齿宽限定范围,可能导致边缘接触;法向压力角an的增大则会使接触迹倾斜角α小幅度增大,接触迹长度基本不变,不会引起接触位置的变化;随着传动比i的增大,接触迹倾斜角α呈现无规律变化,接触迹长度也为无规律变化,由此可得传动比i与接触迹位置无关,接触迹位置并不随传动比的不同而发生变化。
在一对齿轮发生啮合时,接触迹最佳位置应分布在齿宽中部区域,从下向上延伸,接触迹长度应小于齿宽长度,避免发生边缘接触,导致不正确啮合,增加齿轮副振动噪声。因此在进行蜗杆斜齿轮传动副设计,应将螺旋角具体参数设定尽量小,并根据设计尺寸和性能要求,选取合适的模数、法向压力角和传动比。
3 实验分析为了进一步验证本文理论模型的正确性,以表 1中的某型汽车座椅水平调节器中渐开线圆柱蜗杆斜齿轮传动副为例,进行齿面加载接触实验。
3.1 实验方法如图 7所示,将蜗杆斜齿轮装入汽车座椅水平调节器齿轮箱中,保证同轴度等位置公差的安装要求。最后涂入润滑脂,并将汽车座椅水平调节装置装入电动滑轨中进行齿面接触实验。

|
图 7 齿轮箱中蜗杆斜齿轮安装情况 Fig. 7 The installation of worm and helical gear in gearbox |
根据汽车座椅水平调节器的实际工作状态(如图 8所示),将座椅水平调节器安装至电动座椅内部,并安装在实验平台上[16],接通电机,控制座椅水平调节器先向前运动到前端终止位置,随后向后至后端终止位置,以此进行往复运动100 h。打开汽车座椅水平调节器减速箱,取出蜗杆斜齿轮传动副,观察两接触齿面的接触痕迹情况,设定实验具体参数如表 2所示。

|
图 8 汽车座椅水平调节器运行状态 Fig. 8 The operating status of HDM |
| 表 2 齿面接触实验具体参数 Table 2 The specific parameters of tooth surface contact experiment |
实验后的两齿面接触情况如图 9所示,实验前齿面光洁,无印痕,如图 9(a)所示。实验后,斜齿轮出现齿面接触痕迹,位于齿宽中部,并从齿根部位出发,成某一倾斜角度向齿顶部延伸。通过图 9(b)与图 3中的理论齿面接触位置对比可以看出,齿轮副实际啮合接触印痕与理论模型中得出的理论接触迹走向一致,证实了理论模型的正确性。

|
图 9 接触前后齿面情况对比 Fig. 9 Comparison of tooth surface conditions before and after contact |
以渐开线圆柱蜗杆斜齿轮传动副为研究对象,建立了基于空间啮合理论的齿面TCA分析模型,结合实例系统分析了螺旋角、传动比、法向压力角及法向模数等因素对蜗杆斜齿轮接触区域的影响规律,得出结论如下:
1) 传动比变化并不影响接触迹的位置,但对接触区面积的影响最为敏感,为保证齿面接触区域面积和接触强度,设计时应尽量避免改变传动副传动比。
2) 法向模数的变化会导致接触椭圆面积和接触迹长度及位置的变化,但其相对面积变化不大,设计时法向模数不宜过大。
3) 齿面接触面积对螺旋角的变化最为不敏感,但接触迹倾斜角度却受螺旋角的直接影响,设计时应在合理范围内选择小螺旋角。
4) 法向压力角与接触面积呈负相关关系,但对接触迹倾斜角有积极影响,设计时应适当减小法向压力角,以提高传动副承载能力。
| [1] |
王博.塑料斜齿轮钢制蜗杆传动强度与传动性能研究[D].长春: 吉林大学, 2016. WANG Bo. Transmission strength and performance study of plastic helical gear and steel worm drive[D]. Changchun: Jilin University, 2016. (in Chinese) |
| [2] |
李特文.齿轮几何学与应用理论[M].国楷, 叶凌云, 范琳, 等译.上海: 上海科学技术出版社, 2008. LitvinF L. Gear geometry and applied theory[M]. GUO Kai, YE Lingyun, FAN Lin, et al. translated. Shanghai: Shanghai Scientific & Technical Publishers, 2008. (in Chinese) |
| [3] |
张瑞, 武志斐, 王铁, 等. 考虑滚刀安装误差的圆柱斜齿轮接触分析[J]. 机械传动, 2016, 40(12): 61-64, 95. ZHANG Rui, WU Zhifei, WANG Tie, et al. Contact analysis of cylindrical helical gear considering the hob installation error[J]. Journal of Mechanical Transmission, 2016, 40(12): 61-64, 95. (in Chinese) |
| [4] |
He B, Huang S, He X L. Numerical simulation of gear surface hardening using the finite element method[J]. The International Journal of Advanced Manufacturing Technology, 2014, 74(5/6/7/8): 665-672. |
| [5] |
Sohn J, Park N. Geometric interference in cylindrical worm gear drives using oversized hob to cut worm gears[J]. Mechanism and Machine Theory, 2016, 100: 83-103. DOI:10.1016/j.mechmachtheory.2016.02.002 |
| [6] |
Sohn J, Park N. Modified worm gear hobbing for symmetric longitudinal crowning in high lead cylindrical worm gear drives[J]. Mechanism and Machine Theory, 2017, 117: 133-147. DOI:10.1016/j.mechmachtheory.2017.07.004 |
| [7] |
Nomura M, Koide T, Ueda A, et al. Strength of plastic helical wheels meshed with various types of worms[J]. Journal of Materials and Metallurgy, 2015, 14(3): 232-235. |
| [8] |
李传闪, 梁栋, 陈兵奎. 塑料蜗杆与钢质斜齿轮啮合特性分析及实验研究[J]. 机械传动, 2017, 41(12): 58-62. LI Chuanshan, LIANG Dong, CHEN Bingkui. Analysis of the engagement characteristic between plastic worm and steel helical gear and its experimental research[J]. Journal of Mechanical Transmission, 2017, 41(12): 58-62. (in Chinese) |
| [9] |
赵超飞, 魏冰阳. 直廓环面蜗杆-圆柱斜齿轮传动的几何建模与接触特性分析[J]. 机械传动, 2018, 42(11): 123-126. ZHAO Chaofei, WEI Bingyang. Geometric modeling and contact characteristic analysis of hindley worm and cylindrical helical gear transmission[J]. Journal of Mechanical Transmission, 2018, 42(11): 123-126. (in Chinese) |
| [10] |
Dong L Y, Liu P Y, Wei W J, et al. Study on ZI worm and helical gear drive with large transmission ratio[J]. Mechanism and Machine Theory, 2014, 74: 299-309. DOI:10.1016/j.mechmachtheory.2013.12.014 |
| [11] |
Patil S S, Karuppanan S, Atanasovska I, et al. Contact stress analysis of helical gear pairs, including frictional coefficients[J]. International Journal of Mechanical Sciences, 2014, 85: 205-211. DOI:10.1016/j.ijmecsci.2014.05.013 |
| [12] |
Liu Z Y, Huang C C, Hao Y H, et al. The mesh property of the steel involute cylindrical worm with a plastic involute helical gear[J]. Journal of Mechanics, 2014, 30(2): 185-192. DOI:10.1017/jmech.2013.70 |
| [13] |
Zhan J X, Ilie K. Static shear strength calculation of plastic helical gears mating with steel worm[J]. International Journal of Precision Engineering and Manufacturing, 2014, 15(2): 235-239. DOI:10.1007/s12541-014-0330-0 |
| [14] |
王延忠, 赫悦茗. 齿宽方向与法向修形面齿轮接触迹仿真分析[J]. 北京工业大学学报, 2018, 44(9): 1181-1186. WANG Yanzhong, HE Yueming. Simulation analysis of contact trace of face gear modified in the tooth width direction and normal direction[J]. Journal of Beijing University of Technology, 2018, 44(9): 1181-1186. (in Chinese) |
| [15] |
李传闪.塑料蜗杆与钢质斜齿轮传动理论及实验研究[D].重庆: 重庆大学, 2017. LI Chuanshan. Theoretical and experimental study on transmission mechanism of plastic worm and steel helical gear[D]. Chongqing: Chongqing University, 2017. (in Chinese) |
| [16] |
魏波, 陈永洪, 梁栋, 等. 多轴精密传动实验平台设计及动态特性分析[J]. 重庆大学学报, 2017, 40(12): 8-15, 34. WEI Bo, OHEN Yonghong, LIANG Dong, et al. Design and dynamic characteristic analysis of multi-axis precision transmission test platform[J]. Journal of Chongqing University, 2017, 40(12): 8-15, 34. (in Chinese) |
 2020, Vol. 43
2020, Vol. 43


