2. 重庆自主品牌汽车协同创新中心, 重庆 400044
2. Chongqing Automobile Collaborative Innovation Center, Chongqing 400044, P. R. China
发动机是一个复杂的非线性系统,操作参数之间互相影响,直接通过线性拟合无法满足发动机性能预测精度,所以大部分学者通过大量的物理模型和统计模型研究来预测发动机性能及排放。例如Finesso等[1]基于化学反应模型使用现象学方法开发了一种实时零维诊断模型。Guardiola等[2]结合物理模型和经验表,建立半经验NOx预测模型,并研究其计算时间和精度,实现柴油机实时控制; 结果表明这种半经验NOx预测模型全局平均误差约为15%。Gopal等[3]采用多元线性回归模型来预测由柴油、生物柴油和乙醇混合燃料的柴油发动机的性能和排放。但是不管是物理模型还是统计模型的建立都需要大量的实验来寻求相应的规律。而且基于统计模型建立发动机性能的预测模型在涉及多变量预测时预测精度不理想。
考虑到预测模型必须有强大的泛化能力及拟合非线性问题的能力,许多专家学者应用人工智能(包括神经网络(neural network)和支持向量机(support vector machine,SVM))方法预测发动机性能及排放[4-8]。但是大部分人工智能算法需要大量的训练样本才能使其具备目标精度。而广义回归神经网络(general regression neural network,GRNN)和支持向量回归(support vectot regression,SVR)具有强大的泛化能力和鲁棒性,即使在训练样本有限时,其预测精度也能满足要求。因此基于这一优点,GRNN和SVR广泛应用于内燃机领域,比如Niu等[9]通过田口正交实验设计方法设计实验,并比较分析了BP神经网络和SVM基于小样本训练时的预测性能。Bendu等[10]基于2个因素设计了27组实验,拟合得到GRNN模型预测乙醇发动机的热效率和排放等性能参数,其相对误差在2%以内。
为减少预测GDI涡轮增压发动机性能的实验成本和时间成本,笔者利用GRNN和SVR分别建立预测模型,用田口正交实验设计方法设计产生训练数据,用拉丁超立方取样算法获得测试数据,比较分析了GRNN和SVR在有限训练样本的情况下预测GDI涡轮增压发动机性能的效果。
1 仿真模型的建立和数据的获得使用1.5T缸内直喷涡轮增压发动机进行机器学习算法比较研究。缸径为76.0 mm,行程为82.6 mm,连杆长度为133.2 mm,压缩比为10。
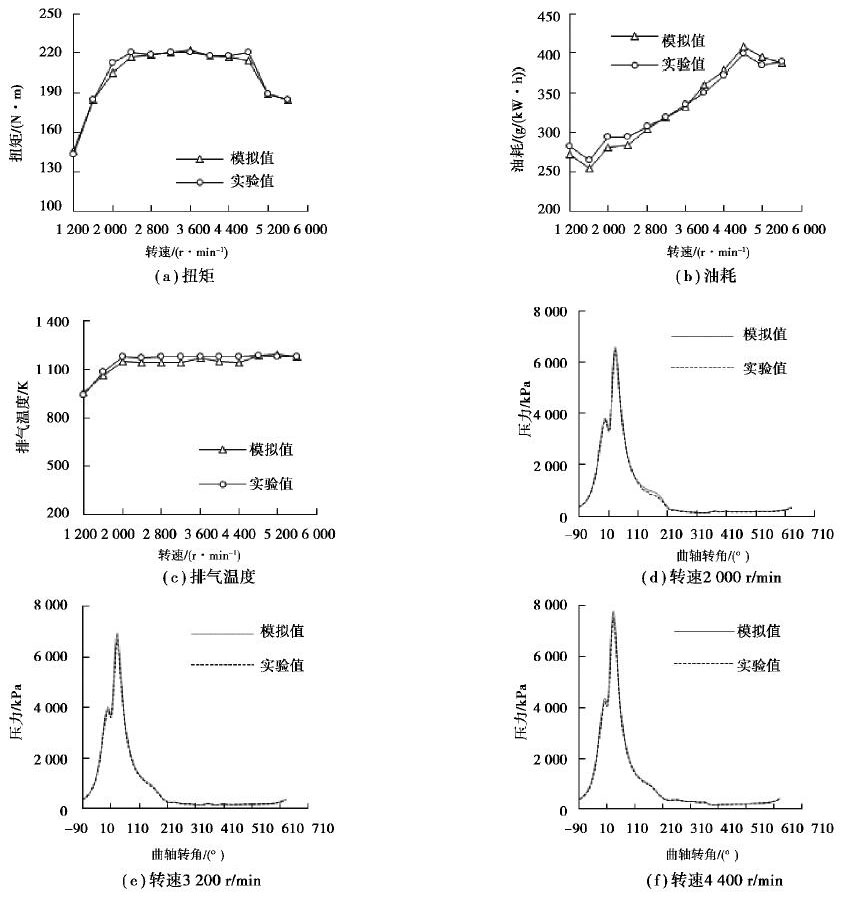
1.1 缸内直喷涡轮增压发动机仿真模型的建立及校正首先对实验数据进行对比校正,得到一个满足性能预测要求的GT-POWER模型,然后通过GT-POWER模拟仿真分别得到训练数据和测试数据。图 1是GT-POWER模型的仿真数据和实验数据的扭矩、比油耗和排气温度的对比图,误差均在5%以内。在发动机仿真计算中燃烧模型对仿真模型非常重要,图 1中列出了2 000, 3 200, 4 400 r/min转速下的缸压对比,误差均在允许范围之内。说明可以在此GT-POWER模型上做发动机外特性性能预测。
|
图 1 GT-POWER仿真值与实验值对比 Fig. 1 Comparison of GT-POWER simulation value with experimental value |
从大量的研究中发现,使用田口正交实验设计方法可以有效地减少所需的实验次数,而不会显著地影响数据的质量[11]。实验设计有4个因素,分别为进气可变气门正时(intake variable valve timing,IVVT)、排气可变气门正时(exhaust variable valve timing,EVVT)、燃烧累积放热量50%所对应的曲轴转角(crank angle 50%,CA50)和喷油始角,其中IVVT和EVVT分别指的是进气门、排气门达到最大升程所对应的曲轴转角。每个因素有5个水平。实验是在缸内直喷涡轮增压发动机定转速全负荷条件下进行的。因此,实验设计中将发动机的转速和节气门设定为常数值,操作变量的变化范围如表 1所示。田口正交设计实验产生的数据作为机器学习算法的训练数据,其操作点的取值如表 2所示。
| 表 1 操作参数变化范围 Table 1 Operating parameter range |
| 表 2 田口正交实验表 Table 2 Taguchi orthogonal experiment table |
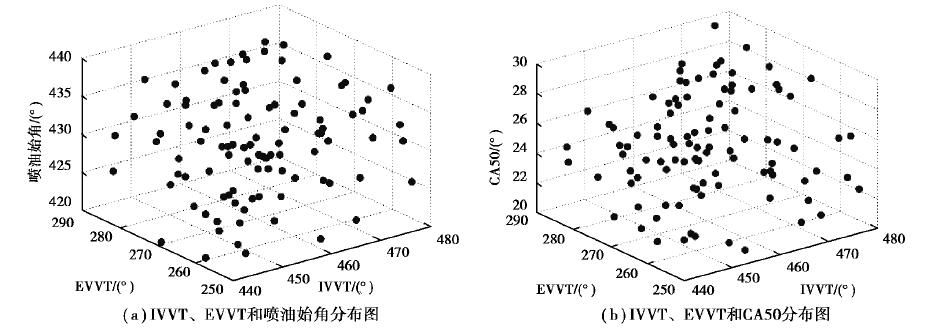
拉丁超立方取样算法(Latin hypercube sampling,LHS)实验设计方法是最常用的空间填充实验设计算法之一,应用LHS实验设计方法可以用较少的试验点覆盖变量的工作空间,而所需的试验点相比全因子实验设计方法少很多[12]。因此应用LHS实验设计方法在保证不丢失重要的系统信息的前提下大幅度降低仿真和实际实验的工作量,但是相比田口正交实验设计法所需的实验次数略多一些。故应用LHS设计实验产生测试点,图 2为应用LHS实验设计方法得到的4个操作变量的三维分布图,其变化范围如表 1所示。
|
图 2 三维分布图 Fig. 2 Three-dimensional map |
GRNN是美国学者Specht于1991提出的一种径向基神经网络[13]。GRNN具有很强的非线性映射能力和柔性网络结构以及高度的容错性和鲁棒性,非常适用于解决非线性问题,并且在样本数据较少时,GRNN具有较好的预测效果[10-11]。
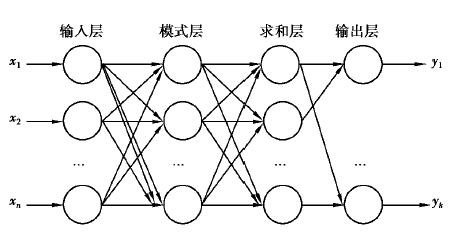
1.4.1 GRNN结构GRNN由4层神经元构成,分别是输入层、模式层、求和层以及输出层,其结构如图 3所示。图中xi (i=1, 2, 3, …, n)为第i个神经元的学习样本,yj(j=1, 2, 3, …, k)为输入对应的输出,k为输出的维度。
|
图 3 广义回归网络结构图 Fig. 3 Generalized regression neural network structure |
1) 输入层的神经元个数与训练样本的输入向量维度相等,数据直接从输入层传递到模式层。模式层神经元数目等于训练样本的数目,模式层的传递函数为:
| $ {{P}_{i}}=\text{exp}\left[- \frac{{{\left( \mathrm{x}-{{x}_{i}} \right)}^{\text{T}}}\left( \mathrm{x}-{{x}_{i}} \right)}{2{{\sigma }^{2}}} \right]。$ | (1) |
式中:Pi为模式层第i个神经元的输出;x为网络输入变量;xi为第i个神经元的学习样本;σ表示高斯函数的宽度系数,即光滑系数。
2) GRNN的求和层由分子层神经元Snj和分母层神经元Sd组成。Snj对模式层神经元输出进行加权求和,表示模式层中第i个神经元与求和层中第j个分子求和神经元之间的连接权值为第i个输出样本yi中的第j个元素;Sd对模式层神经元输出进行算术求和。传递函数如下:
| $ {S_{nj}} = \sum\limits_{i = 1}^n {{y_{ij}}{P_i}} , $ | (2) |
| $ {S_{\rm{d}}} = \sum\limits_{i = 1}^n {{P_i}} 。$ | (3) |
3) 输出层神经元将分子、分母神经元相除从而得到yj估计值:
| $ \mathop {{y_j}}\limits^ \wedge = \frac{{{S_{nj}}}}{{{S_{\rm{d}}}}}。$ | (4) |
GRNN通过从训练样本中得到输入变量与输出变量之间的联合密度函数,从而得到输出变量对输入变量的回归值。假设随机变量x和y的联合概率密度函数为f(x, y),变量x的观测值为xt,那么y相对于xt的回归值,即条件均值为:
| $ \mathop y\limits^ \wedge ({\mathit{\boldsymbol{x}}_{\rm{t}}}) = \frac{{\int_{ - \infty }^\infty {\mathit{\boldsymbol{y}}f({x_t}, \mathit{\boldsymbol{y}}){\rm d}\mathit{\boldsymbol{y}}} }}{{\int_{ - \infty }^\infty {f({\mathit{\boldsymbol{x}}_t}, \mathit{\boldsymbol{y}}){\rm d}\mathit{\boldsymbol{y}}} }}。$ | (5) |
由于在模式层神经元数目等于学习样本容量n,神经元i的输出等于输入变量与对应样本x之间的Euclid距离平方
| $ f\left( {{\mathit{\boldsymbol{x}}_{\rm{t}}}, \mathit{\boldsymbol{y}}} \right) = \frac{{\sum\limits_{i = 1}^n {{{\rm{e}}^-{\frac{{{{\left( {{\mathit{\boldsymbol{x}}_{\rm{t}}}-{x_i}} \right)}^{\rm{T}}}\left( {{\mathit{\boldsymbol{x}}_{\rm{t}}}-{x_i}} \right)}}{{2{\sigma ^2}}}}}{{\rm{e}}^-{\frac{{{{\left( {{\mathit{\boldsymbol{x}}_{\rm{t}}}-{y_i}} \right)}^2}}}{{2{\sigma ^2}}}}}} }}{{n(2{\rm{ \mathsf{ π} }})\frac{{(\mathit{q} + 1)}}{2}{\sigma ^{\mathit{q} + 1}}}}。$ | (6) |
式中:yi为神经i对随机变量y的观测值;q表示随机变量x的维数。将式(5)代入式(4)中,交换积分顺序,且化简(奇函数对称积分为0)得:
| $ \mathop y\limits^ \wedge ({\mathit{\boldsymbol{x}}_{\rm{t}}}){\rm{ = }}\sum\limits_{i = 1}^n {{y_i}{{\rm{e}}^-{\frac{{{{\left( {{\mathit{\boldsymbol{x}}_{\rm{t}}}-{x_i}} \right)}^{\rm{T}}}\left( {{\mathit{\boldsymbol{x}}_{\rm{t}}}-{x_i}} \right)}}{{2{\sigma ^2}}}}}{\rm{/}}} \sum\limits_{i = 1}^n {{{\rm{e}}^-{\frac{{{{\left( {{\mathit{\boldsymbol{x}}_{\rm{t}}}-{x_i}} \right)}^{\rm{T}}}\left( {{\mathit{\boldsymbol{x}}_{\rm{t}}}-{x_i}} \right)}}{{2{\sigma ^2}}}}}} 。$ | (7) |
当宽度系数σ取值较大时,
SVR是一种基于统计学习理论的机器学习方法,通过寻求结构风险最小来提高SVR的泛化能力,其克服了神经网络训练样本需求多、容易陷入局部最优等缺点[15-16]。
设存在样本集合
线性函数设为:
| $ f\left( \mathit{\boldsymbol{x}} \right) = \mathit{\boldsymbol{\omega }}\cdot\mathit{\boldsymbol{x}} + b。$ | (8) |
式中:ω为权值变量;b为线性函数系数。
引入松弛因子ξi、ξi*和惩罚参数C,优化问题表示为:
| $ {{\rm{min}}R\left( {\mathit{\boldsymbol{\omega }}, \xi , {\xi ^ * }} \right) = \frac{1}{2}{\mathit{\boldsymbol{\omega }}^{\rm{T}}}\cdot\mathit{\boldsymbol{\omega }} + C\sum\limits_{i = 1}^s {\left( {{\xi _i} + \xi _i^ * } \right)} },\\ {\rm{s}}{\rm{.t}}{\rm{.}}\left\{ {\begin{array}{*{20}{c}} {{y_i}-(\mathit{\boldsymbol{\omega }}\cdot{x_i} + b) \le \varepsilon + {\xi _i}, }\\ {(\mathit{\boldsymbol{\omega }}\cdot{x_i} + b)-{y_i} \le \varepsilon + \xi _i^ * , }\\ {{\xi _i}, \xi _i^ * \ge 0}。\end{array}} \right. $ | (9) |
式中:ε为不敏感损失函数;R为损失函数。
为便于求解,将上述二次规划优化问题式(9)转换为其对偶问题:
| $ \begin{array}{*{20}{c}} {{\rm{min}}J = \frac{1}{2}\sum\limits_{i, j = 1}^s {\left( {{\alpha _i}-\alpha _i^ * } \right)\left( {{\alpha _j}-\alpha _i^ * } \right)\left( {{x_i}{x_j}} \right)}- \sum\limits_{i = 1}^s {\left( {{\alpha _i}-\alpha _i^ * } \right){y_i}} + \sum\limits_{i = 1}^s {\left( {{\alpha _i}-\alpha _i^ * } \right)} {\rm{ \mathsf{ ε} }}, }\\ {{\rm{s}}{\rm{.t}}{\rm{.}}\left\{ {\begin{array}{*{20}{c}} {\sum\limits_{i = 1}^s {\left( {{\alpha _i}-\alpha _i^ * } \right)} = 0, }\\ {0 \le {\alpha _i}, \alpha _i^ * \le C\left( {i = 1, 2, \ldots , s} \right)}。\end{array}} \right.} \end{array} $ | (10) |
式中:αi、αi*为拉格朗日系数;J为引入拉格朗日系数的损失函数。
近似的回归模型可表示为:
| $ f\left( \mathit{\boldsymbol{x}} \right) = \sum\limits_{i = 1}^s {\left( {{\alpha _i}-\alpha _i^ * } \right)} K\left( {{x_i}, \mathit{\boldsymbol{x}}} \right) + b。$ | (11) |
式中K(xi, x)为核函数,为高斯核,其表达式如下:
| $ K({x_i}, \mathit{\boldsymbol{x}}{\rm{)}} = {\rm{exp}}\left( -{\frac{{||\mathit{\boldsymbol{x}}-{x_i}||{^2}}}{{{\sigma ^2}}}} \right) $ | (12) |
为了保证SVR模型的准确性,需要对惩罚参数C和高斯核参数σ的取值进行优化,本研究中采用常用的网格搜索法确定SVR模型超调参数[17]。
2 结果与讨论GRNN和SVM基于田口正交实验设计方法产生训练数据,分别得到扭矩、油耗和排气温度的预测模型。输入参数为:IVVT、EVVT、喷油始角、CA50。然后基于训练好的预测模型使用拉丁超立方取样算法设计的100组测试数据检验其预测性能。机器学习回归算法的优劣由决定系数(R2)、均方差(eMSE)以及平均绝对百分误差(eMAPE)决定,其定义公式如下:
| $ {R^2} = \frac{{{{(n\Sigma _{i = 1}^n\mathop {{y_i}}\limits^ \wedge {y_i}-\Sigma _{i = 1}^n\mathop {{y_i}} )}^2}}}{{(n\Sigma _{i = 1}^n\mathop {y_i^2-}\limits^ \wedge {{(\Sigma _{i = 1}^n\mathop {{y_i}}\limits^ \wedge )}^2-}(n\Sigma _{i = 1}^n{y_i}^2-{{(\Sigma _{i = 1}^n{y_i})}^2})}}, $ | (13) |
| $ {e_{{\rm{MSE}}}} = \frac{1}{n}\sum\limits_{i = 1}^n {(\mathop {{y_i}}\limits^ \wedge - } {y_i}{)^2}, $ | (14) |
| $ {e_{{\rm{MAPE}}}} = \frac{1}{n}\sum\limits_{i = 1}^n {\left( {\left| {\frac{{\mathop {{y_i}}\limits^ \wedge - {y_i}}}{{{y_i}}}} \right|} \right)} \times 100。$ | (15) |
GRNN模型的预测精度不同于BP神经网络模型,BP神经网络模型的预测精度不仅与其神经元的个数、层数以及初始权重和阈值密切相关,GRNN只需要通过K折交叉验证的方法确定其宽度系数。因此相对于BP神经网络,使用GRNN模型预测发动机性能将大幅度减少预测模型参数调试时间。
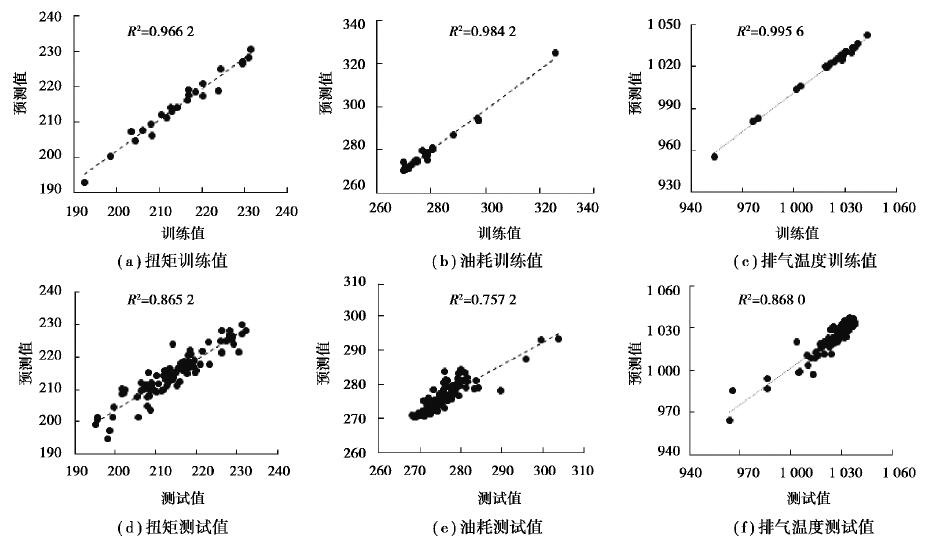
通过选择合适的宽度系数训练得到GRNN模型,训练模型的预测值与扭矩,油耗和排气温度的目标值如图 4所示。从图 4可以看出GRNN预测模型对于训练数据和测试数据的预测效果。对于训练数据,扭矩、油耗、排气温度的R2分别为0.966 2、0.984 2和0.995 6;eMSE分别为4.467 8、2.632 4和16.562 3;eMAPE分别为0.759 9%、0.386 8%和0.312 4%。以上数据说明GRNN预测模型能完美地拟合训练目标值。GRNN预测模型对于测试数据的表现比训练数据略差,对于测试数据,扭矩、油耗和排气温度的R2分别为0.865 2、0.757 2和0.868 0;eMSE分别为11.357 6、9.423 4和28.349 7;eMAPE分别为1.126 9%、0.654 7%和0.423 3%。从以上数据可以看出,GRNN预测模型能很好地预测未在训练数据之内的参数。虽然其R2偏小,但是整个预测值与目标值的相对误差均在5%以内,大部分点的相对误差保持在2%以内,说明GRNN预测模型具有较强的容错性和鲁棒性。
|
图 4 GRNN模型预测结果对比 Fig. 4 Comparison of prediction results of GRNN model |
SVR预测模型相比BP神经网络模型,超调参数只有惩罚参数C和高斯核参数σ,大幅度降低了超调参数的调整难度,但是相比GRNN模型只需优化宽度系数,SVR预测模型的超调参数在选择上难度稍大。目前广泛使用网格搜索法穷举一定范围内的惩罚参数和高斯核参数来搜索SVR模型内的全局最优点。但是使用网格搜索法的缺点在于若搜索区间过大,所需时间会很长。因为本研究的目的主要是讨论SVR和GRNN算法的预测性能,关于网格搜索法的介绍和操作,可以参考文献[17]。
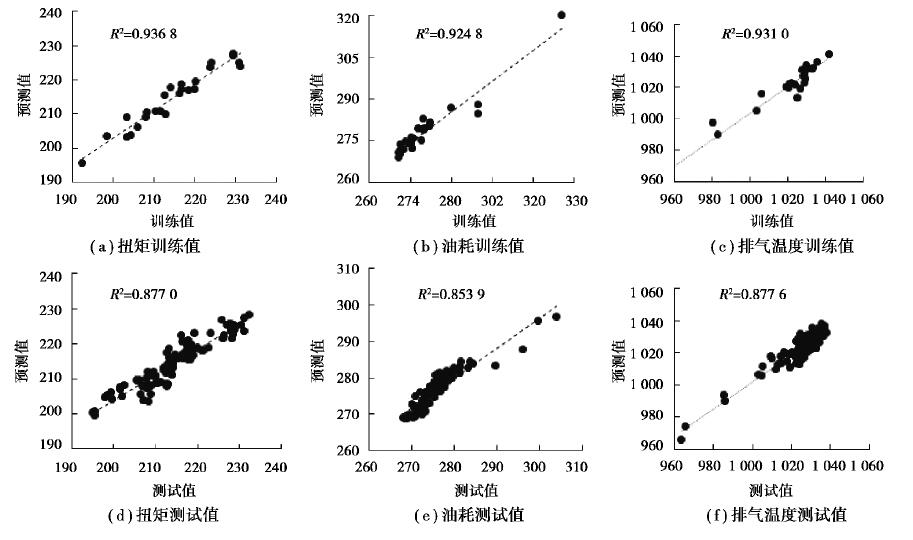
通过网格搜索法得到SVR模型最优的惩罚参数C和高斯核参数σ如表 4所示。从图 5中可以看出,不管是对训练数据还是测试数据,SVR预测的结果都很好。SVR对训练数据的表现明显优于测试数据,但是基于小样本数据,SVR对测试数据的表现相当接近于对训练数据的预测。
| 表 4 SVR模型最优惩罚参数和高斯核参数 Table 4 Optimal penalty parameters and Gauss kernel parameters of SVR model |
|
图 5 SVR模型预测结果对比 Fig. 5 Comparison of predicted results of SVR model |
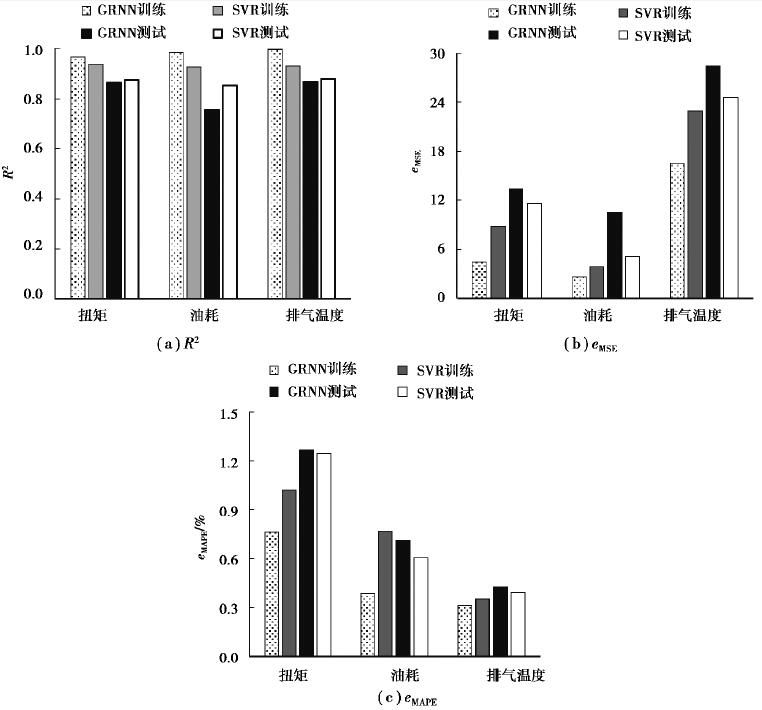
前面一部分讨论了GRNN和SVR各自对训练数据和测试数据的预测性能。从表 5可以看出,SVR模型预测性能比GRNN模型更加精准,SVR模型的预测值与目标值的相对误差几乎全部在3%以内,而GRNN模型的预测值相对分散一些。结合图 6和表 5的误差分析,尽管GRNN模型的训练数据拟合情况优于SVR模型,但是SVR模型对测试数据的预测情况优于GRNN模型,这说明SVR模型的泛化能力优于GRNN,SVR模型的寻优能力也优于GRNN。而且从GRNN模型预测扭矩和油耗的测试点可以看出GRNN可能有收敛于局部最优点的风险。
| 表 5 GRNN和SVR预测测试点的相对误差er占比 Table 5 Relative error ratio of GRNN and SVR prediction test points |
|
图 6 GRNN和SVR的R2、eMSE、eMAPE对比 Fig. 6 Comparison of R2, eMSE, and eMAPE between GRNN and SVR |
GRNN模型和SVR模型均具有强大的处理非线性问题能力、鲁棒性和泛化能力,因此GRNN模型和SVR模型广泛应用于各种研究领域。大部分机器学习算法依赖于大量的数据,为此需要大量的时间成本和经济成本。而GRNN模型和SVR模型处理小样本问题的能力十分突出。笔者基于少量的缸内直喷涡轮增压发动机仿真数据研究GRNN和SVR的预测性能,得出以下结论。
1) 基于田口正交设计实验的25组少量数据,GRNN模型和SVR模型对于测试点的预测准确性都很高。GRNN模型和SVR模型80%以上的测试样本的相对误差均在2%以内。因此可以利用GRNN模型和SVR模型预测发动机的性能,提高发动机开发速度,减少实验成本。
2) 在只有少量样本的情况下,GRNN模型的训练结果明显优于SVR模型,但SVR模型的测试结果比GRNN模型更加准确。表明SVR模型能更加快速准确地找到全局最优点,而GRNN模型有陷入局部最优点的风险。
3) 在后期研究过程中,可以使用启发式优化算法优化GRNN模型和SVR模型的超调参数,以提高GRNN模型和SVR模型的预测精度。
| [1] |
Finesso R, Spessa E. A real time zero-dimensional diagnostic model for the calculation of in-cylinder temperatures, HRR and nitrogen oxides in diesel engines[J]. Energy Conversion and Management, 2014, 79: 498-510. DOI:10.1016/j.enconman.2013.12.045 |
| [2] |
Guardiola C, López J J, Martín J, et al. Semiempirical in-cylinder pressure based model for NOX prediction oriented to control applications[J]. Applied Thermal Engineering, 2011, 31(16): 3275-3286. |
| [3] |
Gopal R, Kavandappa-Goundar M, Ramasamy S, et al. Experimental and regression analysis for multi cylinder diesel engine operated with hybrid fuel blends[J]. Thermal Science, 2014, 18(1): 193-203. DOI:10.2298/TSCI130130127G |
| [4] |
Zhao J X, Xu M, Li M, et al. Design and optimization of an Atkinson cycle engine with the artificial neural network method[J]. Applied Energy, 2012, 92: 492-502. DOI:10.1016/j.apenergy.2011.11.060 |
| [5] |
Yang F B, Cho H, Zhang H G, et al. Artificial neural network (ANN) based prediction and optimization of an organic Rankine cycle (ORC) for diesel engine waste heat recovery[J]. Energy Conversion and Management, 2018, 164: 15-26. DOI:10.1016/j.enconman.2018.02.062 |
| [6] |
胡建军, 秦大同, 杨为. 神经网络的BP算法在发动机建模中的应用[J]. 重庆大学学报(自然科学版), 2004, 27(7): 18-20. HU Jianjun, QIN Datong, YANG Wei. Application of BP NN for engine modeling[J]. Journal of Chongqing University(Natural Science Edition), 2004, 27(7): 18-20. (in Chinese) |
| [7] |
肖汉光, 蔡从中, 王万录. 利用支持向量机SVM识别车辆类型[J]. 重庆大学学报(自然科学版), 2006, 29(1): 61-65. XIAO Hanguang, CAI Congzhong, WANG Wanlu. Vehicle type recognition by using support vector machine SVM[J]. Journal of Chongqing University(Natural Science Edition), 2006, 29(1): 61-65. (in Chinese) |
| [8] |
Niu X X, Wang H C, Hu S, et al. Multi-objective online optimization of a marine diesel engine using NSGA-II coupled with enhancing trained support vector machine[J]. Applied Thermal Engineering, 2018, 137: 218-227. DOI:10.1016/j.applthermaleng.2018.03.080 |
| [9] |
Niu X X, Yang C L, Wang H C, et al. Investigation of ANN and SVM based on limited samples for performance and emissions prediction of a CRDI-assisted marine diesel engine[J]. Applied Thermal Engineering, 2017, 111: 1353-1364. DOI:10.1016/j.applthermaleng.2016.10.042 |
| [10] |
Bendu H, Deepak B B V L, Murugan S. Application of GRNN for the prediction of performance and exhaust emissions in HCCI engine using ethanol[J]. Energy Conversion and Management, 2016, 122: 165-173. DOI:10.1016/j.enconman.2016.05.061 |
| [11] |
皮骏, 马圣, 张奇奇, 等. 基于改进果蝇算法优化的GRNN航空发动机排气温度预测模型[J]. 航空动力学报, 2019, 34(1): 8-17. PI Jun, MA Sheng, ZHANG Qiqi, et al. Aero-engine exhaust gas temperature prediction model based on IFOA-GRNN[J]. Journal of Aerospace Power, 2019, 34(1): 8-17. |
| [12] |
Balki M K, Sayin C, Sarkaya M. Optimization of the operating parameters based on Taguchi method in an SI engine used pure gasoline, ethanol and methanol[J]. Fuel, 2016, 180: 630-637. DOI:10.1016/j.fuel.2016.04.098 |
| [13] |
Specht D F. A general regression neural network[J]. IEEE Trans Neutral Networks, 1991, 2(6): 568-576. DOI:10.1109/72.97934 |
| [14] |
Mansoury M, Jafarmadar S, Talei M, et al. Optimization of HCCI (Homogeneous Charge Compression Ignition) engine combustion chamber walls temperature to achieve optimum IMEP using LHS and Nelder Mead algorithm[J]. Energy, 2017, 119: 938-949. DOI:10.1016/j.energy.2016.11.047 |
| [15] |
Bendu H, Deepak B B V L, Murugan S. Multi-objective optimization of ethanol fuelled HCCI engine performance using hybrid GRNN-PSO[J]. Applied Energy, 2017, 187: 601-611. DOI:10.1016/j.apenergy.2016.11.072 |
| [16] |
Haykin S.神经网络与机器学习(原书第3版)[M].申富饶,徐烨,郑俊,等,译.北京:机械工业出版社, 2011. Haykin S. Neural networks and learning machine (3rd Edition)[M].SHEN Furao, XU Yi, ZHENG Jun, et al, trans. Beijing: China Machine Press, 2011. (in Chinese) |
| [17] |
Liu B, Hu J, Yan F W, et al. A novel optimal support vector machine ensemble model for NOX emissions prediction of a diesel engine[J]. Measurement, 2016, 92: 183-192. DOI:10.1016/j.measurement.2016.06.015 |
 2020, Vol. 43
2020, Vol. 43


