2. 黄冈师范学院 机电与汽车工程学院, 湖北 黄冈 438000;
3. 哈尔滨工业大学 交通科学与工程学院, 哈尔滨 150090
2. School of Electromechanical and Automobile Engineering, Huanggang Normal University, Huanggang, Hubei 438000, P. R. China;
3. School of Transportation Science and Technology, Harbin Institute of Technology, Harbin 150090, P. R. China
路面不平度指的是道路表面对于理想平面的偏离,是车辆行驶过程中的主要激励振源,具有影响车辆动力性能、行驶质量和路面动力载荷三者的数值特征,是车辆的平顺性和耐久性分析中必须考虑的重要因素,因此建立准确的路面模型对车辆设计和性能评估有积极的意义。
路面不平度可利用两种方法得到:一种是通过测量真实路面得到;另一种是采用数值模拟的方法,将路面不平度功率谱密度转换成随机路面不平度,此法非常适用于标准化道路的模拟。关于路面不平度,中国标准GB/T 7031—2005《机械振动道路路面路面谱测量数据报告》[1]给出了A~H共8个道路等级的不平度值,其平均值可以用于道路仿真。
关于一维路面不平度的模拟仿真,比较典型的方法有谐波叠加法(三角级数法)[2-6]、滤波白噪声模型[7-8]、一维逆傅里叶变换法[9-10]和基于时间序列分析的AR模型[11-12]。彭佳等[13]比较了4种建模方法,认为逆傅里叶变换法速度快、适用性强、理论严密,在非特定要求情况下是较为理想的方法。
实际轮胎具有宽度,所以轮胎不仅有纵向包络,也存在侧向包络,因此需要把一维路面不平度模拟仿真向二维扩展,以便适应三维的轮胎模型。
三维随机路面的研究中,吴参等[14]采用谐波叠加法建立了三维随机道路模型,彭佳等[15]采用了本质上与谐波叠加法相同的方法,这两种方法均需要大量的三角函数运算,计算速度较慢。夏均忠等[16]指出路面功率谱密度的表现形式有幂函数和有理函数两种构造,两者在本质上是一致的。唐光武等[17]把路面的有理函数功率谱函数拓展到二维,得到各向同性的二维功率谱,进而利用二维AR模型仿真得到三维随机路面。但采用有理函数功率谱需要确定与路面等级有关的功率谱的参数。罗竹辉等[18]采用了这种有理函数二维功率谱模型,计算了A~H级路面对应的功率谱参数,然后通过二维傅里叶逆变换,建立了三维随机路面。
为避免文献[18]中的参数估计,笔者直接采用中国标准中的幂函数功率谱函数进行拓展,并且根据二维傅里叶逆变换生成三维随机路面,可以使用成熟快速的FFT(Fast Fourier Transform, 快速傅里叶变换)算法。
1 路面不平度的标准路面谱路面不平度表示道路表面对于理想平面的偏离,可以看作是各态历经的平稳随机过程,中国标准[1]按照功率谱密度将路面不平度分为A~H共8个等级。
1.1 路面不平度的一维功率谱密度中国标准[1]采用式(1)拟合路面纵断面高程位移功率谱:
| $ {G_{\rm{d}}}\left( n \right) = {G_{\rm{d}}}({n_0})\left( {\frac{n}{{{n_0}}}} \right)w。$ | (1) |
式中:n为空间频率,即波长的倒数,单位为m-1;n0为参考空间频率,取值为0.1 m-1;Gd(n0)为路面不平度系数,单位为m3,不同等级的路面有不同的不平度系数;w为频率指数,取2,为功率谱密度双对数坐标图下的斜率;Gd(n)为功率谱密度,单位为m3。
由于Gd(n)为单边谱密度,计算时常用的是双边谱,令其对应的双边谱密度为Sd(n),由于Sd(n)为偶函数,有Sd(n)=Gd(n)/2,所以进一步简化式(1)为:
| $ {S_{\rm{d}}}\left( n \right) = \frac{a}{{{n^2}}},$ | (2) |
式中a=Gd(n0)n02/2。
1.2 路面不平度的二维功率谱密度为了得到三维随机路面,需要把路面的功率谱密度扩展到二维。根据Wiener-Khinchin定理,宽平稳随机过程的功率谱密度函数是自相关函数的傅里叶变换。因此对式(2)进行傅里叶逆变换,可以得到路面的一维自相关函数R(x)。通过查表可得
| $ R\left( x \right) = 2{{\rm{ π }}^2}{\rm{a}}\left| x \right|,$ | (3) |
式中x表示波长,单位为m。
根据二维各向同性随机场的性质,可以把路面一维自相关函数R(x)扩展到二维,得到二维路面的自相关函数R(x1, x2):
| $ R({x_1}, {x_2}) = R(\sqrt {{x_1}^2 + {x_2}^2} ) = 2{{\rm{ π }}^2}a\sqrt {{x_1}^2 + {x_2}^2} , $ | (4) |
式中x1和x2分别为两个维度方向的波长,单位为m。
反过来对式(4)进行二维傅里叶变换,即可得到路面的二维功率谱密度。由于R(x1, x2)是径向对称函数,所以经过二维傅里叶变换后,其对应的二维功率谱密度函数Sd(n1, n2)也同样是径向对称的,即
| $ {S_{\rm{d}}}({n_1}, {n_2}) = {S_{\rm{d}}}(\sqrt {n_1^2 + n_2^2} ),$ | (5) |
式中n1和n2为空间频率,单位为m-1。
令x1=rcosθ,x2=rsinθ,这里r为极坐标下的半径,θ为极角,代入式(4)中得到
| $ R\left( r \right) = 2{{\rm{ π }}^2}ar 。$ | (6) |
这样求R(x1, x2)的二维傅里叶变换等同于求R(r)的一维Hankel变换。查变换表得到
| $ {S_{\rm{d}}}\left( \rho \right) = \frac{a}{{2{\rho ^3}}}。$ | (7) |
把a=Gd(n0)n02/2、
| $ {S_{\rm{d}}}({n_1}, {n_2}) = \frac{{{G_{\rm{d}}}({n_0})n_0^2}}{{4(n_1^2 + n_2^2)3/2}}。$ | (8) |
计算机处理的只是有限的、离散化的数据,因此需要建立起三维随机路面连续模型与离散模型之间的联系。
2.1 三维随机路面连续模型令f(x1, x2)为三维路面上坐标点(x1, x2)处路面相对于理想参考面的高程。f(x1, x2)的二维傅里叶变换F(n1, n2)的表达式为:
| $ F({n_1},{n_2}) = \mathop {{\rm{lim}}}\limits_{\begin{array}{*{20}{c}} {{L_1} \to \infty }\\ {{L_2} \to \infty } \end{array}} \int_{ - \frac{{{L_1}}}{2}}^{\frac{{{L_1}}}{2}} {\int_{ - \frac{{{L_2}}}{2}}^{\frac{{{L_2}}}{2}} f } ({x_1},{x_2}){{\rm{e}}^{{\rm{j}}2{\rm{\pi }}(x1n1 + x2n2)}}{\rm{d}}{x_1}{\rm{d}}{x_2} ,$ | (9) |
式中:L1、L2为两个正交方向上路面长度;j为虚数单位。
根据功率谱密度函数的定义,路面二维功率谱密度函数为
| $ S\left( {{n_1},{n_2}} \right) = \mathop {{\rm{lim}}}\limits_{\begin{array}{*{20}{c}} {{L_1} \to \infty }\\ {{L_2} \to \infty } \end{array}} \frac{1}{{{L_1}{L_2}}}{\left| {F({n_1},{n_2})} \right|^2} 。$ | (10) |
实际路面不平度是建立在有限采样点基础之上的。因此L1、L2为有限值。令两正交方向上的采样间隔分别为Δx1、Δx2,采样点数分别为M1、M2,则三维路面的离散高程值为
| $ f[{m_1}, {m_2}] = f({m_1}\Delta {x_1}, {m_2}\Delta {x_2}),$ | (11) |
式中:m1=0, 1, 2, …, M1;m2=0, 1, 2, …, M2-1。
令两个正交方向上的空间频率采样间隔分别为Δn1=1/L1,Δn2=1/L2,则离散的二维空间频率傅里叶变换值为
| $ F\left[ {p, q} \right] = F(p\Delta {n_1}, q\Delta {n_2})。$ | (12) |
式中:p=0, 1, 2, …, M1;q=0, 1, 2, …, M2-1。
同样,离散化的功率谱密度函数为
| $ S\left[ {p, q} \right] = S(p\Delta {n_1}, q\Delta {n_2})。$ | (13) |
根据以上假设,式(9)的离散表达式为
| $ F\left[ {p, q} \right] = \Delta {x_1}\Delta {x_2}\sum\limits_{{m_1} = 0}^{{M_1}1} {\sum\limits_{{m_2} = 0}^{{M_2}1} f } [{m_1}, {m_2}]{{\rm{e}}^{{\rm{j}}2{\rm{ π }}\left( {\frac{p}{{{M_1}}}{m_1} + \frac{q}{{{M_2}}}{m_2}} \right)}}。$ | (14) |
式(10)的离散表达式为
| $ S\left[ {p, q} \right] = \frac{1}{{{L_1}{L_2}}}{\left| {F\left[ {p, q} \right]} \right|^2}, $ | (15) |
式中:L1=(M1-1)Δx1;L2=(M2-1)Δx2。
3 三维随机路面不平度建立流程 3.1 用二维离散功率谱生成二维离散傅里叶变换根据信号分析理论,f[m1, m2]的二维离散傅里叶变换H[p, q]的表达式为
| $ H\left[ {p, q} \right] = \sum\limits_{{m_1} = 0}^{{M_1}1} {\sum\limits_{{m_2} = 0}^{{M_2}1} f } [{m_1}, {m_2}]{{\rm{e}}^{{\rm{j}}2{\rm{ π }}\left( {\frac{p}{{{M_1}}}{m_1} + \frac{q}{{{M_2}}}{m_2}} \right)}}。$ | (16) |
因此,根据式(14)和式(16)有
| $ F\left[ {p, q} \right] = \Delta {x_1}\Delta {x_2}H\left[ {p, q} \right]。$ | (17) |
根据式(15)和式(17)有
| $ S\left[ {p, q} \right] = \frac{{\Delta {x_1}\Delta {x_2}}}{{({M_1}1)({M_2}1)}}{\left| {H\left[ {p, q} \right]} \right|^2}。$ | (18) |
因此
| $ \left| {H\left[ {p, q} \right]} \right| = \sqrt {\frac{{({M_1}1)({M_2}1)}}{{\Delta {x_1}\Delta {x_2}}}S\left[ {p, q} \right]} 。$ | (19) |
通过式(19)得到f[m1, m2]的二维离散傅里叶变换的模值H[p, q]。令H[p, q]的相角为φ[p, q],则
| $ H\left[ {p, q} \right] = H\left[ {p, q} \right]{{\rm{e}}^{{\rm{j}}\varphi \left[ {p, q} \right]}}。$ | (20) |
由于路面不平度是一个平稳随机过程,可令φ[p, q]为[0, 2π)内的随机数。
3.2 利用二维离散傅里叶逆变换生成三维随机路面三维随机路面的离散高程值f[m1, m2]通过二维离散傅里叶逆变换得到:
| $ f[{m_1}, {m_2}] = \frac{1}{{{M_1}{M_2}}}\sum\limits_{{m_1} = 0}^{{M_1}1} {\sum\limits_{{m_2} = 0}^{{M_2}1} H } \left[ {p, q} \right]{{\rm{e}}^{{\rm{j}}2{\rm{ π }}\left( {\frac{p}{{{M_1}}}{m_1} + \frac{q}{{{M_2}}}{m_2}} \right)}}。$ | (21) |
根据上面的推导可知,通过二维离散傅里叶逆变换可以建立三维随机路面。该方法的步骤如下。
步骤1:对路面功率谱进行采样,得到离散的功率谱密度值S[p, q]。当路面功率谱为标准谱时,用标准功率谱Sd替代S;
步骤2:用式(19)得到二维离散傅里叶变换的模值|H[p, q]|;
步骤3:生成随机相位,并用式(20)得到H[p, q];
步骤4:最后用式(21)得到路面离散高程值f[m1, m2],这里可采用成熟快速的FFT算法。
计算过程中,由于f[m1, m2]的值为实数,所以其二维离散傅里叶变换系数H[p, q]组成的矩阵为共轭对称矩阵,因此编码时应先计算非共轭单元和一半的共轭单元,然后通过共轭运算填充另一半的共轭单元。
4 仿真算例 4.1 仿真路面生成路面对轮胎激振频率为f=vn,其中v为车辆速度,单位为m/s,n为路面不平度的空间频率,单位为m-1。根据轮胎与道路激励的时间频率范围[fL, fH],得出路面不平度功率谱密度的有效空间频率范围[nL, nH]。
根据式(8),路面功率谱密度函数的取值如下面的分段函数所示。
| $ S\left[ {p, q} \right] = \left\{ {\begin{array}{*{20}{c}} {\frac{{{G_{\rm{d}}}({n_0})n_0^2}}{{4{{(n_p^2 + n_q^2)}^{3/2}}}}, }& {{n_{\rm{L}}} \le \left| {{n_p}} \right| \le {n_{\rm{H}}}, {n_{\rm{L}}} \le \left| {{n_q}} \right| \le {n_{\rm{H}}}};\\ {0, } & {其他情况。} \end{array}} \right. $ |
利用得到的S[p, q]用式(19)~(21)计算得到三维路面的离散高程值f[m1, m2]。
常见车速一般为36~180 km/h(即10~50 m/s)。一般而言对于汽车振动系统,取fL=0.5 Hz,fH=30 Hz可满足实际需要[4]。对应的空间频率为:
| $ \begin{array}{c} {n_{\rm{L}}} = \frac{{{f_{\rm{L}}}}}{{{v_{{\rm{max}}}}}} = 0.01{{\rm{m}}^{1}};\\ {n_{\rm{H}}} = \frac{{{f_{\rm{H}}}}}{{{v_{{\rm{min}}}}}} = 3{{\rm{m}}^{1}}。\end{array} $ |
因此只需在0.01~3 m-1的空间频率范围内模拟路面不平度,就足以覆盖车辆振动系统固有频率范围,这就保证了利用仿真路面所得到的相关结论符合该车辆真实情况。
为使空间频率的下限准确,也为了避免频率混叠,应当满足
| $ \begin{array}{c} {\rm{max}}(\Delta {x_1}, \Delta {x_2}) \le \frac{1}{{2{n_{\rm{H}}}}} = 0.166{\rm{ }}7{\rm{m}}\\ {\rm{min}}({L_1}, {L_2}) \ge \frac{1}{{{n_{\rm{L}}}}} = 100{\rm{m}} \end{array} $ |
在本例中,采样间隔Δx1=Δx2=0.1 m,L1=L2=409.5 m。因此2个方向上的采样点数M1=M2=4 096。空间频率分辨率为Δn1=Δn2=1/L1=1/L2=0.002 44 m-1。
据统计中国高等级公路基本属于A~C等级,对较差路面的研究更能切合实际应用的需要。
对E级路面的不平度系数Gd(n0)取几何平均值4 096 mm2/m-1。其他变量的意义及取值参考前面的叙述。仿真得到的E级三维路面和切面高程分别见图 1~2。

|
图 1 E级三维路面模拟(片段) Fig. 1 Simulation of Grade E pavement (fragment) |

|
图 2 模拟路面中某一切面的道路高程 Fig. 2 Simulating road roughness of a section in pavement |
利用标准路面谱生成模拟路面后,对生成的路面进行评估,分析模拟路面的功率谱与标准路面谱的接近程度。这里分别采用经典的周期图法和现代AR参数模型进行功率谱估计。
采用周期图法估计的功率谱(图 3)得到的仿真结果与理论一致。其谱线的分辨率较高,但离散性较大,数据波动明显,方差较大,尤其是高频处曲线比较粗糙,信息非常丰富。

|
图 3 周期图法估计的功率谱密度 Fig. 3 Power spectrum density estimated by periodogram method |
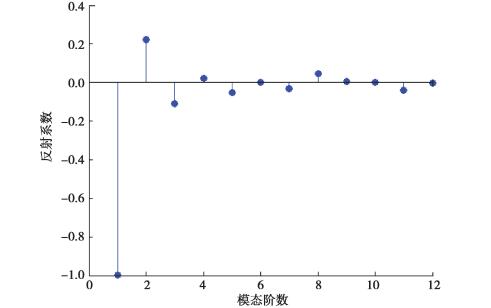
利用AR参数模型估计功率谱,采用公认较好的Burg方法。参数模型估计功率谱需要先定出模型的阶数。图 4中计算的反射系数表明,模型在高于3阶时其均方误差之和已没有太大的变化,因此AR模型可以取阶数为4阶。
|
图 4 利用反射系数确定AR模型阶数 Fig. 4 AR model order determined by reflection coefficient |
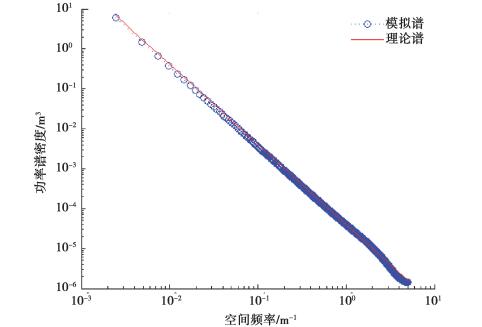
图 5中AR参数模型估计功率谱与理论谱非常吻合,曲线明显比经典谱估计方法光滑,其处理结果的方差比经典谱估计方法的小。
|
图 5 AR参数模型估计的功率谱密度 Fig. 5 Power spectrum density estimated by AR parametric model |
无论是采用经典周期图法谱估计,还是现代AR参数模型谱估计,估计的结果表明仿真模拟的路面与标准路面的理论谱是高度一致的,证明本研究中的方法是有效和适用的。
5 结语笔者把一维逆傅里叶变换法生成随机路面拓展到二维,以生成三维随机路面。利用国家标准中采用的幂函数法路面谱拟合公式,推导并得出幂函数法表示的标准路面二维功率谱解析表达式,避免了有理函数法中的参数估计问题。建立了二维傅里叶逆变换法生成三维随机路面的流程。该方法可以直接使用成熟快速的FFT算法。以某汽车振动系统所关注性能需求,仿真了中国标准中的E级路面。分别采用周期图法和AR参数模型法估计了仿真生成路面的功率谱,两种方法估计的结果表明仿真模拟的路面与标准路面谱是高度一致的。
| [1] |
中华人民共和国国家质量监督检验检疫总局.机械振动道路路面谱测量数据报告: GB/T 7031-2005[S].北京: 中国标准出版社, 2005. General Administration of Quality Supervision, Inspection and Quarantine of the People's Republic of China. Mechanical vibration-road surface profiles-reporting of measured data: GB/T 7031-2005[S]. Beijing: China Standard Press, 2005.(in Chinese) |
| [2] |
Au F T K, Cheng Y S, Cheung Y K. Effects of random road surface roughness and long-term deflection of prestressed concrete girder and cable-stayed bridges on impact due to moving vehicles[J]. Computers & Structures, 2001, 79(8): 853-872. |
| [3] |
Schiehlen W, Hu B. Spectral simulation and shock absorber identification[J]. International Journal of Non-Linear Mechanics, 2003, 38(2): 161-171. DOI:10.1016/S0020-7462(01)00053-1 |
| [4] |
Grigoriu M. On the spectral representation method in simulation[J]. Probabilistic Engineering Mechanics, 1993, 8(2): 75-90. DOI:10.1016/0266-8920(93)90002-D |
| [5] |
Zhang Y L. Time domain model of road irregularities simulated using the harmony superposition method[J]. Transactions of The Chinese Society of Agricultural Engineering, 2003, 19(6): 32-35. |
| [6] |
Wang X, Zhao J B, Wang J Z. An improved road roughness simulation method based on trigonometric series method[J]. Applied Mechanics and Materials, 2014, 513/514/515/516/517: 3277-3282. |
| [7] |
Zhang Y L, Zhang J F. Numerical simulation of stochastic road process using white noise filtration[J]. Mechanical Systems and Signal Processing, 2006, 20(2): 363-372. DOI:10.1016/j.ymssp.2005.01.009 |
| [8] |
Heath A N. Application of the isotropic road roughness assumption[J]. Journal of Sound and Vibration, 1987, 115(1): 131-144. DOI:10.1016/0022-460X(87)90495-0 |
| [9] |
刘献栋, 邓志党, 高峰. 基于逆变换的路面不平度仿真研究[J]. 中国公路学报, 2005, 18(1): 122-126. LIU Xiandong, DENG Zhidang, GAO Feng. Study of simulation of road roughness based on inverse transform[J]. China Journal of Highway and Transport, 2005, 18(1): 122-126. (in Chinese) |
| [10] |
张亚欧, 马吉盛, 吴大林, 等. 基于Fourier逆变换法的路面不平度模拟[J]. 河北工业大学学报, 2005, 34(6): 66-69. ZHANG Yaou, MA Jisheng, WU Dalin, et al. Modeling and simulation of road roughness based on the method of reverse Fourier[J]. Journal of Hebei University of Technology, 2005, 34(6): 66-69. (in Chinese) |
| [11] |
张永林, 李诗龙, 杨建林. 汽车道路随机不平顺的时序模型重构[J]. 武汉理工大学学报(交通科学与工程版), 2005, 29(6): 883-886. ZHANG Yonglin, LI Shilong, YANG Jianlin. Time series model regeneration of random road undulation input to vehicles[J]. Journal of Wuhan University of Technology (Transportation Science & Engineering), 2005, 29(6): 883-886. (in Chinese) |
| [12] |
朱茂桃, 刘建, 王国林. 路面不平度重构的AR模型阶数确定方法研究[J]. 公路交通科技, 2010, 27(7): 25-28, 51. ZHU Maotao, LIU Jian, WANG Guolin. Research on method of determining order of AR model for road roughness reconstruction[J]. Journal of Highway and Transportation Research and Development, 2010, 27(7): 25-28, 51. (in Chinese) |
| [13] |
彭佳, 何杰, 李旭宏, 等. 路面不平度随机激励时域模型的仿真比较与评价[J]. 解放军理工大学学报(自然科学版), 2009, 10(1): 77-82. PENG Jia, HE Jie, LI Xuhong, et al. Simulation comparison and evaluation of common time domain models under road irregularity excitation[J]. Journal of PLA University of Science and Technology (Natural Science Edition), 2009, 10(1): 77-82. (in Chinese) |
| [14] |
吴参, 王维锐, 陈颖, 等. 三维路面谱的仿真建模与验证[J]. 浙江大学学报(工学版), 2009(10): 1935-1938. WU Can, WANG Weirui, CHEN Ying, et al. Simulation and validation of three-dimensional road surface spectrum[J]. Journal of Zhejiang University(Engineering Science), 2009(10): 1935-1938. (in Chinese) |
| [15] |
彭佳, 何杰, 丛颖, 等. 三维随机路面通用模型建立与仿真[J]. 农业机械学报, 2009, 40(3): 1-4, 25. PENG Jia, HE Jie, CONG Ying, et al. Modeling and simulation of general 3D virtual stochastic road model[J]. Transactions of the Chinese Society for Agricultural Machinery, 2009, 40(3): 1-4, 25. (in Chinese) |
| [16] |
夏均忠, 马宗坡, 白云川, 等. 路面不平度激励模型研究现状[J]. 噪声与振动控制, 2012, 32(5): 1-5, 41. XIA Junzhong, MA Zongpo, BAI Yunchuan, et al. State of the research on model for road roughness excitation[J]. Noise and Vibration Control, 2012, 32(5): 1-5, 41. (in Chinese) |
| [17] |
唐光武, 成思源. 二维路面不平度的时域模型及计算机仿真[J]. 重庆大学学报(自然科学版), 2000, 23(6): 31-34. TANG Guangwu, CHENG Siyuan. Time domain model of 2-D road roughness and numerical simulation[J]. Journal of Chongqing University(Natural Science Edition), 2000, 23(6): 31-34. (in Chinese) |
| [18] |
罗竹辉, 魏燕定, 周晓军, 等. 随机激励三维路面空间域模型建模与仿真[J]. 振动与冲击, 2012, 31(21): 68-72. LUO Zhuhui, WEI Yanding, ZHOU Xiaojun, et al. 3-D random excitation road surface modeling and simulation[J]. Journal of Vibration and Shock, 2012, 31(21): 68-72. (in Chinese) |
 2020, Vol. 43
2020, Vol. 43


