2. 重庆大学 山地城镇建设与新技术教育部重点实验室, 重庆 400045;
3. 中国建筑第五工程局有限公司, 长沙 410004
2. Key Laboratory of New Technology for Construction of Cities in Mountain Area, Chongqing University, Chongqing 400045, P. R. China;
3. China Construction Fifth Engineering Division Corp., Ltd., Changsha 410004, P. R. China
关于考虑钢筋混凝土非弹性性质的二阶效应设计方法,Paulay等[1]从有利于工程应用的角度出发,为考虑钢筋混凝土结构的非弹性性质率先引入了按构件分类的刚度折减系数,给出了相应的取值建议,并于1994年修订的新西兰NZS 3101规范中有所体现。在此之后,包括加拿大、美国在内的一些国家,在混凝土结构规范中也推荐使用按构件分类的刚度折减系数来考虑涉及二阶效应的分析问题。中国《混凝土结构设计规范GB 50010—2002》[2]在修订时,为考虑钢筋混凝土框架结构的非弹性性质也引入了“按构件分类的刚度折减系数”。目前大多数结构分析软件采用的是考虑二阶效应的弹性结构分析法,本文中将其简称为弹性二阶分析法。若在弹性二阶分析方法中以折减构件刚度的形式,来近似模拟由于钢筋混凝土的非弹性性质引起的刚度降低,则可称作考虑构件折减刚度的弹性二阶分析法。以这样的方法来进行排架结构的研究,关键是排架柱刚度折减系数的取值如何更加合理、准确。重庆大学团队[3-4]对大量的排架算例做过系统性的研究,提出了基于截面模型的PMM耦合塑性铰的刚度折减系数的建议值,但在通过对基于材料模型的PMM纤维铰的对比分析后发现由此得到的刚度折减系数更为合理。
1 采用PMM纤维铰的非线性分析 1.1 SAP2000两种PMM塑性铰简介及对比这里采用SAP2000分析软件对排架结构做静力非线性分析。在SAP2000分析软件中对于材料非线性主要通过PMM塑性铰来体现并在软件内部提供了2种PMM铰:PMM耦合塑性铰和PMM纤维铰。其中PMM耦合塑性铰是基于截面模型,它的屈服是由P-M2-M3组成的三维空间屈服面,不再是一个点,SAP2000默认采取FEMA-356报告[5]中表 6-8的模型参数和容许准则来自动定义PMM耦合塑性铰属性。而PMM纤维铰是基于材料模型,其依据是平截面假定以及每个纤维材料截面的轴向力轴向和弯矩曲率应变关系[6-7]。
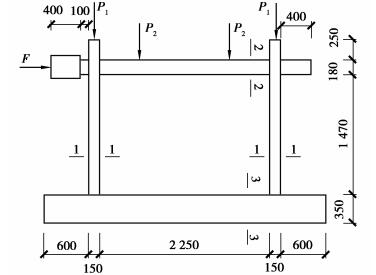
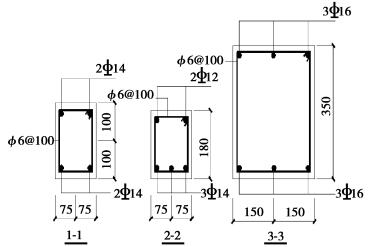
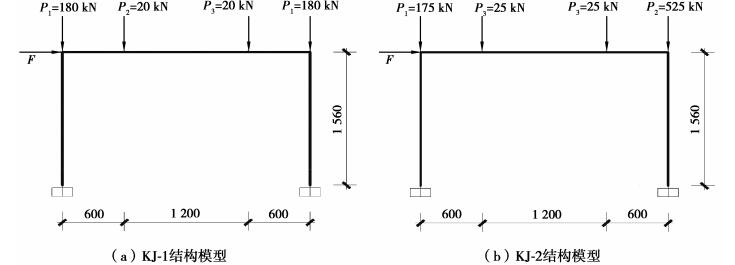
1.2 对自动PMM耦合铰和PMM纤维铰的试验验证通过对重庆大学团队已经完成的两榀门式框架KJ-1、KJ-2进行静载试验[8-9]的模拟。其中KJ-1、KJ-2配筋与模型尺寸完全相同,1号框架设计进行大偏压破坏,2号框架设计进行小偏压破坏[2]。所进行的试验加载分为两步:第一步逐步施加竖向荷载至规定值,第二步逐步进行水平荷载施加直至出铰破坏。分别采用2种不同的塑性铰模型对试验全过程进行模拟。试验模型、截面配筋及SAP2000模型如图 1~3所示。
|
图 1 KJ-1和KJ-2的加载模型 Fig. 1 Loading model of KJ-1and KJ-2 |
|
图 2 KJ-1和KJ-2的梁、柱配筋图 Fig. 2 Beam and column reinforcement of KJ-1 andKJ-2 |
|
图 3 KJ-1和KJ-2的结构模型 Fig. 3 Structural model for KJ-1 and KJ-2 |
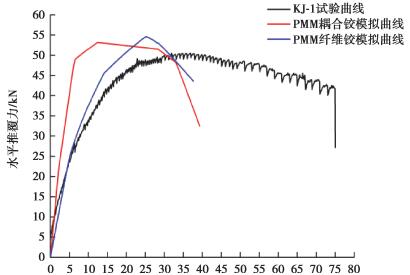
SAP2000中采用与实验相同的加载模式,采用位移控制,钢筋应力应变本构模型选用软件自带的Simple模型。混凝土的应力应变本构模型选取Mander Unconfined混凝土模型。通过模拟发现结构出铰部位多集中在柱端梁端。将试验结果与使用PMM纤维铰和自动耦合铰进行模拟得到的曲线进行对比,详见图 4~5。
|
图 4 KJ-1荷载位移曲线图 Fig. 4 The load-displacement curve of KJ-1 |
|
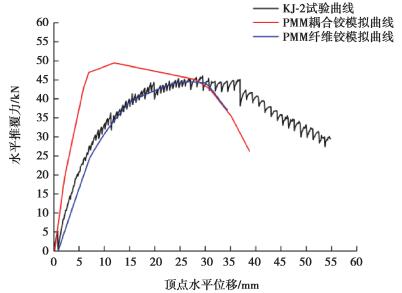
图 5 KJ-2荷载位移曲线图 Fig. 5 The load-displacement curve of KJ-2 |
由图 4和图 5中模拟曲线与试验曲线对比可知PMM纤维铰比PMM耦合塑性铰可以更好地模拟2种框架结构的顶点水平位移和极限承载力,特别是在结构的顶点水平位移上PMM纤维铰可以更加精确地进行模拟,与试验结果非常接近。并且在对2个框架荷载位移反应曲线上升段的模拟上,PMM纤维铰模拟的准确性要远高于PMM耦合塑性铰的模拟结果。虽然对于试验曲线的下降段2种塑性铰模型都无法很好地模拟,无法很好地考虑混凝土开裂及钢筋与混凝土黏结滑移等因素,但这里是在正常使用极限状态对刚度折减系数进行研究,其对应的曲线处于模拟曲线的上升段,所以对于本次非线性模拟,只要能较为精准的模拟反应曲线的上升段,就满足研究的精度要求,所以下面将选取模拟精度更好的PMM纤维铰模型对排架结构进行静力非线性分析。
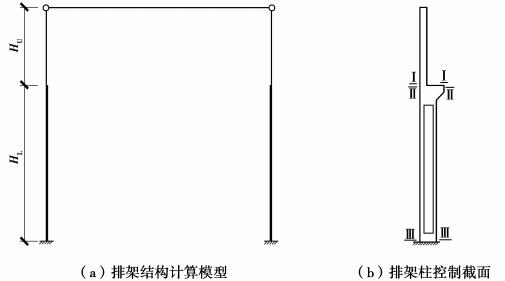
2 排架结构刚度折减系数分析 2.1 荷载分析与结构设计排架结构主要由横向和纵向排架组成,为便于工程设计,建模过程仅取一榀横向平面排架结构进行二阶分析不再考虑空间效应的影响,这样分析得到的结果是偏安全的。屋架按轴向构件处理,水平刚度无穷大且与上柱铰接,保证柱顶水平位移相等。下柱与基础刚接处理均严格按照国家标准图集对排架结构中各构件进行选取。桥式吊车根据大连重工集团的DQQD型起重机进行参数设计,选取10t、20\5t、32\5t和50\10t常用的4种吨位。根据标准图集04G325和04G426进行吊车轨道联接件和吊车梁的相关参数设计。屋架根据标准图集04G415-1进行参数设计。屋面板根据图集04G410-1选用Y-WB-2III预应力屋面板。由以上可设计出计算模型简图,如图 6所示。
|
图 6 排架柱控制截面和排架结构计算模型 Fig. 6 The control section of the bent-columns and the model of bent frames |
在对排架结构进行设计时,考虑到恒荷载作用形式是对称的可作为无侧移荷载处理,而活荷载处理时等效为上柱顶的竖向力和弯矩,考虑上下柱的偏心及牛腿处的弯矩,也可视为无侧移荷载。即通过荷载来考虑上下柱的偏心问题。此外选用排架结构边柱下柱Ⅲ-Ⅲ截面的最不利荷载组合是比较有代表性且合理的组合方式[10],此时截面刚度退化最大。因此根据上述原则,分别设计了34个单层单跨和34个单层双跨排架结构算例进行非线性分析。用于排架结构非线性分析的荷载组合为对应于结构正常使用极限状态下的标准组合,风荷载和吊车荷载组合值系数分别为0.6和0.7。如表 1所示是其具体荷载组合方式[1, 11-12]。
| 表 1 荷载组合 Table 1 Load combination |
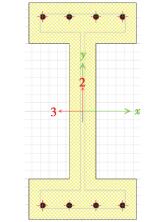
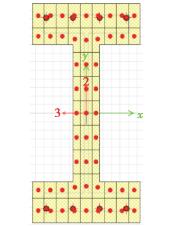
在模型分析时不考虑厂房的空间效应,仍采用有侧移模型进行非线性分析,通过数值实验,将排架下柱中柱和边柱划分成10个单元,中柱上柱和边柱上柱划分成5个单元。横梁整体分成一个单元并将下柱统一考虑为工字型截面,上柱统一考虑为矩形截面,结构分析模型及纤维铰布置见图 7。为较为精准地模拟非线性的反应曲线可将纤维铰的长度取成0.1倍单元的长度。下柱截面分为59个纤维,其中每根钢筋独立划成一个纤维,共8个钢筋纤维,混凝土整体划成51个纤维。排架上柱截面按软件默认进行纤维划分,排架下柱钢筋,纤维的布置与划分参考图 8和图 9。此外钢筋应力应变本构模型选用软件自带的Simple模型。混凝土的应力应变本构模型选取Mander Unconfined混凝土模型。

|
图 7 单层单跨排架模型的纤维铰布置和单元划分 Fig. 7 Fiber hinge arrangement and element partition of single span and single layer bent frame |
|
图 8 下柱截面受力钢筋布置 Fig. 8 Arrangement of reinforced bar |
|
图 9 下柱截面纤维划分 Fig. 9 Section fiber division |
设置合理的目标位移,通过位移控制的加载方式,输出Pushover曲线,得到2种极限状态下的顶点水平位移,方便与弹性二阶状态下分析结果进行对比。
2.3 刚度折减系数计算方法目前排架柱的刚度折减系数计算方法是引入一个整体综合刚度折减系数[13](所有柱段),在运用该系数进行弹性二阶分析时,所得到的结构整体和层间水平位移与非线性分析结果近似相同。对于这里研究的2种排架结构而言,主要是通过排架上柱顶的水平位移来反映结构整体性能,因此这是要考察的重点参数。具体在SAP2000分析软件中为实现刚度折减目标,主要是通过折减混凝土弹性模量,相关公式如(2)式所示。式中,Ec为混凝土初始弹性模量,EI为折减后的刚度,α为刚度折减系数,EcI为混凝土毛截面弹性刚度。
| $ EI = \alpha {E_{\rm{c}}}I。$ | (2) |
这种方法从结构整体性能出发得到刚度折减系数,利于算例的大量展开,可以省去部分繁杂的计算过程,更为简洁高效,也与美国ACI318规范[14]基于结构性能的思想更为契合。
3 排架结构算例分析及刚度折减系数取值建议分别设计了34个典型的单层双跨和单层单跨等高排架算例,以4个影响结构二阶效应的因素为主要变量,在算例中均严格按照国家标准图集[15]对排架结构中各构件进行选取。屋面活载标准值根据最新荷载规范确定为0.5 kN/m2,屋面恒载标准值经计算确定为3.35 kN/m2,风荷载主要考虑作用在排架结构上的3种基本风压:0.8,0.5,0.3 kN/m2。主要考虑3种跨度的横向排架:30,24,18 m,结构上柱、下柱分别为矩形和工字型截面,选用普通C30混凝土以及6 m的纵向排架柱距,排架结构柱的设计参考图集05G335。
3.1 单、双跨排架结构算例参数单、双跨排架算例参数及其编号见表 2。
| 表 2 单层单、双跨排架结构算例参数及其编号 Table 2 The example parameters and their numbers of single-span and double-span bent frames |
由表 3结果可知,非线性二阶分析得到的结果相比于弹性分析而言,主要分为2种情况:算例34, 33, 31, 26, 25, 24, 23, 18, 17, 7, 4, 3的非线性二阶弯矩相比于弹性二阶弯矩略小一点,其余算例相比于弹性二阶弯矩略大一些。并且非线性二阶弯矩在右柱Ⅲ-Ⅲ截面均有较为明显的增加。对于柱顶位移来说,非线性二阶分析所得到的结果相比于弹性二阶分析有明显增大。事实上非线性位移主要是由于混凝土的受拉开裂引起,这部分位移增加了排架柱的P-Δ效应,以及产生的内力重分配,导致左右柱二阶弯矩不同。
| 表 3 单层单跨排架位移及刚度折减系数对比 Table 3 The displacement and stiffness reduction factors comparison of single-span bent frames |
由表 4分析结果可知,单层双跨排架结构非线性分析柱顶位移相比弹性分析有所增大,关于左柱弯矩非线性分析结果略小,但右柱与中柱的弯矩非线性分析结果相较于弹性二阶分析都有一定的增大,其中中柱增大幅度较大。
| 表 4 单层双跨排架结构位移及刚度折减系数对比 Table 4 The displacement and stiffness reduction factors comparison of double-span bent frames |
本文中刚度折减系数的分析是以柱顶变形近似相等为条件,用等效的弹性刚度杆件来模拟非线性状态下结构的内力和变形形态,按这种模拟方法得到的是一种同时针对排架下柱和上柱的综合刚度折减系数α。利用上述结果(表 3和表 4)的刚度折减系数进行散点图绘制,如图 10所示。分析单层单、双跨排架结构相关刚度折减系数的分布。
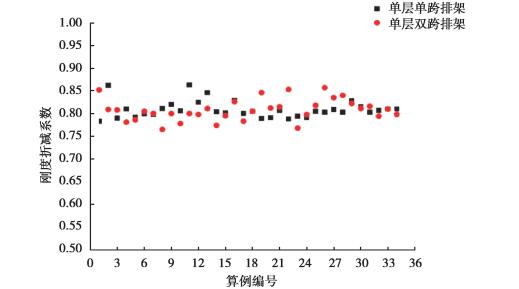
|
图 10 刚度折减系数散点图 Fig. 10 Scatter diagram of stiffness reduction factors |
由图 10可知,在0.75~0.85范围内分布绝大多数的刚度折减系数,且集中于0.80上下,只有个别少数算例超出这个范围。在考虑排架结构的安全储备要求情况下,据此规律,可以给出刚度折减系数的取值建议:单层单、双跨排架结构刚度折减系数均可统一取为α=0.75。
4 结论及建议选取了34个单层单跨排架结构和34个单层双跨排架结构通过精度更高的PMM纤维铰模型对排架结构进行非线性分析,并与弹性二阶分析结果进行对比。以二阶效应等效为条件,得出一系列结构刚度折减系数。并据此绘制出了刚度折减系数散点图,根据其分布规律并结合结构安全储备和工程实用性要求,提出了单层单、双跨排架结构刚度折减系数统一取为0.75的取值建议。
| [1] |
Paulay T, Priestley M J M. Seismic design of reinforced concrete and masonry buildings[M]. New York: John Wiley & Sons, Inc, 1992.
|
| [2] |
混凝土结构设计规范: GB 50010—2002[S].北京: 中国建筑工业出版社, 2002. Code for design of concrete structures: GB 5001020-2002[S]. Beijing: China Architecture & Building Press, 2002. (in Chinese) |
| [3] |
黎波.考虑排架结构二阶效应的设计方法研究[D].重庆: 重庆大学, 2017. LI Bo. Design method of second-order effect of reinforced concrete bent frames[D]. Chongqing: Chongqing University, 2017. (in Chinese) |
| [4] |
刘毅, 刘年朋, 卓子, 等. 考虑刚度折减的弹性二阶分析法在双跨排架结构中的运用[J]. 重庆大学学报, 2017, 40(9): 1-7. LIU Yi, LIU Nianpeng, ZHUO Zi, et al. The application of elastic second-order method with considering stiffness reduction to two-span bent structure[J]. Journal of Chongqing University, 2017, 40(9): 1-7. (in Chinese) |
| [5] |
ASCE, Federal Emergency Management Agency. Prestandard and commentary for the seismic rehabilitation of buildings: FEMA 356[S]. Washington, D C: Federal Emergency Management Agency, 2000.
|
| [6] |
陆新征, 叶立平, 缪志伟, 等. 建筑抗震弹塑性分析:原理、模型与在ABAQUS, MSC.MARC和SAP2000上的实践[M]. 北京: 中国建筑工业出版社, 2009. LU Xinzheng, YE Liping, MIAO Zhiwei, et al. Elasto-plastic analysis of buildings against earthquake: theory, model and implementation on ABAQUS, MSC.MARC and SAP2000[M]. Beijing: China Architecture & Building Press, 2009. (in Chinese) |
| [7] |
Macgregor J G, Hage S E. Stability analysis and design of concrete frames[J]. Journal of the Structural Division, 1977, 103(10): 1953-1970. |
| [8] |
魏巍.考虑非弹性及二阶效应特征的钢筋混凝土框架柱的强度与稳定问题[D].重庆: 重庆大学, 2004. WEI Wei. Strength and stability of reinforced concrete frame columns considering characters of nonlinear and second-order effect[D]. Chongqing: Chongqing University, 2004. (in Chinese) |
| [9] |
刘毅.钢筋混凝土框架柱二阶效应与稳定中若干问题的讨论[D].重庆: 重庆建筑大学, 2000. LIU Yi. Discussion on second-order effect and stability problems of reinforced concrete frame columns[D]. Chongqing: Chongqing Jianzhu University, 2000. (in Chinese) |
| [10] |
Paulay T. Seismic displacement capacity of ductile reinforced concrete building systems[J]. Bulletin of the New Zealand Society for Earthquake Engineering, 2003, 36(1): 47-65. DOI:10.5459/bnzsee.36.1.47-65 |
| [11] |
Li B, Xiang W Z. Effective stiffness of squat structural walls[J]. Journal of Structural Engineering, 2011, 137(12): 1470-1479. DOI:10.1061/(ASCE)ST.1943-541X.0000386 |
| [12] |
建筑结构荷载规范: GB50009—2012[S].北京: 中国建筑工业出版社, 2012. Load code for the design of building structures: GB50009—2012[S]. Beijing: China Architecture & Building Press, 2010. (in Chinese) |
| [13] |
Feng X L, Shen M, Kong X Y, et al. Study on flexural stiffness reduction factor of reinforced concrete column with equiaxial T shaped section[J]. Applied Mechanics and Materials, 2013, 351/352: 319-324. DOI:10.4028/www.scientific.net/AMM.351-352.319 |
| [14] |
ACI Committee 318. 318-14: building code requirements for structural concrete and commentary[S]. Detroit: American Concrete Institute, 2014.
|
| [15] |
中国建筑标准设计研究院.国家建筑标准设计图集05G335: 单层工业厂房钢筋混凝土柱[S].北京: 中国计划出版社, 2005. China Institute of Building Standard Design & Research. National building standard design drawings 05G335: reinforced concrete column of single storey industrial building[S]. Beijing: China Planning Press, 2005. (in Chinese) |
 2020, Vol. 43
2020, Vol. 43

