2. 北京航空航天大学 航空科学与工程学院, 北京 100191
2. School of Aeronautic Science and Engineering, Beihang University, Beijing 100191, P. R. China
在工程实际中,许多结构的危险部位在服役过程中往往承受着复杂的多轴疲劳载荷[1-2],如飞机蒙皮、发动机叶片、轴类零件等;此外,结构中缺口或其他几何形状变化也会引起局部危险部位处于多轴应力状态[3]。如何准确地预测复杂载荷状态即多轴加载下结构的失效行为,引起了工程界的广泛关注。
已有的研究表明,对于不同的材料,其多轴疲劳裂纹萌生及扩展行为不同。Socie等[4]研究发现在多轴疲劳载荷下,Inconel 718的裂纹总是萌生于最大切应变平面,试件的最终失效由表面多处约1 mm长度裂纹的连接形成。尚德广等[5]发现对于45钢,裂纹主要萌生于2个最大切应变幅值平面,相位差的存在会导致裂纹萌生方向的分散性变大。Reis等[6]研究了不同加载路径对3种结构钢裂纹萌生及扩展的影响,发现在相同的加载路径下,不同材料裂纹起裂角度不同;对于相同的材料,不同的加载路径下裂纹起裂角度也不同。Navarro等[7]认为比例加载下,裂纹更倾向萌生于最大切应力平面。
对于多轴疲劳载荷下的裂纹扩展阶段,文献[8-10]发现1045钢在比例加载下,裂纹有明显的扩展第Ⅰ阶段向第Ⅱ阶段的转变,且裂纹总是萌生于最大切应变平面。Ohkawa等[11]、Verreman等[12]和Vu等[13]发现在多轴加载下,S45C钢、C35钢和1045钢的裂纹扩展第Ⅰ阶段沿着最大切应力平面,裂纹由扩展第Ⅰ阶段向第Ⅱ阶段的转变长度受应力幅比的影响。Kim等[14]对SM45C钢研究发现,试件表面裂纹无法明确地区分扩展第Ⅰ阶段和第Ⅱ阶段,疲劳破坏由小裂纹的连接引起。Susmel等[15]研究发现,对于6082-T6铝合金材料,纯弯曲载荷在试件表面产生Ⅰ型裂纹,纯扭转载荷下试件表面产生Ⅱ型裂纹。对于拉扭复合加载,应力幅比大于1时,裂纹形态与纯扭转载荷下裂纹形态相同;应力幅比小于1时,初始裂纹为延最大切应力方向的Ⅱ型裂纹,之后转变为垂直于主应力方向的Ⅰ型裂纹。Liu等[16-17]的研究表明,对于30CrMnSiA高强钢,在应力幅比较小时,裂纹扩展第Ⅰ阶段不明显,随着应力幅比的增大,裂纹出现明显的第Ⅰ阶段到第Ⅱ阶段的转变。第Ⅰ阶段的扩展方向随着应力幅比增大逐渐接近最大切应力幅值平面,第Ⅱ阶段均沿着最大正应力平面方向。Fatemi等[18]对近40年的多轴疲劳研究进行了回顾,认为裂纹的萌生及扩展路径受材料和加载路径的影响。因此,对于不同材料的多轴疲劳裂纹萌生及扩展的研究仍需开展。
2A12-T4铝合金具有良好的成型工艺、断裂韧度较高、耐腐蚀稳定性好,广泛应用在飞机的翼梁、隔框以及机身蒙皮等承力构件上[19-20]。飞机服役过程中,这些部位均承受多轴疲劳载荷作用。笔者通过开展不同应力幅比下2A12-T4铝合金多轴高周疲劳试验,采用光学显微镜观测,记录不同循环数下试件表面裂纹的形态,对表面裂纹萌生和扩展路径进行统计分析和计算,研究了应力幅比裂纹萌生的角度、扩展规律的影响,对处于多轴应力状态下的复杂结构的失效分析具有参考意义。
1 多轴高周疲劳试验试验材料为2A12-T4铝合金,取自直径为40 mm的棒材。材料的化学成分及含量如表 1所示,其静力性能如表 2所示。
| 表 1 2A12-T4铝合金的化学成分及质量分数 Table 1 Chemical composition and weight percent of 2A12-T4 aluminum alloy |
| 表 2 2A12-T4铝合金的静力性能 Table 2 Mechanical properties of 2A12-T4 aluminum alloy |
表 2中E为弹性模型,σy为伸屈服极限,σu为拉伸强度极限,δ为伸长率,G为切变模量,τu为剪切强度极限,τy为剪切屈服强度。
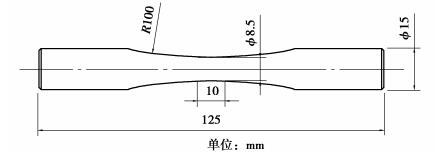
试件依据《金属材料疲劳试验轴向力控制方法》(GB/T 3075—2008)及《金属材料扭应力疲劳试验方法》(GB/T 12443—2017)进行设计,试件如图 1所示。试样测试段长度为10 mm,测试段直径为8.5 mm,并保证测试段光洁度Ra < 0.2, 且过渡圆角尽量加大。
|
图 1 2A12-T4铝合金疲劳试样 Fig. 1 Shape and dimensions of specimens |
多轴疲劳试验在MTS-858电液伺服拉扭组合试验机上进行, 试验环境为室温大气,试验采用载荷和扭矩控制、正弦波加载,加载频率为f=5 Hz,疲劳寿命定义为试件完全断裂。加载应力如下:
| $ {\sigma _x}\left( t \right) = {\sigma _{\rm{a}}}{\rm{sin}}\omega t, $ | (1) |
| $ {\tau _{xy}}\left( t \right) = {\tau _{\rm{a}}}{\rm{sin}}\omega t, $ | (2) |
式中:σa为轴向应力幅值,τa为切应力幅值。
在每个试件加载到一定循环数后,从试验机上取下试件,用金相显微镜观察并记录试件表面的裂纹形态,继续进行试验加载,并重复上述过程,直至试件完全断裂。由于在高倍显微镜下每次观测区域较小,需要多次平移和旋转试件,以保证记录试件表面任意位置可能出现的裂纹。
加载时取相同的等效von-Mises应力幅值σeq, a=300 MPa,应力幅比λ为切向应力幅与轴向应力幅之比,等效von-Mises应力幅值及应力幅比分别如下所示:
| $ {\sigma _{{\rm{eq, a}}}} = \sqrt {\sigma _{\rm{a}}^2 + 3\tau _{\rm{a}}^2} , $ | (3) |
| $ \lambda = {\tau _{\rm{a}}}/{\sigma _{\rm{a}}}。$ | (4) |
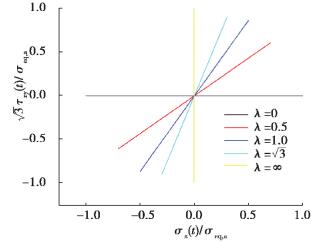
共选取了5个不同的应力幅比λ=0,0.5,1.0,
|
图 2 多轴疲劳试验加载路径 Fig. 2 Load path of the multiaxial fatigue test |
| 表 3 不同加载路径应力幅值及试验寿命 Table 3 Stress amplitude and fatigue life under different load paths |
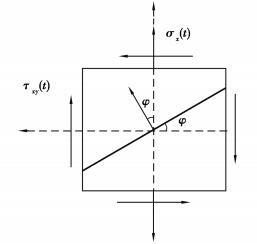
在加载过程中试件表面测试段为最危险应力状态,且处于平面应力状态,试件表面测试段任意点受力状态和该点处任意平面方向φ的定义如图 3所示。
|
图 3 平面方向定义 Fig. 3 Definition of plane direction |
由于疲劳加载下,通常认为最大切应力幅值与最大正应力为影响疲劳失效的2个重要应力分量[2, 5],因此,为了便于分析裂纹的萌生及扩展方向,首先计算得到了不同加载条件下的最大切应力幅值平面(MSSA)和最大正应力平面(MN)的方向,如表 4所示。可以看到,在多轴疲劳载荷下,通常会存在2个相互垂直的最大切应力幅值平面和1个最大正应力平面。
| 表 4 最大切应力幅值平面和最大正应力平面方向 Table 4 Calculated orientations MSSA and MN planes |
开展了5种不同应力幅比下的疲劳试验,使用金相显微镜在每个试件表面均观测到了多条微裂纹,其中形成主裂纹并引起试件最终破坏的往往只有1~2条微裂纹。对于未形成主裂纹的微裂纹可以分为两类:第一类微裂纹在整个加载历程中未发生扩展第Ⅰ阶段向第Ⅱ阶段的转变,并对试件的最终破坏无显著影响;第二类裂纹在加载历程中则出现了明显的扩展第Ⅰ阶段向第Ⅱ阶段的转变。
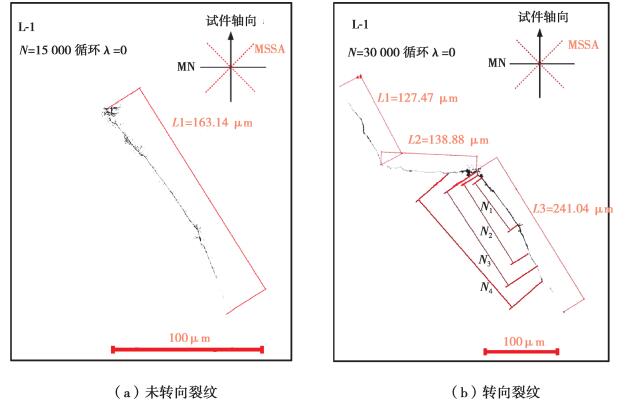
图 4~6给出了L-1~L-3号试件表面2种未引起试件失效的典型微裂纹形态,对于每种应力幅比,分别给出了2条典型的微裂纹:一条未发生扩展2个阶段的转变,另一条具有明显的第Ⅰ阶段向第Ⅱ阶段的转变过程。
|
图 4 λ=0时试件表面典型裂纹形态 Fig. 4 Typical cracks on the surface of the specimen when λ=0 |
|
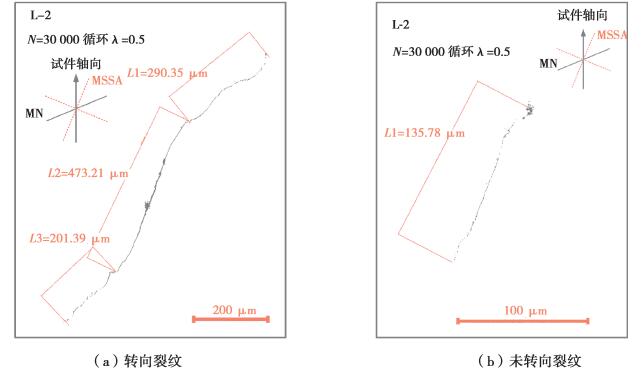
图 5 λ=0.5时试件表面典型裂纹形态 Fig. 5 Typical cracks on the surface of the specimen when λ=0.5 |
|
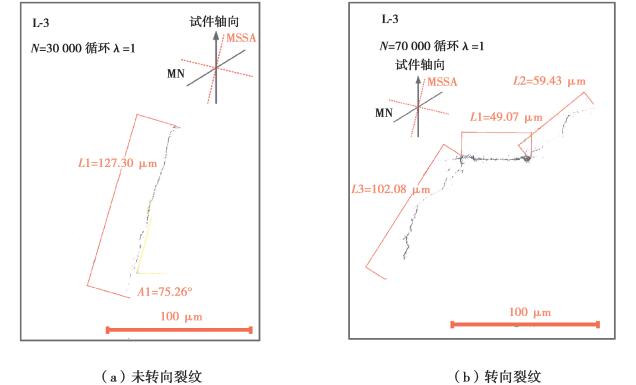
图 6 λ=1.0时试件表面典型裂纹形态 Fig. 6 Typical cracks on the surface of the specimen when λ=1 |
图 4所示为λ=0时试件L-1表面2条典型裂纹形态,可以看到2条裂纹最初均沿着最大剪应力幅值平面萌生,其中图 4(b)所示裂纹在扩展一定的长度后改变方向,沿着最大正应力平面扩展大约140 μm后再次改变方向沿着最大切应力幅值平面扩展。
图 5、图 6所示分别为λ=0.5时试件L-2表面2条典型裂纹形态及λ=1.0时试件L-3表面2条典型裂纹形态,在2种不同的应力幅比下,2条裂纹最初沿着最大切应力幅值平面萌生。对于图 5(a)所示的试件L-2表面裂纹,裂纹沿最大切应力幅值平面扩展约470 μm后方向发生了变化,沿着接近于最大正应力的平面扩展。对于图 6(b)所示的试件L-3表面裂纹,裂纹沿最大切应力幅值平面扩展大约50 μm后再次改变方向,沿着接近于最大正应力的平面扩展。
应力幅比
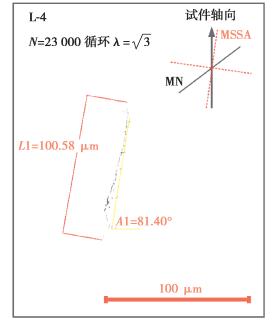
|
图 7 |
|
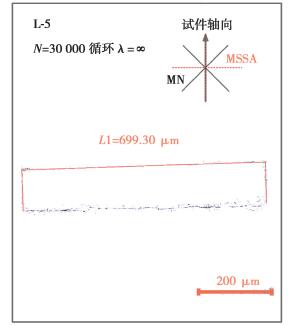
图 8 λ=∞时试件表面典型裂纹形态 Fig. 8 Typical crack on the surface of the specimen when λ=∞ |
通过以上分析可以看到,对于2A12-T4铝合金,试件表面裂纹萌生方向总是接近于最大切应力幅值平面。在不同的应力幅比下,均在裂纹扩展过程中会出现转折,沿最大正应力平面扩展。随着应力幅比的增加,试件表面裂纹出现由最大切应力幅值平面向最大正应力平面转折的数量逐渐减少。
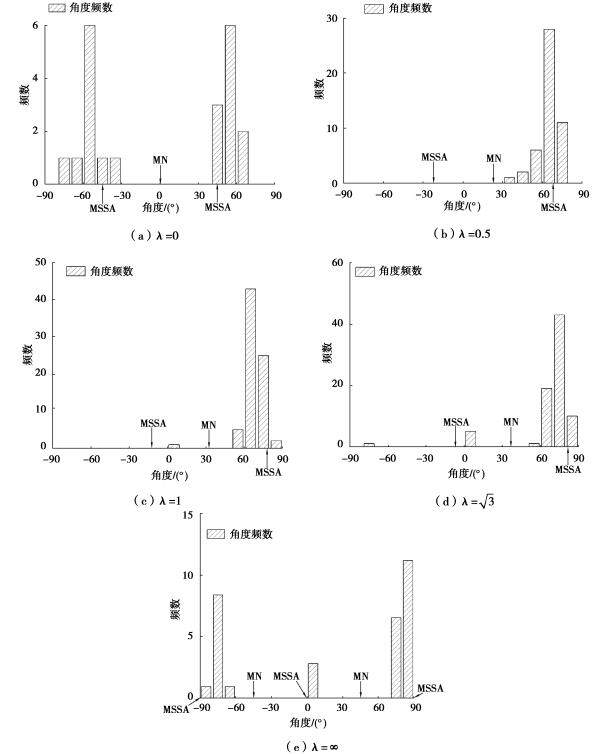
对于每根试件,由于其表面均有大量的裂纹萌生,因此统计了每根试件表面裂纹数量,如表 5所示。针对这些裂纹,统计了其裂纹萌生后初始扩展方向(对于出现方向转变的裂纹为裂纹扩展第Ⅰ阶段)。图 9所示所有裂纹初始扩展方向的统计结果,可以看到,对于所有试件,其裂纹初始方向基本接近于最大切应力幅值平面。
| 表 5 试件表面裂纹统计 Table 5 Number of surface cracks on the specimens |
|
图 9 不同应力幅比下裂纹萌生方向 Fig. 9 Crack initiation orientations under different stress ratios |
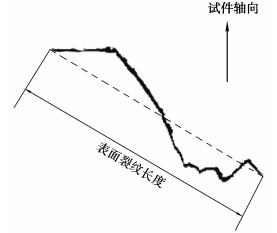
裂纹长度定义如图 10所示。由图 11可以看到裂纹具有明显的扩展第Ⅰ阶段向第Ⅱ阶段的转变,对所有裂纹扩展第Ⅰ阶段的长度进行了统计,统计结果如表 6所示,对于2A12-T4铝合金材料,试件表面裂纹扩展第Ⅰ阶段的长度大约为50~250 μm。不同应力幅比下,裂纹扩展第Ⅰ阶段的长度具有较大的分散性。
|
图 10 试件表面裂纹长度定义 Fig. 10 Definition of the surface crack length |
|
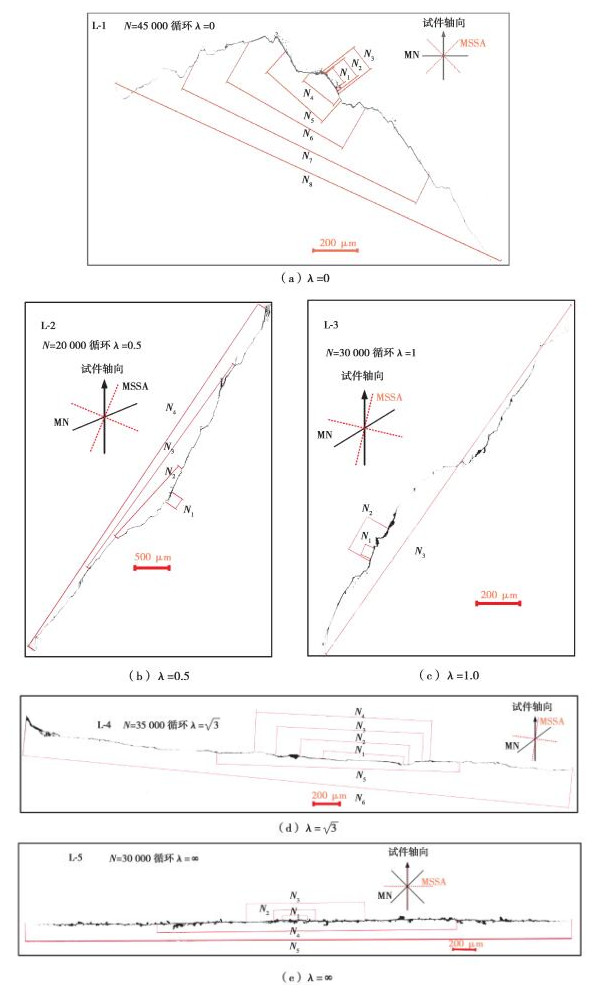
图 11 试件表面主裂纹扩展路径 Fig. 11 Main crack path of test piece surface |
| 表 6 裂纹扩展Ⅰ阶段裂纹长度 Table 6 Length of the stage I crack |
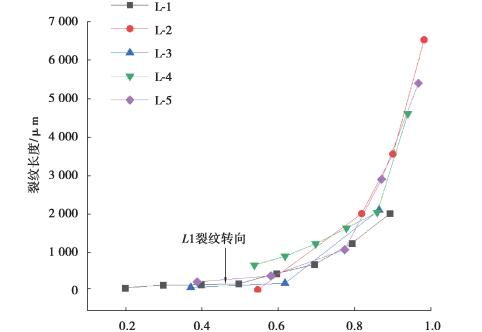
通过对试件表面裂纹的分析,可以得到不同应力主裂纹幅比下主裂纹的长度变化过程,并记录了主裂纹不同循环数下的裂纹长度,如表 7所示。图 11为裂纹完整扩展路径,图 12为不同应力幅比下主裂纹的扩展速率图。
| 表 7 不同应力幅比下试件在不同寿命时的裂纹长度 Table 7 Main crack lengths of different specimens under different fatigue life ratios |
|
图 12 裂纹扩展长度随寿命比的变化 Fig. 12 Variation of crack propagation length with fatigue life ratio |
不同应力幅比下,试件表面主裂纹扩展路径如图 11所示。λ=0时,试件表面主裂纹形态如图 11(a)所示。在循环数N1时,观测裂纹最初在试件表面萌生,此时裂纹长度大约为89 μm,裂纹扩展方向接近于最大切应力幅值平面。随着循环数的增加,裂纹扩展方向在循环数N3~N4(总寿命的39.65%~49.57%)之间时发生转变,开始沿着最大正应力平面扩展;裂纹沿最大正应力平面扩展138 μm,之后(N5~N6)再次改变方向,沿接近最大切应力幅值的平面扩展。
λ=0.5时,试件表面主裂纹没有出现明显的沿最大正应力平面的扩展,裂纹整个扩展过程均沿着接近于最大切应力幅值的平面扩展。λ=1.0时,裂纹扩展路径同应力幅比λ=0.5时相似,试件表面主裂纹扩展过程均沿着接近于最大切应力幅值平面扩展。λ=3与λ=∞时,试件表面主裂纹扩展路径如图所示。可以看到,裂纹在扩展过程中没有出现明显的方向改变,裂纹扩展方向沿着最大切应力平面扩展,扩展过程为Ⅱ型扩展。
通过以上分析可以知道,对于2A12-T4铝合金,其表面疲劳裂纹扩展路径更倾向于沿着接近最大切应力平面扩展,最大切应力幅值是影响裂纹扩展的主要应力分量。
Societ等[4]研究发现对于Inconel718,定义以1 mm长的裂纹作为疲劳失效判据。不同应力幅比下试件表面裂纹扩展长度随寿命比的变化如图 12所示。可以看到,裂纹扩展至1 mm时,大约占疲劳总寿命的70%。对于主裂纹出现明显扩展第Ⅰ阶段向第Ⅱ阶段转变的L-1,裂纹扩展第Ⅰ阶段大约占总寿命的40%。
3 结论针对2A12-T4铝合金,开展了不同应力比下的多轴疲劳试验,研究了其裂纹萌生及扩展路径,可以得到以下结论:
1) 多轴疲劳载荷下,2A12-T4铝合金表面会出现多条裂纹,统计结果表明,对于存在扩展第Ⅰ向第Ⅱ阶段转变的疲劳裂纹,其扩展第Ⅰ阶段的长度为50~250 μm,且第Ⅰ阶段扩展寿命约占总寿命的40%。这可为工程实际中处于多轴应力状态下的2A12-T4铝合金部件的疲劳寿命预测提供参考。
2) 拉扭复合加载下,当λ=0.5,1,
3) 多轴疲劳载荷下,2A12-T4铝合金表面裂纹扩展至1 mm时,扩展寿命占疲劳总寿命的70%。对于多轴应力状态下的2A12-T4铝合金小尺寸结构,该裂纹长度有可能作为其多轴疲劳失效的重要参考依据。
| [1] |
亚伯·斯海维.结构与材料的疲劳[M].吴学仁, 等, 译.北京: 航空工业出版社, 2014. Schijve J. Fatigue of structures and materials[J]. WU Xueren, et al, trans. Beijing: Aviation Industry Press, 2014. (in Chinese) |
| [2] |
尚德广, 王德俊. 多轴疲劳强度[M]. 北京: 科学出版社, 2007. SHANG Deguang, WANG Dejun. Multiaxial fatigue strength[M]. Science Press, 2007. (in Chinese) |
| [3] |
Lieb K C, Horstman R, Peters K A, et al. Multiaxial fatigue: a survey of the state of the art[J]. Journal of Testing and Evaluation, 1981, 9(3): 165. DOI:10.1520/JTE11553J |
| [4] |
Socie D F, Shield T W. Mean stress effects in biaxial fatigue of inconel 718[J]. Journal of Engineering Materials and Technology, 1984, 106(3): 227-232. DOI:10.1115/1.3225707 |
| [5] |
尚德广, 王大康, 孙国芹, 等. 多轴疲劳裂纹扩展行为研究[J]. 机械强度, 2004, 26(4): 423-427. SHANG Deguang, WANG Dakang, SUN Guoqin, et al. Behavior of multiaxial fatigue crack propagation[J]. Journal of Mechanical Strength, 2004, 26(4): 423-427. (in Chinese) |
| [6] |
Reis L, Li B, de Freitas M. Crack initiation and growth path under multiaxial fatigue loading in structural steels[J]. International Journal of Fatigue, 2009, 31(11/12): 1660-1668. |
| [7] |
Navarro A, Vallellano C, Chaves V, et al. A microstructural model for biaxial fatigue conditions[J]. International Journal of Fatigue, 2011, 33(8): 1048-1054. DOI:10.1016/j.ijfatigue.2010.11.001 |
| [8] |
Fatemi A, Socie D F. A critical plane approach to multiaxial fatigue damage including out-of-phase loading[J]. Fatigue & Fracture of Engineering Materials and Structures, 1988, 11(3): 149-165. |
| [9] |
Hua C T, Socie D F. Fatigue damage in 1045 steel under constant amplitude biaxial loading[J]. Fatigue & Fracture of Engineering Materials and Structures, 1984, 7(3): 165-179. |
| [10] |
Hua C T, Socie D F. Fatigue damage in 1045 steel under variable amplitude biaxial loading[J]. Fatigue & Fracture of Engineering Materials and Structures, 1985, 8(2): 101-114. |
| [11] |
Ohkawa I, Takahashi H, Moriwaki M, et al. A study on fatigue crack growth under out-of-phase combined loadings[J]. Fatigue & Fracture of Engineering Materials & Structures, 1997, 20(6): 929-940. |
| [12] |
Verreman Y, Guo H. High-cycle fatigue mechanisms in 1045 steel under non-proportional axial-torsional loading[J]. Fatigue & Fracture of Engineering Materials and Structures, 2007, 30(10): 932-946. |
| [13] |
Vu Q H, Nadot Y, Halm D. High cycle fatigue crack paths in C35 steel under complex loading[C/OL]//International Conference on Crack Paths, March 7, 2013, Vicenza, Italy.[2019-10-12]. https://www.gruppofrattura.it/ocs/index.php/esis/CP2009/paper/viewFile/9372/6207 .
|
| [14] |
Kim K S, Park J C, Lee J W. Multiaxial fatigue under variable amplitude loads[J]. Journal of Engineering Materials and Technology, 1999, 121(3): 286-293. DOI:10.1115/1.2812377 |
| [15] |
Susmel L, Petrone N. Multiaxial fatigue life estimations for 6082-T6 cylindrical specimens under in-phase and out-of-phase biaxial loadings[J]. European Structural Integrity Society, 2003, 31: 83-104. DOI:10.1016/S1566-1369(03)80006-7 |
| [16] |
Liu T Q, Shi X H, Zhang J Y, et al. Crack initiation and propagation of 30CrMnSiA steel under uniaxial and multiaxial cyclic loading[J]. International Journal of Fatigue, 2019, 122: 240-255. DOI:10.1016/j.ijfatigue.2019.02.001 |
| [17] |
Liu T Q, Shi X H, Zhang J Y, et al. Multiaxial high-cycle fatigue failure of 30CrMnSiA steel with mean tension stress and mean shear stress[J]. International Journal of Fatigue, 2019, 129: 105219. DOI:10.1016/j.ijfatigue.2019.105219 |
| [18] |
Fatemi A, Shamsaei N. Multiaxial fatigue: an overview and some approximation models for life estimation[J]. International Journal of Fatigue, 2011, 33(8): 948-958. DOI:10.1016/j.ijfatigue.2011.01.003 |
| [19] |
陈亚军, 王先超, 王付胜, 等. 不同应力幅比加载下2A12铝合金的多轴疲劳性能[J]. 材料工程, 2017, 45(9): 136-142. CHEN Yajun, WANG Xianchao, WANG Fusheng, et al. Multiaxial fatigue properties of 2A12 aluminum alloy under different stress amplitude ratio loadings[J]. Journal of Materials Engineering, 2017, 45(9): 136-142. (in Chinese) |
| [20] |
时新红, 张建宇, 鲍蕊, 等. 比例加载下应力幅比对2A12-T4疲劳寿命的影响[J]. 北京航空航天大学学报, 2010, 36(8): 965-968. SHI Xinhong, ZHANG Jianyu, BAO Rui, et al. Effect of stress amplitude on high-cycle fatigue life of 2A12-T4 aluminum alloy under proportional loading[J]. Journal of Beijing University of Aeronautics and Astronautics, 2010, 36(8): 965-968. (in Chinese) |
 2020, Vol. 43
2020, Vol. 43


