2. 广东技术师范大学 工业实训中心, 广州 510665
2. Industrial Training Center, Guangdong Polytechnic Normal University, Guangzhou 510665, P. R. China
压缩感知理论是近年来信号处理领域的一个研究热点[1-2],它的提出为模式识别和计算机视觉等诸多领域提供了一个新的研究方向。在模式识别领域中,自从J. Wright首次将压缩感知理论核心内容之一的稀疏表示应用于人脸识别[3-4],即面向分类的稀疏表示算法(SRC, sparse representation for classification),该方法受到广泛关注[5-10]。SRC方法在不少情况下可以取得较好的分类或识别效果,尤其是在处理有噪声与遮挡的人脸图像时,若每一类训练样本比较充分,SRC算法的分类效果往往优于最近邻分类器结合Fisherfaces和Laplacianfaces[11]等特征抽取方法的分类效果[12-14]。
然而,在不少应用场合,训练样本很难获取。它们的数目很小,甚至每类只有一个训练样本,这样的数据集为“少样本”数据集。此时,SRC算法的分类效果往往不理想,主要原因是每类数据的训练样本过少,往往不能充分成为与该类训练样本对应的子空间。为解决少样本问题,Deng等[15]人提出了拓展的稀疏人脸识别算法(ESRC, extended sparse representation for classification),该方法目的是处理SRC算法中所遇到的少样本问题。但ESRC也很难获取高维数据中有利于用来分类的非线性信息,为解决这个问题,拟采用一非线性映射将原始输入空间中的数据映射到一高维甚至无穷维的特征空间中。这样,一方面可以从复杂数据集中获取有利于分类的非线性信息[16]。另一方面,把原始输入空间中的数据映射到高维特征空间,避免不同类的样本向量分布于同一方向上[17],使得对样本的线性表示模型变得更简单有效,提高识别效果。
从经典的SRC的表示模型可知,每个训练样本在表示测试样本时所做的贡献不一样。实际上,那些离测试样本越近的训练样本对测试样本的贡献会越大[18-19]。因此,在表示测试样本的过程中,可以将距离测试样本近的训练样本赋予较大的权值,其他训练样本赋予较小的权值,以去除表示测试样本时的干扰因素。为能更好解决上述稀疏表示中的少样本问题,提出特征空间中的核加权拓展稀疏人脸识别算法(KWESRC, kernel weighted extended sparse representation for classification)。在KWESRC中,首先,利用一种非线性映射[20],将这些样本数据非线性映射到高维的特征空间中。它可以通过指定合适的核函数及其参数实现。再利用某一距离度量如高斯核距离[21]计算训练样本的权重,给每个训练样本加权。然后,运用所有的加权训练样本和类内变量矩阵表示测试样本,通过解决l1范数的最小化问题[5]求得测试样本的稀疏表示系数。最后,通过计算每个类别训练样本表示测试样本的l2范数误差,将测试样本分类到误差最小的类别中。实验表明提出的KWESRC算法的分类效果优于其他经典的SRC算法。
1 ESRC算法Deng等人提出的ESRC算法[15], 假设有来自C类的训练样本集X=[X1, X2, …, XC]∈Rm×n与测试样本y∈Rm。第i(i=1, …, C)类的训练样本为Xi=[xi1, xi2, …, xini],其类中心为
| $ {D_i} = \frac{1}{{{n_i}}}\sum\limits_{j = 1}^{{n_i}} {{\mathit{\boldsymbol{x}}_{ij}}} , $ | (1) |
其中,ni为第i类中训练样本个数。由此,再给出类内变量子矩阵如下:Di*=[xi1*, xi2*, …, xini*],其中,xij*=xij-Di(j=1, 2, …, ni)。这些矩阵构成类内变量矩阵:D*=[D1*, D2*, …, DC*]。用所有的训练样本与上述类内变量矩阵共同线性表示测试样本,可得如下式子
| $ y = \mathit{\boldsymbol{X\theta }} + {\mathit{\boldsymbol{D}}^*}\mathit{\boldsymbol{\omega }} + \xi , $ | (2) |
其中:ξ为噪声或表示误差;θ和ω为y的稀疏表示系数,具体如下,θ=[θ11, …, θ1n1, …, θC1, …, θCnC],ω=[ω11, …, ω1n1, …, ωC1, …, ωCnC] (θ, ω∈Rn)。通过解决l1范数的最小化问题求得稀疏表示系数如下
| $ \left[ {\begin{array}{*{20}{l}} {\widehat \theta }\\ {\widehat \omega } \end{array}} \right] = {\rm{arg}}{\kern 1pt} {\kern 1pt} {\rm{min}}{\left\| {\left[ {\begin{array}{*{20}{l}} \theta \\ \omega \end{array}} \right]} \right\|_1},{\rm{ s}}{\rm{.t}}{\rm{. }}{\left\| {y - \mathit{\boldsymbol{X\theta }} - {\mathit{\boldsymbol{D}}^*}\omega } \right\|_2} \le \delta , $ | (3) |
式中,
对于少样本问题,ESRC算法通过引入类内变量矩阵,组成每类训练样本所对应的子空间,再用训练样本集与由它计算得到的类内变量矩阵共同表示单个测试样本,取得一定效果。但是,ESRC算法不能有效获取复杂数据集中的有利于分类的非线性信息。同时,也很难解决不同类的样本向量分布于同一向量方向的问题。为了能够有效获取这样的非线性信息,采用一非线性映射,将数据变换到高维的特征空间。在这一新的空间中,给出KWESRC算法,具体如下。
对来自C类的训练样本集X=[X1, X2, …, XC]∈Rm×n与测试样本y∈Rm来说,可利用非线性映射φ将这些样本映射到高维甚至无穷维的特征空间中。在新的特征空间中,新训练样本集为φ(X)=[φ(X1), φ(X2), …, φ(XC)]∈RM×n, φ(Xi)=[φ(xi1), φ(xi2), …, φ(xini)],
φ(y)∈RM其中i=1, …, C,
| $ \mathit{\boldsymbol{\varphi }}({\mathit{\boldsymbol{D}}_i}) = \frac{1}{{{n_i}}}\sum\limits_{j = 1}^{{n_i}} \mathit{\boldsymbol{\varphi }} ({x_{ij}}), $ | (4) |
其中i=1, …, C, j=1, …, ni。第i类的类内变量子矩阵可表示为
| $ \mathit{\boldsymbol{\varphi }}(\mathit{\boldsymbol{D}}_i^*) = [\mathit{\boldsymbol{\varphi }}(x_{i1}^*),\mathit{\boldsymbol{\varphi }}(x_{i2}^*), \cdots ,\mathit{\boldsymbol{\varphi }}(x_{ini}^*)], $ | (5) |
其中:φ(xij*)=φ(xij)-φ(Di)(j=1, 2, …, ni)。即类内变量矩阵可表示为
| $ \mathit{\boldsymbol{\varphi }}({\mathit{\boldsymbol{D}}^*}) = [\mathit{\boldsymbol{\varphi }}(\mathit{\boldsymbol{D}}_1^*),\mathit{\boldsymbol{\varphi }}(\mathit{\boldsymbol{D}}_2^*), \cdots ,\mathit{\boldsymbol{\varphi }}(\mathit{\boldsymbol{D}}_C^*)]。$ | (6) |
用所有的训练样本与类内变量矩阵共同线性表示测试样本,即
| $ \mathit{\boldsymbol{\varphi }}(y) = \mathit{\boldsymbol{\varphi }}(\mathit{\boldsymbol{X}})\alpha + \mathit{\boldsymbol{\varphi }}({\mathit{\boldsymbol{D}}^*}){\beta ^\prime } + \eta , $ | (7) |
其中,η表示噪声或误差;α,β为φ(y)的稀疏表示系数如下,α=[a11, …, a1n1, …, aC1, …, aCnC], β=[b11, …, b1n1, …, bC1, …, bCnC]。然后通过解决l1范数的最小化问题求得稀疏表示系数,如下式
| $ \left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{\alpha }} ^ \gg }\\ {\mathit{\boldsymbol{\beta }} ^ \gg } \end{array}} \right] = {\rm{arg}}{\kern 1pt} {\kern 1pt} {\rm{min}}{\left\| {\left[ {\begin{array}{*{20}{l}} \alpha \\ \beta \end{array}} \right]} \right\|_1}{\rm{ ,s}}{\rm{.t}}{\rm{. }}{\left\| {\mathit{\boldsymbol{\varphi }}(y) - \mathit{\boldsymbol{\varphi }}(\mathit{\boldsymbol{X}})\mathit{\boldsymbol{\alpha }} - \mathit{\boldsymbol{\varphi }}({\mathit{\boldsymbol{D}}^*})\mathit{\boldsymbol{\beta }}} \right\|_2} \le \varepsilon , $ | (8) |
式中的α, α≫, β, β≫∈Rn。然后,利用经典KPCA算法,得到训练样本的投影轴,并对高维的训练样本数据与类内变量数据进行降维处理。若将每个样本向量降至p维,则有变换矩阵U如下
| $ {\mathit{\boldsymbol{U}}_h} = \sum\limits_{i = 1}^C {\sum\limits_j^{{n_i}} {{v_{hij}}} } \mathit{\boldsymbol{\varphi }}({x_{ij}}) = \mathit{\boldsymbol{\varphi }}(\mathit{\boldsymbol{X}}){v_h},\quad (h = 1, \cdots ,p), $ | (9) |
| $ \begin{array}{*{20}{l}} {\mathit{\boldsymbol{U}} = [{\mathit{\boldsymbol{U}}_1}, \cdots ,{\mathit{\boldsymbol{U}}_h}, \cdots ,{\mathit{\boldsymbol{U}}_p}] = \mathit{\boldsymbol{\varphi }}(\mathit{\boldsymbol{X}})\mathit{\boldsymbol{V}},}\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} = [\mathit{\boldsymbol{\varphi }}(\mathit{\boldsymbol{X}}){v_1}, \cdots ,\mathit{\boldsymbol{\varphi }}(\mathit{\boldsymbol{X}}){\mathit{\boldsymbol{v}}_h}, \cdots ,\mathit{\boldsymbol{\varphi }}(\mathit{\boldsymbol{X}}){v_P}],} \end{array} $ | (10) |
其中,Uh为训练样本的投影轴,vh=(vh11,…,vh1n1…,vhC1,…,vhCnC)T为变换系数向量V=[v1, …, vh…, vp],(h=1, …, p)。在特征空间中,对于任意的2个训练样本φ(x1), φ(x2),可定义核函数为k(x1, x2)=(φ(x1))Tφ(x2)。将样本数据降至P维,则有
| $ \begin{array}{*{20}{l}} {{{\left\| {{\mathit{\boldsymbol{U}}^{\rm{T}}}(\mathit{\boldsymbol{\varphi }}(y) - \mathit{\boldsymbol{\varphi }}(\mathit{\boldsymbol{X}})\alpha - \mathit{\boldsymbol{\varphi }}({\mathit{\boldsymbol{D}}^*})\beta )} \right\|}_2} = }\\ {{{\left\| {{{(\mathit{\boldsymbol{\varphi }}(\mathit{\boldsymbol{X}})\mathit{\boldsymbol{V}})}^{\rm{T}}}(\mathit{\boldsymbol{\varphi }}(y) - \mathit{\boldsymbol{\varphi }}(\mathit{\boldsymbol{X}})\mathit{\boldsymbol{\alpha }} - \mathit{\boldsymbol{\varphi }}({\mathit{\boldsymbol{D}}^*})\mathit{\boldsymbol{\beta }})} \right\|}_2} = }\\ {{{\left\| {({\mathit{\boldsymbol{V}}^{\rm{T}}}{\mathit{\boldsymbol{\varphi }}^{\rm{T}}}(\mathit{\boldsymbol{X}}))(\mathit{\boldsymbol{\varphi }}(y) - \mathit{\boldsymbol{\varphi }}(\mathit{\boldsymbol{X}})\mathit{\boldsymbol{\alpha }} - \mathit{\boldsymbol{\varphi }}({\mathit{\boldsymbol{D}}^*})\mathit{\boldsymbol{\beta }})} \right\|}_2} = }\\ {{{\left\| {{\mathit{\boldsymbol{V}}^{\rm{T}}}(\mathit{\boldsymbol{k}}( \bullet ,y) - K\mathit{\boldsymbol{\alpha }} - G\mathit{\boldsymbol{\beta }})} \right\|}_2} = }\\ {{{\left\| {{\mathit{\boldsymbol{V}}^{\rm{T}}}\mathit{\boldsymbol{k}}( \bullet ,y) - ({\mathit{\boldsymbol{V}}^{\rm{T}}}K\quad {\mathit{\boldsymbol{V}}^{\rm{T}}}G)\left( {\begin{array}{*{20}{l}} \mathit{\boldsymbol{\alpha }}\\ \mathit{\boldsymbol{\beta }} \end{array}} \right)} \right\|}_2},} \end{array} $ | (11) |
其中,k(·, y)=(φ(X))Tφ(y)=[k(x11, y), …, k(xCnC, y)],
| $ \begin{array}{l} \mathit{\boldsymbol{G}} = \left( {\begin{array}{*{20}{c}} {{{(\mathit{\boldsymbol{\varphi }}({x_{11}}))}^{\rm{T}}}\mathit{\boldsymbol{\varphi }}(x_{11}^*)}& \cdots &{{{(\mathit{\boldsymbol{\varphi }}({x_{11}}))}^{\rm{T}}}\mathit{\boldsymbol{\varphi }}(x_{c{n_c}}^*)}\\ \vdots & \ddots & \vdots \\ {{{(\mathit{\boldsymbol{\varphi }}({x_{c{n_c}}}))}^{\rm{T}}}\mathit{\boldsymbol{\varphi }}(x_{11}^*)}& \cdots &{{{(\mathit{\boldsymbol{\varphi }}({x_{c{n_c}}}))}^{\rm{T}}}\mathit{\boldsymbol{\varphi }}(x_{c{n_c}}^*)} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} {k({x_{11}},x_{11}^*)}& \cdots &{k({x_{11}},x_{C{n_c}}^*)}\\ \vdots & \ddots & \vdots \\ {k({x_{C{n_c}}},x_{11}^*)}& \cdots &{k({x_{C{n_c}}},x_{C{n_c}}^*)} \end{array}} \right),\\ \mathit{\boldsymbol{K}} = \left( {\begin{array}{*{20}{c}} {{{(\mathit{\boldsymbol{\varphi }}({x_{11}}))}^{\rm{T}}}\mathit{\boldsymbol{\varphi }}({x_{11}})}& \cdots &{{{(\mathit{\boldsymbol{\varphi }}({x_{11}}))}^{\rm{T}}}\mathit{\boldsymbol{\varphi }}({x_{C{n_C}}})}\\ \vdots & \ddots & \vdots \\ {{{(\mathit{\boldsymbol{\varphi }}({x_{CnC}}))}^{\rm{T}}}\mathit{\boldsymbol{\varphi }}({x_{11}})}& \cdots &{{{(\mathit{\boldsymbol{\varphi }}({x_{C{n_C}}}))}^{\rm{T}}}\mathit{\boldsymbol{\varphi }}({x_{C{n_C}}})} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} {k({x_{11}},{x_{11}})}& \cdots &{k({x_{11}},{x_{C{n_C}}})}\\ \vdots & \ddots & \vdots \\ {k({x_{C{n_C}}},{x_{11}})}& \cdots &{k({x_{C{n_C}}},{x_{C{n_C}}})} \end{array}} \right)\\ = ({K_{11}}, \cdots ,{K_{ij}}, \cdots ,{K_{C{n_C}}})。\end{array} $ |
上面矩阵K的每一列定义如下
| $ {\boldsymbol{K}_{ij}} = \\{\left( {k\left( {{x_{11}},{x_{ij}}} \right), \cdots ,k\left( {{x_{{1_{n1}}}}{x_{ij}}} \right), \cdots ,k\left( {{x_{C1}},{x_{ij}}} \right),, \cdots ,k\left( {{x_{{C_{nC}}}},{x_{ij}}} \right)} \right)^{\rm{T}}},\left( {i = 1, \cdots ,{\boldsymbol{C }},j = 1, \cdots ,{n_i}} \right) $ |
此时,在特征空间中,该训练样本利用定义的核函数可计算得到每一个训练样本的特征向量,矩阵K的每一列定义为该训练样本的特征向量。然后,可衡量训练样本特征在表达测试样本特征时所做的贡献。具体地,计算单个测试样本k(·, y)与Kij(i=1, …, C, j=1, …, ni)之间的高斯核距离,用所计算的距离对Kij进行加权处理。所用的高斯核距离可表示为
| $ {d_g}({\mathit{\boldsymbol{K}}_{ij}},\mathit{\boldsymbol{k}}( \bullet ,y)) = \exp ( - {\left\| {{\mathit{\boldsymbol{K}}_{ij}} - \mathit{\boldsymbol{k}}( \bullet ,y)} \right\|^2}/2{\sigma ^2}), $ | (12) |
其中σ表示高斯核宽度,在实验部分将给出参数σ的计算方法。对K的每一列特征向量加权后的新训练样本特征集K′为
| $ \begin{array}{*{20}{l}} {{\mathit{\boldsymbol{K}}^\prime } = \left( {\begin{array}{*{20}{c}} {{k^\prime }({x_{11}},{x_{11}})}& \cdots &{{k^\prime }({x_{11}},{x_{C{n_C}}})}\\ \vdots & \ddots & \vdots \\ {{k^\prime }({x_{C{n_C}}},{x_{11}})}& \cdots &{{k^\prime }({x_{C{n_C}}},{x_{C{n_C}}})} \end{array}} \right) = ({\mathit{\boldsymbol{K}}^\prime }(1), \cdots ,{\mathit{\boldsymbol{K}}^\prime }(i), \cdots ,{\mathit{\boldsymbol{K}}^\prime }(\mathit{\boldsymbol{C}}))}\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} = ({\mathit{\boldsymbol{K}}^\prime }_{11}, \cdots ,{\mathit{\boldsymbol{K}}^\prime }_{C{n_C}}),} \end{array} $ | (13) |
其中,K′ij=dg(Kij, k(·, y))*Kij,(i=1, …, C, j=1, …, ni)。同时,加权的训练样本特征集K′的类内变量矩阵为G′,即G′可表示为
| $ \begin{array}{l} {\mathit{\boldsymbol{G}}^\prime } = \left( {\begin{array}{*{20}{c}} {{k^\prime }({x_{11}},x_{11}^*)}& \cdots &{{k^\prime }({x_{11}},x_{C{n_c}}^*)}\\ \vdots & \ddots & \vdots \\ {{k^\prime }({x_{C{n_c}}},x_{11}^*)}& \cdots &{{k^\prime }({x_{C{n_c}}},x_{C{n_c}}^*)} \end{array}} \right) = [{\mathit{\boldsymbol{G}}^\prime }(1), \cdots ,{\mathit{\boldsymbol{G}}^\prime }(i), \cdots ,{\mathit{\boldsymbol{G}}^\prime }(\mathit{\boldsymbol{C}})]\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} = [{\mathit{\boldsymbol{K}}^\prime }_{11} - {l_1}, \cdots ,{\mathit{\boldsymbol{K}}^\prime }_{1{n_1}} - {l_1}, \cdots ,{\mathit{\boldsymbol{K}}^\prime }_{C1} - {l_C}, \cdots ,{\mathit{\boldsymbol{K}}^\prime }_{C{n_c}} - {l_C}] \in {R^{M \times n}}, \end{array} $ | (14) |
其中,li(i=1, 2, …, C)表示第i类对应的训练样本特征向量K′(i)=(K′i1, …, K′ini)的均值。即li=
| $ \left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{\alpha ^ \gg }}{_1}}\\ {\mathit{\boldsymbol{\beta ^ \gg}}{ _1}} \end{array}} \right] = {\rm{arg}}{\kern 1pt} {\kern 1pt} {\rm{min}}{\left\| {\left[ {\begin{array}{*{20}{c}} {{\alpha _1}}\\ {{\beta _1}} \end{array}} \right]} \right\|_1},{\rm{s}}.{\rm{t}}.{\left\| {{\mathit{\boldsymbol{V}}^{\rm{T}}}\mathit{\boldsymbol{k}}( \bullet ,y) - \left( {{\mathit{\boldsymbol{V}}^{\rm{T}}}{\mathit{\boldsymbol{K}}^\prime }\quad {\mathit{\boldsymbol{V}}^{\rm{T}}}{\mathit{\boldsymbol{G}}^\prime }} \right)\left( {\begin{array}{*{20}{l}} {{\alpha _1}}\\ {{\beta _1}} \end{array}} \right)} \right\|_2} \le \varepsilon , $ | (15) |
其中V=[v1, …, vp]。即求得此式的稀疏表示系数α≫1,β≫1。然后计算每一类对应的误差大小,将测试样本分到误差最小的类别中。该类别误差可表示为
| $ {r_i}(y) = {\left\| {{\mathit{\boldsymbol{V}}^{\rm{T}}}\mathit{\boldsymbol{k}}( \bullet ,y) - \left( {{\mathit{\boldsymbol{V}}^{\rm{T}}}{\mathit{\boldsymbol{K}}^\prime }\quad {\mathit{\boldsymbol{V}}^{\rm{T}}}{\mathit{\boldsymbol{G}}^\prime }} \right)\left( {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{\delta }}_i}\left( {{\alpha ^ \gg }_1} \right)}\\ {{\beta ^ \gg }} \end{array}} \right)} \right\|_2}, $ | (16) |
其中i=1, 2, …, C,其中新向量δi(α≫1)∈RM中的非零项是α≫1中的仅属于第i类的非零项。具体地,KWESRC算法过程如下。
KWESRC算法
1) 输入:对于给定的测试样本y∈Rm,训练样本的矩阵X=[X1, X2, …, XC]∈Rm×n,将其非线性映射到特征空间中,即新样本集为φ(X)=[φ(X1), φ(X2), …, φ(XC)]∈RM×n,φ(y)∈RM, 误差ε>0。
2) 利用高斯核函数计算得到每个样本的特征向量,即组成了训练样本特征矩阵K与测试样本特征k(·, y)。
3) 利用高斯核距离给每一个训练样本特征向量加权,即产生加权后的新的训练样本特征矩阵K′,并求出K′的类内变量矩阵G′。
4) 通过解决式(15)的l1范数最小化问题求得稀疏表示系数,并利用式(16)来分类测试样本。
3 实验在3个经典的GT,AR和Extended Yale B (EYB)人脸数据集上验证提出的KWESRC算法的识别效果。KWESRC算法将与传统的SRC算法[3]、协同表示分类算法(CRC)[4]、ESRC算法作比较,来验证所提出的算法识别效果。实验中的式(12)表示高斯核距离,其中的参数σ为高斯核宽度,其值为原始输入空间中的全部训练样本平均欧式距离的1e-3倍。式(15)中的误差ε设置为0.01。
3.1 GT人脸数据上的实验第一个实验将在GT(georgia tech)人脸数据集上进行。GT数据集共有50个人的750幅图像,每人有不同姿态,表情,光照等各种条件下的人脸图像。图 1为此人脸数据集的部分图像示例。实验中所有的图像都被转换成为具有256等级的灰度图像,且被裁剪成大小为60×50像素的图像。随机将每类样本分为2类,一部分作为训练样本,剩余的作为测试样本。选定的每类训练样本的数量分别为2和3,即组成2个训练子集。每个算法随机运行10次。

|
图 1 GT人脸数据集的部分图像 Fig. 1 Some images of the GT face data set |
实验中,运用经典的PCA算法将SRC、CRC、ESRC与KED[6]算法中人脸图像降维至不同的维数。图 2和3直观地给出了每类不同训练样本数目N下的各种算法的识别效果,可以看到随着PCA维度的增高,算法的识别精度也随之增高。从图 2和3可知,提出的KWESRC算法优于其它3种算法的识别结果。
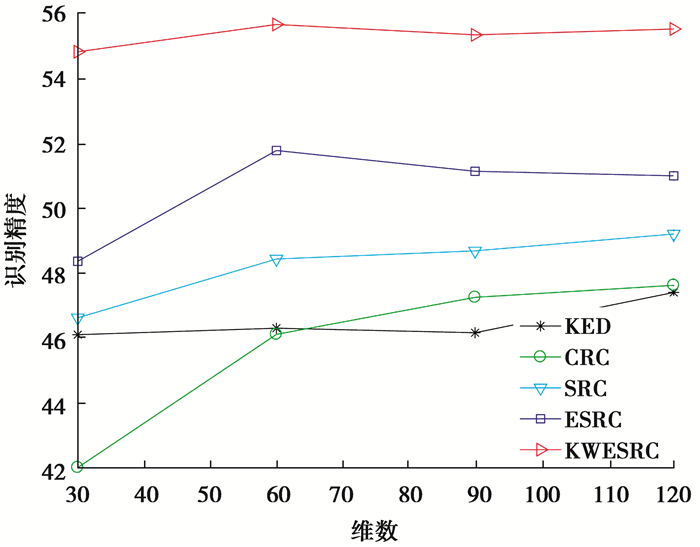
|
图 2 GT数据库上的各种算法的分类效果(N=2) Fig. 2 Classification effect of various algorithms on the GT database (N=2) |
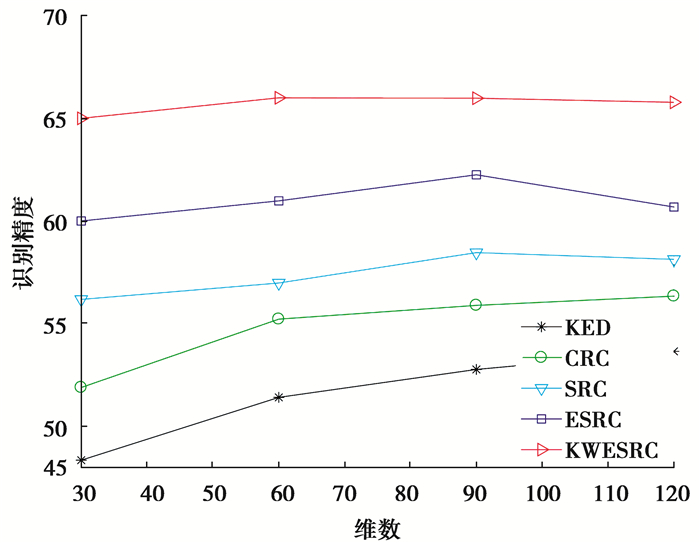
|
图 3 GT数据库上的各种算法的分类效果(N=3) Fig. 3 Classification effect of various algorithms on the GT database (N=3) |
在AR人脸数据集上做第二个实验。AR数据集包含120个人(类)的4 000多幅人脸图像。采用每人不同动作,表情,光照变量条件下的26幅人脸图像。图 4为此人脸数据集的部分图像。实验中所有的图像都被转换成为具有256等级的灰度图像,且被裁剪成大小为20×25像素的图像。同样,随机将每类的样本分为2类,一部分作为训练样本,剩余的作为测试样本。选定的每类训练样本的数量分别为2和3,也组成2个训练子集。同样,每个算法随机运行10次。

|
图 4 AR人脸数据集的部分图像 Fig. 4 Some images of AR Face Data Set |
此实验中,同样运用经典的PCA算法将SRC、CRC、ESRC与KED算法中的人脸图像数据降维至不同的维数。表 1和2给出了每类不同训练样本数目N下的各种算法的识别效果。从表 1,2中可知,所提算法优于其它4种算法的识别结果,并且PCA维度设置的越高,识别精度越高。
| 表 1 AR数据库上的分类精度(平均分类精度±均方差)(%) (N=2) Table 1 Classification accuracy on AR database (average classification accuracy±mean square deviation) (%) (N=2) |
| 表 2 人脸库AR上的分类精度(平均分类精度±均方差)(%) (N=3) Table 2 Classification accuracy on AR database (average classification accuracy±mean variance) (%) (N=3) |
第三个实验是在人脸数据库Extended Yale B(EYB)上实现的。EYB人脸数据库由38个人脸图像构成,总计有2 414幅不同光照条件下的正面人脸图像,每幅人脸图像被裁剪成40×35大小。下图是该人脸库的一些示例图像。同前面的2个实验一样,随机将每类的样本分为两类,一部分作为训练样本,剩余的作为测试样本。选定的每类训练样本的数量分别为3,4和5,组成3个训练子集。每个算法也随机运行10次。
实验中,运用经典的PCA算法将所有的人脸图像数据降至100维。图 6给出了每种算法的识别精度。从此图中可以看出,同前面2个实验结果一致,提出的算法具有最高的识别精度。算法取得理想识别效果的原因主要在于,一方面是利用非线性映射将数据样本从原始输入空间变换到高维特征空间,从理论上使得样本类别之间的边界线性可分。另一方面,考虑了每个样本在表示测试样本的重要程度。给对表示测试样本中贡献大的训练样本赋予较大的权重,进一步增强它们表示测试样本的能力。

|
图 5 EYB人脸库的部分图像 Fig. 5 Some images of the EYB face database |
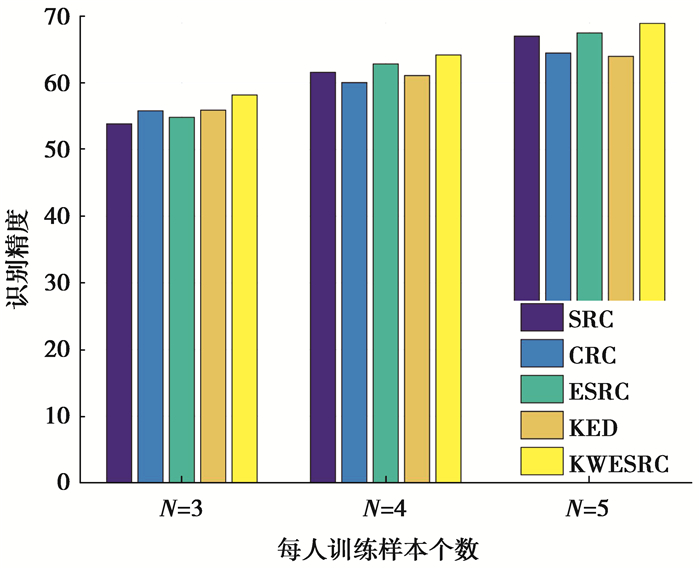
|
图 6 EYB人脸库上的各种算法的分类效果 Fig. 6 Classification effect of various algorithms on EYB face database |
所提出的特征空间中的KWESRC算法可更好处理经典的SRC算法中经常遇到的少样本问题,且有效避免不同类的样本向量分布于同一向量方向的问题。它首先利用一种非线性映射将原来线性不可分数据映射到高维特征空间中,利用高斯核函数求得新样本的特征。然后,考虑不同的训练样本在表示测试样本时所起的作用,即对训练样本进行加权处理,用所求得新样本的类内变量来弥补少样本问题所造成的类内信息缺失。最后用加权的训练样本和类内变量矩阵来线性表示测试样本。实验证明,KWESRC算法的识别精度高于经典的SRC和ESRC算法的识别精度,具有较好的应用前景。
| [1] |
Lu L N, Hu X L, Chen S H, et al. Face recognition based on weighted wavelet transform and compressed sensing[C]//2016 8th International Conference on Wireless Communications & Signal Processing (WCSP). Piscataway, NJ: IEEE, 2016: 1-5.
|
| [2] |
Zhou T Y, Shen F Z, Meng Q Y, et al. Towards real-time through-obstacle imaging based on compressed sensing for sparse objects[J]. IET Microwaves, Antennas & Propagation, 2019, 13(13): 2290-2296. |
| [3] |
Wright J, Yang A Y, Ganesh A, et al. Robust face recognition via sparse representation[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2009, 31(2): 210-227. DOI:10.1109/TPAMI.2008.79 |
| [4] |
Zhang L, Yang M, Feng X C. Sparse representation or collaborative representation: Which helps face recognition?[C]//2011 International Conference on Computer Vision. Piscataway, NJ: IEEE, 2011: 471-478.
|
| [5] |
Yang J, Zhang L, Xu Y, et al. Beyond sparsity:The role of L1-optimizer in pattern classification[J]. Pattern Recognition, 2012, 45(3): 1104-1118. |
| [6] |
Huang K K, Dai D Q, Ren C X, et al. Learning kernel extended dictionary for face recognition[J]. IEEE Transactions on Neural Networks and Learning Systems, 2017, 28(5): 1082-1094. DOI:10.1109/TNNLS.2016.2522431 |
| [7] |
Wu M H, Li S R, Hu J G. Extended class-wise sparse representation for face recognition[C]//2017 3rd IEEE International Conference on Computer and Communications (ICCC). Piscataway, NJ: IEEE, 2017: 1611-1615.
|
| [8] |
Fan Z Z, Zhang D, Wang X, et al. Virtual dictionary based kernel sparse representation for face recognition[J]. Pattern Recognition, 2018, 76: 1-13. DOI:10.1016/j.patcog.2017.10.001 |
| [9] |
Fan Z Z, Wei C. Fast kernel sparse representation based classification for undersampling problem in face recognition[J]. Multimedia Tools and Applications, 2020, 79(11/12): 7319-7337. |
| [10] |
Xu Y, Zhong Z F, Yang J, et al. A new discriminative sparse representation method for robust face recognition via $l2$ regularization[J]. IEEE Transactions on Neural Networks and Learning Systems, 2017, 28(10): 2233-2242. DOI:10.1109/TNNLS.2016.2580572 |
| [11] |
Singh R R, Khandelwal R K, Chavan M. Face recognition using orthogonal locality preserving projections[C]//2016 International Conference on Signal Processing, Communication, Power and Embedded System (SCOPES). Piscataway, NJ: IEEE, 2016: 1323-1328.
|
| [12] |
Miazonzama J F, Hua Q, Wang L. Face recognition using laplacianfaces and artificial neural network[J]. Applied Mechanics and Materials, 2015, 734: 633-636. DOI:10.4028/www.scientific.net/AMM.734.633 |
| [13] |
Chen S B, Ding C H Q, Luo B. Linear regression based projections for dimensionality reduction[J]. Information Sciences, 2018, 467: 74-86. DOI:10.1016/j.ins.2018.07.066 |
| [14] |
Xu X Y, Li S, Liu L. Face recognition based on multi-level histogram sequence center-symmetric local binary pattern and fisherface[C]//2017 IEEE 2nd Advanced Information Technology, Electronic and Automation Control Conference (IAEAC). Piscataway, NJ: IEEE, 2017: 448-451.
|
| [15] |
Deng W H, Hu J N, Guo J. Extended SRC:Undersampled face recognition via intraclass variant dictionary[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2012, 34(9): 1864-1870. DOI:10.1109/TPAMI.2012.30 |
| [16] |
Cheng E J, Chou K P, Rajora S, et al. Deep sparse representation classifier for facial recognition and detection system[J]. Pattern Recognition Letters, 2019, 125: 71-77. DOI:10.1016/j.patrec.2019.03.006 |
| [17] |
Esmaeilzehi A, Abrishami M H. Nonparametric kernel sparse representation-based classifier[J]. Pattern Recognition Letters, 2017, 89: 46-52. DOI:10.1016/j.patrec.2017.02.007 |
| [18] |
Liu X G, Lu L Y, Shen Z X, et al. A novel face recognition algorithm via weighted kernel sparse representation[J]. Future Generation Computer Systems, 2018, 80: 653-663. DOI:10.1016/j.future.2016.07.007 |
| [19] |
Fan Z Z, Ni M, Zhu Q, et al. Weighted sparse representation for face recognition[J]. Neurocomputing, 2015, 151: 304-309. DOI:10.1016/j.neucom.2014.09.035 |
| [20] |
Fan Z Z, Wang J H, Xu B G, et al. An efficient KPCA algorithm based on feature correlation evaluation[J]. Neural Computing and Applications, 2014, 24(7/8): 1795-1806. |
| [21] |
Fu L J, Chen D Y, Lin K Z, et al. An improved SRC method based on virtual samples for face recognition[J]. Journal of Modern Optics, 2018, 65(13): 1565-1576. DOI:10.1080/09500340.2018.1455923 |
 2020, Vol. 43
2020, Vol. 43


