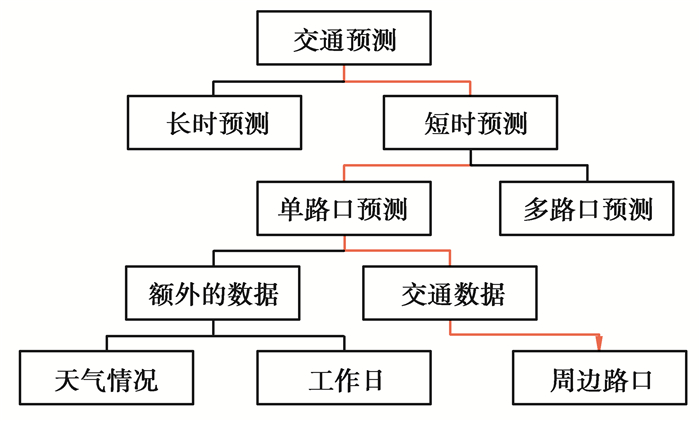
随着社会经济的增长,智能交通系统(ITS,intelligent transport system)[1]在近几年蓬勃发展。智能交通系统主要目的是在大规模的综合交通中实时、准确、高效的感应和控制交通情况,而交通流量的准确预测是ITS的基础,也是ITS的核心研究点之一。现有的交通流量预测通常有2个方向,如图 1所示:一个是涉及多个位置点的区域交通流量预测,比如将道路网络整体看为一个图表,进行整体的预测,这种基于多个位置点的图形研究工作建模复杂度通常比较高,需要大量的人力物力。另一个方向是对单点(单路口)交通流量进行预测,这也是交通预测研究最集中的领域之一。对单路口进行预测的方法受数据源和数据获取方式的限制,大多适用于城郊地域和高速公路等交通情况较简单的地段,在城市中进行预测的方法较少且效果并不理想[2]。所以提出了一种基于城市道路卡口数据的交通流量预测方法,旨在提高城市道路卡口交通流量预测的准确率。
|
图 1 交通预测研究方向图 Fig. 1 Research direction of traffic predicting |
基于观察到城市卡口交通流量数据所呈现的周期性变化,提出了一种有效预测未来一段时间交通卡口流量的方法。该方法利用有监督的机器学习方法,对提取到的车流量周期性变化特征进行建模,然后对未来一段时间的卡口交通流量进行预测。卡口交通流量数据就是对城市中各个路口的监控探头获取到的车辆信息,经过筛选处理后,用来表示每个监控探头所在路口通过车辆数的数据。例如A路口南向北方向车道在早上8:00—8:10的卡口流量是100,表示早上8:00—8:10,A路口南向北方向车道上有100辆汽车通过。这些卡口交通流量数据还包括了卡口所在位置的经纬度、所在的车道方向、所在的道路名称等信息。
在交通流量预测方法中,首先对历史卡口数据进行分析,然后根据其随时间周期性变化特点的提取了以下三种特征:1)日期特征:对时序数据进行特征提取时日期特征是最基础和有效的特征,所以首先提了日期特征,即卡口数据的时间段所属的年、月、日以及整个时间段的开始时刻。2)节日特征:卡口交通流量在节假日、周末、工作日的变化是不同的,考虑卡口数据的时间段属于工作日还是周末,是否属于法定节假日作为第二个特征。3)周期性特征:通过数据分析,可以看到交通卡口数据是随时间呈周期性变化的,比如工作日的早晚高峰车流量会显著增大,而午夜和凌晨时刻的车流量很小,所以将历史每一天相同时刻作为特征进行考虑,此外,同一天预测前的时间段会对预测产生影响,例如8点到8点10分的车流量会对8点半到8点40的车流量产生影响,也将这些相关时间段作为周期性特征进行考虑。最后使用随机森林[3]的方法结合上述3种特征值进行预测,随机森林的方法已经在相关研究[4]被证明有很好的应用。
为了证明方法的有效性,在实验中使用了杭州市真实的卡口交通数据集。实验结果表明,模型有着较好的预测表现,交通卡口数据时间段的不同特征值结合使用在交通卡口流量预测中起着重要作用,贡献可归纳如下:
1) 对数据分析后,根据卡口数据变化的周期性提取了3个特征,包括日期特征、节日特征以及周期性特征。
2) 提出了考虑交通卡口数据周期性特征的一种卡口交通流量预测方法,可以预测未来多个时间段的交通卡口流量。
3) 进行了大量实验并证明了所提方法的有效性。
1 相关工作交通预测领域的相关工作根据预测的范围可以分为两类,一类是对一整个区域进行预测,在城市中就是涉及多个路口和道路,对一整个区域的车流量进行预测。另一类是对单点交通流量进行预测,在城市中便是对一个路口或者一个车道的车流量进行预测,这也是交通预测研究的重点。
第一类方法对整个区域进行预测时会尝试模拟控制交通演变的物理过程来进行分析[5-7]。此类交通预测可用于城市蓝图,道路系统规划等。但是,这种预测需要大量的人力来完成建模,对城市发展有重要意义。也有使用单个车辆轨迹的微观模型来模拟整体交通数据并进一步对整个区域的交通流量变化进行预测[5-6]。但相对于单点预测,对区域进行预测的准确度较低,近些年相关工作并不多。
第二类单点预测的方法在过去的十年中有很多相关研究工作,这也是交通预测的热门研究,其中神经网络(NNet)模型被广泛用于各种交通参数的预测,包括速度的预测[8-9],行程时间的预测[10]和交通流量的预测[11-14],如今,ARIMA,ES和NNet模型已经被用作交通预测的基准方法[13],将ARIMA模型设为对照实验进行考虑。这些传统的交通预测方法使用的数据源为布置于高速公路上记录车速或车辆轨迹等信息的传感器,高速公路交通情况简单,车速较快,所以这些模型取得了很好的预测效果,但这些传感器并不能大规模布置于城市,所以这些方法也不适用于城市区域。在单点预测的相关研究中,过去2年有很多使用新的数据源来进行城市中交通流量预测的方法:Binyu[15]等提出基于出租车GPS数据的k-最近邻模型,对车辆轨迹和车速进行考虑,有不错的效果;LvYIsheng[16]提出了一种新的基于深度学习的交通流量预测方法,该方法考虑了空间和时间的相关性,在城市高架和环城高速上可以进行有效的预测;Fabio Moretti等提出了一种混合建模方法,它结合了人工神经网络和简单的统计方法,以提供一小时的城市交通流量预测,具有良好的预测性能;Kim Y等[17]提出了一种使用多因素模式识别模型的城市交通流量预测系统,该模型将高斯混合模型聚类与人工神经网络相结合,与现有方法相比,可以产生更可靠的预测。以上的方法因为自身数据源和方法的限制,都不能在城市区域有很好的预测表现,模型便是为了弥补这方面工作的欠缺,在城市各个地方都可以有很好的预测结果。
2 数据集使用连续31天真实的杭州市交通卡口数据进行实验。这些数据是800多个交通卡口监控摄像头的记录数据,其中包含完整的属性信息和采集信息1)属性信息,包括监控摄像头编号,摄像机的纬度和经度信息,汽车行驶方向(例如,从南到北等)和所在道路编号等。2)采集信息,包含通过该监控摄像头所在交通卡口的汽车的车牌号和该汽车经过时的时间信息。例如,有2个摄像机,它们相应的交通路口数据显示在表 1和表 2中,分别记录了它们的属性信息和采集信息。每个摄像头都有相应的属性信息,这些是固定不变的,而摄像机的采集信息每天一共约有500万条记录。
| 表 1 属性信息示例表 Table 1 Sample table of own attributes |
| 表 2 采集信息示例表 Table 2 Sample table of acquired data |
表 1和表 2展示了交通卡口数据的原始数据,但需要预测的是路口的车流量,所以需要对上述原始数据进行预处理和结构化,方便之后的模型建模和预测。对原始数据处理后构建例如表 3的数据格式,数字59代表在时间段[20XX-9-1 7:10, 20XX-9-1 7:19]内,路口编号为C123456的路口通过了59辆车。
| 表 3 卡口数据示例表 Table 3 Sample table of traffic intersection data |
为了方便建模和预测工作,提取了卡口数据的以下3部分信息来进行实验:
1) 路口编号:每个时间段中卡口交通流量的唯一标识。
2) 时间段时间戳:每个时间段的开始时间,包含年、月、日、时、分、秒信息。
3) 卡口交通流量:在每个时间段卡口交通流量值。
3 道路卡口交通流量预测方法对交通卡口数据的分析和特征提取工作,然后依据提取的特征建模从而进行卡口交通流量的预测。
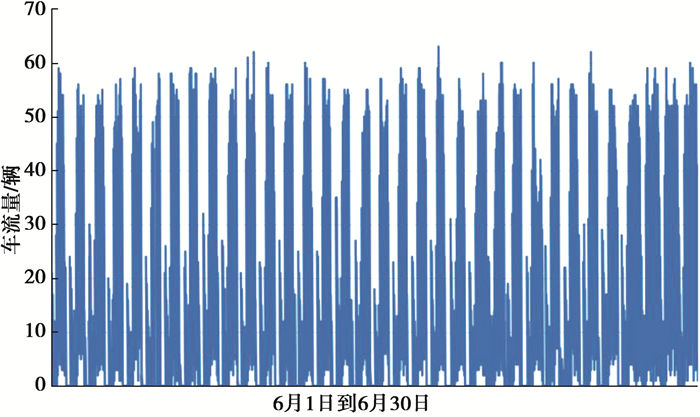
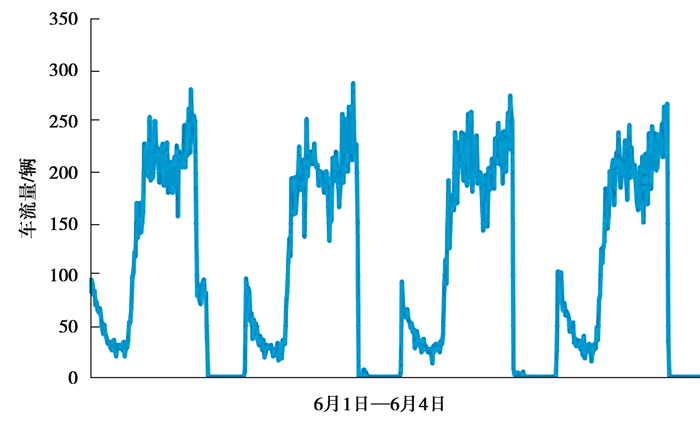
3.1 数据分析和特征提取日期特征:首先对每个卡口的车流量数据分析,发现卡口的车流量呈现周期性变化的规律。图 2展示了一个卡口连续一个月的车流量变化,可以明显看到每一天的车流量是呈周期变化的,每天都有峰值和谷底。如图 3是其中连续4天的车流量变化的对比图,可以看到每一天的车流量变化是呈周期性的,比如在早高峰和晚高峰的时候车流量最大,在午夜和凌晨车流量会非常小,甚至为0,所以将根据卡口交通数据所属日期和时间段开始的时刻提取日期特征。经过预处理的卡口交通数据是精确到分的,即每个时间段的日期包含年、月、日、时、分。但因为数据源限制,数据并没有跨年和跨多个月,所以提取日期中的日、时、分作为特征值。具体来说就是通过时间段的时间戳来获取各个日期的特征,例如一个交通流量值的时间段为“2019-06-10 7:30”,可以提取到时间的日和总分钟的值分别为“2019”、“06”、“10”、“450”,450是这一天的总分钟数,7:30就是这一天的第450 min,同时根据总分钟数450可以得到这个时间段属于7点钟。日期特征也是进行预测的基础特征,可以只使用日期特征进行预测。
|
图 2 一个月车流量变化图 Fig. 2 Changes in traffic folw in a mouth |
|
图 3 四天连续车流量对比图 Fig. 3 Comparison of traffic flow for four consecative days |
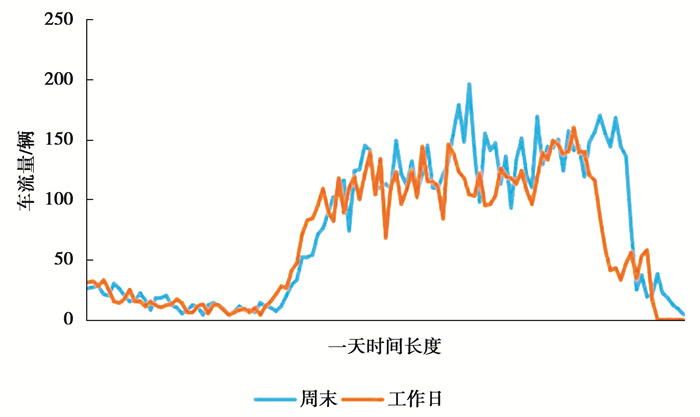
节假日特征:节日分为2种,一种是周末日期(周六和周日),一种是法定节假日。绘制了一天周末和工作日的车流量对比,如图 4所示。可以看到二者的车流量变化是不同的,早高峰开始的时间周末会比工作日晚一点,周末车流量开始下降的时间也比较晚,且一天中车流量最大的时候在中午,白天的车流量都相较于工作日也波动比较大,反观工作日车流量最大的时候在下班高峰,早高峰到晚高峰之间波动幅度比周末小。因此,周末和工作日的车流量变化的周期性是不同的,如表 4所示,将时间段是周末还是工作日也作为特征进行考虑。具体方法就是根据这一天的年、月、日等日期,首先判断这一天属于周一到周日的哪一天,如果属于周一则特征Dayofweek标记为1,周二则标记为2,以此类推。然后判断这天是周六或者周日则标记特征值Isweekend为1,如果是周一到周五则标记为0。
|
图 4 周末和工作日车流量对比图 Fig. 4 Comparison of traffic flow between weekends and weekdays |
| 表 4 周末特征值示意表 Table 4 Examples of weekend eigenvalues |
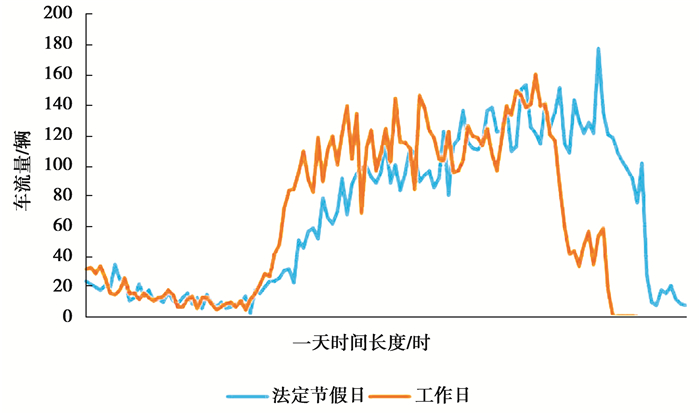
此外在法定节假日,车流量的变化情况也与工作日不同,如图 5所示,法定节假日的早晚高峰时间段车流量并不会显著增大,一天的车流量在平稳增大,然后再中午时候波动,在晚高峰的时候达到最大,然后急剧减少,车流量减少的时间也比工作日要晚一点,因此节假日的变化与工作日也不同,将节假日作为特征进行考虑。与判断周末的方法类似,将时间段的日期进行分析,如果是法定节假日则特征为1,不是则为0。
|
图 5 法定节假日和工作日车流量对比图 Fig. 5 Comparison of traffic folw between statutory |
周期性特征:从图 3观察到每一天交通卡口流量的变化是呈周期性的,比如每天在早高峰和晚高峰的车流量都会增大,早高峰开始时和晚高峰结束后的车流量会急剧变小,在午夜凌晨时分的车流量都会特别小。然后发现同一个路口每天相同时刻的车流量变化都是相似的,比如每天的早上7点左右车流量开始逐渐增大。所以将历史上与预测时间段相同时刻的时间段作为特征进行考虑,如果预测K日[10:00, 10:10]的交通卡口流量,则考虑的特征值为是K-1日,K-2日K-3日,K-4日,K-5日….K-n日等一共n天[10:00, 10:10]的车流量。考虑K日之前多少天的参数n是人为设定的,后续将进行试验求取最适合的值。在表 5中,使用统计学上相关性计算的公式,对连续一周的每个相同时间段进行求余弦相似度,比如对连续一周每天的8:00—8:10、8:10—8:20时间段的车流量分别求余弦相似度,最后取平均值,可以看到连续几天相同时间段的是相关的,特别是日期越相近,余弦值越大,相关性越强,工作日之间的相关性会比工作日和周末的相关性较大。因此考虑预测时间段前几天的相同时刻作为特征值是合理的。
| 表 5 连续7天相同时间段的相关性 Table 5 Correlation of the same time period for 7 consecutive days |
除了连续几天相同时间段是相关的,通过常识判断,同一天前一段时间的交通流量也会对当前的交通流量产生影响。比如K日[10:00, 10:10]的交通卡口流量会受到K日[9:00, 9:10]、[9:10, 9:20]、[9:20, 9:30]、[9:30, 9:40]、[9:40, 9:50]、[9:50, 10:00]等m个时间段的影响(参数m代表当天往前考虑的时间段数量,人为设定,后文也将通过实验求取合适的值),因此将同一天前一段时间的卡口数据作为特征值进行考虑。表 6是使用对连续几个时间段计算其余弦相似度的结果,可以从表中看到与预测时间段时间越相近,二者间的相关性越强,预测时间段之前1 h的时间段相关性已经降低到0.65,所以不能考虑时间间隔太久的时间段。表中证明了连续的时间段是相关的,所以将连续的时间段作为特征值进行考虑。
| 表 6 同一天连续时间段相关性 Table 6 Correlation of consecutive time periods on the same days |
综上所述,通过对相同路口车流量变化进行观察和分析,从卡口数据中提取了日期特征、节假日特征和周期性特征。如表 7所示是将卡口交通数据特征提取后模型的特征和目标输出。Td, i表示第d天第i个时间段,Dd, i表示第d天第i个时间段的日期特征,Jd, i表示第d天第i个时间段的节假日特征,Zd, i表示第d天第i个时间段的周期性特征,Md, i表示第d天第i个时间段的车流量值,也就是经过这些特征希望得到的目标值。下一节将描述使用这些特征,结合随机森林的方法进行模型的构建和预测。
| 表 7 特征值和目标值 Table 7 Eigenvalues and target value |
对原始的卡口交通流量进行预处理和结构化,将车辆数据变为每个卡口随时间变化的连续车流量数据,然后从车流量数据中提取前面提到的3种特征,最后使用这些提取的特征结合随机森林模型进行建模和预测。
首先是预测模型的选择,选择随机森林(RF)进行预测。它是一种灵活且易于使用的机器学习算法,即使没有超参数的调整也能产生良好的实验结果。它是一种监督学习的算法,在做时间序列的预测时,只需要知道每个时间段的特征和目标值就可以放入模型进行训练。在交通预测中,将数据划分为训练集和实验集后,对卡口数据提取前面提到的3种特征来训练模型,这里需要注意的是使用随机森林的模型需要确保特征值不为空,所以周期性特征中需要使用前面几天的数据的作为特征,因此训练时不能选择最前面几天的数据进行训练。
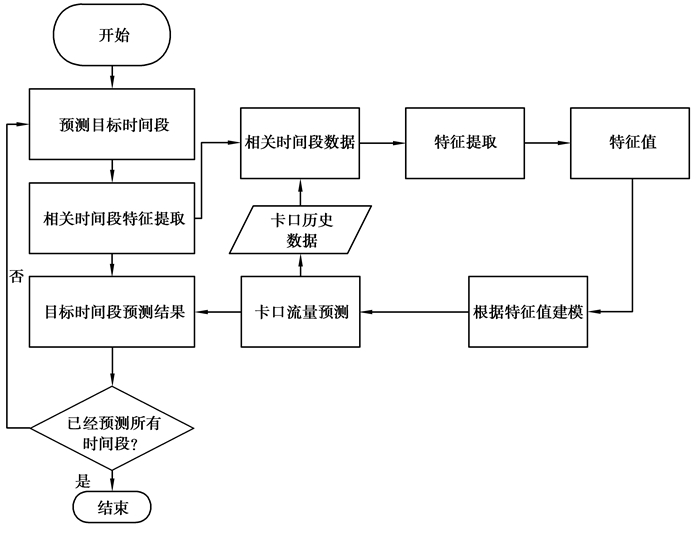
使用随机森林的方法对特征值进行训练,训练好的模型可以输入相应的特征值来得到预测的目标值,预测的步骤如图 6所示。开始之后输入预测的目标时间段,然后根据目标时间段从历史数据中找到相关联的时间段,可以得到目标时间段的周期性特征,然后根据目标时间段自身的时间属性,得到日期特征和节假日特征,最后将3种特征输入训练好的预测模型,最后便可以得到目标时间段的预测交通流量值。
|
图 6 预测模型流程图 Fig. 6 Model prediction process |
根据实验所使用特征的不同,设置了几组对比实验来观察特征选择不同对预测结果的影响。使用进行时序预测比较有效和经典的历史平均预测法[18]和ARIMA[19]模型使用相同的数据对卡口交通流量进行预测,然后对比实验的结果,最后证明使用提出的3种特征的随机森林模型效果较好。
4.1 实验设置使用杭州市一段连续时间的真实数据进行实验,包含完整卡口摄像头自身的属性信息和所获取的数据。首先对原始的卡口数据进行预处理,得到时间长度为1 min的车流量数据,即认为1 min为车流量的最小时间间隔,无法进行时间间隔低于1 min的车流量预测,实验中选择10 min为时间段的长度进行实验[20],10~15 min是进行车流量预测的常用时间粒度。进行实验时,为了避免结果的偶然性,对多个路口进行实验,最后的评估参数取平均值。将数据集的前30 d作为训练集,后4 d作为测试集来评估预测的结果,此外对午夜和凌晨等车流量较少的时间段进行车流量预测现实意义不大,所以选择了每一天早高峰开始到晚高峰结束的时间段进行实验。
为了能够良好的评价和比较仿真结果,采用了如下2种指标来评估模型的优劣:
1) 均方根误差RMSE(root-mean-square error),均方根误差亦称标准误差, 它是观测值与真值偏差的平方与观测次数比值的平方根。均方根误差是用来衡量观测值同真值之间的偏差。标准误差对一组测量中的特大或特小误差反映非常敏感,所以,标准误差能够很好地反映出测量的精密度。可用标准误差作为评定这一测量过程精度的标准。计算公式如下
| $ {\rm{RMSE}} = \sqrt {\frac{{\sum {_{i = 1}^n{{\left( {{y_i} - y_i^*} \right)}^3}} }}{n}} , $ |
其中n是样本量,y是实际值,y*是预测值。
2) 相对百分误差绝对值的平均值MAPE(mean-absolute-percen-tage error):可以用来衡量一个模型预测结果的好坏,计算公式如下
| $ {\rm{MAPE = }}\frac{{\frac{{{\rm{sum}}\left| {{y^*} - y} \right| \times 100}}{y}}}{n}, $ |
其中:n是样本量;y是实际值;y*是预测值。
3) 均方误差(mean square error),准确度预测中均方误差是指预测值与真实值之差平方的期望值,记为MSE,文中即是预测的车流量与实际车流量之差平方的期望值,误差越小,该值越小。
MSE、RMSE表现的是模型预测的结果,越小代表预测效果越好;MAPE表现的是模型预测的趋势效果,数值越小代表对交通流量趋势的预测效果越好,最后我们将每个时间段预测的MSE、MAPE和RMSE值取平均值作为模型评估的结果。
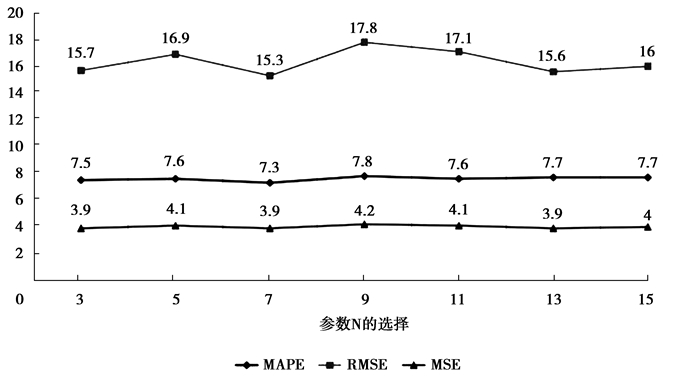
4.2 模型参数实验首先对预测模型中特征提取部分的参数的选择进行了实验,以保证模型的有效性和预测的准确度,当对一个参数进行试验时,其他参数设定为不变。历史时间段特征选择的天数由参数n决定,表示从之前多少天中提取相关时间段的特征,选取了n的值为3到15进行实验,图 7的实验结果可以看出,MAPE的曲线波动较小,预测结果相差不大,每一天的同一时刻的车流量变化对预测结果不大,也就是决定考虑历史多少天的参数n对预测准确度的影响较小。代表误差的MAPE在7~8之间波动,RMSE的值在15~18波动,最终选择预测效果较好的n=7进行之后的实验。
|
图 7 参数n取值变化图 Fig. 7 The value of n |
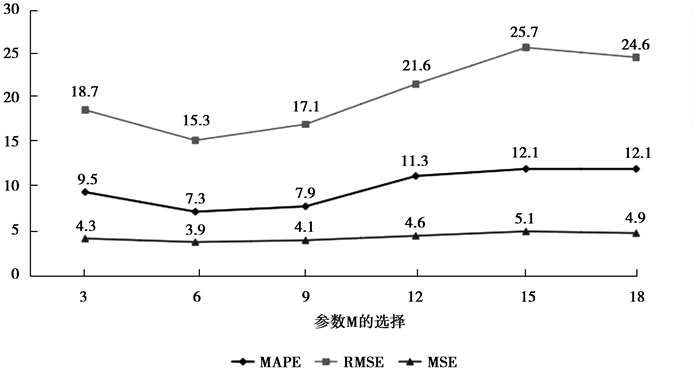
之后对参数m进行实验,参数m表示实验时从当天取多少个时间段的交通流量作为特征进行预测,比如预测时间段为8:00—8:10,当m为3的时候,选择作为相关时间段特征的时间段为7:30—7:40、7:40—7:50、7:50—8:00。选择m的参数为3~18进行实验,即预测时间段的前半小时到前3 h。实验结果如图 7所示,当参数m设定为6时,实验评估的MAPE和RMSE值明显最小,实验效果最好,当参数m太小,即考虑的时间段很相近时,由于参考特征较小,所以预测效果不是最佳,当参数m从12开往大增加时,预测的效果没有太大变化,说明12个时间段是有参考意义的,再远的时间安排产生的影响可以忽略不计。因此设定m=6来进行之后的实验。
|
图 8 参数m取值变化图 Fig. 8 The value of m |
设置几组对比实验来检验各个特征的重要性。日期特征是最基础的特征,每一组实验都需要该特征值,因此就是否考虑节假日特征和相关时间段特征设置了4组模型进行实验:模型RFd是只考虑日期特征,模型RFd, f考虑了日期特征和节假日特征,模型RFd, r考虑了日期特征和周期性特征,最后模型RFd, f, , r将3种特征都考虑在内。
因为日期特征的准确性已经足够高,而且卡口实验数据没有跨多个月或者跨年,作为节假日特征进行模型训练的时间段较少,测试集中日期也没有属于法定节假日的,所以特征实验时节假日特征对预测的影响较小。前面提到交通卡口数据呈现明显的周期性变化,每天都会有增大和减少,且短时间内交通情况比较路面宽度、车流量来源等不会发生大的变化,相关时间段的车流量也不会发生大的变化,所以考虑前几天相同时刻时间段和一天中早些时间段的周期型特征对预测效果的影响会大一些,此外周期型特征的数据比较丰富和准确,对预测结果也会有好的影响。
实验结果如表 8所示,可以看到将所有特征都考虑在内的预测效果最好,只考虑日期特征的预测效果最差,RFd模型是在预测时仅考虑历史数据的日期特征,MAPE值已经降低到了11.2,属于比较准确的预测,说明卡口数据的丰富性和准确性对预测的帮助很大;将节假日特征进去之后,发现RMSE值有所降低,说明对模型误差的减少有一定帮助,但是并没有很大提升,日期的准确性已经足够高,所以RFd, f作为特征的影响不大。RFd, r和RFd, f, r的预测结果也再次印证了这个结论。最后RFd和RFd, r的对比可以看出来将周期型特征考虑的预测结果极好,会大幅提升预测的准确度,说明交通卡口流量受这些周期性特征和基础的日期特征影响较大。
| 表 8 特征模型结果比较 Table 8 Comparison of model results |
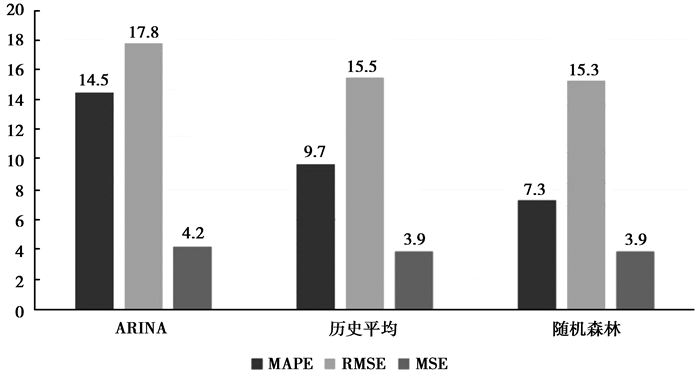
对相同的数据集使用历史平均的方法和ARIMA模型作为对比实验来检测预测模型的效果,预测的时间段和随机森林的选择相同,都是对若干个相同路口4天的早晚高峰时间段进行预测。实验结果如图 9所示,三者相较而言随机森林的预测结果最好,历史平均预测的效果次之,ARIMA模型预测效果最差。因为城市中卡口交通数据的准确性和丰富性,历史每天的相同时间段会呈现相似的变化趋势和相近的车流量,但每一天的周期变化并不是完全相同,有时候高峰会来的早一些,特别是周末的车流高峰期会在午饭和晚饭时间,所以历史平均的预测效果相较于ARIMA模型较好,提出的随机森林方法与历史平均法相比,预测准确性有所提高,因为随机森林的模型是历史平均方法的一种优化,将周期性特征、节假日特征等都考虑在内,而历史平均只考虑了日期特征,所以随机森林的预测效果更好一点。最后的实验结果也证明了方法在城市中使用卡口交通数据有很好的预测效果。
|
图 9 不同模型实验对比图 Fig. 9 Comparison of results of different models |
提出了在交通流密集,道路复杂的城市区域进行准确的交通流量预测的问题。对丰富且准确的城市卡口交通数据进行观察和分析,提出了基于周期性变化的交通卡口流量数据的城市道路卡口的随机森林预测模型,可以对城市中卡口的交通流量进行准确预测。首先对交通卡口数据进行预处理和结构化,将车辆数据整理为每个卡口的交通流量数据,然后从中提取了日期特征、节假日特征和周期性特征,然后使用随机森林的方法基于已经提取的三个特征进行预测模型的构建和预测,对模型的参数的选择进行实验,选择恰当的参数后,再对特征的选择进行实验,验证所提取特征的有效性,最后通过与ARIMA模型和历史平均模型的预测效果进行对比和分析,证明方法的有效性。
| [1] |
陆刚. 简述智能交通系统在我国的发展与应用[J]. 城市公共交通, 2007(10): 28. LU Gang. The development and application of ITS in China[J]. Urban Public Transport, 2007(10): 28. (in Chinese) |
| [2] |
Jin F, Sun S L. Neural network multitask learning for traffic flow forecasting[C]//2008 IEEE International Joint Conference on Neural Networks (IEEE World Congress on Computational Intelligence). Piscataway, NJ: IEEE, 2008: 1897-1901.
|
| [3] |
姚登举, 杨静, 詹晓娟. 基于随机森林的特征选择算法[J]. 吉林大学学报(工学版), 2014, 44(1): 137-141. YAO Dengju, YANG Jing, ZHAN Xiaojuana. Feature selection algorithm based on random forest[J]. Journal of Jilin University(Eng and Technol Ed), 2014, 44(1): 137-141. (in Chinese) |
| [4] |
郭金鑫, 陈玮. 基于HOG多特征融合与随机森林的人脸识别[J]. 计算机科学, 2013, 40(10): 279-282. GUO Jinxin, CHEN Wei. Face recognition based on HOG multi-feature fusion and random forest[J]. Computer Science, 2013, 40(10): 279-282. (in Chinese) |
| [5] |
Gehrke J D, Wojtusiak J. A natural induction approach to traffic prediction for autonomous agent-based vehicle route planning[J/OL].2008[2020-09-29]. http://www.mli.gmu.edu/jwojt/papers/08-3.pdf.
|
| [6] |
Box G E P, Jenkins G M, Reinsel G C, et al. Time series analysis:forecasting and control[M]. Hoboken, USA: John Wiley & Sons, 2015.
|
| [7] |
Jin F, Sun S. Neural network multitask learning for traffic flow forecasting[J]. Proceedings of the International Joint Conference on Neural Networks (IJCNN), 2008, 1898-1902. |
| [8] |
Xiao H, Sun H Y, Ran B, et al. Fuzzy-neural network traffic prediction framework with wavelet decomposition[J]. Transportation Research Record:Journal of the Transportation Research Board, 2003, 1836(1): 16-20. DOI:10.3141/1836-03 |
| [9] |
Ishak S, Alecsandru C. Optimizing traffic prediction performance of neural networks under various topological, input, and traffic condition settings[J]. Journal of Transportation Engineering, 2004, 130(4): 452-465. DOI:10.1061/(ASCE)0733-947X(2004)130:4(452) |
| [10] |
van Lint J W C, Hoogendoorn S P, van Zuylen H J. Freeway travel time prediction with state-space neural networks:modeling state-space dynamics with recurrent neural networks[J]. Transportation Research Record:Journal of the Transportation Research Board, 2002, 1811(1): 30-39. DOI:10.3141/1811-04 |
| [11] |
Lv Y, Duan Y J, Kang W W, et al. Traffic flow prediction with big data:a deep learning approach[J]. IEEE Transactions on Intelligent Transportation Systems, 2014, 1-9. |
| [12] |
Moretti F, Pizzuti S, Panzieri S, et al. Urban traffic flow forecasting through statistical and neural network bagging ensemble hybrid modeling[J]. Neurocomputing, 2015, 167: 3-7. DOI:10.1016/j.neucom.2014.08.100 |
| [13] |
Hu W B, Yan L P, Liu K Z, et al. A short-term traffic flow forecasting method based on the hybrid PSO-SVR[J]. Neural Processing Letters, 2016, 43(1): 155-172. DOI:10.1007/s11063-015-9409-6 |
| [14] |
Sun B, Cheng W, Goswami P, et al. Flow-aware WPT k-nearest neighbours regression for short-term traffic prediction[C]//2017 IEEE Symposium on Computers and Communications (ISCC). Piscataway, NJ: IEEE, 2017: 48-53.
|
| [15] |
Yao B Z, Chen C, Cao Q D, et al. Short-term traffic speed prediction for an urban corridor[J]. Computer-Aided Civil and Infrastructure Engineering, 2017, 32(2): 154-169. DOI:10.1111/mice.12221 |
| [16] |
Polson N G, Sokolov V O. Deep learning for short-term traffic flow prediction[J]. Transportation Research Part C:Emerging Technologies, 2017, 79: 1-17. DOI:10.1016/j.trc.2017.02.024 |
| [17] |
Oh S D, Kim Y J, Hong J S. Urban traffic flow prediction system using a multifactor pattern recognition model[J]. IEEE Transactions on Intelligent Transportation Systems, 2015, 16(5): 2744-2755. DOI:10.1109/TITS.2015.2419614 |
| [18] |
史其信, 郑为中. 道路网短期交通流预测方法比较[J]. 交通运输工程学报, 2004, 4(4): 68-71. SHI Qixin, ZHENG Weizhong. Short-term traffic flow prediction methods comparison of road networks[J]. Journal of Traffic and Transportation Engineering, 2004, 4(4): 68-71. (in Chinese) |
| [19] |
Williams B M, Hoel L A. Modeling and forecasting vehicular traffic flow as a seasonal ARIMA process:theoretical basis and empirical results[J]. Journal of Transportation Engineering, 2003, 129(6): 664-672. DOI:10.1061/(ASCE)0733-947X(2003)129:6(664) |
| [20] |
朱学明.基于神经网络的短时交通流预测方法的研究与应用[D].兰州: 兰州理工大学, 2013. ZHU Xueming. Research and application of short-term traffic flow prediction method based on neural network[D]. Lanzhou: Lanzhou University of Technology, 2013. (in Chinese) |
 2020, Vol. 43
2020, Vol. 43

