荐系统的成功使其在Web应用程序中日益普及[1]。近年来,个性化推荐已在电影[2]、视频[3]、论文引用[4]、地点[5]等方面获得了广泛的应用[6]。到目前为止,已经提出了多种个性化推荐算法[7-9],为了从用户的历史行为来预测用户的偏好,人们投入了许多研究,如协同过滤(CF)。尽管CF方法具有有效性和普遍性,但它无法对物品属性、用户配置文件和各种辅助信息进行建模,因此,在用户和物品交互较少的情况下表现不佳。为了解决这些问题,提出了各种各样的推荐方法,如,知识图谱[10-12]、热传导[13]和质量扩散[14]。Google的PageRank算法[15]根据网页间的超链接随机跳跃被用来进行网页排名,受到PageRank算法的启发,基于推荐系统二部图的随机游走算法PersonalRank[15]被开发出来,传统的PersonalRank算法认为二部图中相关性高的节点具有以下特征:1)两个节点之间有很多路径相连;2)连接两个节点之间的路径长度都比较短;3)连接两个节点之间的路径不会经过出度比较大的节点[16]。
虽然,PersonalRank可以通过随机游走算法对推荐结果进行比较好的理论解释,但该算法在时间复杂度上有明显的缺点。因为,一是在为每个用户进行推荐时都需要在整个二部图上进行迭代,直到图中每个节点的访问概率值收敛;二是该算法对图中节点间边的权重简单依靠有无交互设为1或者0,导致算法推荐准确性不高[17]。
文中在PersonalRank算法的基础上提出了一种新的LWV模型,该模型通过引入自然语言处理,计算商品标签辅助信息在词向量空间中的相似性来生成新的用于交互的边[18],根据其向量空间中的相似性和用户物品历史行为赋予权重,最终在目标用户的三部图中随机游走获取新的推荐物品以更新其他算法的推荐列表。
1 方法 1.1 标签辅助推荐模型基于邻域的算法是推荐系统中最基本的算法,该算法不仅在学术界得到了深入研究,在业界也得到了广泛应用。基于邻域的算法分为两大类,一类是基于用户的协同过滤算法(UCF),另一类是基于物品的协同过滤算法(ICF)。LWV算法实现过程的第一步是通过任意基础推荐算法获取目标用户的前nL(L在本算法中设为50,n>1)个物品推荐值,并将原推荐值作为边的权重,如图 1所示。
|
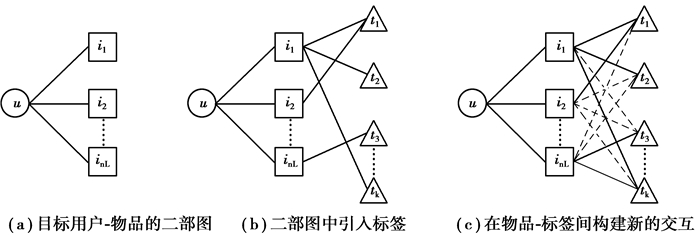
图 1 LWV三部图模型 Fig. 1 LWV three-part graph model |
图 1是LWV方法构建三部图的流程图。图 1(a)构建目标用户物品的二部图,并赋予e(u, i)权重;图 1(b)在二部图中引入标签;图 1(c)在物品标签两两间构建新的交互并由word2vec计算标签相似性结合用户历史行为赋予e(i, t)权重。
通过目标用户与基础算法推荐的nL个物品来构建了用户物品二部图,接着通过在用户物品二部图中引入标签节点建立三部图模型。令G(u, I, T)表示用户物品标签三部图。其中,节点V=u∪Vi∪Vt由单个目标用户u,ICF推荐的nL个物品集合Vi,和这nL个物品在标签数据集中对应的标签集合Vt组成。对于目标用户u和物品节点Vi,图中都有一条对应的边e(u, i),边的权重Wu, i=A(u, i), A(u, i)是任意推荐算法给出的对于目标用户u,物品i的推荐值。对于图中任意二元组(i, t),图中都有一条对应的边e(i, t),值得注意的是用户和标签之间没有交互边。
1.2 边的权重计算赋予三部图中的物品标签之间的边e(i, t)权重。word2vec模型计算的是词与词之间的余弦相似性,范围为-1~1。在建立的模型中,为了最后在整张三部图上进行随机游走推荐,边的权重范围必须是一个正数,且e(u, i)权重范围是0~1,与之对应,运用式(1)将相似性范围缩放到0~1之间:
| $ y = \frac{{{w_{t{t^\prime }}} - \min }}{{\max - \min }}, $ | (1) |
其中,min=-1,max=1,wtt′为word2vec计算出的标签t和标签t′的相似性;y是缩放后标签t和t′的相似性。
传统的图随机游走算法只考虑图中节点间有无交互而构建节点之间边的权重,文中将标签辅助信息引入传统的用户物品二部图,并基于用户历史行为和辅助信息生成新的节点间交互关系构建更加有说服力的权重是成功推荐的重要因素。标签的辅助信息采用在词向量空间中的相似性来为模型在图中构建新的交互关系提供理论依据。如图 1(b)中,实线是数据集中已有的行为交互关系,图 1(c)中的虚线是LWV模型生成的新的交互关系。比如,用户购买了一个物品a,物品a被其他用户打上了“鼠标”这个标签,而物品b有一个“键盘”标签,而“键盘”,“鼠标”两个词在文本上的相似性是比较高的,此时可以生成两条边e(a, “键盘”)和e(b, “鼠标”), 并根据“键盘”,“鼠标”的相似性赋予这两条边一个权重。虽然,e(a, “键盘”)和e(b, “鼠标”)的权重可能远远小于e(a, “鼠标”)和e(b, “键盘”),但是许多条边的生成最终会对最后的推荐列表产生影响。这种处理方式可以更好地挖掘数据间深层次的关系,并使推荐结果具有可解释性。更详细的如图 1(c)中对于物品i1在数据集中被用户打上了t1,t2,tk 3种标签,那么对于i1这个物品,它的标签集合为Ni1={t1, t2, tk},此时,标签t3不在集合中,模型要生成i1到t3的新边,该边的权重要同时受Ni1中所有的元素影响,具体如式(2)所示:
| $ {S_{i,t}} = \left\{ {\begin{array}{*{20}{c}} {{n_{t,i}}t \in {N_i},}\\ {\frac{{\sum\nolimits_t^{} {^\prime \in } {N_i}({w_t}{t^\prime } + 1) * {n_{{t^\prime }i}}}}{{2{m_i}}}t \notin {N_i},} \end{array}} \right. $ | (2) |
其中:wtt′是标签t和t′之间通过word2vec计算出来的相似性;mi是Ni的长度;nt, i是物品i被打上标签t的次数,一个物品被打上相同标签次数越多,证明该标签更加符合这个物品的本质。在数据集中有些标签并不准确,因此,通过引入nt, i,惩罚了这些错误标签对推荐结果的影响。
| $ {S^\prime }_{i,t} = \frac{{{S_{i,t}}}}{{\max ({S_{i,t}})}}, $ | (3) |
同样的,需要将Si, t缩放到0~1之间。
1.3 排名更新在传统二部图的基础上,文中构建了用户物品标签三部图推荐模型,通过引入标签辅助信息,在物品标签间生成新的用于随机游走的带权重的边。
在构造好三部图后,通过随机游走算法来确定最终推荐列表。由于每个用户都拥有一个唯一的三部图,随机游走算法计算所有物品节点相对于用户节点的重要度,按照重要度的高低生成推荐列表,因此,本质是一个图上节点的排名问题。模型要计算用户u的三部图中其余节点相对于用户u的重要度,则从用户u对应的节点开始执行图随机游走算法:每到一个节点都以1-d的概率停止游走并从u重新开始,或者以d的概率继续游走,确定游走概率后从当前节点指向的节点中按照均匀分布随机选择一个节点赋予部分重要度。这样经过很多轮游走之后,每个节点被访问到的概率都会收敛并趋于一个稳定值[19]。
| $ PR(v) = \left\{ {\begin{array}{*{20}{c}} {d\sum\limits_{{v^\prime } \in {\rm{ out }}(v)} {\frac{{PR\left( {{v^\prime }} \right)s}}{{\mid {\rm{ out }}\left( {{v^\prime }} \right)\mid }}} }&{\left( {v \ne {v_u}} \right),}\\ {(1 - d) + d\sum\limits_{{v^\prime } \in {\rm{ out }}(v)} {\frac{{PR\left( {{v^\prime }} \right)s}}{{\mid {\rm{ out }}\left( {{v^\prime }} \right)\mid }}} }&{\left( {v = {v_u}} \right),} \end{array}} \right. $ | (4) |
式中:PR(v)是节点v的访问概率(重要度);vu是用户节点;d是用户继续访问网页的概率,d值在[20]中被认为值为0.85时效果最好;out(v)表示与v有边相连的节点集合。在每次游走的初始,用户的PR值设置为1,其余节点的PR值均设置为0。
文中设置最大迭代次数为100,在图中游走完所有边算一个迭代,在图中迭代100次后每个节点的概率都趋于稳定,最后取重要度最高的前L个物品节点作为最终推荐列表。
模型通过基础算法获取单个目标用户推荐值前nL(n>1)的物品,再由LWV算法更新该nL物品列表中每个物品的推荐系数,对推荐列表进行重新排列来获取最终的长度为L的推荐列表。
2 评价指标为了测试算法性能,将每个实验数据集按照9:1随机分为两部分:训练集和测试集。对于每个用户,根据训练集提供推荐列表,并在测试集上测试性能。为了量化推荐的效果,在此应用6个广泛使用的指标[21],包括3个准确性指标(AUC,Precision,Recall),2个多样性指标(Hamming,Intra-similarity)和1个新颖性指标(Novelty)。
准确性是评估推荐算法质量的最重要指标之一。首先,介绍AUC[22](ROC曲线下的面积),给定测试集中的物品推荐指数,AUC的值可以解释为随机选择的推荐物品的排名高于随机选择的未推荐物品的概率。为了计算AUC,每次选择一对已推荐和未推荐的物品以比较它们的推荐值。经过N次独立比较后,如果推荐物品中有N1次具有更高推荐值,而N2次其推荐值相同,则将所有用户的AUC平均值定义为[23]
| $ {\rm{AUC}} = \frac{1}{m}\sum\limits_{i = 1}^m {\frac{{({N_1} + 0.5{N_2})}}{N}} $ | (5) |
较大的AUC值意味着较高的算法准确性。然后,介绍2个与L相关的精度指标,即Precision和Recall[24]。准确率被定义为测试集中出现的推荐物品数与推荐物品总数之比。在数学上,对于所有用户,Precision的平均值定义为
| $ P(L) = \frac{1}{m}\sum\limits_{i = 1}^m {\frac{{{d_i}(L)}}{L}} , $ | (6) |
其中:di(L)是推荐给用户的物品与测试集中与用户交互物品的交集;L是推荐给用户的物品的总数。召回率定义为用户推荐列表中出现的推荐物品数量与测试集中所有用户有过交互的物品数量的比值。在数学上,对于所有用户,Recall的平均值定义为
| $ R(L) = \frac{1}{m}\sum\limits_{i = 1}^m {\frac{{{d_i}(L)}}{{D(i)}}} , $ | (7) |
更高的召回率意味着更高的精度。多样性是评估由个性化推荐算法推荐的物品种类的重要指标。为了量化物品相似性,使用汉明距离。所有用户的汉明距离[25]平均值定义为
| $ H(L) = \frac{1}{{m(m - 1)}}\sum\limits_{i = 1}^m {\sum\nolimits_{j = 1}^m {\left( {1 - \frac{{C(i,j)}}{L}} \right)} } , $ | (8) |
其中,C(i, j)=|OLi∩OLj|是用户i和j的推荐列表中相同物品的数量。汉明距离的值越大,则多样性越高。
另一个多样性指标是内相似性[26],它是指目标用户的推荐列表中出现对象之间的相似性。数学上,对于所有用户,内部相似性的平均值定义为
| $ I(L) = \frac{1}{{mL(L - 1)}}\sum\limits_{i = 1}^m {\sum\nolimits_{{O_\alpha },{O_\beta } \in O{L_{i,\alpha \ne \beta }}} S } {\rm{Co}}{{\rm{s}}_{\alpha \beta }}, $ | (9) |
其中,SCosαβ是用户i的长度为L的推荐列表OLi中对象α和β之间的余弦相似性[27]。内相似性值越小意味着多样性越高。
新颖性是量化算法推荐新颖(即不热门)物品的能力[28]。在这里,使用推荐对象的平均人气来量化新颖性,其定义为
| $ N(L) = \frac{1}{{mL}}\sum\limits_{i = 1}^m {\sum\nolimits_{{o_\alpha }} { \in O{L_i}{K_{{O_\alpha }}}} } , $ | (10) |
其中,KOα是用户i的推荐列表OLi中物品α的度。较低的N值表示较高的新颖性和潜在的更好的用户体验。
3 实验将实验分为2部分,第1部分是构建word2vec模型并测试其性能。研究发现,在大量数据上用word2vec训练高维词向量时,所得的向量可用于回答单词之间非常微妙的语义关系[29],例如,城市和它所属的国家/地区,例如法国巴黎,德国柏林。具有这种语义关系的词向量可以让模型解释LWV的推荐结果且可以使其他尚未发明算法具有可能性。第2部分在3个公共数据集上对比UCF,ICF,CosRA这3种基础算法通过LWV更新前后的性能表现。在UCF中,将向目标用户推荐具有相似爱好的用户所购买的物品。类似地,在ICF中,将向目标用户推荐与他过去喜欢的物品相似的物品。CosRA算法过程和ICF类似,不过前者对物品相似性做了更多的考虑。文中采用余弦相似性分别量化UCF和ICF中的用户和对象相似性。
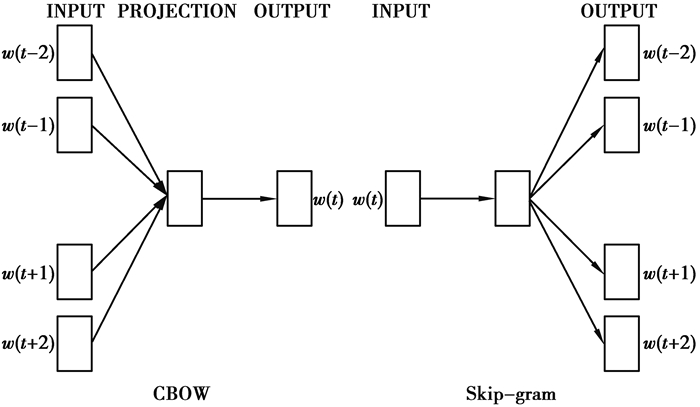
3.1 Word2vec构建2003年,Bengio等[30]发表了一篇开创性的论文,总结出了一套用神经网络建立统计语言模型的框架,首次提出了wordembedding[31]的概念,从而奠定了包括word2vec在内后续研究的基础。word2vec分为2个计算模型,分别是CBOW模型和Skip-gram模型, Skip-gram模式是根据中间词,预测前后词,CBOW模型刚好相反,根据前后的词,预测中间词,如图 2所示。
|
图 2 Word2vec模型 Fig. 2 Word2vec model |
2个模型都包含3层:输入层、投影层和输出层。前者是在已知当前词Wt的上下文Wt-2,Wt-1,Wt+1,Wt+2的前提下预测当前词Wt。而后者恰恰相反,是在已知当前词Wt的前提下,预测上下文Wt-2,Wt-1,Wt+1,Wt+2。文中采用Skip-gram构建word2vec训练模型。
Word2vec本质是一个小型神经网络,神经网络的输出是概率分布,概率代表着输入单词文本上相似性的大小[32]。
对于完整的神经网络模型,输出层需要Softmax[33-35]分类:
| $ softmax (x) = \frac{{ex}}{{\sum\limits_i^N e {x_i}}}, $ | (11) |
其中:神经网络输出层的输出是一个长度为N的向量;xi表示向量第i维的值。计算x的softmax值就是计算x的指数与输出向量中所有元素指数和的比值。Softmax可以将输入映射为0-1之间的实数,而且和为1。文中使用交叉熵作为神经网络的损失函数:
| $ {\rm{Loss}} = - \sum\nolimits_i {{t_i}} \ln {y_i}, $ | (12) |
其中:ti表示真实值;yi表示求出的softmax值,交叉熵损失函数可以衡量ti与yi的相似性。
为了将word2vec模型引用到LWV的推荐算法中需要衡量词向量嵌入的质量,文中定义了1个综合测试集,其中包含5种类型的语义问题和9种类型的句法问题。表 1中显示了每个类别的2个示例。总体而言,共有3 648个语义问题和9 989个句法问题。每个类别中的问题分2个步骤创建:首先,手动创建相似单词对的列表。然后,通过连接2个单词对形成大量问题。例如,文中列出了68个美国大城市及其所属州的列表,并通过随机选择2个单词对形成了约2K个问题。
| 表 1 测试集中的5种语义和9种句法问题的示例 Table 1 Examples of five semantic and nine syntactic problems in the test set |
试验评估所有问题类型的总体准确性。仅当与使用word2vec计算出的向量最接近的词与问题中的正确词完全相同时,才能假定问题得到正确回答;因此,同义词被视为错误。这也意味着达到100%的准确性可能是不可能的。但是,文中认为单词向量在某些应用中的有用性应与此精度的度量值正相关。通过结合有关单词结构的信息,尤其是针对句法问题的信息,可以取得进一步的提升。
3.2 测试数据集为了评估LWV的有效性,使用了3个基准数据集:Movielens-100K,Movielens-1M和Last-FM。他们可公开访问,并且在域、大小和稀疏性方面各不相同。
Movielens-100K & 1M:一个广泛用于电影推荐的数据集,将其中部分不能用于word2vec计算相似性的标签及其所对应的用户交互数据删除。为了确保试验质量,将数据集进行十倍交叉划分,对每一次划分的数据集独立进行试验,最后取实验结果的平均值。
Last-FM:这是从Last.fm在线音乐系统收集的音乐收听数据集,其中,音轨被视为物品,同样删除了其中不能用于word2vec的部分数据,并将数据十倍交叉划分进行试验。
| 表 2 数据集描述 Table 2 Data set description |
文中使用维基百科上随机爬取的六千万篇英文文章作为训练词向量的语料库,并将词汇量限制为一百万个最常用的单词。在综合数据集上就不同词向量的维度做了准确性比较,实验结果如表 3所示。可以看出,随着词向量维度的增加,模型评估语义,句法关系的准确率也随之提升。考虑到维度的增加会提升训练模型的时间,并且维度在300~600的情况下准确率提升不高,文中最终选择300维度下的word2vec模型来计算标签的相似性。
| 表 3 不同词向量维度下Word2vec准确性比较 Table 3 Comparison of Word2vec accuracy under different word vector dimensions |
为了确定LWV对每个目标用户构造的三部图中物品节点的数量,定义了2个参数K和M,其中,K代表原推荐算法给训练集中每个用户推荐的正确物品之和;M代表测试集中每个用户产生过交互的物品数量之和。
| $ C = \frac{K}{M}, $ | (13) |
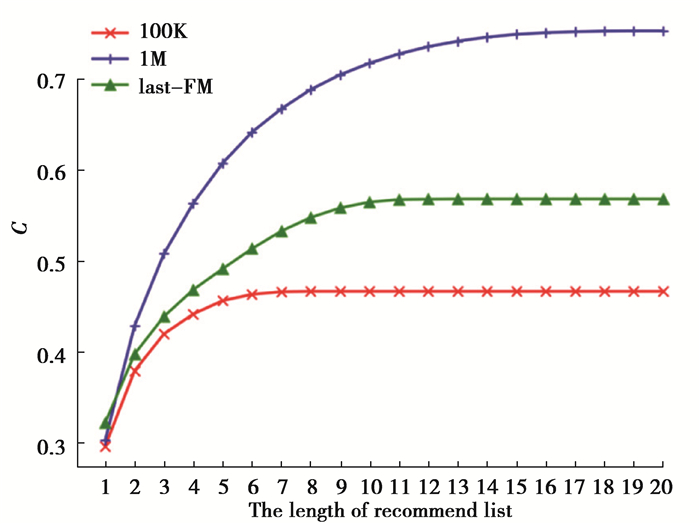
式中:C能够衡量推荐算法的性能,相同长度的推荐列表下C的值越高说明算法发掘用户真正喜欢物品的能力越好。文中在Movielens-100K,Movielens-1M和Last-FM上就不同的推荐列表长度(1L-20L,L=50)进行了比较,如图 3所示。
|
图 3 三种数据集上C值对比 Fig. 3 Comparison of C values on three data sets |
图中在3个不同数据集上对比了UCF,ICF和CosRA算法在不同L下C的平均值,其中,红色、蓝色、绿色分别对应于Movielens-100K,Movielens-1M,Last-FM下的结果。
可以看出,在3个数据集中,C最终在8L,13L,19L的情况下收敛,考虑到推荐列表长度对算法时间复杂度的影响,在C值收敛的情况下,在尽可能短的列表中获得最多的正确的推荐物品。文中选择n=8L作为基础算法生成的推荐列表的长度(用做LWV三部图中目标用户的物品节点)。此时,在100K,1M,Last-FM上发掘正确推荐物品的能力分别达到原算法最大值的100%、91%和96%。
3.4 实验结果文中将基于LWV的方法应用于3个公共数据集,并在3种数据集中分别对基于用户的协同过滤(UCF),基于物品的协同过滤(ICF)和CosRA这3种基础算法来更新推荐列表(L=50),如表 4所示。
| 表 4 3种数据集上算法性能对比(粗体表示更新算法后结果较优的数据) Table 4 Comparison of algorithm performance on the three data sets |
6个公共评价指标显示,被LWV更新过推荐列表的3种推荐算法在3种数据集上相对于原方法在准确性上具有显著优势。另一方面,经由LWV更新过的算法其在多样性上表现不足,说明物品之间的多样性确实可以通过文本上的相似性表示,LWV通过将更多在文本上相似而不仅仅是用户行为上相似的物品推荐给用户,从而提高了推荐算法的准确率。可以得出结论,基于LWV更新过的算法能够发掘传统推荐算法所无法推荐的物品,从而推荐给用户。
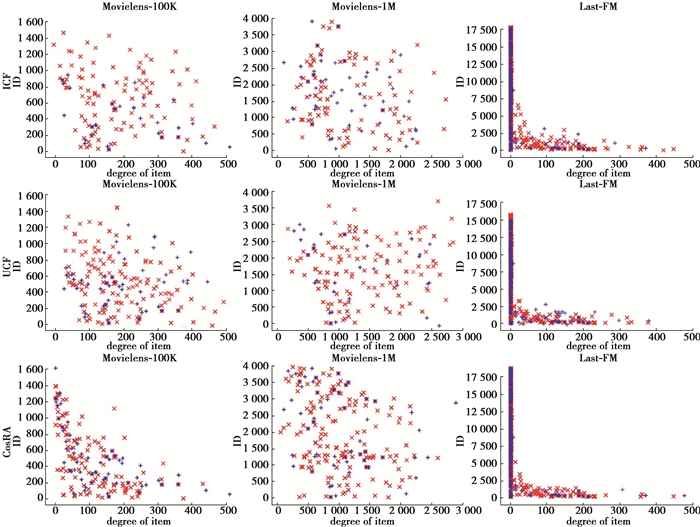
3.5 结果分析文中对3个不同的数据集分别用LWV更新了3种基础算法,每种算法随机抽取了100个用户并由原推荐算法得到长度为50推荐列表,LWV更新过的推荐算法分别给每个用户推荐了50个物品的推荐列表。图 4中红色部分代表原算法通过LWV更新了的那部分物品,该物品确实在测试集中与用户有交互;蓝色部分代表那些在测试集中与用户有过交互但被LWV错误的更新掉的那部分物品。
|
图 4 LWV算法与原算法的散点图显示对比 Fig. 4 Comparison of scatter graph display between LWV algorithm and original algorithm |
可以看出,红色部分明显多于蓝色部分。说明LWV确实能通过标签在向量空间中相似性来提高推荐算法的准确性,可以观察到LWV推荐的物品对度并没有强烈的偏好,这在实际应用中是一个显著的优势。
4 结论提出了一个新的通过增加标签辅助信息在向量空间中的相似性来增强对实际推荐影响的新模型LWV[36]。该模型基于标签辅助信息在向量空间中的相似性生成新的用于随机游走的新边,并结合传统的协同过滤和自然语言处理模型-word2vec构建三部图中各边的权重。在真实数据集上的大量实验表明,通过LWV更新过的算法相比较于原算法具备更好的准确性、多样性和新颖性。为了进一步了解算法工作情况,文中对原算法和经LWV更新过的算法提供了推荐列表更新前后物品在度上的分布[37]。结果表明,该方法对物品的度数没有强烈的偏见。LWV被扩展为了一般形式,也就是说LWV没有任何其他的参数,这在实际应用中是一个显著的优势。
文中探索了自然语言处理在推荐中的潜力,代表利用自然语言处理的方法在三部图中生成新边结合图随机游走算法优化推荐列表的初步尝试。凸显了将机器学习应用在个性化推荐中[38]的重要作用,通过该方法合理的更新推荐列表能够使用户获得更加准确的推荐物品。但是如何在推荐系统中平衡准确性、多样性和新颖性仍然是一个悬而未决的问题。该模型在时间复杂度上仍然有着很大的劣势[38],文中虽然将传统的包含所有用户、物品节点和交互关系的三部图拆分成多个小的三部图,在游走上大大减少了时间的消耗,但由于需要对每一个用户都生成一张唯一的三部图,因此,在面对用户特别多的实际情况中,时间复杂度问题仍不能有效解决[39]。后续研究会考虑矩阵转移的方法来代替在图中一次次迭代以产生推荐列表。
| [1] |
Zheng Z B, Ma H, Lyu M R, et al. QoS-aware web service recommendation by collaborative filtering[J]. IEEE Transactions on Services Computing, 2011, 4(2): 140-152. DOI:10.1109/TSC.2010.52 |
| [2] |
Jinhu L, Tao Z, Zike Z, et al. Promoting cold-start items in recommender systems[J]. PLoS One, 2014, 9(12): e113457. DOI:10.1371/journal.pone.0113457 |
| [3] |
Davidson J, Livingston B, Sampath D, et al. The youtube video recommendation system[C]. Proceedings of the fourth ACM conference on Recommender systems-RecSys'10. New York, USA: ACM Press, 2010: 293-296.
|
| [4] |
Bogers T, van den Bosch A. Recommending scientific articles using citeulike[C]. Proceedings of the 2008 ACM conference on Recommender systems-RecSys'08. New York, USA: ACM Press, 2008: 287-290.
|
| [5] |
Lian D, Xie X, Zhang F, et al. Mining location-based social networks:A predictive perspective[J]. IEEE Data Engineering bulletin, 2015, 38(2): 35-46. |
| [6] |
Schafer J B, Konstan J A, Riedl J. E-commerce recommendation applications[M]. Boston, MA: Springer US, 2001: 115-153.
|
| [7] |
Yao X J, Tan B H, Hu C, et al. Recommend algorithm combined user-user neighborhood approach with latent factor model[M]. Cham: Springer International Publishing, 2017: 275-280.
|
| [8] |
Cheng P, Wang S, Ma J, et al. Learning to recommend accurate and diverse items[J]. Proceedings of the 26th international conference on World Wide Web, 2017, 183-192. |
| [9] |
Ahmedi L, Rrmoku K, Sylejmani K, et al. A bimodal social network analysis to recommend points of interest to tourists[J]. Social Network Analysis and Mining, 2017, 7: 14. DOI:10.1007/s13278-017-0431-8 |
| [10] |
Paulheim H. Knowledge graph refinement:a survey of approaches and evaluation methods[J]. Semantic Web, 2016, 8(3): 489-508. |
| [11] |
Wang Q, Mao Z D, Wang B, et al. Knowledge graph embedding:a survey of approaches and applications[J]. IEEE Transactions on Knowledge and Data Engineering, 2017, 29(12): 2724-2743. DOI:10.1109/TKDE.2017.2754499 |
| [12] |
Dettmers T, Minervini P, Stenetorp P, et al. Convolutional 2D knowledge graph embeddings[J]. 32nd AAAI Conference on Artificial Intelligence, 2018, 1811-1818. |
| [13] |
Zhang Y, Blattner M, Yu Y. Heat conduction process on community networks as a recommendation model[J]. Physical review letters, 2008, 99(15): 154301. |
| [14] |
Zhang Y C, Medo M, Ren J, et al. Recommendation model based on opinion diffusion[J]. Europhysics Letters (EPL), 2007, 80(6): 68003. DOI:10.1209/0295-5075/80/68003 |
| [15] |
Langville A, Meyer C. Deeper inside PageRank[J]. Internet Mathematics, 2004, 1(3): 335-380. |
| [16] |
Hu J, Liu L, Zhang C, et al. Hybrid recommendation algorithm based on latent factor model and personal rank[J]. Journal of Internet Technology, 2018, 19(3): 919-926. |
| [17] |
Xing W, Ghorbani A. Weighted PageRank algorithm[C]. Proceedings Second Annual Conference on Communication Networks and Services Research. Piscataway, NJ: IEEE, 2004: 305-314.
|
| [18] |
Ji S H, Satish N, Li S, et al. Parallelizing word2Vec in shared and distributed memory[J]. IEEE Transactions on Parallel and Distributed Systems, 2019, 30(9): 2090-2100. DOI:10.1109/TPDS.2019.2904058 |
| [19] |
Lofgren P, Banerjee S, Goel A. Personalized pagerank estimation and search[C]. Proceedings of the Ninth ACM International Conference on Web Search and Data Mining-WSDM'16. New York, USA: ACM Press, 2016: 163-172.
|
| [20] |
Kloumann I M, Ugander J, Kleinberg J. Block models and personalized pagerank[J]. Proceedings of the National Academy of Sciences of the United States of America, 2017, 114(1): 33-38. DOI:10.1073/pnas.1611275114 |
| [21] |
Zhou T, Ren J, Medo M, et al. Bipartite network projection and personal recommendation[J]. Physical Review E, 2007, 76(4): 046115. DOI:10.1103/PhysRevE.76.046115 |
| [22] |
Liu R H, Hall L O, Bowyer K W, et al. Synthetic minority image over-sampling technique: How to improve AUC for glioblastoma patient survival prediction[C]. 2017 IEEE International Conference on Systems, Man, and Cybernetics (SMC). Piscataway, NJ: IEEE, 2017: 1357-1362.
|
| [23] |
Zhou T, Lü L, Zhang Y C. Predicting missing links via local information[J]. The European Physical Journal B, 2009, 71(4): 623-630. DOI:10.1140/epjb/e2009-00335-8 |
| [24] |
Herlocker J L, Konstan J A, Terveen L G, et al. Evaluating collaborative filtering recommender systems[J]. ACM Transactions on Information Systems, 2004, 22(1): 5-53. |
| [25] |
Cao Y, Long M S, Liu B, et al. Deep cauchy hashing for hamming space retrieval[C]. 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition. Piscataway, NJ: IEEE, 2018: 1229-1237.
|
| [26] |
Zhou T, Su R, Liu R, et al. Accurate and diverse recommendations via eliminating redundant correlations[J]. New Journal of Physics, 2009, 11(12): 123008. DOI:10.1088/1367-2630/11/12/123008 |
| [27] |
Zhou Y, Lü L, Liu W, et al. The power of ground user in recommender systems[J]. PloS one, 2013, 8(8): e70094. DOI:10.1371/journal.pone.0070094 |
| [28] |
Resnick P, Varian H R. Recommender systems[J]. Communications of the ACM, 1997, 40(3): 56-58. DOI:10.1145/245108.245121 |
| [29] |
Kottur S, Vedantam R, Moura J M F, et al. VisualWord2Vec (vis-W2V): learning visually grounded word embeddings using abstract scenes[C]. 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR). Piscataway, NJ: IEEE, 2016: 4985-4994.
|
| [30] |
Mikolov T, Chen K, Corrado G, et al. Efficient estimation of word representations in vector space[J/OL]. Computer ence, 2013[2020-09-29]. https://arxiv.org/abs/1301.3781.
|
| [31] |
Yao, Li X, Liu X P, et al. Sensing spatial distribution of urban land use by integrating points-of-interest and Google Word2Vec model[J]. International Journal of Geographical Information Science, 2017, 31(4): 825-848. DOI:10.1080/13658816.2016.1244608 |
| [32] |
Church K W. Word2Vec[J]. Natural language engineering, 2016, 23(1): 155-162. |
| [33] |
Wang F, Cheng J, Liu W Y, et al. Additive margin softmax for face verification[J]. IEEE Signal Processing Letters, 2018, 25(7): 926-930. DOI:10.1109/LSP.2018.2822810 |
| [34] |
Jang E, Gu S, Poole B. Categorical reparameterization with gumbel-softmax[J/OL]. arXiv e-prints, 2016[2020-09-29]. https://arxiv.org/abs/1611.01144
|
| [35] |
Liu W, Wen Y, Yu Z, et al. Large-margin softmax loss for convolutional neural networks[J]. ICML, 2016, 507-516. |
| [36] |
Yang Q. A robust recommended system based on attack detection[J]. Concurrency and computation, 2019, 31(12): e4660. |
| [37] |
Babeetha S, Muruganantham B, Ganesh Kumar S, et al. An enhanced kernel weighted collaborative recommended system to alleviate sparsity[J]. International Journal of Electrical and Computer Engineering (Malacca, Malacca), 2020, 10: 447-454. |
| [38] |
Mi H Y, Muruganujan A, Huang X S, et al. Protocol update for large-scale genome and gene function analysis with the PANTHER classification system (v.14.0)[J]. Nature Protocols, 2019, 14(3): 703-721. DOI:10.1038/s41596-019-0128-8 |
| [39] |
Putriany V, Jauhari J, Izwan Heroza R. Item clustering as an input for skin care product recommended system using content based filtering[J]. Journal of Physics:Conference Series, 2019, 1196: 012004. DOI:10.1088/1742-6596/1196/1/012004 |
 2020, Vol. 43
2020, Vol. 43

