2. 北京信息科技大学 计算机学院, 北京 100101;
3. 华南理工大学 机械与汽车工程学院, 广州 510640
2. Computer School, Beijing Information Science and Technology University, Beijing 100101, P. R. China;
3. School of Mechanical and Automotive Engineering, South China University of Technology, Guangzhou 510640, P. R. China
由于齿轮的结构复杂、测量参数多,检测精度易受到人为因素影响;对于尺寸较大的齿轮,测量时装夹与定位困难。根据齿轮的在线检测与精密制造的现实要求,研究人员将计算机视觉引入齿轮各项技术指标的测量,取得了不少研究成果。张少军等[1]采用计算机视觉对齿轮的部分参数如齿数、模数、齿厚等进行检测;陈廉清等[2]提出虚拟圆扫描法,采用计算机视觉实现对齿轮的齿数、模数等的检测。葛动元等[3-4]采用机器视觉对直齿圆柱齿轮的齿距累积总误差等进行检测,该方法将检测点定位于分度圆,使得所检测的齿距符合定义,而不是常规的检测方法所得到的弦齿距。采用机器视觉系统在齿轮齿廓渐开线的法线方向上测量齿廓偏差,以确保该方案所得到的齿廓偏差与其定义相一致。林超等[5]提出高阶椭圆锥齿轮齿距误差的三坐标测量法。齿轮在生产完成后,常常需要对其进行精度等级的确认,而公法线长度及其误差则能反映齿厚与齿槽宽的误差。齿轮公法线长度的传统测量方法是采用公法线千分尺对其进行接触式测量[6],但是随着计算机视觉及图像处理技术的快速发展,实现非接触式测量是可行的。文中以渐开线标准直齿圆柱齿轮为对象,研究基于计算机视觉的齿轮齿数以及公法线长度及其变动的检测算法。
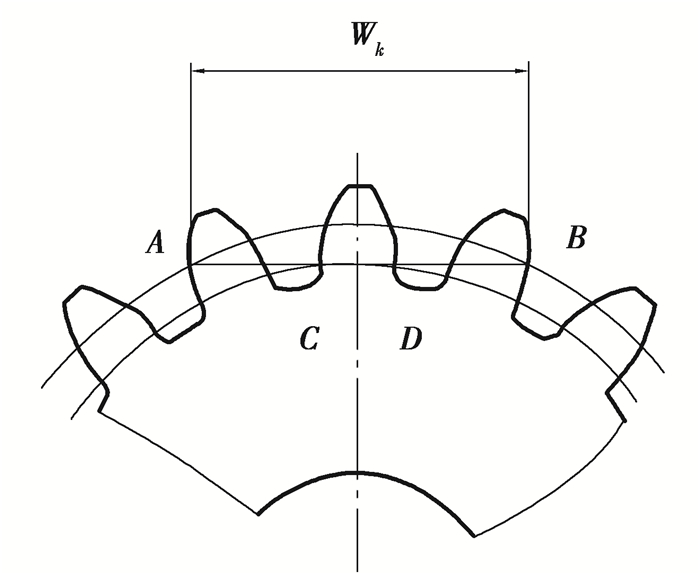
1 检测原理齿轮的公法线是一条与基圆相切,与齿轮异侧渐开线相交的直线,而公法线长度变动是指在齿轮1周范围内, 所有位置的公法线最大值与最小值之差。如图 1所示,Wk表示齿轮的公法线长度;Wk*表示模数为1时的公法线长度;A、B点为公法线与齿廓交点;C、D点为基圆与齿廓交点,外圆是公法线与齿廓相交的点作半径的测量圆,内圆是基圆。
|
图 1 公法线示意图 Fig. 1 Diagram of common normal |
齿轮的公法线长度计算表达式为
| $ {{W_k} = W_k^*m,} $ | (1) |
| $ {W_k^* = \cos \alpha [{\rm{ \mathsf{ π} }}(k - 0.5) + {\rm{zin}}v\alpha ],} $ | (2) |
测量公法线的跨齿数k取决于公式
| $ {k = \frac{\alpha }{{{{180}^\circ }}} + 0.5,} $ | (3) |
式中,α为压力角;k值四舍五入取整数[7]。根据图示测量原理,公法线与齿廓的交点(A、B点)之间的距离即为公法线长度,在算法程序上只需求解A、B两点的图像坐标。
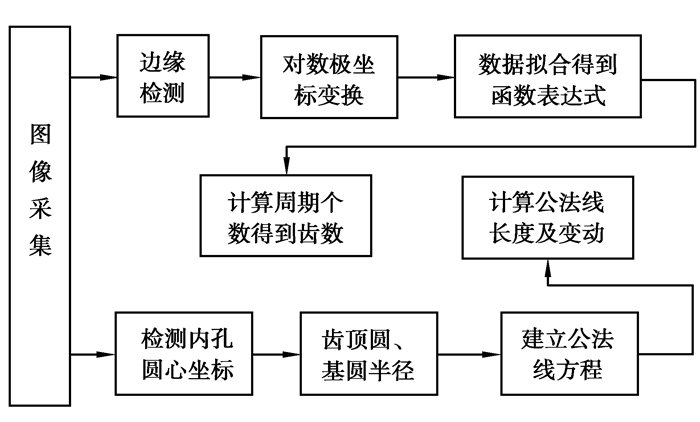
根据公法线的测量原理,得到利用计算机视觉技术检测齿轮公法线长度的流程,如图 2所示。
|
图 2 检测流程图 Fig. 2 Detection flow chart |
齿轮的检测装置如图 3所示,检测装置由实验支架、光源以及摄像机和光源控制器等组成。把摄像机固定在一个不变的位置,摄像机镜头到物体表面的距离为230 mm。拍摄采用的是1个500万像素、型号为(XW500)CCD工业相机,CCD工业相机具有拍摄图像清晰度高,色彩还原好、几何失真小的特点,是一款高分辨率的彩色数字摄像机。检测物体的几何形状采用的光源是型号为(HF-FX100)的背光光源,对检测物体的几何形状、图像特征比较明显。

|
图 3 实验拍摄设备 Fig. 3 Experimental shooting equipment |
对摄像机标定[8-10]求取比例尺采用的方法是通过拍摄30 mm×20 mm的矩形,利用OpenCV库中的算法获得这一矩形的长和宽的像素值之后,计算物理尺寸与像素值之间的比例关系。在标定板上精加工1个30 mm×20 mm的矩形框,经过图像采集,灰度化处理,二值化处理之后,使用OpenCV中的findContours()函数求得外轮廓的点集坐标,drawcontours()函数求取矩形的外接矩形,通过boundingRect()函数[11]提取矩形的左上角坐标以及长和宽的值,即可获得外接矩形的长和宽的像素个数。在实验中,计算得到的标定矩形块的像素值大小为152×227。图像坐标系的原点在图像左上角,水平向右为u轴,垂直向下为v轴,图像坐标系以像素为单位,像素的横坐标u与纵坐标v分别是在其图像数组中所在的列数与所在行数。图像像素与物理尺寸的转换系数k=像素数/物理尺寸,即k=227/30=7.566 667 pixel/mm,验算另一值,物理尺寸d=152/7.566 667= 20.0881 mm,误差为0. 088 1,基本满足使用要求。
2.2 计算齿轮齿数利用三角函数的周期性对齿轮的齿数进行检测。使用对数极坐标将齿廓展开,得到的变换图像可以看作是一条齿距相等且按照一定的周期排布的齿条,类似具有周期的波形图,对其进行正弦函数或者余弦函数拟合,得到展开齿廓的函数表达式,求其周期,展开之后齿廓的总长度与拟合得出的正弦函数的周期的比值即为齿轮齿数。
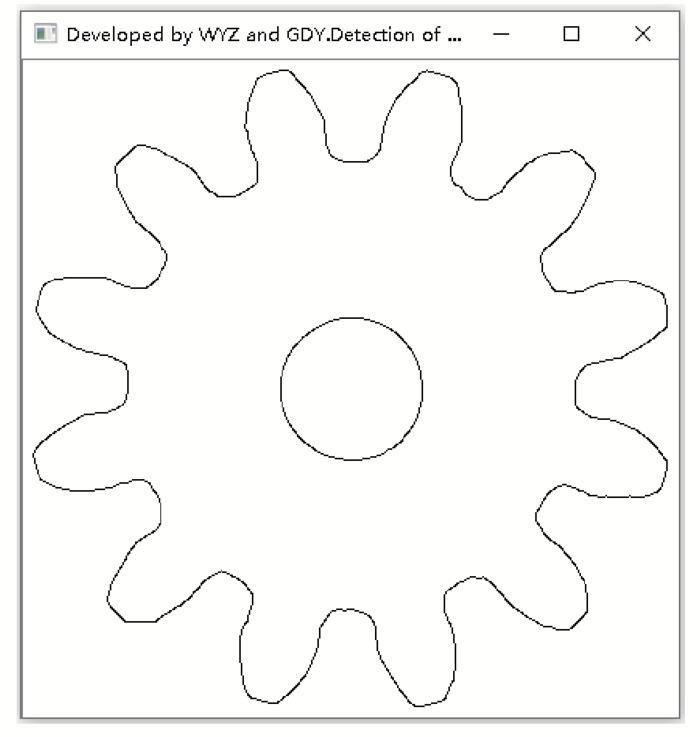
2.2.1 图像采集打开背光光源采集齿轮的轮廓图像,如图 4所示。图像经过二值化后,使用Canny()函数提取图像轮廓,如图 5所示。

|
图 4 齿廓图像采集 Fig. 4 Sampling's gear contour |
|
图 5 齿轮轮廓特征提取 Fig. 5 Feature extract of gear contour |
在对齿数进行检测时,张少军等[1]采用中点画圆法或Bresenham画圆法作一个辅助圆,然后沿辅助圆搜索,得到该辅助圆与齿轮廓线的交点, 实现对齿轮齿数的检测。葛动元等[4]通过计算齿廓的采样点到分度圆的圆心距离,采用异或运算求得分度圆与齿廓的交点,得到所检测齿轮的齿数。首次运用极坐标变换算法对预处理后的齿廓采样数据进行变换,将圆周上的齿廓曲线在水平方向展开,并将得到的齿廓看作正弦曲线,再采用Matlab工具箱中傅里叶变换函数得到正弦曲线的拟合表达式,再对齿廓采样数据的总数(即列数)与拟合函数的周期比值取整,得到所检测齿轮的齿数。
在计算机图像处理中,原图像经过某种变换得到目标图像,根据变换关系将目标图像的像素一个个映射回原图像,由原图像的已知像素求出目标图像的未知像素。对数极坐标有很好的性质,例如,在图像拼接中,经常会见到将图像从笛卡尔直角坐标系转换到对数极坐标系中,进行图像旋转尺度和缩放因子的计算,尺度和旋转变换转化为平移变换, 这就为尺度和旋转不变性带来了方便[12],选用对数极坐标对齿轮轮廓进行展开。
在进行极坐标变换时,(x, y)表示图像中笛卡尔直角坐标系的坐标,ρ表示原图中某一像素点坐标(x1, y1)与中心点(x0, y0)形成的向量的模,θ表示该向量与笛卡尔平面直角坐标系正向横坐标的夹角,对数极坐标是在极坐标的基础上增加了对数运算,将直角坐标系的点(x, y)用向量表示,令向量m=[x y]T,n=[sinθ cosθ]T, 坐标点(x, y)在笛卡尔直角坐标系和极坐标之间的映射关系为
| $ m = \rho n, $ | (4) |
其中,
| $ \left\{ {\begin{array}{*{20}{l}} {\xi = K{\kern 1pt} {\rm{ln}}(\sqrt {{{({x_1} - {x_0})}^2} + {{({y_1} - {y_0})}^2}} ),}\\ {\beta = L \cdot \arctan [({y_1} - {y_0})/({x_1} - {x_0})],} \end{array}} \right. $ | (5) |
式中,K和L是为了调整变换之后的图像的像素值大小而添加的调整参数,K值决定着输出图像x轴(ρ)的尺度,L值决定着y轴(θ)的尺度。rows表示原图像像素的行数,则有L=rows/360,输出的极坐标图像的y轴从0~rows-1表示在笛卡尔直角坐标系下0~360°的变化。cols表示原图像像素的列数,假设把图像的中心定为(cols/2, rows/2), 那么最大半径
| $ {{\rm{ max}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{Radius }} = \sqrt {{{({\rm{rows}}/2)}^2} + {{( {\rm{cols}} /2)}^2}} ,} $ | (6) |
对应的调整参数K为
| $ {K = {\rm{cols}} /\sqrt {{{({\rm{rows}}/2)}^2} + {{( {\rm{cols}} /2)}^2}} }。$ | (7) |
采用OpenCV库中的logPolar()函数对图 5的齿廓进行对数极坐标变换,如图 6所示。图中右边的黑色区域部分是由于对数极坐标在变换过程中因极点(图像中心点)到边缘的距离小于max Radius形成的空洞,其中,最大的半径(max Radius)为极点到四个角点的距离,在变换后会用灰度值全为0来填充空洞区域;极点选择在同心圆心时,同一个圆上的点到圆心的距离相等,所以映射在极坐标中是1组垂直于极轴的平行线。为了方便对中间的齿廓部分进行拟合,使用transpose()函数将图 6逆时针旋转90°,如图 7所示,得到的图像的列数为457,即457个pixel。

|
图 6 对数极坐标变换 Fig. 6 Log-polar transformation |

|
图 7 目标图像旋转 Fig. 7 Target image rotation |
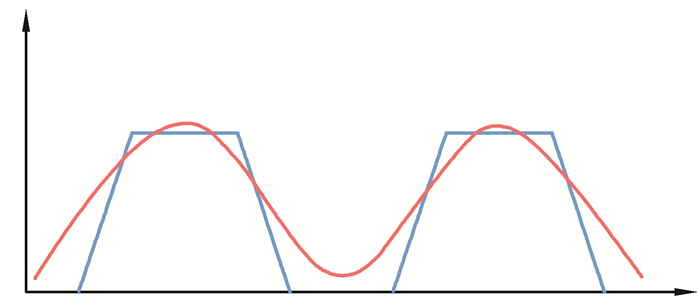
经过对数极坐标变换后的齿廓整齐排布在同一水平线上,且呈现周期性规律变化,这一规律变化类似于三角函数的正弦函数或者余弦函数图像,如图 8所示,若把经过对数极坐标变换的齿廓的齿顶和齿根与正弦曲线的波峰和波谷对应,则拟合的逼近曲线为正弦曲线,一个整齿对应于一个周期曲线,由于在图像处理与数据处理环节受到噪声的影响,使齿轮齿数与拟合的正弦曲线的周期个数存在偏差,求解拟合曲线的周期个数的取值应为与它最接近的整数值,该方法不影响齿数的求解。文中分别采用傅里叶级数和正弦函数与对数极坐标变换后的图形曲线进行拟合,得到拟合表达式。
|
图 8 齿廓拟合曲线 Fig. 8 Fitting curves of teeth profile |
1) 基于傅里叶级数的正弦函数拟合。设拟合的正弦函数的表达式为
| $ y = a + b\sin (\omega x + \varphi ), $ | (8) |
利用正弦函数两角的和差公式,对公式进一步展开得到
| $ y = a + b[\sin (\omega x)\cos (\varphi ) + \sin (\varphi )\cos (\omega x)], $ | (9) |
由于φ值为常数,所以sin(φ)、cos(φ)为定值,令bcos(φ)=b1,bsin(φ)=a1,
则有y=a+a1cos(ωx)+b1sin(ωx),等于n=1时的傅里叶级数,
| $ f(x) = {A_0} + \sum\limits_{n = 1}^\infty {\left[ {{a_n}\cos (n\omega x) + {a_n}\sin (n\omega x)} \right]} 。$ | (10) |
在Matlab的拟合工具箱里有Fourier(傅里叶级数)拟合法,选择Fourier对齿轮的齿廓采样点进行拟合。
在图像坐标系的基础上,选取若干点作为正弦函数的采样拟合点,各采样点的坐标,如表 1所示。
| 表 1 采样点坐标 Table 1 Sampling point coordinates |
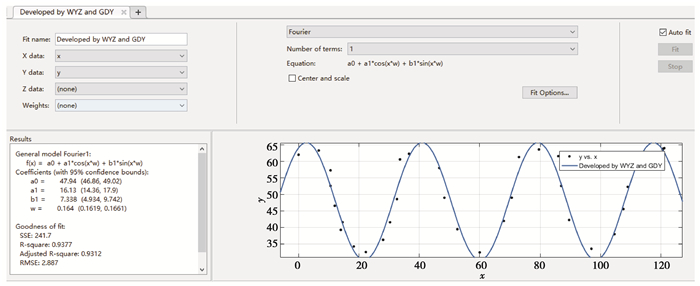
在采用Matlab工具箱拟合正弦曲线时,根据系统的要求,采样点坐标分别以2个向量x和y分别保存,再运行,输入指令cftool,弹出求解对话框,如图 9所示。在X data中选择采样点的x坐标,即为保存的x=[0,6.7,10.6,10.6,10.6,12.0,……,121.3]T,在Y data中选择采样点y坐标,即为保存的y=[62.0,63.3,57.3,52.6,46.6,41.6,……,64.6] T,然后选择Fourier进行拟合,拟合的图像函数,如图 9所示。
|
图 9 拟合结果 Fig. 9 Fitted result |
运行结果如图 9所示,a0=47.94,a1=16.13,b1=7.338,w=0.164,可得正弦曲线的拟合方程为
| $ f(x) = 47.94 + 16.13\cos (0.164x) + 7.338{\kern 1pt} {\kern 1pt} {\kern 1pt} \sin (0.164x)。$ | (11) |
从拟合得到的方程可知,频率ω1=0.164,周期T1=2π/0.164=38.31。经过极坐标变换之后,齿廓的形状可以用正弦曲线来表示,不影响对齿数求解的精度(这与齿轮的模数求解类似)。齿数N1=457/38.31=11.93。根据公式(10),傅里叶级数n=2,拟合得到的频率ω2=0.081 89, 周期T2=38.364,N2=11.91, 比较N1和N2值,N1比N2更趋近齿数12,由此得出傅里叶级数选择n=1的拟合效果更好。
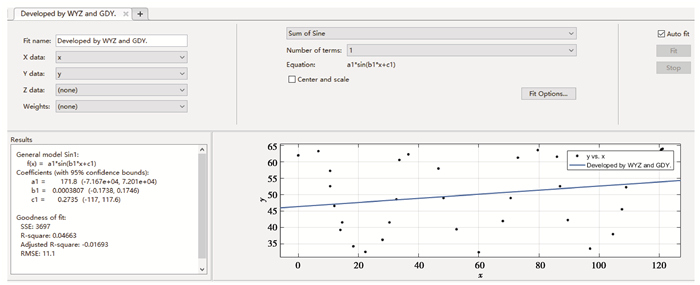
2) 基于通用模型f(x)=asin(bx+c)正弦函数拟合。在Matlab的拟合工具箱中的“Sun of Sine”是对正弦函数曲线的拟合,文中尝试拟合正弦函数曲线,与Fourier作为比较,选择二者中较好的。拟合的数据与上文相同,最终的拟合结果,如图 10所示。
|
图 10 拟合结果 Fig. 10 Fitted result |
根据图 10可得拟合的正弦曲线方程为
| $ f(x) = 171.8\sin (0.000{\kern 1pt} {\kern 1pt} {\kern 1pt} 380{\kern 1pt} {\kern 1pt} {\kern 1pt} 7x + 0.273{\kern 1pt} {\kern 1pt} {\kern 1pt} 5)。$ | (12) |
从拟合方程可以得出,频率b1=0.000 380 7,周期T3=165 04.3,采用Sum of Sine拟合齿廓,且项数(number of terms)为1,得到的拟合曲线与实际的相差很大,经过多次探索,只有当项数(number of terms)为4时,所得到的拟合曲线基本符合实际,但此时无法得到拟合曲线的周期,所以文中检测方法采用傅里叶级数的方式进行。
采用张少军提出的Bresenham画圆法和葛动元采用的求分度圆与齿廓交点检测方法对齿轮齿数进行检测,分别如表 2的第1行与第2行所示。实验结果表明,文中提出的检测方法准确有效、更简洁,从理论创新的角度来看,鲁棒性更好。
| 表 2 齿数检测方法及检测结果 Table 2 Tooth number detection method and detection result |
齿轮的参数包括齿顶圆半径、模数、基圆半径等。Hough变换法检测圆和圆心具有较强的抗噪能力[13],因此,文中用Hough变换法检测齿轮内孔的圆心坐标,此内孔圆心即为齿轮的中心点。在检测齿顶圆半径时,先对采集到的图像进行二值化处理,遍历灰度值全为0的像素点并且计算像素点到中心点的距离,取最大的3组观测值,其平均值即为齿顶圆半径。设这3组观测值的灰度值为0的像素点坐标分别为(x1, y1)、(x2, y2)、(x3, y3),齿轮中心点坐标为(x0, y0),为了方便计算,将坐标向量化,则有γi=[xi yi]T,η=[x0 y0]T,齿顶圆直径的计算公式为
| $ {d_a} = 2/3\sum\limits_{i = 1}^3 {{{\left[ {{{\left( {{\gamma _i} - \mathit{\boldsymbol{\eta }}} \right)}^{\rm{T}}}\left( {{\gamma _i} - \mathit{\boldsymbol{\eta }}} \right)} \right]}^{1/2}}} 。$ | (13) |
根据齿顶圆直径求齿轮在图像上的模数m, m=da/(z+2)。其中,da为齿顶圆直径;z为齿数。齿轮公法线是一条与基圆相切的线段,需要求出基圆直径,基圆直径db=mzcos α。
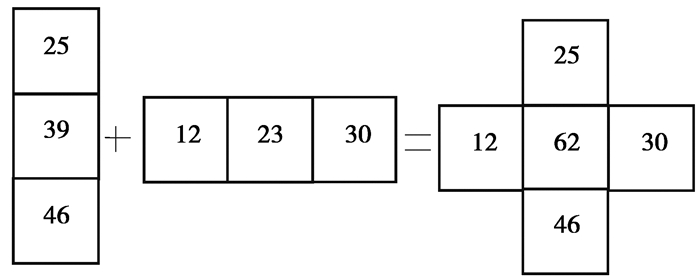
2.4 齿轮公法线长度变动齿廓与基圆的交点,通过两幅图像使用add (pictureA, pictureB)函数相加来获取。两幅大小相同的图像相加,得到的是两者的灰度值之和,并且如果灰度值之和大于255,返回图像的灰度值恒为255, 如图 11所示。
|
图 11 add函数示意图 Fig. 11 add Function diagram |
在picture1中,搜索齿轮轮廓的像素点,并把灰度值设为20,图片大小为m×n;将picture2的图片大小设为m×n、背景灰度值为255,根据上文计算得出的基圆半径和圆心坐标,使用circle函数画出基圆,并把基圆像素点的灰度值设为100,picture1和picture2相加得到picture3,根据picture3得到的交点使用编号0,1,2,……,23进行标记。根据图 1的测量原理,基圆与两侧齿廓的交点(C、D点)的中线经过这一段的基圆圆弧的中点。中线方程可根据(x, y)到C(xc, yc)、D(xd, yd)点的距离相等来获得,如式(14)所示,再经过变换得到该中线在图像坐标系上的坐标,如式(15)所示。将图片picture4大小设为m×n、背景灰度值为255,画出中线,经过该中线的像素点的灰度值设为50,并与基圆的图像picture2相加,得到picture5,搜索灰度值为150的像素点即为这一段基圆圆弧的中点。
| $ {{{(x - {x_c})}^2} + {{(y - {y_c})}^2} = {{(x - {x_d})}^2} + {{(y - {y_d})}^2},} $ | (14) |
| $ {\left\{ {\begin{array}{*{20}{l}} {x = i,i \in [0,m],}\\ {y = (2x{x_c} + x_d^2 + y_d^2 - 2x{x_d} - x_c^2 - y_c^2)/2({y_c} - {y_c})}。\end{array}} \right.} $ | (15) |
由于经过圆弧中点的中线与该点在基圆上的切线相互垂直,可通过计算中线斜率得到切线斜率l,得到公法线方程
| $ y = l(x - {x^\prime }) + {y^\prime }。$ | (16) |
经过公法线的像素点的灰度值设为120,在大小为m×n、背景灰度值为255的图像picture6上根据式(16)画出公法线,picture6与齿廓图像picture1相加,得到齿廓与公法线的交点picture7,搜索灰度值为140的像素点即为公法线与齿廓的交点。
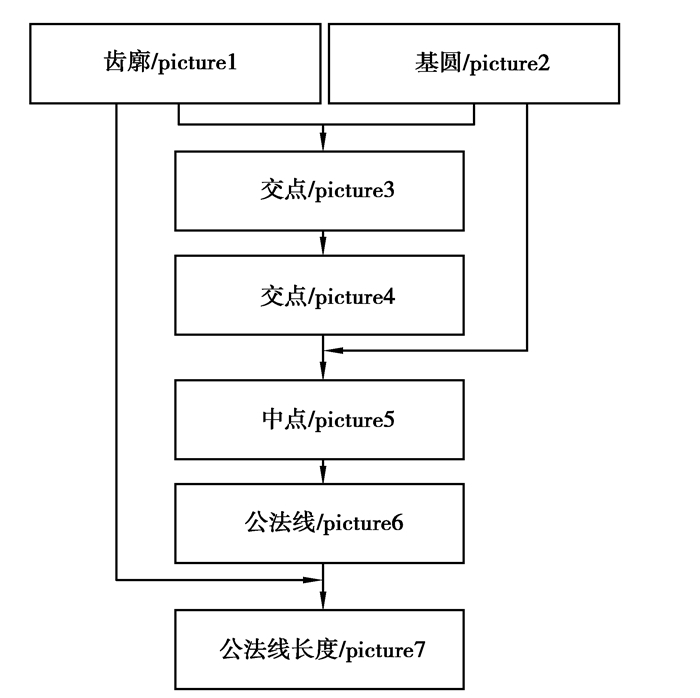
该算法结构如图 12所示。
|
图 12 程序流程图 Fig. 12 Program flow chart |
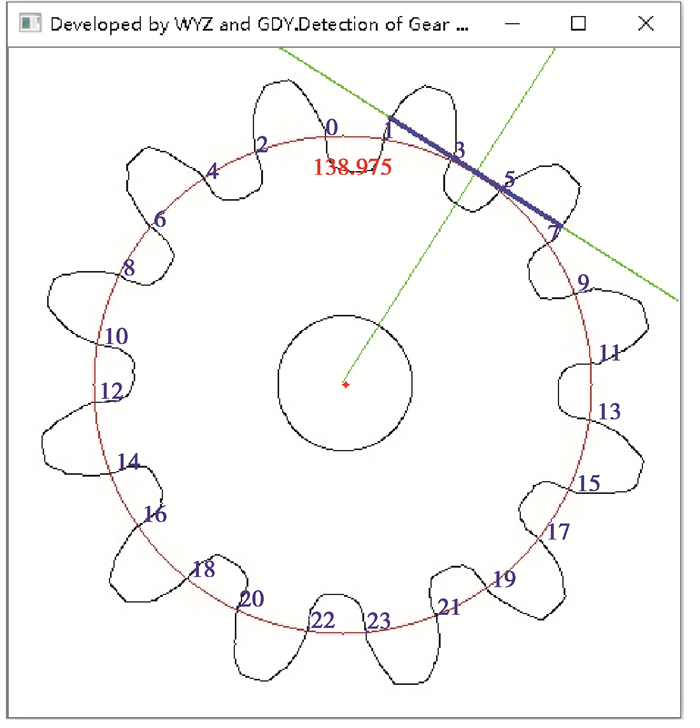
由于公法线与齿廓相交于若干点,而在提取存储这些点的坐标时是无序的,导致无法知道公法线与齿廓相交的端点,在算法上需要在每两个点之间都要进行一次计算并索引其中的最大值,索引得到的最大值即为图像坐标上的公法线长度。蓝色部分加粗的直线段就是图像上的公法线长度。公法线长度的计算结果如图 13所示,在齿轮上的显示的结果,如图 14所示。
|
图 13 公法线计算结果 Fig. 13 Common normal calculation result |

|
图 14 齿轮公法线 Fig. 14 Gear common normal |
遍历齿轮一圈,计算各个位置的公法线长度并将其记录下来,公法线长度变动F′W等于公法线长度W′k最大值与最小值的差值
| $ F_w^\prime = \max (W_k^\prime ) - \min (W_k^\prime )。$ | (17) |
实验对象是齿顶圆直径为56 mm,模数m=4 mm, 齿数z=12,压力角为20°, 分度圆直径为48 mm的标准齿轮。
1) 根据式(13),图像的齿顶圆半径为211.2,图像上的齿轮模数m=422.4/(12+2)=30.17 pixel,基圆直径db=12×30.17×0.939 7=340.21 pixel。
2) 根据式(3),跨齿数k=1.83, 四舍五入之后得到k=2。
3) 计算齿轮图像上所有位置的公法线长度,并转化为物理长度记录,如表 3所示。查阅相关资料得到当模数m=1 mm,压力角α=20°时,Wk*= 4.596 3 mm,根据式(1)得到渐开线标准直齿圆柱齿轮公法线长度Wk=18.385 2 mm[14]。
| 表 3 图像上的齿轮公法线长度 Table 3 Common normal length of the gear on the image |
公法线长度的最大值为18.509 8 mm,最小值为18.261 1 mm, 根据式(17)可得到公法线长度变动Fw=18.509 8-18.261 1=0.248 7 mm。
文中还采用了公法线千分尺对齿轮进行测量,选择被测齿轮的跨齿数,测量时,先将公法线千分尺归零,缓慢地使测量杆与测砧接触,所用的力须和测量时保持一致(一般为2~3 N),然后将被测齿轮移入两测量面之间,微调分筒,使工作面快接触到齿轮后,调测力装置,听到3声“咔咔咔”时停止,最后读数。测量结果如表 4所示。使用公法线千分尺得到的公法线长度的最大值为18.511 mm, 最小值为18.241 mm,公法线长度变动F′W=18.511-18.241=0.270 mm。
| 表 4 公法线千分尺测量结果 Table 4 Common normal micrometer measurement result |
从表 3可以看出,文中的检测方法与使用公法线千分尺测量结果产生了一定的误差,误差产生原因,一方面是由于实验条件的限制,采用的摄像头是普通CCD摄像头,精度不高;另一方面可能是摄像机的标定导致。
4 结论文中对拟合齿廓得到函数表达式的检测齿数方法和采用计算机视觉技术建立公法线方程的检测方法进行了研究,完成了齿轮齿数和公法线长度变动的检测,该方法与传统的检测方法相比,能有效、准确检测出齿轮齿数和公法线,实现了无接触、无损检测。鉴于机器视觉以及计算机视觉的前沿成果,本课题拟继续对机器视觉进行研究分析,并引入机器学习的最新研究成果,实现对齿轮工件的识别与检测。
| [1] |
张少军, 苟中魁, 李庆利, 等. 利用数字图像处理技术测量直齿圆柱齿轮几何尺寸[J]. 光学精密工程, 2004, 12(6): 619-625. ZHANG Shaojun, GOU Zhongkui, LI Qingli, et al. Digital image processing technology for spur gear measurement[J]. Optics and Precision Engineering, 2004, 12(6): 619-625. (in Chinese) |
| [2] |
陈廉清, 高立国, 史永杰, 等. 基于图像识别的微小塑料齿轮检测研究[J]. 中国机械工程, 2007, 18(13): 1535-1539. CHEN Lianqing, GAO Liguo, SHI Yongjie, et al. Research on the on-line inspection of micro plastic gear based on computer vision[J]. China Mechanical Engineering, 2007, 18(13): 1535-1539. (in Chinese) |
| [3] |
Ge D Y, Yao X F, Lian Z T, et al. Applications of computer vision in measuring total cumulative pitch deviation of a gear[J]. Tehnicki Vjesnik, 2017, 24(1): 71-78. |
| [4] |
葛动元, 姚锡凡, 向文江, 等. 面向齿廓偏差等精密检测的机器视觉关键技术[J]. 机械传动, 2019, 43(2): 171-176. GE Dongyuan, YAO Xifan, XIANG Wenjiang, et al. Key technologies of machine vision for precision measuring of profile deviations[J]. Journal of Mechanical Transmission, 2019, 43(2): 171-176. (in Chinese) |
| [5] |
林超, 曾庆龙, 聂玲, 等. 高阶椭圆锥齿轮齿距误差的三坐标测量方法[J]. 重庆大学学报, 2013, 36(10): 1-7. LIN Chao, ZENG Qinglong, NIE Ling, et al. Pitch error measurement of high-order oval bevel gear on three dimensional measuring machine[J]. Journal of Chongqing University, 2013, 36(10): 1-7. (in Chinese) |
| [6] |
杨继东, 李敏. 齿轮公法线长度检测的新方法[J]. 机床与液压, 2007, 35(11): 119-121. YANG Jidong, LI Min. New method on detecting common normal length of gear[J]. Machine Tool & Hydraulics, 2007, 35(11): 119-121. (in Chinese) |
| [7] |
闻邦椿. 机械设计手册·齿轮传动第5版[M]. 北京: 机械工业出版社, 2014: 29-30. WEN Bangchun. Mechanical Design Manual·Gear Transmission 5th Edition[M]. Beijing: China Machine Press, 2014: 29-30. (in Chinese) |
| [8] |
Budiharto W, Irwansyah E, Suroso J S, et al. Design of object tracking for military robot using PID controller and computer vision[J]. ICIC Express Letters, 2020, 14(3): 289-294. |
| [9] |
Caporali R. Overhead crane:An adaptive particle filter for anti-sway closed-loop and collision detection using computer vision[J]. International Journal of Innovative Computing, Information and Control, 2019, 10(1): 1223-1241. |
| [10] |
Gunawan F E. Car-following model:A computer-vision-based calibration method[J]. International Journal of Innovative Computing, Information and Control, 2019, 15(4): 1397-1411. |
| [11] |
Joe M, Joseph H. OpenCV 3计算机视觉[M].刘波, 苗贝贝, 史斌译.北京: 机械工业出版社, 2016: 44-46. Joe M, Joseph H. Learning operCV 3 computer Learning operCV 3 computer[M]. Translated by Liu Bo, Miao Beibei, Shi Bin. Beijing: China Machine Press, 2016: 44-46.(in Chinese) |
| [12] |
汪洋, 黄小红, 陈曾平. 基于对数极坐标变换的目标识别算法[J]. 雷达科学与技术, 2009, 7(2): 111-114. WANG Yang, HUANG Xiaohong, CHEN Zengping. A new algorithm for target recognition based on log-polar transform[J]. Radar Science and Technology, 2009, 7(2): 111-114. (in Chinese) |
| [13] |
翟永立, 丁雷, 裴浩东. 基于改进轮廓提取的Hough变换椭圆检测方法[J]. 现代电子技术, 2019, 42(6): 34-37. ZHAI Yongli, DING Lei, PEI Haodong. A Hough transform ellipse detection method based on improved contour extraction[J]. Modern Electronics Technique, 2019, 42(6): 34-37. (in Chinese) |
| [14] |
《齿轮便查手册》编委会. 齿轮便查手册[M]. 北京: 机械工业出版社, 2013. Editorial Board of "Handbook of Gears Checking". Handbook of Gears Checking[M]. Beijing: China Machine Press, 2013. (in Chinese) |
 2020, Vol. 43
2020, Vol. 43


