2. 金陵科技学院 数据科学与智慧软件江苏省重点实验室, 江苏 南京 211169
2. Jiangsu Key Laboratory of Data Science and Smart Software, Jinling Institute of Technology, Nanjing 211169, P. R. China
如果一个系统是一个由输入组成的过程,这些输入执行特定的功能并产生输出,通过系统的数学表示并引入评估规则,需要用优化方法来解决,这就是优化问题。约束优化问题是优化邻域的重要研究方向,由于约束条件对优化目标的约束,导致目标函数的不可微性及变量空间不可行域的出现,使得对约束优化问题的求解难以用传统优化方法解决[1-3]。近年来,启发式智能优化方法求解约束工程问题得到关注和重视[4-6],比如,为使得进化算法中种群能跨越孤立的可行域,王停等[4, 7]将不可行解加入到差分进化的变异中,并且设置随时间变化的约束违反度最大扩增度ε,以增强探索可行域边界的能力。研究提出了一种基于分段式随机惯性权重和最优反馈机制的鲸鱼优化算法[8];通过解空间变换以有效避免不可行解的狼群算法[9];使用种群最优信息实时更新和局部深度搜索策略改进的果蝇优化算法[10];将差分进化中的差分变异机制引入到蝙蝠算法中来求解工程设计约束优化问题等[11-12]。约束处理方法是约束优化中的关键[13-16],将罚函数应用到不可行解[14],在差分进化变异操作中引入三角变异算子交叉变异的约束处理技术[15],对全局搜索引入帕累托分布和混沌映射、在局部搜索引用随机交叉策略[16],以改善约束工程设计优化问题的效率和性能。
粒子群优化算法(PSO)在解决多峰约束优化问题上不断取得成功,由于分数阶粒子群优化(FOPSO)具有路径轨迹记忆的优点,成为新一代群智能研究的重要主题,并成功应用于CMOS放大器设计、多目标PWR核装载模式优化、风能控制器设计优化等[11, 17-20]。针对FOPSO易于早熟和依赖于初始控制参数,参考文献[9, 21],提出一种邻域自适应的约束分数阶粒子群优化(NAFPSO),增强了对局部区域的探索,并且在NAFPSO中采用微分变异策略以增强种群多样性,从而使粒子摆脱局部状态。对于约束的处理,应用了一种静态惩罚函数方法,该方法通过在违反约束时,施加较大的惩罚将约束问题转化为无约束问题。用9个流行基本约束优化函数验证了文中算法的可行性与稳定性,然后将该算法应用于解决2个实际工程问题。
1 分数阶粒子群优化算法 1.1 粒子群优化算法粒子群优化(PSO)是一种基于随机种群的元启发式方法,其灵感来自于鸟类觅食的聚集行为,如鸟类聚集觅食和鱼类聚集觅食。粒子群优化算法的主要特点是利用轨迹记忆来更新粒子的位置。与其他的元启发式方法相比,PSO方法在获得最优解方面更简捷有效、更鲁棒。通过将粒子群算法的概念与其他元启发式方法相结合,或者将新的机制引入到粒子群算法中,得到并发展了许多粒子群算法的变体及其混合方法。在PSO中,每个粒子代表超空间中的一个可能解,其当前位置用x(i, k)表示,其中,i是单个粒子,k是迭代次数。每个粒子都记录它的当前位置和到目前为止它的最优解,用xp(i, k)表示。算法跟踪的另一个值是用xGk表示的全局最优解。粒子速度v(i, k)为第k次迭代时粒子位置的变化。粒子群优化算法试图通过更新粒子的速度来达到自己的最优速度和全局最优解[9, 11]。v(i, k)和x(i, k)都分别通过以下2个方程式迭代更新:
| $ {v^{(i,k + 1)}} = {v^{(i,k)}} + {c_1}{\kern 1pt} {\kern 1pt} {\rm{rand}}_1^{(k)}(x_P^{(i,k)} - {x^{(i,k)}}) + {c_2}{\kern 1pt} {\kern 1pt} {\rm{rand}}_2^{(k)}(x_G^{(k)} - {x^{(i,k)}}), $ | (1) |
| $ {x^{(i,k + 1)}} = {x^{(i,k)}} + {v^{(i,k + 1)}}, $ | (2) |
其中,i=1~N,c1和c2分别为认知和社会参数,统称为加速度系数。rand1(k)和rand2(k)为第k次迭代(0≤rand≤1)产生随机数的向量,N表示群体大小。一旦计算出粒子的新速度和位置,xp(i, k)和xGk迭代更新如下:
| $ x_p^{(i,k)} = \left\{ {\begin{array}{*{20}{l}} {{x^{(i,k)}},}&{f({x^{(i,k)}}) < f(x_p^{(i,k)}),}\\ {x_p^{(i,k)},}&{f({x^{(i,k)}}) \ge f(x_p^{(i,k)});} \end{array}} \right. $ | (3) |
| $ x_G^{(k)} = \left\{ {\begin{array}{*{20}{l}} {{x^{(i,k)}},}&{f({x^{(i,k)}}) < f(x_p^{(i,k)}),}\\ {x_p^{(i,k)},}&{f({x^{(i,k)}}) \ge f(x_p^{(i,k)})}。\end{array}} \right. $ | (4) |
粒子的位置和速度都有一个预定义的值域,其动态范围由设计变量值域确定。在初始化时,粒子的位置在超空间中是随机分布的,一般地,初始速度设置为零[12]。方程式(1)~(4)每次迭代更新,直到满足预定义的终止条件。通常,一旦获得一个可接受的全局解决方案,或者达到预定义的最大函数计算次数或迭代次数,算法就会终止。
1.2 分数阶粒子群算法利用分数阶微积分的概念来记忆粒子群中粒子的运动轨迹,Zameer等提出分数阶粒子(FOPSO)算法,由FOPSO算法中得到启示,进一步提出一种分数阶达尔文粒子群(FDPSO)算法,较大程度提高了收敛速度和解精度[17-20]。分数阶微积分有多种定义,其中Grünwald-Letnikov定义为
| $ aD_\alpha ^t = \mathop {\lim }\limits_{h \to 0} \frac{1}{{{h^\alpha }}} \times \sum\limits_{k = 0}^{\left[ {\frac{{t - a}}{h}} \right]} {{{( - 1)}^k}} \times \left( {\begin{array}{*{20}{l}} \alpha \\ k \end{array}} \right) \times f(t - k \times h), $ | (5) |
| $ \left( {\begin{array}{*{20}{l}} \alpha \\ k \end{array}} \right) = \frac{{\Gamma (\alpha + 1)}}{{\Gamma (k + 1) \times (\alpha - k + 1)}}, $ | (6) |
其中,aDαt表示函数f(t)的α阶微积分。如果t是离散时间,则可以近似为
| $ aD_\alpha ^t = \frac{1}{{{T^\alpha }}} \times \sum\limits_{k = 0}^r {{{( - 1)}^k}} \times \left( {\begin{array}{*{20}{l}} \alpha \\ k \end{array}} \right) \times f(t - k \times T), $ | (7) |
其中,t是采样区间,r是截断阶数。
FPSO利用分数阶来更新粒子速度,将式(1)速度项移至等式左边,得到以下方程式:
| $ {v^{(i,k + 1)}} - {v^{(i,k)}} = {c_1}{\kern 1pt} {\kern 1pt} {\rm{rand}}_1^{(k)}(x_P^{(i,k)} - {x^{(i,k)}}) + {c_2}{\kern 1pt} {\kern 1pt} {\rm{rand}}_2^{(k)}(x_G^{(k)} - {x^{(i,k)}}), $ | (8) |
式中,左边是速度的一阶差分,由于在PSO算法中,粒子飞行是离散时间的,其最小间隔T=1,其差分形式为
| $ aD_\alpha ^t = {c_1}{\kern 1pt} {\kern 1pt} {\rm{rand}}_1^{(k)}(x_P^{(i,k)} - {x^{(i,k)}}) + {c_2}{\kern 1pt} {\kern 1pt} {\rm{rand}}_2^{(k)}(x_G^{(k)} - {x^{(i,k)}}), $ | (9) |
根据式(7),取截断阶数r=4,将式(9)通过整理得出以下速度更新方程:
| $ \begin{array}{l} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {v^{(i,k + 1)}} = \alpha {v^{(i,k)}} - \frac{1}{2}\alpha (\alpha - 1){v^{(i,k - 1)}} + \frac{1}{6}\alpha (\alpha - 1){v^{(i,k - 2)}} - \\ \frac{1}{{24}}\alpha (\alpha - 1)(\alpha - 2)(\alpha - 3){v^{(i,k - 3)}} + {c_1}{\kern 1pt} {\kern 1pt} {\rm{rand}}_1^{(k)}(x_P^{(i,k)} - {x^{(i,k)}}) + {c_2}{\kern 1pt} {\kern 1pt} {\rm{rand}}_2^{(k)}(x_G^{(k)} - {x^{(i,k)}})。\end{array} $ | (10) |
需要对FOPSO进行修改才能处理约束问题。为了粒子可以搜索整个设计空间,通过保留可行解,使粒子只能跟踪可行解,这可以通过跟踪约束违反来实现[9, 13]。在算法中,处理约束时应用了以下逻辑条件:选择任意可行解而不是不可行解;在2个可行解之间,目标函数值较好的解为优。
通过应用这些条件,算法使自己倾向于可行解而不是非可行解,在2个可行解选择较优解,将搜索指向具有更好解的可行区域。通过对不可行解施加惩罚,迫使粒子向可行区域收敛。惩罚函数中包含2条信息——违反约束的次数和违反约束的值大小。修改后的FOPSO算法求解目标函数为
| $ {F_i}(x) = \left\{ {\begin{array}{*{20}{l}} {{f_i}(x),{\rm{ 若 }}x{\rm{ 可行; 否则 }}}\\ {{f_i}(x) + {\beta _1}(\sum\limits_{i = 1}^d h ) + {\beta _2}(\sum\limits_{i = 1}^d y )}。\end{array}} \right. $ | (11) |
其中,Fi(x)为惩罚函数;fi(x)为原始目标函数;
NAFPSO算法利用反馈参数作为自适应粒子的机制,以便为每个粒子生成特定的分数阶系数和加速度系数。
2.1 邻域拓扑结构在粒子群算法中,粒子的邻域结构可分为2种,即局部和全局结构,这2种拓扑结构是固定的。将邻域引进粒子群中,使得在局部范围内粒子能更好地协同进化。
在PSO算法中,每个粒子通常是基于欧式距离来选择邻域,粒子i的邻域可由以下方程式确定[21]:
| $ \left\{ {\begin{array}{*{20}{l}} {{D^{(i)}} = \{ {d_{ij}}|{d_{ij}} = \left\| {{x^{(i,0)}} - {x^{(j,0)}}} \right\|\} ,j \in {N_s}}\\ {{\rm{ neighbor}}{{\rm{ }}_i} = \arg (\min ( sort ({D^{(i)}}),n)),} \end{array}} \right. $ | (12) |
其中,D(i)表示在初始阶段当前粒子i和其他粒子的欧式距离集合;Ns表示种群规模;neighbori表示离粒子与i欧氏距离最近的n个粒子; sort(D)表示对集合D从小到大排序。如果n=Ns/3,粒子的邻域从开始到结束阶段是固定不变的。在上述公式(10)的基础上,将粒子向全局历史最优解的引力改为向邻域历史最优解的引力,于是基于邻域的速度更新方程式为
| $ \begin{array}{l} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {v^{(i,k + 1)}} = \alpha {v^{(i,k)}} - \frac{1}{2}\alpha (\alpha - 1){v^{(i,k - 1)}} + \frac{1}{6}\alpha (\alpha - 1){v^{(i,k - 2)}} - \\ \frac{1}{{24}}\alpha (\alpha - 1)(\alpha - 2)(\alpha - 3){v^{(i,k - 3)}} + {c_1}{\kern 1pt} {\kern 1pt} {\rm{rand}}_1^{(k)}(x_P^{(i,k)} - {x^{(i,k)}}) + {c_2}{\kern 1pt} {\kern 1pt} {\rm{rand}}_2^{(k)}(x_G^{(i,k)} - {x^{(i,k)}}), \end{array} $ | (13) |
其中,xG(i, k)为粒子i邻域历史最优解。
2.2 基于进化状态反馈的邻域自适应策略Isiet等[9]根据粒子i在第k次迭代时的个体最优、邻域历史最优及其当前适应度,设计了粒子i第k次迭代时的进化状态(ES(i, k))如下:
| $ {\rm{E}}{{\rm{S}}^{(i,k)}} = \frac{{f(x_P^{(i,k)}) - f(x_G^{(i,k)})}}{{f(x_f^{(i,k)})}}, $ | (14) |
其中:f(xP(i, k))为粒子i个体最优解的适应度;f(xG(i, k))为粒子i邻域历史最优解的适应度;f(xf(i, k))是当前粒子i的适应度。由于任何给定的约束问题都包含可行解和不可行解,粒子根据不可行解进行自适应将导致粒子指向不必要的位置。为此,f(xf(i, k))的选择过程如下:
| $ f(x_f^{(i,k)}) = \left\{ {\begin{array}{*{20}{l}} {f(x_P^{(i,k)}),{\rm{ 若 }},k = 1}\\ {f({x^{(i,k)}}),{\rm{ 若 }}{x^{(i,k)}}{\rm{ 可行, 否则 }},}\\ {f(x_f^{(i,k - 1)})}。\end{array}} \right. $ | (15) |
在第一次迭代中,f(xf(i, k))=f(xP(i, k)),因为所建立的约束处理技术不能保证可行解。在随后的迭代(k>1)中,解的可行性决定了最新可行解的选择过程。当粒子的进化状态ES较大时,表明该粒子的最新可行解接近其个体最优解;而较小时,表明粒子的个体最优解接近邻域历史最优解或者粒子的最新可行解离其个体最优解和邻域历史最优解都较远。据此,对文中改进算法的控制参数进行了设计:
1) 分数阶系数(α)。由于分数阶系数α的大小影响着粒子的收敛速度,随着α的增加,粒子的收敛速度会逐渐减小。在粒子处于探索阶段时,进化状态较大,将分数阶系数α调大,减小收敛速度;而在粒子处于收敛阶段时,进化状态会越来越小,分数阶系数α调小,增大收敛速度。传统分数阶α的调整是在[0.5, 0.8]范围内逐步减小,依据进化状态,分数阶系数α的调整如下:
| $ \alpha = \frac{1}{{1 + {e^{ - 1.3863 \times {\rm{ES}}。}}}} $ | (16) |
根据式(14),可以发现,在函数值都取正值时,ES的取值范围在区间[0, 1]之间,式(16)是在变量ES上的单调递增函数,所以,α的取值区间在[0.5, 0.8]间,随着ES从1到0减小,α也从0.8到0.5减小。
2) 加速度系数(c1, c2)。通常PSO加速度系数被设置为常数2。然而,在随后的研究中,线性变化的版本被证明是非常成功的。在基于邻居的小范围内,认知因子c1平均上大于社会因子c2,有利于在邻域范围内更开拓的搜索更优解。基于进化状态ES,c1和c2调整如下:
| $ {c_1} = \left( {\begin{array}{*{20}{l}} {2.5 - 1.5{\kern 1pt} {\kern 1pt} {\kern 1pt} * {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{step }}/{\rm{max\_step,}}}&{{\rm{ }}0 \le {\rm{ES}} \le 0.5}\\ {1 + 1.5{\kern 1pt} {\kern 1pt} {\kern 1pt} * {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{step }}/{\rm{max\_steps,}}}&{{\rm{ }}0.5 < {\rm{ES}} \le 1} \end{array}} \right. $ | (17) |
| $ {c_2} = \left( {\begin{array}{*{20}{l}} {0.5 + 1.5{\kern 1pt} {\kern 1pt} {\kern 1pt} * {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{step }}/{\rm{max\_step,}}}&{{\rm{ }}0 \le {\rm{ES}} \le 0.5}\\ {2 - 1.5{\kern 1pt} {\kern 1pt} {\kern 1pt} * {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{step }}/{\rm{max\_steps,}}}&{{\rm{ }}0.5 < {\rm{ES}} \le 1,} \end{array}} \right. $ | (18) |
其中,step为当前迭代次数,max_steps为总的迭代次数。
2.3 差分变异算子基于邻居的自适应分数阶粒子群优化缺少全局信息,易陷入局部解,且在后期粒子无法快速收敛到最优解。研究者试图通过在速度更新方程中引入一个混沌因子来避免这种情况,而另一些研究人员则通过修改方程来避免这种情况,比如,排斥性粒子群优化(RPSO)[12, 15, 19]。RPSO算法试图通过在粒子之间引入斥力来增强全局搜索,从而增加确定全局最优值的概率。在NAFPSO中,当算法在某些迭代中陷入局部最优时,引入差分变异算子来更新粒子。引入差分变异算子的主要作用是为了增强种群多样性。具体来说,当种群中某一粒子i的个体最优解在次数T内没有更新,则对此粒子i的当前位置进行变异。首先,从种群中随机选择3个不同的粒子l,n和m(i≠l≠n≠m)。然后,计算粒子n,m个体历史最优位置之间的差异,形成一个差分向量。最后,用差分向量对粒子l个体历史最优位置进行缩放和求和,该操作式为
| $ {x^{(i,k)}} = {x_P}^{(i,k)} + F(x_P^{(n,k)} - x_P^{(m,k)}), $ | (19) |
其中,F为缩放因子,经验证F=0.8性能最好。
2.4 提出的算法在Darwin分数阶PSO算法中,粒子更新采用基于进化状态反馈的邻域拓扑动态自适应策略,同时设计了差分变异算子以增强粒子逃脱局部最优能力,提出邻域自适应的微分变异约束分数阶粒子群优化算法(NAFPSO),其算法伪代码,如图 1所示。

|
图 1 NAFPSO的算法伪代码 Fig. 1 Pseudocode of the proposed algorithm |
通过解决多个基准约束优化问题检验NAFPSO的性能。选择了9种标准的基准约束函数和2种约束工程问题,比较NAFPSP与其他智能算法的性能。NAFPSO的性能将通过统计方法分析。对于9种基准约束函数,考虑的统计性能包括最优函数值、最差函数值、均值函数值和标准差,其中,种群大小为45,迭代次数为2 000,而对于约束工程问题,为了更好地比较,在原有统计性能上加入函数评估(FEs),其中,种群大小为15,迭代次数为2 000。对于所有问题,最大速度设置为设计变量的上下界范围。
文中提出的NAFPSO算法实验测试及比较分析由李智等在Win10系统上使用软件Python 3.7版本编写。将所有约束优化问题独立运行30次,以分析评估算法的统计性能。
3.1 基准约束函数实验测试从文献[16]选取了9个比较约束问题基准函数。通过文中算法求解基准问题的全局最优解,数值结果如表 1所示,显示了最优、最差和平均函数值、标准差。从表中可以看出,NAFPSO能在所有问题中获得全局最优解,统计性能表明了该方法的鲁棒性和有效性。表 2反映了与NAFPSO对比的其他算法计算结果[3, 9, 13, 16],包括基于变化范围的遗传算法(CRGA)、自适应速度粒子群优化(SAVPSO)、基于小规模的粒子群优化(Micro-PSO)、动态目标粒子群算法(RVPSO)、文化差分进化算法(CDE)。从表 1和表 2对比可以看出,对于G1、G7和G10,除了CDE,在最优值、平均值、最差值和标准差方面,NAFPSO都优于其他方法;对于G2,NAFPSO在各方面的性能只优于RVPSO;对于G4,NAFPSO在各方面性能优于CRGA和Micro-PSO;对于G6、G9, NAFPSO的各方面性能优于CRGA,SAVPSO和Micro-PSO,相比另外2种算法,标准差稍大;对于G8, 所有算法都表现很好,但NAFPSO在标准差稍大;对于G12,所有算法性能相同。总之,NAFPSO在各方面表现良好,平均性能优于大部分方法,体现了该算法的有效性。
| 表 1 NAFPSO算法对基准函数的实验测试结果 Table 1 Test Results of NAFPSO on Constrained Benchmarks |
| 表 2 其他智能算法对基准函数的实验比较结果 Table 2 Comparison Results of Other Five Algorithms on Constrained Benchmarks |
为了直观描述文中算法综合性能,图 2(a)~图 2(i)刻画了FOPSO和NAFPSO在各个基准函数上的收敛曲线图。可以看出,FOPSO比NAFPSO收敛速度快,但是FOPSO容易较早地陷入局部解,并且难以摆脱,而NAFPSO虽然收敛速度慢,但是收敛曲线一般是较光滑的,在到全局最优区域前,不会像FOPSO会在很大迭代次数内最优解停滞不前。从结果上看,NAFPSO的最优解一般要比FOPSO更优。
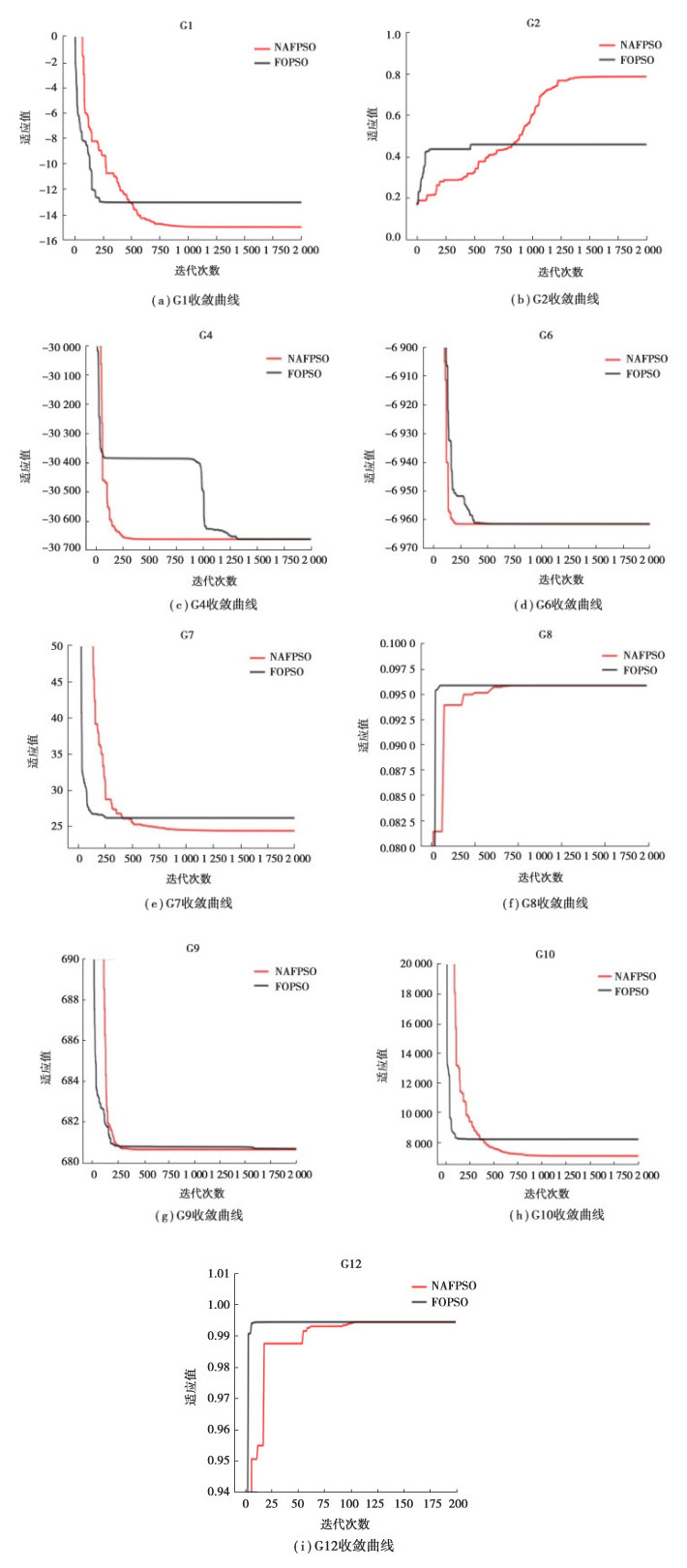
|
图 2 FOPSO和NAFPSO在9个基准约束函数上的收敛曲线图(a)~(i) Fig. 2 Plots for both FOPSO and NAFPSO on 9 Constrained Benchmark Functions (a)~(i) |
减速机优化问题是测试和比较优化方法的常用基准实例,如图 3所示。在这个问题上, 目标是最小化减速器的重量且优化7个设计变量——分别是表面宽度(b), 模件的宽度(m), 小齿轮的齿数(z), 第一轴轴承之间的长度(l1), 轴承之间的第二轴的长度(l2)和第一轴的直径(d1)和第二轴的直径(d2)。除z为整数值外,所有设计变量均为连续的。由于这是一个混合整数问题,所以,NAFPSO算法被修改为在迭代过程中处理离散变量(z)与连续变量的方法相同,但是在迭代结束时,z被四舍五入到最接近的整数值。
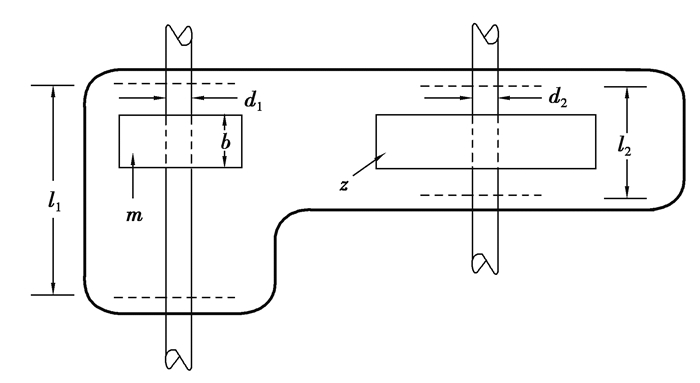
|
图 3 减速器设计问题示意图 Fig. 3 Diagram of Speed reducer design |
减速器设计问题的约束优化函数如下:
| $ \begin{array}{*{20}{l}} {\min f(x) = 0.785{\kern 1pt} {\kern 1pt} {\kern 1pt} 4{x_1}x_2^2(3.333{\kern 1pt} {\kern 1pt} {\kern 1pt} 3x_3^2 + 14.933{\kern 1pt} {\kern 1pt} {\kern 1pt} 4x - 43.093{\kern 1pt} {\kern 1pt} {\kern 1pt} 4) - 1.508{x_1}(x_6^2 + x_7^2) + 7.477{\kern 1pt} {\kern 1pt} 7(x_6^3 + x_7^3) + }\\ {0.785{\kern 1pt} {\kern 1pt} {\kern 1pt} 4({x_4}x_6^2 + {x_5}x_7^2)} \end{array} $ |
| $ c{(x)_1} = \frac{{27}}{{{x_1}x_2^2{x_3}}} - 10,c{(x)_2} = \frac{{397.5}}{{{x_1}x_2^2x_3^2}} - 1 \le 0 $ |
| $ c{(x)_3} = \frac{{1.93x_4^3}}{{{x_2}x_6^4{x_3}}} - 1 \le 0,c{(x)_4} = \frac{{1.93x_5^3}}{{{x_2}x_6^4{x_3}}} - 1 \le 0,c{(x)_5} = \frac{{\sqrt {754{{(\frac{{{x_4}}}{{{x_2}{x_3}}})}^2} + 16.9 \times {{10}^6}} }}{{110x_6^3}} - 1 \le 0, $ |
| $ c{(x)_6} = \frac{{\sqrt {754{{(\frac{{{x_5}}}{{{x_2}{x_3}}})}^2} + 157.5 \times {{10}^6}} }}{{85x_7^3}} - 1 \le 0,c{(x)_7} = \frac{{{x_2}{x_3}}}{{40}} - 1 \le 0,c{(x)_8} = \frac{{5{x_2}}}{{{x_1}}} - 1 \le 0, $ |
| $ c{(x)_9} = \frac{{{x_1}}}{{12{x_2}}} - 1 \le 0,c{(x)_{10}} = \frac{{1.5{x_6} + 1.9}}{{{x_4}}} - 1 \le 0,c{(x)_{11}} = \frac{{1.1{x_7} + 1.9}}{{{x_5}}} - 1 \le 0 $ |
| $ {{\rm{where}}{\kern 1pt} {\kern 1pt} {\kern 1pt} 2.6 \le {x_1} \le 3.6,0.7 \le {x_2} \le 0.8,17 \le {x_3} \le 28,} $ |
| $ {7.3 \le {x_4} \le 8.3,7.3 \le {x_5} \le 8.3,2.9 \le {x_6} \le 3.9,5.0 \le {x_7} \le 5.5{\rm{ }}}。$ |
用以比较的算法有混合进化算法和自适应约束处理技术(HEA-ACT)、水平比较的差分进化(DELC)、改进的差分进化(MDE)、粒子群与差分进化混合算法(PSO-DE)、基于模拟退火的回溯搜索优化算法(BSAISA)、人工蜂群算法(ABC)、煤矿爆炸算法(MBA)、动态随机选择的差分进化(DSS-MDE)和加权叠加的引力(WSA),表 3给出了NAFPSO和其他方法的统计性能比较[9, 10, 12-16]。如表 3所示,在获得最优解方面,DELC,BSAISA、DSS-MDE和NAFPSO获得了最优解,f(x)=299 4.471 066,而HEA-ACT、MDE、PSO-DE、ABC、MBA和WSA则不能。在30, 000函数评估内,NAFPSO比所考虑的方法表现得更好,体现了NAFPSO平均得到的解更优,更稳定。图 4为减速器问题的NAFPSO和FOPSO的收敛曲线图。可以看出,NAFPSO收敛速度虽然比FOPSO慢,但求得的最优解更优。
| 表 3 NAFPSO与其它算法在减速器问题上的性能统计 Table 3 Performances of Algorithms Tested on reducer design problem |
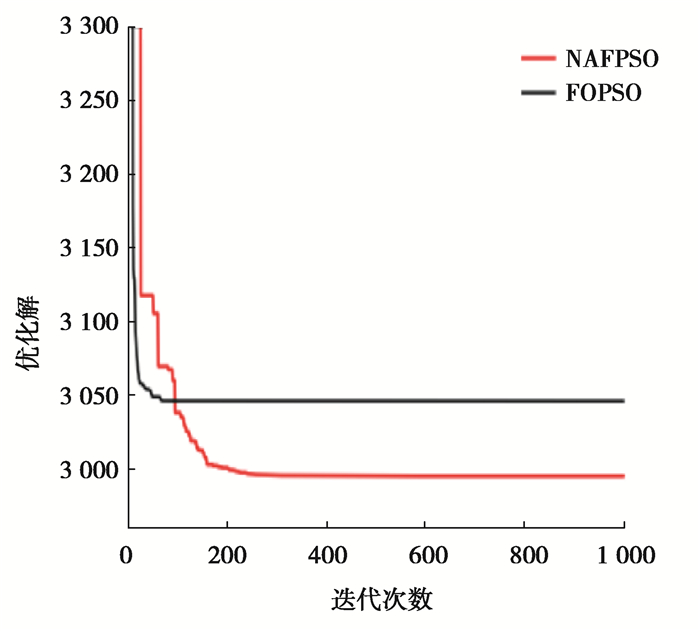
|
图 4 减速器问题的收敛曲线 Fig. 4 plot for speed reducer problem |
焊接梁设计问题由1个带有7个非线性不等式方程的非线性目标函数组成,如图 5所示。这个问题的目标是把成本降到最低,成本受到剪应力(τ),梁中的弯曲应力(σ),杆上的屈曲载荷(Pc),梁的端挠(δ)和边限制的约束。该问题中包含的设计变量是焊缝高度h(x1),梁的长度l(x2),梁的厚度t(x3)和梁的宽度b(x4)。焊接梁问题的优化函数如下:
| $ {\min f(x) = 1.10471{x_2}x_1^2 + 0.04811{x_3}{x_4}(14.0 + {x_2}),c{{(x)}_1} = \tau (x) - {\tau _{\max }} \le 0,} $ |
| $ {c{{(x)}_2} = \sigma (x) - {\sigma _{\max }} \le 0,c{{(x)}_3} = {x_1} - {x_4} \le 0,} $ |
| $ {c{{(x)}_4} = 0.10471x_1^2 + 0.04811{x_3}{x_4}(14.0 + {x_2}) - 5 \le 0,c{{(x)}_5} = 0.125 - {x_1} \le 0,} $ |
| $ {c{{(x)}_6} = \delta (x) - {\delta _{\max }} \le 0,c{{(x)}_7} = P - {P_c}(x) \le 0,} $ |
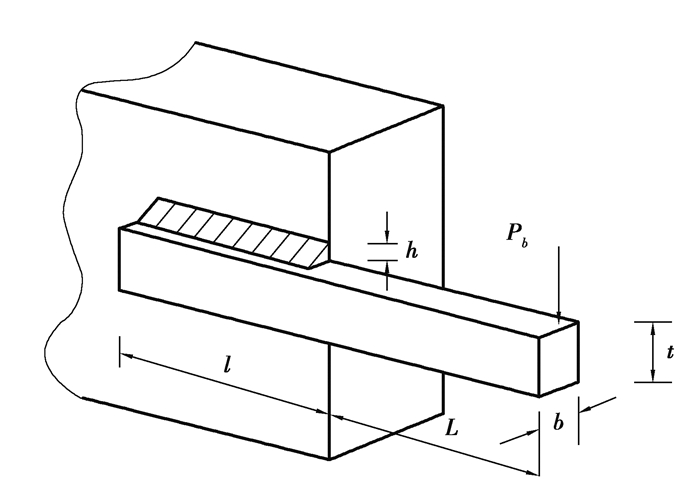
|
图 5 焊接梁问题的示意图 Fig. 5 Diagram of welded beam structure problem |
其中:
| $ \tau (x) = \sqrt {{{({\tau ^\prime })}^2} + 2{\tau ^\prime }{\tau ^{\prime \prime }}(\frac{{{x_2}}}{{2R}}) + {{({\tau ^{\prime \prime }})}^2}} ,{\tau ^\prime } = \frac{P}{{\sqrt 2 {x_1}{x_2}}},{\tau ^{\prime \prime }} = \frac{{MR}}{J},M = P(L + \frac{{{x_2}}}{2}),R = \sqrt {\frac{{x_2^2}}{4} + {{(\frac{{{x_1} + {x_3}}}{2})}^2}} , $ |
| $ J = 2\sqrt 2 {x_1}{x_2}(\frac{{x_2^2}}{{12}} + {\left( {\frac{{{x_1} + {x_3}}}{2}} \right)^2}) $ |
| $ \sigma (x) = \frac{{6PL}}{{x_3^2{x_4}}},\delta (x) = \frac{{4P{L^3}}}{{Ex_3^3{x_4}}},{P_c}(x) = \frac{{4.013\sqrt {EG\left( {\frac{{x_3^2x_4^6}}{{36}}} \right)} }}{{{L^2}}}\left( {1 - \frac{{{x_3}}}{{2L}}\sqrt {\frac{E}{{4G}}} } \right), $ |
| $ {P = 6{\kern 1pt} {\kern 1pt} {\kern 1pt} 000lb,L = 14{\rm{in}},E = 30 \times {{10}^6}{\rm{psi}},G = 30 \times {{10}^6}{\rm{psi,}}} $ |
| $ {{\tau _{\max }} = 13{\kern 1pt} {\kern 1pt} {\kern 1pt} 600{\rm{psi}},{\sigma _{\max }} = 30{\kern 1pt} {\kern 1pt} {\kern 1pt} 000{\rm{psi}},{\delta _{\max }} = 0.25{\rm{in}}} $ |
| $ {0.1 \le {x_i} \le 2(i = 1,4),0.1 \le {x_i} \le 10(i = 2,3).} $ |
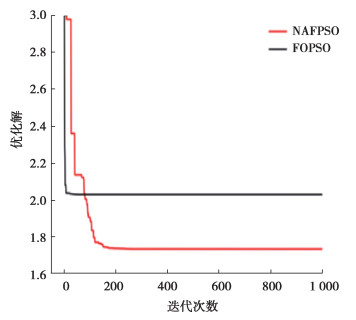
比较NAFPSO与其他算法在焊接梁问题方面的统计性能,如表 4所示[9-10, 12, 16]。在获得最优解方面,HPSO、PSO-DE、BSAISA、BSA-SA,WSA, DELC、CSA、ABC和NAFPSO获得了最优解f(x)=1.724 852,而CPSO、MBA、CDE、GA-DT、TEO不能。在算法稳定性方面,除了MBA外,NAFPSO表现优于其他各种方法,产生了更低标准差。总的来说,在鲁棒性和有效性方面,NAFPSO优于所考虑的方法。图 6为焊接梁问题的FOPSO和NAFPSO的收敛曲线。可以看出,NAFPSO收敛速度虽然比FOPSO慢,但求得的最优解更优,验证了NAFPSO改进的性能。
| 表 4 NAFPSO与其他算法在焊接梁问题上统计性能比较。 Table 4 Performances of Algorithms Tested on welded beam problem |
|
图 6 焊接梁问题的收敛曲线 Fig. 6 Plot for welded beam problem |
针对分数阶粒子群优化算法收敛速度慢、对初始控制设置敏感等问题,为每个粒子依据邻域设置进化状态来自适应参数,提出了一种自适应算法。同时,在NAFPSO中,通过保留可行解和惩罚不可行解来满足约束。考虑了一组约束优化问题,验证了该方法的性能和有效性。结果表明,与所考虑的方法相比,文中方法在所有问题上都能接近最优解,并且通过不断迭代更精确求出接近全局最优的解,提高了算法的效率。基于文中的结果,NAFPSO表明了它是一种解决约束问题的有效方法,因为克服了粒子早熟收敛,具有较好的稳定性和效率。
未来可以对粒子邻域的拓扑结构进一步研究,为反馈系统提供有用的信息,粒子与邻近粒子的相互作用直接影响其搜索信息和空间,因此,需要研究不同的群学习机制来确定最优拓扑,并考虑所使用的约束处理技术的类型对算法的整体性能有影响,以适应更广泛的工程设计问题。
| [1] |
Abdel-Basset M, Wang G G, Sangaiah A K, et al. Krill herd algorithm based on cuckoo search for solving engineering optimization problems[J]. Multimedia Tools and Applications, 2019, 78(4): 3861-3884. DOI:10.1007/s11042-017-4803-x |
| [2] |
Ferreira M P, Rocha M L, Silva Neto A J, et al. A constrained ITGO heuristic applied to engineering optimization[J]. Expert Systems With Applications, 2018, 110: 106-124. DOI:10.1016/j.eswa.2018.05.027 |
| [3] |
刘衍民. 一种求解约束优化问题的粒子群算法[J]. 清华大学学报(自然科学版), 2013, 53(2): 242-246. LIU Yanmin. Hybrid particle swarm optimizer for constrained optimization problems[J]. Journal of Tsinghua University(Science and Technology), 2013, 53(2): 242-246. (in Chinese) |
| [4] |
王停, 夏克文, 唐黎军, 等. 改进狼群算法用于多约束稀布线阵综合[J]. 计算机应用研究, 2020, 37(8): 2324-2328. WANG Ting, XIA Kewen, TANG Lijun, et al. Improved wolf pack algorithm for multi-constrained sparse array Synthesis[J]. Application Research of Computers, 2020, 37(8): 2324-2328. (in Chinese) |
| [5] |
Rana N, Latiff M S A, Abdulhamid S M, et al. Whale optimization algorithm:A systematic review of contemporary applications, modifications and developments[J]. Neural Computing and Applications, 2020, 32(20): 16245-16277. DOI:10.1007/s00521-020-04849-z |
| [6] |
刘景森, 马义想, 李煜.改进鲸鱼算法求解工程设计优化问题[J/OL].计算机集成制造系统, 2020: 1-20[2020-10-15].http://kns.cnki.net/kcms/detail/11.5946.TP.20200320.1144.006.html. LIU Jinseng, MA Yixiang, LI Yu. Improved whale algorithm for solving engineering design optimization problems[J/OL]. Computer Integrated Manufacturing Systems, 2020: 1-20[2020-10-15]. http://kns.cnki.net/kcms/detail/11.5946.TP.20200320.1144.006.html. (in Chinese) |
| [7] |
Kaveh A, Zaerreza A. Shuffled shepherd optimization method:a new Meta-heuristic algorithm[J]. Engineering Computations, 2020, 37(7): 2357-2389. DOI:10.1108/EC-10-2019-0481 |
| [8] |
邱少明, 胡宏章, 杜秀丽, 等. 基于DDE改进蝙蝠算法的动态火力分配方法[J]. 现代防御技术, 2019, 47(6): 61-67, 87. QIU Shaoming, HU Hongzhang, DU Xiuli, et al. Dynamic fire distribution method using improved bat algorithm based on DDE[J]. Modern Defence Technology, 2019, 47(6): 61-67, 87. (in Chinese) |
| [9] |
Isiet M, Gadala M. Self-adapting control parameters in Particle Swarm optimization[J]. Applied Soft Computing Journal, 2019, 83(10): 105653. |
| [10] |
石建平, 李培生, 刘国平, 等.求解约束优化问题的改进果蝇优化算法及其工程应用[J/OL].控制与决策, [2019-10-23].https://doi.org/10.13195/j.kzyjc.2019.0557. SHI Jianping, LI Peisheng, LI Guoping, et al. Improved fruit fly optimization algorithm for solving constrained optimization problems and engineering applications[J]. Control and Decision, [2019-10-23]. https://doi.org/10.13195/j.kzyjc.2019.0557. (in Chinese) |
| [11] |
Hosseini S A, Hajipour A, Tavakoli H. Design and optimization of a CMOS power amplifier using innovative fractional-order particle swarm optimization[J]. Applied Soft Computing, 2019, 85: 105831. DOI:10.1016/j.asoc.2019.105831 |
| [12] |
Xiao W S, Liu Q, Zhang L C, et al. A novel chaotic bat algorithm based on catfish effect for engineering optimization problems[J]. Engineering Computations, 2019, 36(5): 1744-1763. DOI:10.1108/EC-04-2018-0181 |
| [13] |
Yang Y K, Liu J C, Tan S B. A constrained multi-objective evolutionary algorithm based on decomposition and dynamic constraint-handling mechanism[J]. Applied Soft Computing, 2020, 89: 106104. DOI:10.1016/j.asoc.2020.106104 |
| [14] |
Palar P S, Liem R P, Zuhal L R, et al. On the use of surrogate models in engineering design optimization and exploration[C]//Proceedings of the Genetic and Evolutionary Computation Conference Companion, Prague Czech Republic. New York, USA: ACM, 2019: 1592-1602.
|
| [15] |
粟朝阳, 封全喜, 韦彦婷, 等. 改进的自适应约束差分进化算法[J]. 微电子学与计算机, 2019, 36(9): 30-37. SU Zhaoyang, FENG Quanxi, WEI Yanting, et al. Improved self-adaptive constrained differential evolution algorithm[J]. Microelectronics & Computer, 2019, 36(9): 30-37. (in Chinese) |
| [16] |
Gandomi A H, Yang X S, Alavi A H, et al. Bat algorithm for constrained optimization tasks[J]. Neural Computing and Applications, 2013, 22(6): 1239-1255. DOI:10.1007/s00521-012-1028-9 |
| [17] |
Zameer A, Muneeb M, Mirza S M, et al. Fractional-order particle swarm based multi-objective PWR core loading pattern optimization[J]. Annals of Nuclear Energy, 2020, 135: 106982. DOI:10.1016/j.anucene.2019.106982 |
| [18] |
翟兆睿, 苏守宝. 一种动态压缩因子的分数阶粒子群优化[J]. 重庆理工大学学报(自然科学), 2019, 33(7): 94-101. ZHAI Zhaorui, SU Shoubao. A fractional-order particle swarm optimization with dynamic constriction factor[J]. Journal of Chongqing Institute of Technology, 2019, 33(7): 94-101. (in Chinese) |
| [19] |
Alaviyan Shahri E, Alfi A, Tenreiro Machado JA. Fractional fixed-structure H∞ controller design using Augmented Lagrangian Particle Swarm Optimization with Fractional Order Velocity[J]. Appl Soft Comput, 2019, 77(3): 688-695. |
| [20] |
Tenreiro Machado JA, Jasmine Machado X A, Agees Kumar C, et al. Iot based sustainable wind green energy for smart cites using fuzzy logic based fractional order darwinian particle swarm optimization[J]. Measurement, 2020, 166: 108208. DOI:10.1016/j.measurement.2020.108208 |
| [21] |
刘衍民, 赵庆祯, 隋常玲, 等. 一种基于动态邻居和变异因子的粒子群算法[J]. 控制与决策, 2010, 25(7): 968-974. LIU Yanmin, ZHAO Qingzhen, SUI Changling, et al. Particle swarm optimizer based on dynamic neighorhood topology and mutation operator[J]. Control and Decision, 2010, 25(7): 968-974. (in Chinese) |
 2020, Vol. 43
2020, Vol. 43

