摆线针轮减速器具有传动比大、传动效率高、承载能力强、体积小等优点,被广泛应用于工业机器人关节驱动系统[1-3]。传动精度是减速器性能的重要指标,摆线齿轮的修形以及制造误差是影响摆线齿轮传动精度的关键因素。为了提高摆线针轮传动精度,中外学者在摆线齿轮制造误差、摆线针轮传动误差等方面做了大量研究。
在摆线齿轮制造误差方面,Li等[4]根据测得的摆线齿廓误差计算出带有齿廓误差的实际齿面坐标点,通过B样条曲线拟合获得齿廓误差,并基于啮合原理对数字化齿面进行了齿面接触分析(TCA),得到了齿廓误差影响下的摆线针轮传动误差曲线,为评估齿廓误差对传动精度的影响提供了理论依据。莫靖宇等[5]提出一种摆线齿廓偏差非接触检测的方法,对摆线齿轮所有齿的齿廓偏差进行测量,分析引起摆线齿轮齿廓偏差的因素,对摆线齿轮设计制造有一定的指导意义。郭广新等[6]根据摆线齿轮展成原理,分析其齿形加工误差并找到影响齿形加工误差的因素,提出了减少齿形加工误差来提高齿形精度的方法,但仅限于理论分析计算,未进行实物测量分析。
在高精度RV(rotational vector)减速器及摆线针轮减速器的传动误差分析方面,Yang等[7]采用纯几何方法推导出若干装配误差和加工误差引起的齿隙计算公式,分析了齿形误差对传动误差的影响规律,但只分析了针齿半径变化引起的齿形误差和传动误差。日高照晃等[8]采用质量弹簧等价模型,建立机构回转传动误差分析数学模型,分析各构件误差对传动误差的单独影响和组合影响,但分析和计算的过程十分复杂。Lin等[9]采用齿廓离散法对摆线减速器的运动误差进行分析,并分析了零件的加工误差对运动误差的影响。Lin等[10]基于轮齿接触分析来计算摆线针轮传动误差,定量地分析了不同修形组合引起的传动误差变化,未考虑零件的加工和装配误差的影响。刘玉婷[11]和Shan等[12]通过采用质量集中法和动态子结构法,构建RV传动系统的非线性动力学模型,采用计算机求解方程组得到传动误差变化曲线,但只分析各零件单项误差对系统传动误差的影响。韩林山等[13-14]凭借“等价模型”法,对整机建立了动态传动误差的数学分析模型,并进行仿真分析,以期得到误差最佳分配比,进而达到降低生产成本的目的。李充宁等[15]对2K-V型传动机构的传动误差进行分析,得到齿廓啮合误差与传动误差之间的关系,通过综合啮合误差来评价减速器的传动性能,对实际加工生产有一定参考意义。
从上述研究工作可以看出,现有研究多基于单因素法对摆线针轮的传动特性进行研究,而综合考虑多因素作用下摆线传动误差分析的文献比较少。鉴于此,笔者基于齿轮啮合原理,建立摆线针轮齿面接触分析模型,将齿廓修形、加工误差和装配误差等因素考虑到模型中,得到多因素综合作用下的摆线针轮啮合副误差分析模型,分析各误差因素以及多因素作用对传动误差产生的影响。
1 摆线齿廓形成理论 1.1 标准摆线齿廓采用包络法推导标准摆线齿廓方程。坐标系设定如图 1所示,坐标系
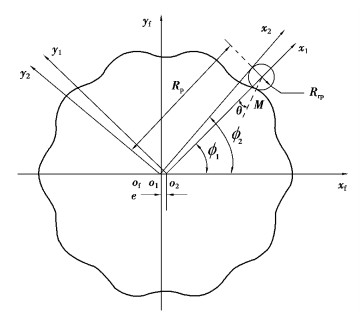
|
图 1 标准摆线齿廓生成的坐标系 Fig. 1 Coordinates system for the standard cycloid tooth profile |
| $ {i_{12}} = \frac{{{\omega _2}}}{{{\omega _1}}} = \frac{{{\phi _2}}}{{{\phi _1}}} = \frac{{{z_{\rm{c}}} + m}}{{{z_{\rm{c}}}}}。$ | (1) |
针齿齿廓在坐标系S1中的位置矢量可表示为:
| $ {\mathit{\boldsymbol{r}}_1}(\theta ) = {[{R_{\rm{p}}} - {R_{{\rm{rp}}}}\cos \theta \quad - {R_{{\rm{rp}}}}\sin \theta \quad 0\quad 1]^{\rm{T}}}。$ | (2) |
根据坐标变换,标准摆线齿廓在坐标系S2中的位置矢量可表示为:
| $ {\mathit{\boldsymbol{r}}_2}(\theta ,{\phi _1}) = {\mathit{\boldsymbol{M}}_{21}}({\phi _1}){\mathit{\boldsymbol{r}}_1}(\theta ) = {\mathit{\boldsymbol{M}}_{{\rm{2f}}}}({\phi _2}){\mathit{\boldsymbol{M}}_{{\rm{fl}}}}({\phi _1}){\mathit{\boldsymbol{r}}_1}(\theta ) = \\ \left[ {\begin{array}{*{20}{c}} {{R_{\rm{p}}}\cos \left( {\frac{{m{\kern 1pt} {\phi _1}}}{{{z_{\rm{c}}}}}} \right) - {R_{{\rm{rp}}}}\cos \left( {\theta - \frac{{m{\kern 1pt} {\phi _1}}}{{{z_{\rm{c}}}}}} \right) - e\cos \frac{{(m + {z_{\rm{c}}}){\phi _1}}}{{{z_{\rm{c}}}}}}\\ {{R_{\rm{p}}}\sin \left( {\frac{{m{\kern 1pt} {\phi _1}}}{{{z_{\rm{c}}}}}} \right) + {R_{{\rm{rp}}}}\sin \left( {\theta - \frac{{m{\kern 1pt} {\phi _1}}}{{{z_{\rm{c}}}}}} \right) - e\sin \frac{{(m + {z_{\rm{c}}}){\phi _1}}}{{{z_{\rm{c}}}}}}\\ 0\\ 1 \end{array}} \right]。$ | (3) |
式中:
摆线针轮传动实际啮合过程中,为了补偿制造误差,方便装配和保证充足的润滑,有必要对摆线轮齿廓进行修形从而产生侧隙[16]。摆线齿廓修形方法包括等距修形、移距修形和转角修形,如图 2所示。
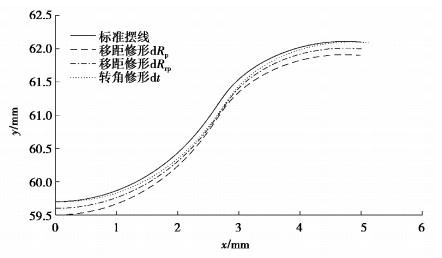
|
图 2 三种修形方法 Fig. 2 Three modification methods |
考虑修形后的摆线齿廓方程表示如下:
| $ {\mathit{\boldsymbol{r}}_2}({\phi _1};{\rm{d}}{R_{\rm{p}}},{\rm{d}}{R_{{\rm{rp}}}},{\rm{d}}t) = {[{x_{\rm{c}}}\cos ({\rm{d}}t) + {y_{\rm{c}}}\sin ({\rm{d}}t) - {x_{\rm{c}}}\sin ({\rm{d}}t) + {y_{\rm{c}}}\cos ({\rm{d}}t)\quad 0\quad 1]^{\rm{T}}}。$ | (4) |
式中:xc和yc为考虑了移距修形和等距修形的齿廓参数,只需将dRp和dRrp分别加到式(3)中的Rp和Rrp上;t为转角修形。
2 齿面接触分析(TCA)模型 2.1 坐标系统设定通过齿面接触分析(TCA)可以求出实际接触点的位置和输出角度,从而分析由轮廓变化引起的传动误差[17]。首先必须建立组装坐标系如图 3所示,其中S1为针齿坐标系,S2为摆线齿轮坐标系,Sf为固定坐标系,且S1与Sf重合。
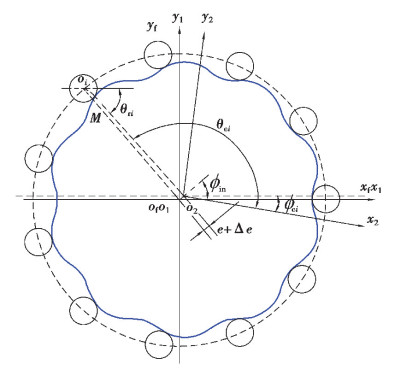
|
图 3 摆线齿轮齿面接触分析(TCA) Fig. 3 Tooth contact analysis of the cycloidal gear |
针齿齿廓上接触点的位置矢量在坐标系Sf中可表示为:
| $ \mathit{\boldsymbol{r}}_{\rm{f}}^{(1)}({\theta _{{\rm{r}}i}}) = {[{R_{\rm{p}}}\cos i{A_{\rm{P}}} + {R_{{\rm{rp}}}}\cos {\theta _{{\rm{r}}i}}\quad {R_{\rm{p}}}\sin i{A_{\rm{P}}} - {R_{{\rm{rp}}}}\sin {\theta _{{\rm{r}}i}}\quad 0\quad 1]^{\rm{T}}}。$ | (5) |
式中:Ap为两相邻针齿间的夹角,其值为2π/zb;i为针齿数目序号。
修形摆线轮齿廓上接触点在坐标系S2中可表示为:
| $ {\mathit{\boldsymbol{r}}_2}({\theta _{{\rm{c}}i}};{\rm{d}}{R_{\rm{p}}},{\rm{d}}{R_{{\rm{rp}}}},{\rm{d}}t) = {[{x_{\rm{c}}}\cos ({\rm{d}}t) + {y_{\rm{c}}}\sin ({\rm{d}}t) - {x_{\rm{c}}}\sin ({\rm{d}}t) + {y_{\rm{c}}}\cos ({\rm{d}}t)\quad 0\quad 1]^{\rm{T}}}。$ | (6) |
式中:
| $ \left[ {\begin{array}{*{20}{l}} {{x_{\rm{c}}}}\\ {{y_{\rm{c}}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{l}} {({R_{\rm{p}}} + {\rm{d}}{R_{\rm{p}}})\cos ({\theta _{{\rm{c}}i}}) - ({R_{{\rm{rp}}}} + {\rm{d}}{R_{{\rm{rp}}}})\cos ({\theta _{\rm{m}}} - {\theta _{{\rm{c}}i}}) - e\cos ({z_{\rm{b}}}{\theta _{{\rm{c}}i}})}\\ {({R_{\rm{p}}} + {\rm{d}}{R_{\rm{p}}})\sin ({\theta _{{\rm{c}}i}}) + ({R_{{\rm{rp}}}} + {\rm{d}}{R_{{\rm{rp}}}})\sin ({\theta _{\rm{m}}} - {\theta _{{\rm{c}}i}}) - e\sin ({z_{\rm{b}}}{\theta _{{\rm{c}}i}})} \end{array}} \right], $ |
| $ {\theta _{\rm{m}}} = {\tan ^{ - 1}}\left[ {\frac{{ - \sin ({z_{\rm{c}}}{\theta _{{\rm{c}}i}})}}{{\cos ({z_{\rm{c}}}{\theta _{{\rm{c}}i}}) - ({R_{\rm{p}}} + {\rm{d}}{R_{\rm{p}}})/e{z_{\rm{b}}}}}} \right]。$ |
摆线针轮啮合副在实际加工中各零件会产生加工误差,对其传动精度有影响。因此有必要将加工误差考虑到模型中进行分析,本研究中主要考虑针齿半径误差、针齿位置半径误差、针齿位置角度误差、摆线轮廓度误差以及摆线轮齿距误差等加工误差对啮合副传动误差的影响。
针齿半径误差、针齿位置半径误差和角度误差如图 4所示,考虑三者的加工误差后,针齿齿廓上接触点在坐标系Sf中可表示为:
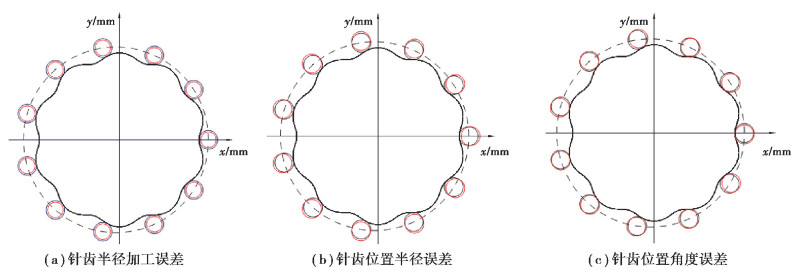
|
图 4 针齿半径和针齿位置加工误差 Fig. 4 Manufacture errors of pin radius and pin positions |
| $ \mathit{\boldsymbol{r}}_{\rm{f}}^{(1)}({\theta _{{\rm{r}}i}};\Delta R,{\theta _{\rm{p}}},\Delta r) = \left[ {\begin{array}{*{20}{c}} {{R_{\rm{p}}} \cos i{A_{\rm{P}}} + ({R_{{\rm{rp}}}} + \Delta r)\cos {\theta _{{\rm{r}}i}} + \Delta R\cos {\theta _{\rm{p}}}}\\ {{R_{\rm{p}}}\sin i{A_{\rm{P}}} - ({R_{{\rm{rp}}}} + \Delta r)\sin {\theta _{{\rm{r}}i}} + \Delta R\sin {\theta _{\rm{p}}}}\\ 0\\ 1 \end{array}} \right]。$ | (7) |
式中:ΔR和θp为针齿位置半径误差和角度误差,Δr为针齿半径误差。
考虑摆线齿轮轮廓度误差时,不选用传统齿轮分析中曲线拟合的方法,用更简单的方法来生成轮廓公差。这里通过将小增量±de增加到方程(6)中的偏心距e上,摆线轮齿廓误差模拟如图 5所示。考虑轮廓度误差的摆线齿轮齿廓上接触点的位置矢量表示为:
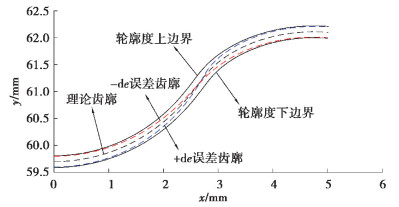
|
图 5 轮廓度误差示意图 Fig. 5 Profile errors of cycloidal |
| $ {\mathit{\boldsymbol{r}}_2}({\theta _{{\rm{c}}i}};{\rm{d}}{R_{\rm{p}}},{\rm{d}}{R_{{\rm{rp}}}},{\rm{d}}t;{\rm{d}}e)。$ | (8) |
摆线齿轮齿距误差由摆线轮的旋转轴的跳动引起,并沿着齿的圆周方向发生,齿距误差示意如图 6所示。在分析由于齿距误差引起的传动误差时,将齿距误差
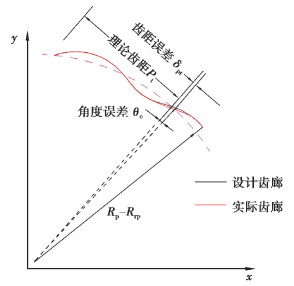
|
图 6 齿距误差示意图 Fig. 6 Pitch error of cycloidal profile |
| $ {\theta _{\rm{c}}} = {\delta _{{\rm{pt}}}}/({R_{\rm{p}}} - {R_{{\rm{rp}}}})。$ | (9) |
考虑齿距误差的摆线齿廓上接触点在坐标系S2中可表示为:
| $ {\mathit{\boldsymbol{r}}_2}({\theta _{{\rm{c}}i}};{\rm{d}}{R_{\rm{p}}},{\rm{d}}{R_{{\rm{rp}}}},{\rm{d}}t;{\rm{d}}e;{\theta _{\rm{c}}}) = {\mathit{\boldsymbol{M}}_2}({\theta _{\rm{c}}}){\mathit{\boldsymbol{r}}_2}({\theta _{{\rm{c}}i}};{\rm{d}}{R_{\rm{p}}},{\rm{d}}{R_{{\rm{rp}}}},{\rm{d}}t;{\rm{d}}e)。$ | (10) |
式中
| $ {\mathit{\boldsymbol{M}}_2}({\theta _{\rm{c}}}) = \left[ {\begin{array}{*{20}{c}} {\cos {\theta _{\rm{c}}}}&{\sin {\theta _{\rm{c}}}}&0&0\\ { - \sin {\theta _{\rm{c}}}}&{\cos {\theta _{\rm{c}}}}&0&0\\ 0&0&1&0\\ 0&0&0&1 \end{array}} \right]。$ |
为分析装配误差对摆线针轮啮合副传动误差的影响,将摆线齿轮的装配误差Δe添加到偏心距e中,得出考虑装配误差下摆线齿轮在固定坐标系Sf中的位置矢量如下式所示。
| $ \mathit{\boldsymbol{r}}_{\rm{f}}^{(2)}({\theta _{{\rm{c}}i}};{\rm{d}}{R_{\rm{p}}},{\rm{d}}{R_{{\rm{rp}}}},{\rm{d}}t;{\rm{d}}e;{\theta _{\rm{c}}};\Delta e) = {\mathit{\boldsymbol{M}}_{{\rm{f2}}}}({\phi _{{\rm{c}}i}},{\phi _{{\rm{in}}}},\Delta e){\mathit{\boldsymbol{r}}_2}({\theta _{{\rm{c}}i}};{\rm{d}}{R_{\rm{p}}},{\rm{d}}{R_{{\rm{rp}}}},{\rm{d}}t;{\rm{d}}e;{\theta _{\rm{c}}})。$ | (11) |
式中
| $ {\mathit{\boldsymbol{M}}_{{\rm{f2}}}} = \left[ {\begin{array}{*{20}{c}} {\cos {\phi _{{\rm{c}}i}}}&{\sin {\phi _{{\rm{c}}i}}}&0&{(e + \Delta e)\cos {\phi _{{\rm{ in }}}}}\\ { - \sin {\phi _{{\rm{c}}i}}}&{\cos {\phi _{{\rm{c}}i}}}&0&{(e + \Delta e)\sin {\phi _{{\rm{ in }}}}}\\ 0&0&1&0\\ 0&0&0&1 \end{array}} \right]。$ |
考虑齿廓修形、加工误差和装配误差等多因素综合作用下的针齿和摆线齿轮上接触点的法向量可表示为:
| $ \mathit{\boldsymbol{n}}_{\rm{f}}^{(1)}({\theta _{{\rm{r}}i}};\Delta R,{\theta _{\rm{p}}},\Delta r) = \frac{{\mathit{\boldsymbol{r}}_{\rm{f}}^{(1)}({\theta _{{\rm{r}}i}})}}{{\partial {\theta _{{\rm{r}}i}}}} \times k/\left| {\frac{{\mathit{\boldsymbol{r}}_{\rm{f}}^{(1)}({\theta _{{\rm{r}}i}})}}{{\partial {\theta _{{\rm{r}}i}}}} \times \mathit{\boldsymbol{k}}} \right|。$ | (12) |
| $ \mathit{\boldsymbol{n}}_2^{(2)}({\theta _{{\rm{c}}i}};{\rm{d}}{R_{\rm{p}}},{\rm{d}}{R_{{\rm{rp}}}},{\rm{d}}t;{\rm{d}}e;{\theta _{\rm{c}}};\Delta e) = \frac{{{\mathit{\boldsymbol{r}}_2}({\theta _{{\rm{c}}i}})}}{{\partial {\theta _{{\rm{c}}i}}}} \times \mathit{\boldsymbol{k}}/\left| {\frac{{{\mathit{\boldsymbol{r}}_2}({\theta _{{\rm{c}}i}})}}{{\partial {\theta _{{\rm{c}}i}}}} \times \mathit{\boldsymbol{k}}} \right|。$ | (13) |
式中
多因素综合作用下的摆线齿轮齿廓上接触点的单位法向量nf(2)在坐标系Sf中表示为:
| $ \mathit{\boldsymbol{n}}_{\rm{f}}^{(2)} = {\mathit{\boldsymbol{L}}_{{\rm{f2}}}}{\kern 1pt} \mathit{\boldsymbol{n}}_2^{(2)}。$ | (14) |
式中
若要满足共轭接触条件,则在同一坐标系下,两个连续曲面上的接触点位置坐标必须相同,且接触点上的单位法向量也必须相等[17],故可列出位置矢量与其法向量相等的方程式:
| $ \left\{ {\begin{array}{*{20}{l}} {\mathit{\boldsymbol{n}}_{\rm{f}}^{(1)}({\theta _{{\rm{r}}i}};\Delta R,{\theta _{\rm{p}}},\Delta r) = \mathit{\boldsymbol{n}}_{\rm{f}}^{(2)}({\theta _{{\rm{c}}i}};{\rm{d}}{R_{\rm{p}}},{\rm{d}}{R_{{\rm{rp}}}},{\rm{d}}t;{\rm{d}}e;{\theta _{\rm{c}}};\Delta e);}\\ {x_{\rm{f}}^{(1)}({\theta _{{\rm{r}}i}};\Delta R,{\theta _{\rm{p}}},\Delta r) = x_{\rm{f}}^{(2)}({\theta _{{\rm{c}}i}};{\rm{d}}{R_{\rm{p}}},{\rm{d}}{R_{{\rm{rp}}}},{\rm{d}}t;{\rm{d}}e;{\theta _{\rm{c}}};\Delta e);}\\ {y_{\rm{f}}^{(1)}({\theta _{{\rm{r}}i}};\Delta R,{\theta _{\rm{p}}},\Delta r) = y_{\rm{f}}^{(2)}({\theta _{{\rm{c}}i}};{\rm{d}}{R_{\rm{p}}},{\rm{d}}{R_{{\rm{rp}}}},{\rm{d}}t;{\rm{d}}e;{\theta _{\rm{c}}};\Delta e)}。\end{array}} \right. $ | (15) |
上式得到3个独立的非线性方程,可通过Matlab软件编程求解,计算出考虑齿廓修形、加工误差和装配误差等多因素综合作用下摆线针轮啮合副的传动误差。
传动误差为摆线齿轮实际输出转角与理论输出转角的差值:
| $ {\rm{d}}{\phi _{\rm{c}}} = {\phi _{\rm{c}}} - {\phi _{{\rm{in}}}}/{z_{\rm{c}}}。$ | (16) |
式中
为了验证模型的正确性,采用与文献[9]相同摆线设计参数,取摆线轮和针齿数分别为10和11,针齿分布圆半径30 mm,针齿半径3 mm,偏心距1.1 mm,移距和等距修行量分别为0.01 mm和0.03 mm。将模型计算结果与文献[9]计算结果进行对比如图 7所示。从图中可以看出,本研究中提出的方法和文献[9]计算得到的传动误差曲线基本一致,验证了本文方法分析摆线轮齿针轮传动误差的正确性。
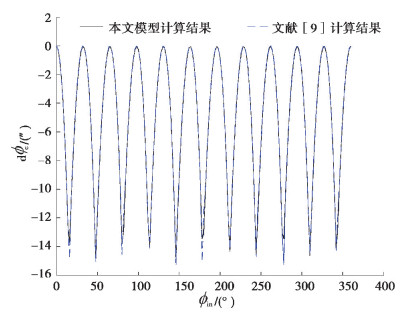
|
图 7 传动误差 |
根据上文提出的考虑齿廓修形、加工误差和装配误差等多因素综合作用下的摆线针轮传动误差分析模型,分别考察各误差因素以及多因素作用对传动误差产生的影响。取摆线齿轮的设计参数如表 1所示,通过仿真求解得到的传动误差曲线如图 8所示。从图中可以看出,传动误差由周期性的波形所组成,其值为1.75″。
| 表 1 摆线齿轮设计参数 Table 1 Design parameters of cycloidal gears |
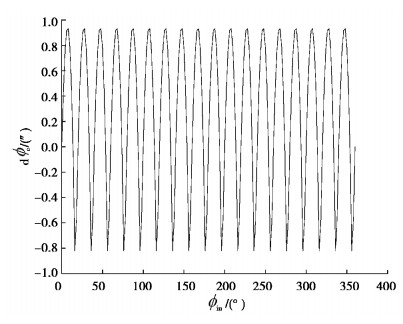
|
图 8 传动误差 |
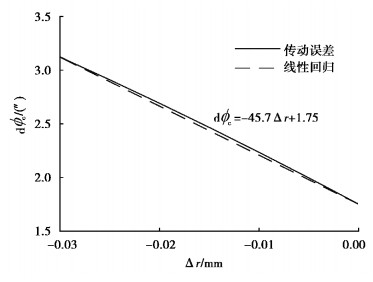
分析针齿半径误差Δr在0~-0.03 mm范围内以-0.001 mm步进增量变化对传动误差的影响,结果如图 9所示。图中虚线为线性回归线,其斜率为灵敏度。可以看出,当针齿半径减小,针齿与摆线轮之间的啮合间隙增大,传动误差增大,针齿半径误差与传动误差近似呈线性关系。
|
图 9 针齿半径误差Δr对传动误差 |
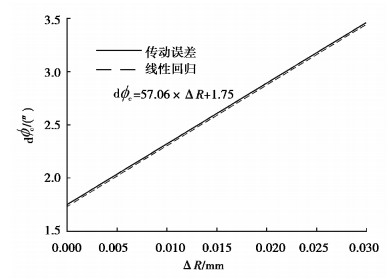
分析针齿位置半径误差ΔR在0~0.03 mm范围内以0.001 mm步进增量变化对传动误差的影响,结果如图 10所示。图中虚线为线性回归线,其斜率为灵敏度。可以看出针齿位置半径误差越大,传动误差越大,针齿位置半径误差与传动误差近似呈线性关系。
|
图 10 针齿位置半径误差ΔR对传动误差 |
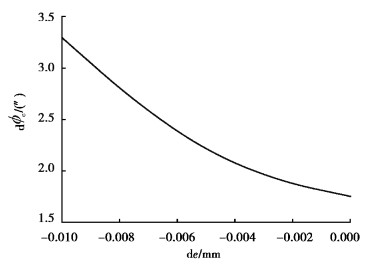
分析摆线轮廓度误差de在0~-0.01 mm范围内以-0.001 mm步进增量变化对传动误差的影响,结果如图 11所示。从图中可看出,随着轮廓度误差减小,传动误差增大,轮廓度误差de与传动误差近似呈指数关系。
|
图 11 轮廓度误差de对传动误差 |
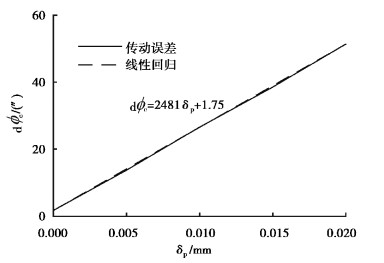
分析齿距累积误差
|
图 12 齿距累积误差 |
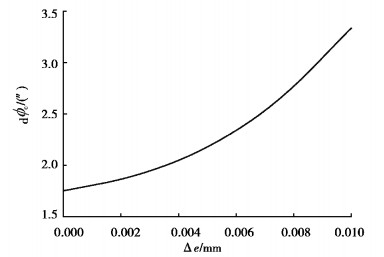
分析装配误差Δe在0~0.01 mm范围内以0.001 mm步进增量变化对传动误差的影响,结果如图 13所示。从图中可看出,随着Δe增大,传动误差也增大,装配误差Δe与传动误差近似呈指数关系。
|
图 13 装配误差Δe对传动误差 |
为了分析考虑齿廓修形、加工误差和装配误差等多因素综合作用对摆线针轮传动误差的影响,本研究中通过一个案例计算进行说明,其中摆线齿轮的设计参数见表 1,加工误差和装配误差参数如表 2所示。
| 表 2 加工和装配误差参数 Table 2 Manufacture and assembly errors parameters |
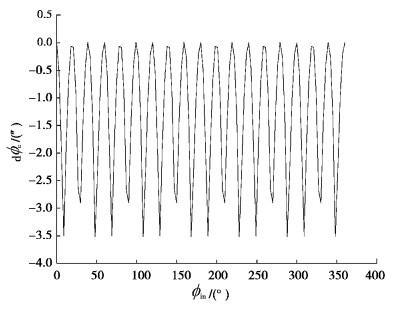
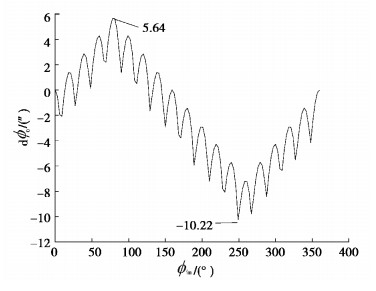
考虑除齿距累积误差的多因素综合作用下的摆线针轮传动误差曲线如图 14所示,从图中可以看出,最大传动误差值为3.52″;考虑齿廓修形、加工误差和装配误差等所有因素综合作用下的摆线针轮传动误差曲线如图 15所示,从图中可以看出,最大传动误差值为15.86″,传动误差曲线近似呈正弦波形,这主要是由于齿距累积误差影响造成。
|
图 14 考虑除齿距累积误差的多因素综合作用下传动误差 Fig. 14 Transmission error under consideration of multiple factors except cumulative pitch error |
|
图 15 考虑所有因素综合作用下的传动误差 Fig. 15 Transmission error under consideration of all factors |
表 3为考虑不同影响因素的4种情况下的传动误差结果对比。在只考虑齿廓修形的情况下,摆线针轮啮合副传动误差相对较小;在修形的基础上又考虑了除齿距累积误差的其他误差因素后,传动误差变大;考虑所有误差因素后,传动误差明显变大;说明加工和装配误差对摆线针轮传动精度的有较大影响,摆线轮齿距累积误差对传动精度的影响最大并形成正弦波形,各误差因素的综合影响并不等同于各种误差简单的叠加。
| 表 3 考虑不同影响因素的4种情况下的传动误差结果对比 Table 3 Comparison of transmission error results in four cases considering different influecing factors |
1) 基于齿轮啮合原理和齿面接触分析,提出一种考虑齿廓修形、加工误差和装配误差等多因素综合作用下的摆线针轮传动误差分析模型,可实现齿廓修形参数、加工误差参数和装配误差参数下摆线针轮传动误差的分析计算。
2) 分析各误差因素对传动误差的影响,结果表明针齿半径误差Δr、针齿位置半径误差ΔR及齿距累积误差
3) 通过比较各误差因素对传动误差的影响程度得出:齿距累积误差
4) 数值案例分析结果表明:加工和装配误差对摆线针轮传动精度有较大影响,摆线轮齿距累积误差对传动精度的影响最大并且会造成正弦波形的影响,各误差因素的综合影响并不等同于各种误差简单地叠加。
本文中模型研究的是无负载条件下各误差因素及多因素对静态传动误差的影响,没有考虑有负载的情况下对动态传动误差的影响,需进一步探讨承载情况下多因素综合作用的摆线针轮传动误差;各误差因素的综合影响不等同于各种误差简单地叠加,需要对误差的相关性进行研究,对于多项误差共同作用对传动误差的耦合影响机理有待更进一步研究。
| [1] |
Wang H, Shi Z Y, Yu B, et al. Transmission performance analysis of RV reducers influenced by profile modification and load[J]. Applied Sciences, 2019, 9(19): 4099. DOI:10.3390/app9194099 |
| [2] |
Pham A D, Ahn H J. High precision reducers for industrial robots driving 4th industrial revolution:state of arts, analysis, design, performance evaluation and perspective[J]. International Journal of Precision Engineering and Manufacturing-Green Technology, 2018, 5(4): 519-533. DOI:10.1007/s40684-018-0058-x |
| [3] |
缪嘉成, 李朝阳, 陈兵奎.结合Kriging与改进NSGA-II的RV减速器优化[J/OL].重庆大学学报, [2020-02-21]. http://kns.cnki.net/kcms/detail/50.1044.N.20190927.1329.004.html. DOI: 10.11835/j.issn.1000-582X.2020.212. MIAO Jiacheng, LI Chaoyang, CHEN Bingkui. Optimization of RV reducer by integrating Kriging with improved NSGA-II[J]. Journal of Chongqing University, [2020-02-21]. http://kns.cnki.net/kcms/detail/50.1044.N.20190927.1329.004.html. DOI: 10.11835/j.issn.1000-582X.2020.212.(inChinese) |
| [4] |
Li T X, Wang G F, Deng X Z, et al. Contact analysis of cycloidal-pin gear of RV reducer under the influence of profile error[J]. Journal of Physics:Conference Series, 2019, 1168: 022095. DOI:10.1088/1742-6596/1168/2/022095 |
| [5] |
莫靖宇, 罗善明, 毛玲霞, 等. 基于投影法的摆线齿轮齿廓偏差检测及分析[J]. 机械传动, 2018, 42(1): 88-93. MO Jingyu, LUO Shanming, MAO Lingxia, et al. Detection and analysis of tooth profile deviation of cycloidal gear based on projection method[J]. Journal of Mechanical Transmission, 2018, 42(1): 88-93. (in Chinese) |
| [6] |
郭广新, 牟魁元, 张淑英, 等. 摆线齿轮的齿形误差分析[J]. 齿轮, 1982(4): 12-19. GUO Guangxin, MOU Kuiyuan, ZHANG Shuying, et al. Analysis of tooth profile error of cycloidal gear[J]. Gear Journal, 1982(4): 12-19. (in Chinese) |
| [7] |
Yang D, Blanche J. Design and application guidelines for cycloid drives with machining tolerances[J]. Mechanism and Machine Theory, 1990, 25(5): 487-501. DOI:10.1016/0094-114X(90)90064-Q |
| [8] |
日高照晃, 王宏猷, 石田武. ほか.サイクロイド齒車を用ぃたK-H-V形遊星齒車装置の回转传达误差に开する研究(第1报, 解析方法)[C]//日本耭械学会论文集(C编).东京: [s.n.], 1994, 60(570): 645-653. Hidaka T, Wang H Y. Rotational transmission error of K-H-V-type planetary gears with cycloid gears (1st report. analytical method of the rotational transmission error)[C]//Proceedings of Japan Society of Mechanical Engineers(C Series). Tokyo: [s.n.], 1994, 60(570): 645-653. (in Japanese) |
| [9] |
Lin K S, Chan K Y, Lee J J. Kinematic error analysis and tolerance allocation of cycloidal gear reducers[J]. Mechanism and Machine Theory, 2018, 124: 73-91. DOI:10.1016/j.mechmachtheory.2017.12.028 |
| [10] |
Lin W S, Shih Y P, Lee J J. Design of a two-stage cycloidal gear reducer with tooth modifications[J]. Mechanism and Machine Theory, 2014, 79: 184-197. DOI:10.1016/j.mechmachtheory.2014.04.009 |
| [11] |
刘玉婷. RV减速器传动误差分析[D].辽宁大连: 大连交通大学, 2012. LIU Yuting. Transmission error analysis of RV reducer[D]. Dalian, Liaoning: Dalian Jiaotong University, 2012. (in Chinese) |
| [12] |
Shan L J, Liu Y T, He W D. Analysis of nonlinear dynamic accuracy on RV transmission system[J]. Advanced Materials Research, 2012, 510: 529-535. DOI:10.4028/www.scientific.net/AMR.510.529 |
| [13] |
韩林山, 沈允文, 董海军, 等. 2K-V型传动装置动态传动精度理论研究[J]. 机械工程学报, 2007, 43(6): 81-86. HAN Linshan, SHEN Yunwen, DONG Haijun, et al. Theoretical research on dynamic transmission accuracy for 2K-V-type drive[J]. Chinese Journal of Mechanical Engineering, 2007, 43(6): 81-86. (in Chinese) DOI:10.3321/j.issn:0577-6686.2007.06.015 |
| [14] |
韩林山, 沈允文, 董海军, 等. 2K-V型传动装置制造误差对传动精度的影响[J]. 机械科学与技术, 2007, 26(9): 1135-1140. HAN Linshan, SHEN Yunwen, DONG Haijun, et al. Effect of manufacturing errors on transmission accuracy for 2K-V-type drive[J]. Mechanical Science and Technology, 2007, 26(9): 1135-1140. (in Chinese) DOI:10.3321/j.issn:1003-8728.2007.09.010 |
| [15] |
李充宁, 刘继岩, 孙涛. 2K-V型行星传动中摆线针轮啮合的传动精度研究[J]. 机械工程学报, 2001, 37(4): 61-65. LI Chongning, LIU Jiyan, SUN Tao. Study on transmission precision of cycloidal pin gear in 2K-V planetary drives[J]. Journal of Mechanical Engineering, 2001, 37(4): 61-65. (in Chinese) DOI:10.3321/j.issn:0577-6686.2001.04.014 |
| [16] |
杨云.时变等距摆线的啮合特性研究[D].重庆: 重庆大学, 2018. YANG Yun. Meshing characteristics study of the time-varying equidistance cycloid[D]. Chongqing: Chongqing University, 2018. (in Chinese) |
| [17] |
Li X, Li C Y, Wang Y W, et al. Analysis of a cycloid speed reducer considering tooth profile modification and clearance-fit output mechanism[J]. Journal of Mechanical Design, 2017, 139(3): 033303. DOI:10.1115/1.4035541 |
 2020, Vol. 43
2020, Vol. 43


