差动式行星滚柱丝杠(differential planetary roller Screw,DPRS)由德国宇航中心于1992年研制成功,与标准型行星滚柱丝杠(planetary roller screw,PRS)相比,DPRS结构更加紧凑,在相同体积和质量下可以承受更高的载荷,并且具有更高的输入转速和更小的导程,能够很好地满足航天航空等恶劣工况条件下机电伺服系统对重载直线传动部件的需求[1]。
DPRS作为一种精密直线传动机构,其承载特性对传动精度和寿命有直接或间接影响[2]。近年来,国内外对DPRS的研究主要集中在工作原理[3-4]、运动特性[5]、预紧转矩[6]和效率及精度[7]等方面,而对于DPRS啮合承载特性的研究还不够深入。在啮合接触方面,徐强等[8]基于空间螺旋面的啮合原理,建立了DPRS的空间啮合模型,求出了啮合点的位置和满足良好啮合状态的啮合中心距;Fu等[9]建立了综合啮合接触分析模型,分析出丝杆和滚柱的初始啮合点会偏向二者螺纹牙顶,从而引起的接触点位置变化,而螺母和滚柱的啮合点位于螺纹中径切点处,接触点位置没有变化。在承载接触方面,主要是针对PRS,Aurégan等[10]在建立有限元模型的基础上,开展了PRS接触点的研究,分析出最大接触应力发生在丝杆与滚柱啮合处;Jones等[11]将丝杠等效成弹簧系统,对PRS的刚度及承载能力开展了研究,分析了滚柱个数与滚柱螺纹牙个数对载荷分布的影响;杨家军等[12]依据Hertz弹性接触理论,将滚柱作为整体,建立了载荷分布模型,并进一步研究了PRS的刚度特性。上述研究为DPRS承载接触特性分析的研究奠定了理论基础,但未考虑接触点位置变化和载荷分布不均对DPRS承载能力的影响,导致承载接触计算结果不准确,而且DPRS结构参数对载荷分布和承载能力的影响规律研究也尚不充分。
笔者基于DPRS结构特点,重点研究了由于滚柱与丝杆初始啮合点偏置引起的接触点位置变化对承载特性的影响,建立了DPRS空间啮合模型,采用数值方法对滚柱与丝杆啮合点处的主曲率进行求解;在此基础上,结合赫兹接触理论和弹塑性力学,对DPRS滚柱载荷分布和承载能力进行理论计算;并进一步系统分析了牙型角、螺距、滚柱螺纹节数、丝杆与滚柱材料弹性模量比等因素对DPRS滚柱载荷分布和承载能力的影响规律。
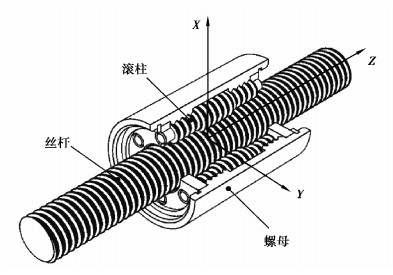
1 DPRS啮合分析 1.1 DPRS结构组成DPRS的结构形式如图 1所示,组成元件有螺母、滚柱及丝杆等部分,螺母内表面和滚柱外表面分布有等距环槽,丝杆外表面为螺距、牙型角及牙型齿廓与螺母均相同的多头螺纹面,多个滚柱均匀布置于丝杠、螺母之间[1]。
|
图 1 DPRS结构组成 Fig. 1 Structure of DPRS |
DPRS通过滚柱大直径段与丝杠螺纹的啮合和小直径段与螺母环槽的啮合来传递运动和动力。滚柱两端安装在保持架的孔中。为方便下一步啮合分析,建立滚柱和丝杆啮合固定空间坐标系(O-X, Y, Z),如图 1所示,其中Z轴与丝杆轴线重合,X轴同时穿过丝杆和滚柱轴线, 并位于与滚柱啮合的丝杆螺纹牙中间面。
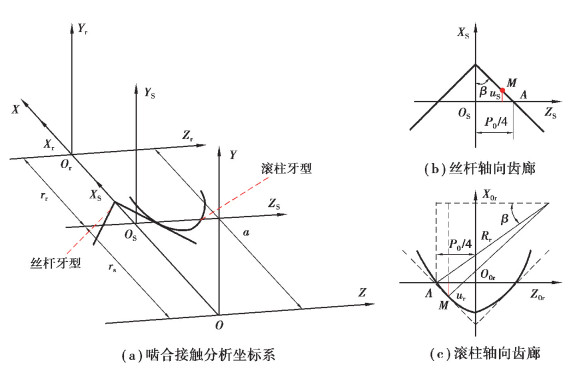
1.2 齿面几何模型为获得良好的接触状态和承载性能,DPRS丝杆和螺母螺纹牙的轴向截面轮廓为直线,滚柱的轴向截面牙型轮廓为圆弧形,圆心位于滚柱轴线[1],滚柱和丝杆牙型轮廓如图 2(b)和(c)所示。根据上文的结构和固定坐标系,可以建立如图 2(a)所示的滚柱丝杆啮合接触坐标系,包括滚柱坐标系
|
图 2 啮合接触分析坐标系及轴向牙型齿廓 Fig. 2 Meshing contact analysis coordinate system and axial tooth profile |
考虑到对称性,这里仅对以Z轴为正方向的丝杆上螺旋曲面和滚柱下环槽曲面建立参数方程,利用图 2(b)和(c)中的轴截面坐标系可以将丝杆螺旋曲面和滚柱环槽曲面上的点表示为
| $ \left\{ {\begin{array}{*{20}{l}} {{x_{{\rm{sM}}}} = {u_{\rm{s}}},}\\ {{z_{{\rm{sM}}}} = {P_0}/4 - {u_{\rm{s}}}\tan \beta }。\end{array}} \right. $ | (1) |
| $ \left\{ {\begin{array}{*{20}{l}} {{x_{{\rm{0rM}}}} = - {u_{\rm{r}}},}\\ {{z_{{\rm{0rM}}}} = R\cos \beta - {P_0}/4 - \sqrt {{R^2} - {{({r_{\rm{r}}} + {u_{\rm{r}}})}^2}} } \end{array}} \right.。$ | (2) |
式中:us与ur为参变量,R=rr/sin β。
依据DPRS的结构特点,为保证图 2中零件坐标系
| $ {\theta _{{\rm{0s}}}^k = (k - 1)2{\rm{ \mathsf{ π} }}/{n_{\rm{s}}},} $ | (3) |
| $ {{\theta _{{\rm{0s}}}} = {\rm{ \mathsf{ π} }}}。$ | (4) |
式中:θ0sk为丝杆第k条螺纹面上螺旋曲面的起始角度,k=1, 2, …, ns,ns为丝杠螺纹头数; θ0r为滚柱环槽起始角度。
由式(1)和(3)可知丝杆上螺旋曲面可以表示为
| $ \left\{ {\begin{array}{*{20}{l}} {{x_{\rm{s}}} = ({r_{\rm{s}}} + {u_{\rm{s}}})\cos ({\theta _{\rm{s}}} + \theta _{{\rm{0s}}}^k),}\\ {{y_{\rm{s}}} = ({r_{\rm{s}}} + {u_{\rm{s}}})\sin ({\theta _{\rm{s}}} + \theta _{{\rm{0s}}}^k),}\\ {{z_{\rm{s}}} = {P_0}/4 - {u_{\rm{s}}}\tan \beta + {\theta _{\rm{s}}}{P_{\rm{s}}}/2{\rm{ \mathsf{ π} }}}。\end{array}} \right. $ | (5) |
式中:θs为丝杆上螺旋面的螺旋参数,即丝杆轴截面绕Z轴旋转角度; Ps为丝杆螺旋面的导程,有Ps=nsP0。
同理根据滚柱下环槽曲面的轴截面方程,可知滚柱曲面方程为
| $ \left\{ {\begin{array}{*{20}{l}} {{x_{\rm{r}}} = a + ({r_{\rm{r}}} + {u_{\rm{r}}})\cos ({\theta _{\rm{r}}} + {\theta _{{\rm{0r}}}}),}\\ {{y_{\rm{r}}} = ({r_{\rm{r}}} + {u_{\rm{r}}})\sin ({\theta _{\rm{r}}} + {\theta _{{\rm{0r}}}}),}\\ {{z_{\rm{r}}} = R\cos \beta + {P_0}/4 - \sqrt {{R^2} - {{({r_{\rm{r}}} + {u_{\rm{r}}})}^2}} }。\end{array}} \right. $ | (6) |
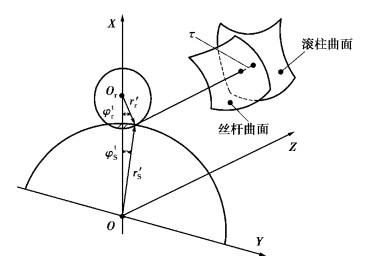
一般为了保证DPRS的正常装配和运动的流畅性,各零件的螺纹牙之间通常具有一定的间隙。图 3给出了DPRS两螺旋曲面相啮合的一般情况,τ为丝杆曲面和滚柱曲面之间的轴向间隙。进一步分析丝杆和滚柱的啮合机理,在图 2基础上,将丝杆与滚柱接触点投影到固定坐标系下的XOY平面上。
|
图 3 丝杆与滚柱啮合示意图 Fig. 3 Screw and roller meshing diagram |
根据丝杆螺纹牙的特点,可将丝杆上螺旋面的螺旋参数表示为
| $ \left\{ {\begin{array}{*{20}{l}} {{x_{\rm{s}}} = r_{\rm{s}}^\prime \cos \varphi _{\rm{s}}^\prime ,}\\ {{y_{\rm{s}}} = r_{\rm{s}}^\prime \sin \varphi _{\rm{s}}^\prime ,}\\ {{z_{\rm{s}}} = {P_0}/4 - (r_{\rm{s}}^\prime - {r_{\rm{s}}})\tan \beta + \varphi _{\rm{s}}^\prime {P_{\rm{s}}}/2{\rm{ \mathsf{ π} }} + {P_0}(t - 1)}。\end{array}} \right. $ | (7) |
滚柱为等距环槽面,有
| $ \left\{ {\begin{array}{*{20}{l}} {{x_{\rm{r}}} = a - r_{\rm{r}}^\prime \cos \varphi _{\rm{r}}^\prime ,}\\ {{y_{\rm{r}}} = r_{\rm{r}}^\prime \sin \varphi _{\rm{r}}^\prime ,}\\ {{z_{\rm{r}}} = R\cos \beta + {P_0}/4 - \sqrt {{R^2} - r_{\rm{r}}^{\prime 2}} + {P_0}(t - 1)}。\end{array}} \right. $ | (8) |
DPRS滚柱环槽面与丝杆螺旋面保持连续啮合,必须要满足在传动中时刻处于相切接触状态,则两曲面在啮合点处存在公共的切线与法线,即满足条件[13]:
| $ {\mathit{\boldsymbol{v}}_{{\rm{rs}}}} \cdot \mathit{\boldsymbol{n}} = 0。$ | (9) |
式中:
| $ \mathit{\boldsymbol{n}} = ({n_x},{n_y},{n_z}) = \left( {\left| {\begin{array}{*{20}{l}} {\frac{{\partial y}}{{\partial z}}}&{\frac{{\partial z}}{{\partial r}}}\\ {\frac{{\partial y}}{{\partial \varphi }}}&{\frac{{\partial z}}{{\partial \varphi }}} \end{array}} \right|\quad \left| {\begin{array}{*{20}{l}} {\frac{{\partial z}}{{\partial r}}}&{\frac{{\partial x}}{{\partial r}}}\\ {\frac{{\partial z}}{{\partial \varphi }}}&{\frac{{\partial x}}{{\partial \varphi }}} \end{array}} \right|\quad \left| {\begin{array}{*{20}{l}} {\frac{{\partial x}}{{\partial r}}}&{\frac{{\partial y}}{{\partial r}}}\\ {\frac{{\partial x}}{{\partial \varphi }}}&{\frac{{\partial y}}{{\partial \varphi }}} \end{array}} \right|} \right)。$ | (10) |
式中:r为
由于滚柱的环槽面的轴向齿廓为圆弧曲线,丝杆的螺旋面的轴向齿廓为直线,因此在同一侧接触区域有且只有一个啮合点。即两曲面在啮合处点坐标相等且各自法线矢量满足:
| $ {\mathit{\boldsymbol{n}}_{\rm{r}}} = k{\mathit{\boldsymbol{n}}_{\rm{s}}},k{\kern 1pt} {\rm{为比例系数。}} $ | (11) |
则由式(7) ~ (11)可得,DPRS滚柱与丝杆之间的啮合方程为
| $ \left\{ {\begin{array}{*{20}{l}} {{x_{\rm{s}}} = {x_{\rm{r}}},}\\ {{y_{\rm{s}}} = {y_{\rm{r}}},}\\ {{z_{\rm{s}}} = {z_{\rm{r}}} + \tau ,}\\ {\frac{{{n_{{\rm{s}}x}}}}{{{n_{{\rm{r}}x}}}} = \frac{{{n_{{\rm{s}}y}}}}{{{n_{{\rm{r}}y}}}} = \frac{{{n_{{\rm{s}}z}}}}{{{n_{{\rm{r}}z}}}}}。\end{array}} \right. $ | (12) |
式(12)可得到具有5个未知数
赫兹理论适用于计算点接触的两物体在弹性范围内发生接触变形的应力应变问题,当DPRS受负载作用后,滚柱和丝杆、螺母接触点处会出现接触变形,由于其接触都为点接触,可采用赫兹接触理论对其弹性接触变形进行分析。
由赫兹理论[15]可知,丝杆和滚柱接触面的接触应力σ和弹性变量δ分别为
| $ \sigma = \frac{{3Q}}{{2{\rm{ \mathsf{ π} }}ab}},\delta = \frac{{K(e)}}{{{\rm{ \mathsf{ π} }}{m_{\rm{a}}}}}\sqrt[3]{{\frac{{9{E^2}{Q^2}\sum \rho }}{4}}}。$ | (13) |
式中:Q为法向接触力;a,b分别为接触椭圆的长、短半轴,
对于DPRS,丝杆与滚柱接触时,第一、二主曲率[16]分别为
| $ \left\{ {\begin{array}{*{20}{l}} {{\rho _{11}} = 1/R\quad {\rho _{11}} = \sin \alpha /{r_{{\rm{mr}}}};}\\ {{\rho _{21}} = 0\quad {\rho _{22}} = \sin \alpha /{r_{{\rm{ms}}}}}。\end{array}} \right. $ | (14) |
式中:α为丝杆与滚柱的接触角,α=90°-β;R为滚柱接触点处对应的圆弧半径
由式(13)和(14)可知,丝杆与滚柱接触时的赫兹接触变形量分别为
| $ \delta = KQ_t^{\frac{3}{2}}, $ | (15) |
式中:K为丝杆的赫兹接触刚度;Qt为在第t节螺纹啮合处所受的法向载荷。
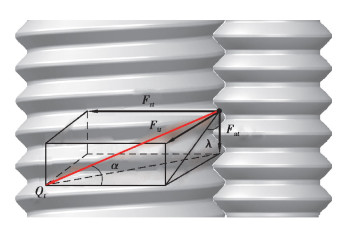
2.2 滚柱载荷分布对于DPRS滚柱载荷分布的求解,假设每根滚柱的载荷分布情况相同。根据滚柱丝杠的特点,滚柱具有多体多点接触的特征,基于假设,以丝杆为研究对象,在与滚柱接触的半个节距中,丝杆受力情况[17]如图 4所示。
|
图 4 丝杆与滚柱接触力示意图 Fig. 4 Diagram of screw rod and roller contact force |
从t-1节到t节,丝杆受滚柱传递的力为
| $ {F_{{\rm{a}}t}} = T - n\sum\limits_{i = 1}^{t - 1} {{Q_i}} \sin \alpha \cos \lambda , $ | (16) |
式中:
根据滚柱和丝杆接触的受载情况,可将丝杆当作圆柱处理,以半个螺距为标定长度,则其第t节螺纹牙轴向变形为
| $ {\varepsilon _{t - 1,t}} = \frac{{{F_{{\rm{a}}t}}{P_0}}}{{2{E_{\rm{s}}}{A_{\rm{s}}}}}, $ | (17) |
式中As为有效接触面积,
由于在t-1节到t节螺纹牙之间,丝杆受到滚柱的压力作用,则在标定长度内的压缩量与第t-1节到第t节螺纹牙的赫兹接触变形量的轴向分量之差相同。
| $ {\varepsilon _{t - 1,t}} = \frac{{{\delta _{t - 1}} - {\delta _t}}}{{\sin \alpha \cos \lambda }}。$ | (18) |
由式(15) ~ (18)可得基于螺旋空间啮合理论的DPRS滚柱螺纹牙载荷分布的迭代公式为
| $ Q_{t - 1}^{2/3} - Q_t^{2/3} = \frac{{nP}}{{2{E_{\rm{s}}}{A_{\rm{s}}}K}}\sum\limits_{i = t}^z {{Q_i}} {\sin ^2}\alpha {\cos ^2}\lambda 。$ | (19) |
根据上述DPRS精确承载分析几何模型进行实例计算,取某一规格DPRS为例,其基本结构参数如表 1所示。
| 表 1 DPRS的结构参数 Table 1 Structural parameters of DPRS |
为了验证本文模型的正确性,将模型计算结果与文献[11]采用的直接刚度法计算结果进行对比。直接刚度法是将DPRS等效成一个弹簧系统,根据接触点变形、刚度和力的关系建立矩阵方程,求解各接触点力。
根据DPRS丝杆两接触侧相邻螺纹牙变形协调关系导出考虑接触点位置变化的承载分布计算模型,而文献[11]求解承载分布没有考虑,故式(14)中直接代入滚柱和丝杆直径。将表 1中数据代入,滚柱和丝杆材料参数取Es=Er=2.07×102 MPa,μs=μr=0.27,取外加轴向载荷为12 kN,计算结果如图 5所示。
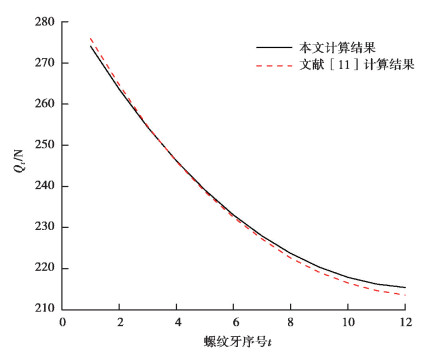
|
图 5 滚柱载荷分布情况 Fig. 5 Roller load distribution |
由图 5可知,本文的滚柱承载分布计算结果与使用文献[11]中方法计算的结果吻合较好,特别是前几节螺纹牙承载变化趋势吻合程度较高,验证了所建模型的有效性。从图 5中可以看出,当DPRS外加载荷一定时,随着滚柱上螺纹序号的增加,每节螺纹上所承受的载荷逐渐减少,并且第1节螺纹牙所受载荷最大,这与普通螺纹连接的载荷分布情况类似。因此在外加载荷和DPRS参数确定下,第1节螺纹牙所受载荷最大,因而在此处的接触应力最大,最有可能引起失效。
3 承载特性规律分析根据笔者提出的基于螺旋空间啮合理论的DPRS滚柱的精准承载几何学模型,分别考察牙型角、螺距、滚柱螺纹节数和丝杆与滚柱材料弹性模量比等因素对DPRS载荷分布和承载能力的影响。
3.1 牙型角对承载特性的影响滚柱螺纹牙载荷分布和承载能力与牙型角有直接关系,以表 1实例参数为基础,牙型半角取β∈(30°, 60°),其余参数不变,牙型角对滚柱螺纹牙载荷分布和承载能力影响规律如图 6所示。
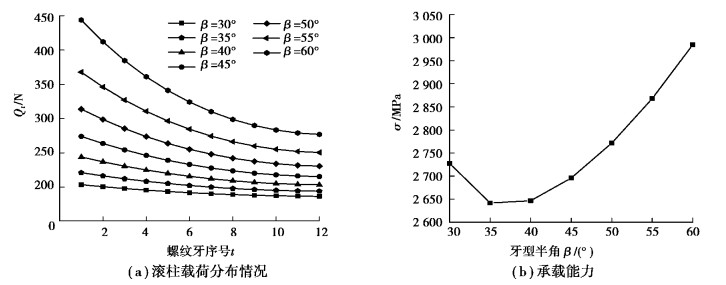
|
图 6 牙型角对滚柱载荷分布和承载能力的影响 Fig. 6 Effect of tooth angle on roller load distribution and carrying capacity |
从图 6中可以看出,随着牙型角的增大,滚柱载荷分布越趋于不均。这是由于牙型角越大,则接触角越小,导致刚度系数越大,前面节数所受载荷变化也越大。在本文实例所取参数条件下,DPRS承载能力在60°~70°范围内随着牙型角增加而增强,在70°~120°范围内随着牙型角增大逐渐减弱。
3.2 螺距对承载特性的影响考察螺距P0对滚柱螺纹牙载荷分布和承载能力的影响,这里取P0∈(1, 6),其余参数不变,螺距对滚柱螺纹牙载荷分布和承载能力影响规律如图 7所示。
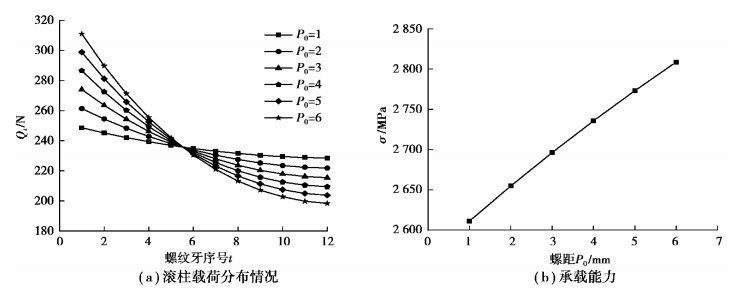
|
图 7 螺距对滚柱载荷分布和承载能力的影响 Fig. 7 Effect of screw pitch on roller load distribution and carrying capacity |
从图 7中可以看出,随着螺距P0逐渐增大,滚柱前面节数所受载荷逐渐增大,对滚柱螺纹牙载荷分布的影响也增大,使载荷分布不均匀性增大,DPRS的承载能力逐渐减小。可见螺距较小时,螺纹牙载荷分布更加均匀,承载能力更强。与此同时,螺距的大小决定了DPRS的直线进给速度。因此,在进行DPRS结构设计时,应综合考虑速度和承载能力要求。
3.3 滚柱螺纹节数对承载特性的影响滚柱螺纹节数直接影响着滚柱螺纹牙载荷分布和承载能力,取z∈(9, 14),其余参数不变,计算所得载荷分布和接触应力结果如图 8所示。
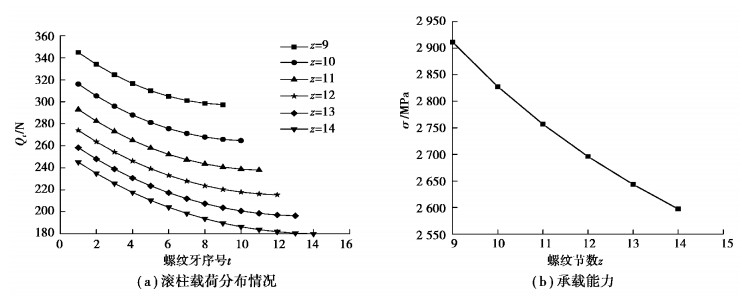
|
图 8 滚柱螺纹节数对滚柱载荷分布和承载能力的影响 Fig. 8 Effect of the number of threads of the roller on roller load distribution and carrying capacity |
从图 8中可以看出,滚柱螺纹节数越多,分配到每个螺纹牙上载荷就越小。在本文实例所取参数条件下,当螺纹节数z>9时,滚柱载荷分布变化趋势保持相同。对于承载能力,DPRS的承载能力随着螺纹节数增加而增大。但是螺纹节数增加会产生更多的摩擦损耗和摩擦热,进而会降低DPRS的传动效率。因此,在进行DPRS结构设计时,为了提供高效的性能传动,在满足强度的条件下,应适量减小滚柱螺纹节数。
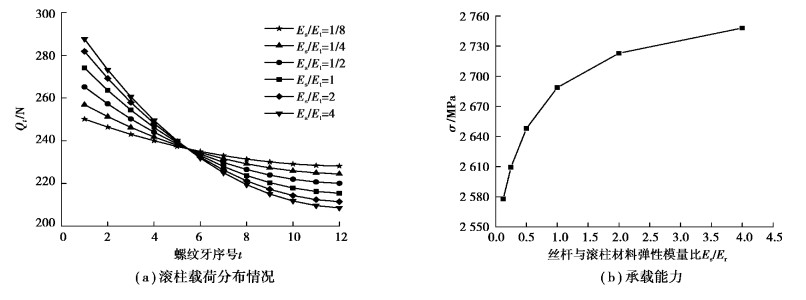
3.4 材料弹性模量比对承载特性的影响考察丝杆和滚柱所用材料对滚柱螺纹牙载荷分布和承载能力的影响,在其余参数不变下,这里取丝杆和滚柱材料弹性模量比为1/8,1/4,1/2,1,2和4对接触特性进行分析,计算结果如图 9所示。
|
图 9 材料弹性模量比对滚柱载荷分布和承载能力的影响 Fig. 9 Effect of elastic modulus ratio of material on roller load distribution and carrying capacity |
由图 9可以看出,滚柱弹性模量越大,对滚柱螺纹牙载荷分布影响越小,前面几节螺纹所受载荷逐渐减小,载荷分布均匀性越好。对于承载能力,DPRS的承载能力随着滚柱弹性模量增加而逐渐增大。这是由于丝杆弹性模量小于滚柱弹性模量时,丝杆更容易变形,滚柱前几节螺纹载荷分布集中度降低,使更多载荷分配到后面各螺纹牙。因此,增加滚柱弹性模量,特别是保证Es/Er<1,可以有效地改善滚柱载荷分布,提高DPRS承载能力。
4 结论以DPRS单对滚柱与丝杆啮合副为研究对象,建立了基于螺旋空间啮合理论的承载特性计算模型,系统分析了牙型角、螺距、滚柱螺纹节数、丝杆与滚柱材料弹性模量比等因素对DPRS滚柱载荷分布和承载能力的影响,得出结论如下:
1) 当丝杠外加载荷一定时,随着滚柱上螺纹序号的增加,每个螺纹上所承受的力逐渐减少,第1节螺纹接触应力最大,最有可能引起失效。
2) 牙型角越大,滚柱载荷分布越趋于不均,前面螺纹牙所受载荷变化越大,均呈增大趋势。在一定范围内,随着牙型角增加,DPRS承载能力先增强后逐渐减弱。
3) 螺距对滚柱螺纹牙载荷分布影响较大,螺距较小时,螺纹牙载荷分布相对更加均匀,DPRS承载能力更强。
4) 滚柱螺纹节数越多,分配到每个螺纹上的接触力就越小。滚柱载荷分布越趋于相同,DPRS承载能力越强。
5) 提高滚柱弹性模量,降低丝杆弹性模量,特别是保证Es/Er<1,可以有效地改善滚柱载荷分布,提高DPRS承载能力。
差动式行星滚柱丝杠结构较复杂,由于滚柱和丝杆的刚度及变形性质不同,即使制造和装配都很精确,每根滚柱的受力也是不同的,因此在计算承载特性时,需进一步探讨每根滚柱的受力情况。在螺纹载荷分布的研究中只考虑了接触变形,未考虑螺纹牙的变形情况,其计算结果可能存在一定的误差,有待更加深入的研究。
| [1] |
Karam W, Mare J C. Modelling and simulation of mechanical transmission in roller-screw electromechanical actuators[J]. Aircraft Engineering and Aerospace Technology, 2009, 81(4): 288-298. DOI:10.1108/00022660910967273 |
| [2] |
刘更, 张文杰, 马尚君, 等. 行星滚柱丝杠副承载特性研究进展[J]. 机械科学与技术, 2017, 36(4): 598-604. LIU Geng, ZHANG Wenjie, MA Shangjun, et al. Review on load bearing characteristics of planetary roller screw mechanism[J]. Mechanical Science and Technology, 2017, 36(4): 598-604. (in Chinese) |
| [3] |
陈曼龙. 差动丝杠机构的传动性能[J]. 机械传动, 2008, 32(1): 98-100. CHEN Manlong. Drive performance of differential roller screw[J]. Journal of Mechanical Transmission, 2008, 32(1): 98-100. (in Chinese) DOI:10.3969/j.issn.1004-2539.2008.01.031 |
| [4] |
祝明路, 陈兵奎. 基于空间螺旋理论的行星滚柱丝杠副自由度计算与分析[J]. 重庆大学学报, 2018, 41(7): 1-7. ZHU Minglu, CHEN Bingkui. Calculation and analysis of planetary roller screw deputy freedom based on spatial screw theory[J]. Journal of Chongqing University, 2018, 41(7): 1-7. (in Chinese) |
| [5] |
Jones M H, Velinsky S A, Lasky T A. Dynamics of the planetary roller screw mechanism[J]. Journal of Mechanisms and Robotics, 2016, 8(1): 014503. DOI:10.1115/1.4030082 |
| [6] |
徐强, 王水铭, 赵国平, 等. 差动式行星滚柱丝杠预紧转矩分析与求解[J]. 机械设计与制造, 2015(3): 1-4, 9. XU Qiang, WANG Shuiming, ZHAO Guoping, et al. The analysis and calculation of pre-loading torque of differential planetary roller screw[J]. Machinery Design & Manufacture, 2015(3): 1-4, 9. (in Chinese) |
| [7] |
Velinsky S A, Chu B, Lasky T A. Kinematics and efficiency analysis of the planetary roller screw mechanism[J]. Journal of Mechanical Design, 2009, 131(1): 011016. DOI:10.1115/1.3042158 |
| [8] |
徐强, 王水铭, 赵国平, 等. PWG型差动丝杠的啮合干涉分析与消除[J]. 组合机床与自动化加工技术, 2015(9): 107-109, 113. XU Qiang, WANG Shuiming, ZHAO Guoping, et al. The analysis of meshing interference and elimination of PWG planetary roller screw[J]. Modular Machine Tool&Automatic Manufacturing Technique, 2015(9): 107-109, 113. (in Chinese) |
| [9] |
Fu X J, Liu G, Ma S J, et al. A comprehensive contact analysis of planetary roller screw mechanism[J]. Journal of Mechanical Design, 2017, 139(1): 012302. DOI:10.1115/1.4034580 |
| [10] |
Aurégan G, Fridrici V, Kapsa P, et al. Experimental simulation of rolling-sliding contact for application to planetary roller screw mechanism[J]. Wear, 2015, 332. |
| [11] |
Jones M H, Velinsky S A. Stiffness of the roller screw mechanism by the direct method[J]. Mechanics Based Design of Structures and Machines, 2014, 42(1): 17-34. DOI:10.1080/15397734.2013.839385 |
| [12] |
杨家军, 韦振兴, 朱继生, 等. 行星滚柱丝杠副载荷分布及刚度计算[J]. 华中科技大学学报(自然科学版), 2011, 39(4): 1-4. YANG Jiajun, WEI Zhenxing, ZHU Jisheng, et al. Calculation of load distribution of planetary roller screws and static rigidity[J]. Journal of Huazhong University of Science and Technology (Nature Science), 2011, 39(4): 1-4. (in Chinese) |
| [13] |
Litvin F L. Gear geometry and applied theory[M]. New Jersey: PTR Prentice Hall, 1994: 267-271.
|
| [14] |
陈宝林. 最优化理论与算法[M]. 北京: 清华大学出版社, 2005. CHEN Baolin. Optimization theory and algorithm[M]. Beijing: Tsinghua University Press, 2005. (in Chinese) |
| [15] |
万长森. 滚动轴承的分析方法[M]. 北京: 机械工业出版社, 1987. WAN Changsen. Analysis method of rolling bearings[M]. Beijing: China Machine Press, 1987. (in Chinese) |
| [16] |
祝明路.行星滚柱丝杠副运动及承载特性研究[D].重庆: 重庆大学, 2018 ZHU Minglu. The motion and loading characteristics study of planetary roller screws[D]. Chongqing: Chongqing University, 2018. (in Chinese) |
| [17] |
Tselishchev A S, Zharov I S. Elastic elements in roller-screw mechanisms[J]. Russian Engineering Research, 2008, 28(11): 1040-1043. DOI:10.3103/S1068798X08110026 |
 2020, Vol. 43
2020, Vol. 43


