2. 国网宁夏电力有限公司检修公司, 银川 750011;
3. 华通科技有限公司, 重庆 400112;
4. 重庆大学 机械传动国家重点实验室, 重庆 400044
2. Overhaul Company, State Grid Ningxia Electric Power Co., Ltd., Yinchuan 750011, P. R. China;
3. Huatong Technology Co., Ltd., Chongqing 400112, P. R. China;
4. State Key Laboratory of Mechanical Transmissions, Chongqing University, Chongqing 400044, P. R. China
滚动轴承广泛应用于国民经济和国防事业的各个领域,不管在大型机械设备上(如航空转子系统、舰船传动系统等),还是在小型自动控制机构上(如驱鸟自动装置、电站巡检机器人等)都是十分重要的机械基础件。特别是对于长期在恶劣工况环境下运行的机械或机器人系统,其轴承部件受风沙、雨雪、酷暑和严寒等自然条件及自身运行震动、遇障冲击、爬行、横移等外界因素影响很大,容易出现故障状态,其故障状态的自动识别对于保证其正常运行,延长其使用寿命起着至关重要的作用。
由于机器人或机械系统在服役过程中的工况复杂多变,其轴承的振动信号是典型的非线性和非平稳信号,通常包含多个低频谐波、高频冲击、干扰噪声等多个信号分量,使得故障特征信息难以被有效提取出来[1-2]。如何有效地从多分量振动信号中提取敏感特征分量进行智能状态识别对提高轴承服役状态的可靠性,保证机器人或机械机构的正常运行具有重要意义。轴承的故障类型较多,具有不确定性,常采用多域多指标进行故障状态的表征。对用高维度输入的人工智能状态识别方法(BP网络[3]、支持向量基[4]、卷积神经网络[5]等),往往面临着网络参数的选择困难,网络结构优化难、运算速度慢、易陷入局部最优等问题。特征聚类法是一种基于统计学的模式识别方法,无须进行参数的设置与结构设计,具有对样本要求低,时效性强的优点。
目前,广泛用于轴承故障状态识别的特征聚类方法有层次聚类、密度聚类、网格聚类、模型聚类及最近邻分类器(K-nearestneighborsclassifier,KNNC)等。层次聚类算法可伸缩性差,输出结果为聚类树,无聚类中心概念,因此不适用于样本精简[6]。密度聚类算法容易造成密度较小的聚类被划分为多个类或密度较大且离得较近的聚类被合并成一个类[7]。而网格聚类算法只能用于边界是水平或垂直的聚类,不能检测斜边界,且不适用于高维数据[8]。模型聚类算法需要找到与给定数据相适应的数学模型。划分聚类算法通常需要事先确定聚类数目和初始化聚类中心。KNNC聚类方法能直接利用训练样本的局部信息与类标签信息对测试样本分类决策,训练过程简单,分类特性好,在轴承的故障模式识别得到了广泛的应用[9-10]。要说明的是,传统的K均值聚类需要输入聚类数K,且随机选择K个初始聚类中心易导致初始聚类中心过于邻近而大大增加迭代过程复杂度,影响输出结果质量。因此,笔者采用改进的二分K均值聚类算法对轴承故障敏感分量的特征训练样本进行精简,从而克服了处理大容量训练样本时间长的缺点,降低了不良样本与干扰点的影响。
1 故障敏感分量提取局部均值分解(local mean decomposition, LMD)旨在将原始信号分解为若干个乘积函数(product function,PF)的线性组合,各PF分量表示了轴承振动信号中自高频到低频的频率成分,然而仅部分PF分量与轴承故障密切相关,因此需要对敏感PF分量进行筛选。设正常状态下振动信号为xnorm(t),被分析状态下振动信号为x(t),笔者基于两类相关系数对x(t)的敏感PF分量进行选取,即x(t)与其各PF分量的相关系数和xnorm(t)与x(t)各PF分量的相关系数,具体选取步骤如下:
1) 计算信号x(t)与其PF分量Pi(i=1, 2, …, L)间的相关系数αi。
2) 计算信号xnorm(t)与x(t)各PF分量Pi间的相关系数βi。
3) 定义并计算x(t)的第i个PF分量Pi的敏感系数
| $ {\gamma _i} = {\alpha _i} - {\beta _i}。$ | (1) |
4)依据敏感系数大小对信号x(t)各PF分量进行重排,得到新PF序列
5) 计算新序列
| $ {d_i} = {\gamma '_1} - {\gamma '_i}。$ | (2) |
6) 找到di最大值所对应序号λ,则序列{Pi′}中前λ个PF分量为敏感PF分量。
x(t)与其分量Pi间的αi反映了Pi相对于x(t)的重要程度。βi可反映分量Pi是否与xnorm(t)中某频率成分相对应,显然,当Pi为由故障引起的频率成分时,由于xnorm(t)不含有与Pi相对应的频率成分,βi接近于零;当Pi为正常信号频率时,由于该频率成分存在于不同状态振动信号中,故βi取值较大。敏感系数γi综合考虑αi和βi的影响,当且仅当Pi为x(t)的主要频率成分且xnorm(t)不含有与Pi相对应的频率成分时,γi取值较大。因此,敏感系数γi可作为信号x(t)中敏感PF分量选取的依据。按照上述方法选取敏感PF分量后,对所选敏感PF分量进行叠加重构,并提取重构信号的均值、最大值、最小值、歪度、峭度、方差、方根幅值、绝对平均幅值、均方根值、峰峰值、波形指标、脉冲指标、峭度指标、峰值指标、裕度指标和偏斜度指标共计16个指标组成特征向量。
2 改进的KNNC算法KNNC以各样本的质心为代表不断迭代,从训练样本集中搜索与待分类数据点d最近的K个邻域样本,并以这K个样本的类标签来决策d的类别[11]。为了弥补KNNC算法训练时间较长,易受不良样本影响的缺点,提高故障特征的聚类辨识率,笔者对随机选择初始聚类中心和收敛条件进行改进,提出一种基于二分K均值聚类的改进算法,具体步骤如下:
1) 找到样本数据集相距最远的2个点。传统的算法要从数据集中选出相距最远的数据对需要比较两两之间的距离,其时间复杂度是O(n2),计算量很大,为了降低复杂度,采用如下算法计算。首先从数据集X={x1, x2, …, xn}中随机选取数据点xi,按式(3)计算xi与所有点之间的距离d(xi, xj),其中j=(1, 2, …, n),并找到距xi最远的点xj,然后计算xj与所有点之间的距离d(xj, xk),其中k=(1, 2, …, n),找出距xj最远的点xk,则xj, xk为整个数据集相距最远的2个点。
| $ d({x_i}, {x_j}) = \sqrt {\sum\limits_i^l {{{({x_i} - {x_j})}^2}} } ,$ | (3) |
式中l为向量空间维数。
2) 以相距最远的2个点为初始聚类中心,用传统的K均值聚类方法进行聚类,直到满足K均值聚类的收敛条件为止。以t表示循环次数,则样本数据集被聚类为t+1个簇。
3) 按照式(4)分别计算以上聚类簇的误差平方和Et1, Et2, …, Et(t+1),并把所有簇的误差平方和相加得到St (t+1)。
| $ E = \sum\limits_{j = 1}^N {\sum\limits_{x \in {C_j}} {{{\left\| {x - {m_j}} \right\|}^2}} } , $ | (4) |
式中:N为聚类数目;Cj (j=1, 2, …, N)为聚类第j个簇,x为簇Cj中任意数据样本;mj为簇Cj的均值。
4) 设ε=St(t+1)-S(t-1) t(初始化S01=0),若ε>Δ(Δ为收敛预设阈值),则以误差平方和最大的簇替换样本数据重复步骤1)~3),否则,结束循环,输出聚类结果。
5) 找出离t+1个聚类中心最近的数据点组成精简的训练样本,再输入到KNNC算法进行训练。
上述改进的KNNC算法,以相距最远的2个点为初始聚类中心,执行了多次二分实验并选择具有最小的簇聚类误差平方和的试验结果,每步只有2个质心,不但精简了大容量的训练样本,还能有效去除不良样本和干扰点。
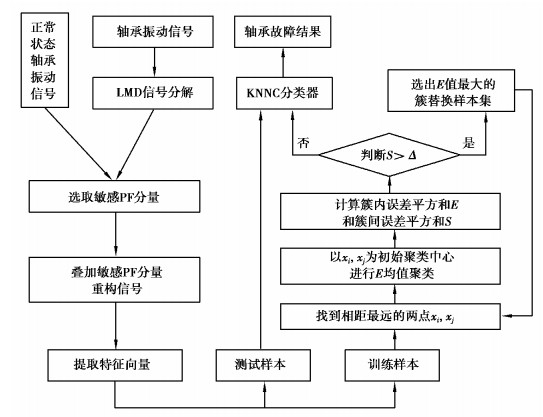
3 基于故障敏感分量和改进KNNC的轴承故障诊断方法笔者基于LMD算法分解轴承振动信号,参考轴承正常状态下的振动信号,选取故障敏感PF分量进行故障特征提取,然后利用改进的KNNC算法实现轴承故障识别,其故障诊断模型如图 1所示,具体步骤如下:
|
图 1 算法结构框图 Fig. 1 structure frame of algorithm |
1) 对采集的轴承振动信号分别进行LMD分解。
2) 依据第2节方法,选取与故障信号分量相关的敏感PF分量,并叠加选取的所有敏感PF分量以重构信号。
3) 从重构信号中提取第2节所述信号的特征向量。
4) 以3)中所提取的特征向量分别作为训练样本和测试样本,然后利用改进的二分K均值聚类算法对训练样本进行精简。
5) 将精简后的训练样本和测试样本输入KNNC,KNNC根据训练样本的邻域信息和类标签信息对测试样本进行状态辨识。
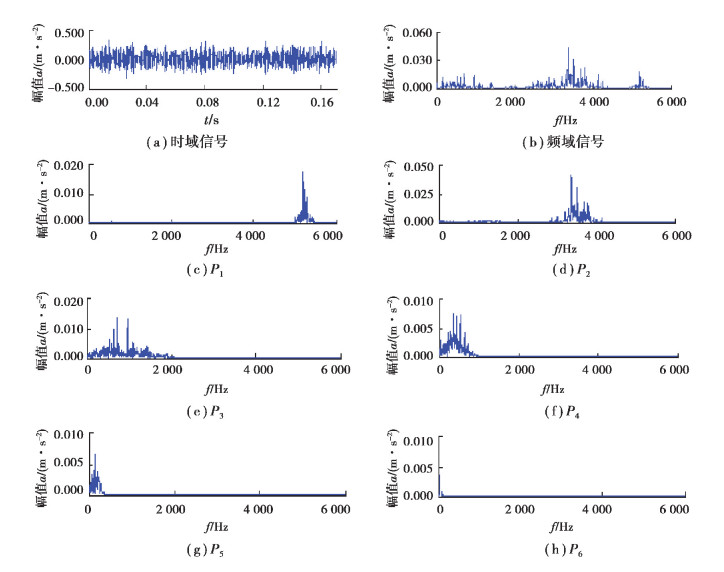
4 实验验证为了验证本文方法的有效性,采用文献[12]滚动轴承振动数据进行实例分析。实验中采用6205-2RS型深沟球轴承,通过人工引入不同类型及不同程度的轴承单点模拟故障。在电机转速1 772 r/min,负载0.736 kW的工况下,测取5种不同故障状态(内圈故障、0.18 mm外圈故障、0.36 mm外圈故障、0.53 mm外圈故障和滚动体故障,分别记为S1→S5)轴承振动信号,并测取正常轴承振动信号一组作为参考信号。取不同故障状态下振动信号各100组,随机抽取其中80组数据作为训练样本,剩余的20组数据作为测试样本,使用前2 048个数据采样点进行分析。为强化振动信号中故障特征分量,对各信号进行LMD分解,并对敏感PF分量进行选取以重构原信号。图 2(a)和(b)分别为0.36 mm外圈故障振动信号及其频谱,图 2(c)~(h)给出了该信号LMD分解所得前6个PF分量(P1,P2,P3,P4,P5,P6)的频谱。从图 2中分量频谱与原信号频谱的对比可知,LMD可有效分离原信号中的各主要频率成分。依据式(1)计算出图 2中各PF分量(P1→P6)的敏感系数γ分别为0.740,0.830,0.230,0.170,0.040,-0.007。
|
图 2 0.36 mm外圈故障信号及其PF分量频谱 Fig. 2 0.36 mm outer ring fault vibration signal and its PF components |
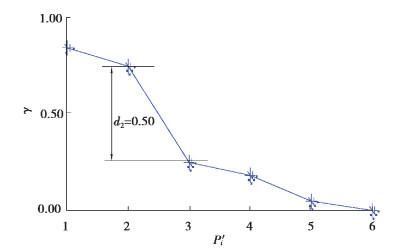
图 3给出0.36mm内圈故障信号重排PF序列{Pi′}的敏感系数,由于P2′与P3′间敏感系数具有最大差值,故敏感系数最大的前2个PF分量(即图 2中所示P2, P1)为敏感PF分量,分别与外圈故障信号中2个故障冲击高频成分相对应。因此,基于LMD敏感PF分量的选取方法能有效分离轴承故障相关频率成分,强化信号故障特征信息。对训练样本和测试样本各信号分别进行敏感PF分量的选取,并以此重构信号和从重构信号中提取特征向量用于后续故障状态识别。
|
图 3 按照敏感系数重排PF顺序 Fig. 3 Reorder PF by sensitive coefficient |
为了验证本文方法的有效性,实验对比了4种不同故障诊断方法,分别记为“PF选取特征提取优化KNNC”,“特征提取优化KNNC”,“小波分解特征提取优化KNNC”和“PF选取特征提取KNNC”,对应的编号分别为“A”“B”“C”“D”。方法“A”为笔者所提基于敏感PF分量特征提取并通过改进的KNNC算法进行模式识别;方法“B”为从原始振动信号中直接提取第2节所述时域统计特征;方法“C”为采用db4小波对原信号进行3层小波分解,从小波分量中提取上述方法相同的特征作为输入;方法“D”为将笔者提出的敏感分量特征输入到传统的KNNC中得的分类结果。
由表 1的比较结果可以看出,基于4种故障诊断方法均能较为准确地识别出滚动轴承状态。对比方法“A”与“B”的结果易知,基于PF分量的特征提取降低了不同状态信号中干扰分量对特征提取的影响,提升了特征向量的状态识别能力。
| 表 1 不同诊断模型分类性能对比 Table 1 Comparison of different diagnosis model's performance |
在实际的工程应用中,外界复杂环境带来的干扰噪声增加了轴承故障特征提取的难度。为检测笔者提出方法在噪声干扰下的故障辨识能力,在测试样本中人为加入随机噪声干扰,从而测试样本更改为
| $ x' \left( t \right) = [1 + \alpha \cdot {\rm{rand}}\left( 1 \right)]'x{\rm{ }}\left( t \right), $ | (5) |
式中:x(t)为原始测试数据;rand(1)为(-1, 1)间的随机数;α为干扰系数。对干扰系数α=0.1,α=0.3和α=0.5时的测试样本进行分类辨识,其统计识别结果如表 2所示(为降低随机性的影响,α=0.1,α=0.3和α=0.5分别运行10次并以其平均值作为识别结果)。显然,相比于“特征提取-优化KNNC”故障诊断模型,“PF选取-特征提取-优化KNNC”及“小波分解-特征提取-优化KNNC”具有更强的识别能力,取得更高的故障诊断精度且基于PF选取的性能略优于小波分解;“PF选取-特征提取-优化KNNC”与“PF选取-特征提取-KNNC”相比较,可看出优化的KNNC算法能明显提高正确识别率。
| 表 2 不同诊断模型抗干扰性能对比 Table 2 Comparison of different diagnosis model's interference-free performance |
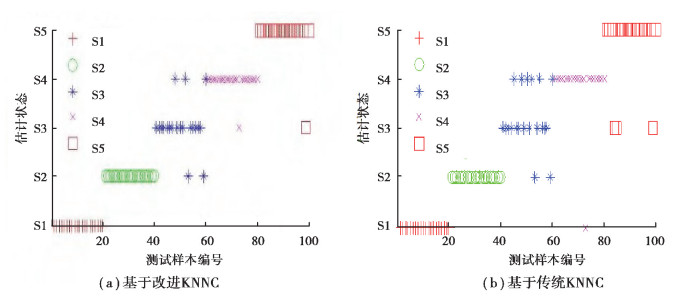
图 4(a)与图(b)分别为方法“A”和“D”在α=0.5时某单次运行中对测试样本的识别结果。两者相比可以看出基于改进的KNNC算法的正确识别率由88%提高到93%,抗干扰性能明显提高。根据图 4(b)可以看出整体误判率仍有7%,主要集中在S2,S3及S4的误判上,他们均属轴承外圈故障,而在内圈故障、外圈故障和滚动体故障的分类上误判率仅有1%。图 4(a)中,整体误判率降低到4%,优化后的KNNC算法在轴承故障是否同类的识别率也有明显提高。对比图 4(a)与4(b)还可以看出,0.36 mm外圈故障的识别率由传统的60%提高到改进后的75%,优化的KNNC算法对外圈故障不同程度损伤的识别率有显著提高。因此,基于故障敏感分量选取特征值能有效地强化故障特征,优化的KNNC能减小干扰信号的影响,提高正确识别率,结果表明两者的有效结合在强噪声干扰下无论是对不同类型的故障还是对同类型故障不同程度的损伤均具有较高的识别能力。
|
图 4 故障识别结果 Fig. 4 Results of faultidentification |
1) 笔者提出基于敏感PF分量选取的特征提取方法用于轴承故障诊断,该方法降低了轴承正常信号频率成分的干扰,强化了故障特征信息。
2) 提出了基于改进的二分KNNC方法,增强了其对不良样本的抗干扰性和降低了对K值的依赖性。
3) 将基于PF分量和改进的二分KNNC算法应用到轴承多类故障状态识别中,结果表明该方法能够有效辨识不同类型和同类型不同程度损伤的轴承故障,且具有较高诊断精度,该方法不仅能对轴承故障进行准确有效地识别,同样适用于机械或机器人系统的其他关键部件的故障检测。鉴于较好的识别精度及抗噪性能,该方法特别适用于野外运行的驱鸟、巡检机器人系统中的旋转类关键部件的故障检测。该方法的应用将有利于提高智能巡检机器人和驱鸟机器人的工作寿命和巡检性能其在机械设备或机器人系统故障检测和状态识别中具有广泛的应用前景。
| [1] |
Zeng M, Chen Z. SOSO boosting of the K-SVD denoising algorithm for enhancing fault-induced impulse responses of rolling element bearings[J]. IEEE Transactions on Industrial Electronics, 2020, 67(2): 1282-1292. |
| [2] |
Yang B Y, Liu R N, Chen X F. Sparse time-frequency representation for incipient fault diagnosis of wind turbine drive train[J]. IEEE Transactions on Instrumentation and Measurement, 2018, 67(11): 2616-2627. |
| [3] |
徐星, 李垣志, 田坤云, 等. ACPSO-BP神经网络在矿井突水水源判别中的应用[J]. 重庆大学学报, 2018, 41(6): 91-101. XU Xing, LI Yuanzhi, TIAN Kunyun, et al. Application of ACPSO-BP neural network in discriminating mine water inrush source[J]. Journal of Chongqing University, 2018, 41(6): 91-101. (in Chinese) |
| [4] |
李嫄源, 袁梅, 王瑶, 等. SVM与PSO相结合的电机轴承故障诊断[J]. 重庆大学学报, 2018, 41(1): 99-107. LI Yuanyuan, YUAN Mei, WANG Yao, et al. Fault diagnosis of motor bearings based on SVM and PSO[J]. Journal of Chongqing University, 2018, 41(1): 99-107. (in Chinese) |
| [5] |
冯新扬, 张巧荣, 李庆勇. 基于改进型深度网络数据融合的滚动轴承故障识别[J]. 重庆大学学报, 2019, 42(2): 52-62. FENG Xinyang, ZHANG Qiaorong, LI Qingyong. Fault recognition of rolling bearing based on improved deep networks with data fusion in unbalanced data sets[J]. Journal of Chongqing University, 2019, 42(2): 52-62. (in Chinese) |
| [6] |
Martín-Fernández J D, Luna-Romera J M, Pontes B, et al. Indexes to find the optimal number of clusters in a hierarchical clustering[M]. Cham: Springer International Publishing, 2019: 3-13.
|
| [7] |
Rojas-Thomas J C, Santos M, Mora M. New internal index for clustering validation based on graphs[J]. Expert Systems With Applications, 2017, 86: 334-349. |
| [8] |
Yunbin H E, Yupeng X, Jing W, et al. Improved K-means algorithm based on expectation of density and clustering validity index[J]. Computer Engineering & Applications, 2013, 49(24): 105-111. |
| [9] |
KouhiEsfahani R, Shahbazi F, Akbarzadeh M. Three-phase classification of an uninterrupted traffic flow:a k-means clustering study[J]. Transportmetrica B:Transport Dynamics, 2019, 7(1): 546-558. |
| [10] |
Li F, Wang J X, Chyu M K, et al. Weak fault diagnosis of rotating machinery based on feature reduction with Supervised Orthogonal Local Fisher Discriminant Analysis[J]. Neurocomputing, 2015, 168: 505-519. |
| [11] |
Lu J Y, Zhu Q S, Wu Q W. A novel data clustering algorithm using heuristic rules based onk-nearest neighbors chain[J]. Engineering Applications of Artificial Intelligence, 2018, 72: 213-227. |
| [12] |
Bearing test data from Case Western Reserve University (CWRU)[EB/OL](2001-01-05)[2019-07-17].http://csegroups.case.edu/bearingdatacenter/pages/download-data-file.
|
 2020, Vol. 43
2020, Vol. 43


