1b. 重庆理工大学 车辆工程学院, 重庆 400054;
2. 重庆大学 机械传动国家重点实验室, 重庆 400044
1b. School of Vehicle Engineering, Chongqing University of Technology, Chongqing 400054, P. R. China;
2. State Key Laboratory of Mechanical Transmission, Chongqing University, Chongqing 400044, P. R. China
不同于传统汽车,电动汽车在研发过程中会遇到很多问题,例如动力匹配问题、续航里程问题、安全性问题等,这些问题成为电动汽车的快速发展的瓶颈。为了有效地解决这些问题,研发人员分别运用计算机仿真、硬件在环测试、台架及实车测试等相关技术手段对零部件的性能和控制进行了深入研究。虽然计算机仿真具有快速、高效的特点,但相比于实车测试有一定的差别,而实车测试由于周期长、成本高、危险系数大等,通常只在后期进行整车性能测试。为了在仿真和实车测试之间找到平衡,有关学者将台架测试和硬件在环测试两者相结合,在研发快速和高效的同时又能保证测试的全面性和可靠性,目前正迅速成为汽车厂商们主要的研发手段。
在国外,很多企业对试验台架测控系统进行了深入研究。例如奥地利AVL公司,在台架测控方面已经开发出了先进的动态测试试验台,即虚拟现实模拟动态测试系统,但价格昂贵,控制复杂;HORIBA公司也研发出能够满足整车以及零部件所有稳态和动态测试的台架测控系统[1-3]。
与国外相比,国内对台架测控系统的技术研究起步晚,还存在较大的差距。高校及研究机构方面如北京交通大学、武汉理工大学以及苏州凌创电子等对台架测控系统的研究主要集中在测功机的控制算法上,而对台架系统实际评估研究较少;企业方面如南峰机电和湘仪动力测试仪器等虽具有对测功机系统集成能力,但大多只针对传统汽车而且被测对象比较单一;清华大学在汽车台架测试方面研究较多,能够对电动汽车系统设计测试方案和搭建台架测试系统,基本具备台架系统的评估能力[4-5]。
目前,电动汽车结构呈现多样化,开发周期需求越来越短,为了提升台架测试效率和产品研发周期,在测试过程中最大限度地模拟实车运行状况,以达到在实验室环境下对汽车动力总成各零部件性能进行整车级的集成测试。笔者提出了整车仿真与试验台架相结合的设计方法,首先搭建了基于台架的车辆系统动力学仿真模型,然后引入虚拟现实驾驶模拟系统并于台架动态加载控制系统集成,最后进行了EM-CVT(electric mechanical continuously variable transmission)台架测试试验,验证了所设计的基于虚拟交通场景的台架测控系统的可行性。
1 基于台架的车辆系统动力学研究为了使台架测试能够达到实车测试的效果,在试验时,根据实际台架测试的需求,对不同的被测对象调用对应匹配的仿真模型,构建出整车测试的环境。首先利用MATLAB/Simulink平台搭建了车辆部件模型库,然后通过前向和后向仿真对比分析,确定与实车动力传动路线一致的前向仿真作为本文台架模型的仿真方法,这种仿真方法不仅在仿真过程中能反映出车辆动态的变化,同时也避免了需求转矩计算超出车辆本身要求所导致的仿真错误[6-9]。
笔者以EM-CVT测试为例,引入一款搭载EM-CVT传动系统的电动汽车。在所搭建的模型库中分别调用如图 1所示的车辆模块,并根据表 1进行整车相关参数设置。其中,EM-CVT是一种新型的无级变速器,结构原理如图 2所示。动力传递同样采用金属带和带轮实现,但调速和夹紧方式不同,它采用由直流电机、齿轮减速器以及丝杆螺母机构组成的机械电子调速驱动机构推动主动带轮做轴向移动,从而改变金属带的有效工作半径,实现速比的调节。夹紧力则通过碟簧的弹性变形来实现。相比于传统CVT,该套系统完全摆脱了加压系统对油压的依赖,其结构和控制大大简化,更加适用于电动汽车的行驶工况,传动效率提高了10%。
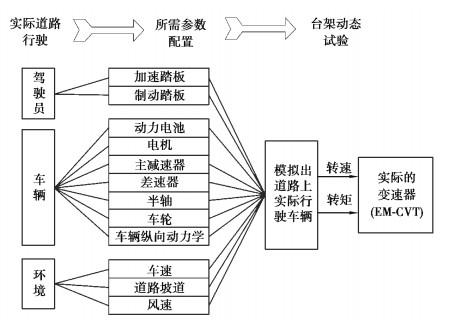
|
图 1 车辆仿真模型架构 Fig. 1 Vehicle simulation model architecture |
| 表 1 整车主要参数 Table 1 Vehicle main parameters |
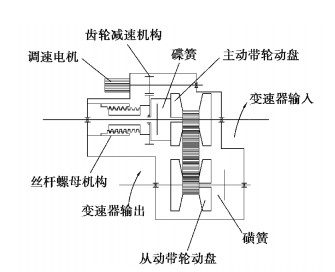
|
图 2 EM-CVT结构原理 Fig. 2 EM-CVT structure principle |
负载电机主要模拟汽车行驶中受到的各种阻力,故在动态加载时,除汽车行驶阻力外,还要对不同加载点进行分析,以模拟车辆在行驶过程中的惯量[10]。台架测试中需要模拟电动汽车的电机、变速器、主减速器、差速器、半轴、车轮等部件的旋转惯量以及整车平移质量。笔者对EM-CVT进行台架测试,负载电机加载点设定为主减速器输入轴处,因此采用飞轮转动惯量来模拟主减速器、差速器、半轴、驱动车轮、从动车轮等的转动惯量以及整车的平移质量,其数学计算表达式为:
| $ {J_{\rm{v}}} = \frac{{m{r^2} + {J_{\rm{w}}} + {J_{\rm{d}}}}}{{i_0^2}},$ | (1) |
式中:m为整车质量;r为车轮半径;Jw为驱动车轮和从动车轮转动惯量之和;Jd为主减速器、差速器和半轴的转动惯量之和;i0为主减速器速比。
2.2 台架动态工况加载原理汽车在行驶过程中,动力系统产生的驱动力除用于克服由滚动阻力、爬坡阻力、加速阻力、空气阻力组成的道路阻力外,有时还用于克服制动器产生的制动阻力,其三者关系如式(2)所示:
| $ {F_{\rm{p}}} = {F_{\rm{f}}} + {F_{\rm{w}}} + {F_{\rm{i}}} + {F_{\rm{j}}} + {F_{{\rm{brk}}}}, $ | (2) |
式中:Fp是动力系统产生的驱动力,在电动汽车中,由于存在制动能量回收,Fp经常会在正负之间切换,为正时表示驱动,为负时表示制动;Ff为滚动阻力;Fw为空气阻力;Fi为爬坡阻力;Fj为加速阻力;Fbrk为机械制动阻力。
在台架测试系统中,驱动力对应的是驱动电机输出的扭矩,各项阻力之和对应的是负载电机输出的扭矩。其中,驱动力加载点为驱动电机和被测对象的结合点,负载力加载点为负载电机和被测对象的结合点。试验时可根据被测对象的不同,选择不同的加载点。
2.3 基于转速的前向模型跟踪方法随着计算机控制工程的不断发展,目前,基于转速闭环的前向模型跟踪方法被广泛用于负载电机的控制,这种方法可以有效地避免系统在跟踪模型微分计算时导致的不稳定性[11-13]。通过测量驱动电机的输出扭矩作为车辆模型的驱动输入,计算得到车辆模型所能达到的响应速度,利用该速度计算出对应的转速值,将该转速值作为负载电机加载点的目标转速,并计算出相应的目标转矩,将目标转矩输送给负载电机控制器,使得负载电机跟随模型速度响应,从而实现模拟车辆负载的目的。图 3为基于转速闭环的前向模型跟踪控制原理图,负载电机动态加载控制器的设计为虚线部分。
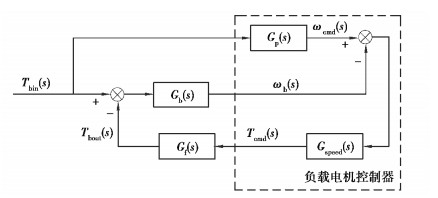
|
图 3 基于转速的前向模型跟踪控制 Fig. 3 Speed-based forward model tracking control |
图 3中:Tbin为被测对象输入端扭矩,Tbout为被测对象输出端扭矩;Gv(s)为整车传递函数;Gb(s)为台架传递函数;ωcmd为目标转速;ωb为被测对象输出转速;Gspeed(s)为速度跟踪控制函数;Tcmd为负载电机目标输入扭矩;Gf(s)为负载电机传递函数,并简化为1。
在实际控制过程中,由于外界干扰、数据传输延迟以及参数设定不准确等因素,负载电机动态加载响应会产生一定的偏差,负载电机真正实现道路负载的动态加载,可由以下2个条件进行判定:
1) 在输入扭矩相同时,被测对象在台架测试中输出端转速应和实车中转速相等。
2) 在车速和加速度相同时,台架中驱动电机输出端扭矩应和实车中扭矩相等。假设模型足够精确,则应满足公式(3)(4)。
| $ \left( {\begin{array}{*{20}{l}} {{\omega _{{\rm{re}}{{\rm{l}}_ - }{\rm{wh}}}} = {\omega _{\rm{b}}}}\\ {{\omega _{{\rm{cmd}}}} = {\omega _{{\rm{re}}{{\rm{l}}_ - }{\rm{wh}}}}} \end{array} \Rightarrow {\omega _{\rm{b}}} = {\omega _{{\rm{cmd}}}}} \right.。$ | (3) |
| $ {T_{{\rm{bin }}}} = {T_{{\rm{b\_rel}}\_{\rm{wh}}}}。$ | (4) |
对图 3进行归纳整理,为简化模型,将外部输入作为实际被测对象的一个干扰即Tbin,且负载电机传递函数为1,得到式(5)。
| $ {G_{{\rm{simple }}}}(s) = \frac{{{\omega _{\rm{b}}}}}{{{\omega _{{\rm{cmd }}}}}} = \frac{{{G_{{\rm{speed }}}}(s){G_{\rm{b}}}(s)}}{{1 + {G_{{\rm{speed }}}}(s){G_{\rm{b}}}(s)}} = \frac{{{K_{\rm{p}}}s + {K_{\rm{i}}}}}{{\sum J {s^2} + \left( {\sum D + {K_{\rm{p}}}} \right)s + {K_{\rm{i}}}}}, $ | (5) |
式中:Gspeed(s)=Kp+Ki*(1/s)为速度跟踪控制函数;Kp为比例系数;Ki为积分系数;Gb(s)=1/(∑Js+∑D)为台架传递函数;∑J为台架各旋转部件转动惯量之和;∑D为台架各旋转部件阻尼系数之和。
稳态加载时,被测对象输入扭矩Tbin不变,相应变化频率为0,Gsimple(s)为1,此时被测对象实际和目标转速保持一致,从而实现稳态加载;动态加载时,由于被测对象输入转矩Tbin变化大,响应的频率也就越大,对应的|Gsimple(s)-1|绝对值也会越大,此刻负载电机模拟和实际负载偏差也会越大[9]。为消除动态加载带来的偏差,在整车传递函数Gv(s)后面加入相应的补偿函数Gbc(s),如公式(6)所示,使得Gsimple(s)*Gbc=1。
| $ {G_{{\rm{bc}}}}(s) = \frac{{{\omega _{{\rm{cmd}}}}}}{{{\omega _{\rm{b}}}}} = \frac{{\sum J {s^2} + \left( {\sum D + {K_{\rm{p}}}} \right)s + {K_{\rm{i}}}}}{{{K_{\rm{p}}}s + {K_{\rm{i}}}}}。$ | (6) |
由Gbc(s)表达式可知,补偿函数分子阶数为2,大于分母阶数,不符合系统因果关系,因此试验中可以增加时间常数很小的一阶惯性环节Ginertia(s)=1/(T1s+1),使模拟负载无限接近于负载,故新的补偿函数为
| $ {G_{{\rm{b}}{{\rm{c}}_ - }{\rm{new }}}}(s) = {G_{{\rm{bc}}}}(s)*{G_{{\rm{inertial }}}}(s)。$ | (7) |
从而得到
| $ \frac{{{\omega _{\rm{b}}}}}{{{\omega _{{\rm{cmd}}}}}} = {G_{{\rm{simple }}}}(s)*{G_{{\rm{bc\_new}}}}(s) = \frac{1}{{{T_1}s + 1}}。$ | (8) |
图 4为加入干扰补偿函数后的台架控制器框图,从图中看出,如果Gb_disturb(s)等于1,则干扰Tbin被完全消除。但事实上,由于数据采集系统的延迟作用,Gb_disturb(s)不可能等于1,除非Tbin保持不变,否则干扰无法消除。因此,要尽可能避免干扰,试验中可以设Gb_disturb(s)=1/(T2s+1),时间常数T2由台架硬件设备数据采集频率所决定。
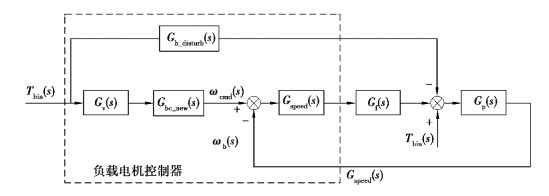
|
图 4 干扰补偿后的前向模型跟踪控制 Fig. 4 Forward model tracking control after interference compensation |
虚拟交通场景是对现实交通的模拟,主要由车辆行驶道路、车辆行驶环境和驾驶车辆3个部分组成,其中车辆行驶环境的定义尤其重要,因为它们的状态时刻影响着驾驶员的行为操作。
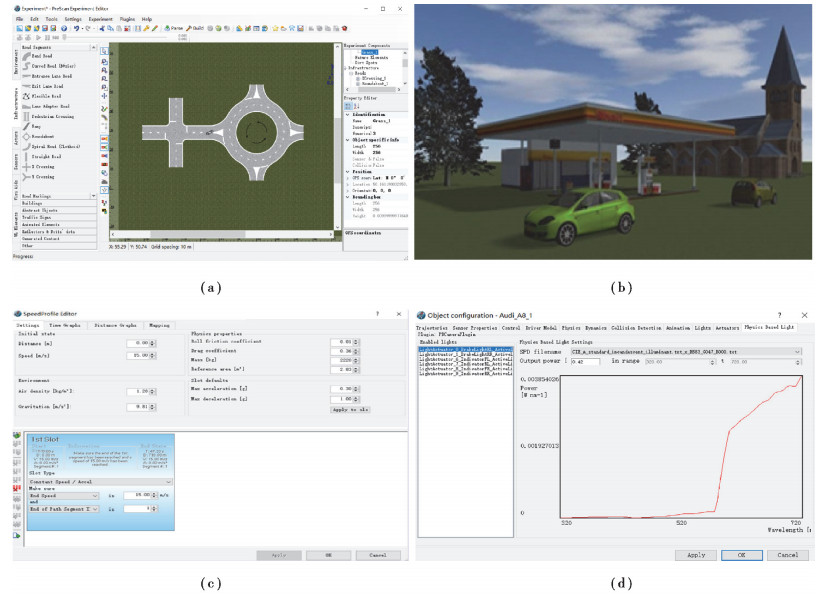
为了使被测对象台架测试更接近实际装车测试,搭建了虚拟交通场景并与台架测试相关联,使测试人员在室内通过交通场景操纵真实的驾驶舱,实现负载电机的动态加载,使台架测试更能体现出实车测试效果,以此来加快被测对象开发速度,降低开发成本。笔者利用Prescan软件分别进行了虚拟道路建模、虚拟环境建模、周围车辆行驶状态建模以及目标车辆的定位等工作,使其更真实地表现出实车测试的环境。图 5所示(a)(b)(c)(d)分别为虚拟交通场景建模等工作。
|
图 5 虚拟交通场景建模 Fig. 5 Virtual traffic scene modeling |
在完成虚拟道路、虚拟周围环境、虚拟周围车辆行驶状态以及目标车辆的定位开发后,编译生成相应的MATLAB/Simulink模型,在模型中添加接收驾驶舱加速/制动踏板和转向盘各信号需要的CAN模块包,建立相应的通讯,完成系统集成。
4 试验台架测控系统集成利用NI公司的LabView编程软件和VeriStand测试软件对台架测控系统进行开发。整个试验台架测控系统的开发主要包括Simulink模型的编译、VeriStand工程的建立、通讯系统的连接、驱动配置和程序下载等几个步骤[11-15]。
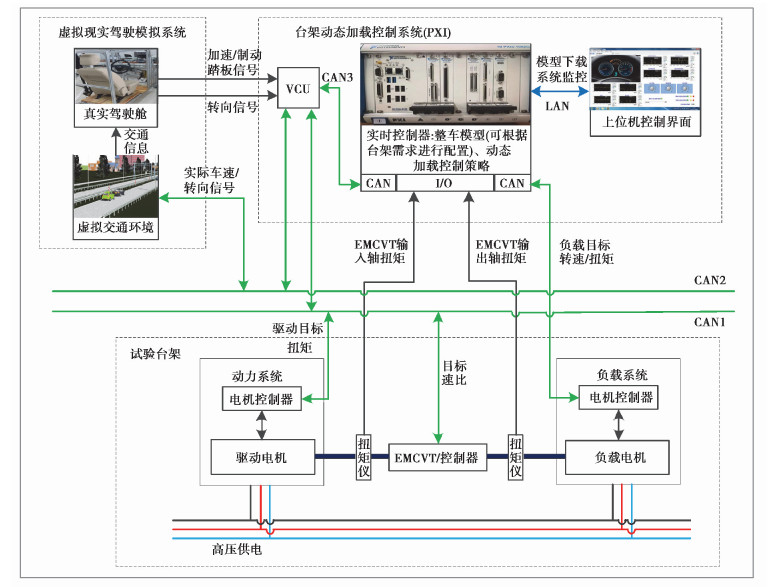
笔者基于NI PXI硬件在环实时仿真系统对整个台架测控进行集成,集成原理图如图 6所示,其中包含了虚拟驾驶仿真系统、台架动态加载控制系统、试验台架动力系统、被测对象、负载系统、高压供电系统以及数据采集系统。
|
图 6 台架测控系统集成原理图 Fig. 6 Bench measurement and control system integration schematic |
该试验台架动力系统由驱动电机和被测对象EM-CVT组成,负载系统连接EM-CVT输出轴,高压供电系统采用双向电源,在制动能量回收时,可以把能量回馈给电网。
动态加载控制系统由两部分组成,一部分是动力系统控制,控制核心是VCU,VCU通过CAN1和CAN2控制驱动电机与EM-CVT协调工作、接收和发送车速信号以及加速/制动踏板和转向信号;另一部分是负载系统控制,控制核心是台架动态加载控制器,台架动态加载控制器包括两路高速CAN口,一路LAN口、多路频率采集以及多路模拟/数字量I/O口,控制器通过一路CAN控制负载电机工作,另一路CAN与VCU的CAN3进行通讯,扭矩仪接入I/O口以读取EM-CVT输出轴端的扭矩值,LAN口与上位机相连,用于模型下载及系统实时监控。
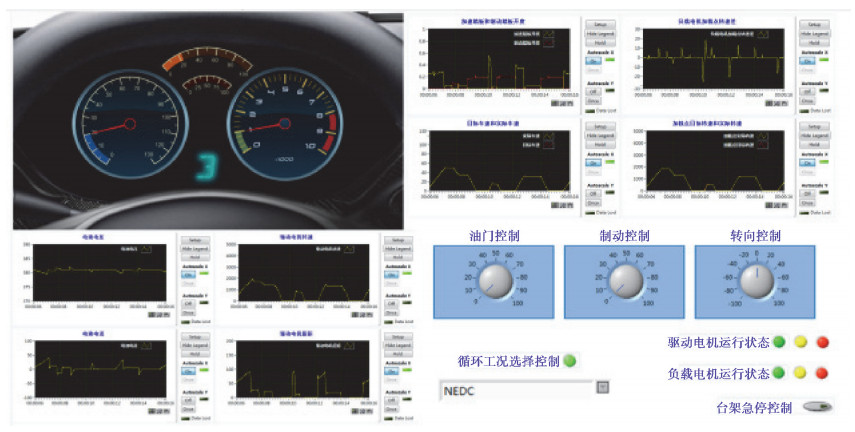
台架动态加载控制系统和虚拟现实驾驶模拟系统位于控制室,驾驶员从虚拟交通场景中获取当前交通信息,并操作驾驶舱中的加速/制动踏板和转向盘,产生的相应信号发送给整车控制器VCU,VCU根据制定的控制策略计算出驱动电机目标扭矩和EM-CVT目标速比,分别将控制指令发送给对应的控制器,控制其协调工作。变速器输出轴扭矩由扭矩仪测得并作为实时控制器中整车模型的输入,根据整车相关数据计算出相应转速作为试验台架负载电机的目标转速,目标转速和当前转速的差值做PI调节,再经过转速跟踪控制算法计算出相应的负载电机扭矩并输送到负载电机控制器中,控制负载电机运行。负载电机的转速可通过换算得出实际车速,实际车速传回VCU,VCU与Prescan中设定的目标车辆通过CAN进行信息交互,从而实现虚拟驾驶环境、驾驶舱、台架系统之间的动态联动变化。如图 7所示,为EM-CVT试验台架测试场景,如图 8所示,为台架测控界面。

|
图 7 EM-CVT台架测试场景 Fig. 7 EM-CVT bench test scenario |
|
图 8 台架测控界面 Fig. 8 Bench measurement and control interface |
为了验证台架测控系统的可行性,以EM-CVT为被测对象,对测控系统进行了驱动电机和负载电机转速及扭矩响应测试以及整车模型验证等测试,在该测试中,驾驶员通过虚拟交通场景获取实时交通信息,对驾驶舱进行相关操作,台架动态加载控制系统接收到相应的输入目标转速计算输出负载电机扭矩指令控制台架进行测试,上位机控制界面实时显示并记录相关数据,从而实现了整个台架测控系统的自动化测试。如图 9~11所示,为台架测控系统试验验证数据。
|
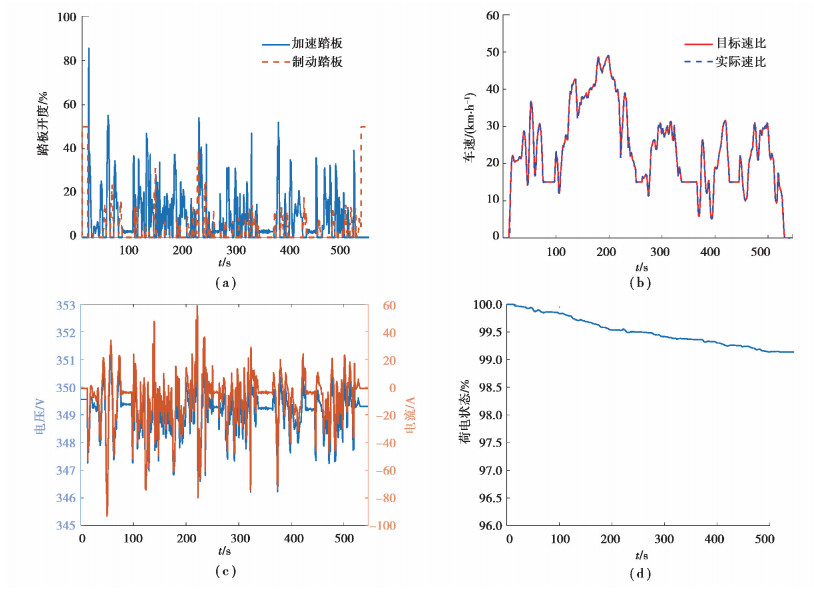
图 9 整车模型验证结果 Fig. 9 Vehicle model verification results |
|
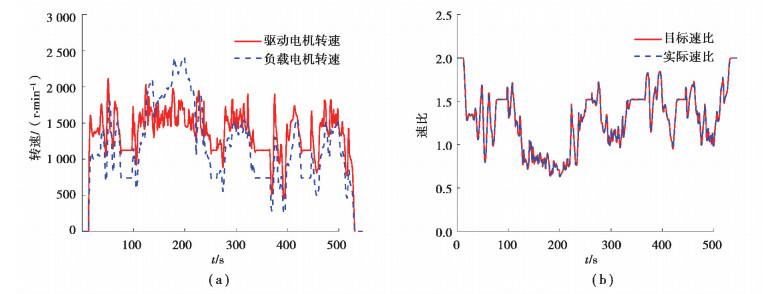
图 10 EM-CVT测试验证结果 Fig. 10 EM-CVT test verification results |
|
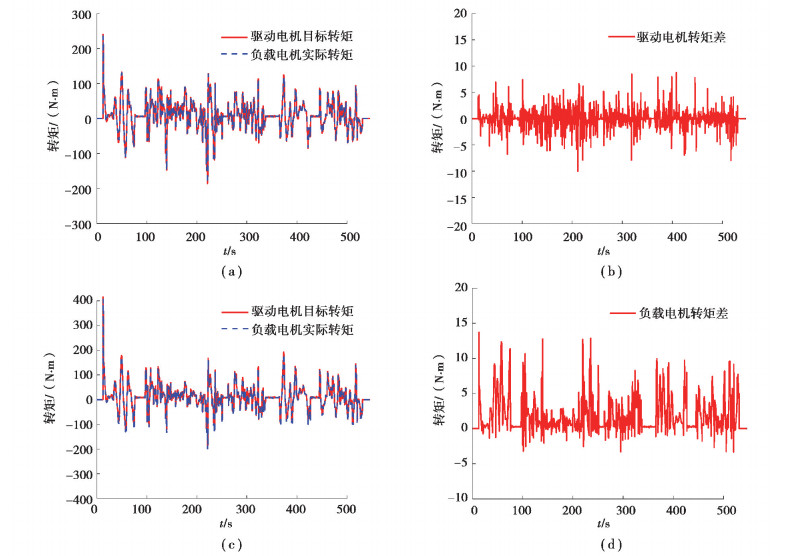
图 11 台架动力系统与负载系统验证结果 Fig. 11 Bench power system and load system verification results |
图 9为整车模型验证结果。从图中可以看出,目标车速和实际车速跟随性良好,两者车速差最大不超过1 km/h,且能够快速响应加速踏板和制动踏板的变化,电池电压、电流、荷电状态变化均符合加速、匀速及减速下的运行情况(电流负表示放电、正表示充电),加速模式和制动能量回收模式均符合整车控制要求,因此验证了本文所搭建的车辆模型的有效性。
图 10为EM-CVT测试验证结果。在台架测试时,驱动电机连接EM-CVT输入轴,驱动电机转速即为EM-CVT输入转速,负载电机连接EM-CVT输出轴,负载电机转速即为EM-CVT的输出转速,两者的比值即为EM-CVT的实际速比,从图(a)(b)中可以看出,目标速比和实际速比跟随性良好,驱动电机转速和负载电机转速符合EM-CVT的调速变化。
图 11为台架动力系统和负载系统验证结果。(a)图是驱动电机目标转矩和实际转矩曲线,驱动电机目标转矩是由整车控制策略理论计算得出的,是车辆在道路上行驶时电机输出的转矩,而输出的实际扭矩通过扭矩仪测得。从图中可以看出驱动电机目标转矩与实际转矩一致性好,偏差大小不超过10 N·m。(c)图是负载电机目标转矩和实际转矩曲线,负载电机目标转矩是理论计算的车辆在道路上行驶时所需要克服的阻力矩。从图中可以看出,负载电机目标转矩与实际转矩一致性好,偏差大小不超过15 N·m。因此,验证了负载电机动态加载控制策略的有效性。
6 结论1) 通过对目前电动汽车研发手段的对比和测试需求的分析,提出了整车仿真测试与试验台架相结合的设计方法,在该方法的指导下搭建了基于台架的车辆动力系统动力学模型,在转速控制负载模拟算法的基础上,设计出基于转速闭环的前向模型跟踪负载电机动态加载方法。
2) 运用Prescan软件建立虚拟交通场景,并和真实驾驶舱进行通讯,完成虚拟现实驾驶模拟系统集成,运用NI硬件在环仿真软件创建试验台架测控系统,最后将前两者与试验台架进行集成。
3) 通过EM-CVT台架试验,验证了所计的虚拟交通场景与试验台架融合的测控系统的可行性,为台架测控系统的优化和二次开发提供了基础。
| [1] |
Yang S B, Li Z Z, Xu F, et al. A electric vehicle powertrain simulation and test of driving cycle based on AC eletric dynamometer test bench[J]. Mems. Ervice Academy Conference Center(SACC-China): 上海禹捷文化传播有限公司, 2012: 4.
|
| [2] |
Kyslan K, Ďurovský F. Control of a test bench for dynamic emulation of mechanical loads[J]. Procedia Engineering, 2012, 48: 352-357. |
| [3] |
Gerard M. Tests and comparison of two electrical powertrain systems by vehicle simulation test bench and vehicle modeling[C]//2012 IEEE Vehicle Power and Propulsion Conference. Piscataway, NJ: IEEE, 2012: 826-829.
|
| [4] |
李文礼, 石晓辉, 施全, 等. 车辆动力总成试验台动态模拟控制方法[J]. 中国机械工程, 2015, 26(2): 278-283. LI Wenli, SHI Xiaohui, SHI Quan, et al. Research on dynamic load emulation for powertrain testbench[J]. China Mechanical Engineering, 2015, 26(2): 278-283. (in Chinese) DOI:10.3969/j.issn.1004-132X.2015.02.027 |
| [5] |
叶晓, 金振华, 高大威, 等. 测功机动态负载模拟算法[J]. 清华大学学报(自然科学版), 2013, 53(10): 1492-1497. YE Xiao, JIN Zhenhua, GAO Dawei, et al. Dynamometer controller algorithm for road load emulations[J]. Journal of Tsinghua University(Science and Technology), 2013, 53(10): 1492-1497. (in Chinese) |
| [6] |
黄妙华, 陈飚, 陈胜金. 电动汽车仿真结构比较[J]. 武汉理工大学学报, 2005, 27(3): 66-69. HUANG Miaohua, CHEN Biao, CHEN Shengjin. Comparison of simulation structures in electric vehicle[J]. Journal of Wuhan University of Technology, 2005, 27(3): 66-69. (in Chinese) DOI:10.3321/j.issn:1671-4431.2005.03.020 |
| [7] |
孙冬野, 陈元, 范曾雁. 搭载回流式动力传动系统的PHEV参数优化[J]. 重庆大学学报, 2019, 42(6): 1-12. SUN Dongye, CHEN Yuan, FAN Zengyan. Optimization of PHEV parameters with reflux power coupling transmission system[J]. Journal of Chongqing University, 2019, 42(6): 1-12. (in Chinese) |
| [8] |
秦大同, 王禺寒, 胡明辉. 考虑运行工况的纯电动汽车动力传动系统参数设计[J]. 重庆大学学报, 2014, 37(1): 7-14. QIN Datong, WANG Yuhan, HU Minghui. Powertrain parameter design for driving the electric vehicle considering cycle[J]. Journal of Chongqing University, 2014, 37(1): 7-14. (in Chinese) |
| [9] |
叶明, 程越, 丁锐. 搭载机电式CVT的纯电动系统动力性调速策略[J]. 机械传动, 2012, 36(6): 29-33. YE Ming, CHENG Yue, DING Rui. Power shifting strategy of electric system equipped with mechanic-electric continuously variable transmission[J]. Journal of Mechanical Transmission, 2012, 36(6): 29-33. (in Chinese) DOI:10.3969/j.issn.1004-2539.2012.06.008 |
| [10] |
李洪山, 孙英达, 庆振华. 电惯量模拟机械转动惯量方法的研究[J]. 制造业自动化, 2009, 31(6): 20-21, 28. LI Hongshan, SUN Yingda, QING Zhenhua. Research on method that electronic inertia simulates mechanic moment of inertia[J]. Manufacturing Automation, 2009, 31(6): 20-21, 28. (in Chinese) DOI:10.3969/j.issn.1009-0134.2009.06.006 |
| [11] |
Alcala I, Claudio A, Guerrero G. Test bench to emulate an electric vehicle through equivalent inertia and machine dc[C]//2008 11th IEEE International Power Electronics Congress. Piscataway, NJ: IEEE, 2008: 198-203.
|
| [12] |
刘力康, 闻居博, 董逾. 汽车传动系动态性能试验台驱动模拟方案的控制与仿真[J]. 传动技术, 2011, 25(3): 26-31, 10. LIU Likang, WEN Jubo, DONG Yu. The control and simulation of dynamic drive emulation on the automotive transmission dynamometer[J]. Drive System Technique, 2011, 25(3): 26-31, 10. (in Chinese) DOI:10.3969/j.issn.1006-8244.2011.03.004 |
| [13] |
莫志勇, 张为公, 吉同舟. 基于模型参考控制的汽车试验台动态加载[J]. 中国机械工程, 2010, 21(7): 877-881. MO Zhiyong, ZHANG Weigong, JI Tongzhou. Dynamic loading of automobile test bench based on model reference control[J]. China Mechanical Engineering, 2010, 21(7): 877-881. (in Chinese) |
| [14] |
Hendriks F, Tideman M, Pelders R, et al. Development tools for active safety systems: Prescan and VeHIL[C]//Proceedings of 2010 IEEE International Conference on Vehicular Electronics and Safety. Piscataway, NJ: IEEE, 2010: 54-58.
|
| [15] |
Feng H Z, You Y G, Huang Z Y, et al. Study and realization of test bench for electric vehicle drive system based on HIL[J]. Applied Mechanics and Materials, 2013, 401/402/403: 1255-1259. |
 2020, Vol. 43
2020, Vol. 43


