2. 中国直升机设计研究所, 江西 景德镇 333000;
3. 重庆大学 航空航天学院, 重庆 400044;
4. 中国空气动力研究与发展中心 旋翼空气动力学 重点实验室, 四川 绵阳 621000
2. China Helicopter Research and Development Institute, Jingdezhen, Jiangxi 333000, P. R. China;
3. College of Aerospace Engineering, Chongqing University, Chongqing 400044, P. R. China;
4. Rotor Aerodynamics Key Laboratory, China Aerodynamics Research and Development Center, Mianyang, Sichuan 621000, P. R. China
现代战争作战环境极为复杂,要求新一代武装直升机能够承担多种任务使命并且具备良好操纵品质。精确的姿态控制能力和优良的稳定性对于近地悬停、贴地飞行,特别是在低能见度环境或单驾驶员操纵时是非常必要的;空对空作战则要求更快的直升机响应。为满足这些要求,先进武装直升机必须具备多模式、高增益、高带宽等操纵品质特点。高带宽飞行控制设计技术不仅可用于我国新型武装直升机设计,还可用于升级大量已有直升机装备,具有重要意义。
自美国陆军启动先进数传/光传控制系统研究项目以来,显模型跟踪控制技术获得广泛关注[1-4]。Landis等[1]提出将显模型跟踪控制设计过程分为反馈控制设计和操纵响应设计两个独立部分,并采用包含旋翼动力学模型的高阶飞行动力学模型开展反馈控制设计研究,指出为提高直升机操纵带宽需要采用高增益控制设计,但过高的控制增益容易引起旋翼稳定性问题,成为限制直升机控制增益和操纵带宽的主要因素。Tischler[2]发现,高增益控制能够提升机体稳定性,但旋翼等高阶动力学系统的时间延迟是限制高带宽直升机飞行控制设计的主要因素。美国科曼奇和黑鹰等直升机的飞行试验和理论分析结果[5-7]表明,显模型跟踪控制系统能够显著提升直升机悬停、低速飞行状态以及在低能见度环境的操纵品质,但过大的控制增益容易导致旋翼/机身耦合振荡。研究人员[8, 9]提出在反馈控制中引入旋翼运动信息增强旋翼/机身耦合稳定性,从而可以增大控制增益,提升直升机操纵带宽。大量理论分析[10-13]和试验研究[14-15]也进一步证实在飞行控制设计中引入旋翼运动信息能够有效提升旋翼动稳定性,实现高带宽飞行控制设计。Guo等[16]在研究变转速旋翼的直升机操纵品质时发现,旋翼转速变化导致正常转速下稳定的旋翼/机身耦合模态逐渐发散,基于模型跟踪/动态逆控制系统,提出一种可以无缝整合到既有控制系统的旋翼反馈控制设计方法[17],解决旋翼转速变化导致的旋翼/机身耦合振荡问题。但由于模型跟踪/动态逆控制系统的限制,旋翼与机体的控制增益设计是相互独立的,没能实现两者参数的最优化设计,也没有提出相应的显模型优化方法以提升直升机操纵响应带宽。最近,吉洪蕾等[18-20]通过旋翼/机体控制增益的协同优化设计,将集成旋翼控制的飞行控制系统用于抑制大气紊流对直升机的干扰,降低驾驶员操纵负荷,取得良好效果。
为发展集成旋翼控制的直升机高带宽飞行控制设计方法,基于显模型跟踪控制技术,在反馈控制模块引入旋翼运动信息增强直升机动稳定性,采用旋翼/机体反馈控制和前馈增强控制协同提升直升机动稳定性和操纵频率。进一步提出基于有效跟踪的显模型设计方法,提升直升机小幅高频和中等幅度姿态控制的操纵品质。最后,基于高阶直升机飞行动力学模型开展直升机操纵品质研究,通过与显模型跟踪控制系统对比研究旋翼控制对直升机动稳定性、操纵响应带宽/相位延迟、姿态快捷性等操纵品质指标的提升作用。
1 直升机飞行动力学模型采用一种高阶直升机飞行动力学模型进行飞行控制设计和操纵品质分析,模型对象为黑鹰直升机,建模过程见文献[21-25]。飞行动力学模型具有33个运动状态量,包括机体运动的9个速度、角速度和欧拉角状态量,旋翼的8个挥舞角和角速度状态量,8个摆振角和角速度状态量,2个弹性扭转角和角速度状态量,旋翼动态入流的3个状态量、尾桨入流的1个状态量,以及机体对尾部的2个下洗和侧洗状态量,模型线性空间形式如下:
| $ \mathit{\boldsymbol{\dot x}} = \mathit{\boldsymbol{Ax}} + \mathit{\boldsymbol{Bu}}, $ | (1) |
式中:A为稳定导数矩阵,B为操纵导数矩阵,x=[E, F, G, H, I, J]T,其中E=[u, v, w, p, q, r, Φ, Θ, Ψ],为机体速度、角速度和欧拉角;F=[
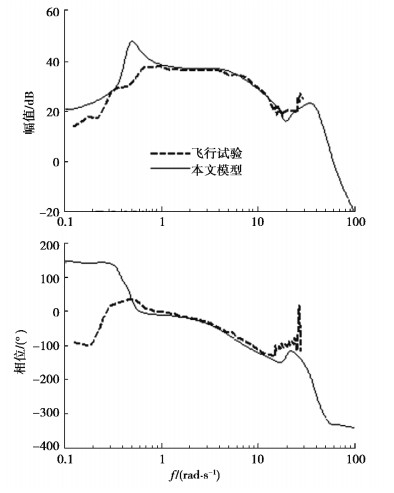
图 1所示为直升机悬停状态时横向操纵输入的滚转角速度频域响应验证结果,其中试验数据取自文献[26]。从图 1中可以看出,与试验数据相比,虽然模型预测结果在小于1 rad/s和大于10 rad/s的频段吻合较差,但在直升机飞行品质关注的主要频率范围内(1~10 rad/s)吻合良好,因此满足直升机飞行控制设计对模型精度的要求。直升机俯仰、偏航和垂向主轴响应的计算精度与之类似,这里不再赘述。
|
图 1 横向操纵输入的滚转角速度频域响应验证结果 Fig. 1 Comparison of helicopter roll rate frequency response to lateral input |
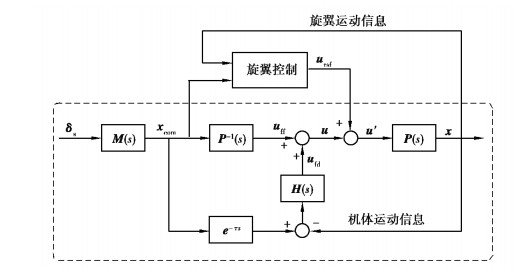
图 2虚线框中所示为显模型跟踪控制系统,从图 2中可以看出,整个系统由显模型M(s),前馈增强控制模块P-1(s)和反馈控制模块H(s)三个部分构成。其中,δs为座舱杆操纵输入,xcom为显模型输出,uff为前馈增强控制操纵,ufd为反馈控制操纵,u为总操纵量,P(s)代表直升机动力学特性,x为直升机运动状态量。
|
图 2 集成旋翼控制的显模型跟踪控制系统 Fig. 2 Integrated explicit model-following and rotor control system |
由图 2可知,如果将前馈增强控制取为直升机动力学特性P(s)的逆P-1(s),则直升机/飞行控制组合系统的传递函数为:
| $ \frac{{\mathit{\boldsymbol{x}}(s)}}{{{\mathit{\boldsymbol{\delta }}_{\rm{s}}}(s)}} = \mathit{\boldsymbol{M}}(s) \cdot [{\mathit{\boldsymbol{P}}^{ - 1}}(s) + \mathit{\boldsymbol{H}}(s)] \cdot \frac{{\mathit{\boldsymbol{P}}(s)}}{{1 + \mathit{\boldsymbol{P}}(s)\mathit{\boldsymbol{H}}(s)}} = \mathit{\boldsymbol{M}}(s), $ | (2) |
即前馈增强控制模块完全抵消直升机动力学运动,直升机运动状态量x与显模型状态量xcom完全一致,仅需要通过显模型设计即可实现对飞行控制的操纵品质要求。详细的显模型、前馈增强控制和反馈控制模块设计方法可以参考文献[1-4],这里不再赘述。
3 集成旋翼控制的高带宽飞控设计在显模型跟踪控制系统基础上,通过引入旋翼控制增强旋翼/机体耦合稳定性,根据系统有效操纵频率优化显模型设计,提升直升机操纵响应带宽,具体思路如下。
3.1 反馈控制反馈控制的作用是确保直升机动稳定性、抑制外部扰动,并精确跟踪显模型输出。高反馈控制增益能够使直升机拥有更高的操纵频率,但也会导致阻尼比较小的旋翼/机体耦合运动模态发散。飞行试验[5-7]表明,旋翼/机体耦合运动的发散主要集中于旋翼挥舞/摆振运动的前进型和后退型模态,因此在反馈控制模块引入与之相关的旋翼挥舞和摆振运动信息
|
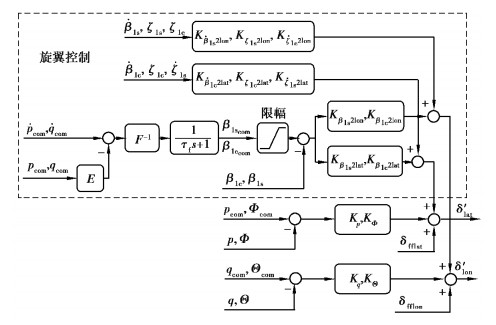
图 3 旋翼控制系统框架 Fig. 3 Architecture of rotor control system |
由于旋翼/机体耦合系统的线速度以及桨叶集合型和无反作用型角和角速度对其俯仰、滚转运动影响很小,因此可以解耦得到旋翼/机体耦合系统的俯仰、滚转运动方程为:
| $ {\mathit{\boldsymbol{\dot x}}_1} = {\mathit{\boldsymbol{A}}_1}{\kern 1pt} {\mathit{\boldsymbol{x}}_1} + {\mathit{\boldsymbol{B}}_1}{\kern 1pt} {\mathit{\boldsymbol{u}}_1}, $ | (3) |
式中:
基于式(3)的旋翼/机体耦合动力学方程,采用LQR最优控制方法[27]对旋翼/机体反馈控制增益进行最优化设计,LQR求解的性能指标为:
| $ J = \int_0^\infty {(\mathit{\boldsymbol{x}}_{\rm{b}}^{\rm{T}}{\kern 1pt} {\mathit{\boldsymbol{Q}}_{\rm{b}}}{\kern 1pt} {\mathit{\boldsymbol{x}}_{\rm{b}}} + \mathit{\boldsymbol{x}}_{\rm{f}}^{\rm{T}}{\kern 1pt} {\mathit{\boldsymbol{Q}}_{\rm{f}}}{\kern 1pt} {\mathit{\boldsymbol{x}}_{\rm{f}}} + \mathit{\boldsymbol{u}}_{{\rm{in}}}^{\rm{T}}\mathit{\boldsymbol{R}}{\kern 1pt} {\mathit{\boldsymbol{u}}_{{\rm{in}}}})} {\rm{d}}t, $ | (4) |
式中:加权矩阵Qb用来限制过大的机体俯仰、滚转姿态角和角速度;加权矩阵Qf用来限制过大的旋翼挥舞角;加权矩阵R用来限制旋翼控制系统产生过大的纵、横向操纵。之所以在式(4)的性能指标计入纵、横向挥舞角是因为它们与机体俯仰、滚转运动相互耦合,对直升机姿态响应产生很大的影响,在最优化性能指标中引入旋翼纵、横向挥舞角能够增强旋翼稳定性,进而提升直升机反馈控制增益。
LQR最优化设计的旋翼/机体全状态控制增益并不适合显模型跟踪控制系统实现,取消影响不大的交叉控制项再微调保留的主控制增益,确保控制系统稳定性并便于将旋翼控制集成到显模型跟踪控制系统。基于以上考虑,机体交叉控制增益Kp2lon, KΦ2lon, Kq2lat, KΘ2lat及旋翼控制增益K
在反馈控制模块引入旋翼状态信息容易导致飞行控制系统无法有效跟踪显模型输出,主要原因在于旋翼反馈控制会降低旋翼操纵灵敏度[18]。采用一种旋翼前馈增强控制提升飞行控制系统[18-20]的操纵频率,形成如图 3所示的旋翼控制系统框架。旋翼纵、横向挥舞角与机体俯仰、滚转运动相互耦合,它们之间存在以下关系:
| $ \left( {\begin{array}{*{20}{c}} {\dot p}\\ {\dot q} \end{array}} \right) \approx \left[ {\begin{array}{*{20}{c}} {{L_p}}&{{L_q}}\\ {{M_p}}&{{M_q}} \end{array}} \right]\left( {\begin{array}{*{20}{l}} p\\ q \end{array}} \right) + \left[ {\begin{array}{*{20}{c}} {{L_{{{\rm{ \mathit{ β} }}_{{\rm{1c}}}}}}}&{{L_{{{\rm{ \mathit{ β} }}_{{\rm{1s}}}}}}}\\ {{M_{{{\rm{ \mathit{ β} }}_{{\rm{1c}}}}}}}&{{M_{{{\rm{ \mathit{ β} }}_{{\rm{1s}}}}}}} \end{array}} \right]\left( {\begin{array}{*{20}{l}} {{\beta _{{\rm{1c}}}}}\\ {{\beta _{{\rm{1s}}}}} \end{array}} \right) \equiv \mathit{\boldsymbol{E}}\left( {\begin{array}{*{20}{l}} p\\ q \end{array}} \right) + F\left( {\begin{array}{*{20}{l}} {{\beta _{{\rm{1c}}}}}\\ {{\beta _{{\rm{1s}}}}} \end{array}} \right), $ | (5) |
式中:Lp、Lq为滚转角加速度
| $ \mathit{\boldsymbol{E}} = \left[ {\begin{array}{*{20}{c}} {{L_p}}&{{L_q}}\\ {{M_p}}&{{M_q}} \end{array}} \right], F = \left[ {\begin{array}{*{20}{c}} {{L_{{\rm{ \mathit{ β} 1c}}}}}&{{L_{{\rm{ \mathit{ β} 1s}}}}}\\ {{M_{{\rm{ \mathit{ β} 1c}}}}}&{{M_{{\rm{ \mathit{ β} 1s}}}}} \end{array}} \right]。$ | (6) |
反解式(5)得到与机体滚转角加速度指令
| $ \left( {\begin{array}{*{20}{l}} {{\beta _{{\rm{1}}{{\rm{c}}_{{\rm{com}}}}}}}\\ {{\beta _{{\rm{1}}{{\rm{s}}_{{\rm{com}}}}}}} \end{array}} \right) = {\mathit{\boldsymbol{F}}^{ - 1}}\left[ {\left( {\begin{array}{*{20}{l}} {{{\dot p}_{{\rm{com}}}}}\\ {{{\dot q}_{{\rm{com}}}}} \end{array}} \right) - E\left( {\begin{array}{*{20}{l}} {{p_{{\rm{com}}}}}\\ {{q_{{\rm{com}}}}} \end{array}} \right)} \right]。$ | (7) |
旋翼前馈增强控制的目的是提升飞行系统的有效操纵频率,但是如果旋翼控制的速度超过旋翼本身固有的响应速度,容易导致过大的作动器超调,不利于对旋翼的控制。在旋翼增强控制的输出环节增加一阶惯性延迟系统,并将该惯性延迟系统的时间常数τf近似为旋翼挥舞角响应的上升时间软化旋翼控制信号。
3.3 显模型设计采用旋翼前馈增强控制能够显著提升飞行控制设计的有效操纵频率,因此能够进一步增大显模型带宽以提升直升机操纵响应带宽和姿态快捷性。为发展一种基于有效跟踪的显模型参数设计方法,下文推导滚转姿态显模型的设计过程,俯仰姿态显模型的设计过程与之类似。
采用一种有效跟踪延迟时间指标定量评估系统对显模型输出状态量的跟踪效果,计算式为
| $ {\tau _{{\rm{mf}}}} = \frac{{135 - |{\varphi _{{\rm{com}}}}({\omega _{{\rm{BDW}}}})|}}{{57.3{\omega _{{\rm{BDW}}}}}}, $ | (8) |
式中:τmf为有效跟踪延迟时间,ωBDW为系统操纵响应带宽,φcom(ωBDW)为操纵带宽频率ωBDW的显模型相位角。
一般情况下直升机在更小的频率范围内对显模型输出的跟踪效果更佳,根据ωBDW频率的有效跟踪延迟时间τmf,那么ω≤ωBDW时有,
| $ \frac{{ - [{\varphi _{\varPhi /{\delta _{{\rm{ lat }}}} }}({\rm{j}}\omega ) - {\varphi _{{\varPhi _{{\rm{com}}}}/{\delta _{{\rm{ lat }}}}}}({\rm{j}}\omega )]}}{{57.3\omega }} \le {\tau _{{\rm{mf}}}}, $ | (9) |
式中:φΦ/δlat(jω)和φΦcom/δlat(jω)为传递函数Φ(s)/δlat(s)和Φcom(s)/δlat(s)在频率ω的相位角,j为虚数符号。
传递函数Φ(s)/δlat(s)和Φcom(s)/δlat(s)的相位角存在以下关系,
| $ {\varphi _{\varPhi /{\delta _{{\rm{ lat }}}}}}({\rm{j}}\omega ) = {\varphi _{{\varPhi _{{\rm{ com }}}}/{\delta _{{\rm{ dat }}}}}}({\rm{j}}\omega ) + {\varphi _{\varPhi /{\varPhi _{{\rm{ com }}}}}}({\rm{j}}\omega ), $ | (10) |
式中:φΦ/Φcom(jω)为传递函数Φ(s)/Φcom(s)在频率ω的相位角。
将式(10)代入式(9)后得
| $ {\varphi _{\varPhi /{\varPhi _{{\rm{com}}}}}}({\rm{j}}\omega ) \ge - 57.3\omega {\tau _{{\rm{mf}}}}, $ | (11) |
其中,ω≤ωBDW。
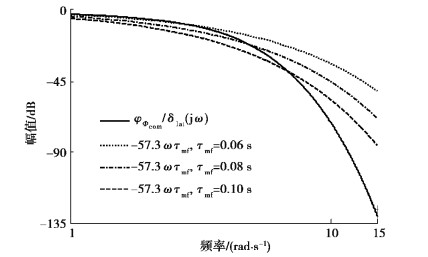
图 4为φΦ/Φcom(jω)与-57.3ωτmf的对比算例。从图 4中可以看出,如果想要实现针对显模型更加有效的跟踪,要求有效跟踪延迟时间τmf更小,那么可以达到的直升机操纵响应带宽更低。直升机操纵响应带宽受到有效跟踪延迟时间τmf的约束。因此,直升机可以实现的最大操纵响应带宽由式(12)确定,
|
图 4 φΦ/Φcom(jω)与-57.3ωτmf对比 Fig. 4 Comparison between φΦ/Φcom(jω) and -57.3ωτmf |
| $ {\varphi _{\varPhi /{\varPhi _{{\rm{com}}}}}}({\rm{j}}{\omega _{{\rm{BDW}}}}) = - 57.3{\omega _{{\rm{BDW}}}}{\tau _{{\rm{mf}}}}。$ | (12) |
因此,传递函数Φcom(s)/δlat(s)在操纵带宽ωBDW频率的相位角为
| $ {\varphi _{{\varPhi _{{\rm{com}}}}/{\delta _{{\rm{lat}}}}}}({\rm{j}}{\omega _{{\rm{BDW}}}}) = - 135 + 57.3{\omega _{{\rm{BDW}}}}{\tau _{{\rm{mf}}}}。$ | (13) |
由于滚转姿态角显模型常采用以下二阶传递函数形式,
| $ \frac{{{\varPhi _{{\rm{com}}}}(s)}}{{{\delta _{{\rm{ lat }}}}(s)}} = \frac{{{K_{{\rm{AC}}}}}}{{\frac{1}{{\omega _{\rm{n}}^2}}{s^2} + \frac{{2\zeta }}{{{\omega _{\rm{n}}}}}s + 1}}, $ | (14) |
其相位角为,
| $ {\varphi _{{\varPhi _{{\rm{com}}}}/{\delta _{{\rm{lat}}}}}}({\rm{j}}\omega ) = - {\rm{arctan}}\left( {\frac{{2\zeta {\omega _{\rm{n}}}\omega }}{{\omega _{\rm{n}}^2 - {\omega ^2}}}} \right)。$ | (15) |
将式(15)代入式(13)可得
| $ \frac{{2\zeta {\omega _{\rm{n}}}{\omega _{{\rm{BDW}}}}}}{{\omega _{\rm{n}}^2 - \omega _{{\rm{BDW}}}^2}} = {\rm{tan}}(135 - 57.3{\omega _{{\rm{BDW}}}}{\tau _{{\rm{mf}}}})。$ | (16) |
通过求解式(16)可得滚转角显模型的固有频率ωn为
| $ {\omega _{\rm{n}}} = \alpha \zeta {\omega _{{\rm{BDW}}}} + {\omega _{{\rm{BDW}}}}\sqrt {1 + {{(\alpha \zeta )}^2}} , $ | (17) |
式中:α=1/tan(135-57.3ωBDWτmf)。
根据给定的有效跟踪延时间和显模型阻尼比,求解式(12)和式(17)可以得到与系统对显模型有效跟踪能力匹配的显模型固有频率,从而实现基于有效跟踪的显模型参数设计。
4 操纵品质分析基于悬停状态的高阶线性直升机飞行动力学模型,将集成显模型跟踪控制系统的直升机频域稳定裕度、操纵响应带宽/相位延迟等指标与集成旋翼控制高带宽飞行控制设计对比,分析旋翼控制对提升直升机操纵品质的影响。其中,显模型跟踪控制系统和集成旋翼控制高带宽飞行控制设计的显模型参数及有效跟踪延迟时间见表 1。从表中可以看出,与传统控制方法相比,虽然集成旋翼控制飞行控制设计的显模型固有频率均提高0.5 rad/s,但仍然保持相对更好的显模型跟踪性能。
| 表 1 显模型参数及有效跟踪延迟时间 Table 1 Parameters of command models and effective tracking time delays |
显模型跟踪控制系统和集旋翼控制高带宽飞行控制设计的直升机频域稳定裕度见表 2。从表 2中可以看出,与前者相比,集成旋翼控制高带宽飞行控制设计具有更大的相位和幅值穿越频率,尤其是相位穿越频率显著增大,但仍然保持了同等程度的稳定裕度,这也是高带宽飞行控制设计的目标,即引入旋翼控制增强系统稳定性,在保持原控制系统稳定性条件下通过提升飞行控制设计的有效操纵频率并进一步提升显模型带宽,达到提升直升机操纵响应带宽的目的。
| 表 2 频域稳定裕度对比 Table 2 Comparison of stability margins |
直升机的操纵响应带宽是驾驶员小幅高频操纵的关键操纵品质指标[28],更大的操纵响应带宽意味着驾驶员能够以更快的速度修正外部小幅度高频扰动的作用。在分析直升机操纵响应带宽/相位延迟指标之前,采用Tischler等[29]出的失配性能参数评估飞行控制系统对显模型的跟踪效果。适配性能参数采用定量化的分析方法通过在频域内比较显模型和直升机响应计算系统对显模型输出的跟踪效果[29],定义如下
| $ {J_{{\rm{mis}}}} = \frac{{20}}{N}\sum\limits_{{\omega _1}}^{{\omega _N}} {\left\{ {{{[|\mathit{\boldsymbol{M}}({\rm{j}}\omega )| - |\mathit{\boldsymbol{P}}({\rm{j}}\omega )|]}^2} + {\gamma _{\rm{p}}}{{[\angle \mathit{\boldsymbol{M}}({\rm{j}}\omega ) - \angle \mathit{\boldsymbol{P}}({\rm{j}}\omega )]}^2}} \right\}} , $ | (18) |
式中:Jmis为失配性能指标,ω1,ω2,…,ωN为离散角频率,N为离散角频率点数,γp为相角加权系数,取值为0.017 45。|M(jω)|和|P(jω)|表示显模型和直升机频域响应的幅值,∠M(jω)和∠P(jω)表示显模型和直升机频域响应的相位角。
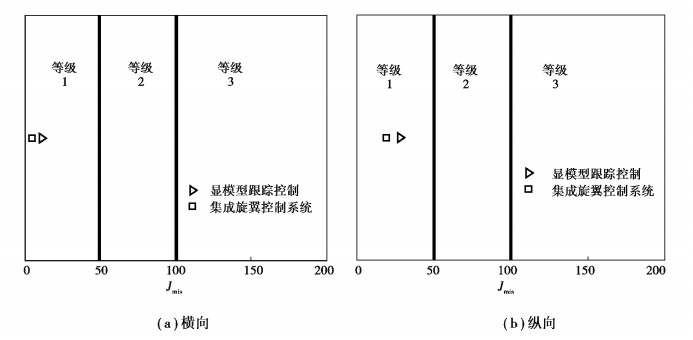
如果直升机呈现出与显模型同样的动力学特性则两者之间的失配性小于50,表明直升机能够很好地跟踪显模型输出;如果直升机响应表现出部分的本体动力学特性则两者之间的失配性大于50但是小于100,但是仍然可以认为飞行控制系统具有可以接受的显模型跟踪能力;如果显模型与直升机频域响应的失配性大于100则表明飞行控制系统对显模型的跟踪效果很差。两种飞行控制系统的直升机失配性能参数对比结果见图 5。可以看出,两种飞行控制系统对显模型的跟踪能力都处于等级1范围,虽然集成旋翼控制高带宽飞行控制系统的显模型带宽更大,但是由于旋翼反馈和前馈增强控制的作用,仍然保持更佳的显模型跟踪能力,该结果与表 1有效跟踪延迟时间的分析结果吻合。
|
图 5 系统失配性能参数对比 Fig. 5 Comparison of mismatch performance |
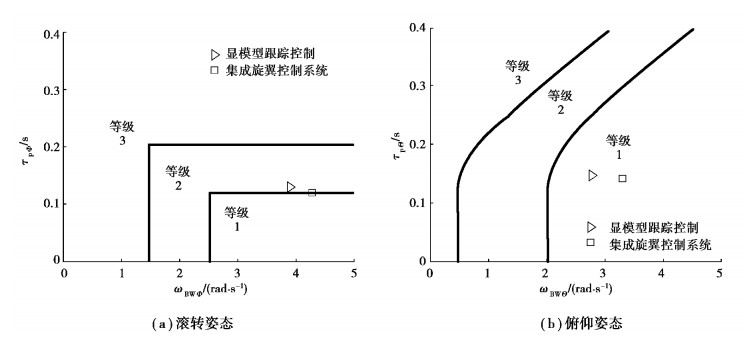
图 6为显模型跟踪控制和集成旋翼控制高带宽飞行控制设计的操纵响应带宽/相位延迟对比结果。可以发现,与显模型跟踪控制系统相比,虽然两者的操纵带宽/相位延迟都达到等级1标准,但后者由于具有更大的有效操纵频率并且显模型带宽更大,集成旋翼控制高带宽飞控设计的横向操纵带宽较显模型跟踪控制提升10%,由3.90 rad/s增加到4.28 rad/s,纵向提升18%,由2.81 rad/s增加到3.32 rad/s,旋翼控制的引入导致系统相位延迟也略有降低。
|
图 6 操纵带宽/相位延迟对比(目标捕获和追踪) Fig. 6 Comparison of bandwith/phase delay (target acquisition and tracking) |
姿态快捷性指标[28]表示直升机中等幅度姿态响应的快慢。由于集成旋翼控制的飞行控制设计对显模型具有良好的跟踪性能,因此,认为集成飞行控制系统的直升机具有与显模型一致的姿态快捷性,通过对比显模型跟踪控制和集成旋翼控制高带宽飞行控制设计所采用的显模型的姿态快捷性分析旋翼控制对直升机滚转、俯仰姿态快捷性的提升作用。
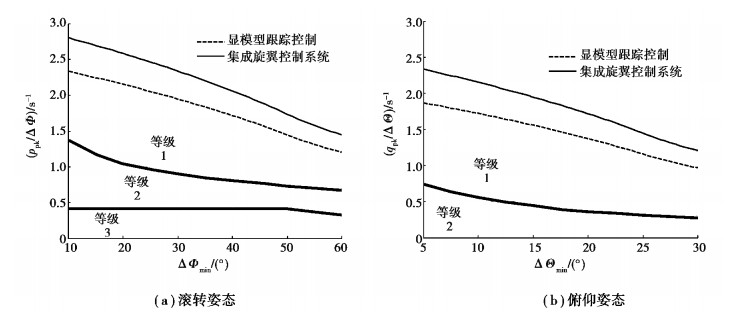
图 7为两种飞行控制系统姿态快捷性分析结果。可以发现,虽然显模型跟踪控制和集成旋翼控制高带宽飞行控制设计的姿态快捷性指标都为等级1,但与前者相比,集成旋翼控制飞行控制设计的横向姿态快捷性平均提升20%,纵向平均提升25%。这是因为,虽然集成旋翼控制飞行控制设计没有直接针对姿态快捷性提升设计,但是在提升显模型带宽的同时提升了直升机姿态快捷性。
|
图 7 姿态快捷性对比 Fig. 7 Comparison of attitude quickness |
将显模型跟踪控制系统和集成旋翼控制飞控系统分别集成到经过验证的高阶非线性飞行动力学模型开展直升机操纵响应数值模拟,验证集成旋翼控制飞行控制系统的控制效果。高阶非线性直升机飞行动力学模型的建模过程及验证见文献[22-25]。
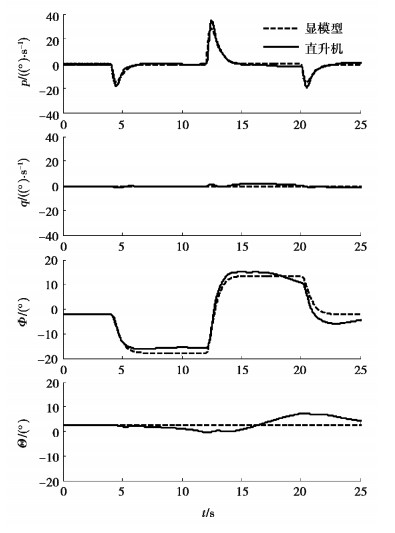
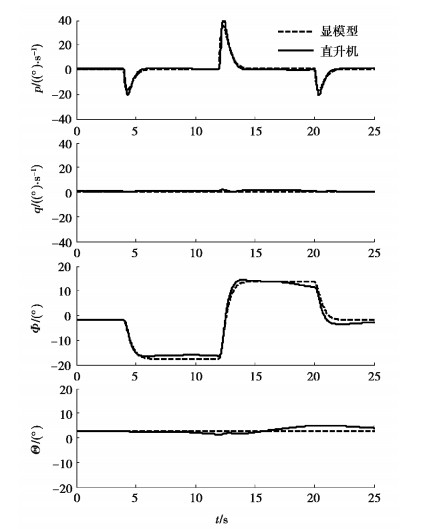
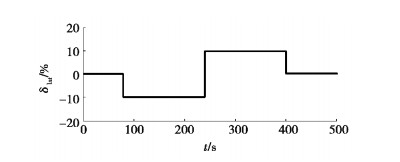
图 8和图 9分别为集成两种飞行控制系统的直升机对驾驶员横向偶极方波输入的响应时间历程,其中横向偶极方波输入的时间历程如图 10所示。从图中可以看出,由于集成旋翼控制飞行控制系统采用了具有更高带宽的显模型,与图 8集成显模型跟踪控制系统的直升机响应相比,图 9显示集成旋翼控制的飞行控制系统使直升机具有更大的滚转角速率峰值,这有助于实现更快的直升机响应。然而,虽然具有更高的操纵带宽,但与显模型跟踪控制系统相比,集成旋翼控制的飞行控制系统显示出更加良好的显模型跟踪性能和更小的异轴响应,证明集成旋翼控制的飞行控制系统不仅能够显著提升直升机操纵响应,而且能够实现更好的各通道解耦性能。
|
图 8 显模型跟踪控制系统对直升机响应控制效果 Fig. 8 Effect of explicit model-following control system on helicopter response |
|
图 9 集成旋翼控制飞控系统对直升机响应控制效果 Fig. 9 Effect of integrated rotor control system on helicopter response |
|
图 10 横向操纵杆输入时间历程 Fig. 10 Time history of lateral stick input |
1) 在已有控制设计中引入旋翼反馈控制能够显著提升直升机相位和幅值穿越频率,进而提升直升机有效操纵频率,同时还可以保持与原飞行控制设计同等程度的稳定性。
2) 综合旋翼反馈控制和前馈增强控制能够提升直升机有效操纵频率,基于有效跟踪的显模型参数设计方法能够在保持对显模型良好跟踪性能的前提下提升显模型固有频率和带宽,从而提高直升机操纵响应带宽。
3) 线性分析结果表明,集成旋翼控制的高带宽飞行控制设计能够将已有飞行控制系统纵、横向操纵响应带宽分别提升18%、10%,纵、横向姿态快捷性分别提升25%和20%。
4) 非线性仿真结果表明,与已有显模型跟踪控制系统相比,集成旋翼控制飞行控制系统能够实现更高的直升机响应速度、显模型跟踪性能以及各通道解耦性能。
| [1] |
Landis K H, Glusman S I. Development of ADOCS controllers and control laws, vol. 2, NASA CR-177339[R]. Washington, D C: NASA, 1985.
|
| [2] |
Tischler M B. Digital control of highly augmented combat rotorcraft, NASA TM-88346[R]. Washington, D C: NASA, 1987.
|
| [3] |
Tischler M B, J W Fletcher, P M Morris, et al. Applications of flight control system methods to an advanced combat rotorcraft, NASA TM-101054[R]. Washington, D C: NASA, 1989.
|
| [4] |
Tischler M B, Fletcher J W, Morris P M, et al. Flying quality analysis and flight evaluation of a highly augmented combat rotorcraft[J]. Journal of Guidance, Control, and Dynamics, 1991, 14(5): 954-963. DOI:10.2514/3.20736 |
| [5] |
Dryfoos J B, Kothmann B D, Mayo J. An approach to reducing rotor-body coupled roll oscillations on the RAH-66 comanche using modified roll rate feedback[C]//American Helicopter Society 55th Annual Forum. Fairfax: AHS, 1999: 1-14.
|
| [6] |
Frost C R, Hindson W S, Moralez E, and et al. Design and testing of flight control laws on the RASCAL research helicopter[C]//AIAA Modeling and Simulation Technologies Conference and Exhibit. Reston: AIAA, 2002: 1-11.
|
| [7] |
Fletcher J W, Lusardi J, Mansur M H, et al. UH-60M upgrade fly-by-wire flight control risk reduction using the RASCAL JUH-60A in-flight simulator[C]//American Helicopter Society 64th Annual Forum. Fairfax: AHS, 2008: 1-26.
|
| [8] |
Ellis C W. Effects of rotor dynamics on helicopter automatic control system requirements[J]. Aeronautical Engineering Review, 1953, 12(7): 30-38. |
| [9] |
Hall W E, Bryson A E. Inclusion of rotor dynamics in controller design for helicopters[J]. Journal of Aircraft, 1973, 10(4): 200-206. DOI:10.2514/3.60214 |
| [10] |
Chen R T N, Hindson W S. Influence of high-order dynamics on helicopter flight-control system bandwidth[J]. Journal of Guidance, Control, and Dyanmics, 1986, 9(2): 190-197. DOI:10.2514/3.20089 |
| [11] |
Chen R T N. An exploratory investigation of the flight dynamics effects of rotor RPM variations and rotor state feedback in hover, NASA-TM-103968[R]. Washington, D C: NASA, 1992.
|
| [12] |
Takahashi M. Rotor-state feedback in the design of flight control laws for a hovering helicopter[J]. Journal of the American Helicopter Society, 1994, 39(1): 50-62. DOI:10.4050/JAHS.39.50 |
| [13] |
Takahashi M D. H-infinity helicopter flight control law design with and without rotor state feedback[J]. Journal of Guidance, Control, and Dynamics, 1994, 17(6): 1245-1251. DOI:10.2514/3.21340 |
| [14] |
Howitt J, Howell S E, McCallum A T, et al. Experimental evaluation of flight control system designs exploiting rotor state feedback[C]//American Helicopter Society 57th Annual Forum. Fairfax: AHS, 2001: 1-9.
|
| [15] |
Howitt J. Application of non-linear dynamic inversion to rotorcraft flight control[C]//American Helicopter Society 61th Annual Forum. Fairfax: AHS, 2005, 2: 1160-1169.
|
| [16] |
Guo W, Horn J F. Rotor state feedback control for rotorcraft with variable rotor speed[C]//AIAA Guidance, Navigation, and Control Conference Proceedings. Reston: AIAA, 2009: 1-12.
|
| [17] |
Horn J F, Guo W, Ozdemir G T. Use of rotor state feedback to improve closed-loop stability and handling qualities[J]. Journal of the American Helicopter Society, 2012, 57(2): 1-10. |
| [18] |
吉洪蕾, 陈仁良, 李攀. 用于直升机在大气紊流中的旋翼状态反馈控制[J]. 航空学报, 2017, 38(5): 48-57. JI Honglei, CHEN Renliang, LI Pan. Rotor-state feedback control for helicopter in atmospheric turbulence[J]. Acta Aeronautica et Astronautica Sinica, 2017, 38(5): 48-57. (in Chinese) |
| [19] |
Ji H L, Chen R L, Li P. Rotor-state feedback control to alleviate pilot workload for helicopter shipboard operations[J]. Journal of Guidance, Control, and Dynamics, 2017, 40(12): 3088-3099. DOI:10.2514/1.G002304 |
| [20] |
Ji H L, Chen R L, Li P. Rotor-state feedback control design to improve helicopter turbulence alleviation in hover[J]. Proceedings of the Institution of Mechanical Engineers, Part G. Journal of Aerospace Engineering, 2018, 232(1): 156-168. DOI:10.1177/0954410016683731 |
| [21] |
Howlett J J. UH-60A Black hawk engineering simulation program, NASA CR-166309[R]. Washington, D C: NASA, 1981.
|
| [22] |
李攀, 陈仁良. 直升机急拉杆机动飞行仿真建模与验证[J]. 航空学报, 2010, 31(12): 2315-2323. LI Pan, CHEN Renliang. Formulation and validation of a helicopter model for pull-up maneuver simulation[J]. Acta Aeronautica et Astronautica Sinica, 2010, 31(12): 2315-2323. (in Chinese) |
| [23] |
吉洪蕾, 陈仁良, 李攀. 适用于直升机飞行力学分析的三维空间大气紊流模型[J]. 航空学报, 2014, 35(7): 1825-1835. JI Honglei, CHEN Renliang, LI Pan. A model of three-dimensional-field atmospheric turbulence for helicopter flight dynamics analysis[J]. Acta Aeronautica et Astronautica Sinica, 2014, 35(7): 1825-1835. (in Chinese) |
| [24] |
Ji H L, Chen R L, Li P. Distributed atmospheric turbulence model for helicopter flight simulation and handling-quality analysis[J]. Journal of Aircraft, 2016, 54(1): 190-198. |
| [25] |
Ji H L, Chen R L, Li P. Distributed turbulence model with accurate spatial correlations for helicopter handling-quality analysis[J]. Journal of the American Helicopter Society, 2019, 64(3): 042000. |
| [26] |
Ballin M G, Dalang-Secre'tan M A. Validation of the dynamic response of a blade-element UH-60 simulation model in hovering flight[J]. Journal of the American Helicopter Society, 1991, 36(4): 77-88. DOI:10.4050/JAHS.36.77 |
| [27] |
陈复扬. 自动控制原理[M]. 北京: 国防工业出版社, 2010: 433-438. CHEN Fuyang. Principles of automatic control[M]. Beijing: National Defense Industry Press, 2010: 433-438. (in Chinese) |
| [28] |
United States Army Aviation and Missile Command. ADS-33E-PRF Aeronautical design standard performance specification handling qualities requirements for military rotorcraft[S]//Aviation Engineering Directorate. Redstone Arsenal, United States: United States Army Aviation, 2000: 6-21.
|
| [29] |
Tischler M B, Remple R K. Aircraft and rotorcraft system identication[M]. Reston, VA: AIAA, 2006.
|
 2020, Vol. 43
2020, Vol. 43


