水处理工艺中,反应器内流态通常为紊流,紊流脉动与反应器中溶解氧浓度、氧气与水体的混合程度、污染物扩散速度等密切相关,因而它对污染物处理效果产生重要的影响[1]。在生物反应器中,紊流脉动也对生物膜的理化与生物特性产生显著影响,选择合适的水动力及紊流条件,既可保证反应器的处理效果又能有效降低运行费用[2]。
通常,紊流的瞬时流速包括时均流速和脉动流速,两者相互影响、相互耦合,难以将它们各自在反应器运行中的作用区分。现有的有关紊流流速对生物反应器生物膜特性以及处理效率等的研究多是针对的时均流速,所获结果表面上好像仅为时均流速的作用,但实际上应为时均流速和脉动流速两者的共同作用。为单独研究紊流脉动速度所产生的作用,采用振动格栅装置是一种有效的方法[3],这是因为该装置所产生的紊流,能在离格栅一定距离的水体中产生时均流速为零的近似各向同性紊流,称为格栅紊流(vibrating grid turbulence,VGT)[4]。由于格栅紊流为无时均速度仅有脉动速度的紊流,因此它被广泛应用于研究紊流脉动的作用,如Chiapponi等[5]用其研究紊流脉动对污染物的降解速率,McCorquodale等[6-7]研究的紊流脉动对能量传递的影响及其与边界的相互作用等。但现有文献中却鲜有紊流脉动对生物反应器中生物膜理化特性及处理效果的研究。
由于紊流的复杂与随机性、速度场测量难度大,通过建立数学模型,借助计算机进行数值模拟是一种有效研究手段。迄今为止,有关的模拟研究[8-10]均采用的方法是让格栅固定,通过使流体不断运动来实现相对的格栅“振动”,采用这种方法对于模拟具有自由表面的液体或非连续流反应器中的流动存在明显的缺陷。此外,构建的格栅紊流的流体运动模型基本上是采用的单相流模型,而非气液两相流模型。
为此,笔者针对所设计的振动格栅反应器中的流体运动,构建气液两相流模型,借助Fluent 18.2软件,采用动网格中的重叠(Overset)网格,对所构建气液两相流模型进行了数值模拟。结合振动格栅生物反应器在特定工况下的运行数据对模型以及模拟结果进行了验证,证实了所构建模型和模拟方法的合理性。通过对不同工况下的格栅紊流的数值模拟,分别得到紊流脉动强度与气含率、紊流脉动强度与氧转移系数和紊流脉动强度与雷诺应力之间的关系。结合相应的实验研究,分析紊流脉动对生物反应器的气液传质效果、生物膜生长及污染物去除率的影响,为生物反应器的结构设计、参数优化和高效运行提供参考。
1 格栅紊流概述本文中所设计的格栅紊流生物反应器装置示意如图 1(a)所示(图 1(c)为实物图),装置主体尺寸为31 cm×31 cm×50 cm。格栅由相互平行的正交格栅条所组成(图 1(b)),栅条宽度及厚度均为1.0 cm,格栅孔为5 cm×5 cm的矩形。格栅由电机驱动,在水箱中做垂向振动。格栅中平面距水槽底端距离为39.0 cm,大于2.5倍栅孔间距,这可减少二次回流的影响[11]。为减小格栅边缘及边壁间的相互作用,格栅边缘与边壁的距离为0.2 cm。随着格栅的往复运动,在格栅开口处形成射流,格栅条上下方形成尾流,射流与尾流相互作用,在距格栅一定范围内生成时均速度为零的近似各向同性的紊流[12]。当格栅以不同频率振动时,形成不同强度的紊流脉动。
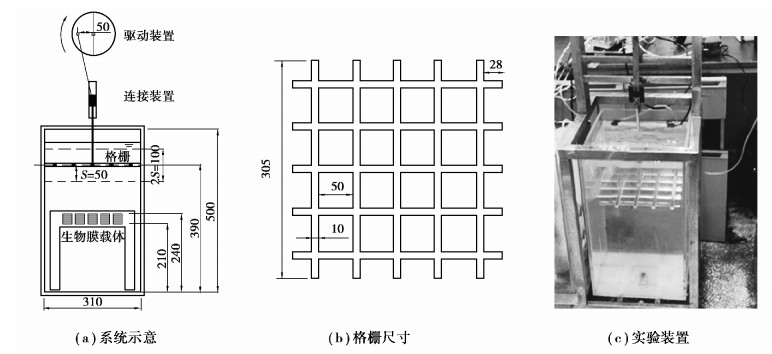
|
图 1 振动格栅生物反应器(单位:毫米) Fig. 1 Vibrating grille bioreactor(mm) |
相应完成的实验用水为配水:COD质量浓度约300 mg/L,TN质量浓度约60 mg/L,TP质量浓度约5 mg/L,近似中等污染的城市污水。通过在反应器内增设生物填料并挂膜,对不同振动频率下水体中的污染物浓度进行了隔日测试(反应器中水温恒定26 ℃),每批实验同时启动运行三组振动格栅生物膜反应器装置进行重复试验,测定数据的计算结果见表 1。
| 表 1 实验中振动频率与污染物次日去除率 Table 1 Vibration frequency and pollutant removal rate in the experiment |
实验结果表明,污染物去除率随振动频率(紊流脉动强度)的增加呈现先升后降的趋势,在频率为4 s-1去除效率均较高,因此选其作为代表性工况对模型及模拟方法的合理性进行验证。
2 数学模型与数值模拟 2.1 数学模型和数值格式模型反应器中气液流动采用多相流Eulerian模型,其控制方程如下。
| $ \frac{\partial }{{\partial t}}\left( {{\alpha _q}{\rho _q}} \right) + \nabla \cdot \left( {{\alpha _q}{\rho _q}{\mathit{\boldsymbol{v}}_q}} \right) = \sum\limits_{p = 1}^n {{{\dot m}_{pq}}} , $ | (1) |
式中:αq为q相的体积分数;ρq为q相的物理密度;vq是q相的速度;
| $ \begin{array}{*{20}{c}} {\frac{\partial }{{\partial t}}\left( {{\alpha _q}{\rho _q}{\mathit{\boldsymbol{v}}_q}} \right) + \nabla \cdot \left( {{\alpha _q}{\rho _q}{\mathit{\boldsymbol{v}}_q}{\mathit{\boldsymbol{v}}_q}} \right) = }\\ { - {\alpha _q}\nabla p + \nabla \cdot \overline {\overline {{\tau _q}} } + \sum\limits_{p = 1}^n {\left( {{\mathit{\boldsymbol{R}}_{pq}} + {{\dot m}_{pq}}\;{\mathit{\boldsymbol{v}}_{pq}}} \right)} + {\alpha _q}{\rho _q}\left( {{\mathit{\boldsymbol{F}}_q} + {\mathit{\boldsymbol{F}}_{{\rm{lift}}, q}} + {\mathit{\boldsymbol{F}}_{{\rm{Vm}}, q}}} \right), } \end{array} $ | (2) |
式中:
紊流模型选用标准κ-ε两方程模型。为模拟流动过程中气泡的破碎及凝聚现象,得到不同大小气泡的组分数分布,耦合群体平衡(Population Balance Model,BPM)模型,BPM模型采用Discrete方法。Eulerian模型采用有限体积法对整个计算域进行空间离散,压力速度耦合算法选择Coupled算法,梯度项离散采用Least Square Cell Based算法,瞬态项格式采用First Order Implicit进行迭代求解;BPM模型采用Discrete算法。
2.2 网格划分研究的流动区域如图 1所示,为实现紊流场动态模拟,选择沿格栅开口断面为特征断面,采用重叠(Overset)网格实现格栅的运动,模拟过程设置两套网格,反应器内的流体(空气和水)为背景网格,振动格栅振动范围为前景网格。通过ICEM进行模型的网格划分,采用结构化网格保证网格质量,背景网格数为6 840;前景网格中栅条断面处采用O-BLOCK划分,网格数为7 600。
2.3 边界条件两相流模型中,液体为主相,空气为第二相。对模型进行两相流初始化,设定静止时水深为45 cm,液相不含任何气体,水面上方设为空气;反应器顶部与大气相通。数值求解PBM模型时,设置10组不同尺寸的空气气泡,最小直径设置为0.001 m,最大直径为0.102 m,气液相间表面张力系数设置为0.071 N/m。
格栅的振动通过前景网格的运动实现,其运动方式与实验格栅振动一致,即
| $ v=\omega A \cos (\omega t+\varphi), $ | (3) |
式中:v为格栅运动速度;ω为角频率;A为格栅振幅;t为运动时间;φ为初相位。
格栅振动幅度为5 cm,振动频率分别取0.5,1.0,1.5,2.0,2.5,3.0,4.0,6.0,8.0,10.0 s-1,针对这10种运行工况进行数值模拟。模拟时间步长设为0.001 s,总时长为20 min。借助Fluent软件数值模拟各方向的均方脉动流速、雷诺应力、湍动能、湍动能耗散率和不同尺寸的气泡分布分数等参数用于后续计算分析。
3 模拟结果与分析 3.1 流场的验证与紊流强度首先对瞬时脉动流速进行分析,其频率分布可近似为正态分布(见图 2),与实验数据较吻合,也与已有的研究结论[11]一致,且时均流速近似为零。因此,该反应器可用于研究紊流脉动的单独作用。
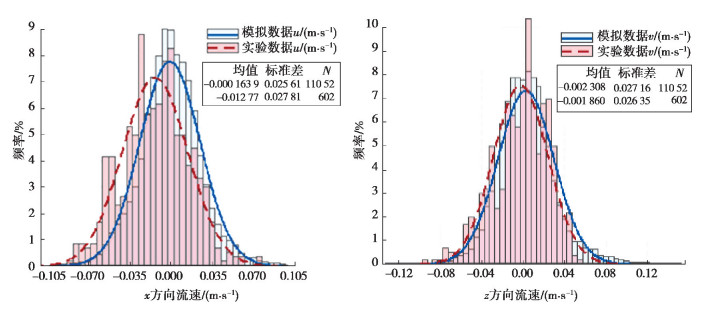
|
图 2 某点流速频率密度分布及验证 Fig. 2 Distribution and verification of velocity frequency density at a certain point |
如图 3所示,由于反应器内紊流脉动分布复杂且不断随时间变化,为更直观和定量地分析紊流脉动的影响,提取各点位动态的流速后,采用平均紊流强度q来表征紊流脉动的作用(式(4))。
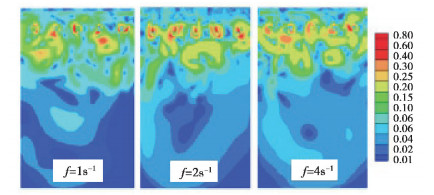
|
图 3 部分工况下反应器瞬时速度云图 Fig. 3 Cloud diagram of instantaneous velocity of reactor under partial working conditions |
| $ q = \sqrt {\frac{1}{N}\sum\limits_{i = 1}^N {\left( {\frac{{u_i^{\prime 2} + v_i^{\prime 2} + w_i^{\prime 2}}}{3}} \right)} } , $ | (4) |
式中:u′i,v′i,w′i是某点处均方脉动流速在x,y,z方向的分量,且u′i=v′i[13]。10种工况下模拟的紊流强度如图 4所示。
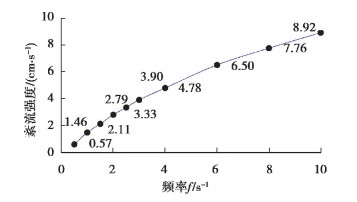
|
图 4 不同工况下紊流强度模拟值 Fig. 4 Simulation value of turbulent intensity under different working conditions |
紊流脉动使得水体强烈紊动,水面翻滚卷入大量空气形成气泡。气含率体现了反应器气液的传动和混合效果,对反应器内传质及生物膜生长有重要影响,是紊流脉动对生物反应器运行影响的最直观体现。为验证该数值模拟计算的可靠性,对代表工况f=4 s-1时模拟统计得到的反应器随运行时间变化的气含率与该工况下测得的实验数据进行对比验证。平均气含率采用体积膨胀法测量,即紊流裹挟气体进入液体使得体积增大的比例,计算公式如式(5)所示。图 5为代表工况下反应器气含率的模拟值与实验值的对比。
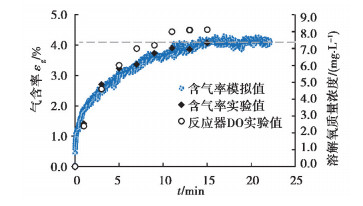
|
图 5 气含率的模拟值与实验值(f=4 s-1) Fig. 5 Gas holdup predications and experimental results |
| $ {{\rm{\varepsilon }}_{\rm{g}}} = \frac{{\Delta V}}{{{V_0} + \Delta V}} = \frac{{{V_1} - {V_0}}}{{{V_1}}} = \frac{{{{\bar h}_1} - {h_0}}}{{{{\bar h}_1}}}, $ | (5) |
式中:εg为气含率;V0为气体进入前的液体体积;V1为气体进入后的液体体积;ΔV为气体进入后液体变化的体积;h1为气体进入后的液体平均高度;h0为反应器静止时水面高度。
由图 5可知反应器内气含率的模拟数值与实验数据较为吻合,反应器的溶解氧浓度变化趋势与气含率变化趋势基本一致,表明本文中所构建的模型和模拟方法在模拟流动和气液传质两方面具有可行性及准确性。不同工况下反应器运行稳定时的气含率与紊流强度的关系见图 6,随着紊流强度的增大,反应器的气含率增大,但增大趋势逐渐减缓,当紊流强度q≥4 cm/s时,气含率变化已较为平缓(< 5%)。因紊流脉动干扰气泡上浮路径,延长气泡的停留时间、气液两相接触时间,增加了反应器的整体气含率,强化了气液传质效果。
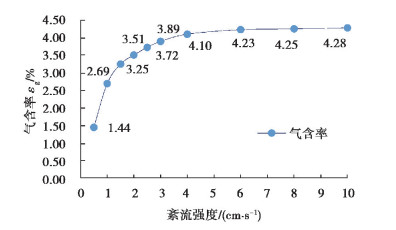
|
图 6 紊流强度与气含率的关系 Fig. 6 Relationship between turbulence intensity and gas holdup |
氧转移系数KLa是直接体现传质效果的参数,也是控制生物反应器好氧区中溶解氧浓度的关键因素。为研究紊流脉动对氧转移系数影响,将代表工况的动态氧转移系数模拟值与该工况下测得的实验值进行对比验证。
实验根据Fick第一定律测定氧转移系数:
| $ {\frac{{{\rm{d}}M}}{{A{\rm{d}}t}} = \frac{V}{A}\frac{{{\rm{d}}C}}{{{\rm{d}}t}} = - {D_{\rm{L}}}\frac{{{\rm{d}}C}}{{{\rm{d}}X}}, } $ | (6) |
即,
| $ \frac{{{\rm{d}}C}}{{{\rm{d}}t}} = {K_{{\rm{La}}}}\left( {{C_{\rm{s}}} - C} \right)\frac{{{\rm{d}}C}}{{{\rm{d}}t}} = {K_{{\rm{La}}}}\left( {{C_{\rm{s}}} - C} \right), $ | (7) |
式中:dM/dt为氧传递率;A为气、液两相界面接触面积;V为水体体积;DL为氧在液膜中的扩散系数;Cs为氧在水中达到饱和时的浓度。
数值模拟中氧转移系数的计算方法,采用薛胜伟等[14]利用溶质渗透理论和各项湍流理论建立的液相体积传质系数模型:
| $ {K_{{\rm{La}}}} = \frac{2}{{{{\rm{ \mathsf{ π} }}^{ - 0.5}}}}\sqrt {{D_{\rm{L}}}} \left( {\frac{{{\rho _{\rm{L}}}\varepsilon }}{\mu }} \right)0.25\frac{{6{\varepsilon _{\rm{g}}}}}{{d\left( {1 - {\varepsilon _{\rm{g}}}} \right)}}, $ | (8) |
式中:ε为湍动能耗散率;d为气泡直径;εg为平均气含率;μ为剪切黏度;ρL为液相流体密度;DL为液相扩散系数。
由图 7可知,代表工况下的氧转移系数模拟值与实验值基本吻合。反应器启动后,氧转移系数随运行时间增大而增加,然后逐渐稳定在0.007 4 s-1左右。不同工况下反应器运行稳定时的氧转移系数与紊流强度关系见图 8,在紊流强度q=0.5~5.0 cm/s时,氧转移系数与紊流强度有良好的线性关系(R2=0.957)。由3.2节的结果可知,紊流脉动增大使反应器的整体气含率增加,气液接触面积增大。适宜的紊流强度使气泡分布更加均匀,从而降低了气泡聚集概率,增加了气泡比表面积[15]。气泡受脉动影响破碎后产生大量微小气泡,进一步强化了气液传质效果。紊流强度q≥5.0 cm/s时,随着气液氧分压、溶解氧浓度差值等传质推动力减小,传质系数出现边界递减效应,氧转移系数与紊流强度不再呈线性关系。
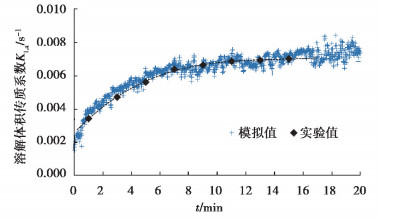
|
图 7 氧转移系数的模拟与实验值(f=4 s-1) Fig. 7 Volumetric mass transfer coefficient predications and experimental results |
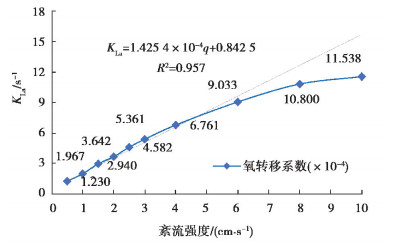
|
图 8 紊流强度与氧转移系数的关系 Fig. 8 Relationship between turbulence intensity mass and transfer coefficient of liquid phase volume |
紊流脉动有利于生物膜表面的传质,促进生物量的积累[16],而脉动产生的切应力影响生物膜脱落。紊流切应力τ为黏性切应力τ1和雷诺应力τ2(紊流附加切应力)之和,当紊动强烈时,τ1≪τ2,前者可忽略不计。因此,研究不同强度紊流脉动产生的雷诺应力对生物膜生长、脱落及污染物处理效果的影响十分必要。雷诺应力计算式如下。
| $ {\tau _2} = - \rho \overline {{u^\prime }{v^\prime }} , $ | (9) |
式中:ρ为液体的密度;u′、v′分别为x方向与y方向上的均方脉动速度。
将雷诺应力模拟值与该条件下实验测得的生物膜物理指标(生物膜平均厚度Lf和生物膜平均密度ρs)进行对比分析。实验工况选择氧传质系数和紊流强度线性关系明显的区间,格栅振动频率分别为0.5,1.0,1.5,2.0,2.5,3.0,4.0 s-1。每批实验同时运行3组振动格栅生物膜反应器,设置相同的运行频率与实验条件进行平行实验,生物膜成功接种后培养10 d进行测量,用于测定的生物膜如图 9所示。

|
图 9 不同工况下用于测定的部分生物膜 Fig. 9 Partial biofilms for determination under different working conditions |
图 10反映了生物膜平均厚度、密度与雷诺应力的关系:随着雷诺应力增大,紊流使反应器中的氧气和营养成分传质加强,生物膜的厚度开始不断增加,但生物膜膜结构多孔且松散,故密度较小。在τ2=2.37 Pa/m2时,生物膜厚度达最大值(0.95 mm±0.06 mm)。之后雷诺应力增大,剪切作用开始明显,生物膜厚度逐渐变薄,同时生物膜的密度也迅速增大,表明较大的雷诺应力将导致生物膜更为紧密,尤其在τ2=2.37~3.82 Pa/m2时,雷诺应力增大了约75%,生物膜密度增大了约230%。
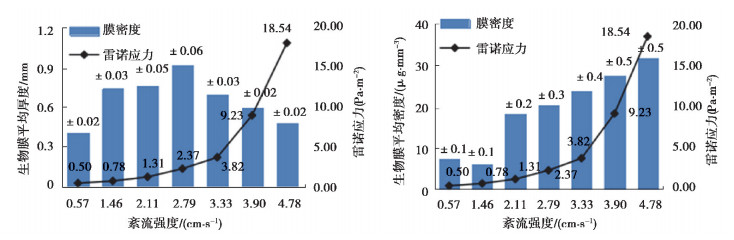
|
图 10 生物膜平均厚度、密度与雷诺应力的关系 Fig. 10 The relationship between the average thickness, density and Reynolds stress of the biofilm |
在生物膜反应器实际运行中,若生物膜厚度太薄,往往出现污水处理效率低、出水指标不满足设计要求等现象。若生物膜太厚,则会抑制膜内传质,导致生物膜过早脱落,造成反应器膜污染等问题。因此污水处理中生物膜的厚度须适中,以保证污水处理效果、减少生物膜凋落。Tijhuis等[17]提出了式(10)表征生物膜脱离凋落速率。
| $ {R_{{\rm{dt}}}} = {K_{\rm{d}}}\rho {L_{\rm{f}}}, $ | (10) |
式中:Rdt为生物膜的脱离凋落速率,Kd为生物膜的脱离率系数。结合反应器模拟的各项参数与实验装置运行数据,分析生物膜反应器中最佳紊流强度,见图 11。
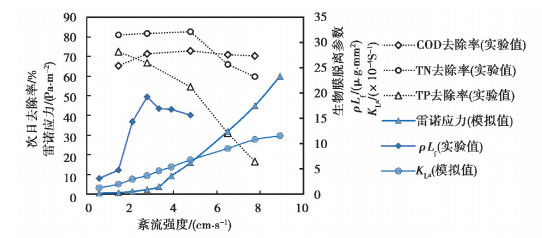
|
图 11 紊流强度与反应器内各参数关系 Fig. 11 Relationship between turbulence intensity and parameters in reactor |
图 11结合表 1实验测定的污染物去除率,综合呈现了紊流脉动强度变化下生物反应器运行的各项参数变化趋势:随着紊流强度q增大,氧气传质系数KLa及雷诺应力τ2都随之增大,水体紊动促进营养成分扩散,使微生物加速代谢,从而增加了污染物去除率。紊动强度q≥2.7 cm/s-1时,雷诺应力作用显著增强,生物膜的脱离凋落参数ρLf快速增大,微生物细胞受到机械损伤,生物膜受剪切力开始脱落。当紊动强度进一步增大(q≥4.8 cm/s-1),COD去除率略有下降,ρLf呈下降趋势,生物膜厚度减小、密度增大,仍有足够的生物量降解有机物,因此去除率总体变化不大。此时死亡细胞中的氮磷再度释放到水中,TN、TP去除率出现明显下降。由于含气率升高与紊流脉动作用加剧了N2、NH3的吹脱[18],而磷未能有效去除,导致TP去除率下降早于TN且下降速度快。在综合考虑污染物处理效果与生物膜生长情况后,选择紊动强度q=3.4~4.8 cm/s为较优工况。
4 结语为研究紊流脉动对生物反应器运行的影响,构建气液两相流模型,借助Fluent软件进行数值模拟。根据数值模拟的结果,结合已开展的实验研究,得到以下结论:
1) 建立了格栅紊流的气液两相流仿真模型,模拟结果与实验数据吻合较好,验证了模型和模拟方法在模拟流动和传质两方面的可行性及准确性。
2) 紊流脉动作用能增加氧气在水体停留时间,提高氧的传质效率。增大紊流脉动可有效提高反应器内的气含率和氧转移系数,促进气液两相进行高效传质,为微生物提供良好生存环境。
3) 较大的雷诺应力会使生物膜变薄加密。结合实验测得的生物膜的物理参数及反应器运行情况,当紊流强度q=3.4~4.8 cm/s时,对应的雷诺应力τ2=4.8~18.6 Pa/m2,本反应器中气液传质效果较好,污染物去除效率较高。
| [1] |
Li J, Li R, Li K F, et al. Experimental study of turbulence effect on re-aeration[J]. Progress in Natural Science, 2000, 10(9): 693-697. |
| [2] |
Gillot S, Héduit A. Effect of air flow rate on oxygen transfer in an oxidation ditch equipped with fine bubble diffusers and slow speed mixers[J]. Water Research, 2000, 34(5): 1756-1762. DOI:10.1016/S0043-1354(99)00323-1 |
| [3] |
Wan Mohtar W H M, Munro R J. Threshold criteria for incipient sediment motion on an inclined bedform in the presence of oscillating-grid turbulence[J]. Physics of Fluids, 2013, 25(1): 015103. DOI:10.1063/1.4774341 |
| [4] |
Rouse H. Experiments on the mechanics of sediment suspension[C]//Proceedings of the Fifth International Congress for Applied Mechanics. New York: John Wiley & Sons, 1939: 550-554.
|
| [5] |
Chiapponi L, Longo S, Tonelli M. Experimental study on oscillating grid turbulence and free surface fluctuation[J]. Experiments in Fluids, 2012, 53(5): 1515-1531. DOI:10.1007/s00348-012-1367-4 |
| [6] |
McCorquodale M W, Munro R J. Analysis of intercomponent energy transfer in the interaction of oscillating-grid turbulence with an impermeable boundary[J]. Physics of Fluids, 2018, 30(1): 015105. DOI:10.1063/1.5007020 |
| [7] |
McCorquodale M W, Munro R J. Experimental study of oscillating-grid turbulence interacting with a solid boundary[J]. Journal of Fluid Mechanics, 2017, 813: 768-798. DOI:10.1017/jfm.2016.843 |
| [8] |
邱旭, 王昊, 李峰, 等. 格栅湍流场湍流特性的数值模拟[J]. 沈阳建筑大学学报(自然科学版), 2016, 32(5): 863-870. QIU Xu, WANG Hao, LI Feng, et al. Numerical simulation of wind characters of grid-generated wind field[J]. Journal of Shenyang Jianzhu University(Natural Science), 2016, 32(5): 863-870. (in Chinese) |
| [9] |
白桦, 何晗欣, 刘健新, 等. 格栅紊流风特性参数模拟规律研究[J]. 振动与冲击, 2016, 35(22): 209-214. BAI Hua, HE Yixin, LIU Jianxin, et al. Study on simulation law of turbulent wind characteristic parameters of grating[J]. Journal of Vibration and Shock, 2016, 35(22): 209-214. (in Chinese) |
| [10] |
Zhang J F, Zhang Q H, Maa J P Y, et al. Lattice Boltzmann simulations of oscillating-grid turbulence[J]. Journal of Hydrodynamics, 2017, 29(1): 68-74. DOI:10.1016/S1001-6058(16)60718-7 |
| [11] |
王得祥, 王得军, 李艳. 水槽中振动格栅紊流特性实验研究[J]. 华北水利水电学院学报, 2007, 28(2): 19-21. WANG Dexiang, WANG Dejun, LI Yan. Experimental study on characteristics of oscillating-grid turbulence in flume[J]. Journal of North China Institute of Water Conservancy and Hydroelectric Power, 2007, 28(2): 19-21. (in Chinese) DOI:10.3969/j.issn.1002-5634.2007.02.006 |
| [12] |
Djenidi L, Tardu S F, Antonia R A. Relationship between temporal and spatial averages in grid turbulence[J]. Journal of Fluid Mechanics, 2013, 730: 593-606. DOI:10.1017/jfm.2013.351 |
| [13] |
Hopfinger E J, Toly J A. Spatially decaying turbulence and its relation to mixing across density interfaces[J]. Journal of Fluid Mechanics, 1976, 78(1): 155-175. DOI:10.1017/S0022112076002371 |
| [14] |
薛胜伟, 尹侠. 气升式内环流反应器流场及传质特性数值模拟[J]. 化学工程, 2006, 34(5): 23-27. XUE Shengwei, YIN Xia. Numerical simulation of flow behavior and mass transfer in internal airlift-loop reactor[J]. Chemical Engineering, 2006, 34(5): 23-27. (in Chinese) DOI:10.3969/j.issn.1005-9954.2006.05.007 |
| [15] |
Belchior C A C, Araújo R A M, Landeck J A C. Dissolved oxygen control of the activated sludge wastewater treatment process using stable adaptive fuzzy control[J]. Computers & Chemical Engineering, 2012, 37: 152-162. |
| [16] |
戚韩英, 汪文斌, 郑昱, 等. 生物膜形成机理及影响因素探究[J]. 微生物学通报, 2013, 40(4): 677-685. QI Hanying, WANG Wenbin, ZHENG Yu, et al. Mechanism of biofilm formation and analysis of influencing factors[J]. Microbiology China, 2013, 40(4): 677-685. (in Chinese) |
| [17] |
Tijhuis L, van Loosdrecht M C M, Heijnen J J. Dynamics of biofilm detachment in biofilm airlift suspension reactors[J]. Biotechnology and Bioengineering, 1995, 45(6): 481-487. DOI:10.1002/bit.260450604 |
| [18] |
Zinatizadeh A A L, Ghaytooli E. Simultaneous nitrogen and carbon removal from wastewater at different operating conditions in a moving bed biofilm reactor (MBBR):process modeling and optimization[J]. Journal of the Taiwan Institute of Chemical Engineers, 2015, 53: 98-111. DOI:10.1016/j.jtice.2015.02.034 |
 2020, Vol. 43
2020, Vol. 43


